在浅海和水文条件复杂的区域,水声定位性能受到影响,磁定位在浅海环境下具有受环境影响小、暴露风险低等优点[1],可作为声学定位的有效补充。舰船磁场定位技术多采用传感器阵列实现运动参数解算,可分为静磁场定位技术和交变磁场定位技术。静磁定位采用舰船静磁场信息,利用磁场建模、最优化搜索手段求解目标轨迹信息,但由于静磁场衰减速度快,检测距离有限,只能实现舰船小区域内的精确定位。
相对于静磁场,用于舰船定位的交变磁场由于受到地磁场影响较小,信噪比较高,易于检测。舰船由于自身辐射和对外部激励磁响应会产生交变磁场,且防腐电流经螺旋桨调制产生的交变磁场频率较低,衰减速率慢,具有一定的传播距离,并且带有明显的基频及谐波信息,因此可作为舰船定位的重要信号源[2]。通过对浅海中腐蚀相关交变磁场信号的提取分析可知,舰船在海水中运动时产生的交变磁场可以用低频时谐电偶极子进行模拟[3]。
有关水下电磁场及其对舰船探测定位的研究,相关学者已经开展了一些研究。吴云超等[3]、毛伟等[4]针对电偶极子源产生水下电磁场的相关机理进行了阐述,并通过仿真分析了磁场信号的空间分布特性;卢成新等[5]针对于深海环境下的准近场水平电偶极子定位进行了研究,但该方法只适用于空气-海水二层界面条件下的深海环境;张华等[6]研究了对基于静电场模型的目标速度及方向对制导方法的影响;李涛等[7]利用时谐水平电偶极子产生的电场信号对目标定位中最优化算法进行了研究,基于Matlab仿真软件验证了算法可靠性,但并未开展算法可行性的实验室验证工作。
基于已有研究成果,针对空气—海水—海床三层界面条件下的浅海环境时谐电偶极子源产生的交变磁场,通过建立定位目标函数,利用模型最优化反演算法,进行反演定位,实时计算电偶极子源的空间位置。通过仿真分析与实验室水池可控源试验相结合的方法,采用传感器阵列对磁场信号进行采集,对该定位方法的有效性及定位精度进行验证。
1 偶极子模型产生机理假定海洋环境为空气—海水—海床3层界面,且每层界面均为线性、均匀、各向同性媒质模型。设
如图1所示,空气-海水界面位于

|
图 1 空气—海水—海床3层界面计算模型示意图 Fig. 1 Schematic diagram of calculation model of three layers of air-seawater-seabed |
| $ \begin{array}{*{20}{l}} {\nabla ^2}{A_0} + k_0^2{A_0} = 0,(z < 0) ,\\ {\nabla ^2}{A_1} + k_1^2{A_1} = - J_e^s\delta (x - {x'})\delta (y - {y'})\delta (z - {z'}),(0 < z < D) ,\\ {\nabla ^2}{A_2} + k_2^2{A_2} = 0,(z > D) 。\end{array} $ | (1) |
对于3层界面的水平电偶极子,其分界面的边界条件可以如下表述:
| $ {A_{0x}}{|_{z = 0}} = {A_{1x}}{|_{z = 0}} ,$ | (2) |
| $ {A_{1x}}{|_{z = D}} = {A_{2x}}{|_{z = D}},$ | (3) |
| $ \frac{{\partial {A_{0x}}}}{{\partial z}}{|_{z = 0}} = \frac{{\partial {A_{1x}}}}{{\partial z}}{|_{z = 0}} ,$ | (4) |
| $ \frac{{\partial {A_{1x}}}}{{\partial z}}{|_{z = D}} = \frac{{\partial {A_{2x}}}}{{\partial z}}{|_{z = D}},$ | (5) |
| $ {A_{0z}}{|_{z = 0}} = {A_{1z}}{|_{z = 0}},$ | (6) |
| $ {A_{1z}}{|_{z = D}} = {A_{2z}}{|_{z = D}} ,$ | (7) |
| $ \frac{1}{{{\sigma _0}}}\left(\frac{{\partial {A_{0x}}}}{{\partial x}} + \frac{{\partial {A_{0z}}}}{{\partial z}}\right){|_{z = 0}} = \frac{1}{{{\sigma _1}}}\left(\frac{{\partial {A_{1x}}}}{{\partial x}} + \frac{{\partial {A_{1z}}}}{{\partial z}}\right){|_{z = 0}} ,$ | (8) |
| $ \frac{1}{{{\sigma _1}}}\left(\frac{{\partial {A_{1x}}}}{{\partial x}} + \frac{{\partial {A_{1z}}}}{{\partial z}}\right){|_{z = D}} = \frac{1}{{{\sigma _2}}}\left(\frac{{\partial {A_{2x}}}}{{\partial x}} + \frac{{\partial {A_{2z}}}}{{\partial z}}\right){|_{z = D}}。$ | (9) |
根据Helmholtz方程的通解形式,式(1)的通解可表述为:
| $ {H_{exw}}{\kern 1pt} = \int {({f'}_{1z}{e^{ - {u_1}z}} + {g'}_{1z}{e^{{u_1}z}}){\rm{d}}\lambda } \left[\frac{{2\lambda xy}}{{{\rho ^3}}}{J_1}(\lambda \rho ) - \frac{{{\lambda ^2}xy}}{{{\rho ^2}}}{J_0}(\lambda \rho )\right] ,$ | (10) |
| $ \begin{split} {H_{eyw}} =& - \frac{{{P_e}z}}{{4\pi }}{e^{ - i{k_1}r}}\left(\frac{1}{{{r^3}}} + \frac{{i{k_1}}}{{{r^2}}}\right) - \\ &\int {\left({f_{1x}}{e^{ - {u_1}z}} - {g_{1x}}{e^{{u_1}z}}\right){u_1}{J_0}(\lambda \rho ){\rm{d}}\lambda } -\\ &\int {({f'}_{1z}{e^{ - {u_1}z}} + {g'}_{1z}{e^{{u_1}z}}){\rm{d}}\lambda } \times\\ &\left[\left(\frac{{2{x^2}}}{\rho } - \frac{1}{\rho }\right)\lambda {J_1}(\lambda \rho ) - \frac{{{\lambda ^2}{x^2}}}{{{\rho ^2}}}{J_0}(\lambda \rho )\right] ,\end{split} $ | (11) |
| $\begin{split} {H_{ezw}} = &\frac{{{P_e}y}}{{4\pi }}{e^{ - i{k_1}r}}\left(\frac{1}{{{r^3}}} + \frac{{i{k_1}}}{{{r^2}}}\right) + \\ &\frac{y}{\rho }\int {({f_{1x}}{e^{ - {u_1}z}} + {g_{1x}}{e^{{u_1}z}})\lambda {J_1}(\lambda \rho ){\rm{d}}\lambda },\end{split} $ | (12) |
| $ \left\{ \begin{gathered} {g_{1x}} = \frac{{{P_e}}}{{4\pi }}\frac{\lambda }{{{u_1}}}\frac{{{r_{21}}{e^{ - {u_1}(2D - h)}} - {r_{10}}{r_{21}}{e^{ - {u_1}(2D + h)}}}}{{1 + {r_{10}}{r_{21}}{e^{ - 2{u_1}D}}}} ,\hfill \\ {f_{1x}} = - \frac{{{P_e}}}{{4\pi }}\frac{\lambda }{{{u_1}}}{r_{10}}{e^{ - {u_1}h}} - {r_{10}}{g_{1x}},\hfill \\ {r_{10}} = \frac{{\lambda - {u_1}}}{{\lambda + {u_1}}} ,\hfill \\ {r_{21}} = \frac{{{u_1} - {u_2}}}{{{u_1} + {u_2}}} ,\hfill \end{gathered} \right. $ | (13) |
| $ \left\{ \begin{gathered} {g'}_{1z} = - \frac{{{f_{2x}}\left(\dfrac{1}{{{\sigma _1}}} - \dfrac{1}{{{\sigma _2}}}\right){e^{ - ({u_1} + {u_2})D}} + \dfrac{{{g_{0x}}}}{\lambda }{X_1}{e^{ - 2{u_1}D}}}}{{{X_1}{e^{ - 2{u_1}D}} + {X_2}}} ,\hfill \\ {f'}_{1z} = - \frac{1}{\lambda }{g_{0x}} - {g'}_{1z} ,\hfill \\ {X_1} = \frac{{{u_1}}}{{{\sigma _1}}} - \frac{{{u_2}}}{{{\sigma _2}}} ,\hfill \\ {X_2} = \frac{{{u_1}}}{{{\sigma _1}}} + \frac{{{u_2}}}{{{\sigma _2}}} 。\hfill \end{gathered} \right. $ | (14) |
其中,
船舶电性交变磁场定位是利用船体金属结构流经海水形成交变电流激发的磁场信号进行定位[7]。如果将电性源交变磁场等效为偶极子模型,在已知电偶矩条件下,便可计算出其在空间任一点产生的磁场信号。反之,如果已知偶极子源在空间激励的磁场信号分布,反之也可通过模型反演的算法,计算偶极子源的位置参数。根据水平电偶极子产生的交变磁场公式,可得多测点磁场值和测点坐标以及电偶极矩的关系可以简化为线性超定方程组,写成矩阵形式为:
| $ {\boldsymbol{B}} = {\boldsymbol{FM}} 。$ | (15) |
式中:
1)根据磁场传感器获取的交变磁场信号,通过信号截取、滤波等前处理,获取对应性噪比相对较高的交变磁场信号曲线;
2)在前处理获取信号基础上,通过窄带滤波等方法,提取对应频率的轴频磁场信号特性,获取对应频率轴频磁场信号的包络信号;
3)在水平电偶极子正演模型的基础上,建立目标函数,构建轴频磁场反演模型,其中目标函数中包含偶极子源的三维坐标参数;
4)将对应轴频磁场的包络信号作为输入信号代入反演模型,通过数值求解,得出满足要求的信号源坐标参数的值,实现反演信号相对于输入信号的最优求解;
5)将反演得到的偶极子源坐标参数是实际源运动轨迹参数对比,实现基于模型反演的交变磁场定位技术的验证。
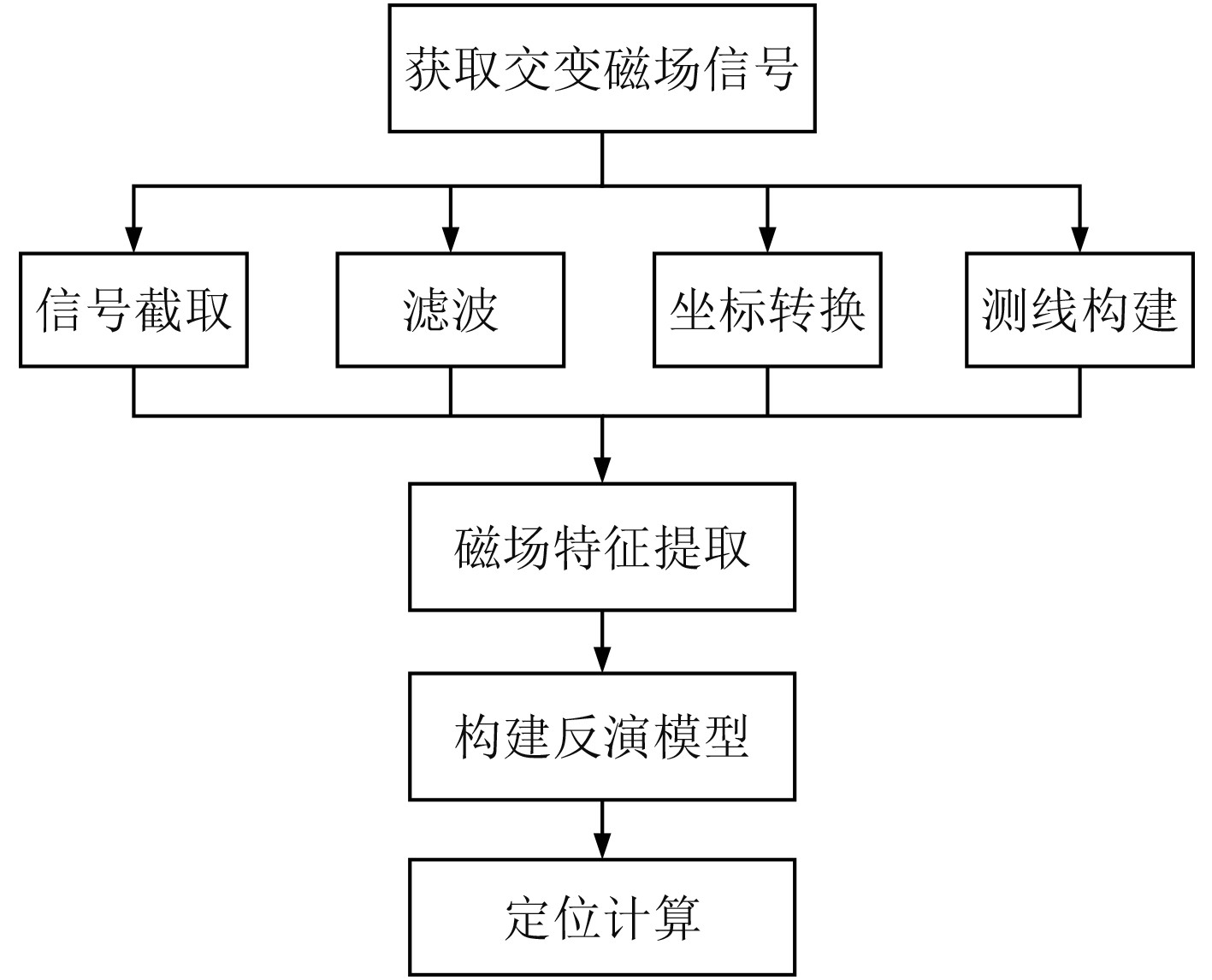
|
图 2 交变磁场定位技术验证流程图 Fig. 2 Flow chart of verification of alternating magnetic field positioning technology |
对偶极子源交变磁场定位方法的验证采用虚拟数值仿真与实际模型在实验室水池测试相结合的方法进行,通过仿真结果与模型实际定位效果进行对比分析,用以证实方法可靠性与精确性。
3.1 仿真分析假设偶极子源航速均匀,在同一深度同一航向进行航行,从磁传感器阵列上方通过。模型航向为20°测线的仿真计算结果如图3所示。

|
图 3 磁场三分量包络曲线 Fig. 3 Three-component envelope curve of the magnetic field |
偶极子源运动方向与传感器阵列垂向夹角为20°,传感器分别在相对于偶极子源正横距离y=−15 m, y=10 m测线上对偶极子源进行反演定位,定位结果如图4所示。

|
图 4 模型轨迹对比 Fig. 4 Trajectory contrast |
通过模型仿真分析结果可知,偶极子源原始运动轨迹与反演定位轨迹几乎完全吻合,仿真分析验证了定位算法的稳定性。
3.2 实验室验证测试水池的尺寸长为8m,宽为6m,深度2.5 m,3个测量磁场传感器经密封后安装在水池桁架上,分别为节点1、节点2和节点3。验证中采用的偶极子源模型示意图如图5所示,模型采用非金属材质,自身材质不造成磁性干扰,在模型下方水平方向放置一对水平电偶极子作为激励源。
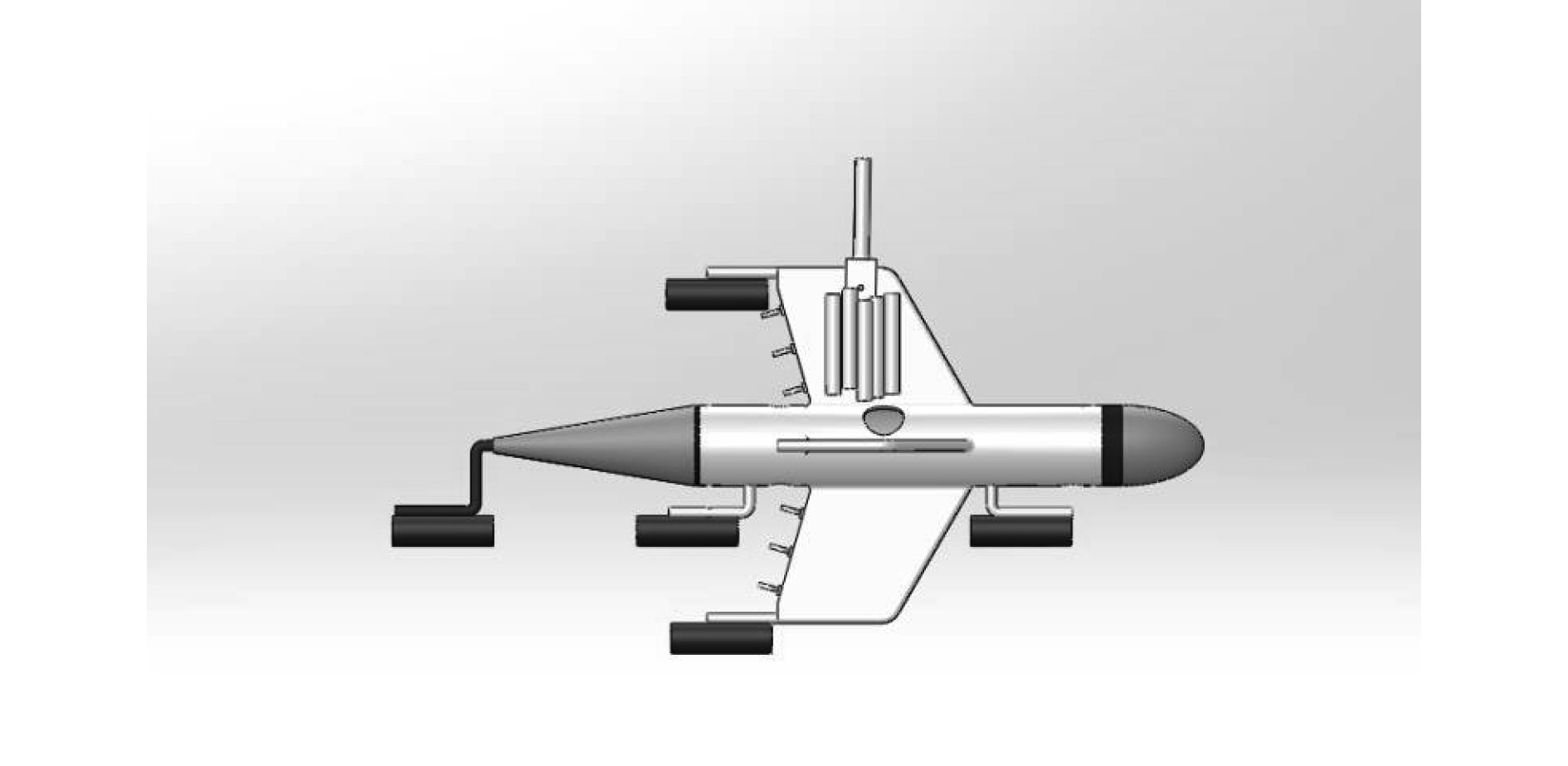
|
图 5 偶极子源模型示意图 Fig. 5 Schematic diagram of dipole source model |
水平偶极子源产生3.5 Hz的交变磁场信号,电机的输入电压约为0.5Vp-p,结合水池环境参数,进行空气—海水—海床3层界面条件下,交变磁场模型计算,得出基于偶极子模型的磁场分布曲线。仿真条件为:
1)水平偶极子深度根据偶极子源中心线入水深度,取0.5 m;
2)磁场传感器深度为1.16 m;
3)水池中溶液深度为1.57 m;
4)偶极子偶极矩为0.25A×0.2 m=0.05 Am,频率为3.5 Hz;
5) 溶液电导率为1.32 S/m,池底电导率相对溶液较小,取0.1 S/m,溶液温度为8.9℃;
由于采用水平电偶极子源,其在水平x方向感应产生的交变磁场较小,磁信号较为微弱,因此本次仿真主要采用y和z分量计算结果进行分析,如图6所示。

|
图 6 水平偶极子源模型计算与实测值对比 Fig. 6 Comparison of horizontal dipole source model calculation and measured values |
|
|
表 1 模型数据与实测数据表 Tab.1 Model data and measured data table |
对比可知,3层界面条件下,基于时谐偶极子模型的磁场计算结果与实测结果的幅值大小及衰减特性具有很好的一致性。
试验中,模型航速预设为0.09 m/s,航行深度为0.5 m,产生3.5 Hz的磁场信号,测量传感器深度为1.16 m,实验室水池深度为1.57 m,溶液电导率为1.32 S/m,溶液温度为8.9℃,模型运动方向与传感器阵列垂向夹角为90°,利用传感器相对于偶极子源的正横距离y=−1 m测线上的测量数据(做测线对称获取正横距离y=1 m测线上的测量数据)对模型进行反演定位。磁场三分量及频率3.5 Hz交变磁场曲线如图7所示,通过频谱分析获取三分量磁场频谱曲线,如图8所示,通过窄带滤波获取频率3.5Hz交变磁场包络曲线,如图9所示。

|
图 7 交变磁场及磁场三分量信号曲线 Fig. 7 AM field and magnetic field three component signal |

|
图 8 三分量磁场信号的频谱特性曲线 Fig. 8 Spectrum characteristic curve of three-component magnetic field signal |

|
图 9 三分量磁场信号包络曲线 Fig. 9 Three component magnetic field signal envelope curve |
在建立水平电偶极子正演模型及磁场反演模型的基础上,利用目标函数求解出偶极子源的三维坐标参数,然后在对传感器采集的信号进行包络信号提取,将信号作为输入代入反演模型,运用最优化算法反演求解出最优坐标参数解。
在实际模型定位计算中,通过多次迭代反演,最终计算出定位结果,其中x0=−2.97 m,极矩IL=0.05 A,航向角为0.1°。反演结果和实测数据对比结果如图10所示。其定位轨迹为一基本垂直于传感器阵列的直线,与实际运行轨迹基本一致,实际航速为(6.5−1.0)/58=0.094 m/s,与反演航速0.09 m/s比较接近。
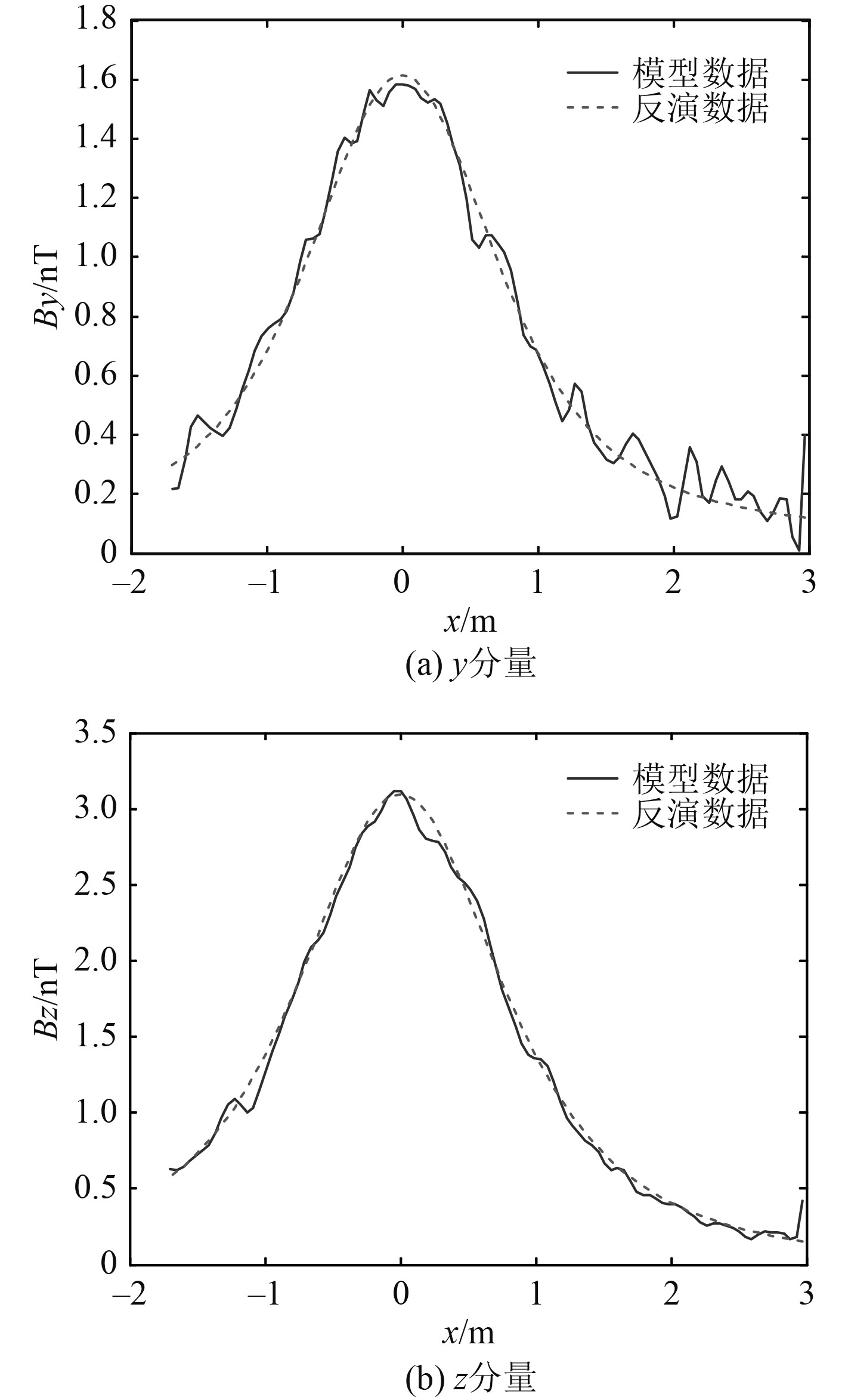
|
图 10 磁场y、z分量实测与模型反演对比曲线 Fig. 10 Contrast curve between measured magnetic field y and z component and model data |
由图11可知,偶极子模型在x=−3 m,y=−1 m和z=0.5 m的位置,沿着测线从−3 m到2 m运动,根据磁场传感器的实际测量数据,采用最优化求解算法对数据进行偶极子位置反演计算,运动轨迹与反演计算轨迹基本重合。
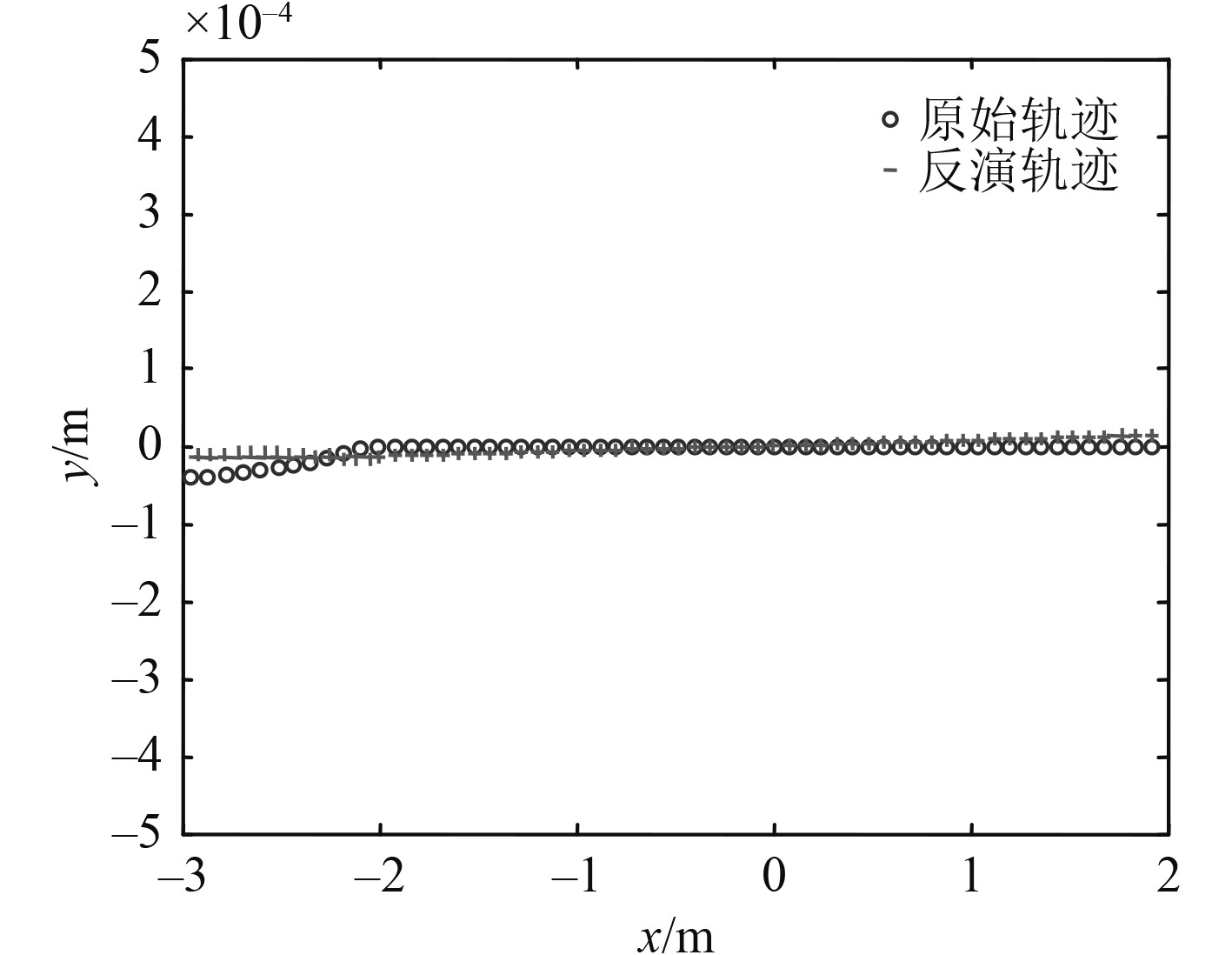
|
图 11 偶极子源磁场定位轨迹曲线 Fig. 11 Dipole source magnetic field positioning trajectory curve |
首先建立了基于空气—海水—海床3层界面条件下的偶极子模型,利用电偶极子源产生交变磁场,通过频谱分析、窄带滤波等信号处理技术进行信号提取,将包络信号作为信号输入通过反演模型反演定位,并根据实测数据对模型运动轨迹与反演定位轨迹比较分析。实验结果表明,该方法可成功解算出模型在空间的位置坐标,定位轨迹与运动轨迹基本重合,定位方法稳定可靠。
需要说明的是由于提出的方法主要在实验室水池中进行验证,受环境因素影响较小,但在实际海洋环境中,由于受到海浪、海流和人为干扰等因素影响,利用电性源激励交变磁场对舰船进行定位,其工程应用的适用性仍需要进一步验证。
| [1] |
向前, 马小龙. 基于磁偶极子模型的水下目标定位与跟踪[J]. 探测与控制学报, 2019, 41(3): 70-75. XIANG Q, MA X L. Underwater target passive location and tracking based on magnetic dipole model[J]. Journal of Detection & Control, 2019, 41(3): 70-75. |
| [2] |
林春生, 龚沈光. 舰船物理场[M]. 北京: 兵器工业出版社, 2007, 45-46.
|
| [3] |
吴云超, 刘永志, 苏建业, 等. 舰船交变电偶极子模型产生的交变磁场计算[J]. 舰船科学技术, 2009, 31(10): 123-128. WU Y C, LIU Y Z, SU J Y, et al. The computation of the AM field of a ship using the AC electric dipole[J]. Ship Science and Technology, 2009, 31(10): 123-128. DOI:10.3404/j.issn.1672-7649.2009.10.036 |
| [4] |
毛伟, 张宁, 林春生. 在三层介质中运动的时谐水平电偶极子产生的电磁场[J]. 电子学报, 2009, 9: 2077-2081. MAO W, ZHANG N, LIN C S. The EM FIELDS produced by a moving Horizontally-Directed time-harmonic dipole in three-layer medium[J]. ACTA Electronic Sinica, 2009, 9: 2077-2081. DOI:10.3321/j.issn:0372-2112.2009.09.035 |
| [5] |
卢新成, 龚沈光, 周骏, 等. 海水中时谐水平电偶极子的准近场定位[J]. 武汉理工大学学报, 2005, 29(3): 331-334. LU X C, GONG S G, ZHOU J, et al. Quasi-near field localization of a time-harmonic HED in sea water[J]. Journal of Wuhan University of Technology, 2005, 29(3): 331-334. |
| [6] |
张华, 王向军, 单潮龙, 等. 基于目标静电场的水中兵器制导方法研究[J]. 电子学报, 2013, 41(3): 470-474. ZHANG H,WANG X J, SHAN C L, et al. Research of guidance method based on the electrostatic field of target for underwater weapon[J]. ACTA Electronica Sinica, 2013, 41(3): 470-474. DOI:10.3969/j.issn.0372-2112.2013.03.009 |
| [7] |
李涛, 王向军, 嵇斗. 浅海中时谐水平电偶极子定位研究[J]. 舰船电子工程, 2015, 35(5): 142-146. LI T, WANG X J, JI D. Time-harmonic horiziontal dipole in coastal[J]. Ship Electronic Engineering, 2015, 35(5): 142-146. |
| [8] |
吕俊军, 陈凯, 苏建业, 等. 海洋中的电磁场及其应用[M]. 上海: 上海科学技术出版社, 2020, 207-208.
|
| [9] |
徐杰. 一种高效的舰船磁性定位方法[J]. 舰船科学技术, 2011, 33(12): 69-71. XU J. A efficient vessel magnetic location method[J]. Ship Science and Technology, 2011, 33(12): 69-71. DOI:10.3404/j.issn.1672-7649.2011.12.015 |
 2022, Vol. 44
2022, Vol. 44
