在汽车电子和航空航天等领域,基于模型的设计(MBD)方法已被充分证实是一种有效的控制器设计方法,将该方法移植到船用柴油机电子调速器的设计开发中无疑是一种有效的思路,而其首要问题是要建立能准确反映柴油机特性及满足MBD开发实时计算要求的数学模型。对于船用柴油机这种强非线性对象,传统建模方法很难兼顾仿真精度和高实时性,因此建立兼顾精度与仿真实时性的非线性模型,成为开发柴油机高性能调速器的关键基础。此外,在基于模型设计流程中,快速控制原型测试阶段是检验控制算法和部署控制器的重要环节,该阶段也要求建立精度高、实时性好的柴油机模型作为被控对象参与测试,所以建立的模型在研究控制算法、部署控制策略过程中同样起着举足轻重的作用。
常用的柴油机建模方法有用于控制系统综合分析的线性化模型、用于研究柴油机外部特性的准稳态模型、基于放热规律建立的充排模型和用于柴油机稳态性能精确预测的压力波模型等4种,均针对不同的研究目的和实际应用对柴油机模型做了较大简化,导致模型精度与实时性难以兼顾。考虑到基于神经网络的系统辨识已得到有效应用,且RBF神经网络具有逼近精度高、收敛速度快等特点,可满足在线辨识、实时控制的需求[1],故本文着重研究基于RBF神经网络的模型辨识方法,并以PA-6型柴油机为对象进行试验验证。
1 船用柴油机外特性及动力学方程描述船用柴油机通常采用四冲程中高速柴油机,柴油机有效扭矩
| $ {M}_{e}={M}_{i}{\eta }_{m}=\frac{{H}_{u}{g}_{c}{\eta }_{i}{\eta }_{m}}{\tau \pi } 。$ | (1) |
式中:
| $ {\eta }_{i}={a}_{0}({({N}_{d}-{N}_{d0})}^{2}+{a}_{1}^{2}{(\alpha -{\alpha }_{0})}^{2})+{a}_{2}。$ | (2) |
式中:
| $ \alpha =\frac{{G}_{tr}}{{G}_{f}{L}_{0}},$ | (3) |
式中:
| $ {G}_{f}=\frac{{g}_{c}\cdot {N}_{d}}{30\tau },$ | (4) |
| $ {G}_{tr}=\frac{i\cdot {V}_{s}\cdot {N}_{d}\cdot {p}_{3}\cdot {\eta }_{v}}{120\cdot R\cdot {T}_{i}} 。$ | (5) |
式中:
| $ {\eta }_{v}=a{N}_{d}^{2}+b{N}_{d}+c 。$ | (6) |
参数
在柴油机作为推进主机的舰船动力装置中,可根据如下动力学方程计算柴油机转速:
| $ \frac{{{\text{π}} I}_{e}}{30}\cdot \frac{{{\rm{d}}N}_{d}}{{\rm{d}}{\rm{t}}}={M}_{e}-{M}_{B}-{M}_{f1} ,$ | (7) |
| $ {N}_{d}=\frac{30}{{{\text{π}} I}_{e}}\int {(M}_{e}-{M}_{B}-{M}_{f1}){\rm{d}}t 。$ | (8) |
式中:
但据上建立的准稳态模型用于仿真计算时过程复杂、对计算资源要求高,不便用于高实时性要求的MBD的设计开发与调试中。利用RBF神经网络的连续非线性函数逼近特性,建立MBD开发与测试中需要的的高实时非线性模型。
2 RBF神经网络的柴油机模型辨识 2.1 基本原理RBF神经网络为具有单隐藏层的3层前馈网络,网络结构相对较为简单。其3层前馈网络结构中,
| $ {h}_{j}=\mathrm{exp}\left(-\frac{{‖X-{C}_{j}‖}^{2}}{2{b}_{j}^{2}}\right)(j=\mathrm{1,2},\cdots ,m) 。$ | (9) |
式中:
| $ {y}_{m}\left(k\right)={W}^{{\rm{T}}}H,$ | (10) |
与训练集对应标签
| $ E\left(k\right)=y\left(k\right)-{y}_{m}\left(k\right) ,$ | (11) |
根据梯度下降原则,对输出权值、节点中心以及节点基宽等参数进行迭代调整,算法如下:
| $\begin{split} {w}_{j}\left(k\right)=&{w}_{j}\left(k-1\right)+\eta \left(y\left(k\right)-{y}_{m}\left(k\right)\right){h}_{j} +\\ &\alpha ({w}_{j}\left(k-1\right)-{w}_{j}\left(k-2\right)),\end{split} $ | (12) |
| $ \Delta {b}_{j}=\left(y\left(k\right)-{y}_{m}\left(k\right)\right){w}_{j}{h}_{j}\frac{{‖X-{C}_{j}‖}^{2}}{{b}_{j}^{3}} ,$ | (13) |
| $ {b}_{j}\left(k\right)={b}_{j}\left(k-1\right)+\eta \Delta {b}_{j}+\alpha ({b}_{j}\left(k-1\right) -{b}_{j}\left(k-2\right)) ,$ | (14) |
| $ \Delta {c}_{ji}=\left(y\left(k\right)-{y}_{m}\left(k\right)\right){w}_{j}{h}_{j}\frac{{x}_{j}-{c}_{ji}}{{b}_{j}^{2}} ,$ | (15) |
| $ {c}_{ji}\left(k\right)={c}_{ji}\left(k-1\right)+\eta \Delta {c}_{ji}+\alpha ({c}_{ji}\left(k-1\right) -{c}_{ji}\left(k-2\right)) 。$ | (16) |
其中,
在研究供油量与柴油机转速关系过程中,忽略转速对供油量的影响,得到循环供油量与供油齿杆位移的线性关系为:
| $ {F}_{r}=\frac{{g}_{c}-{g}_{c0}}{{g}_{cH}-{g}_{c0}} 。$ | (17) |
式中:
根据柴油机动力学模型,柴油机有效扭矩
| $ {M}_{e}=f({F}_{r},{N}_{d}) ,$ | (18) |
那么,有
| $ {\Delta M}_{e}\left(k\right)={M}_{e0}\left(k\right)-{\hat{M}}_{e}\left(k\right) ,$ | (19) |
式中:
将试验采集得到的供油齿杆位置量
| $ {\hat{M}}_{e}\left(k\right)={W}^{{\rm{T}}}H ,$ | (20) |
所以:
| $ {\Delta M}_{e}\left(k\right)={M}_{e0}\left(k\right)-{W}^{{\rm{T}}}H=E\left(k\right) 。$ | (21) |
再由式(12)~式(16)对网络参数进行修正,使神经网络逼近被辨识系统。
2.2.2 柴油机机理模型与辨识模型设计选用PA-6型柴油机准稳态模型作为被辨识对象。实验中柴油机空载运行,即
根据神经网络辨识原理,设计柴油机离线辨识建模试验,辨识系统的结构如图1所示。
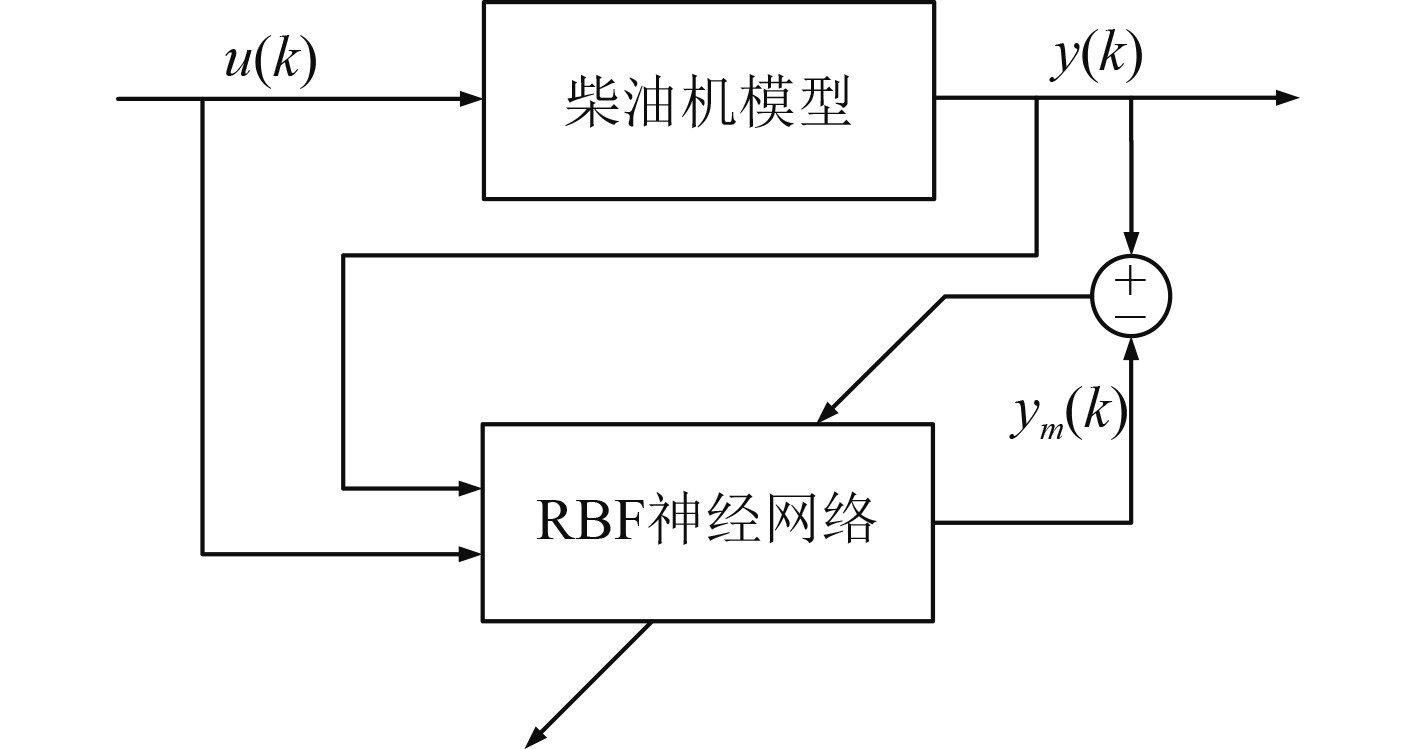
|
图 1 RBF神经网络辨识结构图 Fig. 1 RBF neural network identification structure diagram |
实验通过模型仿真采集柴油机供油齿杆位置量、转速以及有效扭矩等数据,经过预处理后输入神经网络,通过对比预测输出与模型仿真输出的差值调节神经网络参数以减小偏差,最终建立模型。
考虑利用RBF神经网络收敛速度快、全局最优等特性,依据模型和神经网络辨识原理,设计在线辨识模块进行实验,如图2所示。图中
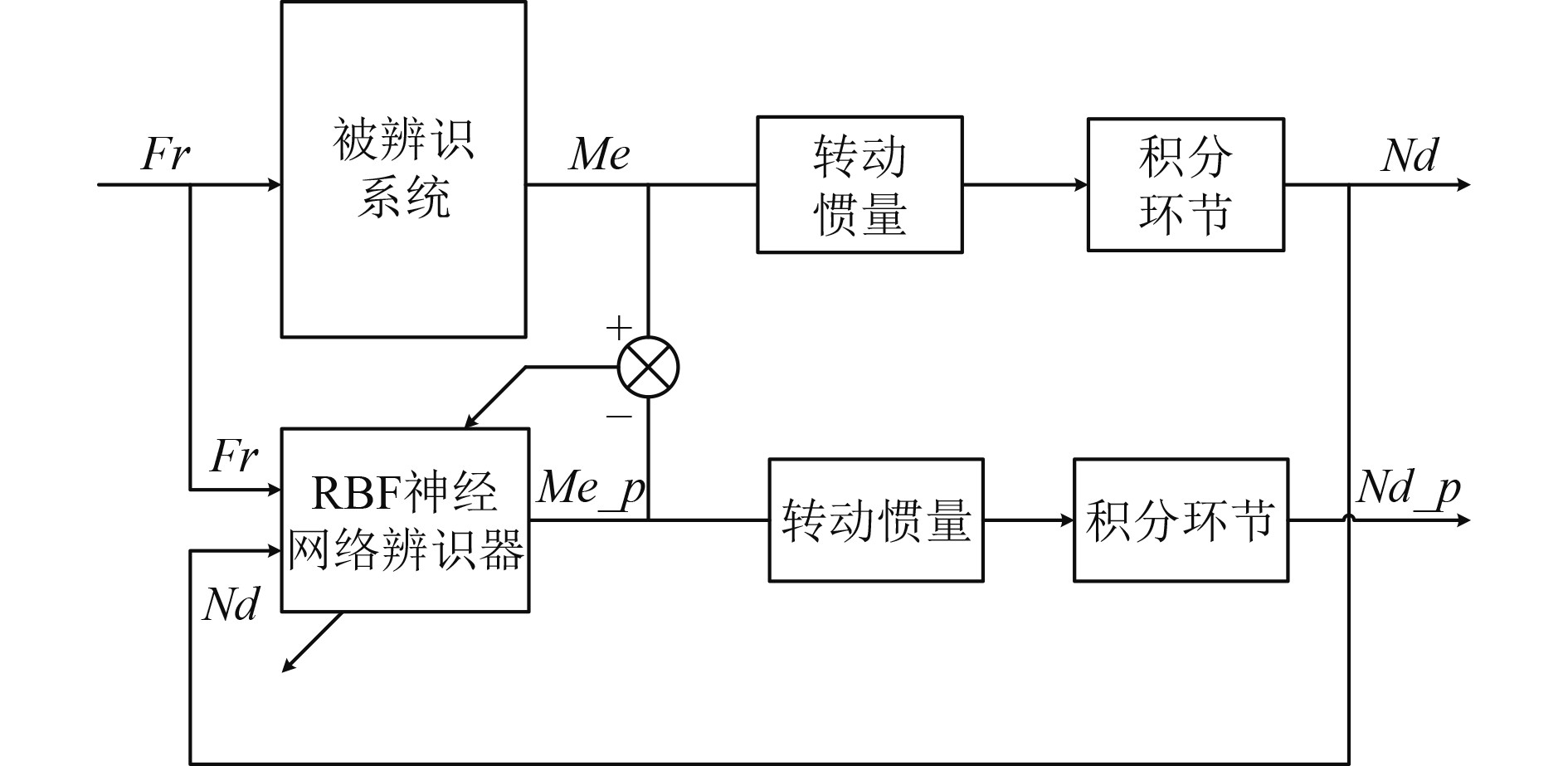
|
图 2 在线辨识原理图 Fig. 2 Online-identification schematic diagram |
应用Simulink拓展功能S-Function对RBF神经网络进行封装。
2.3 神经网络参数设置实验在神经网络初次训练时,需要设置网络参数包括:隐藏神经元数量
为说明神经元数量
首先设置训练迭代轮次为
|
|
表 1 隐藏神经元对训练效果影响 Tab.1 Influence of hidden neuron on training effect |
实验结果表明,随着隐藏神经元数量的增加,训练效果显著提高,但只增加神经元数量,而不增加训练迭代轮次,会导致网络训练不充分,反而使得均方误差值增大。
设置隐藏神经元数量
|
|
表 2 训练迭代轮次对训练效果影响 Tab.2 Influence of training iteration round on training effect |
实验结果表明,增加训练迭代轮次有助于提高训练效果,而当误差较小时,单纯增加迭代轮次会导致预测误差在小范围内震荡变化,体现在均方误差上,其结果会随着迭代轮次的增加而变大。
3 仿真实验 3.1 RBF神经网络离线辨识实验考虑训练过程耗时与训练效果,设置神经网络隐藏神经元数量
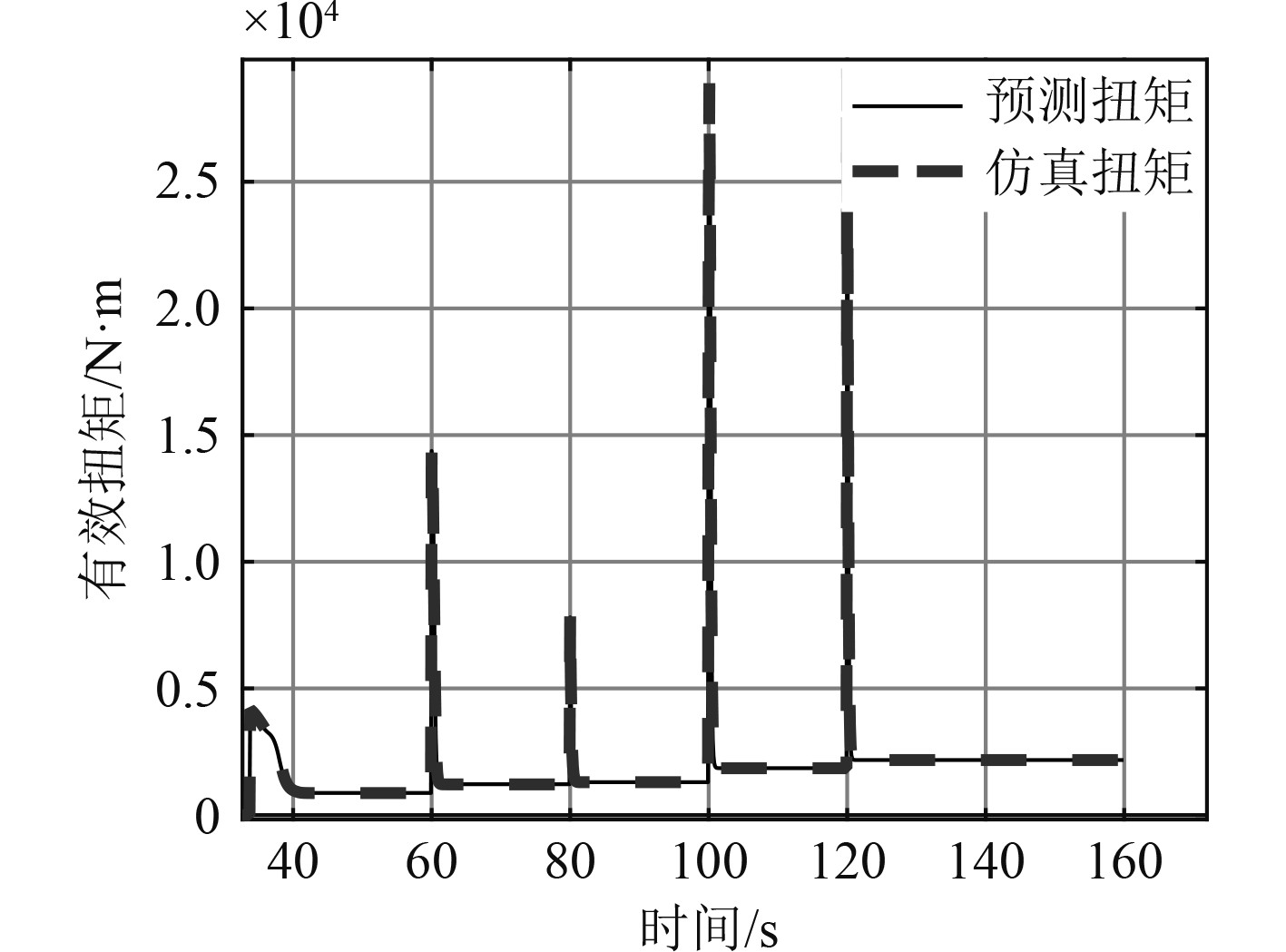
|
图 3 预测扭矩与仿真扭矩曲线图 Fig. 3 Curves of predicted torque and simulated torque |
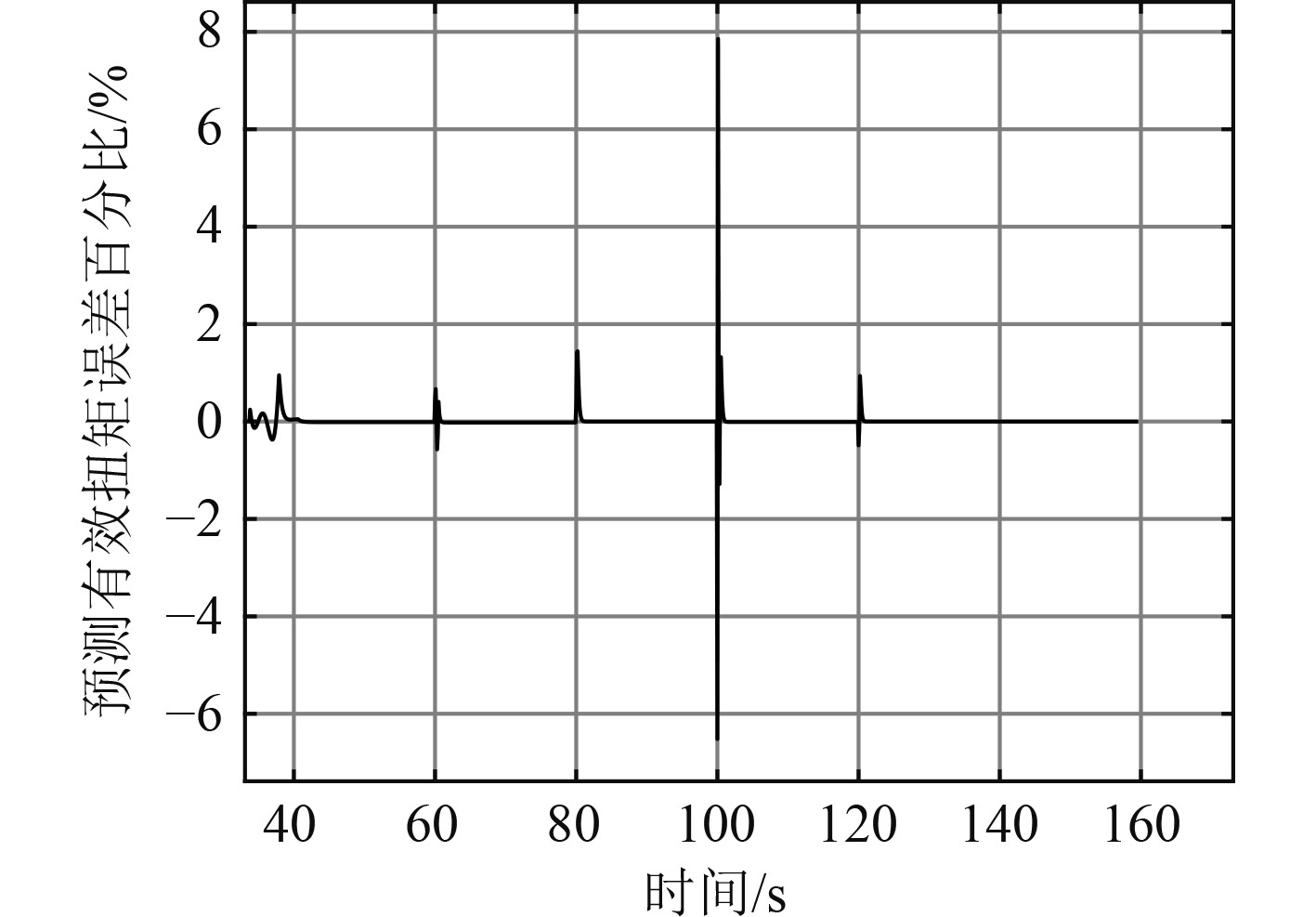
|
图 4 预测扭矩误差曲线图 Fig. 4 Curve of prediction torque error |
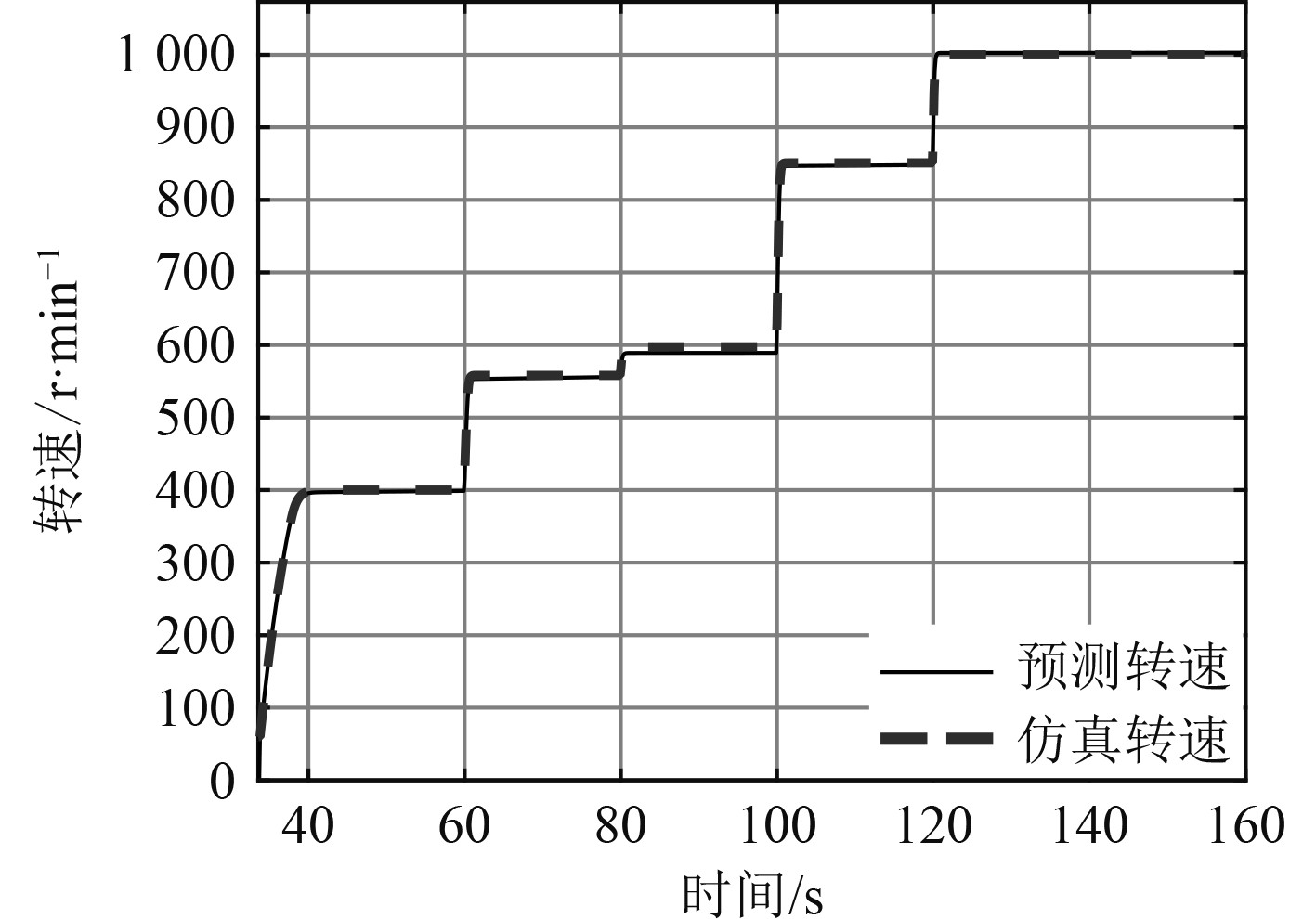
再由式(8)计算得到转速,结果如图5所示。
|
图 5 预测转速与仿真转速曲线图 Fig. 5 Curve of predicted speed and simulated speed |
从图中可以直观看出,神经网络对柴油机有效扭矩的预测效果良好,工况发生突变瞬间,预测误差突然变大,最大误差在8%以内。训练辨识生成模型对系统逼近效果良好,能够真实反映柴油机外部特性。
3.2 RBF神经网络在线辨识实验在线辨识仿真环境为Matlab/Simulink环境,利用封装好的辨识模块,对柴油机准稳态模型进行在线辨识。
为检验辨识器对频繁变化的输入信号的追踪特性,选取正弦信号输入到油门位置
| $ {F}_{r}=0.25\;{\rm{sin}}\left(0.314{t}_{s}\right)+0.7。$ | (22) |
其中,
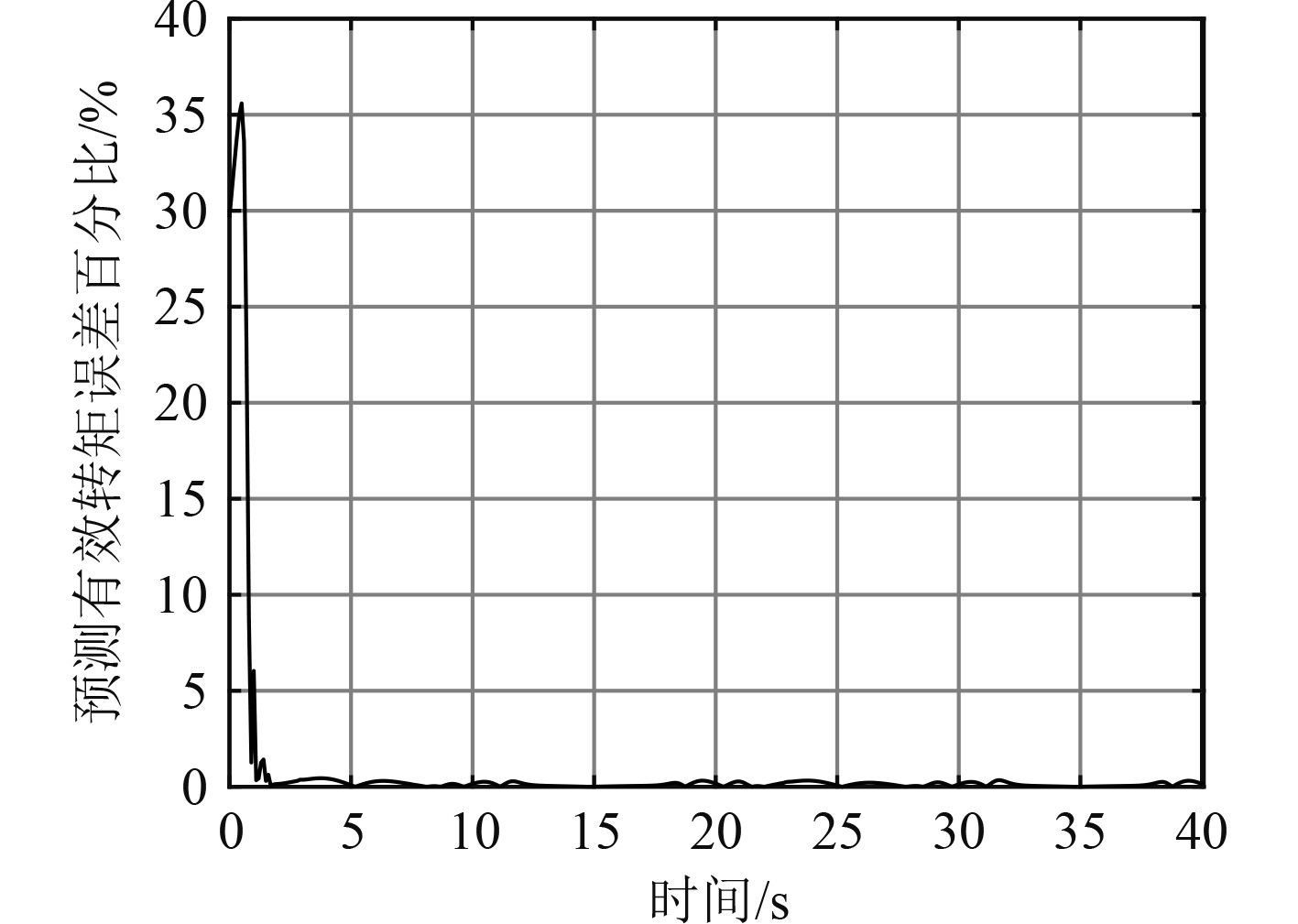
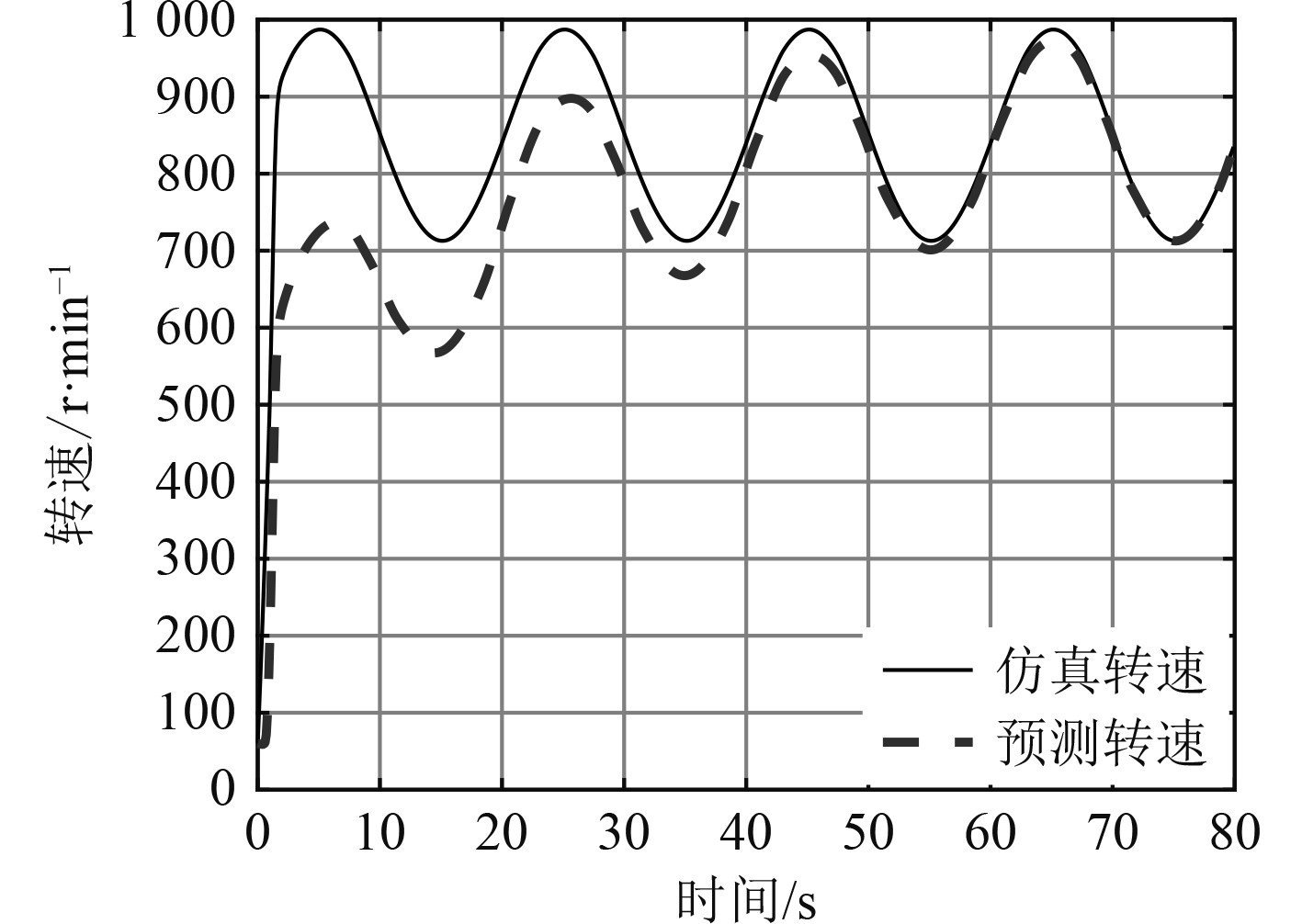
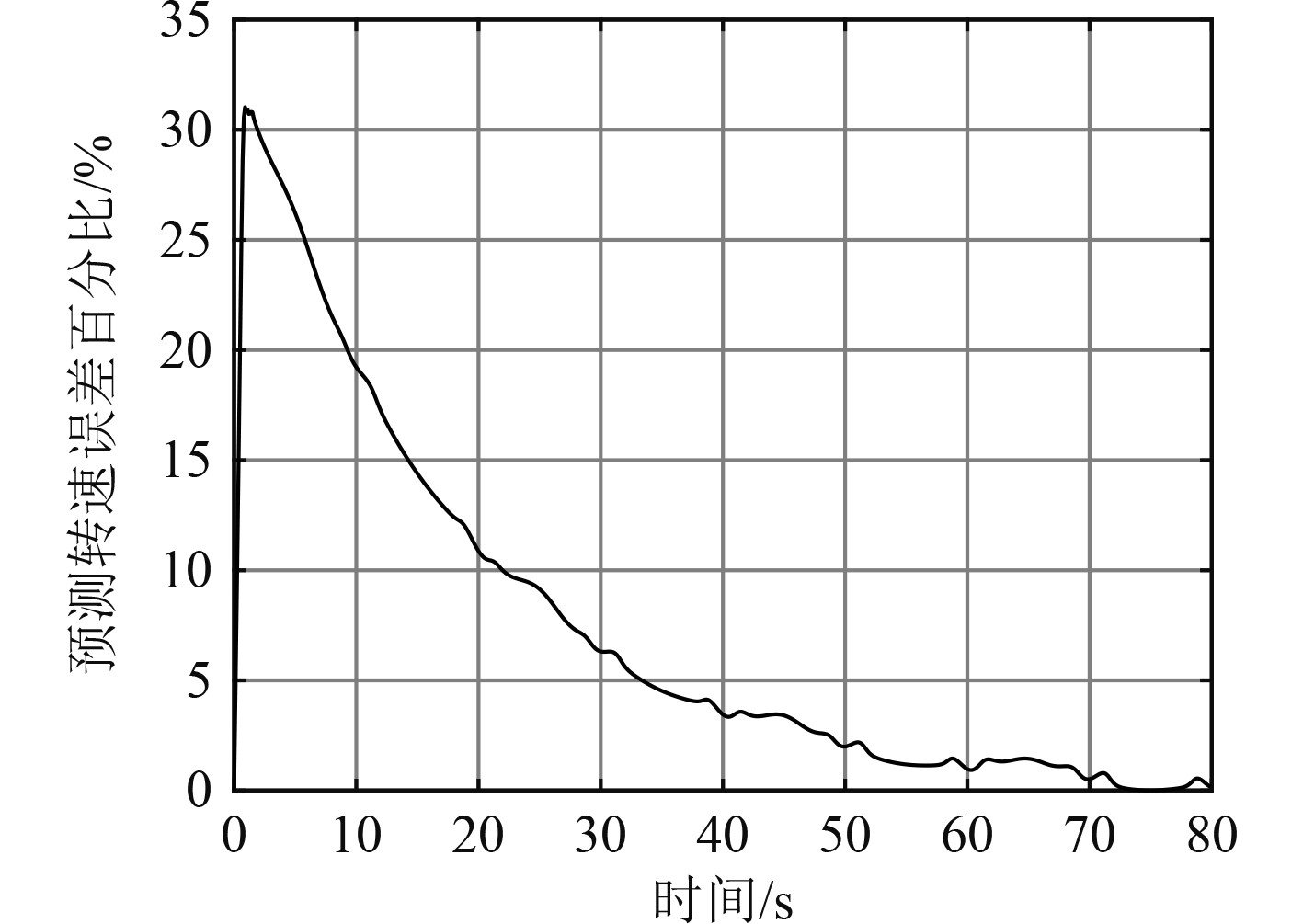
从图6~图8可以看出,在启动过程初始误差较大,随着学习过程迭代轮次增加,预测误差减小,预测转速不断逼近仿真转速。
|
图 6 预测扭矩误差曲线图 Fig. 6 Curve of prediction torque error |
|
图 7 预测转速与仿真转速曲线图 Fig. 7 Curve of predicted speed and simulated speed |
|
图 8 预测转速误差曲线图 Fig. 8 Curve of prediction speed error |
RBF神经网络系统辨识方法可对不同被辨识对象进行辨识建模,这与通过分析柴油机内部机理从而建立模型的方式相比,有着更加便捷、高效的特点,更为非线性、时变“黑箱”系统的逼近问题提供了解决方案。辨识建立的柴油机模型具有仿真精确度高、实时性强的优点,可应用于电子调速器的设计、调试,也可为实船训练系统提供模型基础。
| [1] |
刘金琨, 沈晓蓉, 赵龙. 系统辨识理论及MATLAB仿真[M]. 北京: 电子工业出版社, 2013: 120–121.
|
| [2] |
刘金琨. RBF神经网络自适应控制及MATLAB仿真[M]. 北京: 清华大学出版社, 2018: 18–20.
|
| [3] |
石勇, 宋恩哲. 船用柴油机转速控制系统辨识及自适应控制技术仿真研究[J]. 系统仿真学报, 2014, 26(5): 1078-1083,1101. |
| [4] |
钟婧佳, 赵洪, 佟泽友, 等. 基于RBF神经网络的控制器参数优化设计研究[J]. 导弹与航天运载技术, 2020, 374(3): 76-80. DOI:10.7654/j.issn.1004-7182.20200314 |
| [5] |
张惠臣, 那健, 翟春平. 基于卷积神经网络的声信标信号识别方法[J]. 舰船科学技术, 2021, 43(1): 150-153. |
| [6] |
冯子凯. 基于结构自适应滤波方法的非线性系统辨识[D]. 郑州: 河南大学, 2020.
|
| [7] |
KARAMI K, FATEHI P, YAZDANI A. On-line system identification of struc-tures using wavelet-Hilbert transform and sparse com-ponent analysis[J]. Comput Aided CIV INF. 2020: 1–17.
|
| [8] |
XU Qiangrong, SHENG Zhichao, FANG Yong, et al. Measurement matrix optimization for compressed sensing system with constructed dictionary via takenaka–malmquist functions[J]. Sensors 2021, 21(4): 1229–1229.
|
 2022, Vol. 44
2022, Vol. 44

