海洋立管将海底油田井口与海上工程结构物组成一体,是21世纪海洋油气资源开发和运输的重要水下通道。在进行油气传输的过程中,立管长期处于高温高压的环境中,导致立管成为了现代海洋工程结构系统中最薄弱、最易损坏的工程构件之一。
海洋立管在结构上可分为顶张式立管、钢悬链线式立管、柔性立管和混合式立管等。立管所处的海洋环境复杂,其影响因素繁多。立管在顶张力、自重、浮力、海洋波流、TLP平台初始偏移的综合作用下,立管结构易产生大形变,具有强烈的几何非线性[1]。
本文建立在1500 m水深下的顶张式立管(TTR)有限元模型,同时考虑立管在顶张力、TLP平台运动和复杂海洋载荷作用下的动力响应分析。在此基础上,分析各参数对立管管内弯矩的影响。
1 数学模型在海洋工程结构物设计中,一个关键指标就是计算结构物的波浪力。计算波浪力是研究计算海洋结构物所受载荷中最基本的任务,也是最艰难的任务之一[2]。设计波法和随机分布方法是确定作用于海洋结构物上波浪载荷的2种常用方法。对于小直径构件(直径波长比小于等于0.2,本文研究的TTR立管属于小直径构件),可将波浪力分解成为速度力和惯性力。常用的波浪力计算方法是莫里森在1950年基于模型试验结果提出的Morison方程。根据莫里森理论,假设认为在深水中立管的存在对海流流动没有影响,并认为海流对立管柱体的作用可分解成黏滞效应和附加质量效应[3]。多适用于纵横比较大柱体的波浪力求解[4],所以该方法在海洋工程界应用十分广泛。
Morison方程把作用在垂直立管上的力分解成两部分:惯性力项和拖曳力项,惯性力项和流体加速度成正比,拖曳力项和流体速度二次方成正比。
作用于TTR立管单位高度
| $ {F}_{I}={C}_{M}\rho \frac{{\text{π}} {D}^{2}}{4}\frac{\partial V}{\partial T} ,$ | (1) |
作用于TTR立管单位高度
| $ {F}_{D}=\frac{1}{2}{C}_{D}\rho {D}_{V}\left|V\right|,$ | (2) |
在水深z处,作用在立管的单位高度
| ${F}={F}_{I}+{F}_{D}={C}_{M}\rho \frac{{\text{π}} {D}^{2}}{4}\frac{\partial V}{\partial T}+\frac{1}{2}{C}_{D}\rho {D}_{V}\left|V\right|。$ | (3) |
将公式取定积分可得到立管在深水中受到的纵波浪力(Morison方程):
| $ {F}_{total}={\int }_{0}^{1}({C}_{M}\rho \frac{{\text{π}} {D}^{2}}{4}\frac{\partial V}{\partial T}+\frac{1}{2}{C}_{D}\rho {D}_{V}\left|V\right|{){\rm{d}}}_{s} 。$ | (4) |
其中:
要得到上述公式中的流体质点速度和加速度等量需要用到波浪理论。目前应用的主要有线性和非线性理论2种,线性波浪理论(AIRY波)是假设深水中的波浪振幅极其小,可以忽略非线性的影响而得到速度势的近似解[5];非线性波浪理论主要包括Stokes波理论、椭圆余弦波理论、驻波理论以及流函数波理论等[6],该理论认为在实际海洋中,真实波浪振幅足够大,由波动自由面产生的非线性影响显著,不能再被忽略。
通常使用Morison方程去计算立管在深水受到的波浪力,还存在一个关键性问题,面对具体问题和实际情况时,怎么确定系数
|
|
表 1 各国规范所采用的
|
由于TTR立管的垂直高度远远大于其水平宽度(即纵横比远远大于1),所以立管在外形上可看作是标准细长结构物,不易发生剪切变形,TTR立管的运动微分方程如下:
| $ EI\frac{{\partial }^{4}{x}({z},{t})}{{\partial z}^{4}}-\frac{\partial }{\partial z}\left[{T}_{t}\frac{\partial \left(z,t\right)}{\partial z}\right]+m\frac{{\partial }^{2}{x}\left({z},{t}\right)}{\partial {t}^{2}}={f}_{x}\left(z,t\right) 。$ | (5) |
其中:
本文选取的立管模型来自运营在我南海海域的一座张力腿平台(TLP),TLP平台所受的浮力大于平台重量产生的剩余浮力,承受剩余浮力的张力腿具有较大的预张力,由此来维持平台整体的运动稳定性,海域水深为达1500 m。顶张式立管主要用于干式采油树,该系统可进行完井操作,完成生产、回注、钻进和外输等功能。顶张式立管需要的张力随水深的增加而增加,其通过张力支撑立管质量,防止底部压缩,限制相邻立管间的碰撞[7]。因此TTR立管在海洋中作业时主要受到立管顶部的顶张力、波浪和海流的作用,以及立管自身的重力和浮力等[8]。立管的模型简图如图1所示。
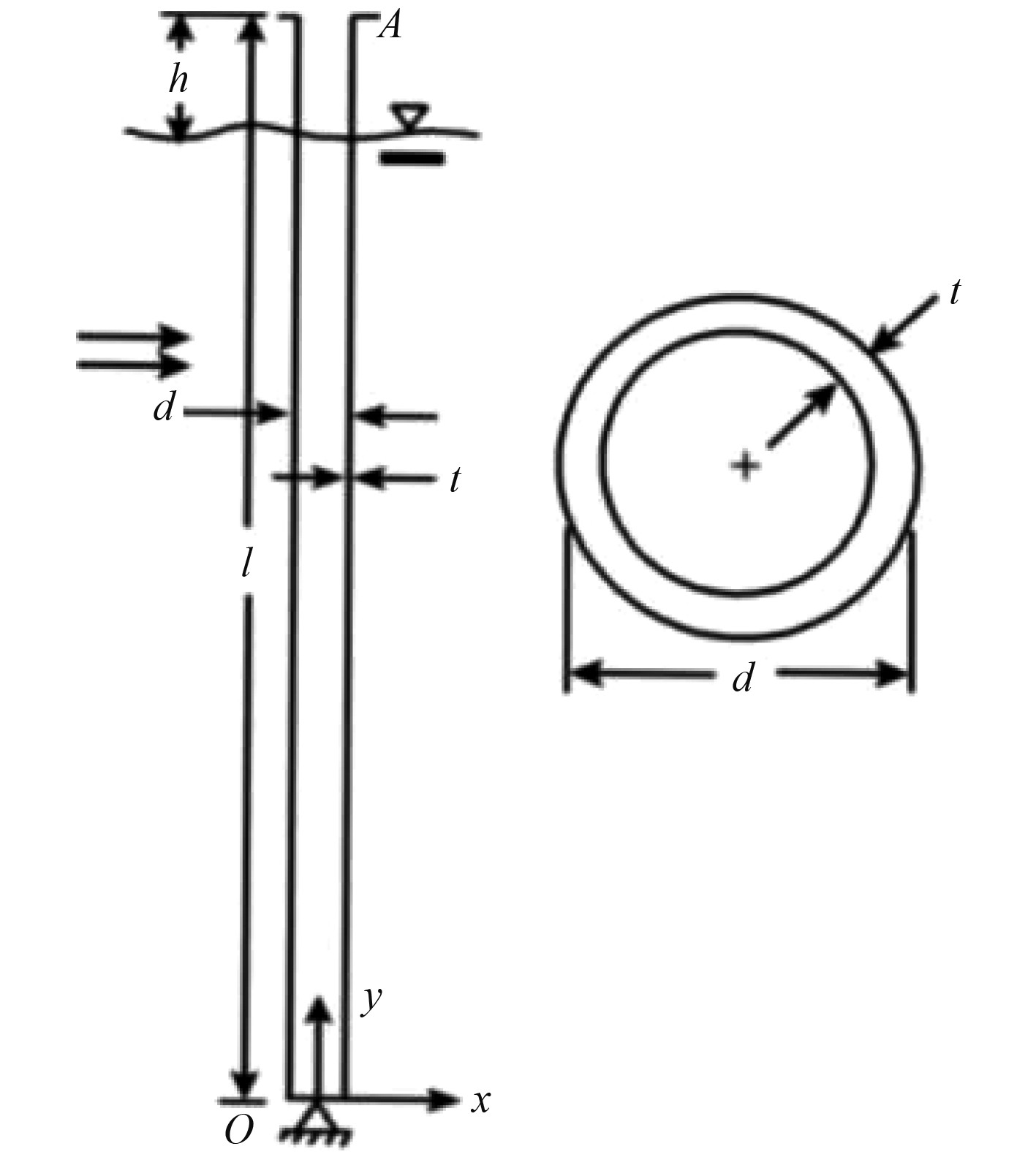
|
图 1 TTR立管模型图 Fig. 1 TTR riser model diagram |
TTR立管使用的钢材是API 5L X80级别钢材,该钢材具有高效、安全、可靠、经济、环保等诸多优点。立管的几何参数和物理特性如表2所示。立管作业的海域海况参数来自参考文献[9]。
|
|
表 2 TTR立管参数 Tab.2 TTR riser parameters |
由于TTR立管底部通过井口与海底相连,连接方式为应力连接,所有立管底部可以视为固定边界条件;TTR立管顶部通过张紧器与TLP平台相连,所以将立管顶部设为运动边界条件[9]。立管顶端的运动主要来源于TLP平台的慢漂运动,平台运动不同于波浪,直接影响着立管顶部的动力特性。TLP平台的运动模型包括:TLP平台的平均漂移、TLP平台的长期慢漂运动以及TLP平台对不规则波浪的瞬时响应3个方面,TLP平台慢漂运动模型:
| $ \begin{split} {S}\left({t}\right)=&{S}_{0}+{S}_{L}\mathrm{sin}\left(\frac{2{\text{π}} t}{{T}_{L}}-{\alpha }_{L}\right)+\\ &\sum _{n=1}^{N}{S}_{n}\mathrm{c}\mathrm{o}\mathrm{s}[{k}_{n}{S}\left({t}\right)-{\omega }_{n}t+{\varnothing }_{n}+{\alpha }_{n}]。\end{split} $ | (6) |
式中:
|
|
表 3 管顶部位移条件 Tab.3 Top displacement condition of riser |
|
|
表 4 海况参数 Tab.4 Sea state parameters |
固定边界条件:立管底部O点位移
立管顶部运动边界条件:
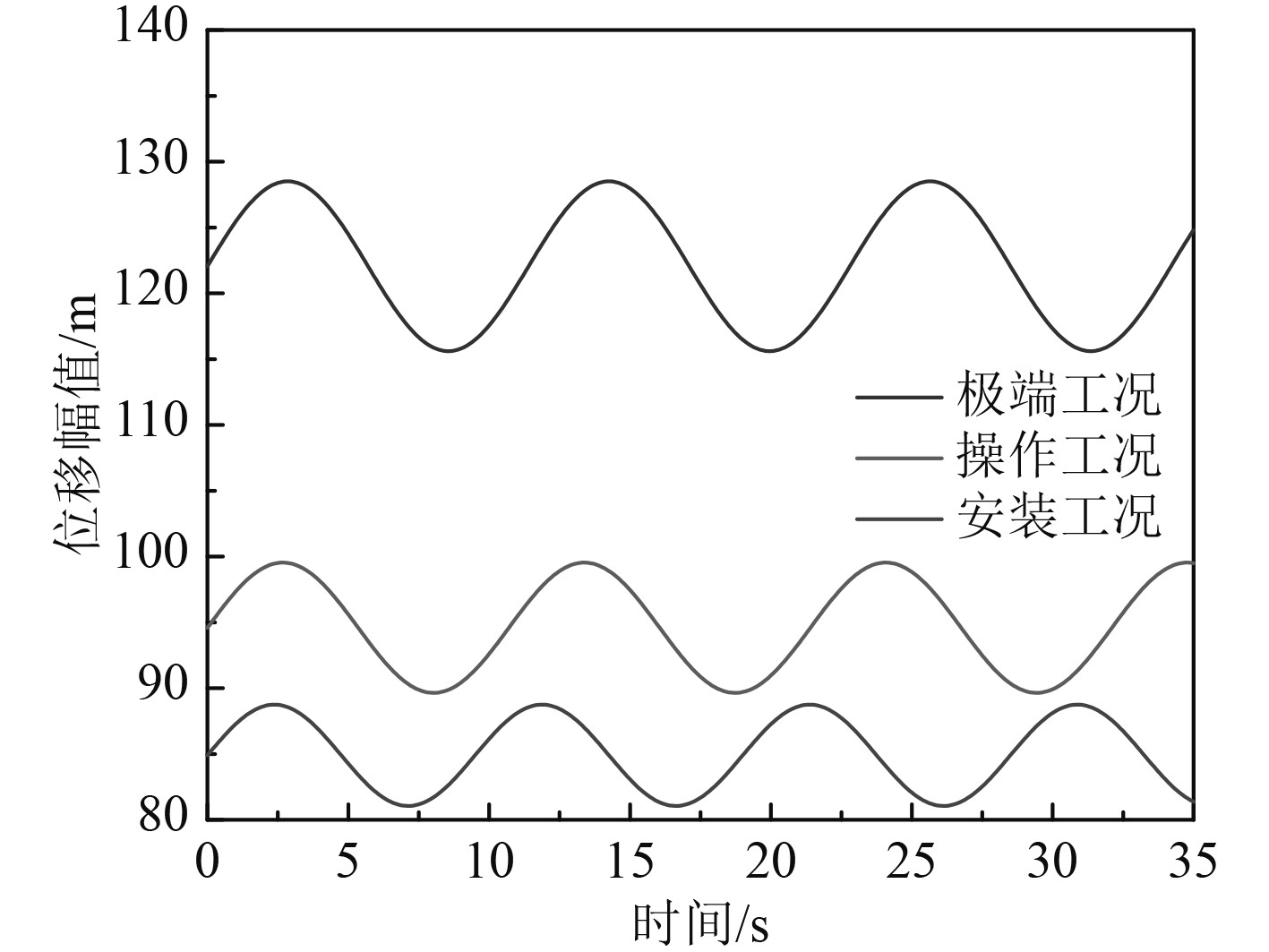
|
图 2 幅值曲线图 Fig. 2 Amplitude curve |
TTR立管在极端工况下作业时主要受到的载荷有:1)立管顶部的顶张力,
根据规范API RP 2A中描述:在海洋中的波浪载荷作用是以动态形式变化的,为了降低计算难度,在很多设计中动态载荷都被静态化了。当水深达到一定程度时,对作用在结构物上的动态效应就不能忽略。所以从静态和动态两方面出发分析立管的动力响应[4]:
步骤1 静态步,考虑立管的自重、浮力、顶张力以及顶部的水平位移;
步骤2 动态步,在静态步响应的基础之上加入波浪载荷的动态效应,动态效应是波浪和海流对立管的耦合效应。
3.2 计算结果用Abaqus中的BEAM 21梁单元建立TTR立管的有限元模型、模型的单元长度取为2 m,对立管使用Stokes波及安装、操作和极端3种工况进行分析,计算并提取各个单元节点受载荷作用的响应结果。对立管模型进行时域分析,部分TTR立管在极端工况下的应力与位移云图,如图3所示。
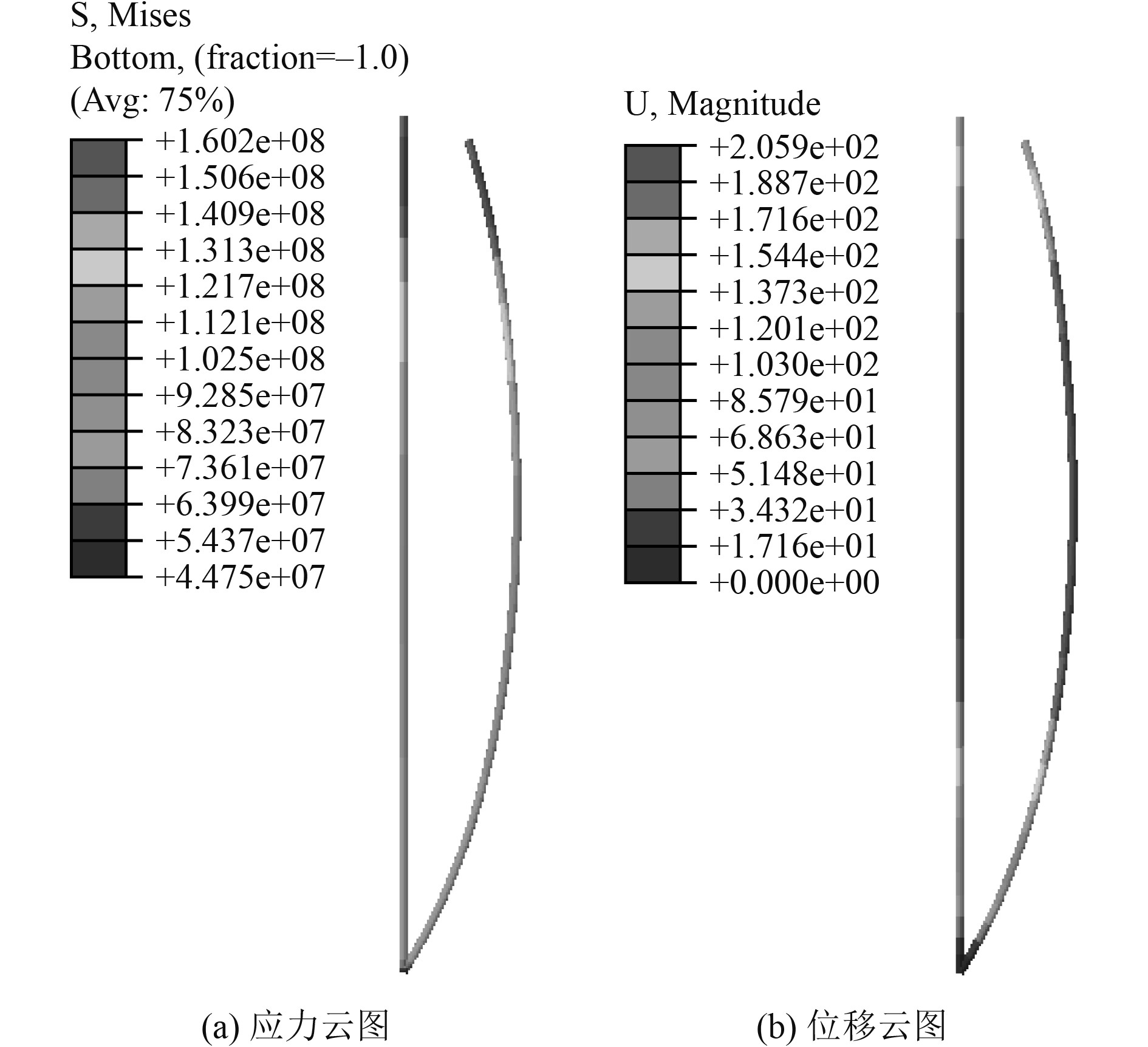
|
图 3 应力云图和位移云图 Fig. 3 Stress nephogram and displacement nephogram |
根据Abaqus软件的计算输出文件可以得到最大应力和最大位移的节点位置,如表5所示。
|
|
表 5 最大应力、位移节点号 Tab.5 Node number of maximum stress and displacement |
由Abaqus计算输出文件可知,立管在极端工况下,最大应力出现在720号节点,最大值为160.2 MPa;最大位移出现在440号节点,最大值为206 m。应力、位移响应曲线如图4所示。
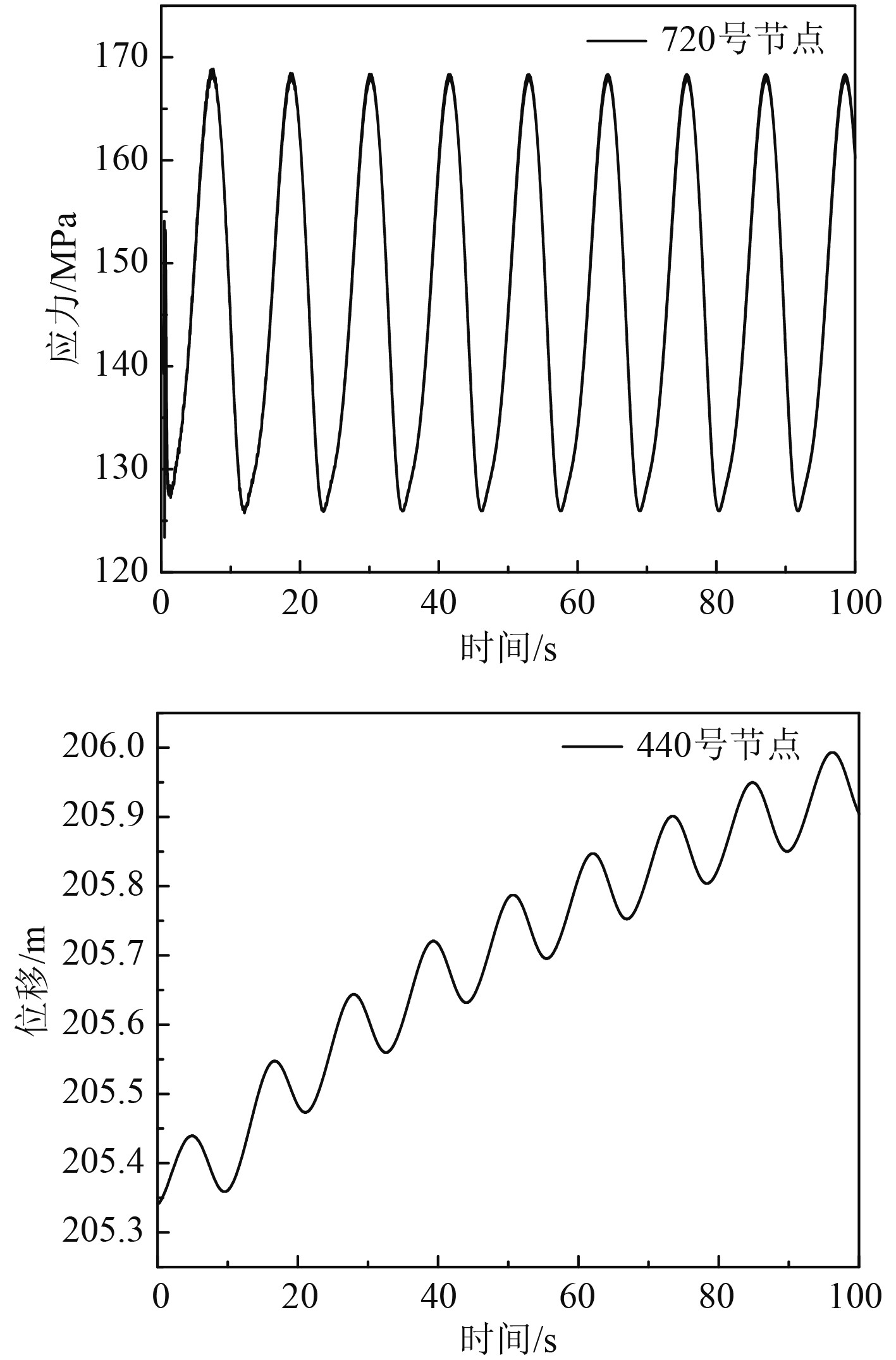
|
图 4 应力和位移响应曲线 Fig. 4 Stress and displacement response curve |
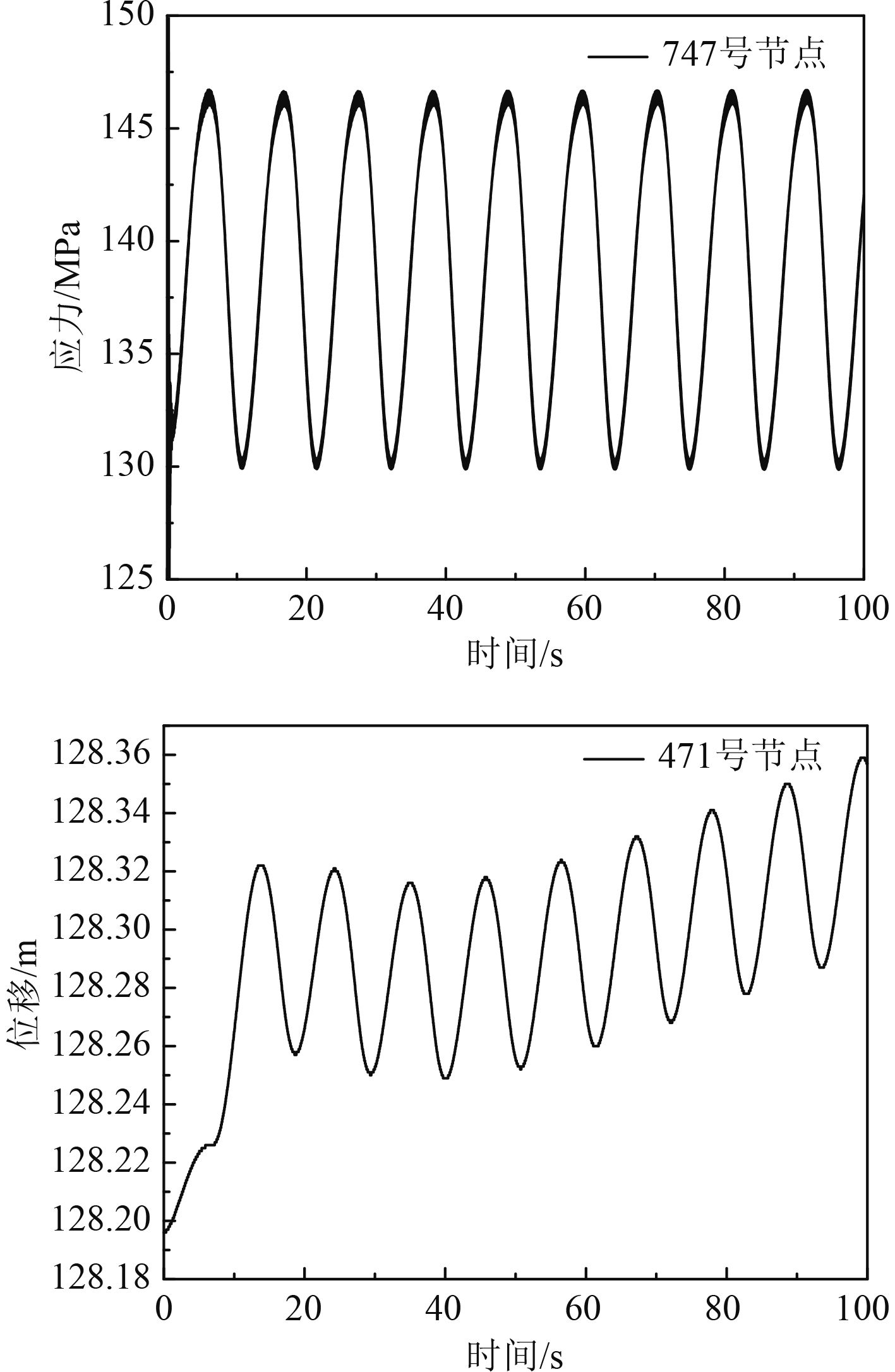
立管在操作工况下,最大应力出现在747号节点,最大值为142.1 MPa;最大位移出现在471号节点,最大值为128.4 m。应力、位移响应曲线如图5所示。
|
图 5 应力和位移响应曲线 Fig. 5 Stress and displacement response curve |
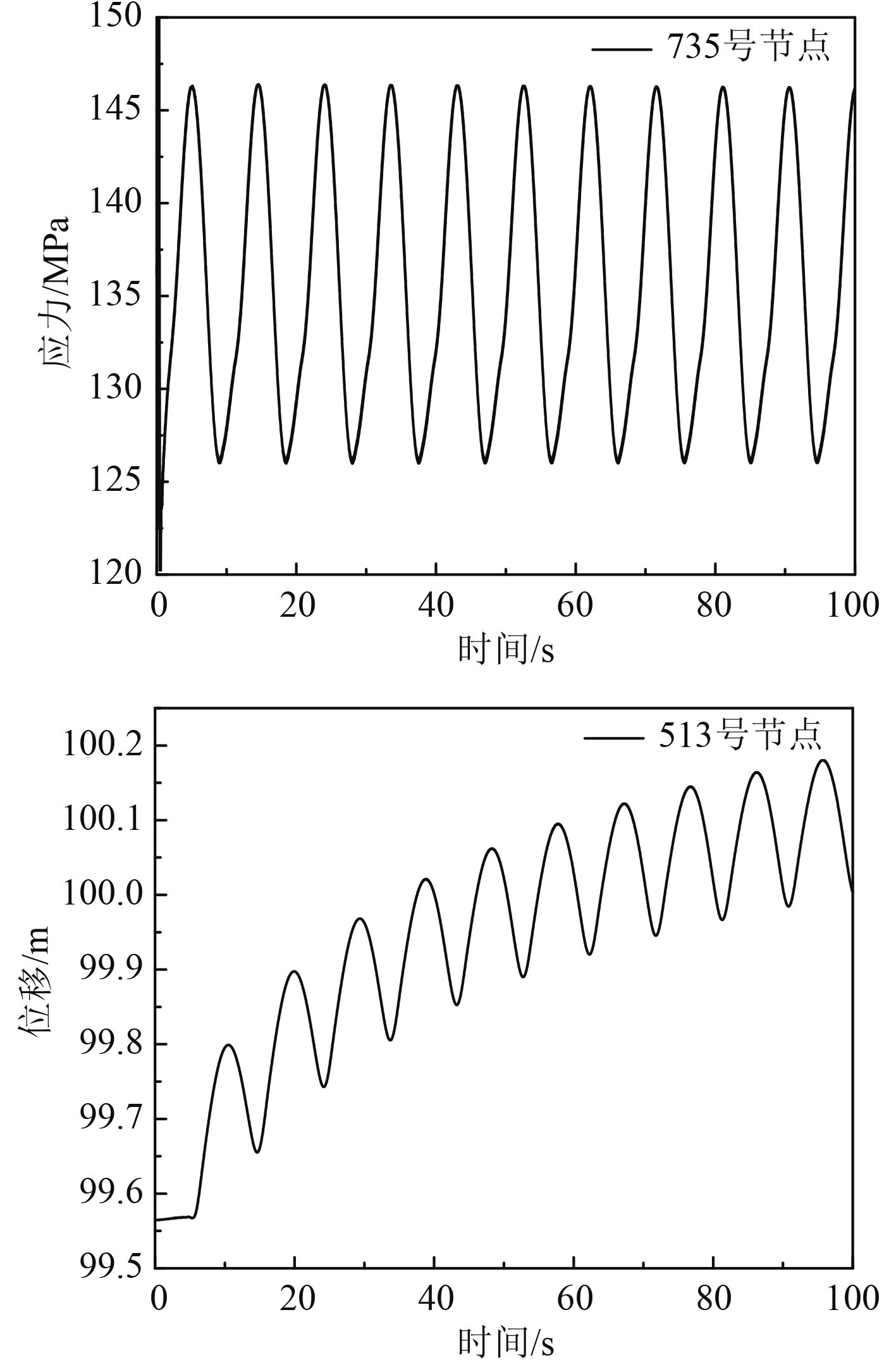
立管在安装工况下,最大应力出现在735号节点,最大值为146.2 MPa;最大位移出现在513号节点,最大值为100.3 m。应力、位移响应曲线如图6所示。
|
图 6 应力和位移响应曲线 Fig. 6 Stress and displacement response curve |
根据各个工况下的Mises应力云图和输出文件知,在极端工况、操作工况和安装工况下的最大Mises应力值分别为160.2 MPa,142.1 MPa,146.2 MPa,均小于X80级别钢材的许用应力,故可以认定该TTR立管是安全的。
3.3 分析各个参数对立管的影响为了更好地研究TTR立管在复杂海洋载荷下的非线性分析,防止立管发生结构弯曲破坏,研究各个参数对管内弯矩的影响同样具有工程意义。本文从立管管径、平台平均偏移量以及顶张力系数的变化,总结立管内部弯矩的变化规律。
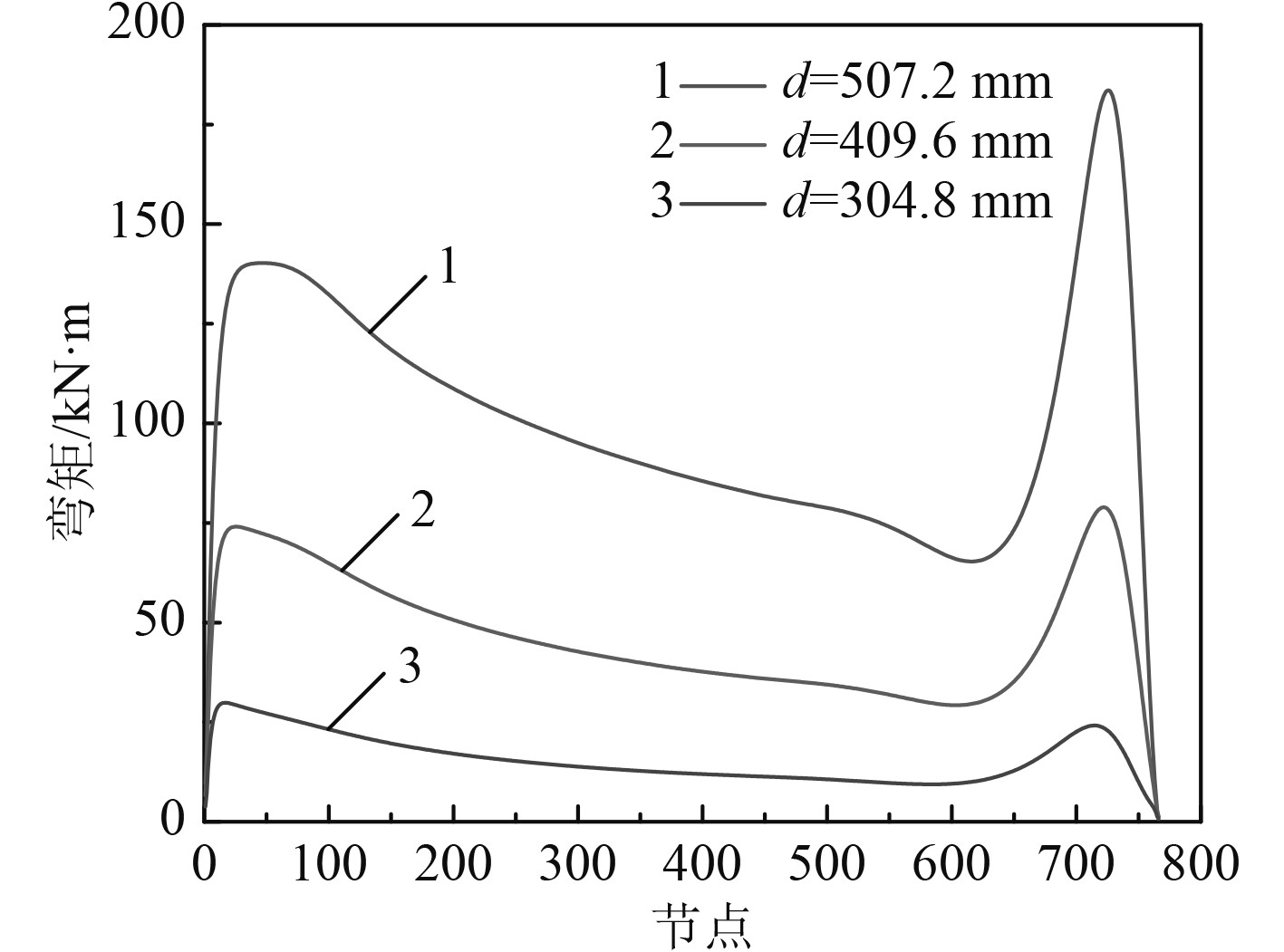
3.3.1 立管管径取立管管径为304.8 mm,409.6 mm,507.2 mm,分析其立管内部弯矩的影响,如图7所示,由图可见,管内弯矩在海平面与深水区均有极值出现,随着立管管径的加大,海平面与深水区管内弯矩均增大,且增加幅度较大,说明管内弯矩对管径的变化比较敏感。
|
图 7 不同管径管内弯矩曲线 Fig. 7 Bending moment curves in different pipe diameters |
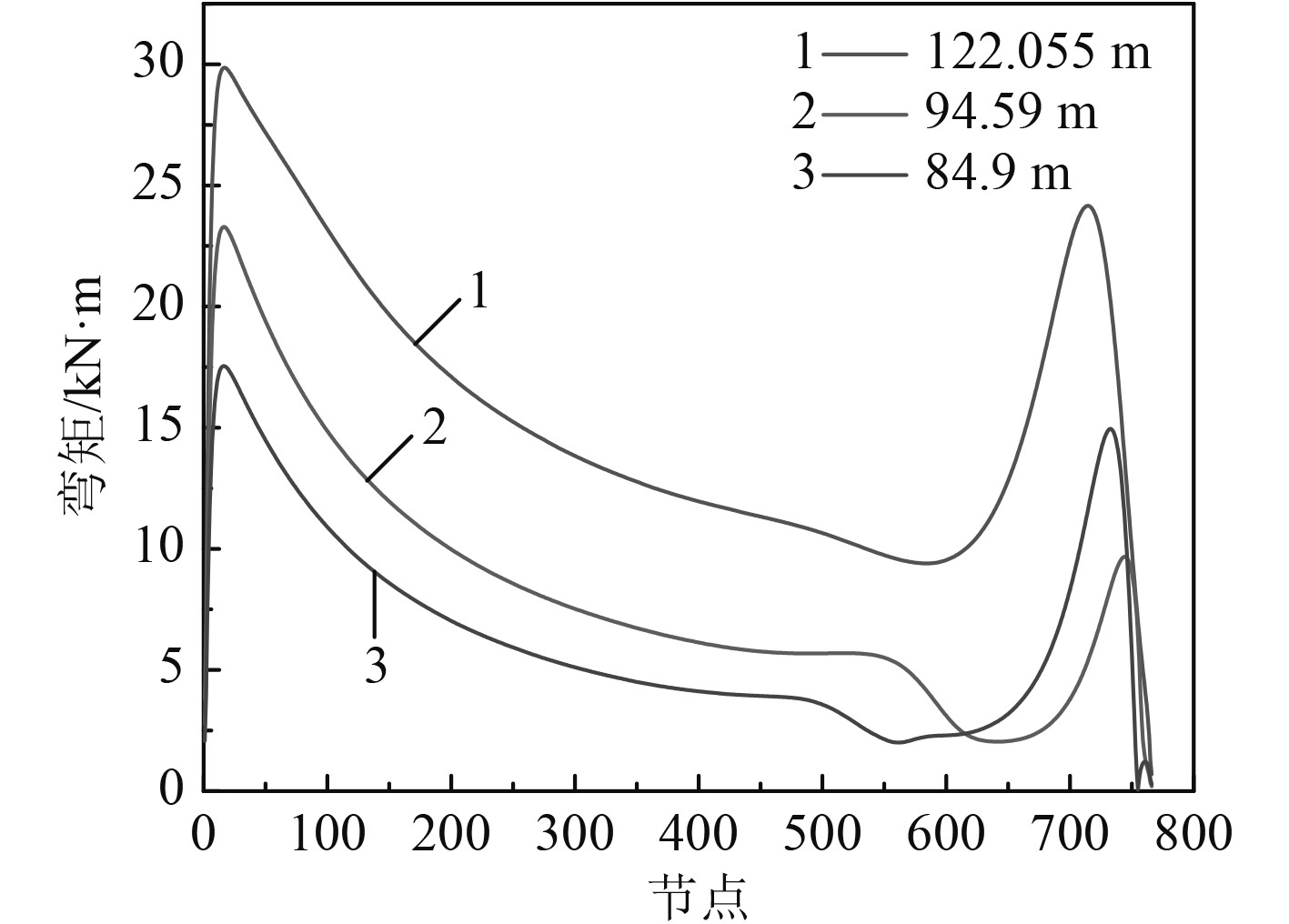
取平台平均偏移量为84.9 m,94.59 m,122.055 m,分析立管内部弯矩的影响,如图8所示。由图可见,管内弯矩在海平面与深水区均有极值出现,随着平台平均偏移量的加大,海平面管内弯矩增幅不明显,但深水区管内弯矩明显增大,但幅度较小。
|
图 8 不同平台平均偏移量管内弯矩曲线 Fig. 8 Bending moment curve in pipe with different platform average offset |
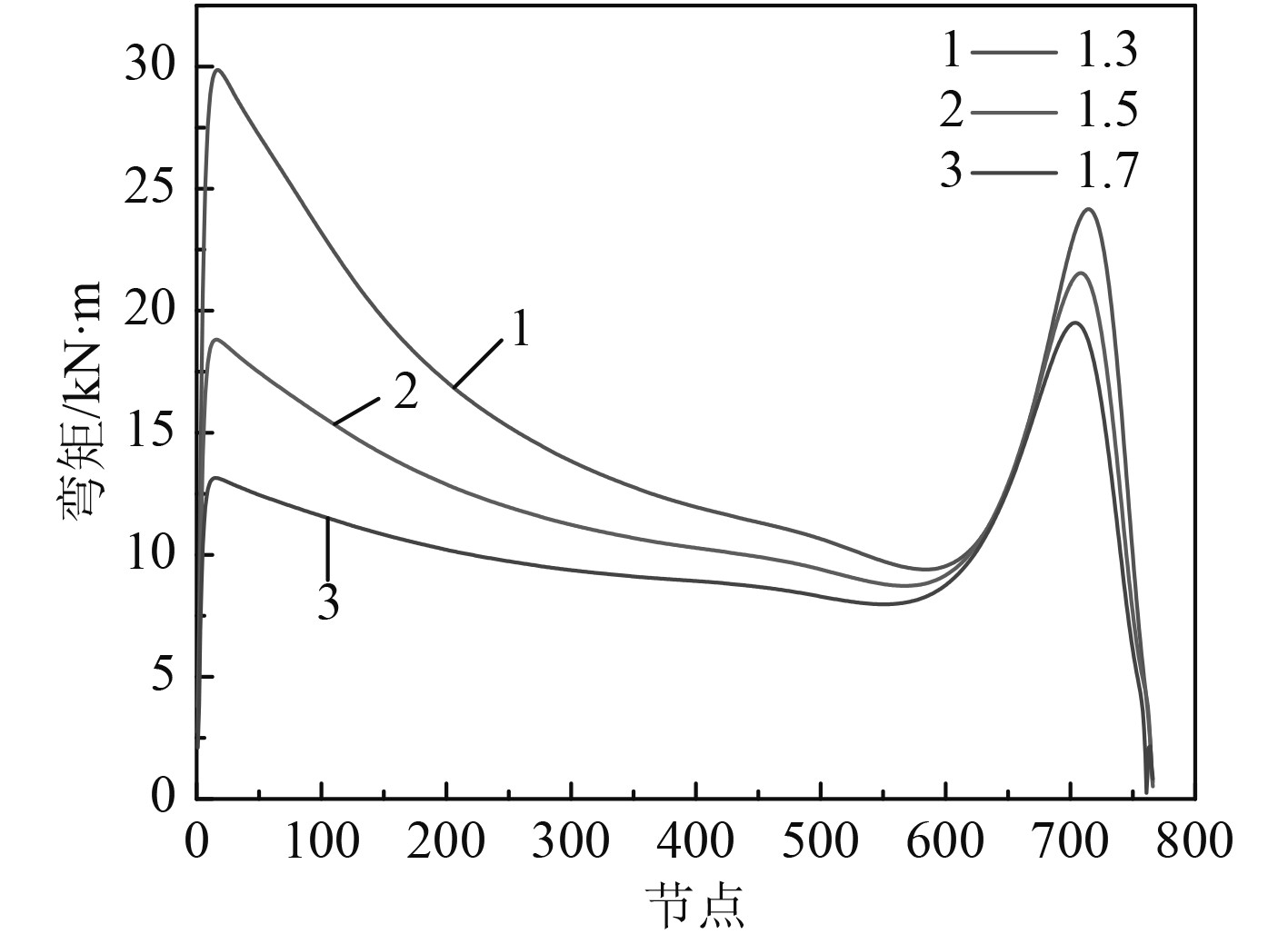
取顶张力系数为1.3,1.5,1.7,分析其立管内部弯矩的影响,如图9所示。由图可见,管内弯矩在海平面与深水区均有极值出现,张力系数对海平面管内弯矩极值影响不大,在深水区管内弯矩极值随顶张力系数增加而减小。
|
图 9 不同顶张力系数管内弯矩曲线 Fig. 9 Bending moment curve in pipe with different top tension coefficient |
1)采用有限元软件Abaqus对TTR进行简化建模、加载自重、浮力、波浪、海流等载荷以及平台运动,引入海洋工程模块AQUA对立管进行3种工况下的非线性动力响应分析。
2)在极端工况、操作工况和安装工况下的最大Mises应力值分别为160.2 MPa,142.1 MPa,146.2 MPa,均小于X80级别钢材的许用应力,故可以认定该TTR立管是安全的,立管最大位移为206 m ,128.4 m,100.3 m。
3)随着立管管径的加大,海平面与深水区管内弯矩均增大,且增加幅度较大;随着平台平均偏移量的加大,海平面管内弯矩增幅不明显,但深水区管内弯矩明显增大,但幅度较小;顶张力系数对海平面管内弯矩极值影响不大,在深水区管内弯矩极值随顶张力系数增加而减小。
| [1] |
许亮斌, 畅元江, 蒋世全, 等. 深水钻井隔水管时域非线性动态响应分析技术研究[J]. 中国海上油气, 2008(2): 115-120. DOI:10.3969/j.issn.1673-1506.2008.02.011 |
| [2] |
祝晓燕, 赵光艺, 崔月瑶. 波流耦合作用下导管架平台整体结构静力分析[J]. 船舶工程, 2016, 38(6): 61-64. |
| [3] |
余建星, 吴静怡, 余杨, 等. 局部系泊失效下的TLP平台鲁棒性评估方法研究[J]. 天津大学学报(自然科学与工程技术版), 2020, 53(7): 713-724. |
| [4] |
孙传栋. 深水顶张式立管的非线性动力分析及浪致疲劳研究[D]. 青岛: 中国海洋大学, 2009.
|
| [5] |
冯珩, 李艺, 刘忠彦, 等. 自升式平台桩腿的疲劳寿命计算方法[C]. //中国石油学会石油工程专业委员会海洋工程工作部2012年工作年会暨技术交流会论文集. 2012: 662–665.
|
| [6] |
邓合霞. 海洋立管在非线性波浪载荷下的极值响应研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.
|
| [7] |
余折. 凹陷损伤立管的极限强度和疲劳寿命分析[D]. 上海: 上海交通大学, 2010.
|
| [8] |
周灿丰, 帅潇, 焦向东, 等. API X65钢深水顶端张紧立管动力响应数值仿真研究[J]. 石油化工高等学校学报, 2014, 27(3): 87-91. DOI:10.3969/j.issn.1006-396X.2014.03.019 |
| [9] |
周灿丰, 帅潇, 焦向东, 等. 深水顶端张紧立管疲劳寿命研究[J]. 北京石油化工学院学报, 2014, 22(2): 45-49. DOI:10.3969/j.issn.1008-2565.2014.02.009 |
 2022, Vol. 44
2022, Vol. 44
