0 引　言

船舶碰撞事故会造成严重的后果，不仅会导致货物损失和船体受损，还会引起人员伤亡，造成环境污染。通常，船舶危险事故的原因包括：船员操作不当、船体机械故障、恶劣气象条件影响、船舶碰撞等。其中，船舶碰撞事故是发生频次最高的一种危险事故，一旦船舶出现碰撞事故，轻者造成航线拥堵和物流延误，重者导致船体搁浅和受损，造成燃油泄漏、人员伤亡，引发严重的经济损失。因此，国内外的研究人员针对船舶如何避碰以及船体碰撞的风险评估进行了大量的研究^[1]。

BP神经网络算法是基于非线性映射关系的一种先进算法，在处理非线性系统的寻优等问题上有明显的优势，但BP神经网络也存在收敛速度较慢等问题，神经网络的权值，阈值调整过程也存在一定的随机性。因此，在使用BP神经网络算法进行系统寻优时，往往配合GA遗传算法等其他先进算法，一方面可以提高BP神经网络算法的收敛速度，另一方面也可以提高目标寻优的准确度^[2]。

本文通过建立船舶碰撞的危险度模型，结合BP-GA算法进行详细的风险评估，并利用有限元分析技术，对船体碰撞后的损伤特性进行了仿真。本文的研究有助于提升船舶航行的安全性。

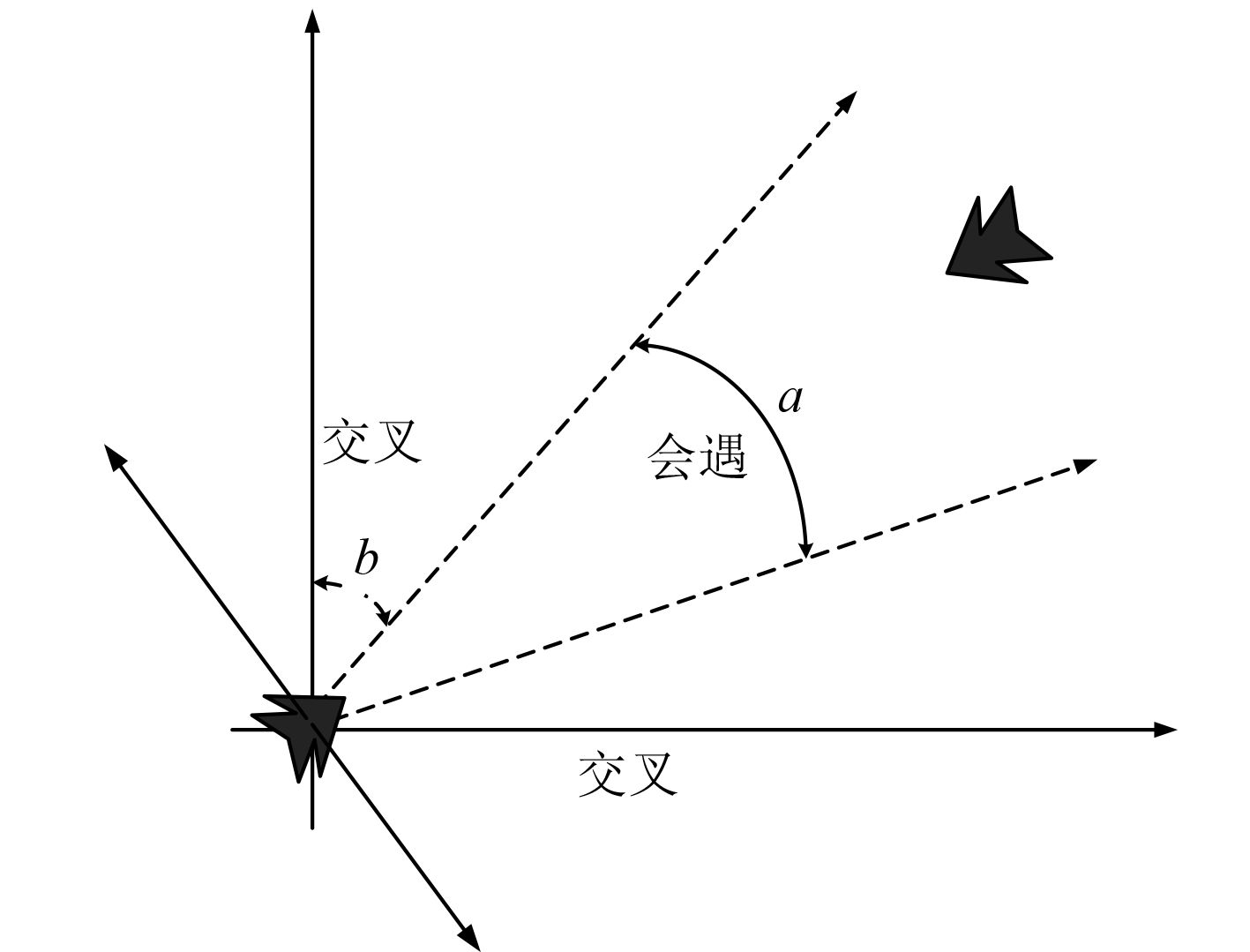
1 船舶碰撞危险度概念

为了分析船舶相遇过程的碰撞危险度，本文将船舶相遇过程的工况划分为会遇、右舷交叉、左舷交叉等情况，如图1所示。

1）会遇

会遇工况是指相遇的2艘船舶在相反的航向上相遇，2艘船的相对方位角度小于60°。

2）右舷交叉

右舷交叉是指两机动船之间有一定的会遇距离，甲船的右舷与乙船的右舷相对交叉，方位角小于45°，在这种会遇态势下，如果船舶驾驶人员出现局面判断不准确或者误操作，很容易导致船舶碰撞事故的发生，因此，右舷交叉是一种较危险的工况。

3）左舷交叉

与右舷交叉相遇类似，左舷交叉是指两机动船之间有一定的会遇距离，甲船的左舷与乙船的左舷相对交叉，方位角小于45°，在这种会遇态势下，船舶同样可能出现碰撞危险。

船舶碰撞危险度是进行船舶避碰评估的基本概念，有助于船舶碰撞风险度的量化。目前，针对船舶碰撞风险度的标准主要有2种：一是采用数学公式和算法，进行船舶碰撞概率的客观描述，通过采集相遇船舶的航行速度、航向以及相对速度等信息，计算船舶的碰撞危险度。二是通过船舶操作人员的主观描述进行船舶碰撞危险度的定义。本文使用日本学者小山健夫等的危险度模型，如下：

定义本船与它船的距离余量为 $ R/d $ ，时间余量为 $ R/{V_c} $ ，定义船舶碰撞危险度为：

$ {\mu _c} = \left( {{m_1}d + {m_2}{V_c}} \right)/R \text{。} $

式中： $ {m_1} $ ， $ {m_2} $ 为2船的质量； $ d $ 为安全距离； $ {V_c} $ 为两船的相对速度； $ R $ 为两船之间的实际距离。

建立船舶会遇的碰撞概率模型为：

$ \begin{gathered} \xi = \int_d^d {{\mu _c}} (t){\rm{d}}t，\hfill \\ {T_0} = dis\;\tan \; ce/{V_c}，\hfill \\ CRI = \xi /{T_0}。\end{gathered} $

式中： $ \xi $ 为概率； $ {T_0} $ 为两船相遇到碰撞发生的时间； $ CRI $ 为概率危险度。

2 基于BP-GA算法的船舶碰撞过程风险评估

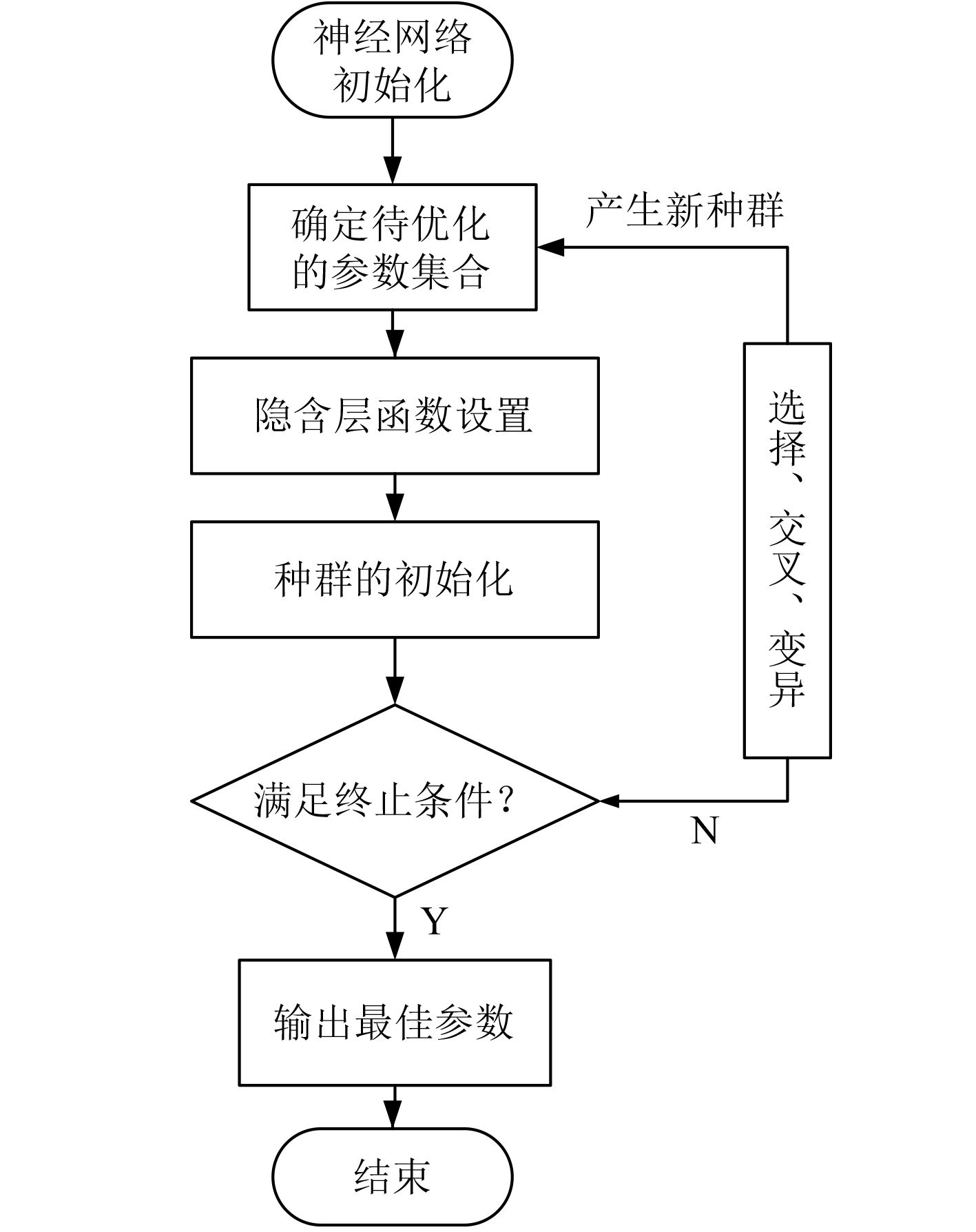
BP神经网络算法的收敛速度相对较慢，且BP神经网络算法在局域极值求解时准确度相对较低，因此，本文提供一种基于GA遗传算法和BP神经网络算法相结合的新型算法，进行船舶碰撞过程的风险评估。BP-GA优化算法的基本流程如图2所示。

1）BP神经网络的初始化

BP神经网络是进行危险度评估的主体算法，需要对BP神经网络的权值、阈值以及迭代上限次数进行初始化。其中，权值 $ W{\text{ = }}\left( {{w_1},{w_2},\cdots,{w_n}} \right) $ 的初始化将（−1,1）范围内的随机数赋予。

2）权值修正

由于BP-GA算法在实际使用时需要根据迭代次数和精度进行不断优化，因此，建立算法的权值修正方程为：

$ {\delta _i}\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}{l}} {\delta _i}\left( t \right) + f\left( t \right)\left[ {{x_i}\left( t \right) - {\delta _i}\left( t \right)} \right]，& i \in {S_i}\left( t \right) ，\\ {\delta _i}\left( t \right)，& i \notin {S_i}\left( t \right) 。\end{array}} \right. $

其中： $ {\delta _i}\left( t \right) $ 为待修正系数； $ f\left( t \right) $ 为效率函数^[2]； $ {S_i}\left( t \right) $ 为待修正系数的邻域； $ {x_i}\left( t \right) $ 为输入信号。

3）隐含层函数设置和初始边界条件

将相遇船舶的相对速度、方位角、位置等信息作为计算的边界条件，隐含层函数^[3]是算法进行寻优的核心，决定了BP-GA算法的效率和精度。设置隐含层函数为：

$ y = \frac{{{a_T} - {\theta _T}}}{{{\varphi _R}V}}\left( {\frac{{{V_R}g{R_T}^3}}{8}} \right) \text{。} $

其中，V为船舶的速度，在2个坐标轴的分量为：

$ \begin{gathered} \left\{ {\begin{array}{*{20}{l}} {{v_{{x_O}}} = {v_O} \cdot \sin \left( {{\varphi _O}} \right)} \text{，} \\ {{v_{{y_0}}} = {v_O} \cdot \cos \left( {{\varphi _O}} \right)} \text{，} \end{array}} \right. \hfill \\ \left\{ {\begin{array}{*{20}{l}} {{v_{{x_T}}} = {v_T} \cdot \sin \left( {{\varphi _T}} \right)} \text{，} \\ {{v_{{y_T}}} = {v_T} \cdot \cos \left( {{\varphi _T}} \right)} \text{。} \end{array}} \right. \hfill \\ \end{gathered} $

式中： $ {\varphi _O} $ 为本船的航向角； $ {\varphi _T} $ 为会遇船舶的航向角。

$ {V_R} $ 为两船的相对速度，用下式计算：

$ \begin{split} &{V_R} = \sqrt {v_{{x_R}}^2 + v_{{y_R}}^2}，\\ & {{v_{{x_R}}} = {v_{{x_T}}} - {v_{_0}}} ，\\ &{{v_{{y_R}}} = {v_{{y_T}}} - {v_{_O}}} 。\end{split} $

$ {\varphi _R} $ 为相对速度的方位角，用下式计算：

$ {\varphi _R} = {a_0} - \arctan \frac{{{v_{{y_R}}}}}{{{v_{{x_R}}}}} \text{，} {a_0} = \left\{ {\begin{array}{*{20}{l}} {90}，&{{\text{if }}{v_{{x_R}}} \geqslant 0} ，\\ {270}，&{{\text{if }}{v_{{x_R}}} < 0} 。\end{array}} \right. $

$ {R_T} $ 为两船直线距离，用下式计算：

$ {R_T} = \sqrt {{{\left( {{x_T} - {x_O}} \right)}^2} + {{\left( {{y_T} - {y_O}} \right)}^2}} \text{。} $

式中： $ \left( {{y_T},{x_T}} \right) $ 为会遇船舶现在位置； $ \left( {{x_O},{y_O}} \right) $ 为本船位置。

$ {a_T} $ 为实际方位角，如下式：

$ {a_T} = {a_1} - \arctan \frac{{{y_T} - {y_O}}}{{{x_T} - {x_O}}} \text{，} $

$ {\theta _T} $ 为实际船舷角，用下式计算：

$ {\theta _T} = {a_T} - {\varphi _O} \pm 360{\rm{^\circ }} 。$

4）遗传交叉和变异

利用GA遗传算法进行危险度评估过程的遗传交叉和变异操作，提高寻优算法的收敛速度。使用GA算法的适应度函数为：

$ F\left( t \right) = F\left( {\min \left| {\sqrt {\sum\limits_{i = 1}^M {{x_i}\left( t \right) - {\delta _i}{{\left( t \right)}^3}} } } \right|} \right) \text{，} $

最后，输出船舶碰撞的风险评估结果。

3 基于有限元分析的舰船碰撞过程损伤评估 3.1 有限元建模

为了进行船舶碰撞过程的损伤评估，采用有限元分析技术建立船体碰撞区域的有限元模型，在Workbench中进行碰撞过程的损伤仿真^[5]。

本文选用10000 t散货船作为有限元仿真的对象，其基本参数如表1所示。

船舶碰撞区域的有限元建模包括几何模型建立、有限元模型建立2个步骤。

1）几何模型建立

在建立船舶碰撞区域的几何模型时，一方面要进行模型基本参数的建立，另一方面也要进行复杂结构的简化。首先确定船舶碰撞区域模型的坐标系，以船舶甲板面为oxy平面，以船首方向为ox轴正方向；以左舷方向为oy轴正方向，以垂直于甲板向上为oz轴正方向。

选取几何建模的单位为mm，力为N，弹性模量为MPa，设定好初始条件后，依次建立点、线、面构建整体模型。

2）有限元模型建立

船舶碰撞区域几何模型建好后，在Workbench的Mechanical^[5]工作环境下进行有限元模型的建立，忽略建模过程的小圆角、倒角等形状特征，模型全部使用四面体单元建模，总共包括9685个单元和263548个节点，船舶碰撞区域的局部有限元模型如图3所示。

3.2 材料属性定义及损伤求解

散货船碰撞区域的材料通常为高强度钢，为了模拟船舶碰撞过程中材料的应力-应变特性，有必要对高强度钢的材料属性进行详细的设置。

使用的材料属性动态模型满足Cowper-Symonds本构方程^[6]，如下式：

$ \frac{{\sigma _o^\prime }}{{{\sigma _o}}} = 1 + {(\varepsilon /D)^{1/q}} \text{。} $

其中： $ \sigma _o^\prime $ 为高强度钢在发生塑性应变时的动态屈服应力； $ {\sigma _o} $ 为静态屈服应力； $ \varepsilon $ 为应变； $ D $ 为常数40.1；q为粘性系数0.5^[7]。

船舶碰撞区域有限元模型的材料参数设置如表2所示。

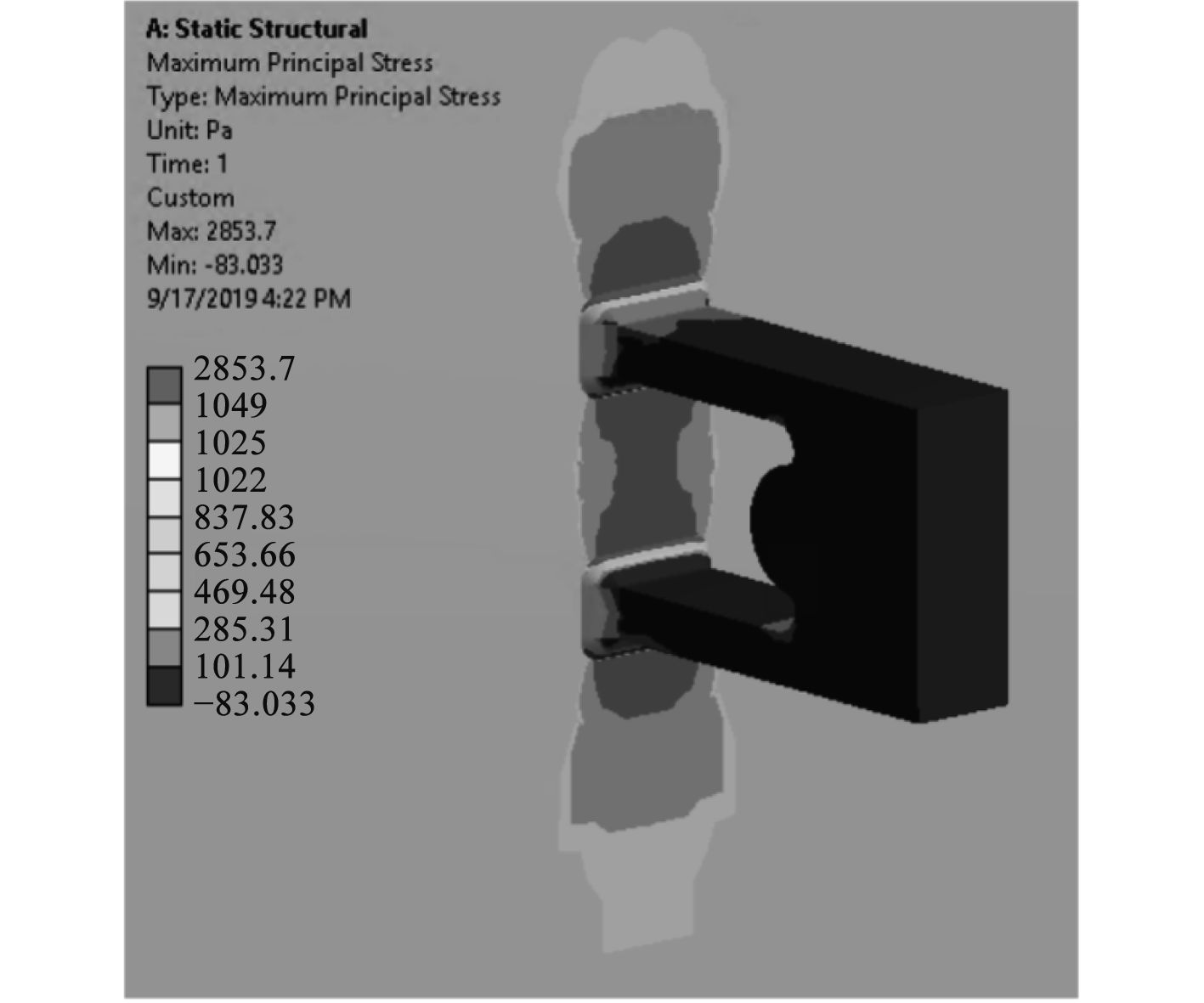
图4为基于Workbench的船体碰撞区域损失有限元仿真云图。

4 结　语

本文针对船舶碰撞过程的风险评估和损伤进行研究，分别采用BP-GA算法进行会遇船舶的碰撞风险评估，采用有限元分析方法对船舶碰撞区域建立有限元模型，在Workbench仿真软件中进行碰撞损失评估，为防止出现船舶碰撞事故提供参考。