0 引　言

AUV作为开发海洋资源的重要工具，具有机动性好、稳定性强、精确度高等一系列优点，已经在环境监测、资源勘探和水下救援等任务中发挥了重要作用^[1]。但由于结构的限制，依靠尾部单推进器和十字舵来控制的小型欠驱动AUV，各自由度之间存在较强的耦合性，加之体积小，易受海浪、洋流的干扰。因此小型欠驱动AUV面对外界干扰和本身的局限性，如何进行精准的控制是水下机器人研究的主要方向之一。

目前，AUV的轨迹跟踪问题可分为3个方面。一是AUV水平面轨迹跟踪。刘丽萍等^[2]将海流速度引入AUV数学模型，提出一种自适应反演滑模控制方法对AUV进行水平面的轨迹跟踪；杨泽文等^[3]通过建立误差方程，基于反步法设计控制器实现了对AUV水平面的轨迹跟踪；严浙平等^[4]通过建立误差方程，在反步法的基础上加入滑模控制进行AUV水平面的轨迹跟踪；钟雨轩等^[5]将轨迹跟踪转化为跟踪误差镇定，利用自适应滑模方法设计误差镇定控制器实现对欠驱动无人艇的轨迹跟踪；Ramezani-Al M R等^[6]用连续项代替离散的传统符号函数，设计具有自适应增益的滑模控制器趋近律减轻抖振和噪声的影响来解决AUV的平面跟踪问题。二是，AUV垂直面轨迹跟踪。王洪斌等^[7]提出了基于粒子群优化的AUV定深跟踪有限时间控制方法，并通过理论证明和仿真实验证明了该方法可以有效实现AUV的定深控制；林荣鹏等^[8]通过定义虚拟误差，设计反步法控制器，同时加入PID控制，实现了AUV无超调垂直面跟踪；饶志荣等^[9]提出一种自适应终端滑模控制方法对AUV进行垂直面的深度控制。三是AUV三维空间轨迹跟踪。张国成等^[10]提出了一种新型2阶滑模控制，并采用自适应调谐律估计扰动上限来对便携式AUV进行轨迹跟踪；王金强等^[11]提出一种基于神经网络的反步滑模控制策略实现三维路径的精确跟踪；徐建等^[12]将姿态跟踪转化为虚拟速度控制满足欠驱动UUV对位置、姿态和速度的时间要求，实现了在系统参数不精确及环境时变扰动情况下的三维轨迹精确跟踪控制。

滑模控制作为一种非线性控制方法，具有控制精度高、结构简单等优点，尤其在系统不确定性和抗干扰方面具有强鲁棒性^[13]。本文在符合“云帆”AUV特性的六自由度数学模型基础上，采用NDO对环境的干扰进行估计补偿，通过反步法和滑模控制相结合设计控制器。在传统反步法控制中，定义跟踪误差，引入虚拟控制量，进行控制器的设计。结合滑模控制后，将AUV的数学模型与NDO相结合，设计滑模面取代虚拟控制量，设计反步滑模控制器，利用李雅普诺夫函数证明系统的稳定性，并通过仿真证明该方法可以完成对AUV的三维轨迹跟踪。

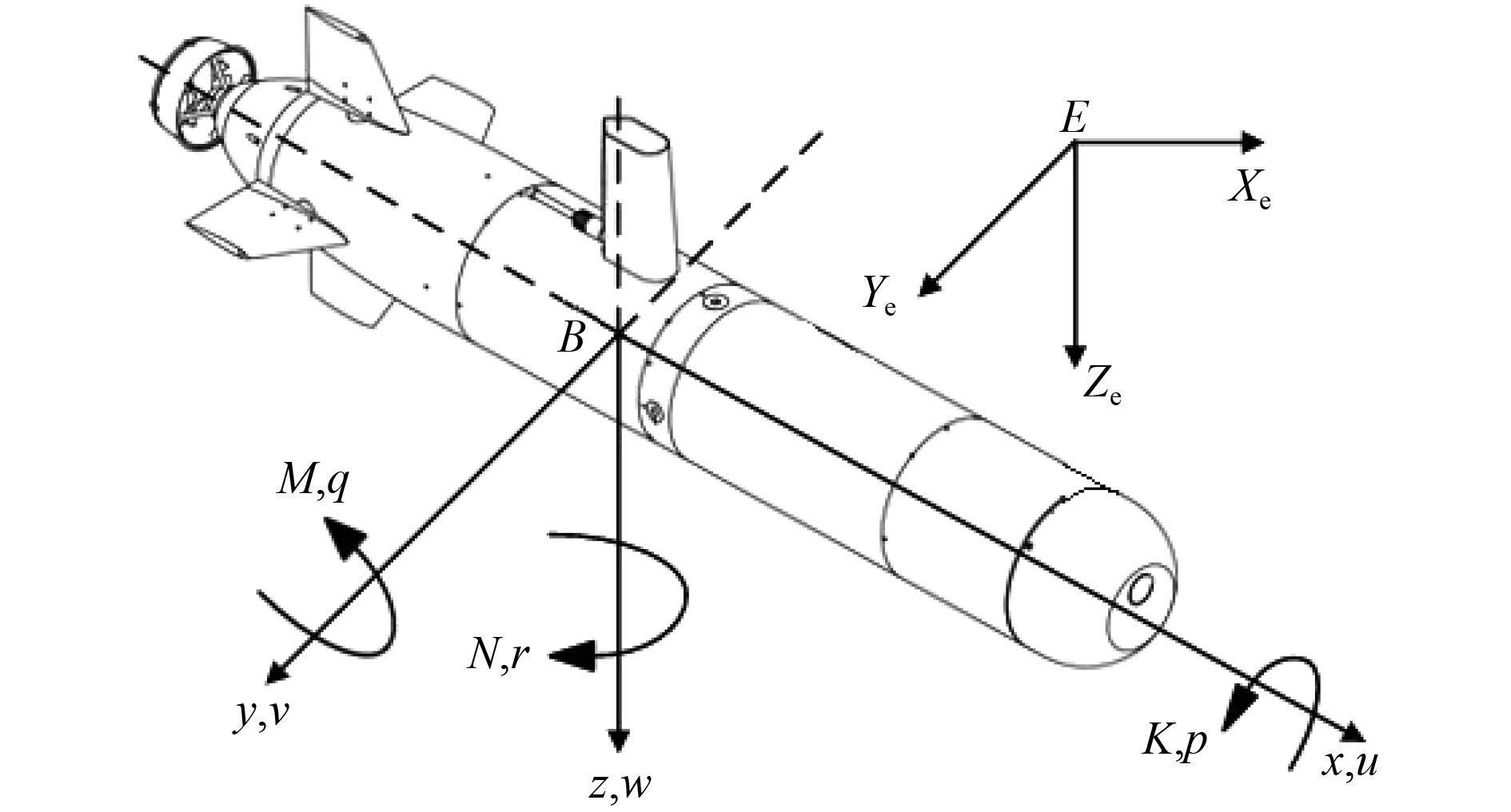
1 AUV运动建模

为了更好地表达AUV在三维空间的位置、姿态等信息，基于“云帆”AUV为模型建立如图1所示惯性坐标系 $E - {X_e}{Y_e}{Z_e}$ 和载体坐标系 $ B - xyz $ 。载体坐标系原点B与AUV浮心重合。

AUV的数学模型可表示为：

$ \left\{ {\begin{array}{*{20}{l}} {\dot \eta {\text{ = }}R\left( \eta \right)v} ，\\ {M\dot v + C\left( v \right)v + D\left( v \right)v + g\left( \eta \right) = \tau + {\tau _d}} 。\end{array}} \right. $

(1)

式中： $\eta = {\left[ {x,y,z,\phi ,\theta ,\psi } \right]^{\rm T}}$ 为广义方位参数，分别表示在惯性坐标系下AUV的纵坐标、横坐标和垂向坐标，横滚角、俯仰角和偏航角； ${v_1} = {\left[ {u,v,w,p,q,r} \right]^{\rm T}}$ 为广义速度参数，分别表示载体坐标系下AUV的纵向、横向和垂向速度，横滚、纵倾和偏航角速度； $ R\left( \eta \right) $ 为坐标转换矩阵， $\tau {\text{ = }}{\left[ {{\tau _u},0,0,0,{\tau _q},{\tau _r}} \right]^{{\rm{T}}}}$ 为控制输入量，分别表示推进器推力，水平舵和垂直舵产生的力矩。 ${\tau _d} = \left[ {\tau _{d1}}, \right. $ $ \left. {\tau _{d2}},{\tau _{d3}},{\tau _{d4}},{\tau _{d5}},{\tau _{d6}} \right]^{\rm T}$ 为外界干扰项。

忽略横滚对AUV的影响，AUV的运动学模型可表示为：

$ \left\{ {\begin{array}{*{20}{l}} {\dot x = u\cos \psi \cos \theta - v\sin \psi + w\sin \theta \cos \psi } ，\\ {\dot y = u\sin \psi \cos \theta + v\cos \psi + w\sin \theta \sin \psi } ，\\ {\dot z = - u\sin \theta + w\cos \theta } ，\\ {\dot \theta = q} ，\\ {\dot \psi = r\sec \theta } 。\end{array}} \right. $

(2)

AUV的动力学模型可表示为：

$ \left\{ {\begin{array}{*{20}{l}} {{m_{11}}\dot u = {m_{22}}vr - {m_{33}}wq - {X_u}u - {X_{u\left| u \right|}}u\left| u \right| + {\tau _u} + {\tau _{d1}}} ，\\ {{m_{22}}\dot v = - m{}_{11}ur - {Y_v}v - {Y_{v\left| v \right|}}v\left| v \right| + {\tau _{d2}}} ，\\ {{m_{33}}\dot w = {m_{11}}uq - {Z_w}w - {Z_{w\left| w \right|}}w\left| w \right| + {\tau _{d3}}} ，\\ \begin{gathered} {m_{55}}\dot q = \left( {{m_{33}} - {m_{11}}} \right)uw - {M_q}q - {M_{q\left| q \right|}}q\left| q \right| + {\tau _q} + {\tau _{d5}} ，\hfill \\ \quad \quad \;\; - \overline {B{G_z}} W\sin \theta ，\hfill \\ \end{gathered} \\ {{m_{66}}\dot r = \left( {{m_{11}} - {m_{22}}} \right)uv - {N_r}r - {N_{r\left| r \right|}}r\left| r \right| + {\tau _r} + {\tau _{d6}}} 。\end{array}} \right. $

(3)

式中： ${m_{11}} = m - {X_{\dot u}}$ ， $ {m_{22}} = m - {Y_{\dot v}} $ ， $ {m_{33}} = m - {Z_{\dot w}} $ ， $ {m_{55}} = $ $ {I_y} - {M_{\dot q}} $ ， $ {m_{66}} = {I_z} - {N_{\dot r}} $ ， $ m $ 为AUV质量，其他为AUV转动惯量和水动力参数。

2 反步滑模控制

为了减轻环境干扰对AUV航行的影响，同时提高AUV三维轨迹跟踪精度。将NDO模型与AUV数学模型相结合，设计反步滑模控制器，最后通过李雅普诺夫函数证明系统的稳定性。

2.1 NDO的设计

面对未知干扰 $ {\tau _d} $ ，根据AUV的数学模型，设计NDO为：

$ \left\{ {\begin{array}{*{20}{l}} {d = z + p(v)}，\\ \begin{gathered} \dot z = - Lz - L(p(v) - (C\left( v \right) + D\left( v \right))v + \tau - g(\eta )) 。\end{gathered} \end{array}} \right. $

(4)

式中： $z$ 为干扰器的状态变量， $L$ 为干扰器的增益，定义为：

$ L = \frac{{\partial p(v)}}{{\partial v}} = {\rm{diag}}({l_1},{l_2},{l_3},{l_4},{l_5},{l_6})。$

(5)

式中， $ {l_1},{l_2},{l_3},{l_4},{l_5},{l_6} > 0 $ 。 $ p(v) $ 为待设计的非线性函数，定义为：

$ p(v) = LMv ，$

(6)

定义观测误差 $ \tilde d = {\tau _d} - d $ ，对时间求导得：

$ \dot {\tilde d} = {\dot \tau _d} - \dot d = {\dot \tau _d} - L\tilde d 。$

(7)

考虑实际情况下，干扰项 $ {\tau _d} $ 未知且无法预知，当 $ {\tau _d} $ 相对于控制系统的动态特性变化缓慢时，认为 ${\dot \tau _d} = 0$ ，则式(7)可改写为：

$ \dot{ \tilde d} = {\dot \tau _d} - \dot d = - L\tilde d ，$

(8)

构建李雅普诺夫函数： $ V = \frac{1}{2}{\tilde d^2} $ ，对时间求导得：

$ \dot V = \dot{ \tilde d}\tilde d = - L{\tilde d^2} \leqslant 0 ，$

(9)

故该非线性干扰观测器是稳定的。同时可得到观测误差方程： $\dot {\tilde d }+ L\tilde d = 0$ ，解方程得：

$ \tilde d\left( t \right) = \tilde d\left( 0 \right){e^{ - Lt}} ，$

(10)

由此可知，通过调节参数 $ L $ ，使误差 $\tilde d$ 快速收敛接近0，即NDO的干扰观测值无限接近外界干扰 $ {\tau _d} $ 。根据式(1)，定义NDO的输出量为：

$ {u_d} = Md。$

(11)

2.2 传统反步法控制

在忽略外部干扰的情况下，结合式(1)，AUV的数学模型可以写为：

$ \left\{ {\begin{array}{*{20}{l}} {\dot \eta = R\left( \eta \right)v} ，\\ {M\dot v = \tau - \left( {C\left( v \right) + D\left( v \right)} \right)v - g\left( \eta \right)} 。\end{array}} \right. $

(12)

为使AUV通过调整输入 $ \tau $ ，使实际轨迹 $ \eta $ 跟随期望轨迹 $ {\eta _d} $ ，定义跟踪误差为 $ {e_1} = \eta - {\eta _d} $ 。构建李雅普诺夫函数： $ {V_1} = \dfrac{1}{2}{e_1}^2 $ ，对时间求导得：

$ {\dot V_1} = {e_1}{\dot e_1} = {e_1}\left( {\dot \eta - {{\dot \eta }_d}} \right) = {e_1}\left( {R\left( \eta \right)v - {{\dot \eta }_d}} \right)，$

(13)

为使跟踪误差 $ {e_1} $ 稳定，引入虚拟控制量 $ {e_2} $ ，取 $ {e_2} = R\left( \eta \right)v - {\dot \eta _d} + {k_1}{e_1} $ ，式中 ${k_1} > 0$ ，则式(13)可改写为：

$ {\dot V_1} = {e_1}\left( {{e_2} + {{\dot \eta }_d} - k{e_1} - {{\dot \eta }_d}} \right) = {e_1}{e_2} - {k_1}e_1^2，$

(14)

为使 $ {\dot V_1} \leqslant 0 $ ，构建关于 $ {e_2} $ 的李雅普诺夫函数为： $ {V_2} = {V_1} + \dfrac{1}{2}e_2^2 $ ，对时间求导得：

$ \begin{gathered} {{\dot V}_2} = {{\dot V}_1} + {e_2}{{\dot e}_2} =\hfill \\ \quad \;\; {e_1}{e_2} - {k_1}e_1^2 + {e_2}(\dot R\left( \eta \right)v + R\left( \eta \right){M^{ - 1}}\tau - \hfill \\ \quad \;\; R\left( \eta \right){M^{ - 1}}\left( {\left( {C\left( v \right) + D\left( v \right)} \right)v + g\left( \eta \right)} \right) + {k_1}{{\dot e}_1} - {{\ddot \eta }_d}) 。\end{gathered} $

(15)

为使 $ {V_2} \leqslant 0 $ ，设计控制器为：

$ \begin{split} \tau =& \left( {C\left( v \right) + D\left( v \right)} \right)v + g\left( \eta \right) + \\ & MR{\left( \eta \right)^{ - 1}}\left( { - {k_1}{{\dot e}_1} + {{\ddot \eta }_d} - {k_2}{e_2} - {e_1} - \dot R\left( \eta \right)v} \right) ，\end{split} $

(16)

式中 ${k_2} > 0$ ，有

$ {\dot V_2} = - {k_1}e_1^2 - {k_2}e_2^2 \leqslant 0。$

(17)

即 $ {\dot V_2} $ 是负半定的，因此，使用式(16)可以使非线性系统(12)渐进稳定。

2.3 反步滑模控制

传统反步法控制不仅需要精确的建模信息，而且不能抵抗外界干扰。为减少模型不确定性对AUV的影响，同时减轻环境干扰对AUV的影响，将反步法与滑模控制相结合，并引入NDO抵消外界干扰，使AUV在环境干扰的情况下可以稳定的运行。

引入NDO后，AUV的数学模型可表示为：

$ \left\{ {\begin{array}{*{20}{l}} {\dot \eta = R\left( \eta \right)v} ，\\ {M\dot v = \tau - \left( {C\left( v \right) + D\left( v \right)} \right)v - g\left( \eta \right) + \zeta } 。\end{array}} \right. $

(18)

式中： $ \zeta = \tilde d $ 为通过NDO得到的干扰误差量。

定义跟踪误差 $ {e_3} = \eta - {\eta _d} $ ，则 $ {\dot e_3} = \dot \eta - {\dot \eta _d} = R \left( \eta \right) v - {\dot \eta _d} $ 。构建李雅普诺夫函数： $ {V_3} = \dfrac{1}{2}{e_3}^2 $ ，对时间求导得：

$ {\dot V_3} = {e_3}{\dot e_3} = {e_3}\left( {R\left( \eta \right)v - {{\dot \eta }_d}} \right) ，$

(19)

为使系统趋于稳定，设计滑模面为 $ s = {\dot e_3} + c{e_3} $ ，其中 $c > 0$ ，对时间求导得：

$ \dot s = \dot R\left( \eta \right)v + R\left( \eta \right)\dot v - {\ddot \eta _d} + c{\dot e_3} ，$

(20)

考虑到非线性干扰观测器 $ d $ ，构建李雅普诺夫函数为：

$ {V_4} = {V_3} + \frac{1}{2}{s^2} + \frac{1}{2}{\zeta ^2}，$

(21)

对时间求导得：

$ \begin{split} &{{\dot V}_4} = {{\dot V}_3} + s\dot s + \zeta \dot \zeta = \hfill \\ & \quad s\left( {\dot R\left( \eta \right)v + R\left( \eta \right)\dot v - {{\ddot \eta }_d} + c{{\dot e}_3}} \right) - L{{\tilde d}^2} +\hfill \\ & \quad \;\; {e_3}\left( {R\left( \eta \right)v - {{\dot \eta }_d}} \right)= \hfill \\ & \quad s\left( {R\left( \eta \right){M^{ - 1}}\left( {\tau - C\left( v \right)v - D\left( v \right)v - g\left( \eta \right) + \zeta } \right)} \right. - \hfill \\ & \quad \;\;\left. { {{\ddot \eta }_d} + c{{\dot e}_3} + \dot R\left( \eta \right)v} \right) - L{{\tilde d}^2} + {e_3}\left( {R\left( \eta \right)v - {{\dot \eta }_d}} \right) = \hfill \\ & \quad s\left( {R\left( \eta \right){M^{ - 1}}\left( {\tau - C\left( v \right)v - D\left( v \right)v - g\left( \eta \right) + \zeta } \right)} \right.- \hfill \\ & \quad \;\;\left. { {{\ddot \eta }_d} + c{{\dot e}_3} + \dot R\left( \eta \right)v} \right) - L{{\tilde d}^2} + {e_3}\left( {s - c{e_3}} \right)，\end{split} $

(22)

为使 $ {\dot V_4} \leqslant 0 $ ，设计控制器为：

$ \begin{split} \tau =& MR{\left( \eta \right)^{ - 1}}\left( { - c{{\dot e}_3} + {{\ddot \eta }_d} - {k_3}s - {e_3} - \dot R\left( \eta \right)v} \right) + \\ & \left( {C\left( v \right) + D\left( v \right)} \right)v - {\rm{a}}{{\rm{sgn}}} (s) + g\left( \eta \right) - \zeta ，\end{split} $

(23)

式中： ${k_3} > 0$ 且 $a > \left| {{\tau _d}} \right|$ ，于是有

$ {\dot V_4} = - L{\tilde d^2} - ce_3^2 - {k_3}{s^2} - {\rm{a}}{{\rm{sgn}}} (s) \leqslant 0 。$

(24)

即 $ {\dot V_4} $ 是负半定的，因此，使用式(23)可以使非线性系统(18)渐进稳定。

3 仿真结果与分析

为验证本文设计的基于NDO的反步滑模控制器的三维轨迹跟踪效果，根据建立的AUV数学模型进行仿真，并在相同初始条件和期望轨迹下，与传统PID控制器进行对比验证。表1给出了“云帆”AUV动态模型的各个参数。

考虑到AUV存在回转半径，设计期望轨迹为螺旋下降曲线： ${\eta _d} = {\left[ {4\cos \left( t \right),4\sin \left( t \right), - t - 1,0,\theta ,\psi } \right]^{\rm T}}$ ，式中，俯仰角 $ \theta $ 和偏航角 $ \psi $ 根据实际轨迹的变化而变化。为保证实际轨迹与期望轨迹起点重，定义AUV的初始位置为： $\eta \left( 0 \right) = {\left[ {4,4,0,0,0.5,0.5} \right]^{\rm T}}$ 、定义AUV的初始速度为 $ v\left( 0 \right) = {\left[ {1,1,1,0,0.1,0.1} \right]^{\rm T}} $ ，定义采样周期为： $ h = 0.02\;{\rm{s}} $ 。定义环境干扰，验证NDO的有效性： ${\tau _d} = \left[ 75\sin \left( t \right) - \right. $ $ \left. 16,65\cos \left( t \right),106\cos \left( {t - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. } 2}} \right) + 30 \right]^{\rm T}$ 。

定义非线性干扰观测器的增益为： $L = {\rm{diag}} \left( 0.01, \right. $ $ \left. 0.002,0.005,0,0,0 \right)$ ；选取设计控制器参数为： ${k_1} = 3.25$ ， ${k_2} = 41.5$ ， ${k_3} = 41.5$ ， $ a = \left| {{\tau _d}} \right| + 0.1 $ ；选取设计滑模面参数为： $c = 3.25$ 。

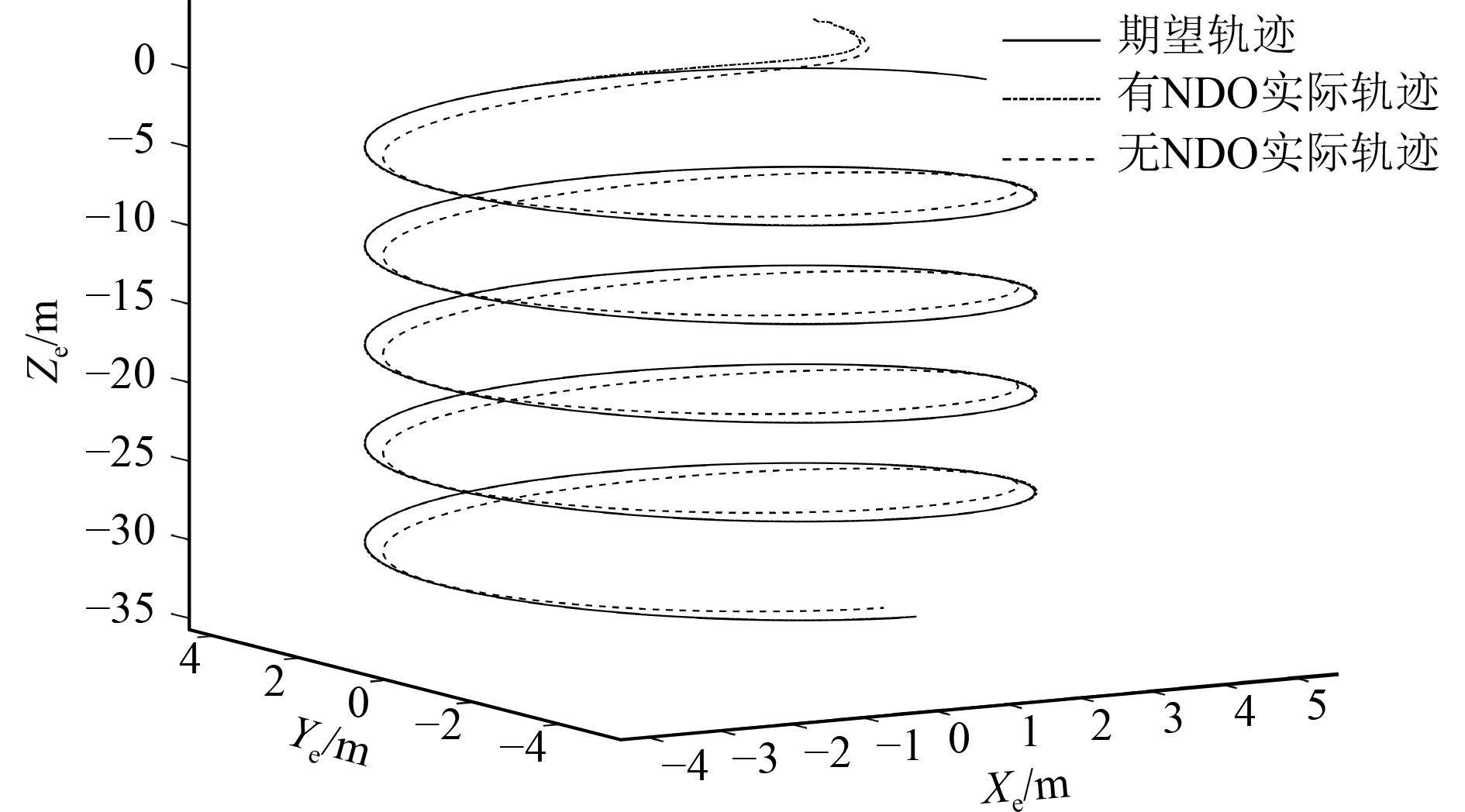
实验1　为验证NDO的有效性，在相同初始条件情况下，分别在控制器中加入NDO和不加入NDO进行对比。图2为AUV期望轨迹和在有无NDO的情况下AUV的实际轨迹对比。

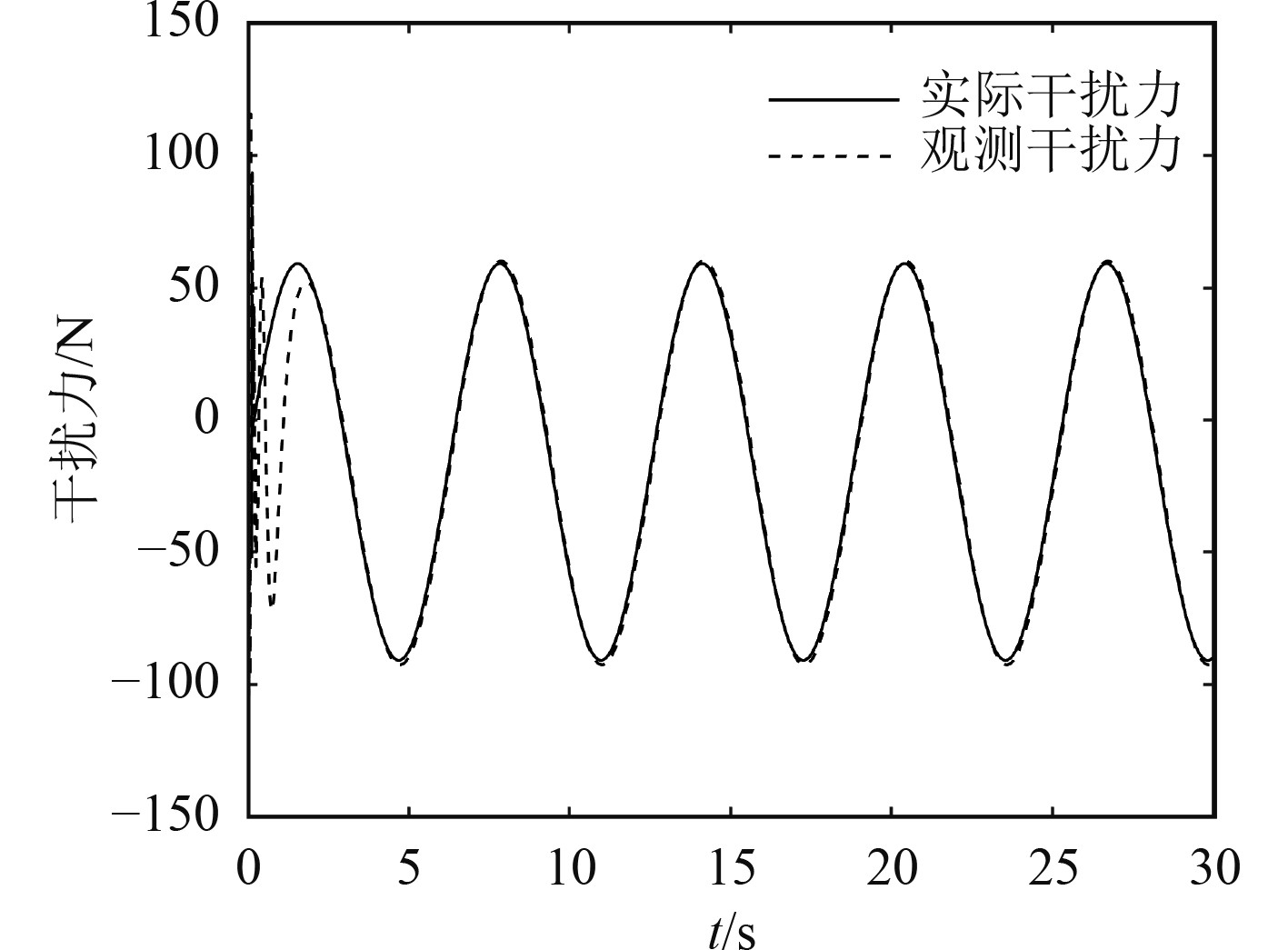
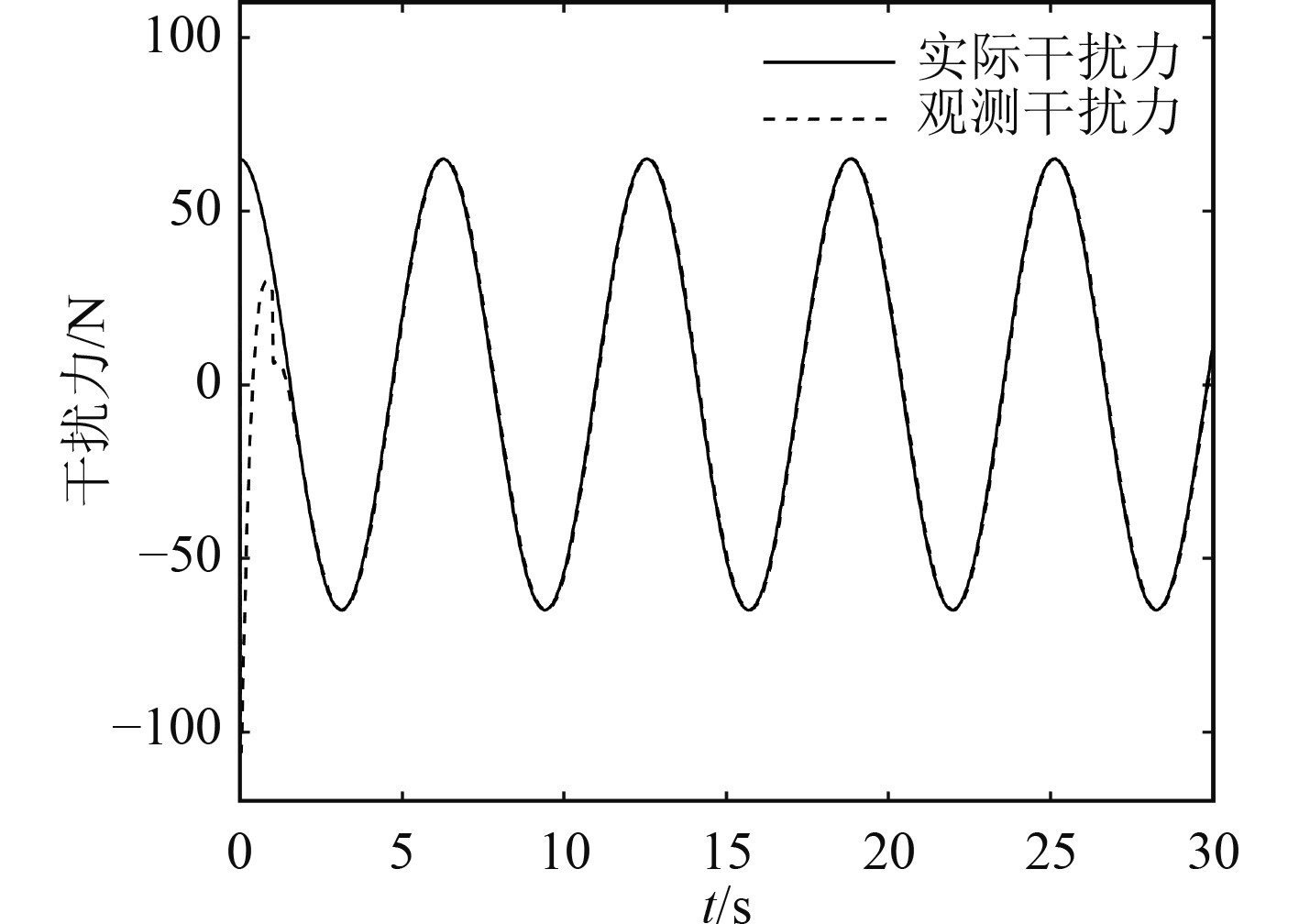
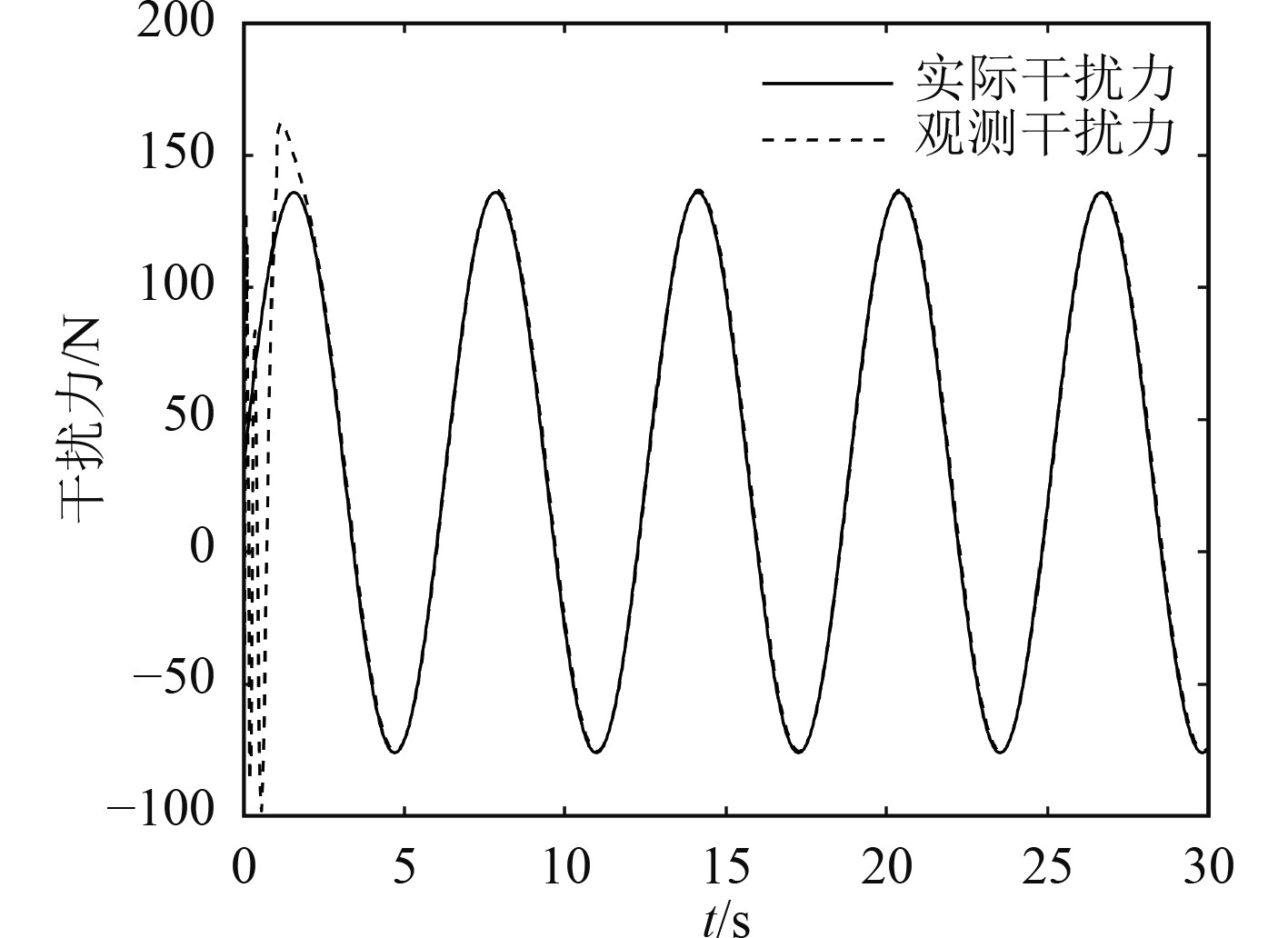
可以看出在存在外界干扰的情况下，有NDO的实际轨迹与期望轨迹几乎重合，但无NDO的实际轨迹与期望轨迹偏差较大。结果表明加入NDO后，控制器的控制效果更好，证明了NDO的有效性。图3～图5为NDO干扰观测值与实际干扰值对比，可以看出NDO干扰观测值在前2 s左右存在较大的振荡后，逐渐趋于稳定，最终与实际干扰值基本重合。图6为3个方向的跟踪误差，可以看出无NDO时，轨迹始终存在误差，且误差波动较大。加入NDO后，经过3 s左右的振荡，误差收敛于零值附近。

实验仿真证明，NDO具有良好的抗干扰能力，可以对环境干扰进行精确的估计，并补偿到AUV，使AUV较好的完成三维轨迹跟踪。

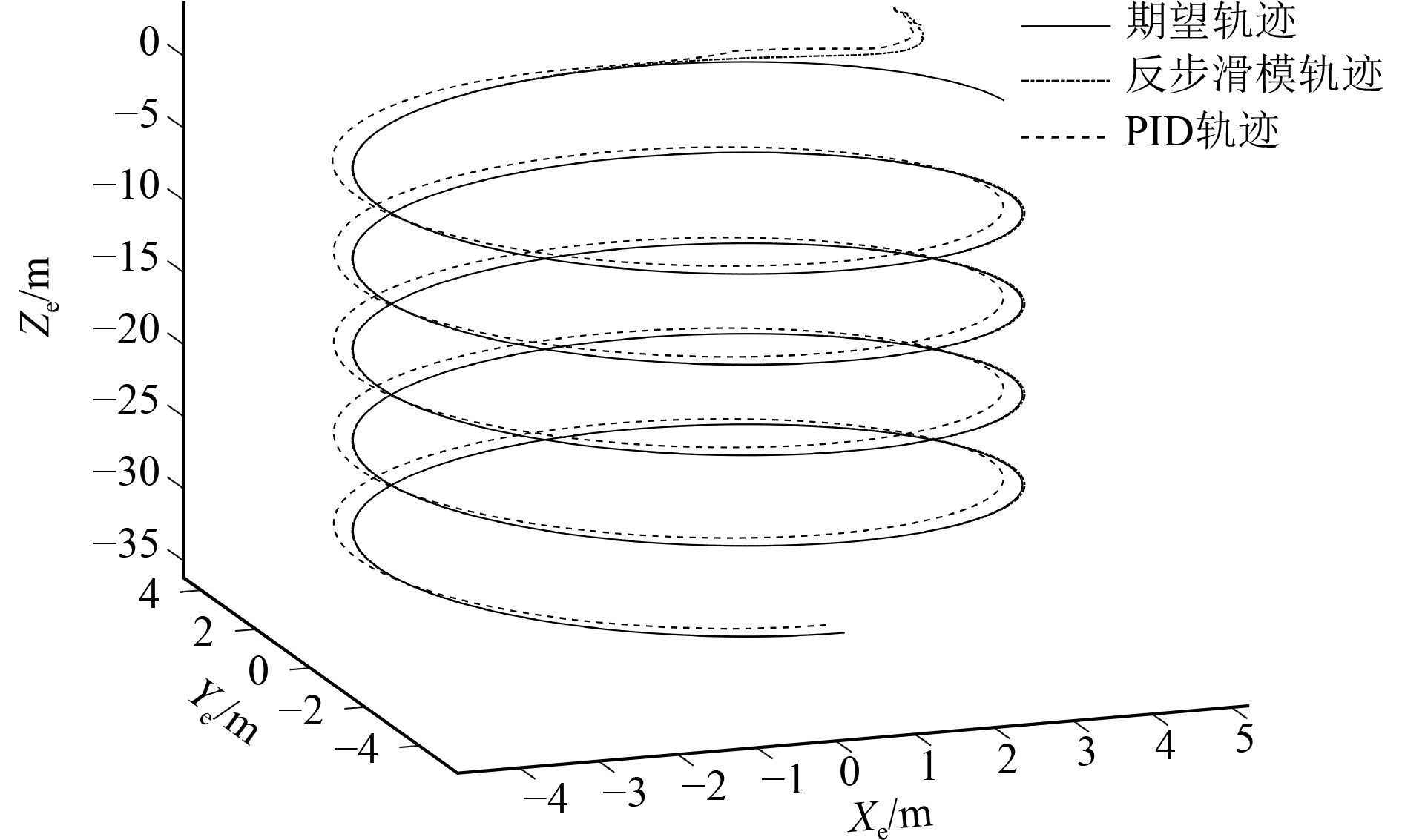
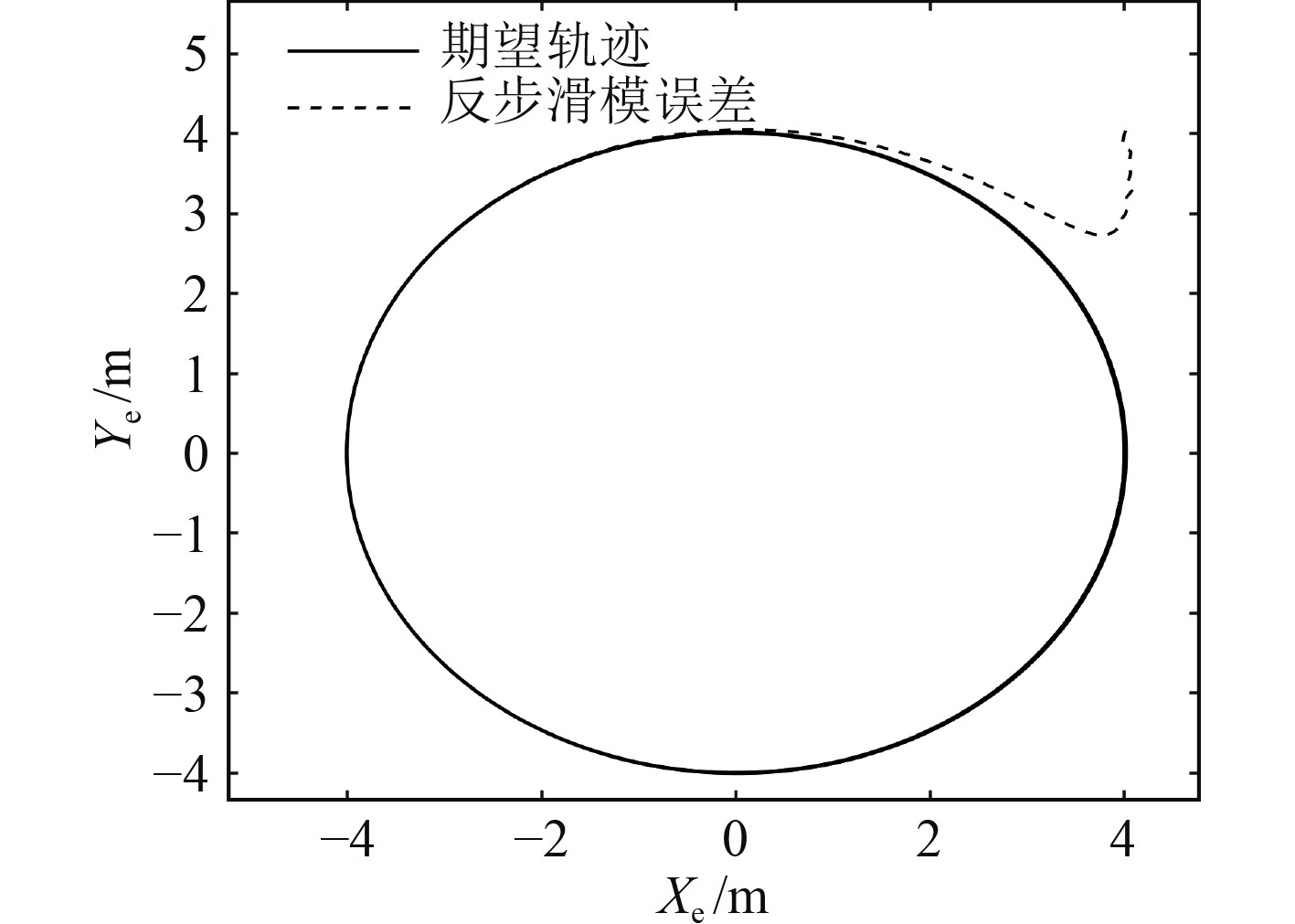
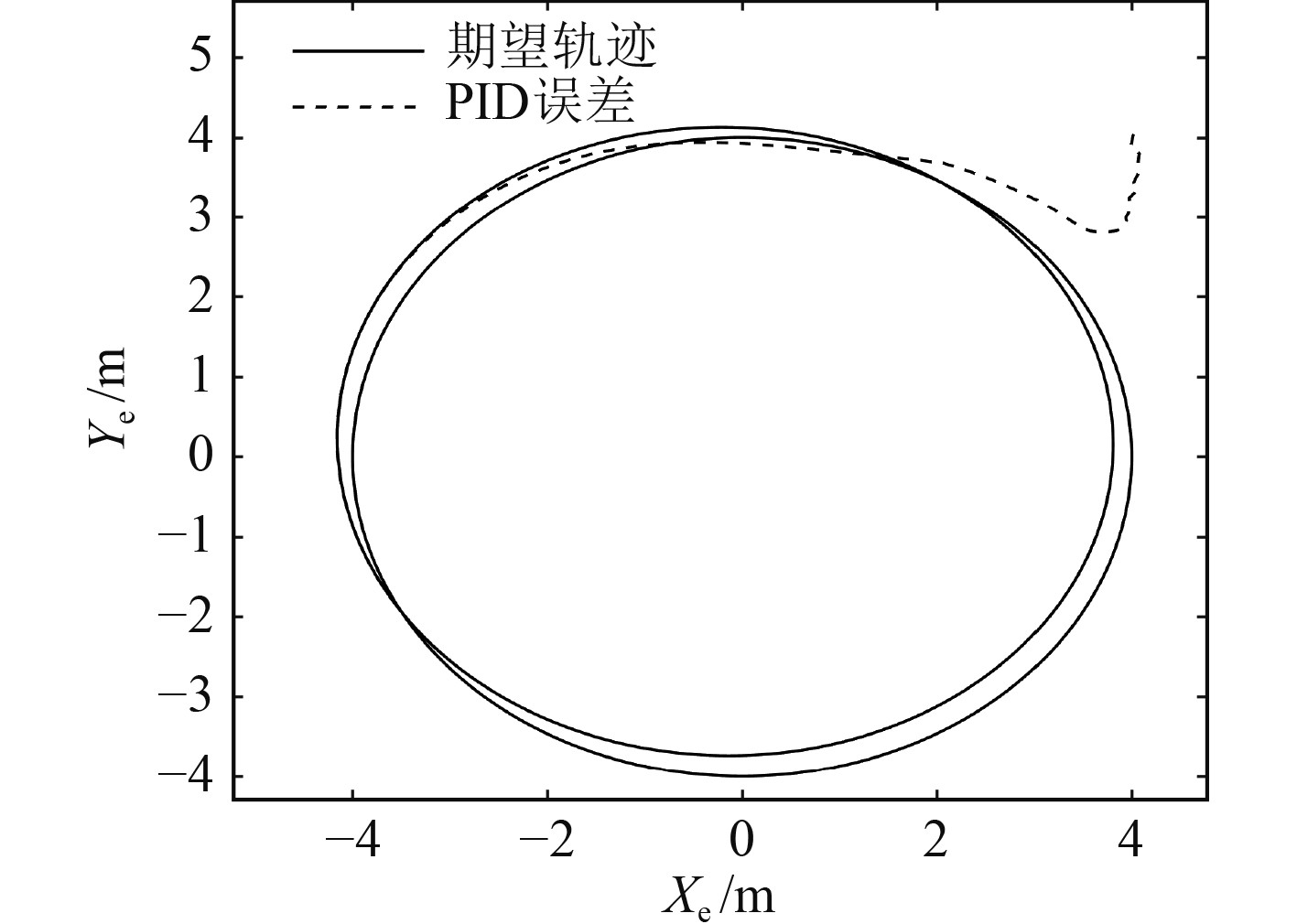
实验2　为验证基于NDO的反步滑模控制器在环境干扰下的鲁棒性，与传统PID控制器进行三维轨迹跟踪效果对比。图7为期望轨迹与在2种控制方法下的实际轨迹，可以看出传统PID控制能够完成控制要求，但存在较大的偏差，而基于NDO的反步滑模控制基本与期望轨迹重合，具有较好的控制能力。为更清楚地表达出2种控制器轨迹跟踪的区别，将三维轨迹分解成垂直面和水平面，如图8～图11所示。可以看出垂直面内，基于NDO的反步滑模控制器相较于传统PID控制器有更好的控制效果，实际轨迹基本与期望轨迹重合，而在传统PID控制器下 AUV 的实际轨迹与期望轨迹始终存在偏差。在水平面内，基于NDO的反步滑模控制器下AUV的实际轨迹依旧与期望轨迹基本重合，但传统PID控制器下AUV的实际轨迹与期望轨迹存在较大偏差。图12为在2种控制器下AUV的实际轨迹与期望轨迹的误差值，可以看出基于NDO的反步滑模控制器在3 s左右时，跟踪误差趋于稳定且收敛于零值附近，而传统PID控制器在航行前期对AUV有调节作用，但在稳定后始终存在误差，跟踪效果不佳。

实验仿真证明，基于NDO的反步滑模控制器相比于传统PID控制器有更好的轨迹跟踪能力，AUV可以获得稳定的控制效果。

4 结　语

针对AUV存在环境干扰时的三维轨迹跟踪问题，基于反步法和滑模控制理论，设计了基于NDO的反步滑模控制器，并通过仿真证明了该方法的有效性。实验1结果表明，NDO对时变干扰有较好的跟踪效果，可以对干扰做出准确的估计，防止环境干扰对AUV航行轨迹产生较大影响。实验2结果表明，基于NDO的反步滑模控制相较于传统的PID控制方法有较强的鲁棒性，控制效果更好。