0 引　言

无人船就是当下智能技术、科学技术创新的典型代表^[1]。目前，无人船在很多领域都得到了广泛应用。虽然无人船具有很多的优势，但是毕竟无人实时操作，运动稳定性难以保证，一旦遭遇恶劣天气，海浪波动较大，且这种波动对船舶影响是无规律的，因此无人船很难进行有效应对和控制，翻船事故时有发生^[2]。针对上述问题，无人船的运行控制成为无人船研究和升级的难点和重点。

目前，关于船舶运动控制的研究有很多，例如基于神经网络的控制模型、基于反馈线性化的控制方法以及模糊控制系统。其中，第1种是在已知船舶运动参数的基础上，利用神经网络3个层次的运算，通过强大的自学习能力，求取船舶运动最佳控制参数，最后将参数发送给船舶控制系统，实现船舶自动化控制^[3]。第2种针对负载力扰动，通过设计的基于反馈线性化的滑模控制器来跟踪船舶运动，以减少干扰到来的误差，实现运动补偿，完成船舶精确化运动控制^[4]。第3种是利用模糊控制模型进行控制，原理是通过计算预期和实际运动参数之间的误差，并进行模糊处理，通过模糊推理获取控制量^[5]。以上这些控制方法的提出虽然在一定程度上提高了无人船运动的稳定性，但是控制方面是有限的，而船舶的非线性运动多样，针对一种运动进行控制，得到的控制效果并不好。

针对上述问题，构建一种基于分数阶微积分的无人船运动非线性数学控制模型。通过该模型以期为无人船海上运动提供参考和借鉴，降低翻船事故发生率。

1 无人船运动非线性数学控制模型设计

无人船作为一种新型无人现场操控的船舶类型，在军民领域都发挥了重要作用。无人船由于无人在船上，可以实现零伤亡。然而，这类船舶的缺点也十分明显，无人现场操控意味着无法有效应对突发状况，对船舶的控制力不够，尤其遭遇风浪较大的天气时，船舶运动非常不稳，很容易发生翻船事故^[6]。针对这种现象，为提高无人船运动稳定性和可靠性，基于分数阶微积分设计一种控制模型。模型构建分为3部分，即无人船运动建模、无人船运动参数采集以及无人船运动非线性数学控制实现。

1.1 无人船非线性运动描述

在实际应用中，船舶的运动异常复杂，整个运动并不呈现线性规律分布，而是呈现非线性特征^[7]。无人船非线性运动主要包括6种类型，即纵荡，横荡，垂荡，横摇，纵摇和首摇，其描述如表1所示。

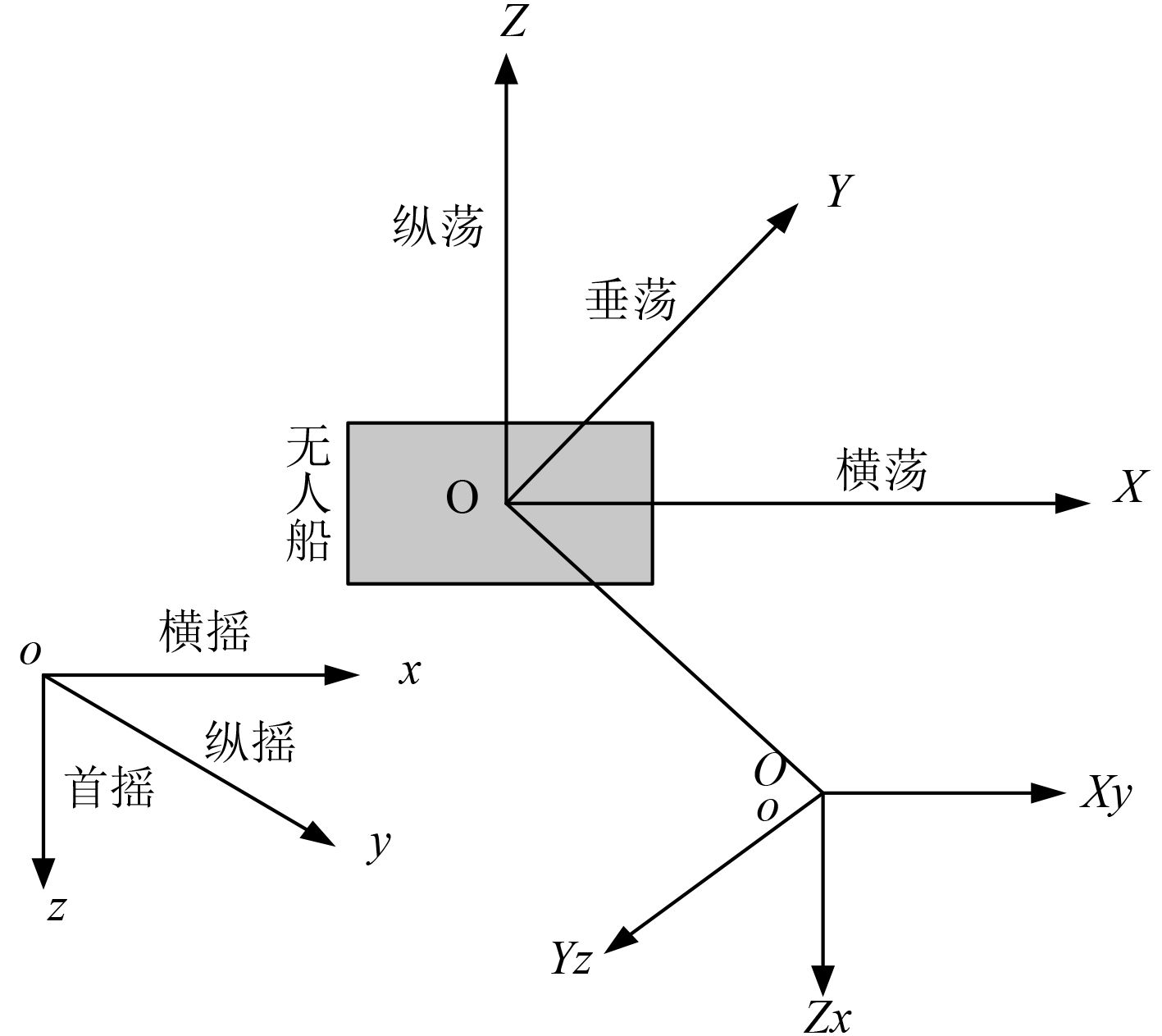
将上述这些非线性运动通过参考坐标系描述出来，如图1所示。可以看出，存在3个坐标系，O-XYZ代表附体坐标系；o-xyz代表绝对坐标系；Oo-XyYzZx代表平衡坐标系。这3个坐标系共同描述了无人船6种非线性运动。

针对6种无人船非线性运动类型，建立耦合模型，用于描述船舶运动几何的特征^[9]。

$ \begin{split} & F\left( {A,A1,A2,B,B1,B2} \right) = \hfill \\ & \frac{{g\left[ \begin{gathered} m\left( {X{\text{ + }}Y + Z} \right) + L\left( {u + v + w} \right) \hfill \\ + m\left( {K + M{\text{ + }}N} \right) + L\left( {p + q + r} \right) \hfill \\ \end{gathered} \right]}}{{m \cdot Q \cdot U}} 。\end{split} $

(1)

式中： $ F\left( {A,A1,A2,B,B1,B2} \right) $ 代表纵荡 $ A $ ，横荡 $ A1 $ ，垂荡 $ A2 $ ，横摇 $ B $ ，纵摇 $ B1 $ 和首摇 $ B2 $ 的耦合运动描述模型； $ m $ 代表船体质量； $ L $ 代表船舶排水量；g代表舵力中心至重心的垂向距离；Q代表静水力恢复力系数；U代表船体附加阻尼系数^[10]。

无人船非线性运动是无规律的，通过对6种运动进行具体描述，为后续运算和分析奠定基础。

1.2 无人船运动参数采集

触发无人船控制的关键是当前无人船运动状态超过稳定阈值，因此了解无人船运动参数是必要的。另外，当前运动参数为后续建立控制模型提供基础数据。需要采集的船舶运动参数包括6种，相应的采集方式如表2所示。

在完成数据采集之后，需要对数据进行去噪处理，保证数据的准确性。

1）输入原始含噪无人船运动参数数据为Y_i。

2）利用主成分分析方法对Y_i进行处理，并转换为矩阵的形式，记为R，公式为：

$ {\boldsymbol{R}} = \left[ \begin{array}{*{20}{c}} {r_{11}}&{{r_{12}}}&{...}&{{r_{1n}}} \\ {r_{21}}&{{r_{22}}}&{...}&{{r_{2n}}} \\ ... \\ {r_{m1}}&{{r_{m2}}}&{...}&{{r_{mn}}} \\ \end{array} \right]。$

(2)

式中：r_ij代表矩阵中第 $ i $ 行第 $ j $ 列的无人船运动数据主成分。

3）选择矩阵中前 $ k $ 个主成分，并让其保持不变。

4）将除了 $ k $ 个主成分外的所有主成分分量转换为二维图像形式，记为 $ H $ 。

5）利用K-SVD 算法对 $ H $ 进行去噪处理，去噪公式如下：

$ H' = \frac{{KT\sum {{r_{ij}}} }}{{\sqrt m }} 。$

(3)

式中： $ H' $ 代表去噪后的二维图像； $ K $ 代表稀疏系数； $ T $ 代表字典原子； $ m $ 代表矩阵 $ {\boldsymbol{R}} $ 中阵子的数量。

6）对去噪后的二维图像进行逆变换。

7）得到去噪后的无人船运动参数数据，完成去噪处理。此外，为保证不同数据具有统一性，需要去除其量纲。公式如下：

$ x' = \frac{{x - \phi }}{\varphi } 。$

(4)

式中： $ \phi $ ， $ \varphi $ 代表原始无人船运动参数数据均值和标准差。

通过采集到无人船运动参数能够明确了解无人船运动状态，为后续建立控制模型奠定基础。

1.3 无人船运动非线性数学控制实现

基于分数阶微积分构建控制模型，得出控制量，以此抵消掉无人船非线性运动带来摇荡能量。分数阶微积分是一种积分和微分混合优化的数学概念，随着不断的研究和发展，这一概念理论逐渐在诸多领域被应用。目前，最广泛的应用就是在控制器设计中，不仅能全面描述控制系统的动态特性，还能提高系统控制的灵活性和适用性，使得控制准确性更高。基于分数阶微积分理论进行无人船运动非线性数学控制，首先建立基于分数阶微积分的控制方程如下：

$ \left\{ \begin{gathered} {X_{t + 1}} = \frac{{P_\beta ^\alpha \left( {{V_t} + {C_t}\sqrt L + {G_t}} \right)}}{2}，\hfill \\ {Y_{t + 1}} = \sqrt {\frac{{f\left( {{D_t} \cdot {C_t}} \right)}}{2}} ，\hfill \\ {Z_{t + 1}} = \frac{{P\left( {{K_t} + {M_t} + {N_t}} \right)}}{{pqr}} 。\end{gathered} \right. $

(5)

式中：X_t+1，Y_t+1，Z_t+1代表t+1时刻x轴、y轴和z轴3个方向上的控制量； $ P_\beta ^\alpha $ 代表分数阶微积分算子；f代表分数阶微积分基本函数。

1）分数阶微积分算子描述为：

$ P_\beta ^{\alpha} = \left\{ \begin{aligned} & \dfrac{{{d^\alpha }}}{{d{t^\beta }}}, \alpha > 0，\\ &{1,} {\alpha = 0}，\\ &{\int_a^{\beta} {{{(d\eta )}^{\alpha} }} ,} {{\alpha} < 0} 。\end{aligned} \right. $

(6)

式中：α，β代表分数阶微积分算子的上下界；η代表算子阶次。

2）分数阶微积分基本函数描述为：

$ f = \sum\limits_{k = 0}^\infty {\frac{{{B^k}}}{{\lambda (\alpha k + \beta )}}} 。$

(7)

式中：B为复数；k为分数阶； $ \lambda $ 代表Gamma函数。

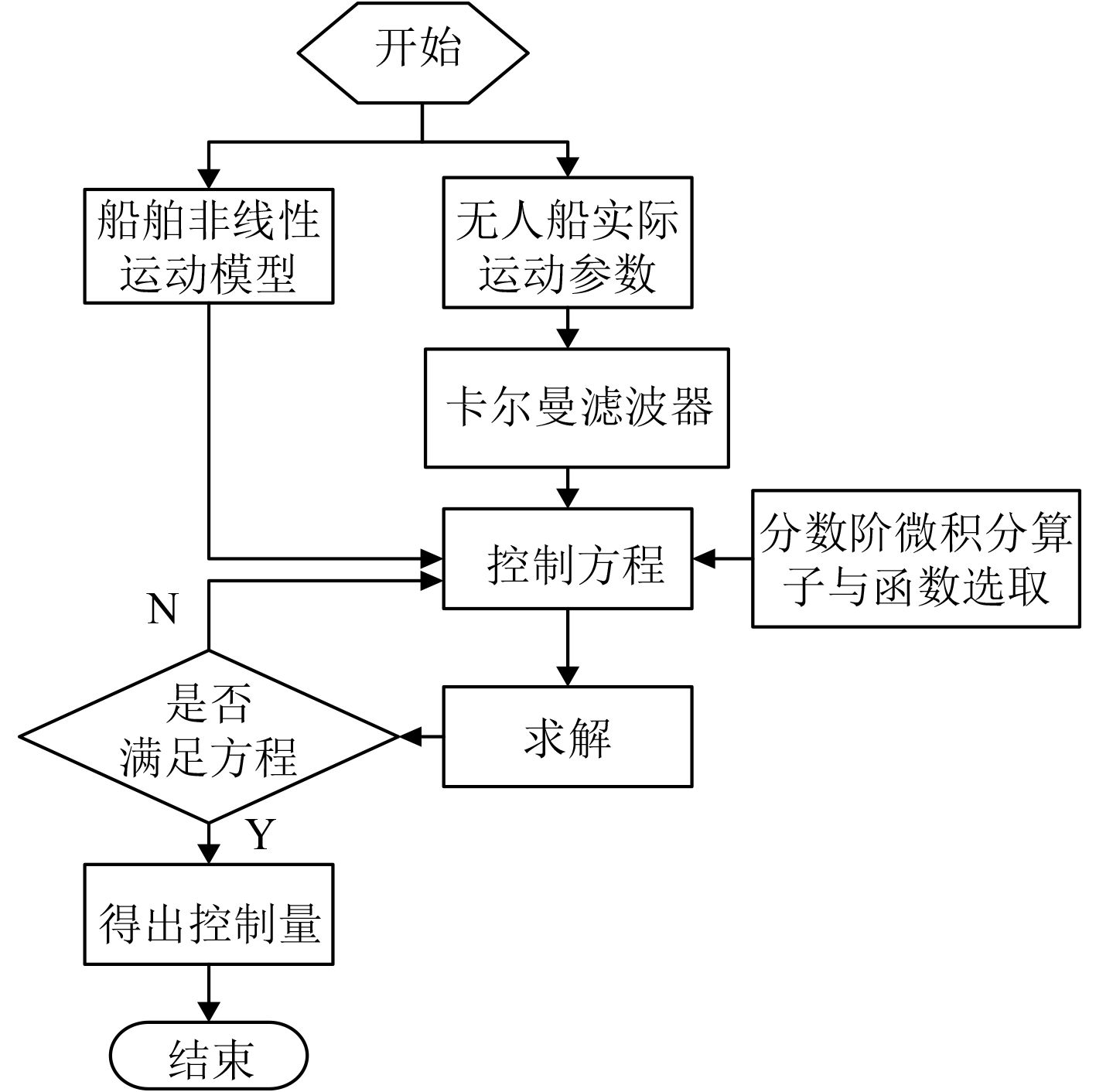
基于构建的分数阶微积分控制方程进行控制，具体过程如图2所示。最后利用预估-校正算法对方程进行数值近似估算，得出 $ t + 1 $ 时刻x轴、y轴和z轴3个方向上的控制量，完成控制模型构建。

2 模型测试与分析

为明确所研究控制模型的应用效果，与基于神经网络的控制模型、基于反馈线性化的控制方法以及模糊控制系统相比，进行模拟测试。

2.1 测试环境搭建

为测试所构建的基于分数阶微积分的无人船运动非线性数学控制模型的应用效果，以某船舶为原型，制作船舶模型，在实验室水池进行船舶运动控制实验。

2.2 工况相关参数设置

将风速风向仪、转速表、陀螺罗经、船舶惯性导航系统、功率指示器、GPS等设备安装在无人船模型上，采集船舶运动过程中的相关参数。结合设定的已知相关参数，工况相关参数如表3所示。

2.3 无人船运动控制量

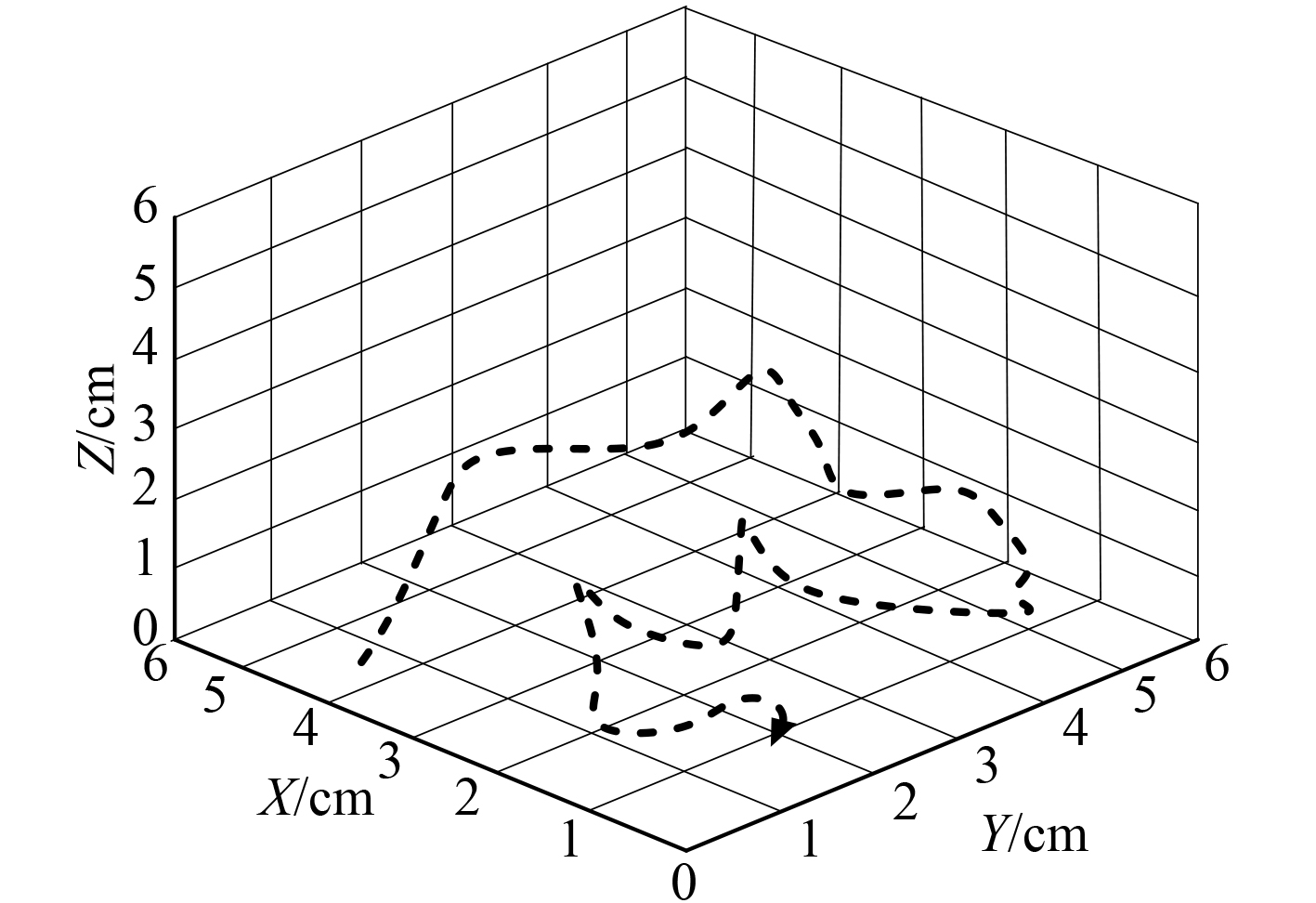
基于已知参数，利用预估-校正算法的求解方程(5)，得出x轴、y轴和z轴3个方向上3 min内的控制量，结果如图3所示。可以看出，在所模拟的工况下，无人船模型主要发生横向运动，所以控制量主要表现在X轴和Y轴，而纵向Z轴的运动波动较小，控制量数据也就相对较少。

2.4 控制效果分析

同样测试环境下，利用基于神经网络的控制模型、基于反馈线性化的控制方法以及模糊控制系统进行船舶运动控制。根据控制结果分析其减摇和减荡效果，结果如表4所示。可以看出，与基于神经网络的控制模型、基于反馈线性化的控制方法以及模糊控制系统相比，所构建模型应用下，减摇和减荡效果更强，说明更能保证船舶在大风、大浪情况下的稳定性，降低翻船事故。

3 结　语

本文设计一种基于分数阶微积分的无人船运动非线性数学控制模型。该模型通过在明确船舶运动参数的基础上，通过求取控制方程在3个方向上的控制量来控制船舶保持平衡。最后通过测试，纵荡，横荡，垂荡，横摇，纵摇和首摇6种运动的控制效果均达到70%以上，证明了所研究模型的控制效果，达到了目标。