水面无人艇由于具有速度快、体积小、运动灵活等优势,近年来在军用和民用领域的应用日益广泛。在大范围水域,使用无人艇尤其是使用多无人艇协同巡逻警戒,对进入任务区域的可疑目标进行协同警戒与跟踪监视,能够大幅提高巡逻警戒任务执行效率。针对该问题,本文定义了区域巡逻警戒任务及任务优化目标,在此基础上提出一种基于人工势场的多无人艇的分布式协同区域警戒跟踪算法,并进一步分析了算法的时间复杂性。算法针对任务定义的优化目标,基于环境感知数据和协同艇之间的交换信息,规划区域巡逻航路或目标跟踪航路。本文提出的分布式算法无需集中控制,每艘无人艇根据获得的信息独立决定任务执行状态,规划任务航路,协同完成区域警戒任务。
1 相关领域国内外研究现状多无人艇协同区域警戒是无线传感器网络领域的一种典型应用场景。在无线传感器网络领域,Mo Li等[1]提出了t-扫描区域覆盖的定义,提出最少传感器t-扫描覆盖问题,通过分析证明该问题是NP难问题,并将其转化为旅行商问题(traveling salesman problem, TSP)进行求解。该研究提出了集中式方案(CSWEEP)和分布式方案(GSWEEP)2种方案。Barun Gorain等[2]针对扫描覆盖问题,提出了一种3-近似算法。当兴趣点(point of interest, POI)具有不同扫描周期的情况时,对算法进行扩展以适应不同情况。最后证明如果传感器具有不同的移动速度,扫描覆盖问题不可收敛。Chuang Liu等[3]提出具有返回时间约束的扫描覆盖问题,并提出采用G-MSCR算法和MinD-Expand算法解决该问题。
Larson等[4] 基于A *算法设计了无人艇在受限时间条件下的路径规划算法。Liu等[5]提出了基于快速前进的无人艇编队路径规划算法,该算法在复杂的环境中也能有效的工作。Niu等[6]结合Voronoi图、能见度算法,提出了基于Dijkstra算法的无人艇路径规划算法。人工势场法常用于无人机[7]和无人艇[8]的局部路径规划算法中。
2 协同区域警戒算法定义协同区域警戒任务,重点针对多无人艇分布式协同区域警戒的算法进行分析研究,并对性能进行初步分析。
2.1 任务定义设无人艇的探测距离为rs、通信半径为rc > 2 rs。给定n艘无人艇和矩形警戒区域,协同区域警戒任务要求n艘无人艇协同配合,持续对任务区域执行警戒巡逻作业,对进入区域内的可疑目标进行跟踪监视直至其离开警戒区域。算法将任务区域划分为均匀栅格集合X,对每个栅格g∈X,x表示g的中心位置。
设Ui.pi(t)为无人艇Ui在t时刻的位置;oj.p(t)为目标oj在t时刻的位置;Ui.O (t)={ oj | Dist(Ui.p(t), oj.p(t)) ≤ rs; j = 1, 2, …, k}为无人艇Ui在t时刻发现的可疑目标集合,Ui.N(t) = { Uj | Dist(Ui.p(t), Uj.p(t)) ≤ rc; j = 1, 2, …, n且j ≠ i}为t时刻与无人艇Ui保持通信连接的无人艇集合。受无人艇的数量、探测距离和通信半径等因素限制,区域警戒任务有如下优化指标:
1)最小化警戒区域任意栅格被探测的最大时间间隔,即对
针对该指标,需优化每艘无人艇的巡逻航路,使警戒区域内的每个位置相邻2次被无人艇巡逻检查的时间间隔最短,优化该指标的目的是为尽早发现进入警戒区的可疑目标。
2)最大化能够同时被跟踪监视的可疑目标数量,对
针对该指标,需要持续预测可疑目标运动趋势并规划出每艘无人艇的跟踪航路,优化该指标的目的是确保任务区域内尽可能多的可疑目标能够被无人艇跟踪监视。
通过分析上述优化指标,2个指标的优化过程存在一定的冲突。因为,欲满足指标1)的相关要求,可能会使无人艇的航路存在偏离被跟踪目标的运动趋势,从而不能完全满足指标1的相关要求;欲满足指标2)的相关要求,无人艇的航路将受到其跟踪目标的约束,从而不能完全遵循指标2的相关要求。因此,多无人艇执行协同区域警戒任务时需要综合考虑合理优化上述2种指标,以确定任务执行的最优策略。
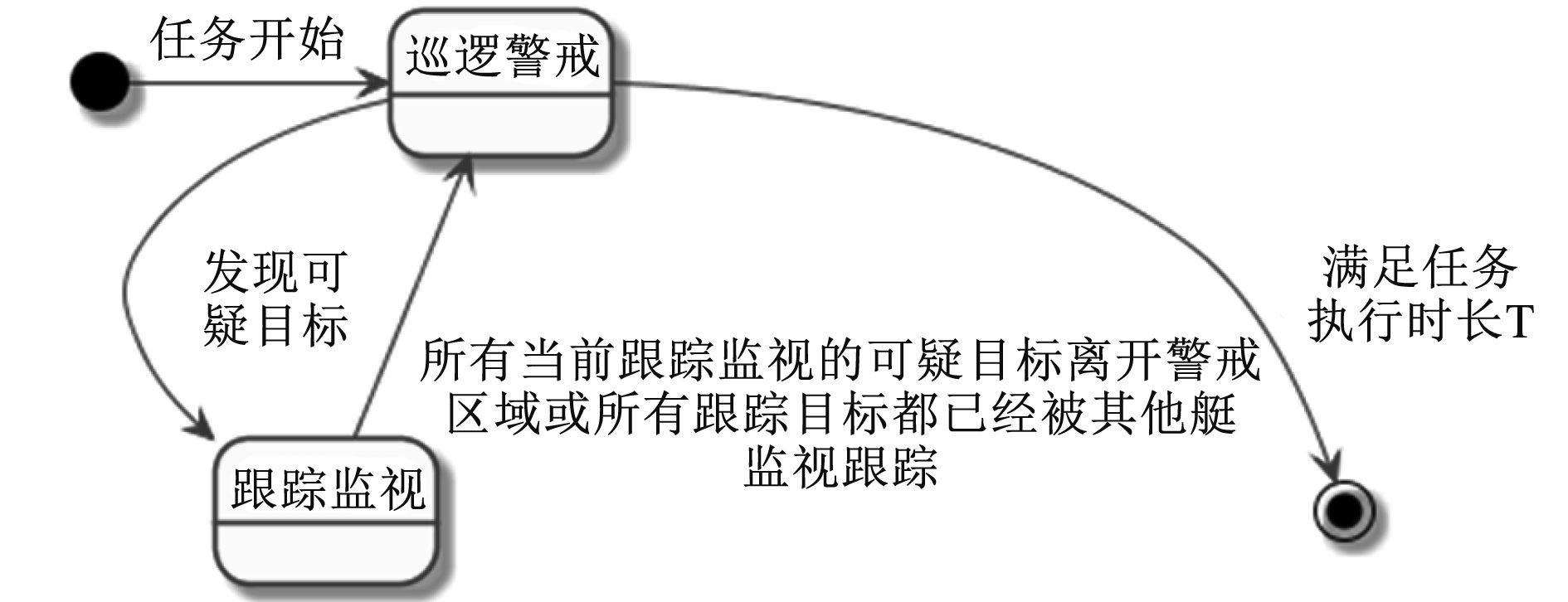
2.2 分布式协同区域警戒算法在任务执行过程中,无人艇可能处于巡逻警戒状态或跟踪监视状态。警戒巡逻警戒状态下,无人艇未发现进入任务区域的可疑目标,此时基于优化指标1来规划巡逻航路;跟踪监视状态下,无人艇正处于可疑目标跟踪状态,则基于优化目标2来规划监视跟踪航路。任务刚刚开始时,所有无人艇均处于警戒巡逻状态,一旦某艘无人艇发现可疑目标,则立即切换为跟踪监视状态。无人艇航行状态转换过程如图1所示。
|
图 1 无人艇航行状态转换图 Fig. 1 State transition of sailing USV |
在任务过程中,每艘无人艇都采用区域巡逻表来记录任务区域内每个栅格最近被探测的时刻。在时刻t,若栅格中心点x和无人艇Ui的距离Dist(x, Ui.p(t)) ≤ rs ,则认为该栅格在时刻t被探测过,则算法设置Ui的区域巡逻表中对应栅格x的记录Ui.g(x) = t。,并使算法始终保持记录栅格x最近一次被检测的时刻,同时每艘无人艇都会不断广播其区域巡逻表。无人艇Ui收到无人艇Uj广播的区域巡逻表后,会根据收到的信息维护其自身的区域巡逻表,确保每个栅格记录为其最近被检测的时间。设Ui.g(x) = t1,Uj.g(x) = t2,若t1 < t2,则算法更新Ui.g(x) = t2。
分布式协同区域警戒算法如下:
Area Guard(X, T)
输入:任务区域栅格集合X,任务执行时长T
输出:区域警戒航路Path
1)Path = φ;
2)无人艇状态 =“巡逻警戒”;
3)While 未达到任务执行时长T
4)根据当前位置及协作艇广播的信息计算并更新区域巡逻表;
5)If 未发现目标 then
6) If 无人艇状态 = “跟踪监视”then
7) 无人艇状态 = “巡逻警戒”;
8) End if
9) Path = Patrol Area(X);
10)Else //发现目标
11) If 无人艇状态 = “巡逻警戒”then
12) 无人艇状态 = “跟踪监视”;
13) End if
14) Path = Track Objects(X);
15) End if
16)执行区域警戒规划航路Path;
17)End While
2.2.1 区域巡逻警戒算法区域巡逻警戒算法基于人工势场法计算无人艇巡逻航路。每艘无人艇基于自身获取的数据以及协作无人艇推送的数据,独立进行航路规划。航路关键点为每个栅格的中心点,算法基于势函数来构建人工势场。无人艇需要巡逻的位置产生引力,其周边的障碍或协同无人艇产生斥力,每个无人艇的航路根据其所处位置的引力场势函数和斥力场势函数之和来计算。
引力场势函数基于优化指标1),引导无人艇选择巡逻收益最大的栅格。在时刻t,无人艇Ui可巡逻栅格集合Gi(t)为:
| $ \left\{ \begin{array}{*{20}{l}}{G}_{i}\left(t\right)=\left\{ x|{\rm{Dist}}\left(x,{U}_{j} \cdot p\left(t\right)\right)\geqslant {\rm{Dist}}\left(x,{U}_{i} \cdot p\left(t\right)\right) >{r}_{s}, \right. \\ \left. {U}_{j}\in {U}_{i}\cdot N\left(t\right)\right\}{U}_{i}\cdot N\left(t\right)\ne \varnothing ,\\ {G}_{i}\left(t\right)=\left\{x|Dist\left(x,{U}_{i}\cdot p\left(t\right)\right) > {r}_{s}\right\}{U}_{i}.N\left(t\right)=\varnothing 。\end{array}\right. $ | (1) |
对任意栅格x,Ui的巡逻收益函数定义如下:
| $ \delta \left(x,{U}_{i},t\right)={\left(t-{U}_{i}.g\left(x\right)\right){\rm{Dist}}\left(x,{U}_{i}.p\left(t\right)\right)}^{\alpha },$ | (2) |
于是,在栅格集合Gi(t)中算法选择使Ui巡逻收益最大的栅格x*作为Ui的巡逻目标,即
| $ {x}^{*}=\underset{x\in {G}_{i}\left(t\right)}{\mathrm{arg max}}\delta \left(x{,U}_{i},t\right) ,$ | (3) |
引力场势函数定义如下:
| $ {Q}_{att}^{i}\left(p\right)=\left\{\begin{array}{*{20}{l}} \dfrac{1}{2}\xi {{\rm{Dist}}\left(p,{x}^{*}\right)}^{2}&{\rm{Dist}}\left(p,{x}^{*}\right)\leqslant {D}^{*},\\ {D}^{*}\lambda {\rm{Dist}}\left(p,{x}^{*}\right)-\frac{1}{2}\xi {\left({D}^{*}\right)}^{2} & {\rm{Dist}}\left(p,{x}^{*}\right) > {D}^{*}。\end{array}\right. $ | (4) |
其中,D*为引力作用阈值范围。当Dist(p, x*) ≤ D*时,引力势能的大小与当前位置到的距离平方x*成正比;当Dist(p, x*) > D*时,降低引力函数的取值,避免远离x*时引力过大。引力场势函数的梯度函数为
斥力场势函数综合考虑了Ui附近无人艇对其航行的潜在影响。设斥力函数f(z,d)定义如下,η为增益常数。
| $ f\left(z,d\right)=\left\{\begin{array}{*{20}{l}}\dfrac{1}{2}\eta {\left(\dfrac{1}{z}-\dfrac{1}{d}\right)}^{2} & 0\leqslant z\leqslant d,\\ 0& z > d。\end{array}\right. $ | (5) |
设t时刻无人艇Ui位于位置Ui.p(t),斥力势函数为:
| $ \begin{array}{cc}{Q}_{rep}^{i}\left(p\right)= \displaystyle\sum _{{U}_{j}\in {U}_{i}.N\left(t\right)}f\left(Dist\left(p,{U}_{j}.p\left(t\right)\right),{d}^{*}\right)0 < {d}^{*}\leqslant {2r}_{s}。\end{array} $ | (6) |
其中,d*为斥力作用阈值范围,在该范围内障碍物才产生斥力,超出该范围则不产生斥力作用。斥力势函数的梯度函数为
综上,将引力场和斥力场叠加就形成了人工势力场。无人艇Ui所在位置的势力场函数定义如下:
| $ \begin{array}{cc}{Q}^{i}\left(q\right)= {Q}_{att}^{i}\left(q\right)+{Q}_{rep}^{i}\left(q\right),\end{array} $ | (7) |
| $ {F}^{i}\left(q\right)= -\nabla {Q}^{i}\left(q\right)=-\left({\nabla Q}_{att}^{i}\left(q\right)+{\nabla Q}_{rep}^{i}\left(q\right)\right) 。$ | (8) |
算法从无人艇Ui当前位置开始计算,沿着负梯度方向不断前进,直至达到梯度为0的位置。
区域巡逻警戒算法如下:
Patrol Area (X)
输入:任务区域栅格集合X
输出:巡逻警戒航路Path
1)Path = φ;
2)If 未发现可疑目标 then
3) 根据式(1)计算可巡逻栅格集合Gi(t);
4) 根据式(3)计算巡逻收益最大的栅格x*;
5) 基于人工势力场函数计算巡逻警戒航路Path;
6)End if
7)输出Path
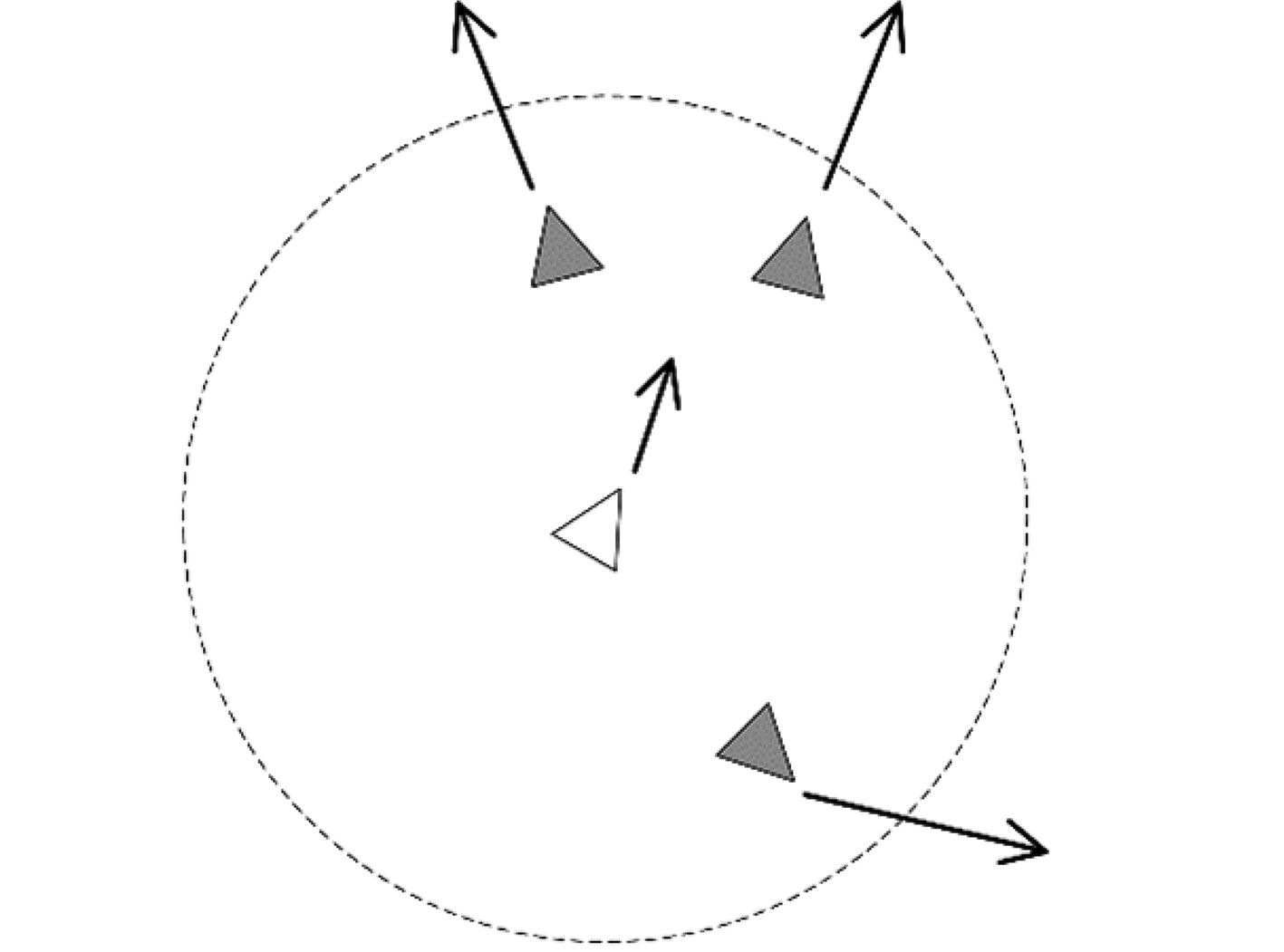
2.2.2 目标跟踪监视算法目标跟踪监视算法基于优化指标2)完成航路规划。当无人艇发现进入任务区的目标后将对其进行持续跟踪监视。由于可疑目标的运动轨迹无法预知,因此只能假设其短时间内保持当前速度不变,并依据此预测下一时刻的目标位置,目标跟踪示意图如图2所示。基于所有当前跟踪目标的预测位置,算法保留所有预测位置仍位于任务区内的目标,计算相关目标预测位置的中心点,并以该中心位置作为目标未来位置,使用人工势场法计算无人艇的跟踪监视航路。
|
图 2 目标跟踪示意图 Fig. 2 Target tracking sketch map |
目标跟踪监视算法如下:
Track Objects (X)
输入:任务区域栅格集合X
输出:目标跟踪监视航路Path
1)Path = φ;
2)计算当前感知目标预测位置;
3)计算预测位置在任务区外内的目标集合中心点位置ρ;
4)将位置ρ作为航路终点,采用与3.2.1节类似的方法计算航路Path;
5)输出Path
2.2.3 算法时间复杂性分析区域巡逻警戒算法步骤3~步骤5均需扫描任务区划分的栅格集合X并进行相应计算,其计算时间复杂性为O(|X|)。
设M为同时进入任务区域的最大目标数,目标跟踪算法2−3步骤需要计算当前跟踪的目标位置,时间复杂性为O(M)。步骤4计算航路的时间复杂性为O(|X|)。通常栅格不会划分的过少,可认为|X|>M。因此,目标跟踪算法的时间复杂性为O(|X|)。
分布式协同区域警戒算法步骤4执行需接收协同艇发来的区域巡逻表并更新本地记录,故时间复杂性为O(n|X|)。因此,每艘艇上执行的分布式协同区域警戒算法的时间复杂性为O(nT|X|)。
3 结 语针对多无人艇协同区域警戒任务,提出了基于人工势场的巡逻警戒算法和目标跟踪算法,并对算法的时间复杂性进行分析。本文提出的分布式算法,无需通过集中式的任务协调节点对巡逻警戒任务进行统一协调,无人艇各自独立执行算法即可完成区域协同警戒任务,因此能够将任何一艘无人艇受损退出任务后产生的不利影响降至最低,提高多无人艇机动部署的灵活性和局部无人艇受损后其他无人艇动态重组的灵活性,为多无人艇大范围水域灵活部署以及任务执行效率提高等应用提供参考。
| [1] |
LI M, CHENG W, LIU K, et al. Sweep coverage with mobile sensors[J]. IEEE Transactions on Mobile Computing, 2011, 10(11): 1534-1545. DOI:10.1109/TMC.2010.237 |
| [2] |
GORAIN B, MANDAL PS. Approximation algorithm for sweep coverage on graph[J]. Information Processing Letters, 2015, 115(9): 712-718. DOI:10.1016/j.ipl.2015.03.011 |
| [3] |
LIU C, DU H, YE Q. Sweep coverage with return time constraint[C]//2016 IEEE Global Communications Conference, 2016: 1–6.
|
| [4] |
LARSON J, BRUCH M, EBKEN J. Autonomous navigation and obstacle avoidance for unmanned surface vehicles[C]//Proc eedings SPIE, 2006: 1–12.
|
| [5] |
LIU Y and BUCKNALL R. Path planning algorithm for unmanned surface vehicle formations in a practical maritime environment[C]//Ocean Engineering, 2015(97): 126–144.
|
| [6] |
NIU H, LU Y, SAVVARIS A, et al. Efficient path planning algorithms for unmanned surface vehicle[J]. IFAC-Papers On Line, 2016, 49(23) : 121–126.
|
| [7] |
闫军涛, 李御驰, 宋志华, 等. 基于改进人工势场方法的无人机覆盖航路规划算法研究[J]. 运筹与模糊学, 2019, 9(4): 264-270. |
| [8] |
王金龙, 无人艇航路规划的算法研究[D]. 长春: 吉林大学, 2019.
|
 2022, Vol. 44
2022, Vol. 44
