路径跟踪是船舶运动控制中的重要内容,可以实现船舶从地图上任意位置作为起点,通过控制系统的控制,使得船舶能够跟踪并最终稳定在期望跟踪路径上,而且不受时间的限制。路径跟踪是船舶导航系统中重要的组成部分[1-2],目前关于船舶路径跟踪的研究中,大多使用直线或者简单的三角函数曲线作为给定路径进行跟踪,没有参考真实的海洋环境,研究内容过于理想化,实际应用性较差。本文将采用路径规划生成的航线作为输入信号,对船舶进行路径跟踪,对于海上航行有重要意义。
制导算法一直都是船舶运动控制的重要研究模块,视线制导方法(line of sight,LOS)是一种应用广泛的船舶制导算法,其主要应用在船舶直线路径跟踪中[3]。LOS算法的原理是将船舶位置映射为船舶首向角,通过实时提供期望首向角,使船舶平滑地行驶在路径上。Healey等[4]首先利用LOS制导律对船舶进行控制,Fossen等[5]运用LOS算法进行船舶路径跟踪,将输出空间减少为两自由度,并且利用矢量反演法开发了一种动态反馈的非线性控制器。上述算法虽然具有控制器简单、算法有效等优点,但其不能实时调整位置误差。Ryeok等[6]提出一种模型预测控制的方法,将前视距离加入到控制器中,使得船舶能根据预测信号调整位置,提高了跟踪效能。朱骋等[7]基于Mamdani模型调整了LOS控制策略,通过自适应模糊控制修正LOS控制参数,改进了传统LOS算法各项参数固定,不能实时调整的特点。
上述算法在建模时没有考虑风、浪、流等真实海洋因素的影响,实用性较差,船舶在大洋航行时路径跟踪困难。为了解决这个问题,Qiu等[8]采用了轨迹线性化控制技术及有限时间干扰观测器,可以准确地观测到不确定的动态因素和未知的外界干扰,提升了路径跟踪的准确性,实现了期望的路径跟踪。Liang等[9]提出了一种模糊反步滑模控制器,该控制器可以抑制外部干扰和避免抖震,实现水下船舶对三维路径的精确跟踪。沈智鹏等[10]使用神经元自适应迭代滑模控制方法,补偿船舶受到的内外扰动和系统建模不确定项,解决了复杂海洋环境干扰下船舶的路径跟踪问题。Fossen等[12]针对风浪流等因素产生的船舶航行漂角问题,将自适应理论与LOS制导律结合,此方法将漂角看作常量引入到LOS制导律中,有效补偿了由于海洋环境引起的漂角,增强了控制器的鲁棒性。
路径规划及跟踪控制是指船舶根据任务需要规划出最优航线,并沿着期望航线航行到目标点。Shen等[13]结合样条路径模板对船舶进行路径规划,利用非线性模型预测控制技术进行船舶路径跟踪,提高了算法的抗干扰性和运行效率。张力行[14]将A*算法与COLREGs相结合对欠驱动船舶进行路径规划,然后将LOS与神经网络控制器结合解决了欠驱动船舶路径跟踪的问题,这种方法在多种海洋环境的仿真实验中行之有效。
综合上述文献可以看出,目前船舶路径规划及跟踪控制中还存在着算法缺陷[15-16]、路径不平滑[17]和路径跟踪信号为虚拟信号等问题。本文使用人工势场法改进统蚁群算法,弥补了传统蚁群算法的不足。并在此基础上对改进蚁群算法规划出的路径进行路径拟合,将拟合后的平滑路线作为输入信号进行路径跟踪,使用双环闭合控制系统作为运动学控制子系统,对船舶进行路径跟踪。使用神经网络对动力学子系统的不确定项进行逼近,实现了对内外扰动及未建模动态的补偿,有效跟踪了运动学控制子系统给出的期望速度。
1 基于改进蚁群算法的船舶路径规划在传统蚁群算法初期,各个路径上的信息素浓度都相等,蚂蚁搜索目标点的随机性比较大,通过引入人工势场法,提高了蚁群算法的搜索效率;蚁群算法依靠蚂蚁个体进行独立的路径搜索,通过蚂蚁间的信息素交换逐步优化路径,避免了人为的干预,算法的全局搜索能力和鲁棒性较好,可以有效解决人工势场法目标不可达和陷入局部最小值等问题。为了让蚂蚁获得更出色的路径寻优能力,本文通过4种方式改进蚁群算法:
1.1 改变信息素的更新策略蚁群算法中信息素浓度可以决定蚂蚁的走向,是一个非常重要的环节。在算法开始时,蚂蚁会随机选择路径进行搜索,部分蚂蚁可能会选择离目标点比较长的路径更新信息素,这会误导后续蚂蚁的路径选择,导致最优路径收敛缓慢,针对这个问题,本文进行以下改进:
由于人工势场法在蚁群算法前期对蚂蚁有指导作用,可以使用人工势场法改进信息素:
| $ {\tau ''_{ij}}\left( h \right) = \left\{ \begin{array}{*{20}{l}} {\tau _{ij}}\left( h \right) + \delta {{\tau '}_{ij}}\left( h \right),&h \leqslant {h_a} ,\\ {\tau _{ij}}\left( h \right){\text{,}}&h > {h_a} 。\end{array} \right. $ | (1) |
式中:
当信息素浓度过大或过小,蚂蚁会停止搜索目标点,导致算法不能正常运算下去。为了避免出现这个问题,引入信息素的浓度极值
| $ {\tau ''_{ij}}\left( h \right) = \left\{ \begin{array}{*{20}{l}} {\tau _{\min }}{\text{,}}\qquad \;\;&{{\tau ''}_{ij}}\left( h \right) < {\tau _{\min }},\\ {{\tau ''}_{ij}}\left( h \right),&{\tau _{\min }} < {{\tau ''}_{ij}}\left( h \right) < {\tau _{\max }} ,\\ {\tau _{\max }}{\text{,}}&{{\tau ''}_{ij}}\left( h \right) > {\tau _{\max }} 。\end{array} \right. $ | (2) |
信息素挥发系数
| $ \lambda = 1 - {e^{\frac{{{N_c} - {N_{\max }}}}{{{N_{\max }}}}}} ,$ | (3) |
| $ \rho ' = \left\{ \begin{array}{*{20}{l}} {\rho _{\min }}{\text{,}}\qquad &\rho < {\rho _{\min }} ,\\ \lambda \times \rho, &{\rho _{\min }} < \rho < {\rho _{\max }} ,\\ {\rho _{\max }},&\rho > {\rho _{\max }} 。\end{array} \right. $ | (4) |
| $ {\tau ''_{ij}}\left( h \right) = \left\{ \begin{array}{*{20}{l}} {\tau _{\min }}{\text{ ,}}\quad &{{\tau ''}_{ij}}\left( h \right) < {\tau _{\min }} ,\\ {{\tau ''}_{ij}}\left( h \right), {\tau _{\min }} < {{\tau ''}_{ij}}\left( h \right) < {\tau _{\max }} ,\\ {\tau _{\max }}{\text{,}}&{{\tau ''}_{ij}}\left( h \right) > {\tau _{\max }} 。\end{array} \right. $ | (5) |
式中:
经过以上改进:
| $ {\tau _{ij}}\left( {h + 1} \right) = \left( {1 - \rho '} \right){\tau ''_{ij}}\left( h \right) + \Delta {\tau _{ij}}\left( h \right) 。$ | (6) |
传统蚁群算法的启发函数由欧氏距离决定,主要依靠启发信息指导蚂蚁进行路径搜索,信息素浓度会随着蚂蚁迭代次数的增多而增大,但是启发信息一直保持着初始值,对蚂蚁的指导作用越来越小。而且在计算启发信息时,没有考虑到欧氏距离中障碍物对蚂蚁的影响,会使算法陷入局部最优解。为了解决上述问题,用人工势场法干预传统蚁群算法中启发信息的计算,表达式如下:
| $ {\eta _A}\left( t \right) = {a^{{F_{total}}(P)\cos \varphi }} 。$ | (7) |
式中:
信息素浓度在算法初期比较低,势场启发信息前期对蚁群的指导作用比较重要,但是前期信息启发信息值较小,后期信息素浓度较大,势场启发函数作用较小。为了增强前期的信息启发信息,削弱后期启发信息,启发信息值的大小由势场启发信息因子控制:
| $ \sigma = \frac{{{N_{\max }} - {N_c}}}{{{N_{\max }}}} ,$ | (8) |
式中:σ代表势场启发信息因子,且
改进后的启发函数为:
| $ {\eta '_{ij}}\left( t \right) = \frac{{{a^{{F_{total}}\left( P \right)\cos \varphi }}}}{{{d_{ij}}}} \times \frac{{{N_{\max }} - {N_c}}}{{{N_{\max }}}} 。$ | (9) |
由上式可以看出,当船舶处于人工势场法合力为零的点时,启发信息不为0,依然可以指导船舶前进,解决了人工势场法中目标不可达的问题。此时状态转移规则更新为:
| $ P_{ij}^k(t) = \left\{ {\begin{array}{*{20}{l}} {\frac{{{{\left[ {{\tau _{ij}}(t)} \right]}^\alpha }{{\left[ {{{\eta '}_{ij}}(t)} \right]}^\beta }}}{{{{\displaystyle\sum\limits_{s \subset allowe{d_k}(t)} {\left[ {{\tau _{is}}(t)} \right]} }^\alpha }{{\left[ {{{\eta '}_{is}}(t)} \right]}^\beta }}}\;\;,\quad j \in allowe{d_k}(t)\quad } ,\\ {0,\quad \qquad \quad \quad \quad \quad \quad \quad \quad \;\,\quad j \notin allowe{d_k}(t)} 。\end{array}} \right. $ | (10) |
此外,算法在迭代后期,随着选择路径的减少,所需要的蚁群规模也会相应的减少。因此可以用迭代次数影响蚁群规模,让蚁群规模随着迭代次数的增加而减少,并设置最小蚁群规模:
| $ m = \left\{ {\begin{array}{*{20}{l}} m \times \dfrac{{{N_{\max }} - {N_c}}}{{{N_{\max }}}},& m > {m_{\min }} ,\\ {m_{\min }},& m \leqslant {m_{\min }} 。\end{array}} \right. $ | (11) |
式中,
在传统人工势场法中,斥力函数是障碍物与船舶间距离的倒数取二次方,斥力势场影响的范围比较广,并且斥力势场容易产生波动,致使船舶在很短的时间内无法做出避碰行动。为了解决上述问题,本文引入斥力指数改进斥力函数:
| $ {U_{rep}}^\prime \left( P \right) = \left\{ \begin{array}{*{20}{l}} \dfrac{1}{2}{k_{rep}}{e^{ - d{{\left( {P,O} \right)}^2}}},\, & d\left( {P,O} \right) \leqslant {d_0} ,\\ 0 , & d\left( {P,O} \right) > {d_0} 。\end{array} \right. $ | (12) |
当目标点附近有一个体积较大的障碍物时,由于船舶和障碍物的距离很近,此时障碍物对船舶的斥力很大,导致船舶不能到达目标点。针对以上问题,引入斥力势场系数
| $ \begin{split} {U_{rep}}^{\prime \prime }\left( P \right) =& \xi {U_{rep}}^\prime \left( P \right) = \\ &\left\{ \begin{array}{*{20}{l}} \dfrac{1}{2}{k_{rep}}d{\left( {P,G} \right)^2}{e^{ - d{{\left( {P,O} \right)}^2}}}, & d\left( {P,O} \right) \leqslant {d_0} ,\\ 0{\text{,}} & d\left( {P,O} \right) > {d_0} 。\end{array} \right. \\[-25pt] \end{split}$ | (13) |
改进后的斥力函数为:
| $\begin{split} {F'_{rep}}\left( P \right) &= - \nabla {U_{rep}}^{\prime \prime }\left( P \right) =\\ &\left\{ \begin{array}{*{20}{l}} {k_{rep}}d{\left( {P,G} \right)^2}d\left( {P,O} \right){e^{ - d{{\left( {P,O} \right)}^2}}}{n_{OP}},& d\left( {P,O} \right) \leqslant {d_0} ,\\ 0,& d\left( {P,O} \right) > {d_0} 。\end{array} \right. \end{split}$ | (14) |
从式中可以看出,当船舶与障碍物距离为0时,船舶受到障碍物的斥力也为0,解决了陷入局部最优和目标不可达等问题。
人工势场法合力函数为:
| $ {F'_{total}}\left( P \right) = {F'_{rep}}\left( P \right) + {F_{att}}\left( P \right) 。$ | (15) |
为了实现
| $ \left\{ {\begin{array}{*{20}{c}} {{{\dot x}_e} = U\cos \theta - {{\dot x}_d}} ,\\ {{{\dot y}_e} = U\sin \theta - {{\dot y}_d}} ,\end{array}} \right. $ | (16) |
当
| $ \left\{ {\begin{array}{*{20}{l}} {U\cos \theta }& = &{{u_1}} ,\\ {U\sin \theta }& = &{{u_2}} ,\end{array}} \right. $ | (17) |
针对
| $ {\dot s_1} = {\dot x_e} = {u_1} - {\dot x_d} ,$ | (18) |
控制律为:
| $ {u_1} = {\dot x_d} - {k_1}{s_1} ,$ | (19) |
式中,
通过以上求解,可以得到
针对
| $ {\dot s_2} = {\dot y_e} = {u_2} - {\dot y_d} ,$ | (20) |
设计控制律为:
| $ {u_2} = {\dot y_d} - {k_2}{s_2} ,$ | (21) |
式中,
通过以上求解,可以得到
由式(17)可以得到
| $ \theta = \arctan \frac{{{u_2}}}{{{u_1}}} 。$ | (22) |
求得的
| $ {\theta _d} = \arctan \frac{{{u_2}}}{{{u_1}}},$ | (23) |
式中,
综上所述,可以得到实际的位置控制律为:
| $ U = \frac{{{u_1}}}{{\cos {\theta _d}}} 。$ | (24) |
当
| $ {\dot s_3} = {\dot \theta _e} = r - {\dot \theta _d} ,$ | (25) |
姿态控制律为:
| $ \omega = {\dot \theta _d} - {k_3}{s_3} - {\eta _3}{{\rm{sgn}}} {s_3} 。$ | (26) |
式中,
通过以上求解,可以得到
取Lyapunov
本文的控制系统是由内外环构成的闭环系统,内环系统为姿态子系统,外环系统为位置子系统,指令信号

|
图 1 具有双环的闭环系统结构 Fig. 1 Closed loop system structure with double loops |
在真实的海洋环境航行时,船舶容易受到海洋环境的干扰,使得船舶运动具有典型的不确定性、大惯性、长时滞等特点。参考文献[17],设计基于径向基神经网络的船舶动力学滑膜控制器,跟踪运动学制导律给出的期望速度。
将设计拓展到动力学控制,动力学控制器的目标是跟踪制导律给定的参考速度。船舶动力模型可以表示为:
| $ \left\{ {\begin{array}{l} {{m_u}\dot u = {f_u}\left( {u,\nu ,r} \right) + {\tau _u} + {\tau _{{\text{nw}}}}},\\ {{m_\nu }\dot v = {f_\nu }\left( {u,\nu ,r} \right) + {\tau _{\nu w}}} ,\\ {{m_r}\dot r = {f_r}\left( {u,\nu ,r} \right) + {\tau _r} + {\tau _{nv}}} ,\end{array} } \right. $ | (27) |
由于
| $ \begin{split} {\dot u = \dot U\cos \left( \theta \right) - U\sin \left( \theta \right)} = { \dot U - 2\dot U{{\sin }^2}\left( {\dfrac{\theta }{2}} \right) - U\sin \left( \theta \right)} 。\end{split} $ | (28) |
可以得到
| $ \left\{ {\begin{array}{*{20}{l}} {{m_u}\dot U = {f_u}\left( {u,\nu ,r} \right) + {u_u} + {u_{dw}} + 2{m_u}\dot U{{\sin }^2}\left( {\dfrac{\theta }{2}} \right) + {m_u}U\sin \left( \theta \right)} ,\\ {{m_r}\dot r = {f_r}\left( {u,\nu ,r} \right) + {u_r} + {u_{rw}}} 。\end{array} }\right. $ | (29) |
动力学控制器的控制目的是让船舶跟踪期望前向速度与期望角速度,即
| $ \left\{\begin{array}{l}\underset{t\to \infty }{\mathrm{lim}}\left|{U}_{t}-U\right|\leqslant {\delta }_{1}\hfill,\\ \underset{t\to \infty }{\mathrm{lim}}\left|r-{r}_{r}\right|\leqslant {\delta }_{2},\hfill \end{array}\right. \left\{\begin{array}{l}\underset{t\to \infty }{\mathrm{lim}}\left|{U}_{t}-U\right|\leqslant {\delta }_{1},\hfill \\ \underset{t\to \infty }{\mathrm{lim}}\left|r-{r}_{r}\right|\leqslant {\delta }_{2}。\hfill \end{array}\right. $ | (30) |
式中,
神经网络用于估计动力学模型不确定性与外部海洋环境的扰动,有界控制律给出控制力与力矩。式(28)可转化为如下一阶非线性控制系统,如下式:
| $ \dot x = f(x) + u + d(t) 。$ | (31) |
式中:
| $ \begin{gathered} {f_1} = {m_u}^{ - 1}({f_u}\left( {u,\nu ,r} \right) + 2{m_u}\dot U{\sin ^2}\left( {\frac{\theta }{2}} \right) + {m_u}U\sin \left( \theta \right)r) ,\hfill \\ {f_2} = {m_r}^{ - 1}{f_r}\left( {u,\nu ,r} \right) 。\hfill \\ \end{gathered} $ | (32) |
取制导律的参考速度为
取滑模函数:
| $ s = c \displaystyle\int_0^t e{{\rm{dt}}} + e(t) ,$ | (33) |
式中,
| $ \begin{split} \dot s =& ce + \dot e = \dot x - {{\dot x}_d} + ce =\\ &u + d(t) + f(x) - {{\dot x}_d} + ce= u + F(x) - {{\dot x}_d} + c\dot e。\end{split} $ | (34) |
式中,
由上述分析可以得出
| $ F(x) - \hat F(x) = {W^{*{\rm{T}}}}h(x) + \varepsilon - {{\hat W}^{\rm{T}}}h(x) = - {{\tilde W}^{\rm{T}}}h(x) + \varepsilon ,$ | (35) |
定义Lyapunov函数为
| $ V = \frac{1}{2}{s^2} + \frac{1}{{2\gamma }}{\tilde W^{\rm{T}}}\tilde W ,$ | (36) |
式中,
可以得到:
| $ \dot V = s\dot s + \frac{1}{\gamma }{\tilde W^{\rm{T}}}\dot {\hat W} = s(ce + F(x) + u - {\dot x_d}) + \frac{1}{\gamma }{\tilde W^{\rm{T}}}\dot {\hat W} ,$ | (37) |
设计控制律为:
| $ u = - ce - \hat F(x) + {\dot x_d} - \eta {sgn} (s) ,$ | (38) |
式中,
| $ \begin{split} \dot V =& s(F(x) - \hat F(x) - \eta {sgn} (s)) + \frac{1}{\gamma }{{\tilde W}^{\rm{T}}}\dot {\hat W} = \\ & s( - {{\tilde W}^{\rm{T}}}h(x) + \varepsilon - \eta {sgn} (s)) + \frac{1}{\gamma }{{\tilde W}^{\rm{T}}}\dot {\hat W} = \\ &\varepsilon s - \eta \left| s \right| + {{\tilde W}^{\rm{T}}}\left(\frac{1}{\gamma }\dot {\hat W} - sh(x)\right) 。\end{split} $ | (39) |
取
| $ \dot {\hat W} = \gamma sh(x) 。$ | (40) |
得到
当
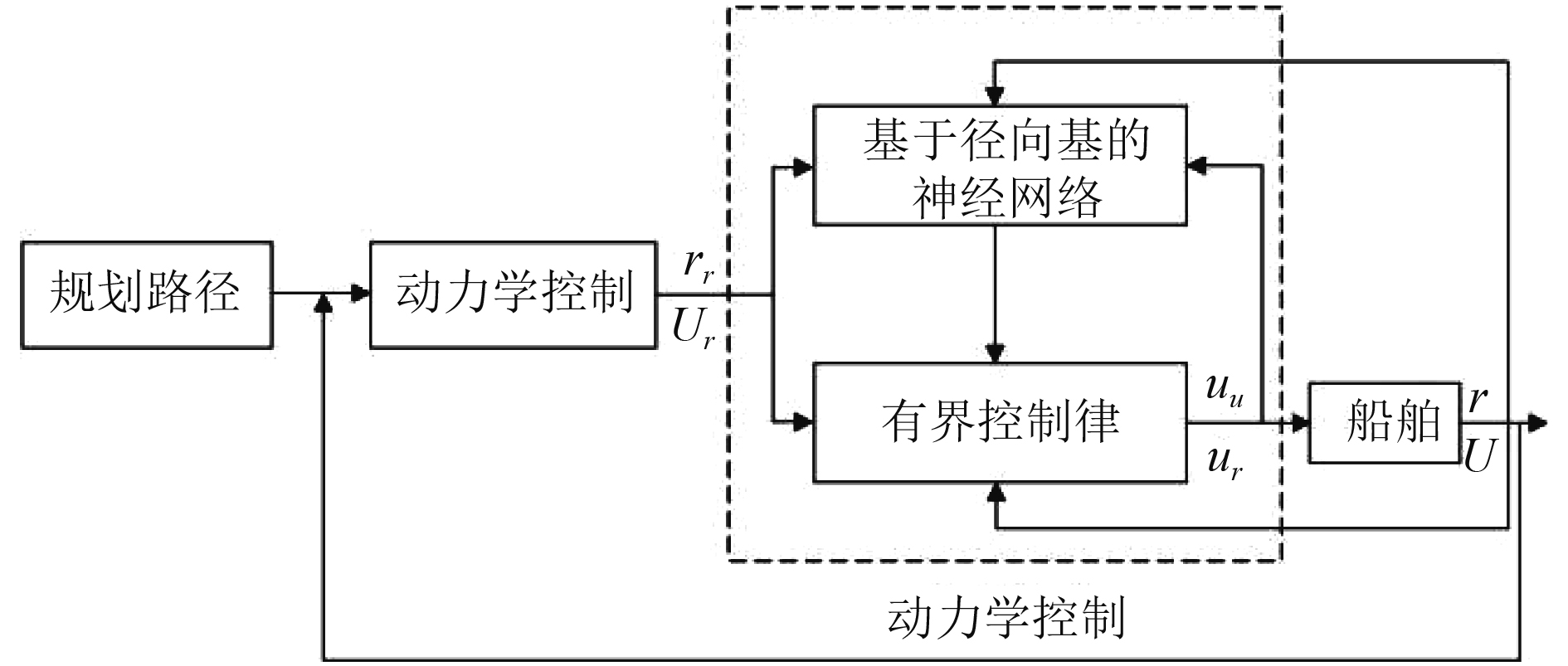
|
图 2 控制系统 Fig. 2 Control system |
控制指令为
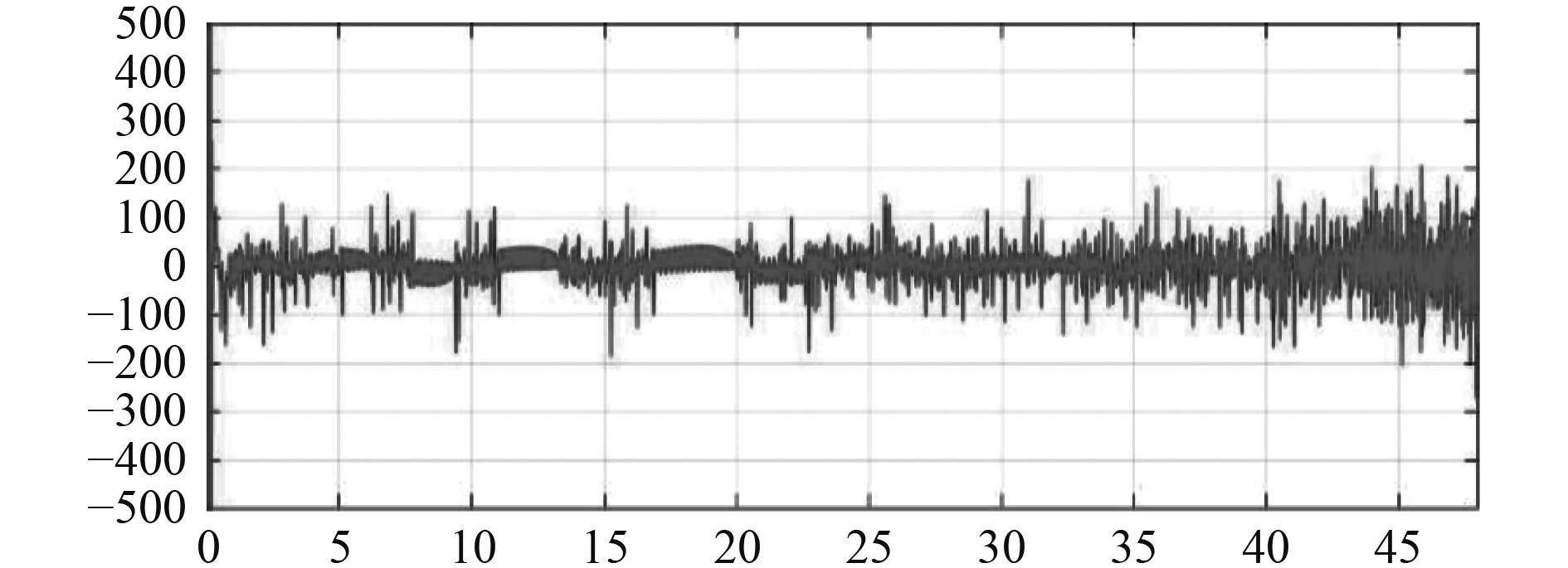
|
图 3 动力学控制力矩 Fig. 3 Dynamic control torque |

|
图 4 动力学系统控制力 Fig. 4 Control force of dynamic system |
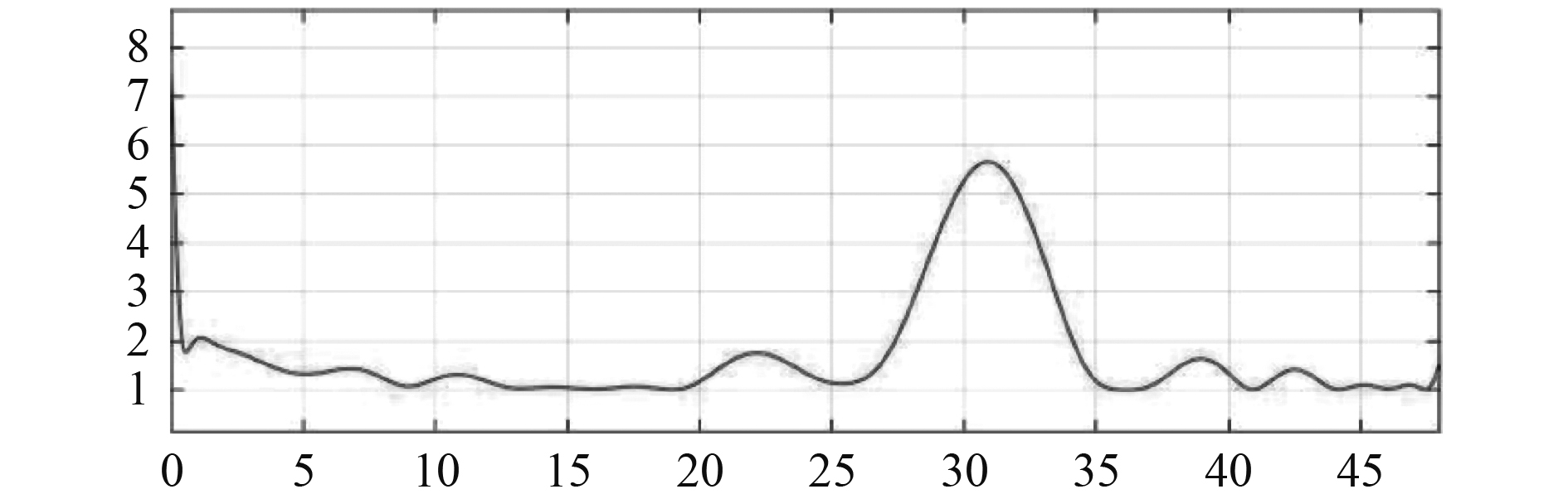
|
图 5 合速度引导律 Fig. 5 Combined speed guidance rate |

|
图 6 系统不确定项 Fig. 6 System uncertainty |

|
图 7 姿态引导律 Fig. 7 Attitude guidance rate |
本文针对船舶路径规划和跟踪控制问题,详细分析了传统蚁群算法与人工势场法存在的问题以及产生原因,使用人工势场法对蚁群算法中的信息素更新规则和启发函数进行了改进,并优化了人工势场法中的斥力势场函数,设计出了运算效率更高的蚁群算法。使用改进蚁群算法规划出的航线作为参考输入信号,通过对船舶运动学控制子系统和船舶动力学控制子系统设计控制率,实现了船舶对改进蚁群算法规划航线的路径跟踪及控制。采用神经网络逼近船舶控制系统中的不确定项,设计一种基于径向基神经网络的船舶动力学控制子系统控制率,补偿了船舶在航行时受到风浪流的干扰,实现了对运动学控制子系统引导律的跟踪,仿真实验验证了控制器的有效性。
| [1] |
NIE J, LIN X. Failos guidance law based adaptive fuzzy finite-time path following control for underactuated msv[J]. Ocean Engineering, 2019, 195: 106726. |
| [2] |
ZHENG Z, XIE L. Finite-time path following control for a stratospheric airship with input saturation and error constraint[J]. International-Journal of Control, 2019, 92(2): 368-393. DOI:10.1080/00207179.2017.1357839 |
| [3] |
曾华宝. 基于终端滑模的欠驱动船舶路径跟踪自适应控制[D]. 大连: 大连海事大学, 2020.
|
| [4] |
HEALEY A J, LIENARD D. Multivariable sliding mode control for autonomous diving and steering of unmanned underwater vehicles[J]. Oceanic Engineering IEEE Journal of, 1993, 18(3): 327-339. DOI:10.1109/JOE.1993.236372 |
| [5] |
FOSSEN T I, BREIVIK M, SKJETNE R. Line-of-sight path following of underactuated marine craft[J]. IFAC Proceedings Volumes, 2003, 36(21): 211-216. DOI:10.1016/S1474-6670(17)37809-6 |
| [6] |
OH S R, SUN J. Path following of underactuated marine surface vessels using line-of-sight based model predictive control[J]. Ocean Engineering, 2010, 37(2-3): 289-295. DOI:10.1016/j.oceaneng.2009.10.004 |
| [7] |
朱骋, 庄佳园, 张磊, 等. 无人水面艇自适应路径跟踪算法[J]. 导航与控制, 2019, 18(1): 44-50. DOI:10.3969/j.issn.1674-5558.2019.01.006 |
| [8] |
QIU B, WANG G, FAN Y, et al. Path following of underactuated unmanned surface vehicle based on trajectory linearization control with input saturation and external disturbances[J]. International Journal of Control Automation and Systems, 2020, 18(4): 1-12. |
| [9] |
LIANG X, QU X, WAN L, et al. Three-dimensional path following of an underactuated auv based on fuzzy backstepping sliding mode control[J]. International Journal of Fuzzy Systems, 2017, 20: 640-649. |
| [10] |
沈智鹏, 景富盛. 欠驱动船舶路径跟踪神经元自适应迭代滑模控制[J]. 哈尔滨工程大学学报, 2019, 40(3): 489-494. |
| [11] |
FOSSEN T I, LEKKAS A M. Direct and indirect adaptive integral line-of-sight path-following controllers for marine craft exposed to ocean currents[J]. International Journal of Adaptive Control and Signal Processing, 2017, 31(4): 445-463. DOI:10.1002/acs.2550 |
| [12] |
FOSSEN T I, PETTERSEN K Y, GALEAZZI R. Line-of-sight path following for dubins paths with adaptive sideslip compensation of drift forces[J]. IEEE Transactions on Control Systems Technology, 2015, 23(2): 820-827. DOI:10.1109/TCST.2014.2338354 |
| [13] |
SHEN C, SHI Y, BUCKHAM B. Integrated path planning and tracking control of an auv: a unified receding horizon optimization approach[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(99): 1163-1173. |
| [14] |
张力行. 欠驱动船舶路径规划及跟踪算法研究[D]. 上海: 上海交通大学, 2017.
|
| [15] |
曾国奇, 赵民强, 刘方圆, 等. 基于网格PRM的无人机多约束航路规划[J]. 系统工程与电子技术, 2016, 38(10): 2310-2316. DOI:10.3969/j.issn.1001-506X.2016.10.13 |
| [16] |
XUE Z, LIU J, W U Zhengxing, et al. Development and path planning of a novel unmanned surface vehicle system and its application to exploitation of qarhan salt lake[J]. Science China(Information Sciences), 2019, 62(8): 084202. DOI:10.1007/s11432-018-9723-5 |
| [17] |
刘陆. 欠驱动无人船的路径跟踪与协同控制[D]. 大连: 大连海事大学, 2018
|
 2022, Vol. 44
2022, Vol. 44
