赫姆霍兹共振器作为一种经典的噪声阻尼器,常用于降低航空发动机以及燃气轮机的排气噪声[1-2]。它的结构很简单,就是一个开口的空腔,开口处插上一个短管。空腔内的空气相当于一个弹簧,管口的空气柱相当于一个质量块。作为一种结构简单的抗性消声器,传统的赫姆霍兹共振器只有一个共振峰,且消声频带较窄[2],所以,为了获得更多的共振峰以及拓宽消声频带,需要对传统的赫姆霍兹共振器进行结构优化。
1 数值模型与数值模拟方法 1.1 赫姆霍兹共振器模型的描述使用的赫姆霍兹共振器基础模型是基于文献中所使用的赫姆霍兹共振器模型。所有的结构变化的新模型全部是赫姆霍兹共振器基础模型的派生品,将对结构变化的赫姆霍兹共振器的数值模型进行实验数据对比验证。赫姆霍兹共振器基础模型的颈部短管半径为Dneck/2,高度为1.2*Lneck; 赫姆霍兹共振器基础模型的共振腔的半径为Dreson/2,高度为Lreson; 其中Dneck=4.044 cm,Lneck=8.05 cm,Dreson=15.32 cm,Lreson=24.42 cm。赫姆霍兹共振器内流动的气体为空气,赫姆霍兹共振器的壳体材料为刚性。1687年,牛顿提出了流体内摩擦概念并且建立了牛顿流体模型,然而在很长的一段时间之内并未得到实际的应用。伯努利所著的经典书籍《水力学》中并未涉及内摩擦力。1755年,欧拉所推导的流体运动方程中也未加入黏性力。随后发现这些理论结果与大量实验结果并不一致,不少力学家试图在欧拉运动方程中加入摩擦项,但一直没有取得广泛的认同,直到法国的力学家纳维和英国的数学家斯托克斯通过不同的途径,成功解决了这一困扰大家多年的难题。纳维认为流体的黏性行为是由于分子之间相互作用导致的,他在欧拉方程中加入了分子之间的动量交换项,即黏性力项。斯托克斯则采取更为简洁的方法,直接从连续介质模型出发,将牛顿黏性定律从一维推广到三维。控制方程为包括质量守恒、动量守恒和能量守恒的线性化Navier-Stokes方程组。
质量方程如下式:
| $ \frac{{\rm{D}}\rho}{{\rm{D}}t}+\rho\frac{\partial u_k}{\partial x_k}=0,$ | (1) |
动量方程如下式:
| $ \rho\frac{\partial u_i}{{\rm{D}}t}=-\frac{\partial p}{\partial x_i}+\frac{\partial \tau_{ij}}{\partial x_j}+\rho F_i。$ | (2) |
式中:ui表示第i个方向的速度分量(x方向为i=1,y方向为i=2),m/s;
能量方程为:
| $ \rho\frac{{\rm{D}}e}{{\rm{D}}t}=-p\frac{\partial u_k}{\partial x_k}+\frac{\partial}{\partial x_k}\left(k \frac{\partial T}{\partial x_k}\right)+\varPhi。$ | (3) |
公式等号左边表示单位体积空气的内能变化率,公式等号右边各项分别表示单位体积空气变化时外部压力所作的压缩功功率、传热功率和流体变形时粘性应力的做功功率。e=e(p,T),
剪切应力方程如下:
| $ \varPhi=\tau_{ij}\frac{\partial u_i}{\partial x_k}\quad \tau_{ij}=\mu\left(\frac{\partial u_j}{\partial x_j}+\frac{\partial u_j}{\partial x_i}-\frac{2}{3}\frac{\partial u_k}{\partial x_k} \delta _{ij}\right)。$ | (4) |
式中:μ代表动力粘度;
瞬时流量参数通过平均值与波动值组成,如下式:
| $ \begin{split} & \rho(x,t)=\rho_0(x)+\rho'(x,t),u(x,t)=u_0(x)+u'(x,t),\\ &v(x,t) =v_0(x)+v'(x,t),p(x,t)=p_0(x)+p'(x,t)。\end{split} $ | (1.5) |
其中:u=u1且v=u2,下标0表示的是平均流量。本模型中,主要考虑了管内流动和声学平面波传播,假设流量扰动是与谐波时间有关的,所以将其转换到了频域。任何的流量参数q'都可以用
将等式(5)代入到等式(1)~式(3)并进行线性化,可以将线性化的N-S纳维-斯托克斯方程推导为
| $ (u_0v_0)\nabla \hat{\rho}+\left(\frac{\partial u_0}{\partial x}+\frac{\partial v_0}{\partial y}-i\omega\right)\hat{\rho}=-\left(\frac{\partial \rho_0\hat u}{\partial x}+\frac{\partial \rho_0 \hat{v}}{\partial y}\right) ,$ | (6) |
| $\begin{split} &\nabla^T\left[ -\left( \begin{array}{*{20}{c}}\dfrac{4}{3}\mu 0\\ 0 \mu \end{array}\right)\nabla \hat{u}\right]+\rho_0(u_0v_0)\nabla\hat{u}+ \rho_0 \left(\frac{\partial u_0}{\partial x}-i\omega\right)\hat{u}=\\ &\rho_0\hat{F}_x- \left( \mu_0\frac{\partial u_0}{\partial x} +v_0\frac{\partial u_0}{\partial y}\right)- c^2 \frac{\partial \hat{\rho}}{\partial x}+\frac{1}{3}\mu\frac{\partial^2\hat{v}}{\partial x\partial y}-\frac{\partial u_0}{\partial y}\hat{v} ,\end{split}$ | (7) |
| $\begin{split} & \nabla^T\left[ -\left( \begin{array}{*{20}{c}}\mu 0 0 \dfrac{4} {3} \mu \end{array} \right) \nabla \hat{v}\right]+ \rho_0(u_0v_0) \nabla\hat{u}+ \rho_0 \left(\frac{\partial v_0} {\partial y}- i\omega\right)\hat{v}=\\ & -c^2 \frac{\partial \hat{\rho}}{\partial y} - \left( \mu_0\frac{\partial v_0} {\partial y} + v_0 \frac{\partial v_0}{\partial y}\right)-\rho_0 \frac{\partial v_0}{\partial x}\hat{u} + \frac{1}{3}\mu\frac{\partial^2\hat{u}}{\partial x\partial y} 。\\[-20pt] \end{split}$ | (8) |
管道中存在切向流,并且由流动带来的扰动将会产生雷诺应力,所以需要去选择适合的湍流模型。很多的湍流模型可供选择,比如说涡流粘度模型、大涡模拟模型以及雷诺应力模型等。出于简单可行的考虑,本模拟选择了涡流粘度模型中的k-ε湍流模型。k代表湍流动能,ε代表湍流耗散率,可以查阅文献[5]获得。
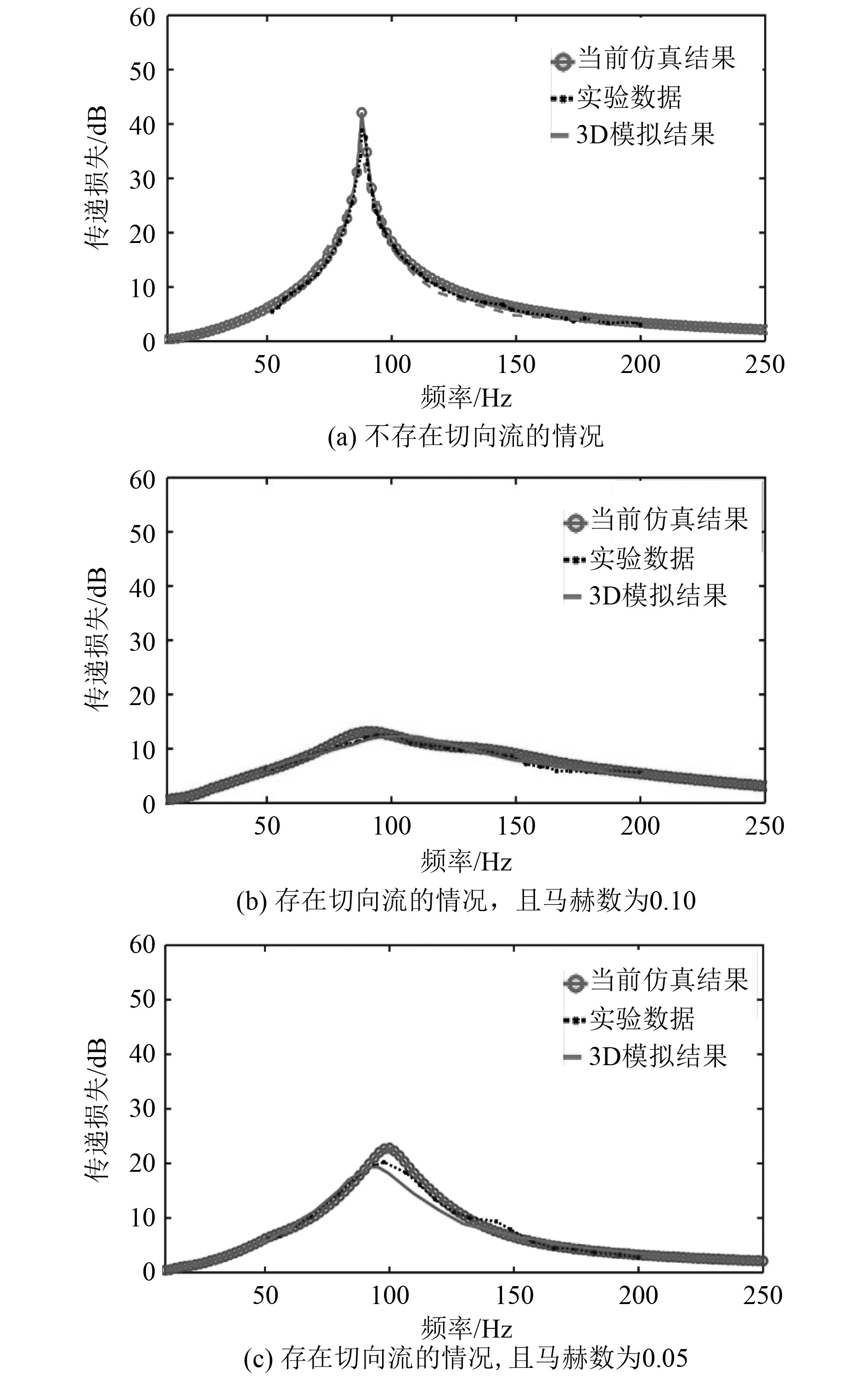
1.2 数值模型准确性验证由于研究的是低频范围,只考虑平面波在管道内传播,与此同时假设入口和出口均为声开放[3-5]。此外,平面波在管道中传播的实验测量中,通常使用的是双麦克风技术,频率范围为[10,250] Hz[6]。建立的数值模型通过和文献中的实验数据和理论推导数据[7]进行对比验证,从而可以证明其可靠性。图1(a)表示存在切向流、温度为293.15 K,共振器颈部和腔体都为传统圆柱体且共振器轴心为X轴正方向的条件下,数值模拟数据与文献中相同条件下实验数值[7]的对比。
|
图 1 当前数值模型模拟结果与文献中实验结果[7]的传递损失性能对比验证 Fig. 1 Comparison and verification of transmission loss performance between the simulation results of the current numerical model (without extended neck) and the experimental results [7] in the literature |
图1(b)和图1(c)表示带延伸颈的赫姆霍兹共振器的数值模拟结果与文献中相同条件下实验数据结果的对比。总的来说,这些比较表明,所使用的模型可以用来估计所提出的赫姆霍兹共振器在存在切向流的作用下的噪声阻尼性能分析。
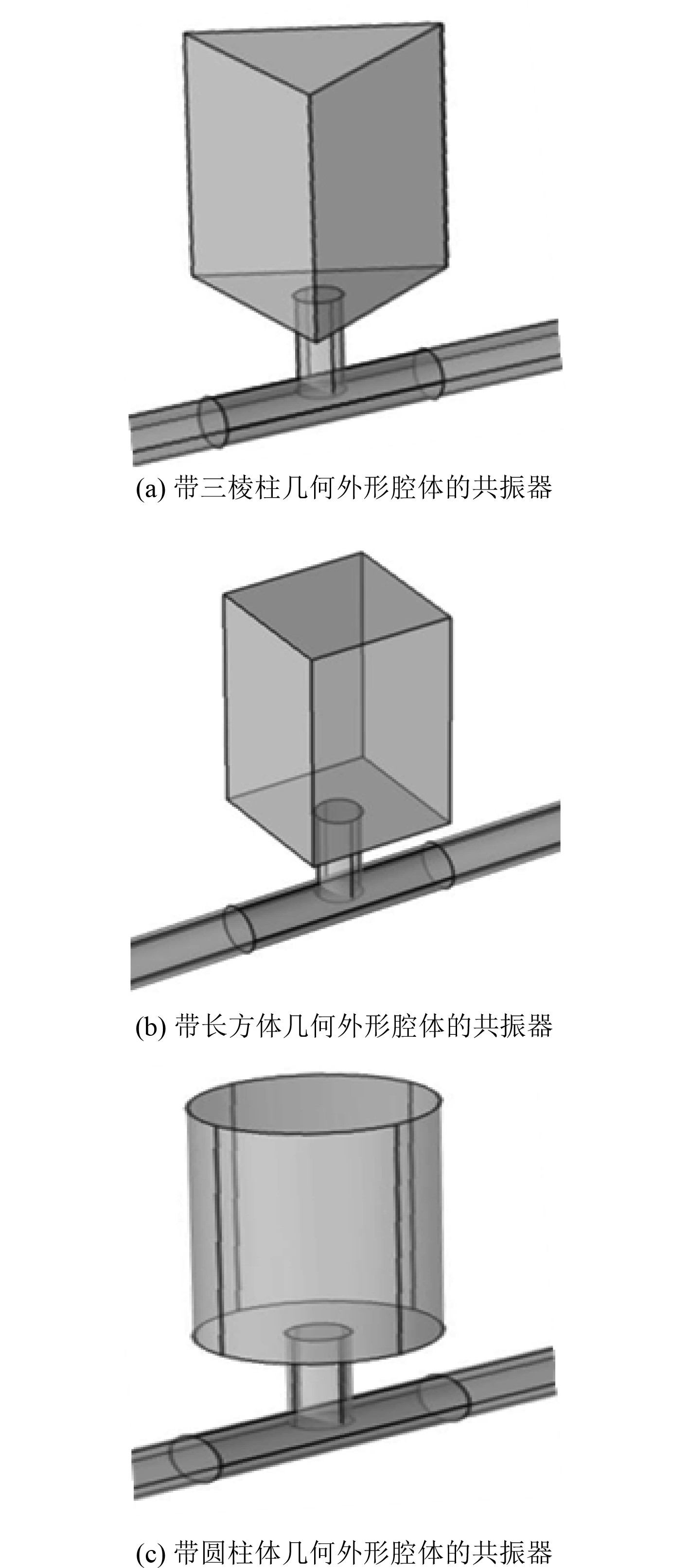
2 结果与讨论 2.1 腔体几何形状对噪声衰减性能的影响讨论腔体的几何形状对噪声衰减性能的影响,图2为结构示意图。研究在切向流作用下,同体积和同截面积的3种不同的几何形状。数值模拟结果表明,三棱柱的整体消声效果最好。三棱柱和长方体腔体的消声效果相对传统的圆柱体腔体要好。
|
图 2 带3种不同几何外形的腔体的赫姆霍兹共振器的三维模型示意图 Fig. 2 Three dimensional model of Helmholtz resonator with three different cavity geometric shapes |
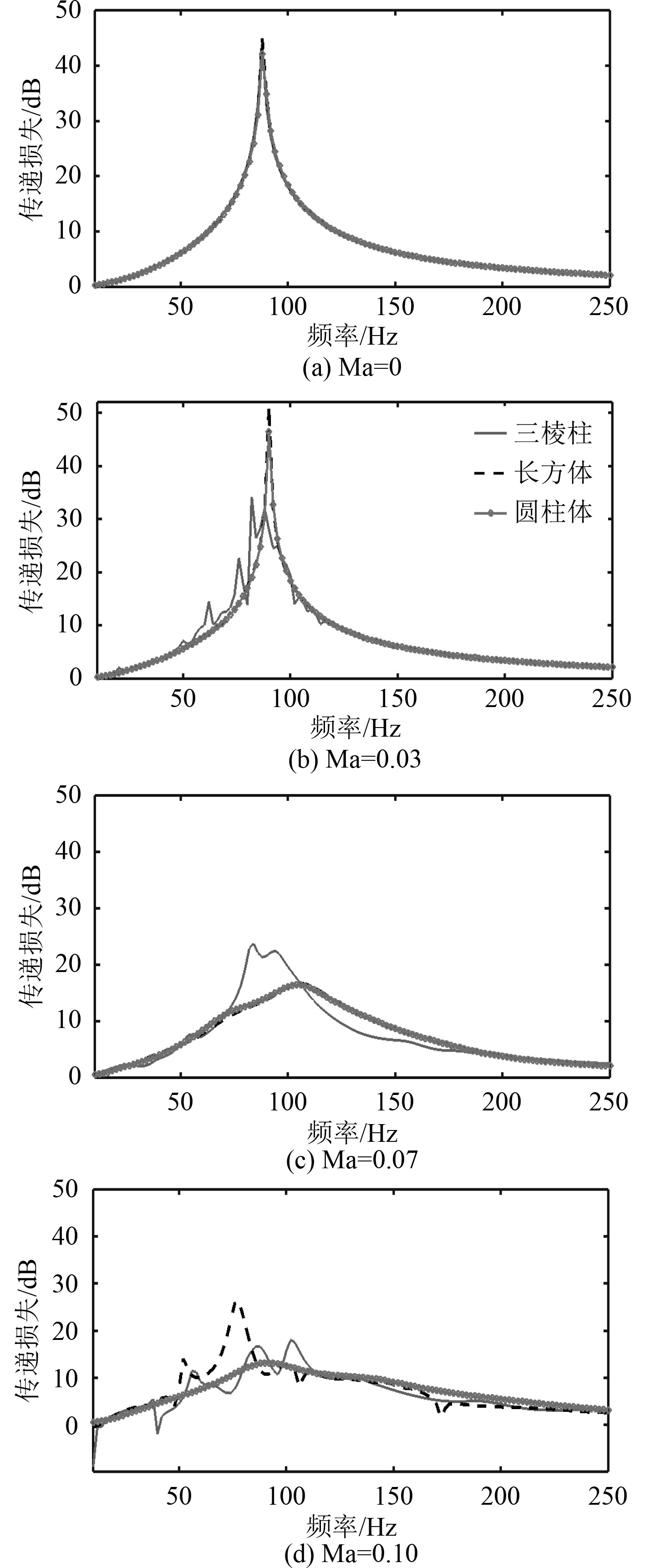
从图3可以发现,在没有切向流的条件下,3种不同几何形状的腔体的效果效果基本一模一样。当有切向流之后,三棱柱的消声效果要远好于圆柱体,并且相对于圆柱体有多个共振峰,如图3(b)~图3(d)所示。
|
图 3 在不同马赫数情况下,3种不同腔体几何形状的传递损失随频率变化的过程 Fig. 3 The transmission loss of three different cavity geometries with different frequencies at different Mach numbers |
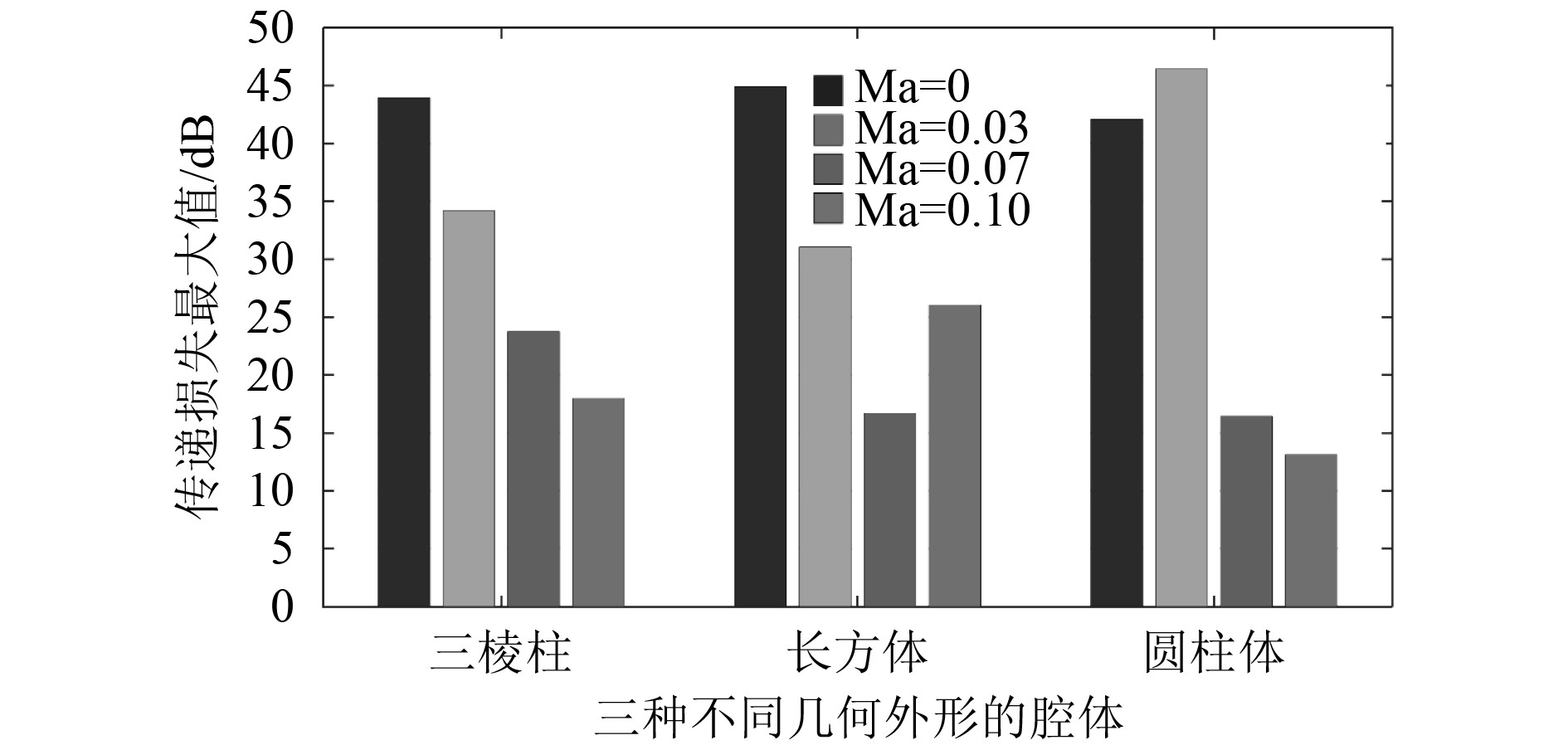
总之,三棱柱和长方体腔体的消声效果要远好于圆柱体颈部,这是由于三棱柱和长方体内部的凹槽导致的结果。通过分析图4,可以看到,整体而言,腔体为三棱柱时,传递损失最大值整体高于腔体为长方体和圆柱体对应的传递损失最大值;这与颈部为三棱柱的情况相反。此外,腔体为三棱柱时,在切向流马赫数为0.1时容易产生“啸叫”现象。表1表明,带三棱柱腔体的赫姆霍兹共振器在一定程度上可以拓宽消声频带。
|
图 4 带3种不同几何外形的腔体模型的传递损失最大值 Fig. 4 The maximum values of the transmission loss of the cavity model with three different geometric shapes |
|
|
表 1 对应于传递损失峰值的共振频率汇总 Tab.1 Summary of resonance frequencies corresponding to peak transmission loss |
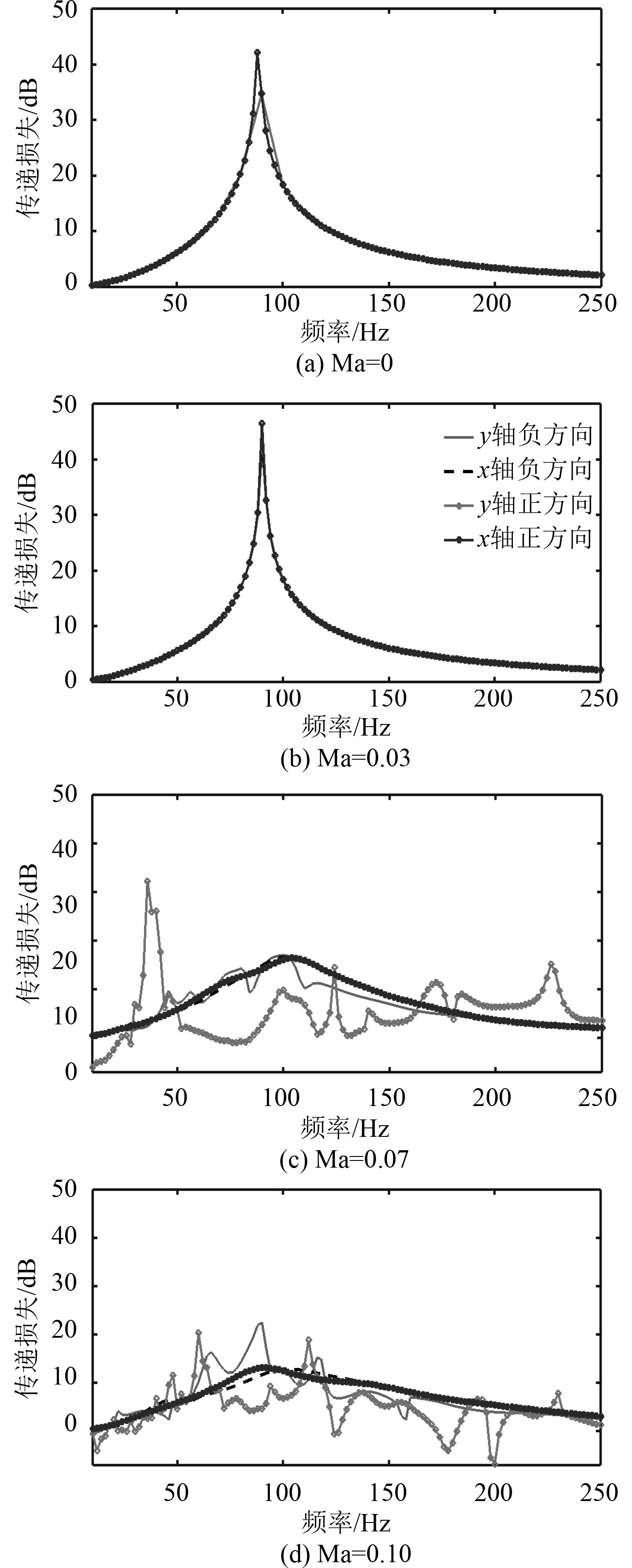
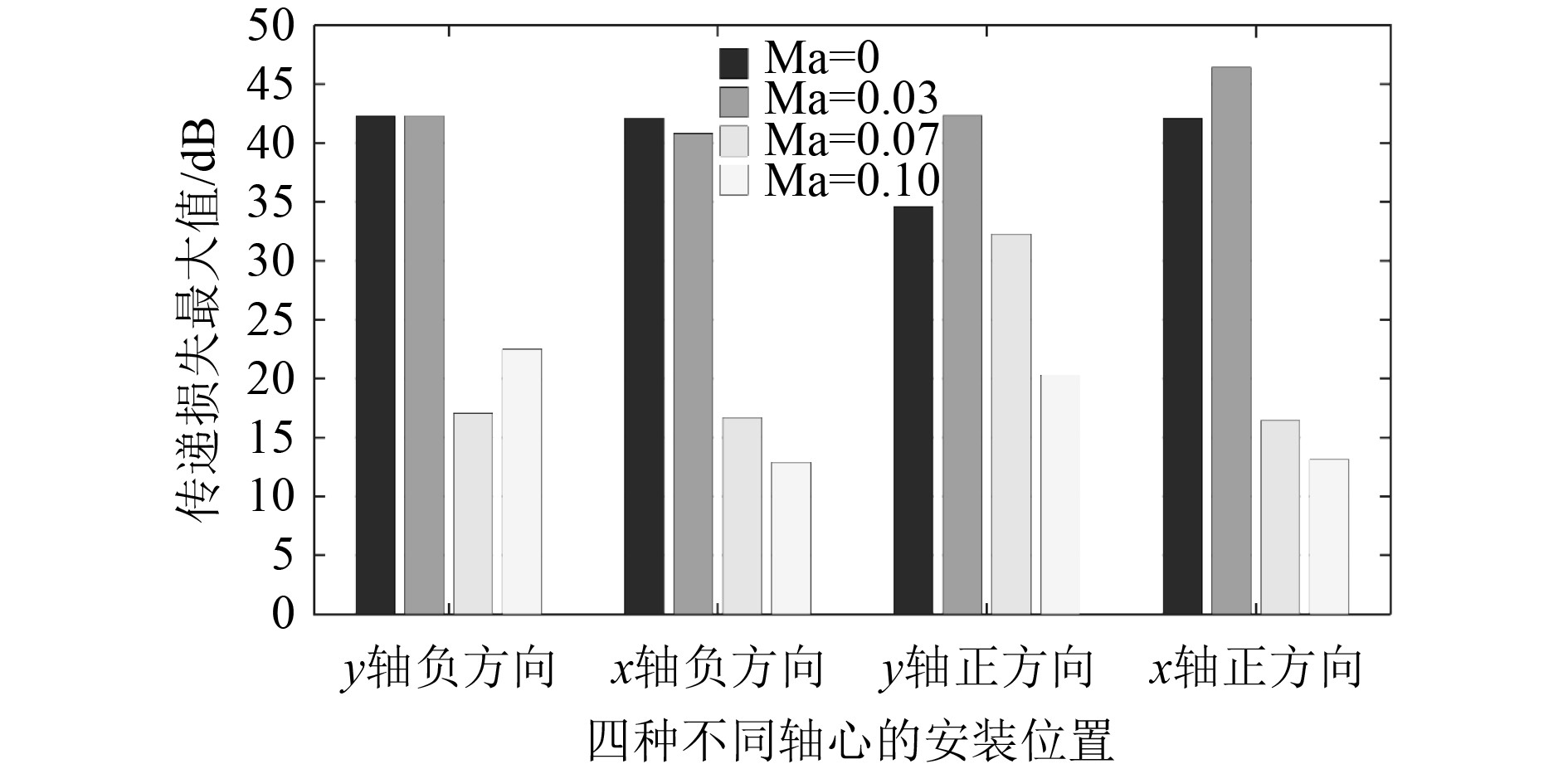
通常研究的赫姆霍兹消声器都是在以x轴正方向为轴心进行研究的,本文对4种不同的轴心方向进行研究,旨在探究不同轴心方向对噪声衰减性能的影响,更希望发现最佳的轴心位置,以便最大化赫姆霍兹共振器的消声性能。通过对图5和图6的分析发现,整体而言,以y轴负方向为轴心的消声效果最好,远好于以x轴正方向为轴心的传统赫姆霍兹共振器。此外,以y轴正方向虽然在[50,150] Hz的范围内传递损失为负值,但是,在30 Hz和230 Hz处产生了共振现象,传递损失峰值分别是传统以x轴为轴心的共振器的200%和110%左右。从图6可以看到,当马赫数相对较高时(如0.07和0.1),共振器设置位置影响传递损失最大值,以y轴负方向和x轴负方向以及y轴正方向安装的共振器的传递损失最大值均高于传统的以x轴正方向为轴心安装的共振器所对应的传递损失最大值。此外,以y轴正方向为轴心安装的共振器在马赫数为0.07和0.1时容易产生“啸叫”现象。表2反映了以y轴负方向为轴心安装的共振器对应传递损失峰值(或最大值)的共振频率与传统的以x轴正方向为轴心安装对应传递损失峰值的共振频率相差无几。但是,以x轴负方向对应传递损失峰值的共振频率则高于传统x轴正方向安装的。此外,以y轴正方向为轴心安装的共振器对应传递损失峰值的共振频率小于传统x轴正方向安装的。
|
图 5 在不同马赫数情况下,不同共振器设置位置的传递损失随频率变化的过程 Fig. 5 The change of transmission loss with frequencies at different positions of resonators at different Mach numbers |
|
图 6 四种不同共振设置位置下的传递损失最大值 Fig. 6 The maximum values of the transmission loss Under four different resonant settings |
|
|
表 2 对应于传递损失峰值的共振频率汇总 Tab.2 Summary of resonance frequencies corresponding to peak transmmission loss |
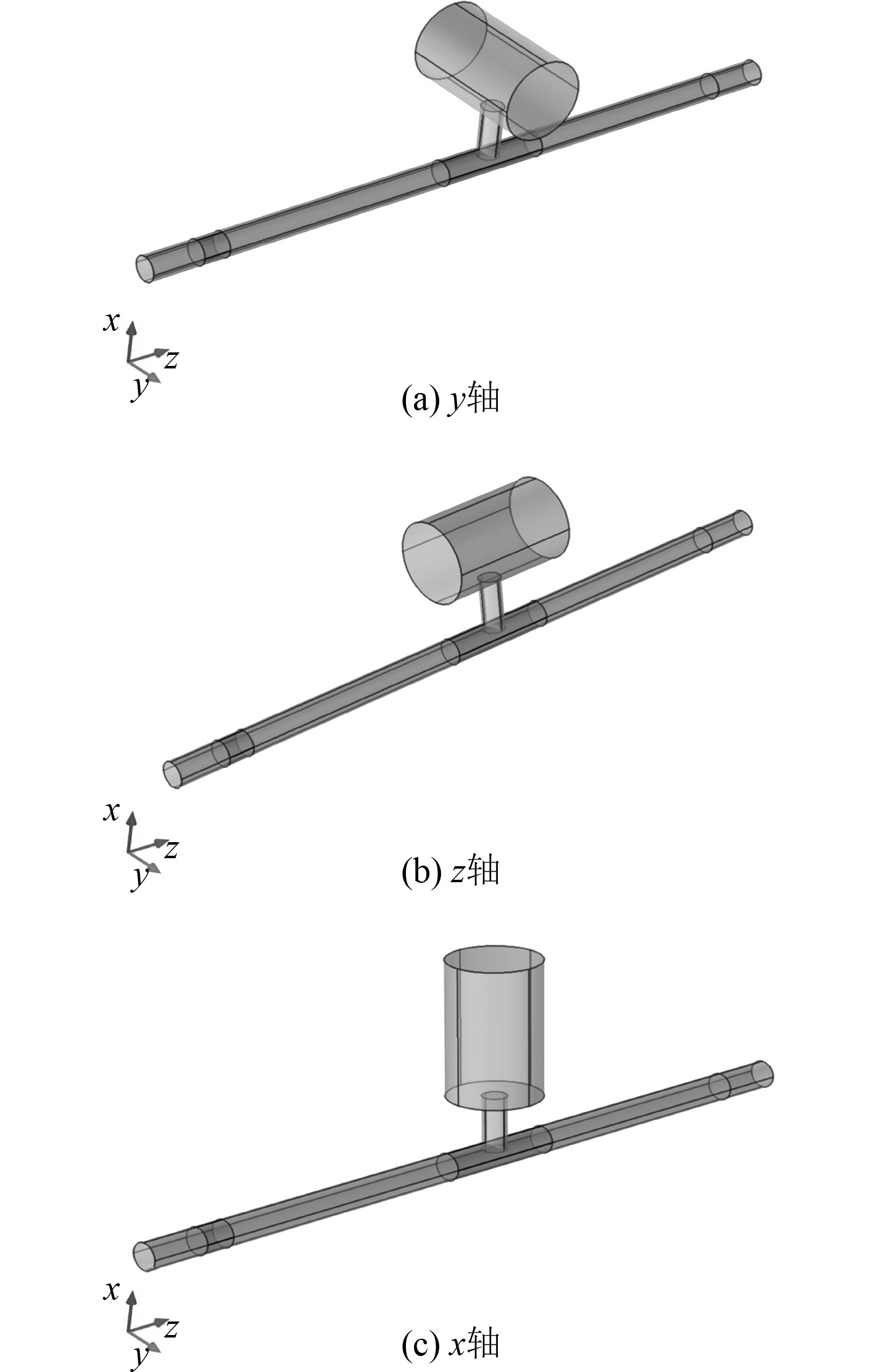
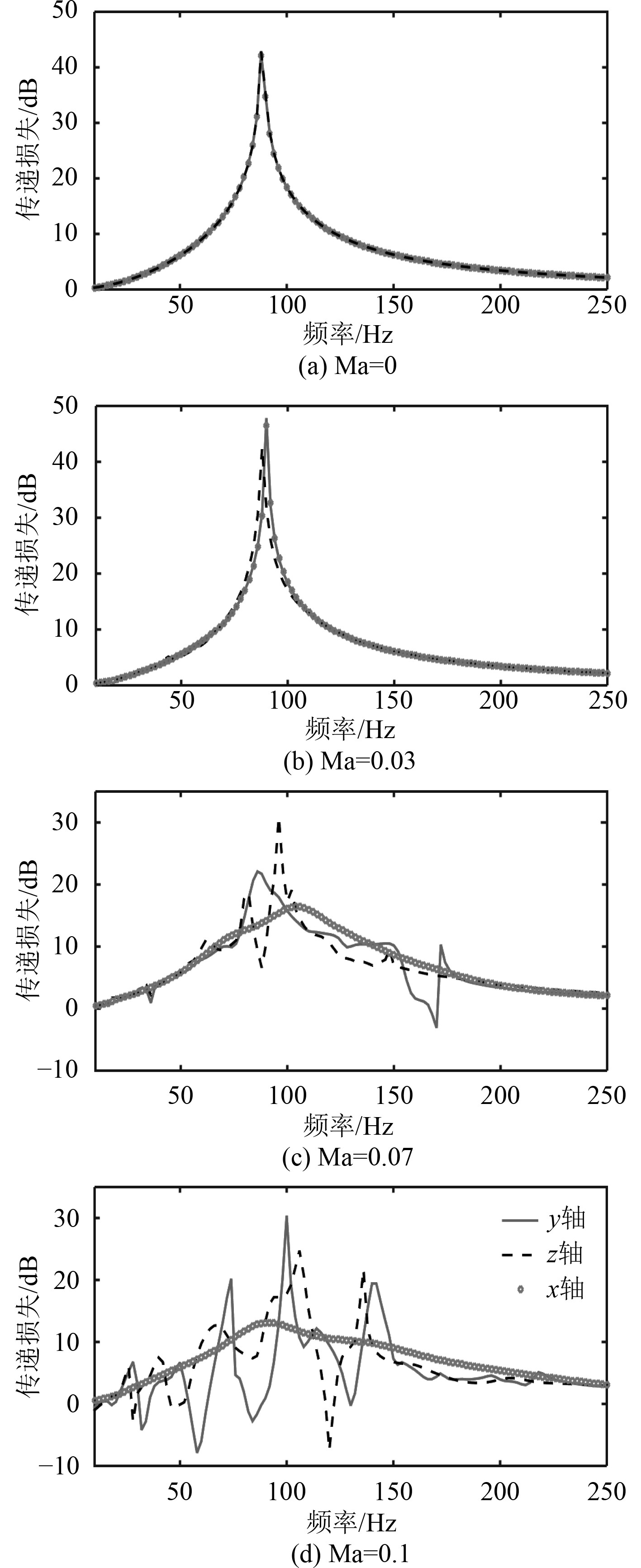
除了共振器整体可以改变其轴心位置外,共振器的腔体同样可以有不同的轴心布置方式,如图7所示。本文主要分析3种不同的轴心布置方式,即x轴、y轴和z轴。从图8可以看出,腔体以y轴为轴心布置的消声效果要好于传统的以x轴为轴心的消声效果。同样的,在没有切向流的条件下,3种布置方式的消声效果几乎一模一样。但是,在切向流作用下,以y轴和z轴的消声效果要远好于以x轴为轴心的消声效果,尤其当马赫数为0.1时,以y轴为轴心的消声器更是产生了6个传递损失峰值。最大消声效果是传统赫姆霍兹消声器的300%,提高了大约20 dB的消声量。
|
图 7 腔体3种不同轴心布置方式的三维示意图 Fig. 7 Three dimensional schematic diagram of three different axis layout of cavity |
|
图 8 在不同马赫数情况下,腔体3种不同轴心布置方式的传递损失随频率变化的过程 Fig. 8 The process of the transmission loss of three different axis arrangement modes of the cavity varies with the frequencies under different Mach numbers |
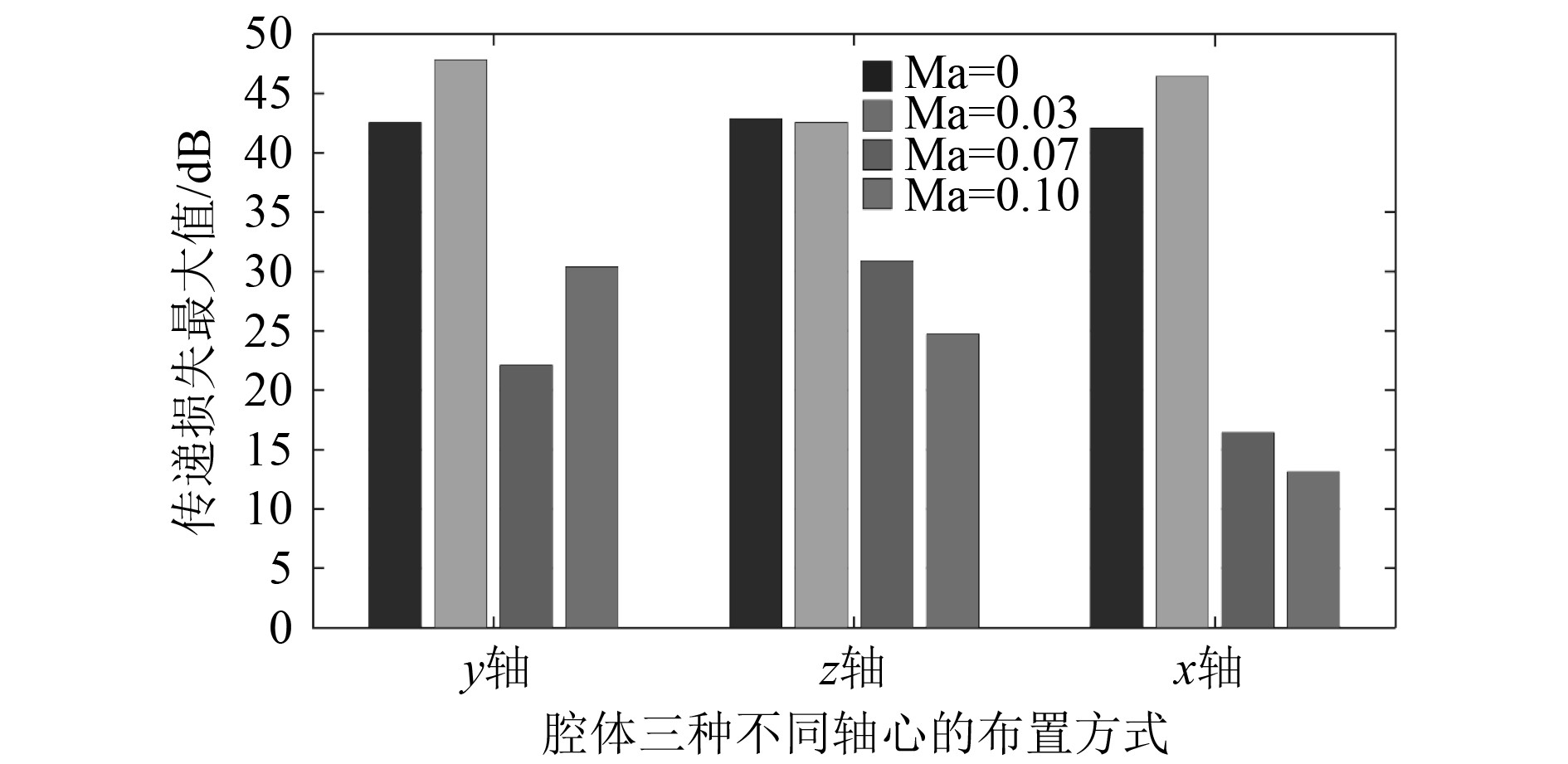
遗憾的是,以y轴为轴心的消声器在一定频率下产生了啸叫现象,也就是“whistling”。在马赫数相对较高为0.07时,共振腔以y轴为轴心安装的传递损失最大值相对传统的以x轴为轴心安装的传递损失最大值的提高值只为振腔以z轴为轴心安装的传递损失最大值相对传统的以x轴为轴心安装的传递损失最大值的提高值的1/3。但是,当马赫数为0.1时,振腔以y轴为轴心安装的传递损失最大值相对传统的以x轴为轴心安装的传递损失最大值的提高值只为振腔以z轴为轴心安装的传递损失最大值相对传统的以x轴为轴心安装的传递损失最大值的提高值的3/2,如图9所示。当马赫数相对较小时,即小于0.03,腔体3种不同轴心布置方式下传递损失最大值几乎一致。但是,当马赫数相对较大时,即马赫数为0.07和0.1,以y轴和z轴为轴心的布置方式的传递损失最大值均高于传统的以x轴为轴心的传递损失最大值。但是,但马赫数较大时,腔体以y轴和以z轴为轴心布置的赫姆霍兹共振器会产生“啸叫”现象。从表3可以看到,腔体以y轴和以z轴为轴心安装的赫姆霍兹共振器对应传递损失最大值的共振频率在马赫数为0.1时整体高于传统的赫姆霍兹共振器。
|
图 9 腔体3种不同轴心布置方式下的传递损失最大值 Fig. 9 The maximum values of the transmission loss Under three different cavity settings |
|
|
表 3 对应于传递损失峰值的共振频率汇总 Tab.3 Summary of resonance frequencies corresponding to peak transmission loss |
本文主要研究在切向流条件下的结构深化和安装轴心变化的赫姆霍兹共振器的噪声衰减性能,分别对变颈、延伸颈、几何外形、安装轴心等在不同切向流马赫数情况下的消声性能进行了数值分析,结果如下:
1)同体积同横截面积下,腔体几何形状不仅会影响传递损失峰值,更会影响共振峰的数量。
2)共振器的设置位置会影响消声性能,优化位置后,会产生2个共振峰,甚至两倍以上的传递损失值。
3)腔体的设置位于对噪声衰减性能有很大的影响,随着马赫数的增加可能会产生3个以上共振峰。
4)用于推导共振频率的理论公式不适用本文研究的部分情况。
总之,在存在不可忽略的切向流马赫数条件下,本文为低频工作的赫姆霍兹共振器,特别是为结构优化的赫姆霍兹共振器的有效设计照亮了前进的路途和提供了理论参考。
| [1] |
ZHAO D, LI X Y. A review of acoustic dampers applied to combustion chambers in aerospace industry[J]. Progress in Aerospaceences, 2015, 74(4): 114-130. |
| [2] |
IAIN D J D, DOWLING A P. The use of Helmholtz resonators in a practical combustor[J]. Journal of Engineering Gas Turbines Power, 2005(127): 268–275.
|
| [3] |
PAN W C, XU X, LI J, et al. Acousitc damping performance of coupled Helmholtz resonators with a sharable perforated sidewall in the presence of grazing flow[J]. Aerospace Science and Technology, 2020, 99(4): 1−9.
|
| [4] |
ZHAO D, MORGANS A S. Tuned passive control of combustion instabilities using multiple Helmholtz resonators[J]. Journal of Sound & Vibration, 2009, 320(4−5): 744−757.
|
| [5] |
SELAMET A, XU M B, LEE I J, et al. Helmholtz resonator with absorbing material[J]. Journal of Acoustical Society of America, 2005, 117(2): 725–733.
|
| [6] |
CAI C, MAK C, SHI X. An extended neck versus a spiral neck of Helmholtz resonator[J]. Applied Acoustiss, 2017, 115(1):74–80.
|
| [7] |
SELAMET E, SELAMET A, IQBAL A, et al. Effect of flow on helmholtz resonator acoustics: a three-dimensional computational study vs. experiments[J]. SAE Technical Paper 2011-01-1521.
|
 2022, Vol. 44
2022, Vol. 44

