21世纪以来,以“蛟龙”号、“勇士”号、“奋斗者”号载人潜水器和“潜龙一号”、“潜龙二号”等无人潜水器为代表的水下高端装备使我国在深海空间的探索与开发领域取得了领先优势[1-2]。
在潜水器设计中,安全性是一项至关重要的技术指标,也是设计人员的技术红线。潜水器设计与水面船舶设计的显著不同是其储备浮力小,通过注排水实现浮力调节,在紧急情况时通常抛弃部分载荷应急上浮。随着潜水器平台的大型化和多功能化要求,部分平台提出了水下铺缆、水下回收等多种作业新需求,对平台的水下起吊、拖曳回收能力有所要求。我国首个实验型35吨级深海移动工作站目前已进行了水池试验,开展了多项试验,初步对水下起吊和拖曳回收能力进行了探索性研究,其未来型将具备水下装备运载投送能力,并配备多种深海机器人,实现长期的水下科学考察与开发研究。
未来在大型多用途潜水器方案设计中,具备一定任务载荷的拖曳和起吊能力将成为一项值得关注的重要指标。拖曳和起吊作业时潜水器的航速低、舵效差,拖曳和起吊过程中缆索传递给潜水器的作用力变化可能对其安全性和作业性能有较大影响,必须对潜水器-缆索-载荷三者间相互耦合作用进行严谨的动力学仿真研究,分析缆索收放过程对缆索张力和潜水器运动相应的影响规律,从而更好为多用途潜水器的储备浮力设计策略和作业流程设计服务。
潜水器-缆索-载荷三者间相互耦合作用的动力学仿真研究问题的难点在于缆索的力学建模。目前针对缆索的仿真方法一般分为两类:一类是基于悬链线方程或缆索微元平衡方程对水下缆索力学问题进行静力学分析,典型用例为系泊系统设计中基于悬链线方程对缆索张力和曲率问题进行求解[3-6];一类是动力学分析,考虑其动态响应过程,按缆索微元的处理方式又分为集中质量法、有限差分法、有限段法、有限元法等。静力学分析不适用于潜水器-缆索-载荷三者间相互耦合作用的仿真分析,后者有一定的适用性,并已在潜艇拖曳线阵动态运动仿真运用中得到较好的仿真精度和效率。
目前上述方法基本未涉及收放缆索过程中变缆索长度、变边界问题的研究,或即使涉及到根据文献调研显示,也未取得较好的仿真效果(效率、精度、稳定性等)。
Ablow等[7]首次将缆索动力学平衡方程与运动学方程投影变换至缆索局部运动坐标系,建立了缆索的偏微分控制方程组,开始基于有限差分法对动态缆索问题进行研究;Burgess[8]和李英辉[9]基于上述方法对深海拖曳系统在二维下拖缆与拖曳体的耦合运动进行了数值模拟。
付薇[10]和王飞[11]等采用集中质量法对拖缆系统的控制方法进行了研究;并且陆肇康等[12]通过增加或减少凝聚质量点的数目,对非定长水下缆索动态运动(缆索收放)进行了初步研究。
Huston[13]和Kamman[14]等基于有限段法对水下缆索进行了动力学仿真;李晓平[15]基于变拓扑多体系统理论对缆索收放过程中的变长度问题进行了初步研究。
有限元分析中一般将缆索采用梁单元或LINK单元近似,即使在Ansys2020正式加入了绳索单元CABLE280,但据了解其适用范围仍仅限于模拟线缆拉压、变形等工况,不适用缆索的大范围运动仿真。任革学团队开发了ALE缆索单元[16],并在缆索驱动多体系统仿真研究方面取得了很大进展,已在部分航天用大伸缩结构中得到运用,尚未清楚该方法是否适用于水下缆索收放仿真。
综上所述,采用集中质量法增加或减少凝聚质量点的数目、采用有限段法中增加或减少缆索段数目均能在一定程度上解决水下缆索收放的仿真问题,但凝聚质量点数目或缆索微元段数目的变化,将导致求解过程中质量矩阵、刚度矩阵等结构的不断改变,严重影响了求解效率和求解稳定性。
本文采用有限差分法、并结合缆索微元长度更新策略,开展潜水器-缆索-载荷三者间相互耦合作用研究中涉及的缆索变长度问题,并通过拖航变深度航行、拖航过程收缆索进行起吊作业2种工况的数值仿真对提出的方法进行验证。
1 仿真方法 1.1 坐标系定义大地坐标系为
| $ \left( {\begin{array}{*{20}{c}} {\boldsymbol{t}} \\ {\boldsymbol{n}} \\ {\boldsymbol{b}} \end{array}} \right) = \left[ {\begin{array}{*{20}{c}} {cos{\varphi _c}cos{\theta _c}}&{cos{\varphi _c}sin{\theta _c}}&{sin{\varphi _c}} \\ { - sin{\varphi _c}cos{\theta _c}}&{ - sin{\varphi _c}sin{\theta _c}}&{cos{\varphi _c}} \\ {sin{\theta _c}}&{ - cos{\theta _c}}&0 \end{array}} \right]\left( {\begin{array}{*{20}{c}} {\boldsymbol{i}} \\ {\boldsymbol{j}} \\ {\boldsymbol{k}} \end{array}} \right)。$ | (1) |

|
图 1 坐标系定义示意图 Fig. 1 Coordinate system definition |
潜水器的运动模型采用Fossen[17]使用的符号表示:
潜水器的运动模型采用美国海军研究院的NPS AUV Ⅱ[18-20],该模型采用尾部2台正反转螺旋桨推进,在首部、尾部有多个姿态调节舵面,与我国首个实验型35t级深海移动工作站具备一定相似性。
NPS AUVⅡ 潜水器的运动方程为:
| $ {{M}}\dot v + {{C}}\left( v \right)v + {{D}}\left( v \right)v + {{g}}\left( \eta \right) = {{Q}} 。$ | (2) |
其中:
Ablow等将缆索视为圆截面理想柔性弹性体,张力始终作用于缆索切向,忽略弯曲、扭转和剪切力的影响,且缆索处于张紧状态。重力加速度为
大地坐标系
| $ {\boldsymbol{u}} = {\boldsymbol{R}}_n^c\left( {{\Theta _c}} \right)({{\boldsymbol{v}}_E} - {{\boldsymbol{J}}_E}) + {{\boldsymbol{v}}_p} ,$ | (3) |
结合文献[7]可得到考虑缆索收放速度变化的缆索偏微分方程组控制方程组:
| $ {\boldsymbol{M}}\left( {s,t} \right)\frac{{\partial {\boldsymbol{Y}}\left( {s,t} \right)}}{{\partial s}} = {\boldsymbol{N}}\left( {s,t} \right)\frac{{\partial {\boldsymbol{Y}}\left( {s,t} \right)}}{{\partial t}} + {\boldsymbol{Q}}\left( {s,t} \right) 。$ | (4) |
式中:
| $ {\boldsymbol{M}}\left( {s,t} \right) = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0 \\ 0&1&0&0&{ - {v_b}\cos \varphi }&{ - {v_n}} \\ 0&0&1&0&{ - {v_b}\sin \varphi }&{{v_t}} \\ 0&0&0&1&{{v_t}\cos \varphi + {v_n}\sin \varphi }&0 \\ 0&0&0&0&{T\cos \varphi }&0 \\ 0&0&0&0&0&T \end{array}} \right],$ |
| $ \begin{gathered} {\boldsymbol{Q}}\left( {s,t} \right) = \hfill \\ \left[ {\begin{array}{*{20}{c}} {w\sin \varphi + 0.5\sqrt {1 + eT} \rho \text{π} d{C_\iota }{u_t}\left| {{u_t}} \right|} \\ 0 \\ 0 \\ 0 \\ {0.5\rho d\sqrt {1 + eT} {C_n}{u_b}\sqrt {u_n^2 + u_b^2} - \rho A{{\dot J}_b}} \\ {wcos\varphi + 0.5\rho d{C_n}\sqrt {1 + eT} {u_n}\sqrt {u_n^2 + u_b^2} - \rho A{{\dot J}_n}} \end{array}} \right] \hfill \\ \end{gathered} ,$ |
| $ \begin{split}{\boldsymbol{N}}\left( {s,t} \right) =& \left[ {\begin{array}{*{20}{c}} {\dfrac{{ - me{v_t}}}{{1 + eT}}}&m&0&0 \\ e&0&0&0\\ 0&0&1&0\\ 0&0&0&1\\ {\dfrac{{ - e({m_1}{v_b} - \rho {\rm A}{J_b})}}{{1 + eT}}}&0&0&{{m_1}}\\ {\dfrac{{ - e({m_1}{v_n} - \rho {\rm A}{J_n})}}{{1 + eT}}}&0&{{m_1}}&0 \end{array}} \right.\\ & \left. {\begin{array}{*{20}{c}} { - ({m_1}{v_b} - \rho {\rm A}{J_b})\cos \varphi }&{({m_1}{v_n} - \rho {\rm A}{J_n})} \\ 0&0 \\ 0&{1 + eT} \\ {(1 + eT)\cos \varphi }&0 \\ {m{v_t}\cos \varphi + ({m_1}{v_n} - \rho {\rm A}{J_n})\sin \varphi }&0 \\ { - ({m_1}{v_b} - \rho {\rm A}{J_b})\sin \varphi }&{m{v_t}} \end{array}} \right]。\end{split} $ |
其中:
根据潜水器拖曳、起吊作业需求,可知缆索上端点为速度约束,下端点根据是否拖曳载荷,分为自由边界或平衡约束。由于有限差分法不能处理缆索张力为零的情况,自由边界约束简化为微小张力的平衡约束。
自由边界:缆索末端未系重物,缆索尾部处于无张力状态,末端缆索单元的姿态角沿缆索长度变化率为0。
平衡约束:拖曳或吊放载荷端在拖曳或起吊过程中,缆索下端点受到的外力为拖曳载荷受到的重力、浮力、流体阻力的合力。
速度约束:缆索上端点在局部坐标系下的速度为潜水器航速在缆索局部坐标下的投影与缆索收放速度的合速度。
求解算法:在偏微分方程的求解中,采用具有2阶精度的中心差分格式。收放缆索的模拟采用在每一步迭代更新中,在求解非线性方程组时增加一次只更新缆索微元的长度的求解过程。
2 数值仿真验证 2.1 稳态过程仿真验证美国海军泰勒舰船研究发展中心在20世纪80年代对水下缆索进行了一系列实船拖曳试验,获得并公开了大量试验数据[21]。采用本文方法对其直航拖曳试验工况进行仿真,通过仿真数据与试验数据对比,对本文方法进行验证。实船拖曳直航试验的试验缆索分为6节,从下拖点编号1~6,各节缆索物理参数如表1所示。缆索杨氏模量为
|
|
表 1 拖曳缆索物理参数 Tab.1 Physical parameters of towing cable |
实船拖曳系统以18.5 kn航速直航,缆索上拖点与拖曳系统速度耦合,下拖点为自由端。数值仿真其监测点A和B深度,在该工况下缆索形态如图2所示。仿真得到的监测点A和B的深度与试验结果基本相符(见表2)。

|
图 2 潜水器直航拖曳缆索形态曲线 Fig. 2 Shape curve of the towing cable |
|
|
表 2 直航拖曳试验监测点深度比较 Tab.2 Results comparison of the towing test and simulation |
潜水器在拖曳、起吊作业工况下,一般航速较低,舵效差。大型潜水器通常具备浮力调节水箱、辅助推进器等设备,在拖曳和起吊作业下提供较大的浮力和姿态调节能力。避免分析因素过多,影响缆索收放影响的分析,在算例中不考虑其浮力变化或辅助推进器推力变化。
本文算例中采用NPS AUV Ⅱ潜水器模型,该模型只有尾部正反转推进器的推进动力及首、尾的水平和垂直操纵舵面。计算潜水器拖曳一定任务载荷调整航行深度后转直航、转直航后进行边拖曳、边收缆的回收任务载荷过程2个工况。通过上述2种工况的分析和比较对缆索收放过程对潜水器运动及缆索最大张力的影响。
缆索和拖曳载荷的基本参数如表3和表4所示。缆索上端点位置位于潜水器的浮心处,潜水器的模型参数、水动力系数见文献[19]。
|
|
表 3 拖曳缆索参数 Tab.3 Towing cable parameters |
|
|
表 4 拖曳物模型参数 Tab.4 Model parameters for towing objects |
表中的参数为默认参数,未明确说明不做改变。
2.2.2 潜水器拖曳载荷变深度转直航工况仿真研究场景演示:潜水器的缆索下端点与任务载荷相连,释放的缆索长度50 m,任务载荷已完成作业任务,准备进行回收任务载荷作业。为保障任务载荷与海底可能的触碰导致载荷损坏情况的发生,首先进行爬升航行高度流程。潜水器模型见文献[19]。
执行步骤:1)设定航行高度并准备;2)推进装置大功率推进,并操上浮舵;3)达到预设航行高度后,调整进入定深直航工况。
仿真工况:螺旋桨推进转速提高至1500 r/min,航行高度调整100 m,自动操舵,仿真时间1000 s。仿真结果如图3~图5所示。
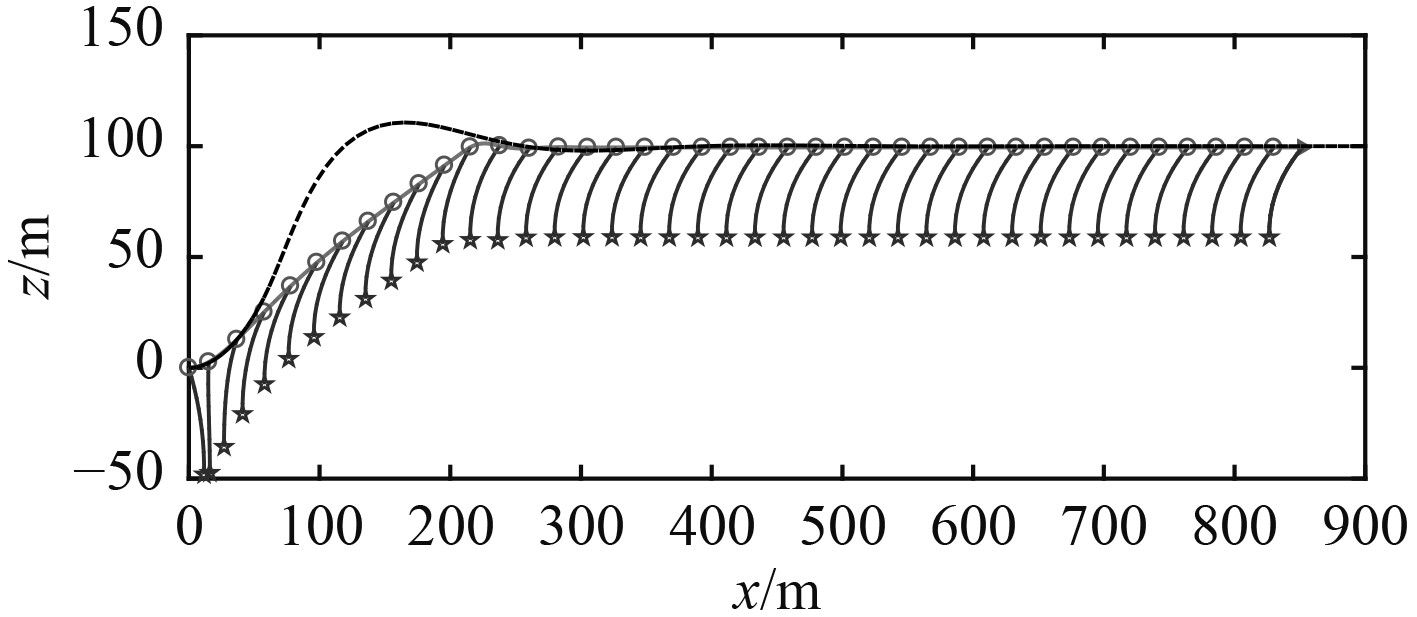
|
图 3 潜水器航行轨迹与缆索形态变化(实线:拖航;虚线:无拖航且同等推进动力) Fig. 3 AUV's trajectory and cable shape change |
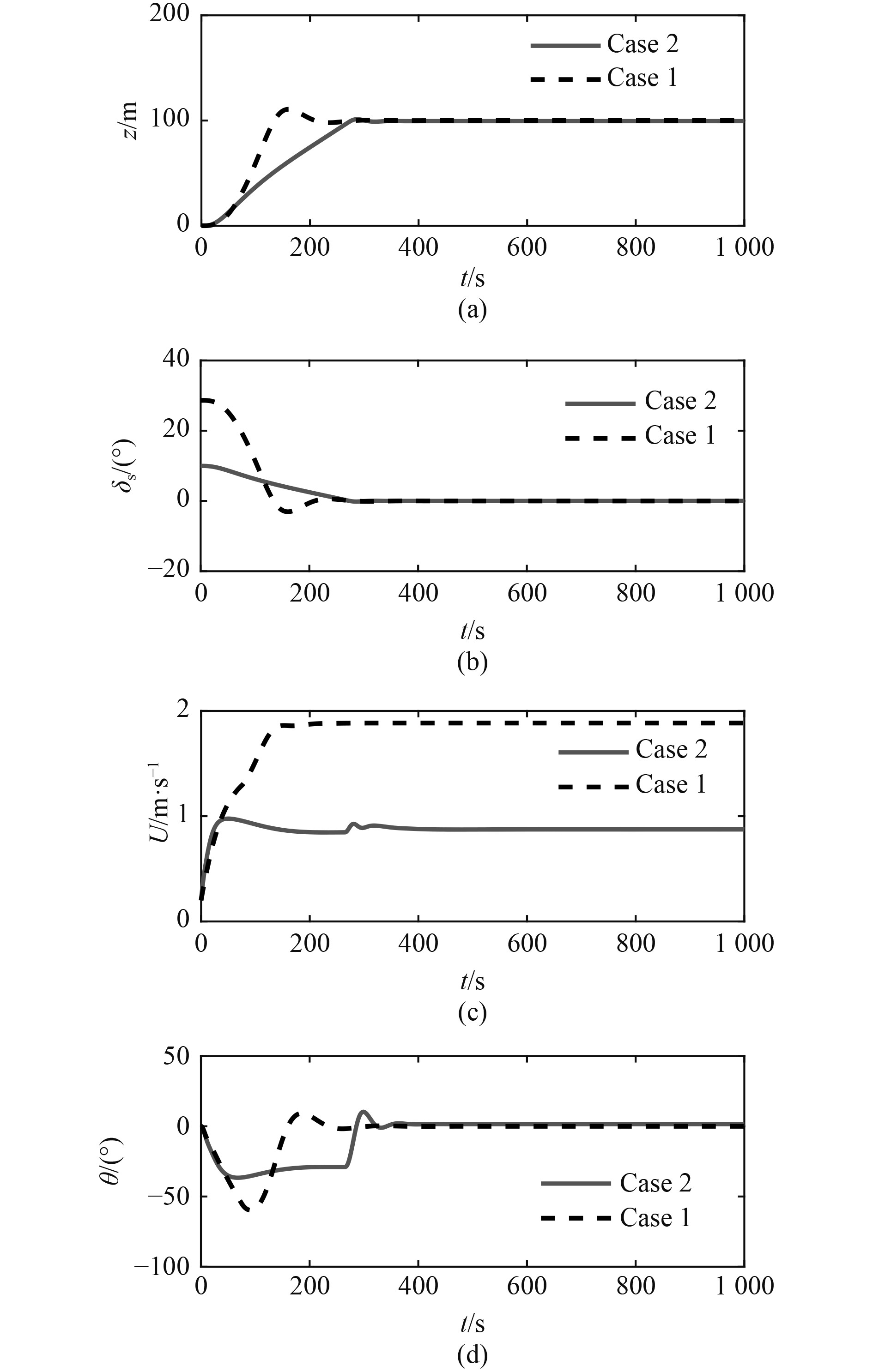
|
图 4 潜水器航行高度、升降舵、航速、纵倾角时间历程图(实线:拖航;虚线:无拖航且同等推进动力) Fig. 4 The time history of the altitude, rudder angle, speed and pitch angle |

|
图 5 拖航工况:缆索上端点张力与缆索长度变化时间历程图 Fig. 5 Towing case:Time history of the tension at the cable’s end point and cable length |
图3为潜水器航行轨迹与缆索形态曲线变化过程。图4为潜水器航行高度、升降舵舵角、航行速度、机身纵倾角随时间的变化历程图。图5为缆索上端点张力与缆索长度的变化时间历程图。
受力分析:开始阶段(稳态过程)潜水器无速度,缆索近乎垂直,缆索上端点张力约等于拖曳载荷及释放的缆索的重力与浮力之差:
| $ {{{T}}^{(1)}}{\text{ = (}}{G_b} - {B_b}{\text{) + }}(m - 0.25\;\rho \;\text{π} {d^2})g \approx 189\; {\text{N}}。$ |
与图5仿真结果的缆索上端点初始张力一致。通过速度及受力分析可以得出以下结论:
1)在相同推进器转速和操舵策略条件下,由于拖曳体与缆索施加给潜水器拖曳阻力,潜水器需更长时间才能调整到预设安全航行高度,并且由于拖航体和拖缆的流体阻力其稳定后的航行速度明显减小;
2)在潜水器爬升段中,拖曳系统施加在潜水器上的缆索张力先增加后减小,潜水器爬升至预定高度后,升降舵减小、潜水器纵倾角减小,上端点缆索张力随之减小,并在潜水器航速稳定后缆索张力逐渐稳定。该过程中缆索张力的变化与潜水器航行速度在缆索局部坐标系
场景演示:进行回收任务载荷作业,已完成爬升航行高度流程,执行缆索回收流程。潜水器模型见文献[19]。
执行步骤:1)完成调整航行高度并转入定深直航;2)稳定直航后收缆;3)缆索长度小于阈值后停止收缆。
仿真工况:从上述算例可知在仿真时间400 s左右,潜水器调整至预设航行高度,且速度稳定在0.9 m/s(1.8 kn)左右。可以认为在仿真时间500 s时,其已经达到稳定直航。并开始以0.1 m/s的速度收缆,缆索总长度小于0.5 m时停止收缆。螺旋桨推进转速维持1500 r/min,自动操舵维持航行高度,仿真时间1500 s。仿真结果如图6~图8所示。
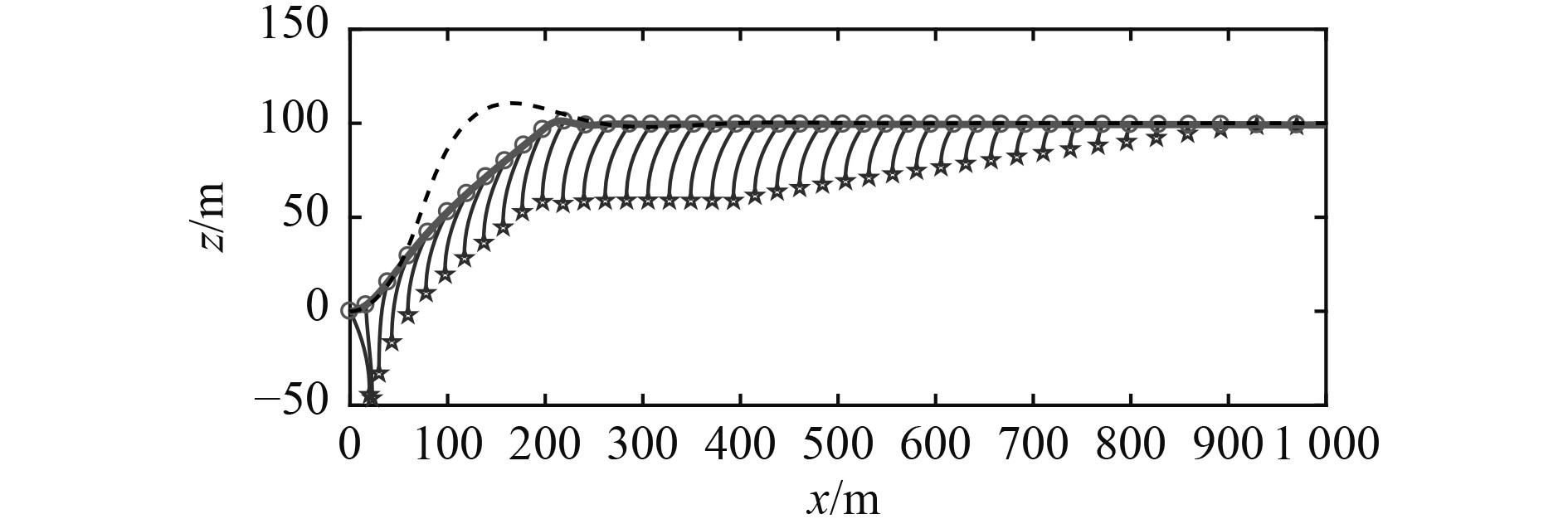
|
图 6 潜水器航行轨迹与缆索形态变化(实线:拖航收缆起吊;虚线:无拖航且同等推进动力) Fig. 6 AUV's trajectory and cable shape change |
图6为拖航收缆工况下潜水器航行轨迹与缆索形态曲线变化过程。图7为仿真过程中潜水器航行高度、升降舵舵角、航行速度、机身纵倾角随时间的变化历程图。图8为缆索上端点张力与缆索长度的变化时间历程图。

|
图 7 潜水器航行高度、升降舵、航速、纵倾角时间历程图(实线:拖航收缆;虚线:无拖航且同等推进动力) Fig. 7 The time history of the altitude, rudder angle, speed and pitch angle |
受力分析:潜水器停止收缆,达到稳定航速后,其缆索上端点张力为拖曳载荷受到的重力、浮力以及流体阻力的矢量合。潜水器定深直航,流阻与重浮力垂直:
通过速度及受力分析可以得出以下结论:
1)在相同推进器转速和操舵策略条件下,在收缆起吊过程中潜水器航行深度和纵倾角均保持在零度附近,并且随着缆索长度减小,拖曳系统施加给潜水器的缆索张力减小,潜水器航速增加。
2)在开始收缆时,拖缆点速度变化导致,缆索张力出现短暂跳变,说明缆索上端点张力对收放缆索的速度变化较敏感,应缓慢改变起吊速度以避免缆索张力剧烈变化。
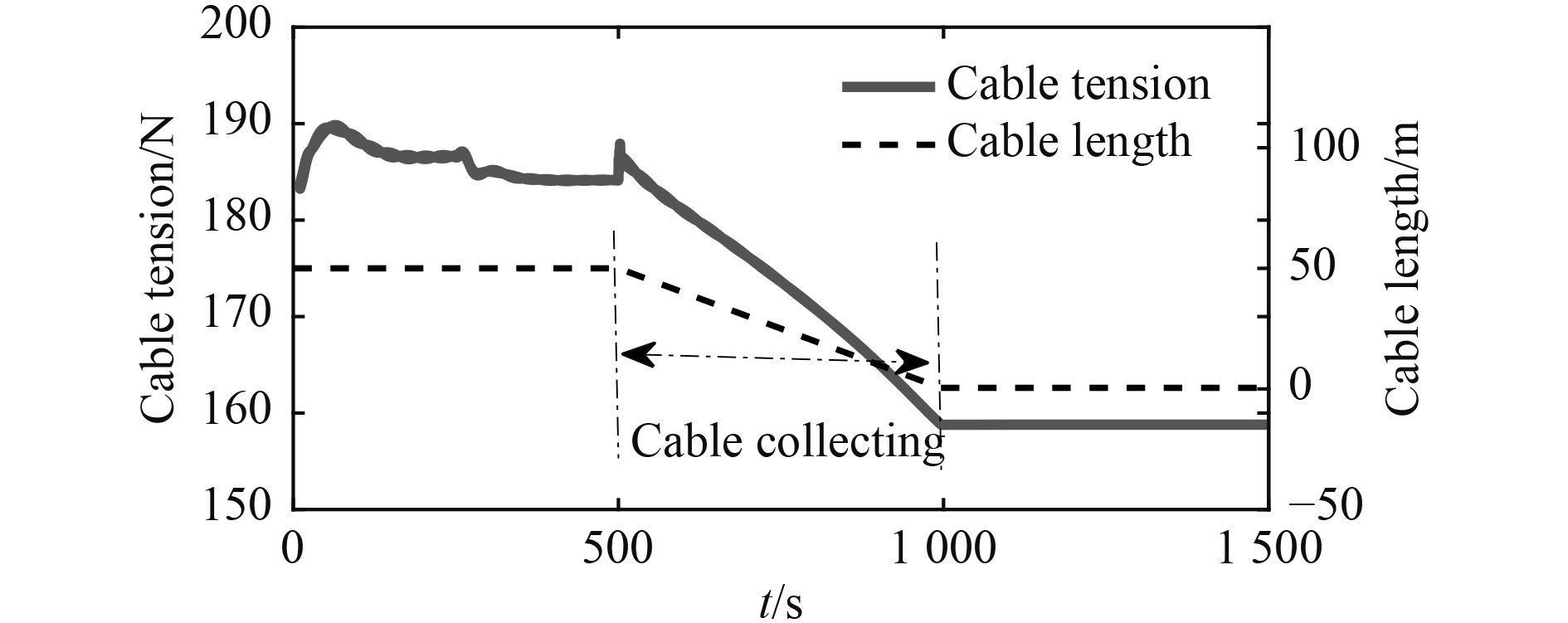
|
图 8 拖航收缆工况下:缆索上端点张力与缆索长度变化时间历程图(实线为缆索张力变化历程;虚线为拖曳缆索总长度) Fig. 8 Towing and lifting case:Time history of the tension at the cable’s end point and cable length |
本文针对潜水器-缆索-载荷三者间相互耦合作用研究中涉及的缆索变长度问题,在仿真办法调研过程中受到集中质量法和有限段法中改变缆索单元数目或凝聚质量点数目来实现缆索变长度问题仿真的启发,基于Ablow推导得到的缆索偏微分控制方程,在非线性方程组迭代时间接更新缆索微元段长度实现缆索收放过程的模拟,并通过稳定拖曳工况与文献对比验证。最后通过拖航变深度航行、拖航过程收缆索进行起吊作业2种算例,对本文方法在水下缆索收放场景模拟中的运用可行性进行了验证,并通过客观分析说明仿真结果的合理性和正确性,相关结论对于开展多用途潜水器拖曳和起吊能力设计具有一定指导意义。主要结论如下:
1)基于Ablow的缆索偏微分控制方程及缆索微元段长度更新策略,可以有效实现缆索收放过程的模拟。
2)潜水器拖曳任务载荷,在相同动力条件下,速度响应与无拖曳工况比较变慢、且稳定航速也降低。潜水器拖曳载荷爬升过程中由于艇体与缆索夹角小,缆索上端点张力较大。
3)在潜水器收缆作业中,缆索张力对收放缆索的速度变化较敏感,应缓慢改变起吊速度以避免缆索张力剧烈变化。同时,随着缆索长度减小,缆索上端点张力也明显减小,说明缆索自身也造成了相当的流体阻力。
本文建立的仿真办法可有效仿真潜水器拖曳航行和起吊航行工况下的运动响应和缆索张力变化,对潜水器水下缆索相关作业的研究提供了合适的仿真手段,但该方法在仿真速度和精度上有待进一步改进。
| [1] |
崔维成, 刘峰, 胡震, 等. 蛟龙号载人潜水器的7000米海上试验[J]. 船舶力学, 2012, 16(10): 1131-1143. CUI Weicheng, LIU Feng, HU Zhen et al. 7000 m sea trials test of deep manned submersible “JIAOLONG”[J]. Journal of Ship Mechanics, 2012, 16(10): 1131-1143. |
| [2] |
曹俊, 胡震, 刘涛, 等. 深海潜水器装备体系现状及发展分析[J]. 中国造船, 2020, 61(1): 204-218. CAO Jun, HU Zhen, LIU Tao et al. Current situation and development of deep-sea submersible equipment[J]. SHIPBUILDING OF CHINA, 2020, 61(1): 204-218. DOI:10.3969/j.issn.1000-4882.2020.01.021 |
| [3] |
丁军, 程小明, 田超, 等. 近岛礁浅水环境下浮式平台系泊系统设计研究[J]. 船舶力学, 2015, 19(7): 28-36. DING Jun, CHENG Xiao-Ming, TIAN Chao et al. Investigation on mooring system design for a floating platform in shallow water near islands and reefs[J]. Journal of Ship Mechanics, 2015, 19(7): 28-36. |
| [4] |
余 龙, 谭家华. 基于准静定方法的多成分系泊线优化[J]. 海洋工程, 2005, 23(1): 69-73. YU Long, TAN Jia-Hua. Research on optimum multi-component mooring lines based on catenary equation[J]. The Ocean Engineering, 2005, 23(1): 69-73. DOI:10.3969/j.issn.1005-9865.2005.01.011 |
| [5] |
王飞, 黄国樑, 邓德衡. 水下拖曳系统的稳态运动分析与设计[J]. 上海交通大学学报, 2008(04): 679-684. WANG Fei, HUANG Guo-Liang, DENG De-Heng. The design and steady-state simulation of underwater towed system[J]. Journal of Shanghai Jiaotong University, 2008(04): 679-684. DOI:10.3321/j.issn:1006-2467.2008.04.035 |
| [6] |
姚晨佼, 许可, 范华涛, 等. 基于载人潜水器的深海敷缆运动仿真[J]. 船舶工程, 2018, 40(11): 93-99. YAO Chen-Jiao, XU Ke, FAN Hua-Tao et al. Motion simulation of deep-sea cable-laying based on manned submarine[J]. Ship Engineering, 2018, 40(11): 93-99. |
| [7] |
Ablow C M, Schechter S. Numerical simulation of undersea cable dynamics[J]. Ocean Engineering, 1983, 10(6): 443-457. DOI:10.1016/0029-8018(83)90046-X |
| [8] |
Burgess JJ. Equations of motion of a submerged cable with bending stiffness[J]. Dynamics, 1992.
|
| [9] |
李英辉, 李喜斌, 戴杰, 等. 拖曳系统计算中拖缆与拖体的耦合计算[J]. 海洋工程, 2002(04): 37-42. LI Ying-Hui, LI Xi-Bin, DAI Jie et al. Calculation of coupling between the cable and the towed-body in the towed system[J]. The Ocean Engineering, 2002(04): 37-42. DOI:10.3969/j.issn.1005-9865.2002.04.007 |
| [10] |
付薇. 水下航行器拖曳系统运动仿真研究[D]. 北京: 中国舰船研究院, 2015.
|
| [11] |
王飞. 海洋勘探拖曳系统运动仿真与控制技术研究[D]. 上海: 上海交通大学, 2007.
|
| [12] |
陆肇康, 朱克强. 海洋非定常缆索系统三维动态仿真[J]. 华东船舶工业学院学报(自然科学版), 2003(02): 6-11. LU Zhao-Kang, ZHU Ke Qiang. Dynamic simulation of system of ocean changeable cable in three dimensions[J]. Journal of East China Shipbuilding Institute(Natural Science Edition), 2003(02): 6-11. |
| [13] |
Huston R L, Kamman J W. Validation of finite segment cable models[J]. Computers & Structures, 1982, 15(6): 653-660. |
| [14] |
Kamman J W, Nguyen T C, Crane J W. Modeling towed cable systems dynamics[C]. Oceans. IEEE, 1989.
|
| [15] |
李晓平. 多体系统动力学建模方法及其在水下缆索中的应用研究[D]. 天津: 天津大学, 2004.
|
| [16] |
彭云, 杨军刚, 肖勇, 等. 重力对大型环形可展天线展开动力学的影响研究[J]. 工程力学, 2018, 35(04): 234-242. PENG Yun, YANG Jun-Gang, XIAO Yong et al. Gravity effect on deployment dynamics of astromesh[J]. Engineering Mechanics, 2018, 35(04): 234-242. |
| [17] |
Fossen, T. I. Nonlinear modeling and control of underwater vehicles[D]. Department of Engineering Cybernetics, Norwegian University of Science and Technology, Trondheim, Norway. 1991.
|
| [18] |
Healey A J, Marco D B. Slow speed flight control of autonomous underwater vehicles: experimental results with NPS AUV II[J]. ISOPE, 1992.
|
| [19] |
Healey A J, Lienard D. Multivariable sliding mode control for autonomous diving and steering of unmanned underwater vehicles[J]. IEEE Journal of Ocean Engineering, 1993, 18(3): 327-339.
|
| [20] |
Healey A J, Marco D B, Mcghee R B, et al. Tactical / execution level coordination for hover control of the NPS AUV II using onboard sonar servoing[J]. Proceedings Of The Ieee Symposium On Autonomous Underwater Vehicle Technology, 1994.
|
| [21] |
Rispin, P. Memorandum. David W, Taylor Naval Ship Research and Development Center. Bethesda, Maryland. 1980.
|
 2022, Vol. 44
2022, Vol. 44
