0 引　言

船舶底边舱折角位置的受力状况比较复杂，且一旦出现撞击，底边舱折角位置往往首当其冲，因此，提高船舶底边舱折角位置的结构刚度、强度很有必要。肘板结构是复杂受力工况下常用的一种机械设计结构，使用肘板结构不仅能够提高机械结构的连续性，防止出现焊接区域的应力集中，也能够提升结构在极限载荷下的静态和动态强度。因此，使用肘板结构提升船舶底边舱折角位置的强度是一种有效的措施。

本文针对船舶底边舱折角位置的舱壁和肘板结构进行结构建模和三维仿真，有限元建模和仿真采用Ansys的参数化设计语言APDL，有助于后续进行快速化模型修改与优化。

1 基于有限元Ansys软件的参数化建模过程

参数化设计指在结构设计中使用参数化建模和分析思路，针对影响结构的重要几何参数进行建模，在修改模型时只需要修改重要参数。利用Ansys的参数化编程方法，可以实现有限元模型建立、修改和分析的快速迭代，目前，该参数化建模与分析技术已经在船舶等领域有非常广泛的应用。

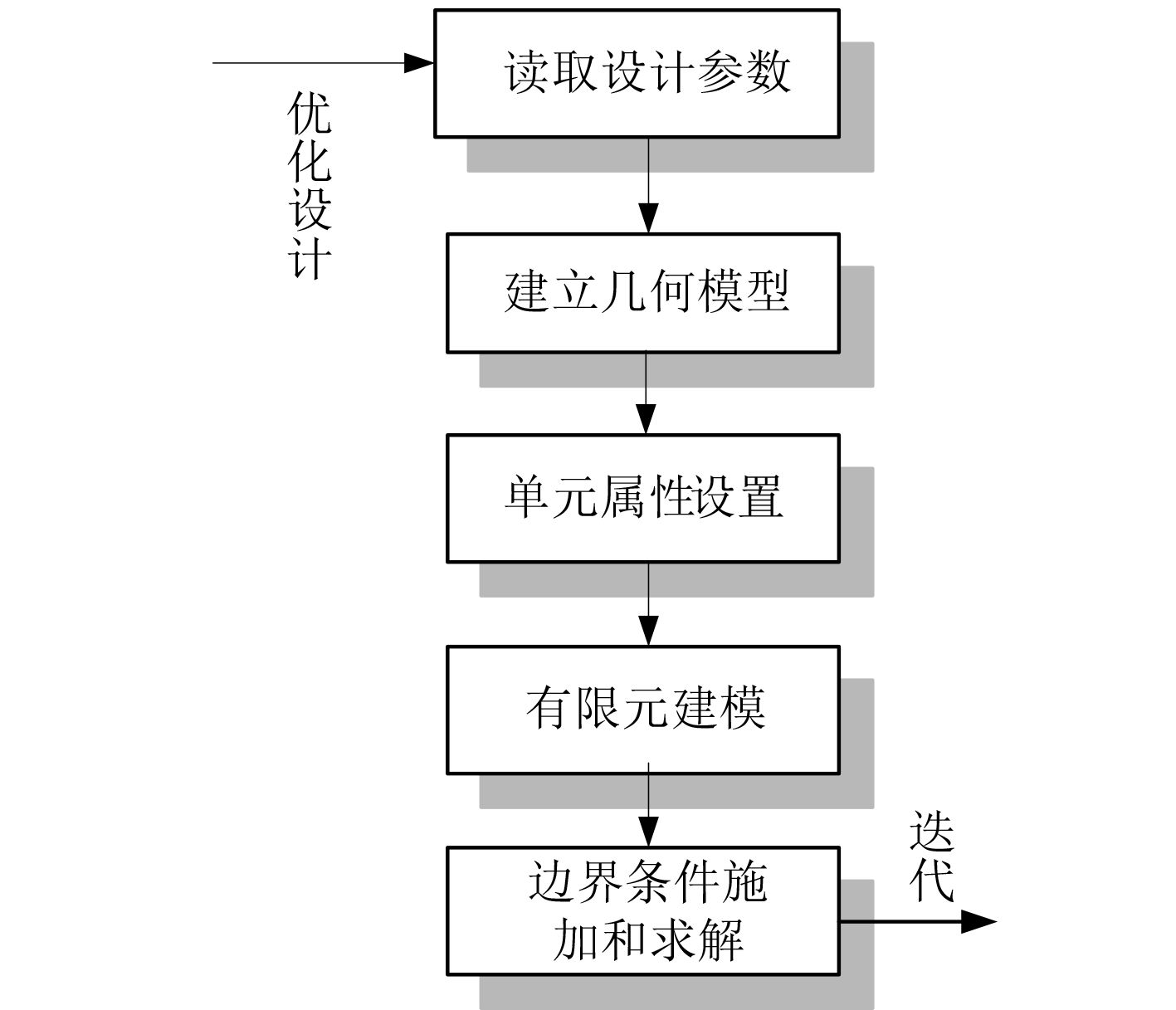
应用Ansys进行结构参数化建模和分析的流程如图1朱示。

1）读取设计参数

设计参数读取是进行参数化建模的基础，通常在进行结构优化设计之前就需要充分考虑当前结构的主要设计参数，将这些关键的设计参数作为Ansys有限元分析的变量，后期进行模型迭代时，分别对这些设计变量进行修改。

船舶底边舱折角结构的关键设计变量包括板材厚度、肘板长度和宽度、槽深等，以肘板长度为例，需要在设计初期确定船舶底边舱折角的坐标系原点和中心线，用空间坐标位置建立点、线、面和体模型，然后依次进行船舶底边舱折角的结构建模。需要注意的是，在进行参数化建模时，在Ansys中的设计变量不唯一，每个设计变量对于整体结构强度的影响需要进行多次仿真寻优。

2）建立几何模型

采用APDL参数化设计语言进行船舶底边舱折角位置的几何模型建立，常用的设计命令包括point（x，y，z）、line（point1，point2）等。由于船舶底边舱折角的结构以板材和壳体为主，因此，在建立几何模型时，需要首先确定该位置的尺寸范围，进而确定该模型的设计变量个数。建模过程包括：

①建立底边舱的壳体板材；

②在壳体板材一定尺寸位置处打断，在垂直板材方向上建立肘板；

③在2层板材之间建立加强肋板，每个肋板之间的距离相同。

3）单元属性设置

单元属性设置是进行有限元仿真的前提，且单元属性设置的准确性直接决定了整个仿真的准确度，采用恰当的单元属性来模拟现实中的机械结构同样是有限元仿真的关键内容。

底边舱折角处以板材和型钢为主，板材之间采用焊接的方式连接，因此，在进行单元属性设置时，主要采用2种单元类型为shell 183和beam 189，2种单元均为二次单元，在有限元仿真时更接近真实值，shell 183单元是一种8节点壳单元，可以模拟板材的塑性、大变形等工况。Beam 189单元是一种6节点单元，能够较真实模拟材料的剪切变形等工况。在进行单元属性设置时，需要将单元的弹性模量、泊松比、截面信息等进行设置。

4）有限元建模

设置好单元属性并建立机械结构的几何模型后，在Ansys中就可以进行有限元模型的建模，将几何模型进行网格划分。主要注意的是，网格划分的精度越高，每个有限单元的尺寸越小，仿真越高，但同时会提高Ansys有限元仿真的计算量，消耗更多的计算机资源和时间。因此，在进行网格划分时，选取恰当的网格大小及mesh方法非常重要。

船舶底边舱折角结构的尺寸较大，为了满足计算精度和计算机资源的需求，在设计整体网格大小时采用80 mm网格，在腹板与肘板的连接位置，由于应力集中现象较明显，进行网格的细化，将此处的网格大小定义为40 mm。

图2为船舶底边舱折角结构的有限元模型。

5）边界条件施加和求解

有限元模型建立后，通过分析底边舱折角结构的固定方式，确定该有限元模型的边界条件，包括外载荷、fix位置、fix自由度等。然后设置有限元模型求解的载荷步，进行模型的求解。

6）模型的优化和迭代计算

完成一轮有限元仿真后，定义Ansys中其他的结构设计变量，进行多轮校核和迭代，通过对比最后的仿真结果，确定设计变量的最优值。

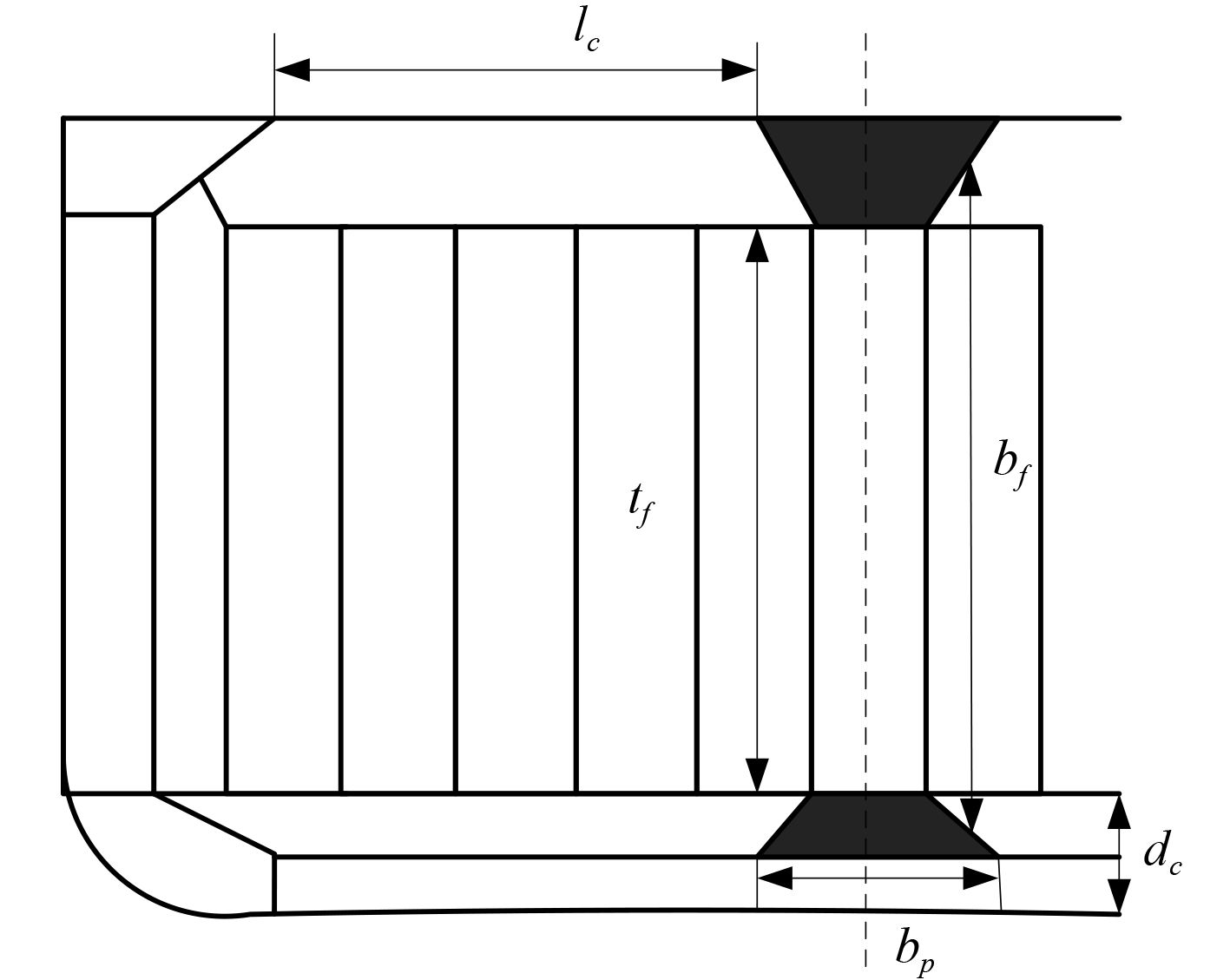
2 基于有限元的船舶底边舱折角处结构优化设计 2.1 船舶底边舱折角的尺度要求

船舶底边舱折角结构的设计尺寸要求见图3。

结合图3，确定在进行底边舱折角结构的优化设计时，需要重点优化的设计变量，主要包括腹板的厚度、肘板的厚度、肋板宽度、槽深等^[1]，分别如下：

1）腹板厚度

在设计底边舱折角位置的腹板厚度时，需要满足下式：

$ {t_f} = 0.015\;8{b_p}\sqrt {\frac{{|P|}}{{{C_a}{\sigma _{yt}}}}} {\rm{mm}}\text{。} $

式中： $ {t_f} $ 为腹板的最低厚度； $ {b_p} $ 为腹板的宽度； $ P $ 为设计载荷； $ {C_a} $ 为腹板的许用弯曲应力系数^[2]； $ {\sigma _{yt}} $ 为腹板的许用屈服应力。

当拼接的2个腹板厚度不一致时，设计板厚需要满足下述方程：

$ {t}_{f1}=\sqrt{\frac{0.000\;5{b}_{p}^{2}\left|P\right|}{{C}_{a}{\sigma }_{yt}}-{t}_{n}{}^{2}} \text{mm} \text{。} $

式中： $ {t_{f1}} $ 为净厚度； $ {t_n} $ 为2个相邻腹板中厚度较小的值； $ {C_a} $ 为腹板的许用弯曲应力系数； $ {\sigma _{yt}} $ 为腹板的许用屈服应力。

2）肘板厚度

肘板是底边舱位置进行结构强化的重要部件，其设计板厚需要满足下式：

$ {t}_{\text{w}}=\frac{1\;000\left|{Q}_{c}\right|}{{d}_{\text{c}}{C}_{t}{\tau }_{yl}} \text{mm} \text{。} $

式中： $ {d_{\text{c}}} $ 为肘板长度； $ {C_t} $ 为肘板许用剪切应力系数； $ {\tau _{yl}} $ 为肘板许用弯曲应力系数； $ {Q_c} $ 为肘板所受的剪切力，按下式计算：

$ {Q_c} = \frac{{{s_c}{l_c}\left| {3{P_1} + {P_u}} \right|}}{{8\;000}} 。$

式中： $ {s_c} $ 为肘板间距； $ {l_c} $ 为肘板长度； $ {P_1} $ 为肘板顶端考虑的设计剪切力； $ {P_u} $ 为肘板底部考虑的设计剪切力。

3）肋板宽度

肋板是连接肘板和腹板的结构，有助于提高整体结构的刚度，其宽度设计尺寸需满足：

$ {d}_{0}=\frac{0.006\;57{b}_{f}\sqrt{{\sigma }_{b}}}{{C}_{f}} \text{mm} \text{。} $

其中： $ {d_0} $ 为肋板宽度； $ {b_f} $ 为相邻肋板之间的距离； $ {\sigma _b} $ 为肋板最大的许用弯曲应力； $ {C_f} $ 为肋板宽度系数，用下式计算：

$ {C_f} = 7.65 - 0.26{\left( {\frac{{{b_{\text{w}}}}}{{{b_f}}}} \right)^2} 。$

2.2 船舶底边舱折角有限元谱分析法

在船舶工程领域，由于船体所受的载荷为波浪谱等连续性载荷，在分析这些载荷工况下的结构强度时，采用谱分析方法进行计算是非常合理的。使用谱分析方法进行船舶底边舱折角结构的疲劳特性分析，并在Ansys中进行疲劳强度的仿真。

整个仿真分析过程如下：

1）确定谱分析方法中的传递函数^[3]

由于船舶底边舱折角结构的疲劳分析需要确定“热点应力”，因此，需要确定应力传递函数 $ {H_\sigma }(\omega \mid $ $ \theta ) $ 。其中， $ \omega $ 为波浪频率， $ \theta $ 为波浪角度。

2）确定船舶结构的疲劳应力响应谱 ${S_\sigma }\left( \omega \mid {H_s}, $ $ {T_Z},\theta \right)$

如下式：

$ {S_\sigma }\left( {\omega \mid {H_s},{T_Z},\theta } \right) = {\left| {{H_\sigma }(\omega \mid \theta )} \right|^2}{S_n}\left( {\omega \mid {H_s},{T_z}} \right) 。$

3）计算谱矩

按照结构仿真的阶数进行谱矩的计算，如下式：

$ {m_n} = \displaystyle\int_0^\infty {\sum\limits_{\theta - 90}^{\theta + 90} {\left( {\frac{2}{\pi }} \right)} } {\cos ^2}\theta {\omega ^n}{S_\sigma }\left( \omega \right){\rm{d}}\omega 。$

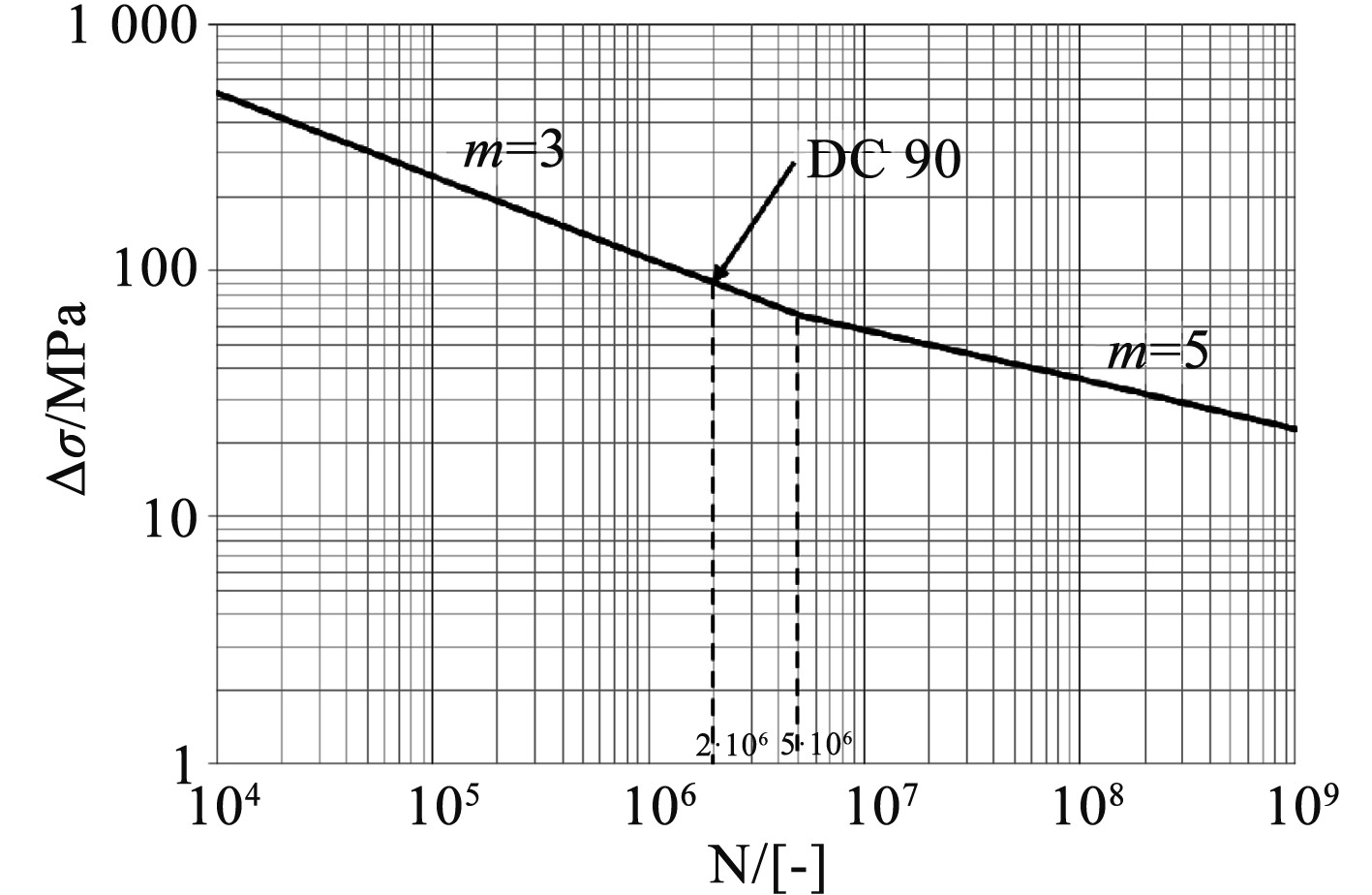
4）确定船舶材料的S-N曲线

选用的船舶结构材料S-N曲线如图4所示。

图中，横坐标代表材料的应力循环次数^[4]，纵坐标代表材料的应力值。

5）计算各工况下的疲劳应力概率密度函数

$ g(s) = \frac{s}{{4{\sigma ^2}}}\exp \left[ { - {{\left( {\frac{s}{{2\sqrt 2 \sigma }}} \right)}^2}} \right] \text{，} $

此外，当应力为交变应力时，需要进行平次次数的修正，如下式：

$ f = \frac{1}{{\sqrt 2 {\text{π}} }}\sqrt {\left( {\frac{{{m_1}}}{{{m_0}}}} \right)} 。$

6）计算累积疲劳损伤

采用miner法则^[5]进行船舶结构的疲劳损伤计算，即

$ D = \sum\limits_{i = 1}^n {{d_i}} 。$

在该S-N曲线下，应力损伤 $ {d_i} $ 用下式计算：

$ {d_i} = \left( {\frac{T}{A}} \right)\int_0^\infty {{s^m}} {f_{0i}}{p_i}{\rm{d}}s \text{。} $

式中： $ {s^m} $ 为应力； $ {f_{0i}} $ 为应力跨零率^[6]； $ {p_i} $ 为当前工况出现的概率； $ T $ 为设计疲劳寿命； $ A $ 为S-N曲线参数。

2.3 船舶底边舱折角有限元仿真

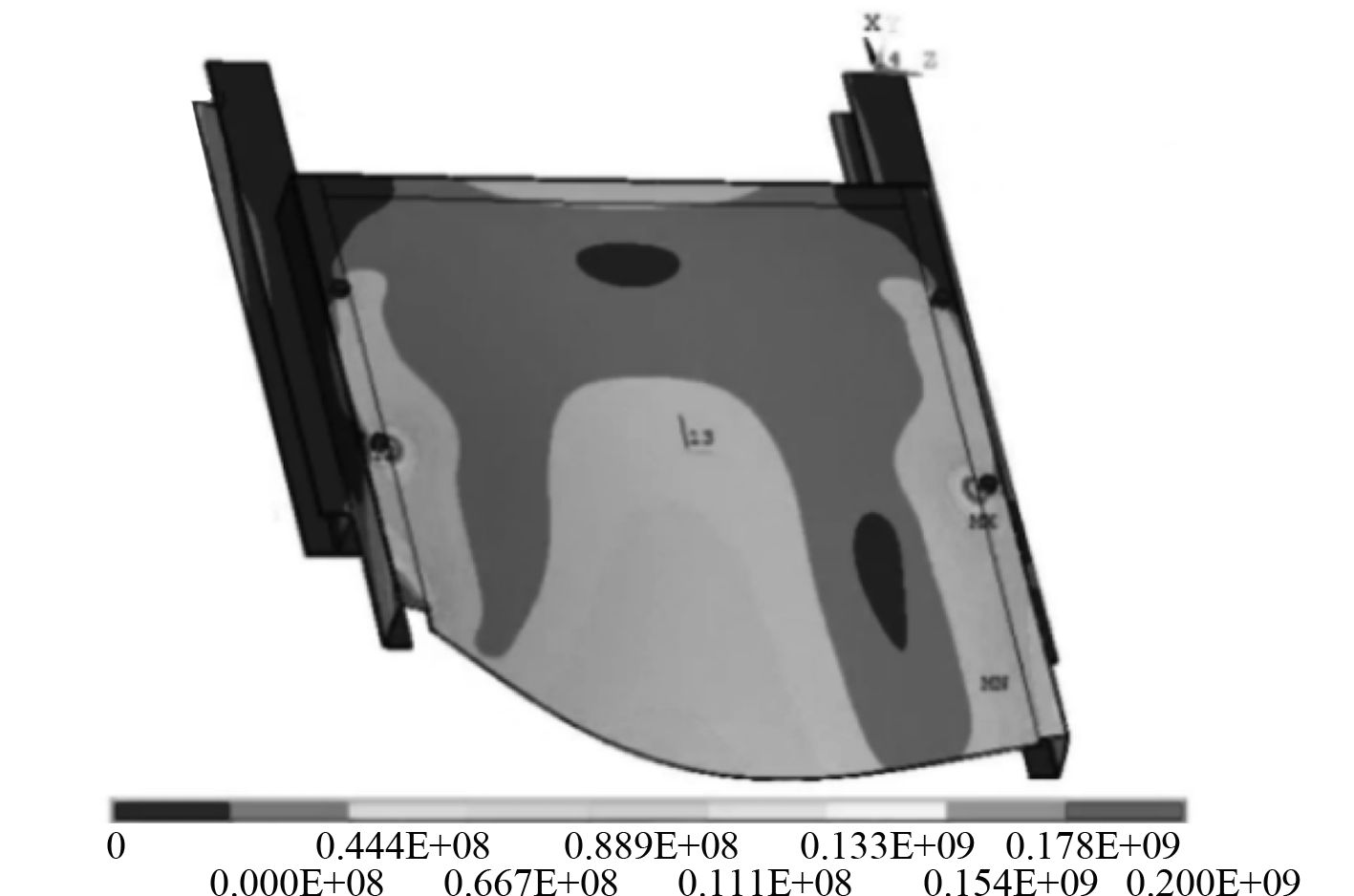
根据设计参数和建模，在Ansys中进行船舶底边舱折角结构的有限元仿真，图5和图6为船舶底边舱折角局部Von Mises应力云图：

可知，船舶底边舱折角局部应力最大值为228 MPa，满足材料的许用应力值。

3 结　语

本文基于Ansys进行船舶底边舱折角结构的参数化建模和仿真，详述了整个建模和仿真过程的关键参数和关键步骤，对于提高船舶底边舱折角结构的设计有参考作用。