0 引　言

随着新材料在水下装备的应用，除了压力环境条件，对压力舱内介质的温度也提出了要求^[1]。压力舱在开展压力-温度试验过程中，即使压力舱本体及其管路在没有结构渗漏的情况下，舱内可能会因为所含气体的析出及温降等能量损失而表现出压力的下降^[2]。

针对温度变化导致压力舱试验压力变化的问题，本文依据弹性力学和水力学的基本理论和相关试验数据，对压力舱温度变化与压力变化关系进行量化分析，以便对压力舱压力-温度耦合试验数据进行合理评判。

1 理论分析

一般来说，压力舱通常为钢制薄壁容器，试验介质通常为水。本文以由圆柱段及2个半球封头组成的钢制薄壁容器为对象，建立温度与压力关系式。

压力舱作为一个密闭容器，水的容积与密闭容器的容积相等，即 $ V{\text{ = }}{V_s} $ ，密闭容器受压力和温度影响容积变化与水受压力和温度影响体积变化也相同^[3-5]，由此可得：

$ {\rm{d}}{V_t}{\text{ + }}{\rm{d}}{V_P}{\text{ = }}{\rm{d}}{V_{st}} + {\rm{d}}{V_{sp}}。$

(1)

式中： ${\rm{d}}{V_{\text{t}}}$ 为水受温度影响的体积变化， $ {{\text{m}}^3} $ ； ${\rm{d}}{V_{\text{p}}}$ 为水受压力影响的体积变化， $ {{\text{m}}^3} $ ； ${\rm{d}}{V_{{\text{s}}t}}$ 为压力舱受温度影响容积的变化， $ {{\text{m}}^3} $ ； ${\rm{d}}{V_{sp}}$ 为压力舱受压力影响容积的变化， $ {{\text{m}}^3} $ 。

1.1 水受温度影响的体积变化计算

水膨胀系数即单位体积的水，温度每增高1℃，体积的增加量，用 $ {\beta _{\text{t}}} $ 表示，其表达式如下：

$ {\beta _{\text{t}}} = \frac{1}{V} \cdot \frac{{{\rm{d}}{V_{\text{t}}}}}{{{\rm{d}}t}}{{ = - }}\frac{1}{{{\rho _{\text{t}}}}} \cdot \frac{{{\rm{d}}{\rho _{\text{t}}}}}{{{\rm{d}}t}} ，$

(2)

$ 即{\rm{d}}{V_{\text{t}}} = {\beta _{\text{t}}}V{\rm{d}}t = {{ - }}\frac{V}{{{\rho _{\text{t}}}}} \cdot {\rm{d}}{\rho _{\text{t}}} 。$

(3)

式中： ${\rm{d}}{V_{\text{t}}}$ 为水受温度影响的体积变化， $ {{\text{m}}^3} $ ； $ V $ 为水体积， $ {{\text{m}}^3} $ ； $ {\rho _{\text{t}}} $ 为水在温度t℃时的密度， $ {\text{kg/}}{{\text{m}}^3} $ ； $ d{\rho _{\text{t}}} $ 为水受温度影响的密度变化值， $ {\text{kg/}}{{\text{m}}^3} $ ； ${\rm{d}}t$ 为温度的变化值，℃； $ {\beta _{\text{t}}} $ 为水的体积膨胀系数，1/℃。

查询1990国际温标水密度表，水的密度-温度曲线如图1所示。通过2阶多项式拟合得

$ {\rho _{\text{t}}}{{ = - 0}}{{.003\;5}}{t^2} - 0.077\;5t + 1\;000.799\;5 ，$

因而：

$ {\rm{d}}{V}_{\text{t}}=\frac{V}{{\rho }_{\text{t}}}(0.007t+0.077\;5){\rm{d}}t 。$

(4)

1.2 水受压力影响的体积变化计算

水的压缩系数即单位体积的水，压力每增加1 $ {\text{MPa}} $ ，体积的减少量，用 $ {\beta _{\text{p}}} $ 表示，其表达式如下：

$ {\beta _{\text{p}}} = {{ - }}\frac{1}{V} \cdot \frac{{{\rm{d}}{V_{\text{p}}}}}{{{\rm{d}}P}}{\text{ = }}\frac{1}{{{\rho _{\text{p}}}}} \cdot \frac{{{\rm{d}}{\rho _{\text{p}}}}}{{dP}} ，$

(5)

$ 即 {\rm{d}}{V_{\text{P}}} = - {\beta _{\text{P}}}V{\rm{d}}P = {{ - }}\frac{V}{{{\rho _{\text{p}}}}} \cdot {\rm{d}}{\rho _{\text{p}}} 。$

(6)

式中： ${\rm{d}}{V_{\text{p}}}$ 为水受压力影响的体积变化， $ {{\text{m}}^3} $ ； $ V $ 为水体积， $ {{\text{m}}^3} $ ； ${\rm{d}}{\rho _{\text{p}}}$ 为水受压力影响的密度变化值， $ {\text{kg/}}{{\text{m}}^3} $ ； ${\rm{d}}P$ 为压力的变化值， $ {\text{MPa}} $ ； $ {\beta _{\text{p}}} $ 为水的压缩系数， $ {1 \mathord{\left/ {\vphantom {1 {{\text{MPa}}}}} \right. } {{\text{MPa}}}} $ 。

查询水的物性手册可知，不同温度下，水的可压缩性-压力曲线，如图2所示。通过线性拟合得:

$\begin{split}& {\left(\frac{V-{\rm{d}}{V}_{p}}{V}\right)}_{0℃}=-0.000\;429p+0.999\;483 \text{，} \\&{\left(\frac{V-{\rm{d}}{V}_{p}}{V}\right)}_{10℃}=-0.000\;405p+0.999\;517 ，\end{split}$

$\begin{split} &{\left(\frac{V-{\rm{d}}{V}_{p}}{V}\right)}_{20℃}=-0.000\;393p+1.001\;183 \text{，} \\&{\left(\frac{V-{\rm{d}}{V}_{p}}{V}\right)}_{40℃}=-0.000\;383p+1.007\;083 , \end{split}$

$\begin{split} &{\left(\frac{V-{\rm{d}}{V}_{p}}{V}\right)}_{60℃}=-0.000\;384p+1.016\;6 \text{，}\\& {\left(\frac{V-{\rm{d}}{V}_{p}}{V}\right)}_{80℃}=-0.000\;398p+1.028\;233 。\end{split}$

在不同温度下，水的压缩系数如表1所示。

1.3 压力舱受温度影响的体积变化计算

在压力舱内介质温度发生变化时，由于钢结构的热膨胀性，压力舱的截面积与长度均发生变化并影响压力舱的容积。

压力舱圆柱段膨胀量：

$ {\rm{d}}{V}_{st,1}=2\pi rL{\rm{d}}r+\pi {r}^{2}{\rm{d}}L=3\alpha \pi {r}^{2}L{{{\rm{d}}}}t ，$

(7)

压力舱2个半球封头膨胀量：

$ {\rm{d}}{V_{st,2}} = 4\pi {r^2}{\rm{d}}r{\text{ = 4}}\alpha \pi {r^3}{{{\rm{d}}}}t ，$

(8)

压力舱膨胀量：

$ {\rm{d}}{V}_{st}={\rm{d}}{V}_{st,1}\text+{\rm{d}}{V}_{st,2}\text=（3\alpha \pi {r}^{2}L+\text{4}\alpha \pi {r}^{3}）{{{\rm{d}}}}t 。$

(9)

式中： ${\rm{d}}{V_{{\text{s}}t}}$ 为受温度影响压力舱容积的变化， $ {{\text{m}}^3} $ ； $ L $ 为压力舱圆柱段长度， $ {\text{m}} $ ； $ r $ 为压力舱圆柱段内径， $ {\text{m}} $ ； ${{{\rm{d}}}}t$ 为温度的变化值，℃ ； $ \alpha $ 为钢材的热膨胀系数，1/℃。

1.4 压力舱受压力影响的体积变化计算

在压力舱加压过程中，会受到内部压力的作用，当内部压力变化时，压力舱的截面积与长度均发生变化并影响压力舱的容积。根据弹性力学理论，压力舱容积受压力影响计算如下：

压力舱圆柱段膨胀量

$ {\rm{d}}{V_{sp,1}}{\text{ = }}2\pi RLdR + \pi {R^2}{\rm{d}}L{\text{ = }}\frac{{1.9\pi {R^3}L}}{{{\xi _1}E}}{\rm{d}}P ，$

(10)

压力舱2个半球封头膨胀量

$ {\rm{d}}{V_{sp,2}}{\text{ = }}\frac{{4\pi {R^3} \times 0.7R{\rm{d}}P}}{{{\xi _2}E}}{\text{ = }}\frac{{2.8\pi {R^4}{\rm{d}}P}}{{{\xi _2}E}} ，$

(11)

压力舱膨胀量

$ {\rm{d}}{V_{sp}}{\text{ = }}{\rm{d}}{V_{sp,1}}{\text{ + }}{\rm{d}}{V_{sp,2}}{\text{ = }}\left( {\frac{{1.9\pi {R^3}L}}{{{\xi _1}E}}{\text{ + }}\frac{{2.8\pi {R^4}}}{{{\xi _2}E}}} \right){\rm{d}}P。$

(12)

式中： ${\rm{d}}{V_{sp}}$ 为受压力影响压力舱容积的变化， $ {{\text{m}}^3} $ ； $ L $ 为压力舱圆柱段长度， $ {\text{m}} $ ； $ r $ 为压力舱圆柱段内径， $ {\text{m}} $ ； $ {\xi _1} $ 为圆柱段厚度， $ {\text{mm}} $ ； $ {\xi _2} $ 为球封头厚度， $ {\text{mm}} $ ； ${\rm{d}}P$ 为压力的变化值， $ {\text{MPa}} $ ； $ E $ 为压力舱本体材料的弹性模量， $ {\text{MPa}} $ 。

1.5 压力舱压力变化-温度变化关系式确立

综上可得，压力舱由温度变化导致压力变化的计算公式：

$ {\rm{d}}P{\text{ = }}\frac{{{\beta _t}V - {k_1}}}{{{k_2}{\text{ + }}{\beta _{\text{P}}}V}}{{{\rm{d}}}}t ，$

(13)

$ \text{或} {\rm{d}}P= \left(\frac{{{k_1}}}{{{k_2} + {\beta _{\text{p}}}V}}{\text{ + }}\frac{{V\left( {0.007t + 0.077\;5} \right)}}{{{\rho _{\text{t}}}({k_2} + {\beta _{\text{p}}}V)}}\right){{{\rm{d}}}}t ，$

(14)

$ \text{其中，}{k_1}{\text{ = }}3\alpha \pi {r^2}L + {\text{4}}\alpha \pi {r^3} ，{k_2}{\text{ = }}\frac{{1.9\pi {R^3}L}}{{{\xi _1}E}}{\text{ + }}\frac{{2.8\pi {R^4}}}{{{\xi _2}E}} 。$

2 实例分析 2.1 实例理论计算

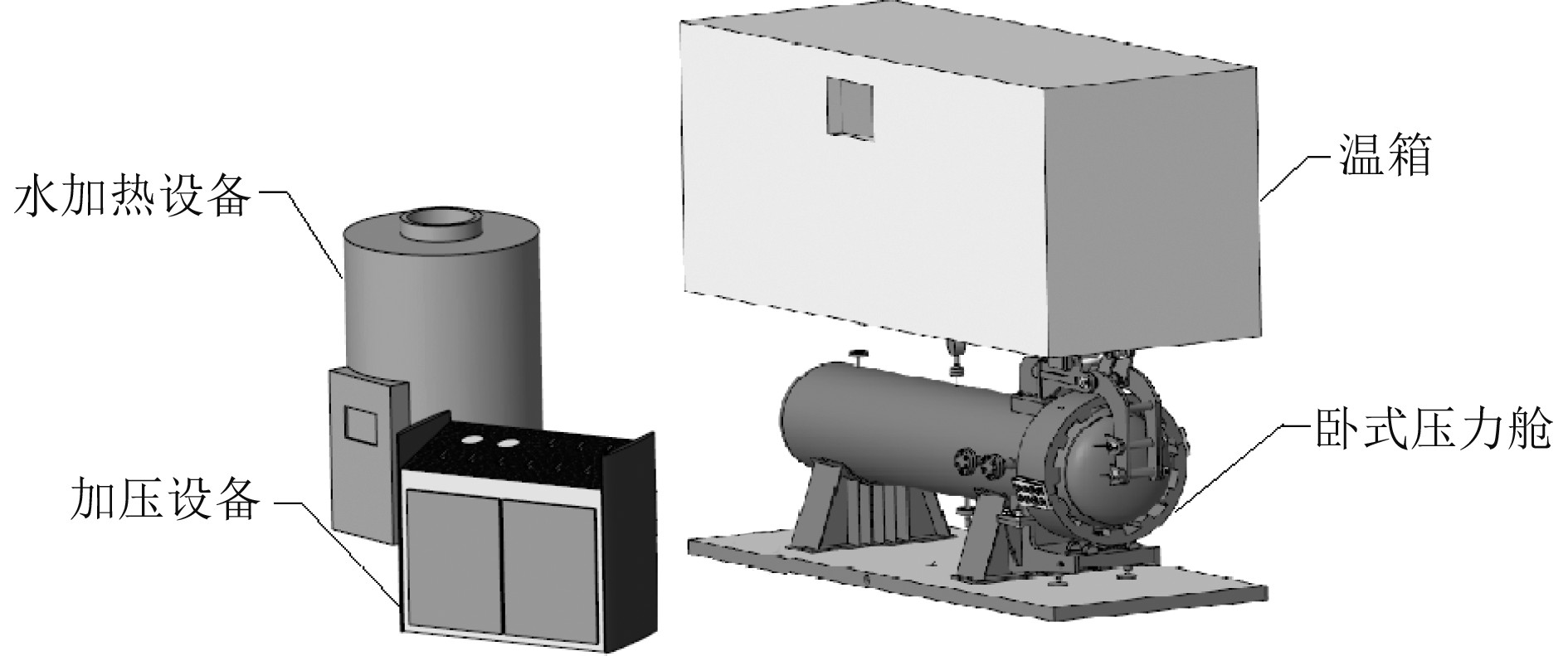
某承压试验设施主要由卧式压力舱、加压设备、水加热设备、温箱等组成，其总体效果图如图3所示。其核心设备卧式压力舱基础数据如表2所示。

查询1990国际温标水密度表，不同温度下水的密度如表3所示。

将表1～表3相关数据代入式（14），可得不同温度下，舱内温降1℃时舱内压降，计算结果如表4所示。

舱内温降1℃时的压降-温降曲线如图4所示。通过最小二乘法线性拟合得舱内温降1℃时的压降计算公式：

$ {\rm{d}}{P_1}{\text{ = }}0.004t + 1.001\;8 。$

(15)

由式（15）可得，舱内温降 $ k $ ℃时的压降计算公式：

$ {\rm{d}}{P_{\text{k}}} = k\left[ {0.004t + 1.001\;8 - \frac{{(k - 1)}}{2} \times 0.004} \right] (0 < k < t,k \in N )。$

(16)

式中： ${\rm{d}}{P_1}$ 为舱内温度变化1℃时，压力的变化值， $ {\text{MPa}} $ ； ${\rm{d}}{P_{\text{k}}}$ 为舱内温度变化 $ k $ ℃时，压力的变化值， $ {\text{MPa}} $ ； $ t $ 为舱内水的温度，℃。

2.2 实例现场试验

首先，水由加热设备加热至78℃，注入卧式压力舱，盖上温箱，静置30 min。加压设备先后将舱内压力加压至5 MPa和10 MPa进行保压，记录舱内压力与舱内温度值。保压过程中，加压设备关闭所有阀门，不进行自动补压，舱内压力和舱内温度实测数据如表5所示，压力-温度曲线如图5所示。

由式（16）计算可得，压力舱温度由75.4℃下降3℃时，压降理论值为3.9 MPa，而实测值为3.74 MPa，相对误差为4%。温度由66.8℃下降1℃时，压降理论值为1.27 MPa，实测值为1.17 MPa，相对误差为7.8%。数据结果表明，现场试验结果与理论计算基本一致。

3 结　语

通过温度变化引起压力舱压降的理论计算和试验数据结果的一致性，为压力舱开展压力-温度试验数据评判提供了计算方法和理论依据。