船舶在水中航行时,需要依靠螺旋桨的推动力向前行驶,如果螺旋桨出现异常状况,则会对船舶的航行造成不利影响。振力异常是螺旋桨较为常见的问题,为避免其对船舶航行安全性和稳定性带来的影响,需要对螺旋桨振力异常进行准确的数值预报[1-3]。为此,就云计算环境下船舶螺旋桨振力异常数值预报展开分析探讨。
1 螺旋桨的水动力性能分析 1.1 建立模型在对螺旋桨的水动力性能计算前,要先构建相关的模型和计算域。建立几何模型时,采用ICEM函数,并对螺旋桨工作状态进行模拟。为确保螺旋桨敞水性能的计算结果准确,要在流场内进行计算,这就需要建立起一个能够模拟敞水状态的计算域。该计算域主要由两部分组成,一部分为大域,用于模拟敞水状态,另一部分为小域,用来模拟螺旋桨的旋转[4-6]。计算螺旋桨的水动力性能时,小域的直径可以取螺旋桨单片桨叶直径的1.2倍,大域的直径则可取螺旋桨单片桨叶直径的8倍。
1.2 划分计算网格对于流体动力学(CFD)的计算而言,网格划分是一个比较重要的环节。划分的网格质量越高,收敛性越好,计算精度也就越高,由此能够为流场中质点流动细节的捕捉提供便利。本文研究中,模型采用六面体网格,该网格最为突出的特点是,能够在保证精度的前提下,减少网络数量[7]。
1.3 敞水性能计算结果桨叶表面的压力梯度随着进速系数的增大变得均匀,由此说明,在重载情况下,螺旋桨存在严重的空泡噪声。
2 云计算环境下船舶螺旋桨振力异常数值预报 2.1 螺旋桨激振力数值计算在对船舶的整体性能进行预估时,较为常用的技术手段和方法有船模数值仿真分析、船模水池试验等。由于船模与实体船舶的雷诺数存在不相等的情况,从而使得数据换算后会出现一定的误差,虽然计算流体动力学技术得到快速发展,并且船桨一体化模型的计算方法也较为完善。但是,受到多方面因素的影响,如模拟网格数量大、收敛时间长等,导致计算过程复杂化,很难有效捕捉到自由液面。依托KCS船和KP505浆,在云计算环境下,运用Fluent软件构建水池模型,借助该模型模拟船桨自航,通过计算获取螺旋桨的激振力,为振力异常数值预报提供依据。在正式计算开始前,要先确定计算模型,并使模型与实体船舶在尺度方面的网络拓扑结构相一致。具体的计算工况如下:实体船舶自航试验模拟计算、基于船桨一体化的螺旋桨激振力计算。可用于螺旋桨旋转运动稳态计算的方法比较多,本文选用的是MRF(多重参考模型),其归属于定常计算模型的范畴,在该模型中假定网格单元匀速运动。通过建立在欧拉网格下的界面追踪方法(VOF)追踪自由液面,以压力校正法(SIMPLEC)实现压力速度耦合迭代。
为了获得更加准确的螺旋桨振力模型,可以对上述的运动模型进行估算,估算模型如下:
| $ {\hat x_k} = E\left( {{x_k}|{z_{1:k}}} \right) = \int {{x_k}} p\left( {{x_k}|{z_{1:k}}} \right){\rm{d}}{x_k} \text{。} $ |
第一步先对估算模型中的
| $ \tilde pN\left( {{x_k}|{z_{1:k}}} \right) = \sum\limits_{i = 1}^N {\tilde w_k^i} \delta \left( {{{\tilde x}_k} - \tilde x_k^i} \right) \text{。} $ |
式中:k为粒子集的权值;
经过计算后,可以将后验概率用如下的离散函数形式进行表示:
| $ \tilde pN\left( {{x_k}|{z_{1:k}}} \right) = \sum\limits_{i = 1}^N {\frac{1}{N}} \delta \left( {{{\tilde x}_k} - \tilde x_k^i} \right) \text{。} $ |
实体船舶在自航试验中,需要对船体的阻力数值加以计算,具体方法和过程如下:对实体船舶自航点确定前,要先计算自由液面下的裸船体阻力,总的阻力系数可通过下式获取:
| $ {SFC}=(1+{k})\left(C_{\mathrm{FM}}-C_{F S}-\Delta \mathrm{C}_{\mathrm{F}}\right)。$ |
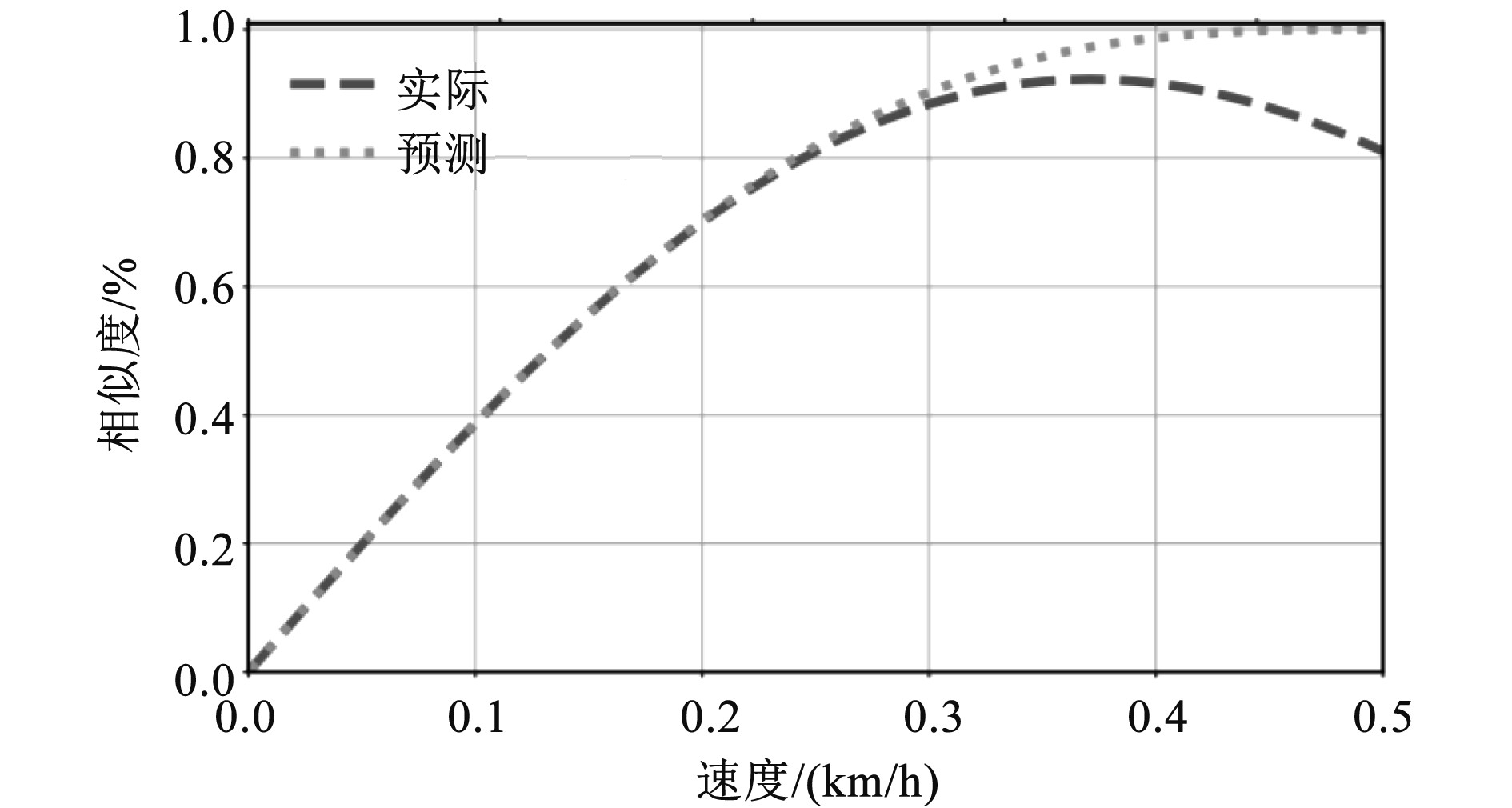
式中:SFC为摩擦阻力修正系数;1+k取1.1;CFM和CFS通过相关公式计算后可得出具体数值,依次为2.1和1. 8。通过计算后发现,实体船舶的总阻力系数要比换算值大一些,二者之间的误差约为3.83%,SFC与计算值的误差为2.63%。1+k存在较大的尺度效应,当雷诺数增大后,尺度会随之增加,与之相关的形状因子也进一步增大。若是在不考虑尺度效应的前提下正常换算,则会导致SFC过小,从而导致总阻力系数偏大。当船舶处于高速航行时,即Fr>0.2时,形状因子1+k会随着Fr的增大而减小。为确保计算结果的准确性,Fr的取值为0.26,与0.16相比,增大了0.1,由此使尺度效应带来的误差被抵消。图1为实体船舶无量纲轴向速度的实际与预测相似度曲线。
|
图 1 实体船舶无量纲轴向速度的实际与预测相似度曲线 Fig. 1 Actual and predicted similarity curves for dimensionless axial velocities of solid ships |
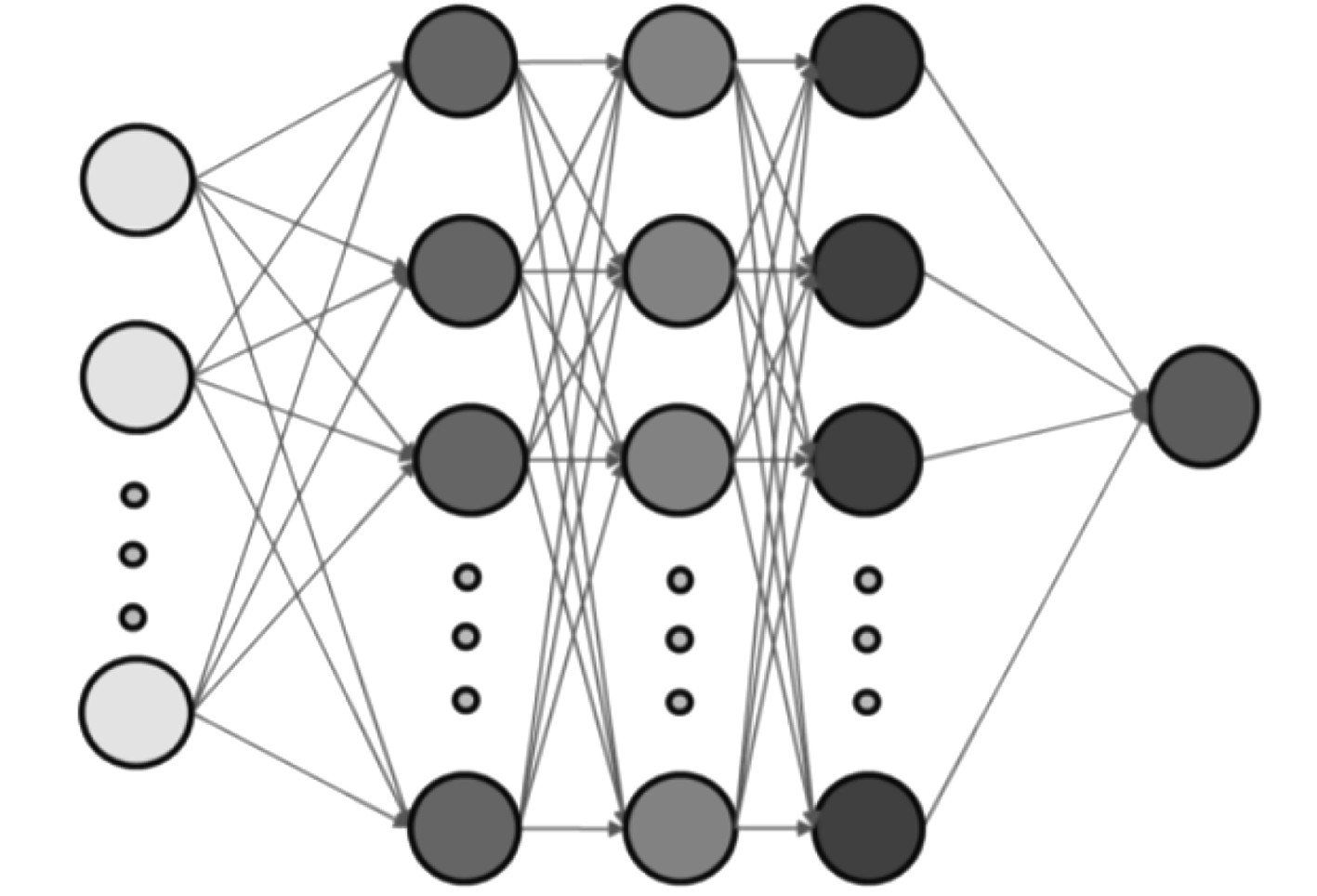
与船模的边界层相比,实体船舶的边界层更薄,其轴向速度等值线向内收缩,桨盘面位置处的轴向速度更大。通过对螺旋桨所处的位置区域进行观察后发现,实体船舶与船模存在较大的伴流差异,前者螺旋桨的进速要明显大于后者,若是以测量得到的伴流分数作为依据,对螺旋桨进行计算,可能使安装在实体船舶上的螺旋桨出现推力不足的现象。基于此,应预留出一定的推力余量,确保螺旋桨推力足够。图2为船模推进系统的输入输出结构框图。
|
图 2 船模推进系统的输入输出结构框图 Fig. 2 Block diagram of input and output structure of ship model propulsion system |
由图2可知,实体船舶和船模的兴波差别非常小,这充分说明,兴波阻力与雷诺数无关。但二者的尾部波形存在差异,实体船舶的尾部波形呈现出整体后移的情况。在对实体船舶的自航点确定时,不需要考虑摩擦阻力,由此使操作步骤得以简化。
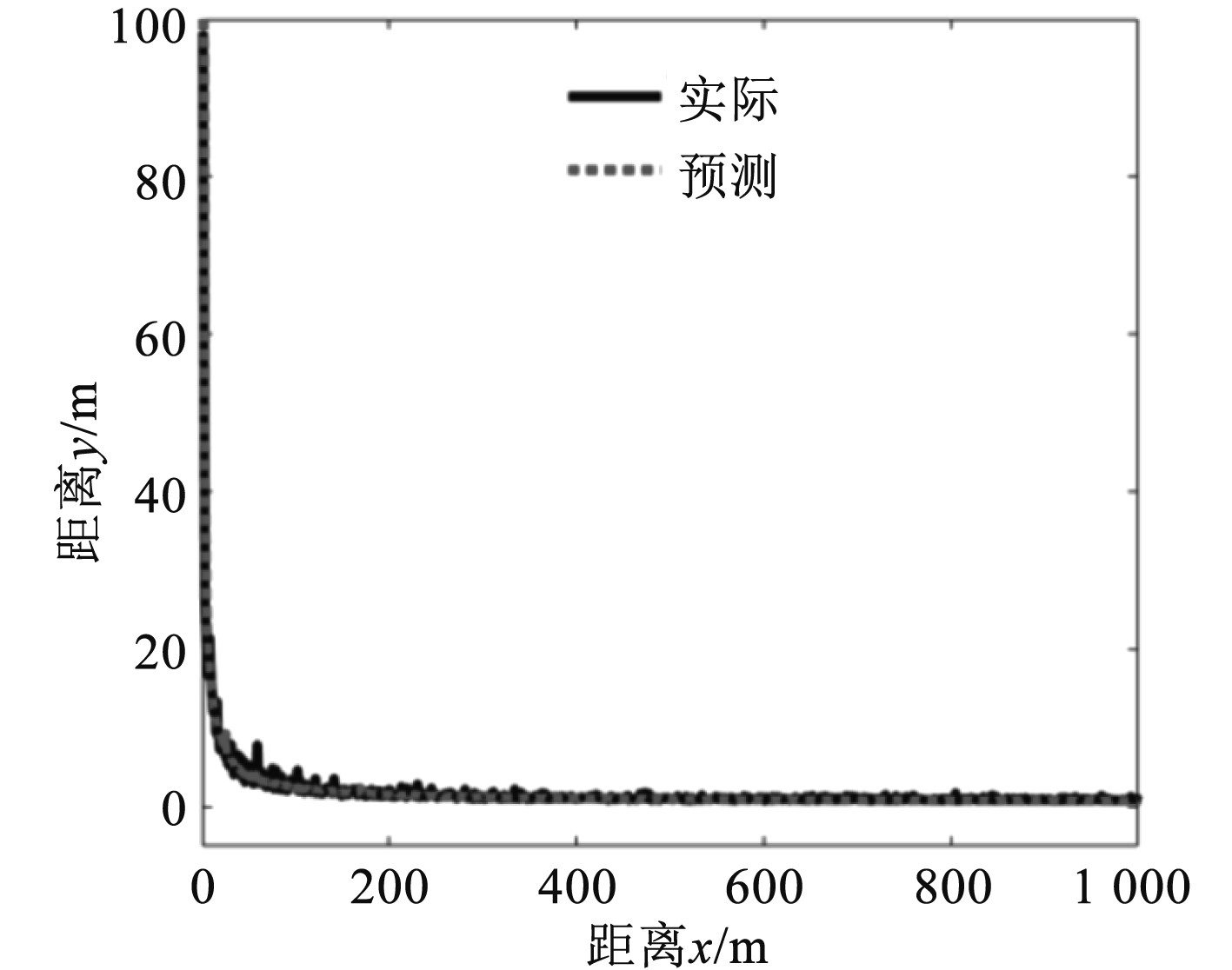
按船模自航试验所得的结果,对实体船舶的自航点进行预估,为简化过程,可应用未经修正的船模自航点,通过缩尺比换算后,直接预估出实体船舶的自航点。在本文中,预估自航点时的船舶螺旋桨转速约为101 r/min。随后分别在该转速的前后各取2个值,在服务航速一定的前提下,对不同螺旋桨转速进行数值模拟。根据模拟所得的结果,绘制出船体阻力与螺旋桨推力之间随转速变化的曲线,2条曲线相交的点,就是实体船舶在该航速下的自航点。实体船舶自航试验曲线如图3所示。
|
图 3 实体船舶自航试验变化曲线示意图 Fig. 3 Schematic diagram of variation curve of self navigation test of solid ship |
通过插值得到实体船舶自航点N的位置,即107.3 r/min。为对计算过程加以简化,并减少计算量,在本次研究中,并未计算螺旋桨的敞水性能,这是因为在水中,尺度作用对推力的影响非常小,基本上可以忽略不计,螺旋桨转矩的系数变化通常不会超过1%,所以实体船舶的螺旋桨与螺旋桨模型的敞水曲线基本处于重合状态。
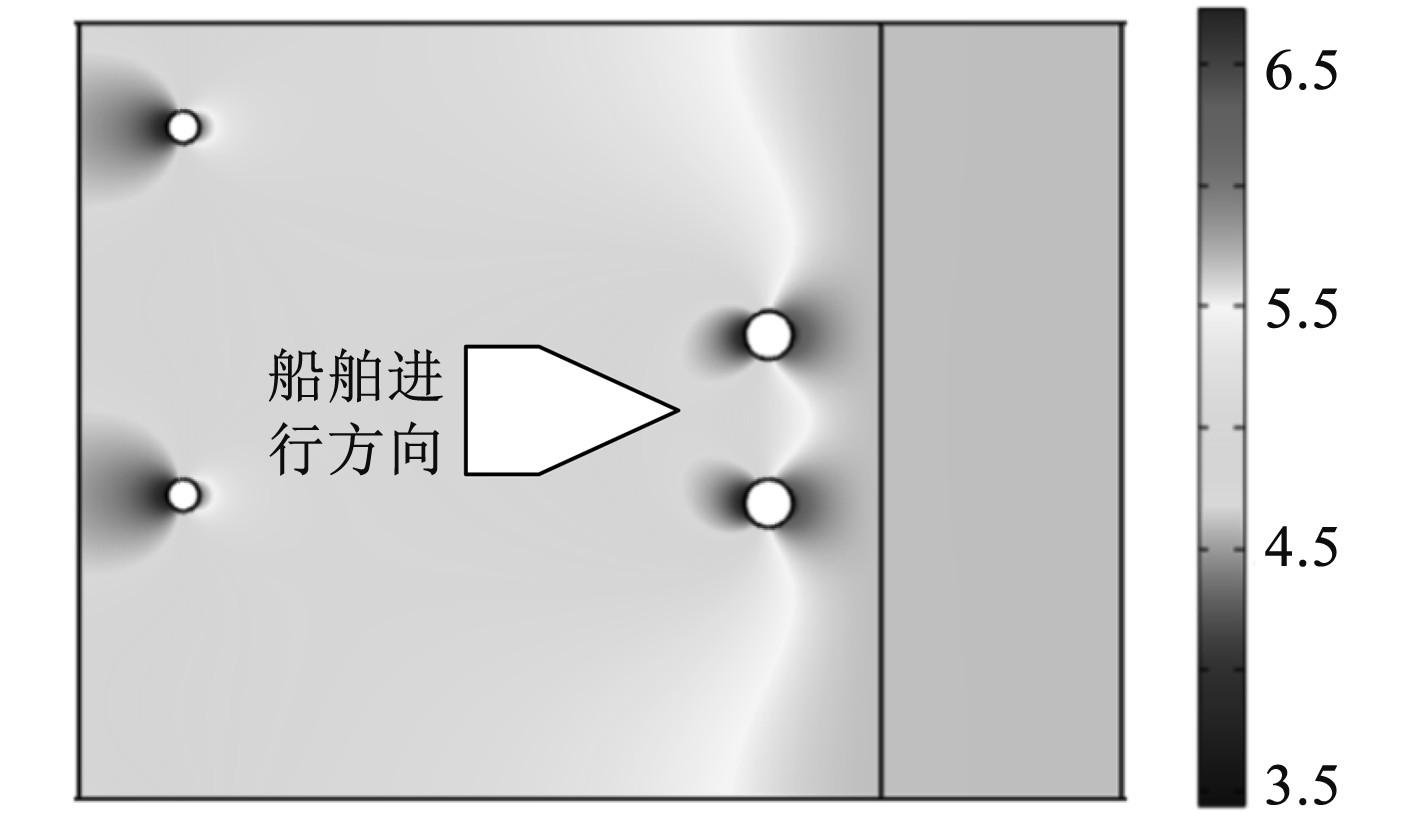
2.3 振力数值计算结果对于螺旋桨而言,其轴承力的强烈程度主要与半流场的均匀性有关。轴向半流是三向非均匀半流中的主要部分。图4为实体船舶和船模桨盘面在自航条件下0.3倍直径处的无量纲轴向速度对比情况。
|
图 4 实体船舶和船模桨盘面在自航条件下0.3倍直径处的无量纲轴向速度对比 Fig. 4 Comparison of dimensionless axial velocity at 0.3 times diameter between solid ship and ship model propeller disk under self navigation condition |
在图4中,圆圈代表的是桨盘面位置,箭头为船舶行进方向。当螺旋桨向右旋转时,桨叶带动水流从右舷侧流动,此时右舷的轴向速度随之增大,并超过左舷侧。中纵剖面处是桨叶产生最大推力和转矩位置。与船模相比,实体船舶的雷诺数更大一些,不仅如此,它的边界层比船模薄很多,伴流场的尺度效应更加显著,等值线收缩的程度更大。桨盘面处的进速超过船模。实体船模桨盘面的等值线分布范围在0.7~0.95之间,而船模则在0.6~0.9之间。只有非常小的一部分区域为0.9~0.95。由此可知,船模的半流场均匀性要优于实体船舶,据此能够推测出船模的螺旋桨推力转矩系数大于实体船舶。由于实体船舶的轴向脉动力比船模大,所以更加容易诱导船体产生振动。自由液面波形情况下的速度变化如图5所示。

|
图 5 自由液面波形情况下的速度变化图 Fig. 5 Velocity change diagram in the case of free surface waveform |
从图5能够清楚看出,模型与试验的自航计算值基本趋于吻合状态,二者不但波高接近,而且波峰与波谷的位置也大体相同。由此可知,CFD对自由液面的捕捉效果比较好。船尾的波形存在一定程度的差别,这是因为船模在计算的过程中,船尾桨产生的影响,致使尾波消散的速度比较快。在自由液面中,波形尺度效应并没有过于明显的表现,但在船尾波形上存在差异,这是因为实体船舶的边界层比船模的薄。
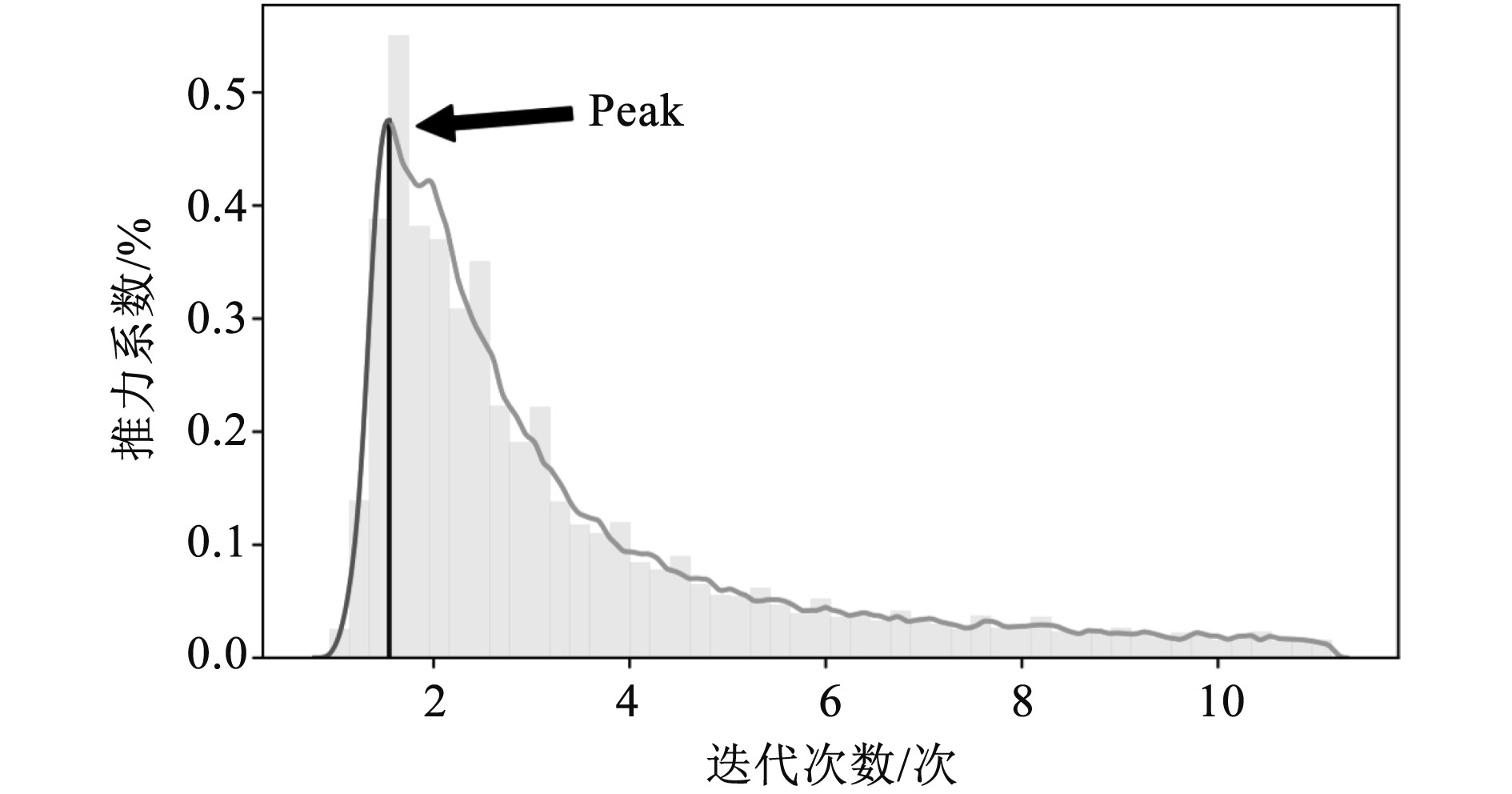
在对螺旋桨的轴承力计算时,可采取随机的方法,从桨叶中任选一片,绘制出单片桨叶推力系数的脉动曲线,如图6所示。
|
图 6 单片桨叶推力系数的脉动曲线示意图 Fig. 6 Schematic diagram of pulsation curve of thrust coefficient of single blade |
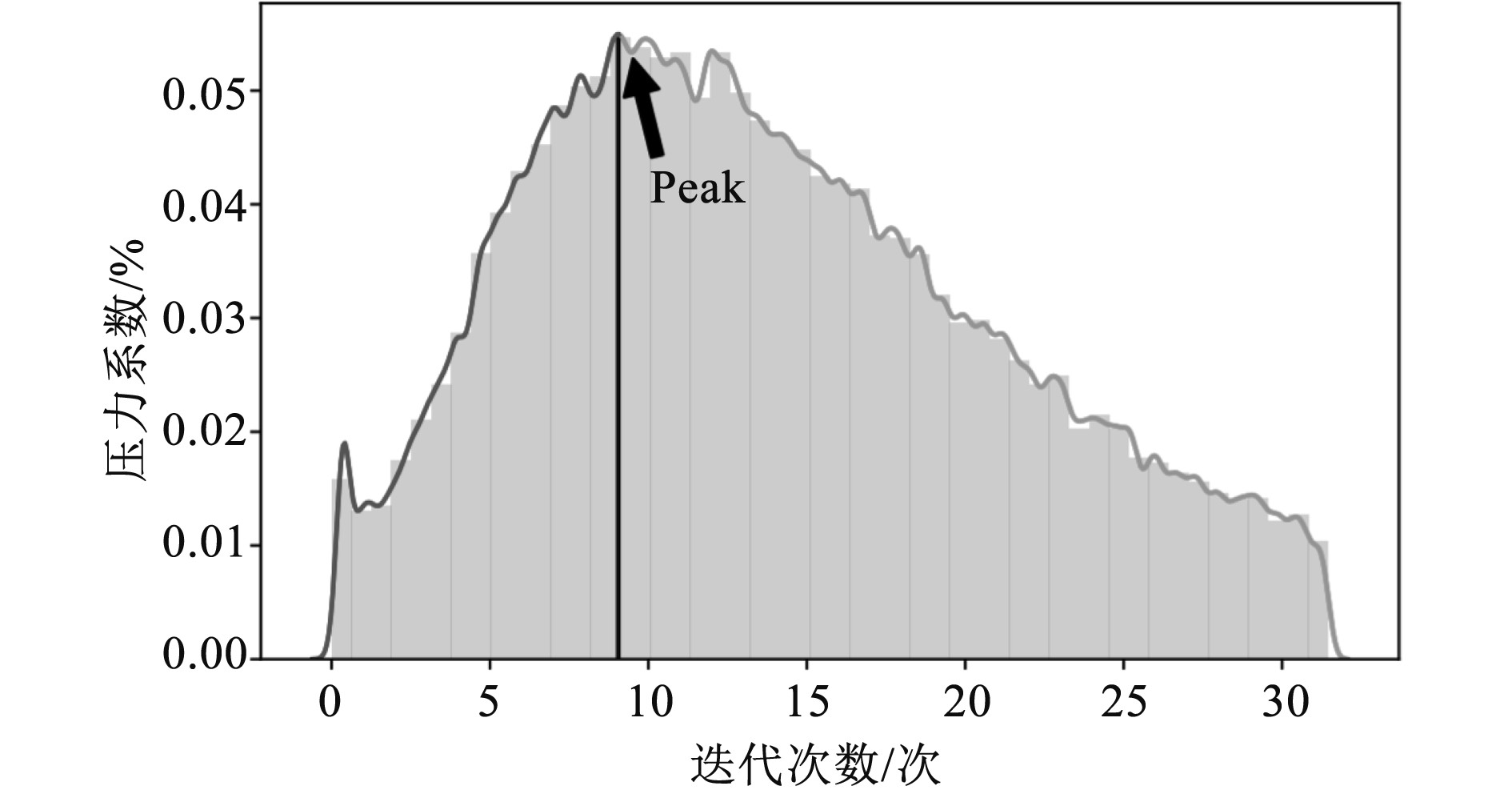
由图6可知,实体船舶中船模的单片桨叶最大推力全都出现在0.48系数处,而最小推力小于0,1位置处,由此能够得出如下结论:即螺旋桨的正上方有最强烈的伴流存在。当浆液接近0°后,进速会随之降低,此时桨叶的攻角增大,与之相应的推力也进一步增大。一般情况下,桨叶在75°~125°这一区间范围内的推力较为平稳,说明这个区间的液体流速均匀;达到150°后,进入低伴流区,桨叶的推力开始下降;达到260°后,进入高伴流区,桨叶推力也会随之增长。实体船舶与船模的桨叶推力系数随时间的变化规律基本相同,但是实体船舶在一定周期的推力系数小于船模,幅度约为7%左右。实体船舶的桨叶推力系数脉动值也比船模小,之所以出现这样的情况,是因为实体船舶桨叶旋转的伴流分数比船模小,致使桨叶的受力相差较大。实体船舶与船模各测点的脉动压力系数均值如图7所示。
|
图 7 实体船舶与船模各测点的脉动压力系数均值 Fig. 7 Mean value of fluctuating pressure coefficient at each measuring point of solid ship and ship model |
由图7可知,实体船舶的脉动压力系数均值比船模大,最大值为0.06左右。这是因为实体船舶的伴流分比船模小,自航点转速比船模大,对应检测点的压力系数大。
3 结 语当螺旋桨出现振力异常后,会影响船舶的航行稳定性,严重时可能会导致船舶倾覆。为避免这一问题的发生,应当采取有效的方法,对螺旋桨振力异常进行准确预报,据此采取相应的措施规避风险,确保船舶航行的安全性。
| [1] |
丁宁, 高占峰, 肖宇. 船舶振动响应计算中螺旋桨脉动压力的模拟方法研究[J]. 船舶, 2021(4): 37-42. |
| [2] |
王路才, 周其斗. 桨叶振动对螺旋桨垂向激励下潜艇结构振动与声辐射的影响[J]. 中国舰船研究, 2020(5): 161-166. |
| [3] |
李亮, 刘登成, 洪方文, 等. 风浪作用下船体纵摇运动对螺旋桨激振力特性影响分析[J]. 中国造船, 2020(2): 1-13. DOI:10.3969/j.issn.1000-4882.2020.02.001 |
| [4] |
刘小磊, 林威, 陈海明. 船艇高速螺旋桨引起的船体振动分析与解决措施[J]. 广东造船, 2019(4): 34-37. DOI:10.3969/j.issn.2095-6622.2019.04.010 |
| [5] |
张雪冰, 田佳彬, 王隽, 等. 螺旋桨非定常力对推力轴承油膜刚度影响的理论与试验研究[J]. 中国造船, 2019(2): 164-170. DOI:10.3969/j.issn.1000-4882.2019.02.016 |
| [6] |
王诗洋, 汤佳敏, 王文全, 等. 艇桨一体的螺旋桨激振力和水动力噪声数值预报[J]. 中国舰船研究, 2019(1): 43-51. |
| [7] |
姚慧岚, 张怀新. 理论和数值方法预报的船舶姿态改变对螺旋桨非定常轴承力的影响[J]. 大连海事大学学报, 2018(3): 1-8. |
 2022, Vol. 44
2022, Vol. 44
