0 引　言

水下航行体运动稳定性是衡量水下航行体的一项重要设计指标，决定了航行体在水下的运动性能，是指物体受到小扰动后回复初始状态的能力。随着计算流体力学的发展，数值计算方法逐渐被应用于操纵性水动力系数预报以评估水下航行体的运动稳定性，且可以提取流场及操纵面详细的信息，为操纵面设计提供有力支撑^[1-3]。旋臂水池试验数值仿真计算方法国内外有许多学者开展了研究^[4-7]，并建立了不同的计算方法。邓峰等^[4]采用旋转坐标系方法将水下航行体旋臂试验数值模拟转化为定常问题。肖昌润等^[5]建立了基于固定坐标系的动网格方法预报旋转导数的数值计算方法。卢锦国等^[6]采用Fluent软件，针对旋臂水池试验，提出控制方程中向心力源项空间离散误差修正方法。Lei等^[7]通过与模型试验数据对比建立了分别利用Cadmv和Fluent两种数值计算代码的旋臂水池数值仿真方法，并通过流场特性分析表明回转运动中在围壳及稳定翼周围出现了流动分离。

围壳作为水下航行体的重要附体之一，与主体之间存在水动力干扰^[8]，在水平面回转时干扰后的流场作用于主体上产生的水动力及力矩，使得水下航行体产生横倾。为了操纵安全，水下航行体应避免产生较大的横倾，且随着现代科技的飞速发展，围壳在水下航行体的布置位置可能更加灵活，因此有必要开展有无围壳及其在水下航行体上的轴向位置对其水动力系数的影响研究。

本文针对Suboff模型，以水平面为例，建立回转运动的线性旋转速度系数数值模拟方法，结合文献[9]斜拖运动的线性速度系数数值模拟方法,针对有无围壳模型、不同围壳轴向位置模型，开展水下航行体水平面水动力系数的计算。根据计算结果分析水下航行体流场特性以及水动力特性，获得有无围壳及围壳轴向位置对水下航行体水平面动稳定性系数的影响规律。

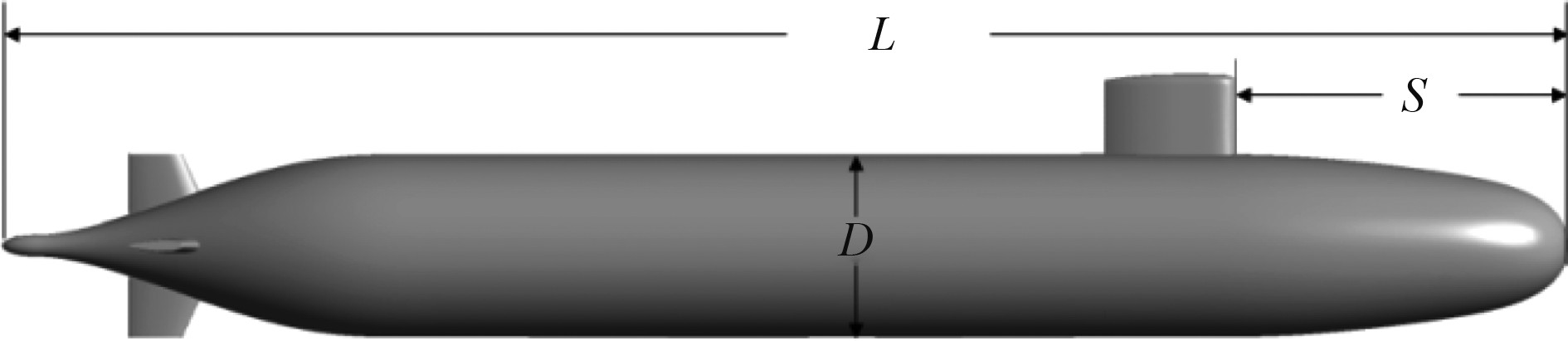
1 计算模型

以Suboff模型为研究对象，采用Ansys Fluent模拟Suboff水平面操纵性试验的线性水动力系数。几何模型如图1所示，Suboff模型的几何尺寸如表1所示。

2 旋臂水池数值计算方法 2.1 水平面运动方程

本文模拟的对象是水下航行体在无漂角无攻角状态下线性角速度范围内水平面的回转状态。该状态下水平面线性运动方程^[10]如下：

$ mur = \frac{1}{2}\rho {L^3}{Y'_r}ur + \frac{1}{2}\rho {L^2}{Y'_*}{u^2}，$

(1)

$ m{x_G}ur = \frac{1}{2}\rho {L^4}{N'_r}ur + \frac{1}{2}\rho {L^3}{N'_*}{u^2} 。$

(2)

其中：m为航行体质量，kg；L为水下航行体长度，m； $ \rho $ 为流体密度，kg/m³； $ {x_G} $ 为重心轴向坐标，m； $ u $ 为航行体轴向分速度，m/s; $ r $ 为航行体z方向上的角速度，rad/s； $ {Y'_r} $ 为横向力线性旋转系数； $ {Y'_*} $ 为无量纲横向力零态值； $ {N'_r} $ 为转首力矩线性旋转系数； $ {N'_*} $ 为无量纲转首力矩零态值。

2.2 计算坐标系

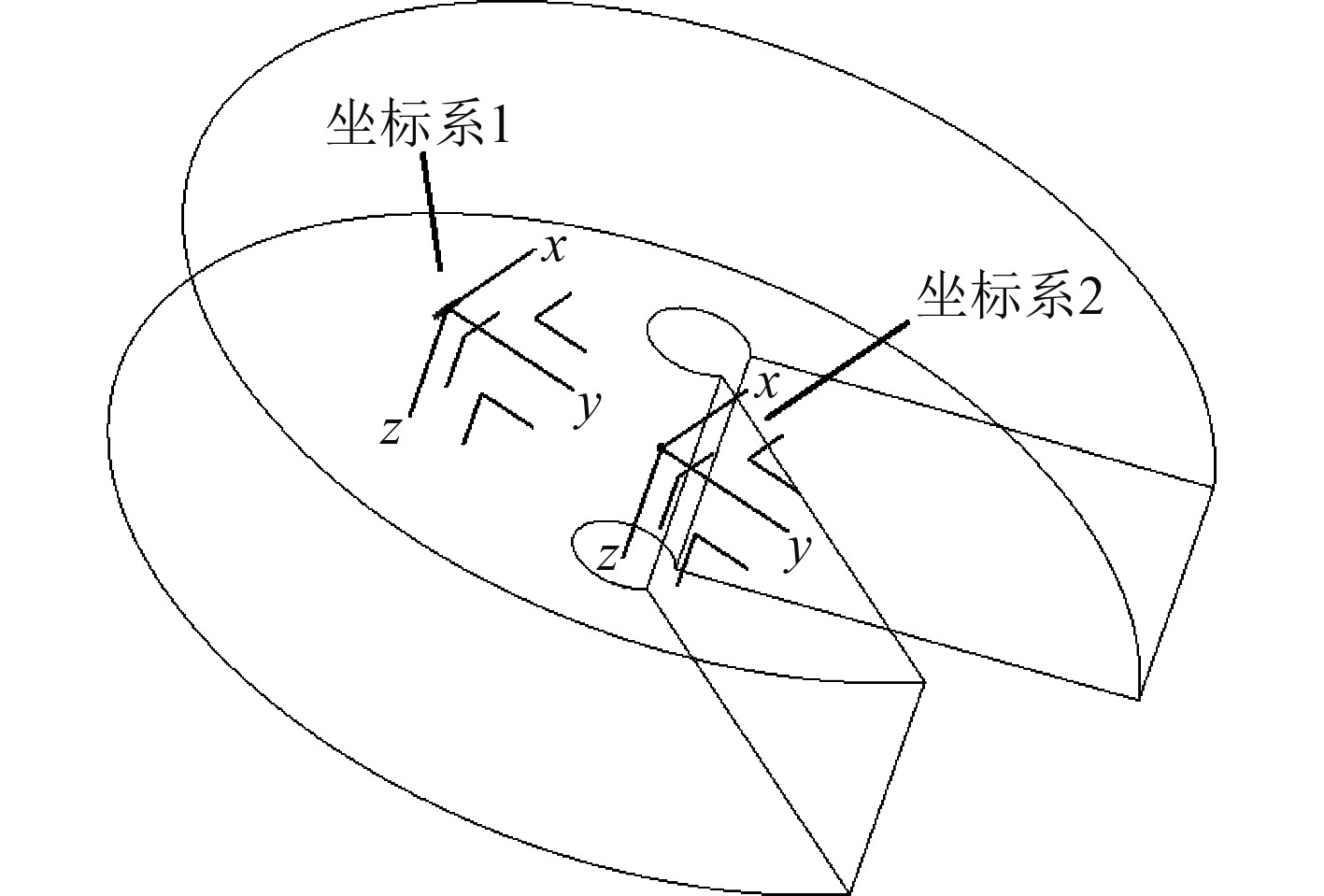
本文的计算对象为Suboff水下航行体，旋臂数值水池计算包括2个坐标系，如图2所示。坐标系1为水下航行体坐标系，坐标原点位于水下航行体轴线与浮心所在横截面交点处，OX轴平行于航行体轴线、指向首部为正；OY轴指向航行体右舷为正；OZ轴位于航行体中纵剖面内、指向航行体下方为正。坐标系2为一个惯性坐标系，用于定义水下航行体的运动，该坐标系原点位于水下航行体回转运动中心。

2.3 计算域与边界条件

求解粘性流动问题就是要求解N-S方程，对于湍流计算，多采用RANS方程求解工程问题。基于相对参考坐标系，采用RANS中的标准 $ k - \varepsilon $ 湍流模型进行操纵性旋臂数值水池仿真技术研究。

计算域为一个扇形的环形域，如图3所示。环形域外径为90D，环形域内径为2D，航行体回转半径为R，扇形环形域的两端分别设置为速度入口、压力出口边界。

2.4 计算网格

整个计算域采用ICEM进行结构化网格划分，网格尺寸在Suboff模型附近加密，在远离Suboff模型的区域较为稀疏，如图4所示。

2.5 数据处理

线性旋转导数反映的是力和力矩相对于旋转角速度 $ r $ 的变化率，为模拟旋臂水池拘束模操纵性试验^[8]，在漂角为0的情况下保持水下航行体线速度 $ u = rR $ 不变，通过改变回转半径R实现水下航行体旋转角速度 $ r $ 的变化。通过不同旋转角速度下横向力 $ Y $ 和转首力矩 $ N $ 的线性回归，得到相应的横向力线性系数 $ {Y'_r} $ 和转首力矩线性系数 $ {N'_r} $ 。根据模型长度雷诺数大于临界雷诺数（1.1×10⁷）确定航行体线速度。

经CFD计算得到的横向力、转首力矩以及旋转角速度按照下式进行无因次处理：

$ r' = rL/u ，$

(3)

$ Y' = Y/(0.5\rho {u^2}{L^2})，$

(4)

$ N' = N/(0.5\rho {u^2}{L^3})。$

(5)

其中： $ Y $ 为横向力，N； $ N $ 为转首力矩， $ {\rm{N}} \cdot {\rm{m}} $ ； $ r' $ 为无量纲旋转角速度； $ Y' $ 为无量纲横向力； $ N' $ 为无量纲转首力矩。 $ N' $ 为无量纲转首力矩。

横向力线性系数 $ {Y'_r} $ 和转首力矩线性系数 $ {N'_r} $ 是采用线性角速度范围的数据，利用式（6）和式（7）进行线性回归得到。

$ Y' = {Y'_*}{u'^2} + {Y'_r}u'r'，$

(6)

$ N' = {N'_*}{u'^2} + {N'_r}u'r' ，$

(7)

水平面阻尼力臂 $ {l'_r} $ 按照下式计算：

$ l{'}_r^{} = - {N{'}_r}/\left( {m{'} - {{Y{'}}_r}} \right) 。$

(8)

其中， $ m' $ 为无量纲质量。

2.6 数值计算精度分析

图5为水平面有无围壳模型不同旋转角速度下的横向力 $ Y' $ 与转首力矩 $ N' $ 数值计算结果曲线。表2为线性旋转速度系数 $ {Y'_r} $ 、 $ {N'_r} $ 数值计算结果与模型试验的对比数据。可知，与试验值相比，有围壳体模型下 $ {Y'_r} $ 、 $ {N'_r} $ 、 $ {l'_r} $ 的计算误差分别为−11.8%，10.1%，6.0%；无围壳模型下 $ {Y'_r} $ 、 $ {N'_r} $ 、 $ {l'_r} $ 的计算误差分别为4.4%，10.3%，13.0%。旋转速度系数的计算误差均在15%以内。

3 围壳对水动力系数的影响 3.1 有无围壳对水动力系数的影响

表3为有无围壳模型的水动力系数数值计算结果。根据表中数据可知，与有围壳模型相比，无围壳状态下水动力系数 $ {Y'_v} $ 增加， $ {N'_v} $ 增加， $ {Y'_r} $ 增加， $ {N'_r} $ 增加，使得水平面静不稳定系数 $ {l'_\beta } $ 增加，阻尼力臂 $ {l'_r} $ 减小，水平面动稳定性系数 $ {K_{hd}} $ 降低。

图6和图7分别为拖曳工况（ $ \beta = - 3^\circ $ ）和回转工况（ $ r' = 0.213 $ ）下有无围壳模型水下航行体中纵剖面上的速度分布等值线图。表4为有无围壳模型相同工况下Suboff主要组成部分的横向力系数对比， $Y{'}_{}^{(H)}$ ， $Y{'}_{}^{(vf)}$ ， $Y{'}_{}^{(fw)}$ 分别表示主体、上垂直稳定翼及围壳上的横向力。

由图6和图7可知，拖曳工况和回转工况下围壳使得主体的速度分布发生改变，使得有无围壳状态下主体上的横向力发生变化（见表4）。拖曳工况下围壳使得上垂直稳定翼前缘速度分布发生了改变，回转工况下围壳对上垂直稳定翼前缘流动影响较小。由表4可知，有无围壳状态下上垂直稳定翼横向力变化幅度拖曳工况大于回转工况，与上述流场特性结论一致。

与有围壳状态相比，无围壳状态下 $ {Y'_v} $ 增加， $ {Y'_r} $ 增加，主要是因为拖曳工况下围壳产生的横向力与主体、垂直稳定翼产生的横向力方向相同，而回转工况下围壳产生的横向力与主体、垂直稳定翼产生的横向力方向相反。此外，可以发现围壳的存在使得横向水动力 $ \left| {{{Y'}_v}} \right| $ 增加，导致回转运动时的横倾力矩增大，从而增加回转中的横倾角，对操纵运动不利。

3.2 围壳的轴向位置

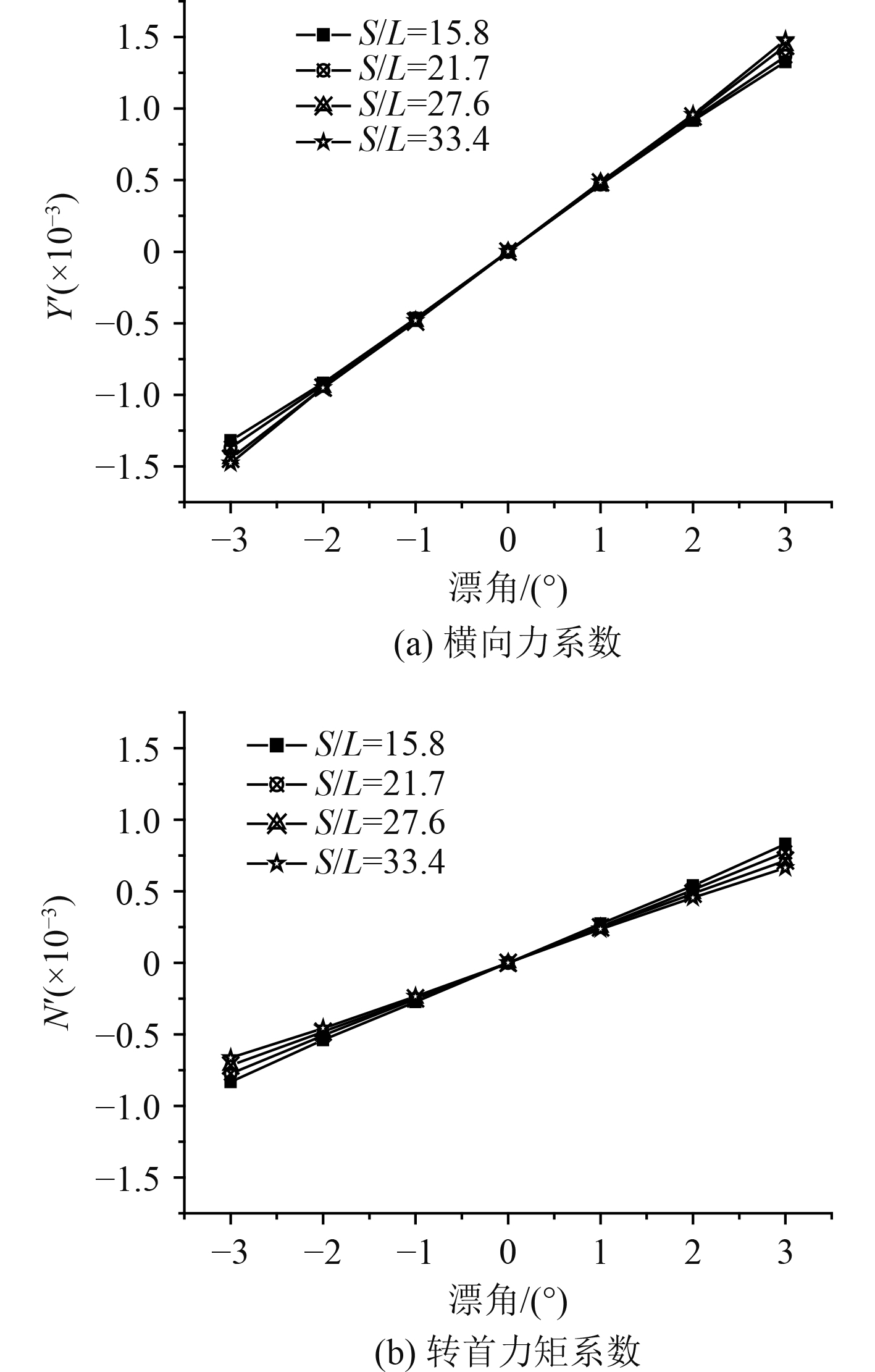
以Suboff围壳前缘距水下航行体首端的距离S与主体长L的比值S/L表示围壳方案的轴向位置。保持围壳尺寸不变，将围壳布置在主体不同的轴向位置上，形成4个围壳方案，依次为围壳方案1、方案2、方案3、方案4，其S/L分别为15.8，21.7，27.6，33.4。图8和图9为4个围壳方案下的横向力和转首力矩的数值计算结果。表5为根据图8和图9中的数据线性回归得到的4个围壳方案的水动力系数。可知，随着围壳距水下航行体首端轴向距离的增加，水动力系数 $ {Y'_v} $ 减小， $ {N'_v} $ 增加， $ {Y'_r} $ 增加， $ {N'_r} $ 增加，使得静不稳定性系数 $ {l'_\beta } $ 减小，阻尼力臂 $ {l'_r} $ 减小，水平面动稳定性系数 $ {K_{hd}} $ 增加。围壳轴向布置位置的改变对静不稳定性系数 $ {l'_\beta } $ 的影响大于阻尼力臂 $ {l'_r} $ 。

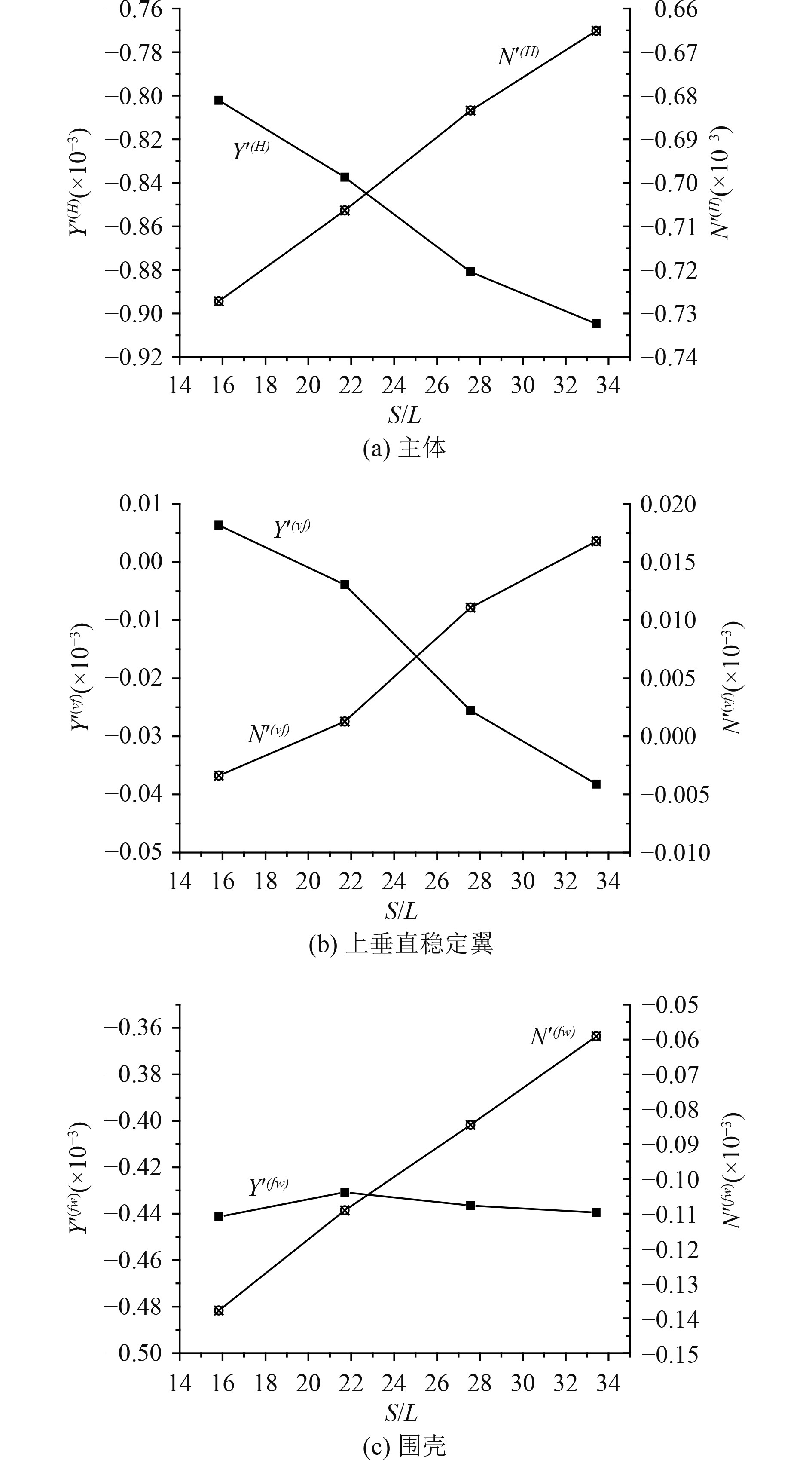
为研究围壳轴向位置对水下航行体在有漂角拖曳工况下主体及各附体的影响，以漂角-3°为例，分别分析主体、上垂直稳定翼及围壳在拖曳工况下的横向力及转首力矩。如图10所示， $N{'}_{}^{(H)}$ ， $N{'}_{}^{(vf)}$ ， $N{'}_{}^{(fw)}$ 分别表示主体、上垂直稳定翼及围壳上的转首力矩。可以看出，拖曳工况下随着围壳轴向位置S/L的增加，主体产生的横向力 $Y{'}_{}^{(H)}$ 减小，转首力矩 $N{'}_{}^{(H)}$ 增加；上垂直稳定翼产生的横向力 $Y{'}_{}^{(vf)}$ 减小，转首力矩 $N{'}_{}^{(vf)}$ 增加；围壳产生的横向力 $Y{'}_{}^{(fw)}$ 基本不变，转首力矩 $N{'}_{}^{(fw)}$ 增加。

随着围壳距水下航行体首端距离的增加，在线性漂角范围内主体、上垂直稳定翼、围壳横向力和转首力矩的变化趋势基本一致，均有利于降低静不稳定性系数 $ {l'_\beta } $ 。

为研究围壳轴向位置对水下航行体在回转工况下主体及各附体的影响，以旋转角速度0.213为例，分别分析主体、上垂直稳定翼及围壳在回转工况下的横向力及转首力矩，如图11所示。可以看出：回转工况下随围壳轴向位置S/L的增加，主体产生的横向力 $Y{'}_{}^{(H)}$ 增加，转首力矩 $N{'}_{}^{(H)}$ 增加；上垂直稳定翼横向力 $Y{'}_{}^{(vf)}$ 减小，转首力矩 $N{'}_{}^{(vf)}$ 增加；围壳产生的横向力 $Y{'}_{}^{(fw)}$ 增加，转首力矩 $N{'}_{}^{(fw)}$ 增加。

随着围壳距水下航行体首端距离的增加，在线性角速度范围内，主体和围壳横向力变化趋势有利于增加阻尼力臂 $ {l'_r} $ ，而其转首力矩的变化趋势不利于增加阻尼力臂 $ {l'_r} $ ；上垂直稳定翼横向力和转首力矩的变化趋势均不利于增加阻尼力臂 $ {l'_r} $ 。

4 结　语

本文针对水下航行体，建立了线性旋转速度系数的数值仿真方法，研究了有无围壳以及围壳轴向位置对水动力系数和流场特性的影响，主要结论如下：

1）在线性角速度范围内，采用Standard $ k - \varepsilon $ 湍流模型预报水平面线性旋转速度系数的计算精度在15%以内；

2）与有围壳状态相比，无围壳状态下水平面静不稳定系数增加，阻尼力臂减小，动稳定性系数降低。围壳的存在使得横向水动力 $ \left| {{{Y'}_v}} \right| $ 增加，导致回转运动时的横倾力矩增大，从而增加回转中的横倾角。

3）围壳主要影响围壳附近主体的流动特性，其次为上垂直稳定翼，且拖曳工况下围壳对上垂直稳定翼流场特性的影响大于回转工况。

4）随着围壳向水下航行体尾部移动，水平面静不稳定性系数减小，阻尼力臂减小，动稳定性系数增加，且围壳轴向位置的改变对静不稳定性系数的影响大于阻尼力臂。