夹层板不仅具有重量轻、强度高的特点,还具有较好的隔音效果、抗弯能力与能量吸收能力[1-2],因此其在船舶设计中的应用有助于提高船舶结构的抗爆性能。然而,为了保证夹层板在船体结构应用中根据具体需求充分发挥其优势,需要开展相关结构综合优化,设计出兼顾结构性、功能性及经济性的结构形式及尺寸组合。
随着计算机技术的发展,神经网络和优化算法打开了传统结构优化设计的突破口。优化算法具有全局优化性能,且通用性强,有严格的理论基础,可以在一定时间内从理论上找到最优解或近似最优解。目前,已越来越多的应用于工程结构优化领域。其中,Xue[3]以多种夹层结构为对象进行了抗爆性能的相关研究,同时实现了夹层板结构的轻量化设计。杨康尧[4]将多目标遗传算法应用于以3D-RH 结构为夹层的夹层板优化设计中,显著提升了夹层板的抗爆性能。亓昌[5]在金字塔点阵夹层板优化中采用第二代非支配排序遗传算法,获得使夹层板面比吸能最大和背板最大变形量最小时的几何参数最优解集。郭少鹏[6]详细研究了结构参数对金字塔夹层板抗爆性能的影响,并进一步用遗传算法对夹层板结构进行了优化设计与比较分析。大量优化算法的应用实例表明,优化算法可以实现夹层板结构的抗爆优化设计。
麻雀搜索算法(sparrow search algorithm,SSA)[7]是受到麻雀觅食行为和反捕食行为的启发,于2020年提出的一种新型群体智能优化算法,与传统的群体智能优化算法相比,该算法具有优化能力强、收敛速度快等优点,将麻雀搜索算法应用于夹层板结构的优化设计是一种新的思路。
神经网络是模仿动物神经网络行为特征的数学模型,能够进行分布式并行信息处理[8],具有超强的学习能力,可以高度处理有限元计算中的非线性信息,从而建立起输入与输出之间的非线性映射,形成响应面模型,在优化过程中代替有限元计算[9]。但是,传统的BP神经网络在训练过程中容易陷入局部极值,即网络在训练过程中容易停留在误差面平坦区域。在平坦区域,权值每次变化很小,使得训练过程几乎停止,很难在短时间内获得高精度的网络模型。因此,本文采用自适应学习率的方法[10],通过控制权值更新的速率,进而提出一种神经网络与麻雀搜索算法相结合的优化方法(back propagation-sparrow search algorithm, BP-SSA),并将其应用于夹层板结构的抗爆性能优化中,实现了多参数、多目标综合优化的效果,可以有效支撑工程设计。
1 优化设计方法 1.1 数学模型结构优化的数学模型一般包含3个要素:设计变量、约束条件和目标函数。结构优化问题即是寻找满足约束条件下能够使目标函数尽可能大或尽可能小的设计方案,其中约束条件一般为关于设计变量的不等式或者等式条件。
波形夹层板结构的优化问题涉及到许多设计变量和优化目标,对于n维的设计变量
| $ \left\{ \begin{gathered} \min {\boldsymbol{F}}({\boldsymbol{X}}) = f({{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2}, \cdots ,{{\boldsymbol{x}}_n}) ,\hfill \\ {\rm{s}}.{\rm{t}}.{{\boldsymbol{g}}_j}({\boldsymbol{X}}) \leqslant 0,j = 1,2, \cdots ,J 。\hfill \\ \end{gathered} \right. $ | (1) |
式中:
为了消除不同维度的影响,需要对设计变量和优化目标进行归一化。采用的归一化公式如下:
| $ {{\boldsymbol{x}}_{{\text{membership}}}} = \frac{{{{\boldsymbol{x}}_{{\text{value}}}} - {{\boldsymbol{x}}_{\min }}}}{{{{\boldsymbol{x}}_{\max }} - {{\boldsymbol{x}}_{\min }}}} ,$ | (2) |
| $ {{\boldsymbol{y}}_{{\text{membership}}}} = \frac{{{{\boldsymbol{y}}_{{\text{value}}}} - {{\boldsymbol{y}}_{\min }}}}{{{{\boldsymbol{y}}_{\max }} - {{\boldsymbol{y}}_{\min }}}}。$ | (3) |
式中:
由于船舶爆炸造成的巨大能量冲击,船舶会产生很大的塑性变形,结构在静、动荷载作用下吸收的动能以及结构的变形和应力在一定程度上能反映结构的抗爆性能。吸能越大,应力和变形越小,结构的抗爆性能越好。同时,为了满足结构轻量化的需要,还应考虑结构的自重。因此,本文选取结构质量、静载时的夹层板上面板的中心位移与应力、动载时的夹层板上面板的中心位移与应力,以及结构吸能作为优化目标。
线性加权法是一种构造多目标函数的方法,先根据每个目标在整个优化问题中的重要性赋予相应的权重系数,再对其线性加权求和。对于本文的夹层板抗爆优化问题,目标函数可以取为:
| $ {\boldsymbol{F}} = \alpha \cdot {{\boldsymbol{f}}_M} + \beta \cdot {{\boldsymbol{f}}_{D1}} + \gamma \cdot {{\boldsymbol{f}}_{S1}} + \lambda \cdot {{\boldsymbol{f}}_{D2}} + \mu \cdot {{\boldsymbol{f}}_{S2}} + \xi \cdot ( - {{\boldsymbol{f}}_E}) 。$ | (4) |
式中:
当优化问题有约束时,通过罚函数将约束问题转化为无约束问题[11]:
| $ {\boldsymbol{F}}{\text{ = }}{\boldsymbol{F}}{\text{ + }}r \cdot {\boldsymbol{P}}\text{,}其中 P = \left\{ {\begin{array}{*{20}{c}} { = 0}&{{\boldsymbol{x}} \in {\boldsymbol{K}}} ,\\ { > 0}&{{\boldsymbol{x}} \notin {\boldsymbol{K}}} 。\end{array}} \right. $ | (5) |
式中:
神经网络的拓扑结构由输入层、隐含层和输出层组成,其中输入样本由正交设计试验[12]生成,用于消除选择样本时设计变量之间不平衡的影响。对于隐含层来说,层数越深,网络拟合能力越强,但模型也趋于复杂,由于本文的数据输入量较小,采用深度神经网络的模型容易出现过拟合问题,因此本文采用单隐层神经网络。研究证明,任何连续函数都可以与仅包含一个隐含层的神经网络建立起映射[13]。在单隐层神经网络的结构中,理论上增加隐含层神经元的数量可以提高网络的准确性,但这并不意味着隐含层神经元的数量越多,网络模型的准确性就越高。实验表明,当输入层的n个神经元与隐含层的m个神经元大致存在m=2n+1的关系时,拟合的网络模型精度最佳。
在神经网络的训练过程中,为了使网络的损失函数最小,需要通过目标优化算法得到一组合适的网络参数。传统的目标优化算法采用批量梯度下降法(BGD)或随机梯度下降法(SGD)。但是,由于这2种方法在调整网络参数时使用相同的学习速率,导致一些参数的更新速度过慢,在训练过程中,网络可能无法跳出局部最优。因此,采用自适应调节学习率的Adam算法作为目标优化算法。
设Wl和bl代表神经网络第L层的权值和阈值,则第l层参数可以整体表示为θl =(Wl, bl),基于Adam算法的优化步骤如下:
1) 输入
初始学习率η,1阶矩估计的指数衰减率β1=0.9,2阶矩估计的指数衰减率β2=0.999,常数δ=1e-8
2) 初始化1阶动量和2阶动量
m0=0,v0=0
m0=0,v0=0
m0=0,v0=0
3) 设置循环迭代次数t为结束条件
4) 从样本集中随机选取s组小批量样本{n1, n2
5) 计算梯度
| $ {g_t} = \frac{1}{s}\nabla {\theta _{t - 1}}\sum\limits_{i = 1}^s {L(f} ({n_{^i}};{\theta _{t - 1}}),{z_{^i}})。$ | (6) |
6) 更新迭代次数
| $ t = t + 1 。$ | (7) |
7) 更新1阶动量
| $ {m_t} = {\beta _1} \cdot {m_{t - 1}} + (1 - {\beta _1}) \cdot {g_t} 。$ | (8) |
8) 更新二阶动量
| $ {v_t} = {\beta _2} \cdot {v_{t - 1}} + (1 - {\beta _2}) \cdot {g_t} \odot {g_t} 。$ | (9) |
9) 计算1阶动量修正偏差
| $ {\hat m_t} = \frac{{{m_t}}}{{(1 - \beta _1^t)}}。$ | (10) |
10) 计算二阶动量修正偏差
| $ {\hat v_t} = \frac{{{v_t}}}{{(1 - \beta _2^t)}}。$ | (11) |
11) 更新参数
| $ {{\boldsymbol{\theta}} _t} = {{\boldsymbol{\theta}} _{t - 1}} + {\text{ - }}\eta \cdot \frac{{{{\hat m}_t}}}{{\sqrt {{{\hat v}_t} + \delta } }}。$ | (12) |
12) 循环采样
当达到迭代次数时,输出参数θ。
可以看出,Adam算法并没有使用固定的学习率,这使得模型的调整难度大大降低。
1.3 麻雀搜索算法麻雀搜索算法(SSA)作为一种新型群智能优化算法,在搜索精度、收敛速度、稳定性和避免局部最优值等方面都优于现有的群智能优化算法。
在麻雀搜索算法中,种群主要分为2类:探索者和跟随者。探索者负责寻找食物,为跟随者提供合理的觅食区域。在实际的优化过程中,探索者和跟随者的身份在群体中是动态变化的,只要能找到更好的食物来源,每只麻雀都有可能成为探索者,但探索者和跟随者占麻雀总数的比例保持不变。若优化问题存在d维设计变量,由n只麻雀组成的种群可以写成:
| $ X = \left[ {\begin{array}{*{20}{c}} {{x_{1,1}}}&{{x_{1,2}}}& \cdots & \cdots &{{x_{1,d}}} \\ {{x_{2,1}}}&{{x_{2,2}}}& \ldots & \ldots &{{x_{2,d}}} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{x_{n,1}}}&{{x_{n,2}}}& \cdots & \cdots &{{x_{n,d}}} \end{array}} \right] 。$ | (13) |
式中:X为麻雀种群,xi,j为种群中位于第j维的第i个个体。
搜索过程中,能量较高的探索者优先获得食物,但如果发现有危险,它就会开始鸣叫,产生报警值,当报警值大于安全值时,探索者会将跟随者带到其他安全区域觅食。探索者的位置更新如下:
| $ x_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {x_{i,j}^t \cdot \exp \left( {\dfrac{{ - i}}{{\alpha \cdot ite{r_{\max }}}}} \right)},&{{\rm{if}}}&{{R_2} < ST},\\ {x_{i,j}^t + Q \cdot {\boldsymbol{L}}},&{{\rm{if}}}&{{R_2} \geqslant ST} 。\end{array}} \right. $ | (14) |
式中:t为当前迭代次数;itermax为常数,表示最大迭代次数;xi,j表示第i只麻雀在第j维中的位置;α∈(0, 1)是一个随机数;R2∈[0, 1],ST∈[0.5,1]分别为报警值和安全值;Q是一个服从正态分布的随机数;L表示一个1 × d的矩阵,矩阵中每个元素都是1。
对于跟随者来说,能量越低,它们在整个种群中的觅食地位就越差。当跟随者找不到食物时,那些能量较低的麻雀更有可能飞到其他地方寻找食物,以获得更多的能量,而在那些最优探索者周围搜寻的跟随者可能会为了食物而竞争,并把自己变成探索者。跟随者的位置更新如下:
| $ x_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {Q \cdot \exp \left( {\dfrac{{x_{worst}^t - x_{i,j}^t}}{{{i^2}}}} \right)},&{{\rm{if}}}\;\;{i > n/2} ,\\ {x_p^{t + 1} + \left| {x_{i,j}^t - x_p^{t + 1}} \right| \cdot {{\boldsymbol{A}}^ + } \cdot {\boldsymbol{L}}},&{{\rm{if}}}\;\;{i \leqslant n/2} 。\end{array}} \right. $ | (15) |
式中:xp为探索者目前所占据的最优位置,xworst为当前全局下的最差位置;A表示一个1 × d的矩阵,矩阵中每一项元素随机分配为1或−1,并且A+ = AT(AAT)−1。
有一些麻雀在觅食时始终保持警惕。当危险逼近时,这些麻雀会放弃它们现有的食物,处于边缘的麻雀向安全的地方移动,处于中间的麻雀随机移动,表示为:
| $ x_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {x_{best}^t + \beta \cdot \left| {x_{i,j}^t - x_{best}^t} \right|},&{{\rm{if}}}\;\;{{f_i} > {f_g}} ,\\ {x_{i,j}^t + K \cdot \left( {\dfrac{{\left| {x_{i,j}^t - x_{worst}^t} \right|}}{{({f_i} - {f_w}) + \varepsilon }}} \right)},&{{\rm{if}}}\;\;{{f_i} = {f_g}} 。\end{array}} \right. $ | (16) |
式中:xbest为当前最优位置;β是步长控制参数,服从均值为0、方差为1的正态分布;K∈[−1,1]是随机数;fi为当前麻雀的适应度值(能量值);fg为当前最佳适应度值;fw为当前最差适应度值;ε是一个常数,用于让分母不为0。
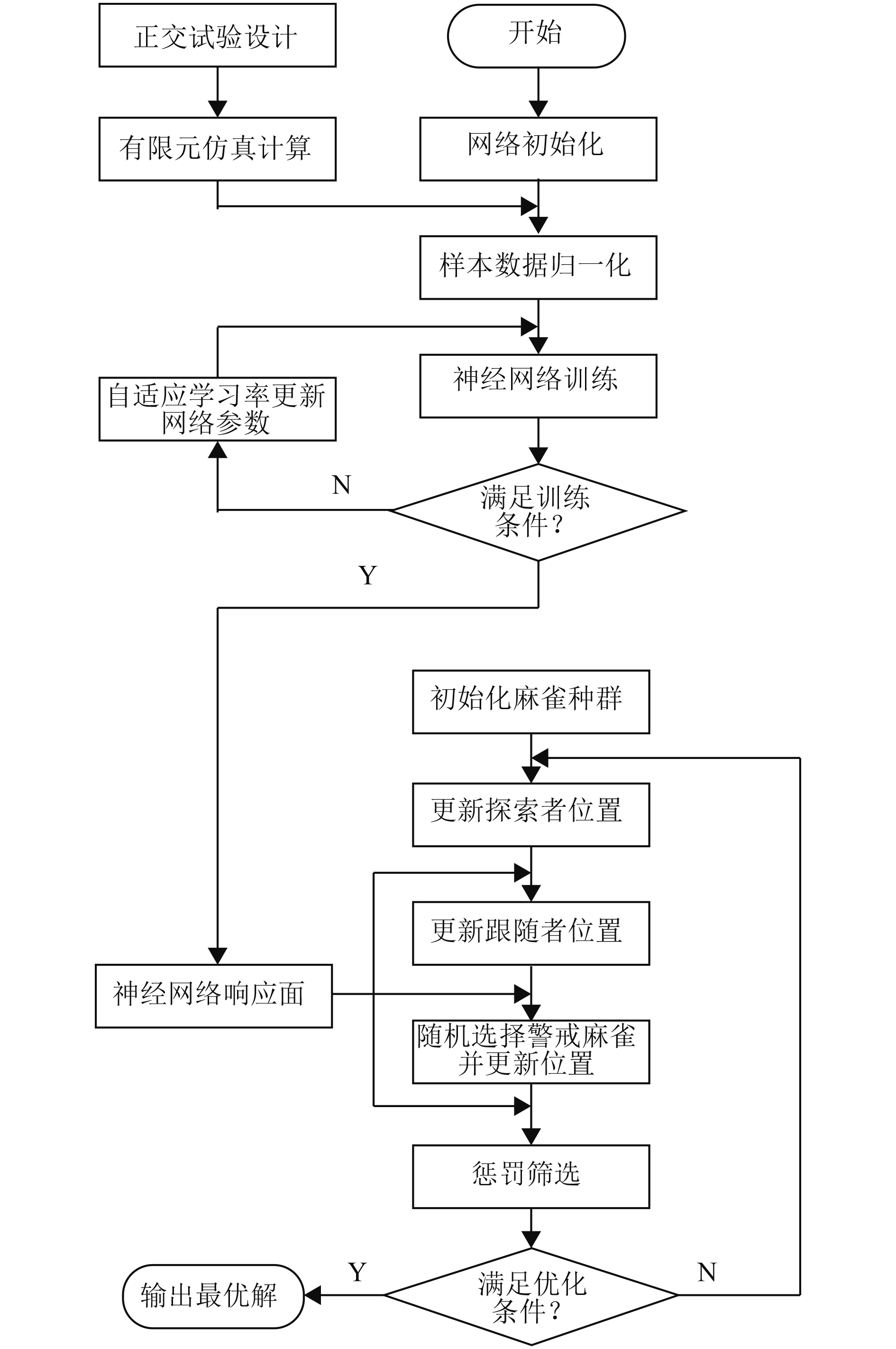
麻雀搜索算法正是仿照麻雀的这些行为进行函数的优化求解,该算法对目标函数基本没有限制,无论是解析函数等显函数还是神经网络等隐函数,都可以作为算法的目标函数。结合神经网络和式(4)作为麻雀搜索算法的目标函数,优化流程图如图1所示。
|
图 1 BP-SSA优化算法流程图 Fig. 1 Flow chart of BP-SSA optimization algorithm |
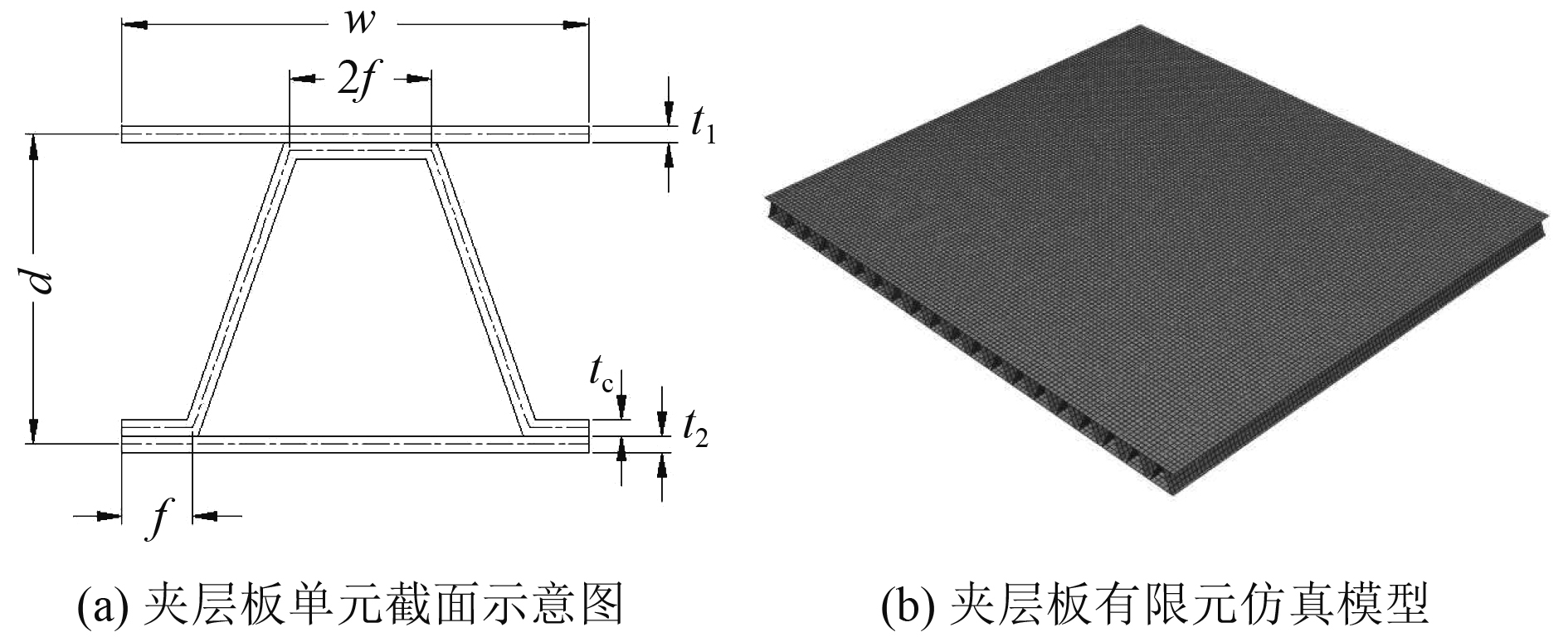
选取夹层板中结构性能较优的Uc型夹层板代替某船上层建筑局部区域,该局部区域板长为2 500 mm,宽为2 300 mm,扶强材为12号球扁钢。Uc型夹层板单元截面示意图如图2(a)所示,夹芯层高度d为100 mm,单位宽度w为125 mm,相邻夹芯层单元之间的间距的一半f为10 mm。
|
图 2 夹层板示意图 Fig. 2 Diagram of sandwich plate |
选取上、下面板厚度和夹芯层厚度为设计变量,上面板厚度t1、下面板厚度t2以及夹芯层厚度tc的设计域均取1~2 mm。优化问题的数学模型可表示为:
| $ \begin{aligned} &\mathrm{min}\;{\boldsymbol{F}}({{\boldsymbol{t}}}_{1}\rm{,}{{\boldsymbol{t}}}_{\rm{c}}\rm{,}{{\boldsymbol{t}}}_{2})=\alpha \cdot {f}_{M}+\beta \cdot {f}_{D1}+\\ &\qquad\qquad \gamma \cdot {f}_{S1}+\lambda \cdot {f}_{D2}+ \mu \cdot {f}_{S2}+\xi \cdot (-{f}_{E}),\\ &\rm{s}.\rm{t}.\quad \rm{1\;mm}\leqslant {{\boldsymbol{t}}}_{\rm{1}}\leqslant \rm{2\;mm},\rm{1\;mm}\leqslant {{\boldsymbol{t}}}_{\rm{2}}\leqslant \rm{2\;mm},\\ &\rm{1\;mm}\leqslant {{\boldsymbol{t}}}_{\rm{c}} \leqslant \rm{2\;mm}。\end{aligned} $ | (17) |
式中:t1为夹层板上面板厚度;t2为夹层板下面板厚度;tc为夹层板夹芯层厚度;
在进行正交设计试验时,采用L9(34) 正交表,各设计变量的水平值取1 mm、1.5 mm和2 mm,并依照正交设计结果,采用有限元软件Abaqus进行仿真计算。建模时采用壳单元,网格类型为S4R(四节点折减单元),网格尺寸为10 mm,边界条件为四边锚固,仿真模型如图2(b)所示。夹层板材料为L907A钢,密度为7850 kg/m3,弹性模量为210 GPa,泊松比为0.3,屈服应力为390 MPa。对模型施加的静载荷为5 kPa,施加的爆炸载荷(动载荷)峰值为500 kPa。选取夹层板上面板中点作为测点,计算得到的正交表样本数据如表1所示。
|
|
表 1 L9(34)正交表与有限元仿真结果 Tab.1 L9(34) orthogonal table and finite element simulation results |
为了能够在提高夹层板结构的抗爆性能的同时实现结构的轻量化,结构质量的权重系数α应取较大值。本文选取α=0.4,β=0.15,γ=0.1,λ=0.15,μ=0.1,ξ=0.1作为优化问题的权重系数,表1中F为通过加权得到的目标函数值。
2.2 神经网络训练采用单隐层神经网络对表1(共3个网络层)中的样本数据进行训练,输入层有3个神经元,隐含层有7个神经元,输出层有6个神经元。激励函数为Sigmoid,损失函数为均方误差函数(MSE),目标优化算法为Adam算法,每次训练从样本集中随机选取8组小批量样本,Adam算法的初始学习率设为0.04。同时,为了突出Adam算法的优势,在其他参数固定、迭代次数相同的条件下,将Adam算法与SGD算法进行了比较。
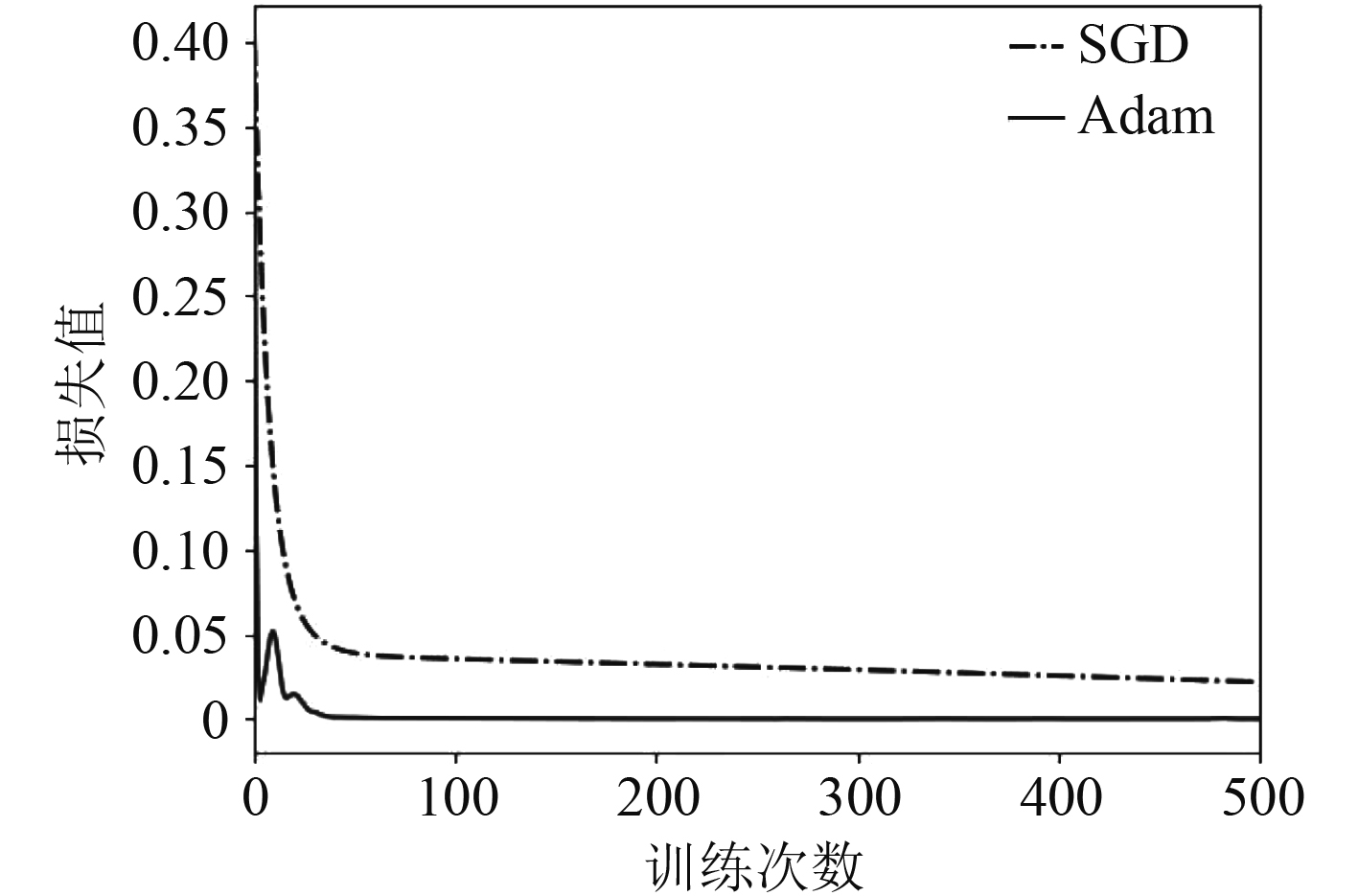
图3为神经网络训练过程中的损失曲线图。可以看出,Adam算法和SGD算法最终都是收敛的,但是Adam算法可以收敛到比SGD算法更小的损失值。这主要是因为传统的SGD算法存在2个缺点:更新方向不稳定、各参数的学习率相同,而Adam算法不仅将历史梯度的平均值记录为动量(惯性),使当前梯度对优化方向影响较小,同时还记录了各参数历史梯度的平方和来表示各参数变化的幅度,然后对变化幅度大的参数自适应地选择较小的学习率。与SGD算法相比,Adam算法能收敛到较小的损失值,有效地解决了SGD算法的2个缺点,成为最终采用的目标优化算法。
|
图 3 神经网络训练过程中的损失曲线图 Fig. 3 Loss curve during neural network training |
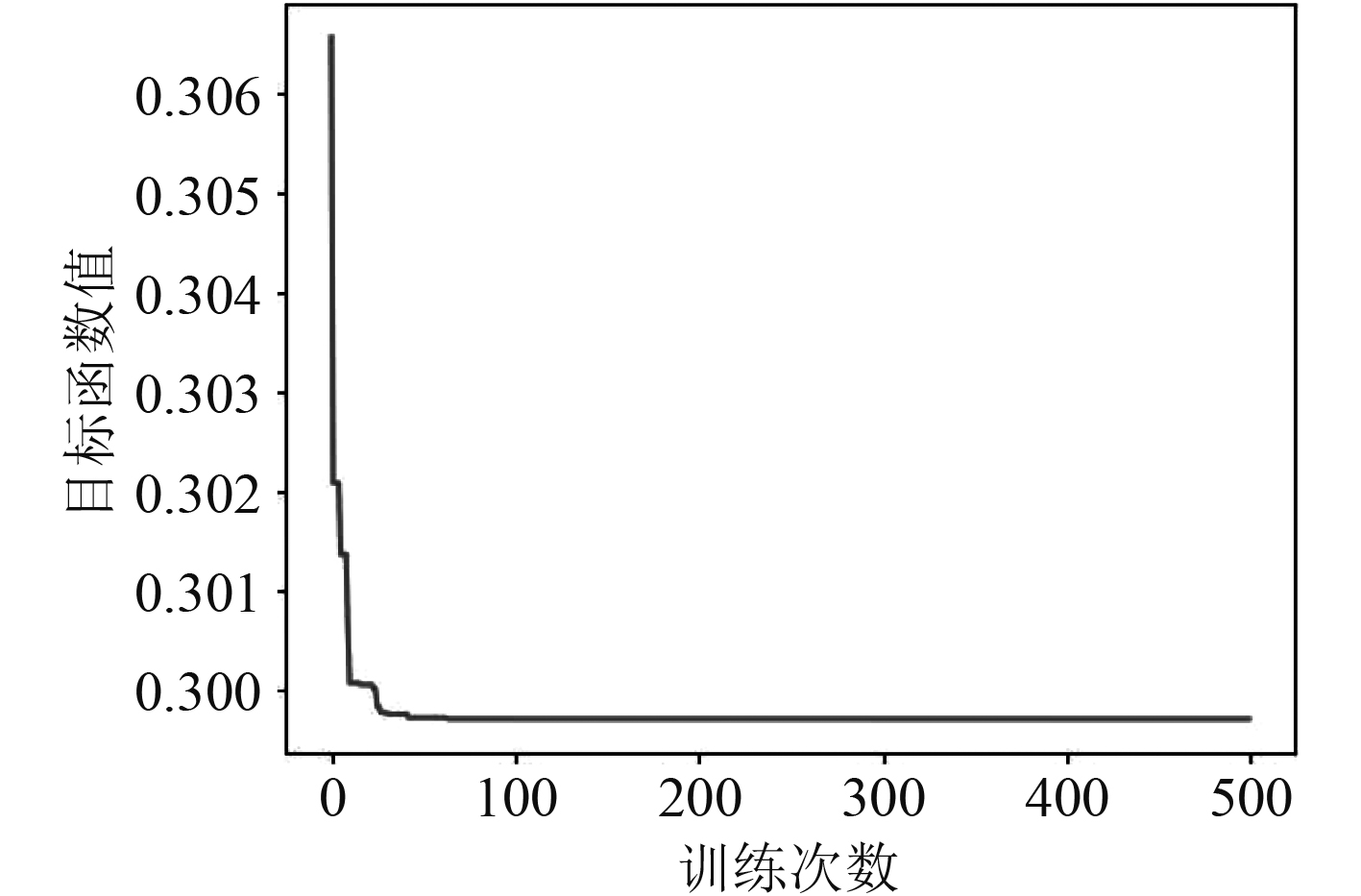
在麻雀搜索算法的优化过程中,神经网络响应面将作为目标函数使用,并对预测值进行线性加权。设置麻雀搜索算法的种群规模为100,生产者比例为20%,安全值为0.8,算法的目标函数曲线如图4所示。
|
图 4 麻雀搜索算法的目标函数变化曲线图 Fig. 4 Objective function curve of sparrow search algorithm |
可以看出,算法经过40次迭代后,目标函数曲线已经收敛,说明算法已经找到了最优解。表2为原结构与优化结果的比较。
|
|
表 2 优化结果与原结构对比 Tab.2 The optimization results are compared with the original structure |
从表2对比结果可以看出,神经网络预测值与有限元仿真值相差不大,说明本文的神经网络响应面具有较好的预测精度。以有限元仿真值作为真实优化结果,优化后的目标函数值相比于原结构降低了31.8%,说明优化后的夹层板结构性能较原设计有所提高;结构的质量比原结构质量降低了8.69%,也满足了结构的减重要求,说明本文的BP-SSA优化算法可以应用于波形夹层板结构的抗爆性能优化设计。与原结构相比,优化后的夹层板的下面板厚度保持不变,上面板厚度增大,芯层厚度减小,这说明在保持下面板厚度不变的情况下,增大上面板的厚度、减小芯层厚度可以提高结构的抗爆性能。
3 结 语本文将神经网络与麻雀搜索算法相结合,形成BP-SSA算法,以提高结构的抗爆性能为目标,对波形夹层板结构进行了优化设计。相比于原结构,采用本文方法得到的优化结果能够使结构的抗爆性能更优,神经网络的预测结果与有限元软件计算的实际结果吻合度较好。主要结论如下:
1)将神经网络与麻雀搜索算法相结合的优化算法可以实现波形夹层板结构的抗爆性能优化设计。优化结果表明,BP-SSA算法在得到具有较好抗爆性能的结构尺寸的同时,还实现了结构的轻量化设计。
2)基于Adam算法优化的神经网络的预测值与有限元软件计算的真实值相差不大,相比于传统的SGD算法,Adam算法可以收敛到更小的损失值,表明采用Adam算法作为目标优化算法进行神经网络的训练,可以让神经网络具有更好的训练精度,神经网络在结构优化中可以代替繁琐的有限元计算。
3)通过对优化结果与原结构进行对比分析,优化后的夹层板结构与原设计相比,下面板厚度保持不变、上面板厚度增大、芯层厚度减小,说明在保持下面板厚度不变的情况下,增大上面板的厚度、减小芯层厚度可以提高结构的抗爆性能。
| [1] |
柯力, 张延昌, 刘昆等. 基于铝质夹层板的上层建筑轻量化设计[J]. 船舶, 2019, 30(5): 25-36. KE L, ZHANG Y C, LIU K, et al. Lightweight design of superstructure based on aluminum sandwich panel[J]. Ship & Boat, 2019, 30(5): 25-36. |
| [2] |
赵相江, 马小敏, 李世强等. 爆炸载荷下双层梯度夹芯板的抗爆性能[J]. 太原理工大学学报, 2021, 52(6): 1022-1028. ZHAO X J, MA X M, LI S Q, et al. The explosion resistance of double-layer honeycomb sandwich panel under blast load[J]. Journal of Taiyuan University of Technology, 2021, 52(6): 1022-1028. |
| [3] |
XUE Z, HUTCHINSON J W. A comparative study of impulse-resistant metal sandwich plates[J]. International Journal of Impact Engineering, 2003, 30(10): 1283-1305. |
| [4] |
杨康尧. 三维内凹蜂窝夹芯板抗爆性能仿真与优化[D]. 大连: 大连理工大学, 2019.
|
| [5] |
亓昌, 郝鹏程, 舒剑等. 金字塔型点阵材料夹芯板抗爆性能仿真与优化[J]. 振动与冲击, 2019, 38(16): 245-252. QI C, HAO P C, SHU J, et al. Simulation and optimization for blast-resistant performances of pyramidal lattice cored sandwich panels[J]. Journal of Vibration and Shock, 2019, 38(16): 245-252. |
| [6] |
郭少鹏. 金字塔点阵与BRAS波纹夹层板抗爆性设计优化研究[D]. 大连: 大连理工大学, 2020.
|
| [7] |
XUE J, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering An Open Access Journal, 2020, 8(1): 22-34. |
| [8] |
王良玉, 张明林, 祝洪涛等. 人工神经网络及其在地学中的应用综述[J]. 世界核地质科学, 2021, 38(1): 15-26. DOI:10.3969/j.issn.1672-0636.2021.01.002 |
| [9] |
闫利鹏, 黄鸿颖, 杨骁等. 基于近似模型技术的高强钢盾构刀盘优化设计[J]. 铁道科学与工程学报, 2021, 18(8): 2156-2164. |
| [10] |
KINGMA D, BA J. Adam: A Method for Stochastic Optimization[C]//Proceedings of the 3rd International Conference for Learning Representations, 2015: 1-15.
|
| [11] |
QUYEN V T B, TIEN D N, DAT P V. Treatment of multi freedom constraints in geometrically nonlinear stability analysis of truss structures using penalty function method[J]. IOP Conference Series:Materials Science and Engineering, 2020, 962(2): 022069. DOI:10.1088/1757-899X/962/2/022069 |
| [12] |
LI L, HUANG B, ZHANG G. Optimization of ammonium sulfate crystals based on orthogonal design[J]. Journal of Crystal Growth, 2021, 570(3): 126217. |
| [13] |
杨灿. 基于BP神经网络故障推理模型的智能网络管理系统的研究与实现[D]. 北京: 北京林业大学, 2020.
|
 2022, Vol. 44
2022, Vol. 44
