0 引　言

大型舰船电气设备中电力变压器运行的可靠性与稳定性，直接影响电气设备的安全稳定性^[1]，严重时甚至威胁大型舰船航运的安全性。在电力变压器负荷量不断增大的条件下，其所承受的故障风险也逐渐增加^[2]，通过估计大型舰船电气设备中电力变压器的剩余寿命，能够优化其检修周期与使用性能，延长其生命周期^[3]。

当前，普遍使用的电力变压器剩余寿命估计方法多为基于隐马尔科夫模型的方法和基于全寿命周期的方法^[4-5]，前者利用故障比率模型分析电力变压器可靠度，获取其剩余寿命概率分布，但该方法所得结果与实际剩余寿命相比普遍偏低，易造成较大的经济损失；后者根据全寿命周期成本最低标准获取电力变压器经济寿命，但该方法所得结果与实际剩余寿命相比普遍偏高，有可能导致各研究对象在末期使用过程中失效，造成电气设备产生故障。

为获取准确的电力变压器剩余寿命，研究一种新的大型舰船电气设备中电力变压器剩余寿命估计方法。

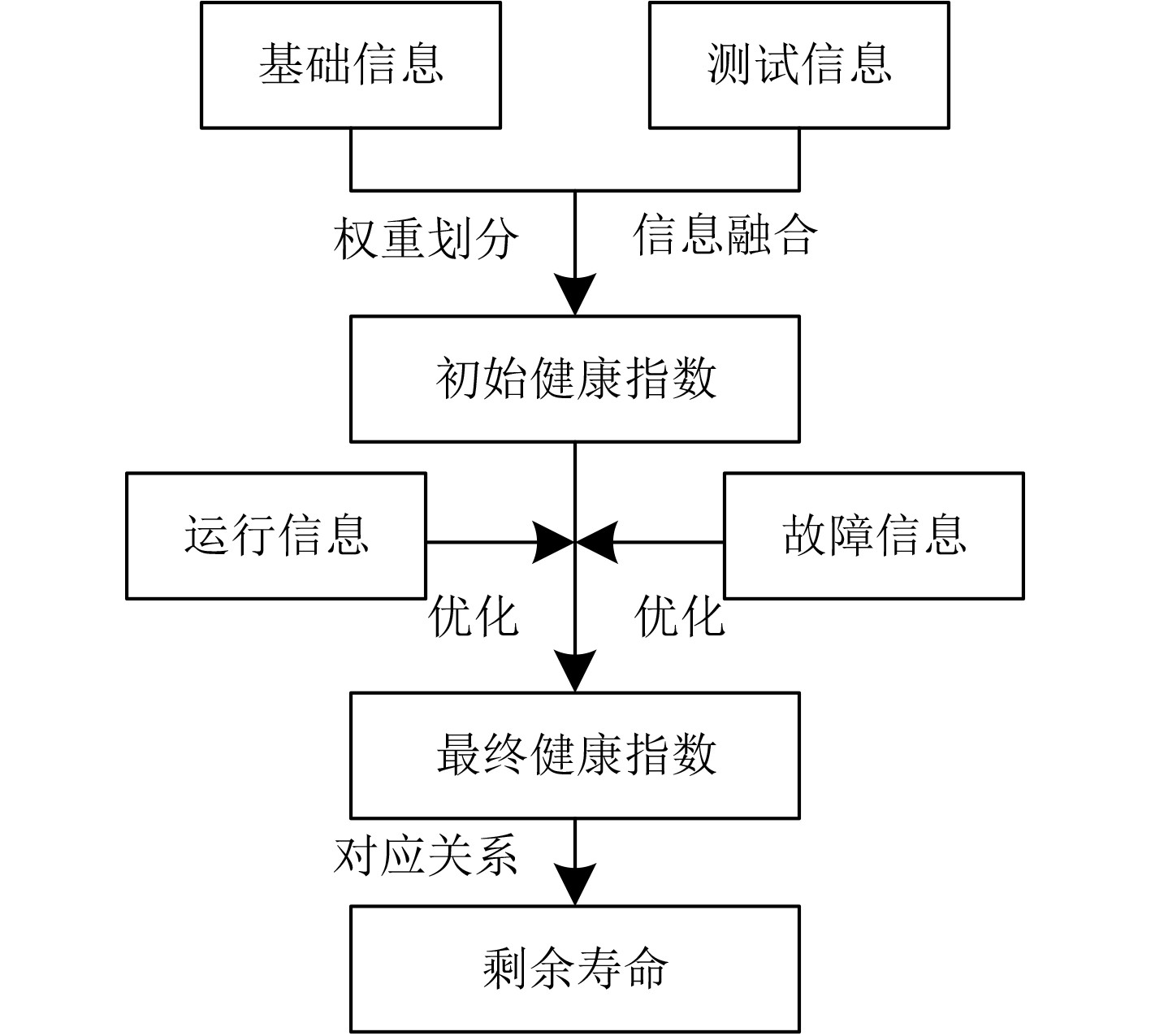
1 电力变压器剩余寿命估计方法 1.1 电力变压器剩余寿命估计模型构建

大型舰船电气设备中电力变压器剩余寿命估计模型如图1所示。该模型以大型舰船电气设备中电力变压器健康状态为基础，根据健康状态与剩余寿命间的对应关系确定大型舰船电气设备中电力变压器剩余寿命。

剩余寿命估计模型采用分层结构将大型舰船电气设备中电力变压器剩余寿命评估信息分为基础信息、测试信息、运行信息以及故障信息4个类别，以基础信息估计为第一层估计模型，获取大型舰船电气设备中电力变压器老化健康指数；以测试信息估计为第二层估计模型，获取大型舰船电气设备中电力变压器老化进程状态；以运行信息以及故障信息为第三层估计模型，优化前2层估计模型所得结果。由此能够防止由于大型舰船电气设备中电力变压器部件健康状态变化显著导致的大型舰船电气设备中电力变压器整体健康状态评估误差显著的问题。利用上述4类信息获取大型舰船电气设备中电力变压器健康指数，根据健康指数与剩余寿命间的对应关系确定大型舰船电气设备中电力变压器剩余寿命。

1.2 大型舰船电气设备中电力变压器健康指数 1.2.1 第一层估计模型

第一层估计模型所采用的基础信息内包含对大型舰船电气设备中电力变压器状态最关键的信息，如大型舰船电气设备中电力变压器产地、型号、预期寿命、工作环境与负荷等^[6]。

根据老化原理^[7]，计算大型舰船电气设备中电力变压器的健康指数 $ H $ ，得到：

$ H{\text{ = }}{H_0} \cdot {e^{G\left( {{T_2} - {T_1}} \right)}} 。$

(1)

式中： $ {H_0} $ 为大型舰船电气设备中电力变压器初始时刻 $ {T_1} $ 的健康指数，通常情况下设定为0.6； $ G $ 为老化率； $ {T_2} $ 为所要计算健康指数的年份。

以 $ {T_d} = \left( {{T_t} - {T_1}} \right) $ 表示大型舰船电气设备中电力变压器预期寿命，其值由厂家处得到，由此能够获取 $ G $ 的估计结果为：

$ G = \frac{{\ln \left( {{H_t} - {H_0}} \right)}}{{{T_d}}}。$

(2)

式中： $ {H_t} $ 为大型舰船电气设备中电力变压器可能产生故障时刻 $ {T_t} $ 对应的健康指数，通常情况下将其设定为6.6，由此能够得到：

$ G = \frac{{\ln \left( {6.6 - 0.6} \right)}}{{{T_d}}} 。$

(3)

在确定老化率后，即可确定大型舰船电气设备中电力变压器工作 $ {T_2} - {T_1} $ 年后的老化健康指数为：

$ {H_j} = {H_0} \cdot {e^{G\left( {{T_2} - {T_1}} \right)}} = \frac{{{e^{G\left( {{T_2} - {T_1}} \right)}}}}{2} 。$

(4)

1.2.2 第二层估计模型

第二层评估模型利用油色谱、糠醛以及油质等测试数据^[8]，间接描述大型舰船电气设备中电力变压器健康状态，对比测试所得数据与大型舰船电气设备中电力变压器使用前的数据，即可获取大型舰船电气设备中电力变压器老化进程状态。

以 $ {H_{z1}} $ 表示油色谱测试所得数据，获取 $ {H_{z1}} $ 的详细过程为：依照氢气、甲烷、乙烷、乙炔乙烯五类气体检测结果^[9]，分别确定气体的含量等级，以V表示。分别以各类气体检测所得气体含量等级与其气体检测对应的权重相乘，能够确定各类气体组分的分值，基于此得到油色谱测试结果为：

$ \left\{ \begin{gathered} {H_{z1}} = {S_{{{\rm{H}}_2}}} + {S_{{{\rm{C}}_2}{{\rm{H}}_6}}} + {S_{{\rm{C}}{{\rm{H}}_4}}} + {S_{{{\rm{C}}_2}{{\rm{H}}_4}}} + {S_{{{\rm{C}}_2}{{\rm{H}}_2}}} ，\hfill \\ {S_i} = {V_i}{W_i} 。\hfill \\ \end{gathered} \right. $

(5)

式中， $ {W_i} $ 和 $ {W_i} $ 分别表示各油色谱测试项目与所对应的权值。

$ {H_{z2}} $ 表示糠醛测试所得数据，通过糠醛测试能够反映大型舰船电气设备中电力变压器绝缘的老化情况^[10]。通常情况下大型舰船电气设备中电力变压器内新的绝缘材料聚合度为1000，在其聚合度降至1/4的条件下需重点关注。纸聚合度 $ DP $ 与糠醛含量间的相关性如下式：

$ DP = - 120 \cdot \ln {F_a} + 469。$

(6)

式中： $ {F_a} $ 表示糠醛含量，在其值为5的条件下， $ DP $ 值为250，由此体现大型舰船电气设备中电力变压器的绝缘达到其使用寿命；在 $ {F_a} $ 值为0.01的条件下， $ DP $ 值为1000，说明大型舰船电气设备中电力变压器的绝缘处于未使用状态。由此能够得到：

$ {H_{z2}} = 2.33{\left( {{F_a}} \right)^{0.68}} 。$

(7)

$ {H_{z3}} $ 表示油质测试所得数据，获取 $ {H_{z3}} $ 的详细过程为：依照击穿水压、介质损耗与酸度的检测结果^[11]，分别确定不同检测项目的检测等级 $ U $ ，并将各 $ U $ 同其对应的权重相乘，由此得到不同气体组分分值，基于此得到油质测试结果为：

$ \left\{ \begin{gathered} {H_{z3}} = {S_a} + {S_b} + {S_c} ，\hfill \\ {S_i} = {U_i}{W_i} 。\hfill \\ \end{gathered} \right. $

(8)

式中， $ {S_i}\left( {i = a,b,c} \right) $ 和 $ {W_i} $ 分别表示各油质测试项目与所对应的权值。

结合第一层估计模型与第二层估计模型能够得到大型舰船电气设备中电力变压器初始健康指数。

在 $ {H_j} $ 为上限的条件下：

$ {H_c} = {H_j} \cdot {f_c} ；$

(9)

在 $ H{I_j} $ 为非上限的条件下：

$ {H_c} = \max \left[ {\left( {{H_{z1}} \cdot {f_c}} \right) \cdot \left( {{H_{z2}} \cdot {f_c}} \right) \cdot \left( {{H_{z3}} \cdot {f_c}} \right)} \right] 。$

(10)

式中， $ {f_c} $ 表示一个非固定的系数。

1.2.3 第三层估计模型

第三层估计模型主要功能是进行优化，基于大型舰船电气设备中电力变压器的运行环境信息优化前2层估计模型所获取的估计结果。第三层评估模型内所使用的优化因子包括以运行信息为核心的优化因子和以故障信息为核心的优化因子2种类型^{[8, 12]}。

根据当前普遍使用的电力变压器状态分析的标准，考虑大型舰船电气设备中电力变压器在检测系统的运行状态，在普遍使用标准的评分项目内挑选关键的部分项目优化前2层估计模型，利用各类方法确定不同优化项目的影响权重，由此确定对应的优化系数。

以运行信息为核心的优化因子包括大型舰船电气设备中电力变压器的投运时间和铁芯接地电流^[13]，二者分别以 $ T $ 和 $ I $ 表示。

1）在大型舰船电气设备中电力变压器的投运时间不小于0年且不大于5年的条件下，投运时间优化因子 $ {A_{11}} $ 值为1；在大型舰船电气设备中电力变压器的投运时间分别在大于5年且不大于10年、大于10年且不大于20年、大于20年且不大于30年和大于30年的条件下，投运时间优化因子 $ {A_{11}} $ 值分别为1.01，1.02，1.05和1.09；

2）在铁芯接地电流值分别为0 A、大于0 A且不大于0.1 A、大于0.1 A且不大于0.3 A和大于0.3 A的条件下，铁芯接地电流优化因子 $ {A_{12}} $ 值分别为1，1.05，1.1和1.2。

以故障信息为核心的优化因子中包括大型舰船电气设备中电力变压器的外观等级、套管可靠等级、冷却方式、近3年故障次数、近区短路和局部放电这6个优化因子^[14]。

1）针对大型舰船电气设备中电力变压器本体、分接开关、冷却系统3个组件内外观等级最高的实施优化。大型舰船电气设备中电力变压器外观等级优化因子 $ {A_{21}} = 0.9 + 0.1L\left( {L = 1,2, \cdots ,5} \right) $ ，其中，等级 $ L $ 为1时表示大型舰船电气设备中电力变压器外观状态为最优状态。

2）大型舰船电气设备中电力变压器套管可靠等级 $ R $ 可划分为5级，在 $ R $ 取值分别为1～5时，可靠性优化值 $ {A_R} $ 分别为0.9，1.0，1.1，1.2和1.4。以某型号三相电力变压器为例，其高、中、低侧套管的可靠性等级有所差异，如果 $ \mathrm{max}\left({A}_{R高}，{A}_{R中}，{A}_{R低}\right) $ >1，则套管可靠等级优化因子 $ {A}_{22}\text{=}{A}_{R高}+{A}_{R中}+{A}_{R低} $ ；如果 $ \mathrm{max}\left({A}_{R高}，\right. $ $ \left.{A}_{R中}，{A}_{R低}\right) $ ≤1，则套管可靠等级优化因子 $ {A}_{22}\text{=} \mathrm{min} $ $ \left({A}_{R高},{A}_{R中},{A}_{R低}\right) $ 。

3）在大型舰船电气设备中电力变压器冷却系统采用油浸自冷与风冷方式时，冷却方式优化因子值为1；在大型舰船电气设备中电力变压器冷却系统，分别采用强迫油循环冷却方式和强迫导向油循环冷却方式时，冷却方式优化因子值 $ {A_{23}} $ 分别为0.96和0.95。

4）在大型舰船电气设备中电力变压器近3年故障次数分别为0，1，2～4，5～10和高于10次的条件下，近3年故障次数优化因子 $ {A_{24}} $ 分别取值0.96，1.00，1.04，1.20和1.40。

5）在大型舰船电气设备中电力变压器形成过近区短路时，近区短路优化因子 $ {A_{25}} $ 取值1.04；相反 $ {A_{25}} $ 取值1。

6）如果大型舰船电气设备中电力变压器产生局部放电问题，那么局部放电优化因子 $ {A_{26}} $ 取值1.2；相反 $ {A_{26}} $ 取值1。

综合运行信息为核心的优化因子 $ {A_{1m}} $ 和故障信息为核心的优化因子 $ {A_{1n}} $ ，得到综合优化因子为：

$ {A_c} = \prod\limits_{m = 1}^2 {{A_{1m}}} \cdot \prod\limits_{n = 1}^6 {{A_{1n}}} ，$

(11)

利用 $ {A_{1m}} $ 和 $ {A_{1n}} $ 优化 $ {H_c} $ ，能够得到大型舰船电气设备中电力变压器最终的健康指数为：

$ H = {H_c}\frac{1}{{\left( {1 - {A_{1m}}} \right)}}{A_{1n}} 。$

(12)

1.3 基于健康指数的剩余寿命估计

基于健康指数的大型舰船电气设备中电力变压器剩余寿命估计就是基于电力变压器当前的 $ H $ 值估算其到无法继续使用的 $ H $ 值的时间。估计结果内若电力变压器 $ H $ 值高于6，其故障形成可能性数值将以较快速度提升。基于此，在基于健康指数的大型舰船电气设备中电力变压器剩余寿命估计过程中，设置相应的裕度，将剩余使用寿命设定为 $ H $ 值为7。在大型舰船电气设备中电力变压器 $ H $ 值为7的条件下，电力变压器故障形成的可能性数值将以较快速度提升，在此条件下，需通过相应的方式对大型舰船电气设备中电力变压器进行修整。基于以上分析，根据健康指数与剩余寿命的对应关系，得到大型舰船电气设备中电力变压器剩余寿命估计结果为：

$ {E_o} = \frac{{\dfrac{{\ln 7}}{I}}}{G} 。$

(13)

2 实验分析

为验证本文研究的大型舰船电气设备中电力变压器剩余寿命估计方法的实际应用性能，选取某批次应用于大型舰船电气设备中的电力变压器为研究对象。该批次研究对象内共包含8个电力变压器，分别命名为1号～8号。各研究对象工作地点均为船内，投入应用时间为2006年，预期使用寿命为40年，冷却方式为油浸自冷，近3年故障次数均为0次，除5号电力变压器产生一次近区短路外剩余电力变压器均未产生近区短路，未产生局部放电问题，预计每6年进行一次整体大检修。基于研究对象的实际情况，采用本文方法估计研究对象剩余寿命。

2.1 健康指数估计结果

以5号电力变压器为目标，采用本文方法估计该研究对象自开始应用至2020年期间历年的健康指数，所得结果如表1所示。

可知，采用本文方法能够得到研究对象自开始应用后历年的健康指数，且历年健康指数在整体上呈现逐渐下降的趋势，这与研究对象的实际应用情况相符。同时研究对象自2006年开始应用后，其健康指数在2011年与2017年2次呈现上升趋势，这与研究对象预计每6年进行一次整体大检修的情况相符。

为进一步验证本文方法对于研究对象健康指数估计结果的精度，对比本文方法所得研究对象自开始应用后历年的健康指数与研究对象历年实际健康指数，所得结果如图2所示。

分析可知，采用本文方法所得研究对象自开始应用至2020年期间历年的健康指数基本同研究对象实际健康指数一致，只在进行整体大检修当年所得的健康指数与实际健康指数存在微弱偏差。由此能够说明采用本文方法能够较为准确地估计研究对象在投入应用后历年的健康指数。

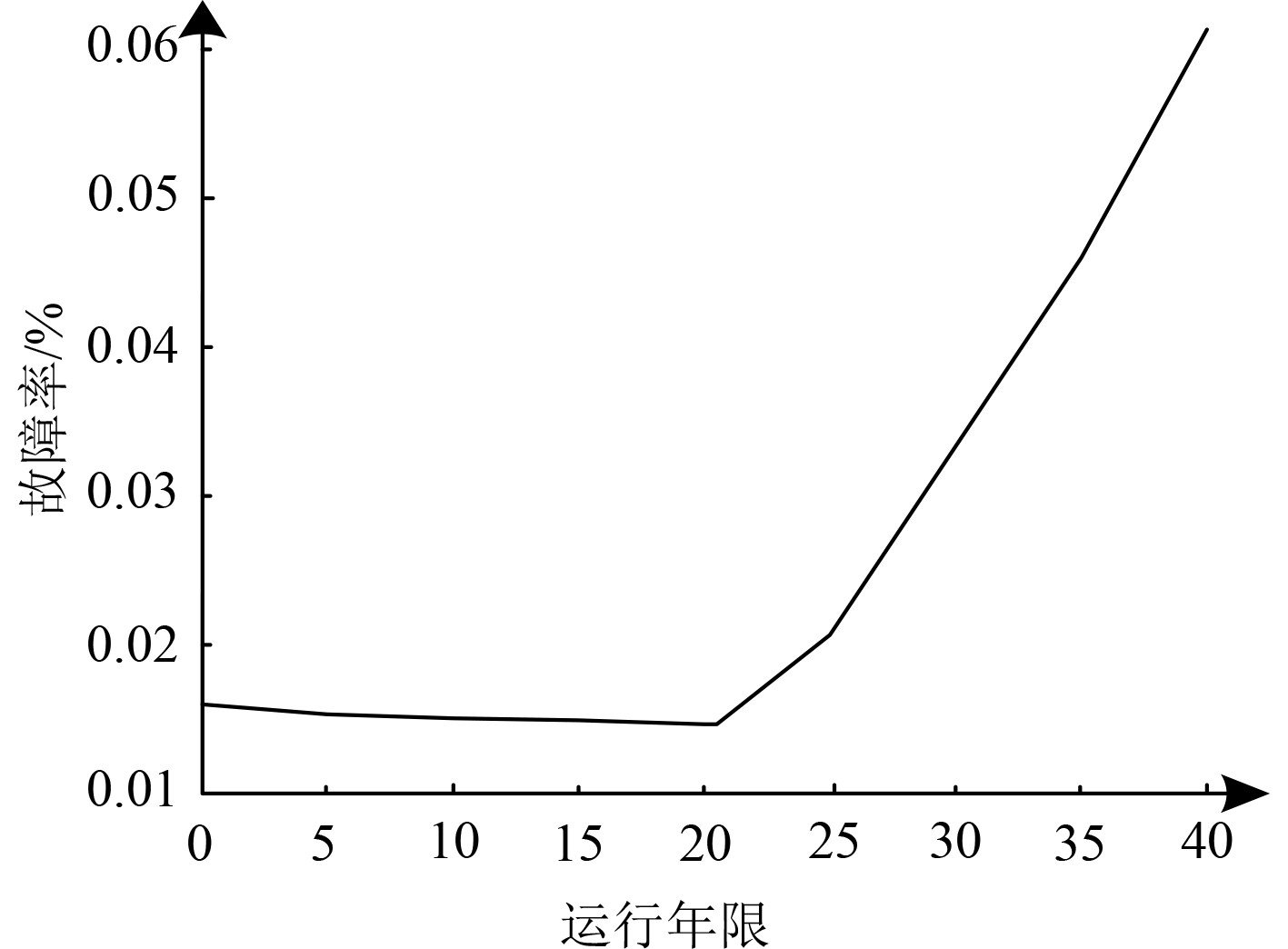
将5号电力变压器健康指数估计结果转换为其故障率，通过曲线拟合得到5号电力变压器的故障率曲线，所得结果如图3所示。

分析可知，由于研究对象在早期应用过程中的故障时间较短，因此所得故障率拟合曲线仅包含2个主要阶段，分别是偶然故障期与耗损故障期。以运行粘性21年为分界点，满足浴盆曲线特征标准，由此说明本文方法能够较好地估计研究对象寿命变化特征。

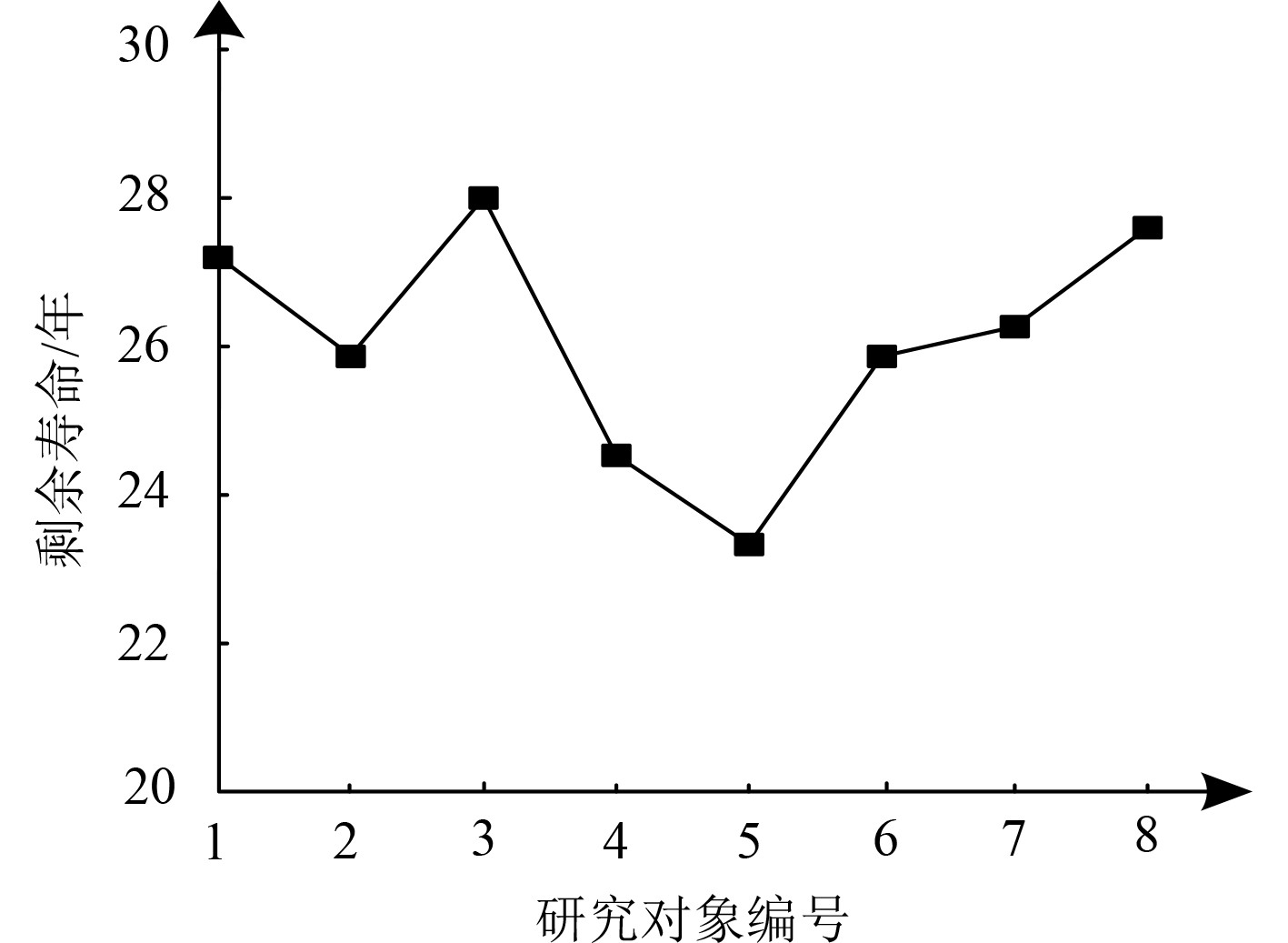
2.2 剩余寿命估计结果

在2021年7月，采用本文方法分别估计各研究对象的剩余寿命，所得结果如图4所示。

可知，采用本文方法所得各研究对象剩余寿命均在23～28年。其中5号研究对象剩余寿命最低，约为23年半左右。

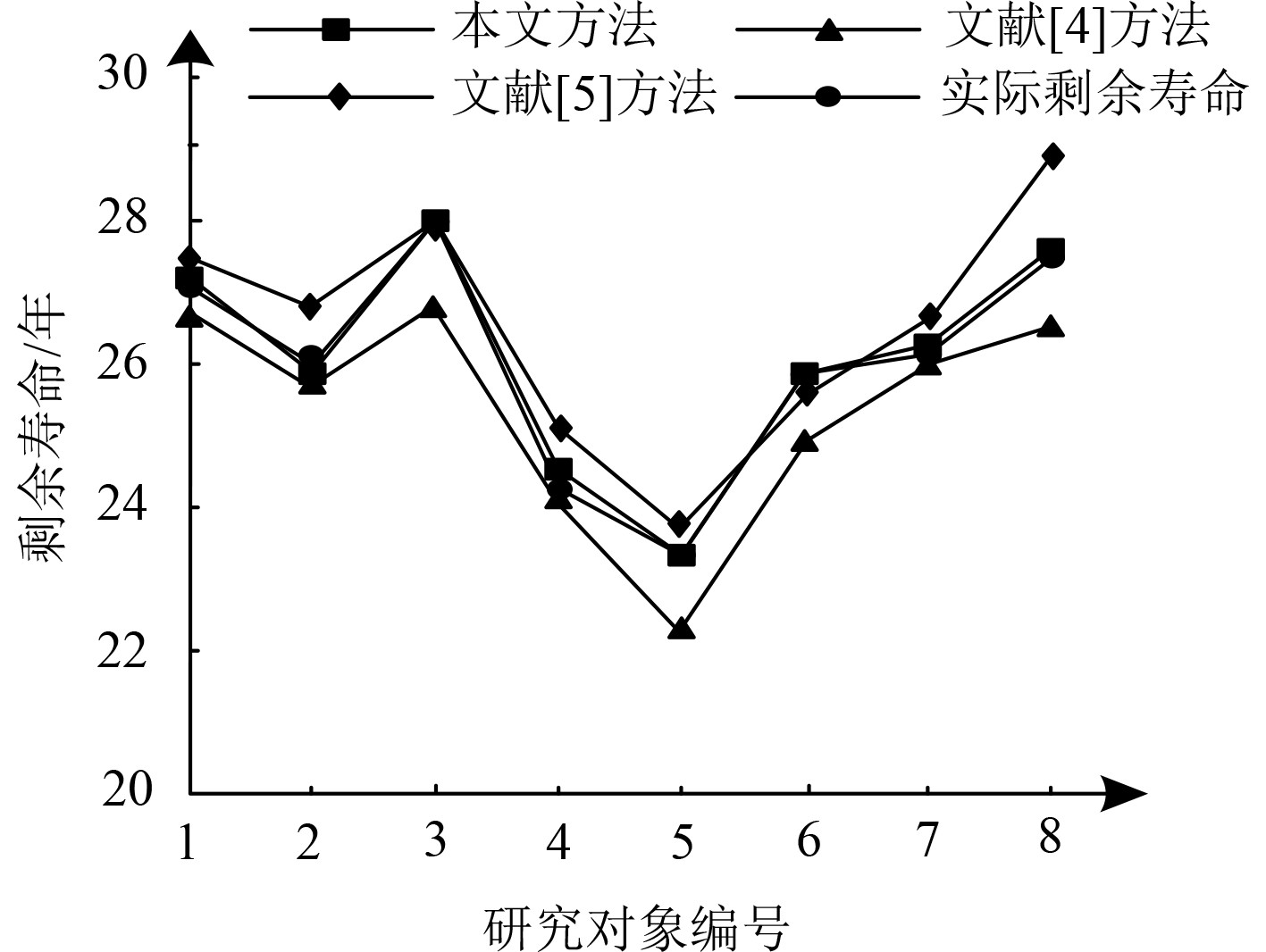
为进一步验证本文方法剩余寿命估计的性能，将文献[4]中基于隐马尔科夫模型的方法和文献[5]中基于全寿命周期的方法为对比方法。将本文方法与2种对比方法估计所得各研究对象剩余寿命同研究对象实际剩余寿命相对比，所得结果如图5所示。

分析可知，3种方法中本文方法对各研究对象估计所得剩余寿命与实际剩余寿命间差异最为微弱。文献[4]方法估计所得结果与各研究对象实际剩余寿命相比普遍偏低，这将导致各研究对象在未达到实际应用年限的条件下被替换掉，造成较大的经济损失。文献[5]方法估计所得结果与各研究对象实际剩余寿命相比普遍偏高，这将导致各研究对象在末期使用过程中存在失效的可能性，造成电气设备产生故障，影响大型舰船航运的安全性。

3 结　语

研究大型舰船电气设备中电力变压器剩余寿命估计方法，以基础信息、测试信息、运行信息与故障信息为基础估计电力变压器健康指数，基于健康指数与剩余寿命间的对应关系确定电力变压器剩余寿命。实验结果表明，本文方法能够准确估计电力变压器剩余寿命，较好估计研究对象寿命变化特征，为大型舰船电气设备中电力变压器的状态检修提供参考。