2. 苏州健雄职业技术学院,江苏 太仓 215411
2. Suzhou Chien-shiung Institute of Technology, Taicang 215411, China
由于船舶运动具有非线性的特征,控制效果不尽人意。对SVM逆系统加以合理运用,以此来实现对船舶航向的广义预测与控制。
1 船舶运动数学模型 1.1 线性模型线性控制是自动控制理论中应用最为广泛的一种控制方式,由于船舶本身具有对称性,所以当船舶在平衡位置处进行小幅运动时,产生的横荡与首摇均为非线性运动。为便于分析,假定船舶的航速为常数,在此基础上,可将前向运动方程删除,当船舶的运动幅度过大时,要应用非线性模型,否则可能会导致误差增大[1-4]。在水面上的船舶做匀速直线运动时,若是受到航向扰动力,在不操纵舵的情况下,船体重心的运动轨迹会在扰动后恢复为直线,但是船舶原本的航向却发生改变,可将该现象称为直线运动稳定性,这是船舶的运动特性之一。在此特性下,船舶受到扰动仍然能够恢复定常运动。通常情况下,可利用稳定性衡准数,判别船舶是否具有定常稳定性。
1.2 非线性模型线性模型的局限性比较大,要求船舶的航速为常数,而当船舶的运动参数过大时,需要运用非线性模型。船舶在航行时定常回转,在无风浪干扰的前提条件下,船舶能够顺利完成回转[5-8]。
1.3 干扰力模型船舶在水上航行,不可避免会受到风浪的影响,对于船舶而言,风浪是其运动的干扰力。随机风对船体运动产生的影响比较小,而当风力为恒值时,舵角可以抵消这部分干扰。海浪对船舶的干扰力矩与波高成正比,即波高越高,干扰力矩越大。
2 广义预测控制与SVM模型 2.1 广义预测控制算法广义预测控制简称GPC,其基础是自适应控制。一些专家学者提出广义预测控制算法,该算法具有GPC的三大特征,即预测模型、滚动优化以及反馈校正。对于预测模型而言,因实际应用中只强调模型的功能,所以很多传统的模型,如状态方程、传递函数等,均能作为预测模型[9-10]。展示系统未来动态行为是预测模型最为突出的功能,在该功能下,可以向系统仿真给出相应的控制策略,对输出变化加以观察,据此比较控制策略的优劣,为选取最优的控制策略提供依据。在GPC中,采用CARIMA模型,对随机干扰的物体进行描述,用传递函数z给出物体的描述,从输入到输出的传递函数为:
| $G\left( z^ {-1} = \frac {z^ {-1}B(z^ {-1})}{A(z^ {-1})} \right)。$ |
按已知的输入与输出信息和未来的输入值,便可预测出未来的输出。
在线优化是预测控制的重要特征之一,该特征使其能够利用某个性能指标的最优确定未来控制。大量实践表明,闭环控制策略的效果要优于开环顺序控制,但在多步预测中进行闭环控制,会导致部分有用的信息无法得到充分利用,并且计算所得的控制量还会受到诸多因素的影响,如误差、干扰等,进而导致虚假波动产生,控制效果随之下降。为此,对多步预测中的有用信息充分利用显得尤为必要,这一目标,可以借助控制律来实现。
从本质上讲,预测控制归属于闭环控制算法的范畴,当未来的控制作用确定后,为了保证控制效果符合预期,需要对模型的抗干扰能力进行强化。当系统进行工作是,需要首先检测初始状态的输出,据此修正预测模型,再进行新的优化,这便是预测控制的反馈校正,它的形式多种多样,能在保持模型不变的前提下,补偿未来的预测误差,还能依据在线辨识,对预测模型进行修改,使其满足应用需要。预测控制始终将优化放在首位,力争在优化时,准确预测出系统的未来行为,由此使得优化成为预测控制模型的基础。GPC会不断修正控制律,这是一种广义的反馈校正行为,它只用一个模型,通过在线修正的方法,便可给出相对比较准确的预测。
2.2 非线性系统广义预测控制实践表明,线性模型能够控制弱非线性对象,但强非线性系统却无法通过线性模型控制。在强非线性系统中运用广义预测控制是目前研究的重要方向,Hammerstein 模型对非线性系统进行分解,其中一部分为线性,另一部分为非线性。也就是说,在一个非线性系统中,既包含线性,也包含非线性,其中的线性部分可以借助GPC,获得参考值,随后找到系统的校准模型,便可得出控制信号。在这一过程中,反函数是否具备唯一性,是算法能否成功的关键。在对未来的输出预测时,要将未来时刻可能存在的非线性影响予以忽略,通过GPC计算出控制量,将之带回后,对未来的输出重新预测,在反复的迭代后,当控制量达到基本稳定,便可停止。上述方法在品阶较低的模型中具有良好的应用效果,当模型的品阶比较高时,应用该方法,计算过程变得较为复杂,计算量也随之增大。单个模型处理非线性系统的效果一般,对此可增加模型的数量,将单个模型变为多模型,应用时,要先对非线性系统的平衡点加以确定,完成线性化后,对得到的模型进行广义预测控制,同时引入参考轨迹,使预测结果逼近期望值。对于具有实质性特点的非线性系统而言,可以在控制周期内,通过递推的方式,预测出未来时刻的工作点,并在该点位附近做线性化处理,借助动态补偿,对系统的控制输入加以确定,这就是广义预测算法。
2.3 SVM模型SVM即支持向量机,与ANN最大的区别在于优化过程不同,ANN可以通过优化训练模型,使得目标最为准确,SVM则是作为限制因素对误差进行控制,优化目标为置信范围的最小值。由此使得SVM的控制效果更好,并且求解得到优化后的结果,求得的解不但是全局最优,而且还是唯一解。SVM所具备的诸多特点,使其一经提出,便得到业内广大专家学者的关注。目前,SVM已被推广到非线性系统当中,在系统识别、预测预报、建模控制等方面的应用越来越广泛。SVM是一种全新的机器学习算法,求解时只要核函数选对即可,对核函数计算求解,能够有效解决维数灾难问题。在实际应用时,需要满足Mercer条件,并且需要具备一定的特征。由此使得选择核函数成为SVM研究的核心。虽然业内的专家学者在该方面做了大量研究,但截止到目前,并未提出一种核函数选择的有效方法,目前,较为常用的核函数有:多项式、径向基、多层感知机等。其中多项式得到的是q阶分类器,径向基的每个函数中心都与一个支持向量相对应,可以自动确定输出权值及算法,多层感知机为多层感知器,可以通过相应的算法确定隐层节点数。
3 船舶航向广义预测控制中SVM逆系统的应用 3.1 航向预测控制的实现由于非线性系统本身所具备的特点,从而使其很难获得精确度比较高的模型,并以此为依托开展多步预测,给广义预测控制的研究造成不利影响。神经网络(ANN)的出现,为非线性系统的描述提供了强有力的支撑,借助神经网络控制非线性系统成为业内研究的重要课题。在通过ANN对非线性系统描述时,可利用输入与输出数据,并在学习与训练中,使结果逼近非线性系统。基于此,结合ANN对船舶航向广义预测控制展开研究。广义预测控制归属于模型预测控制的范畴,这种控制方式最早是基于线性系统CARIMA模型提出的,在不断的应用中发现,该模型可以使线性系统的控制问题得到有效解决。不仅如此,还能解决一些弱非线性系统的控制问题,但要求平衡点在附近工作。如果是强非线性系统,且工作点的变化幅度过大,则无法通过CARIMA模型进行控制。想要解决此类系统的预测控制问题,就需要运用非线性预测模型,对系统的动态特性加以拟合。从目前的实际情况来看,非线性预测控制模型的构建比较困难,并且基于该模型的优化算法过程较为繁琐,求解难度较大。常用的解决方法是借助模糊控制理论和ANN,建立非线性模型,以此来实现预测控制。然而,模糊控制与ANN在建模和训练方面存在一定的缺陷,如局部最小、训练速度慢等。而SVM基于的是风险最小化原理和统计学习理论,函数拟合能力比较强,易于获得全局最优解,训练速度快。船舶在海面上的航行过程较为复杂,随着环境的改变,将会对系统造成影响,导致不确定性增大。而采用SVM构建非线性预测模型,能够使建模难的问题得到有效解决。具体的实现过程如下:
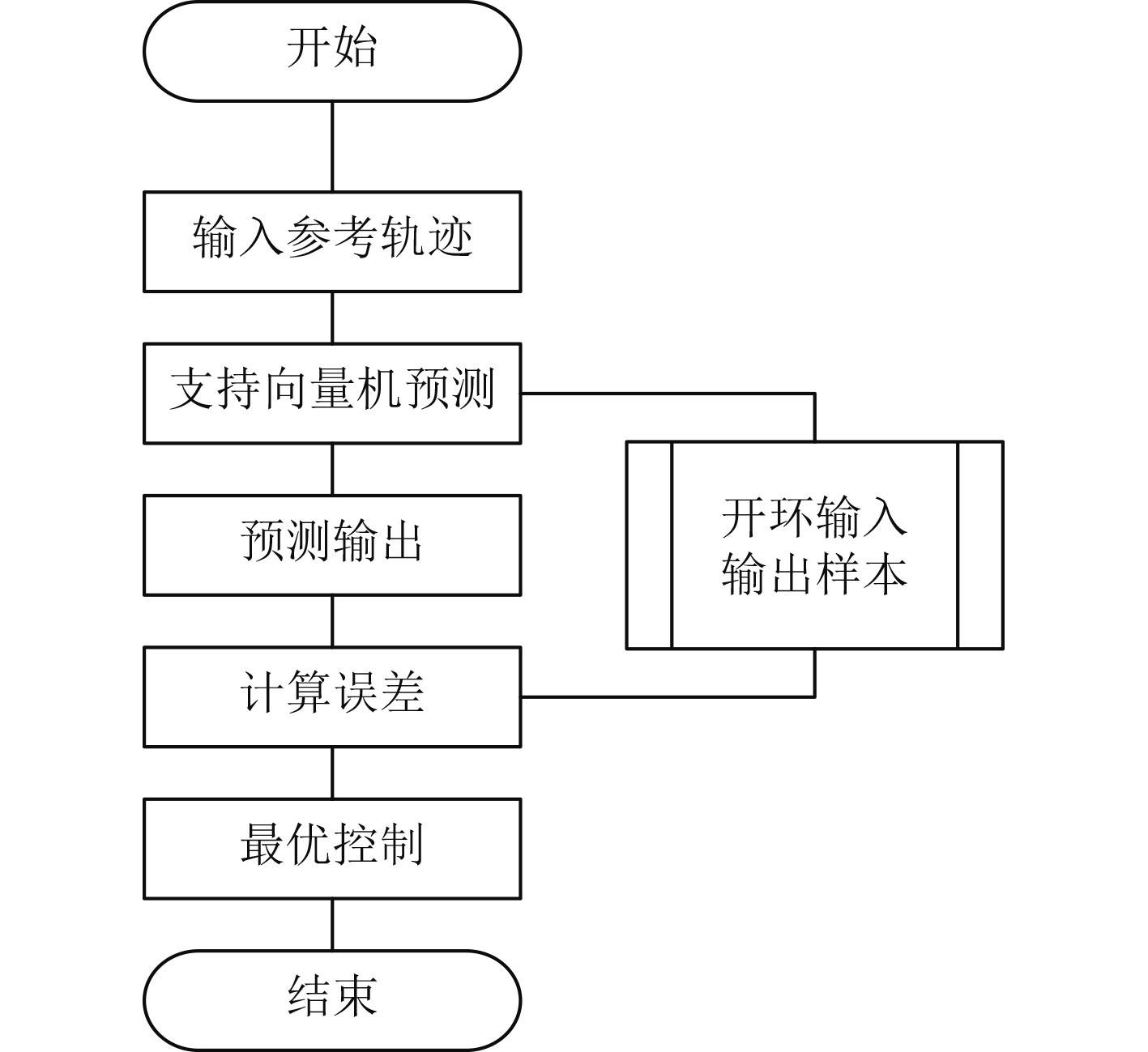
在递推多步预测的过程中,只需要运用一个SVM预测模型,通过对输入与输出信息的存储,连同相应的计算结果,全部传给控制器,借助GPC算法便可获得控制输入。非递推多步预测,使用多个并行的SVM预测模型,经GPC控制器得到控制输入。从实际情况来看,上述2种方法在实现效果上差别不大。因此,本次研究选用递推多步预测方法,预测控制算法的具体过程如下:按照具体的控制要求,获取期望的输出序列,该系列即输入的参考轨迹;测量被控对象的输入和输出数据,将之作为训练SVM的样本,对SVM做离线训练,获得预测模型;通过得到的SVM预测模型,产生系统输出,计算出误差,得到最优的控制量,将之作用于系统,便可实现预测控制。算法流程如图1所示。
|
图 1 支持向量机预测控制算法实现流程示意图 Fig. 1 Implementation flow diagram of support vector machine predictive control algorithm |
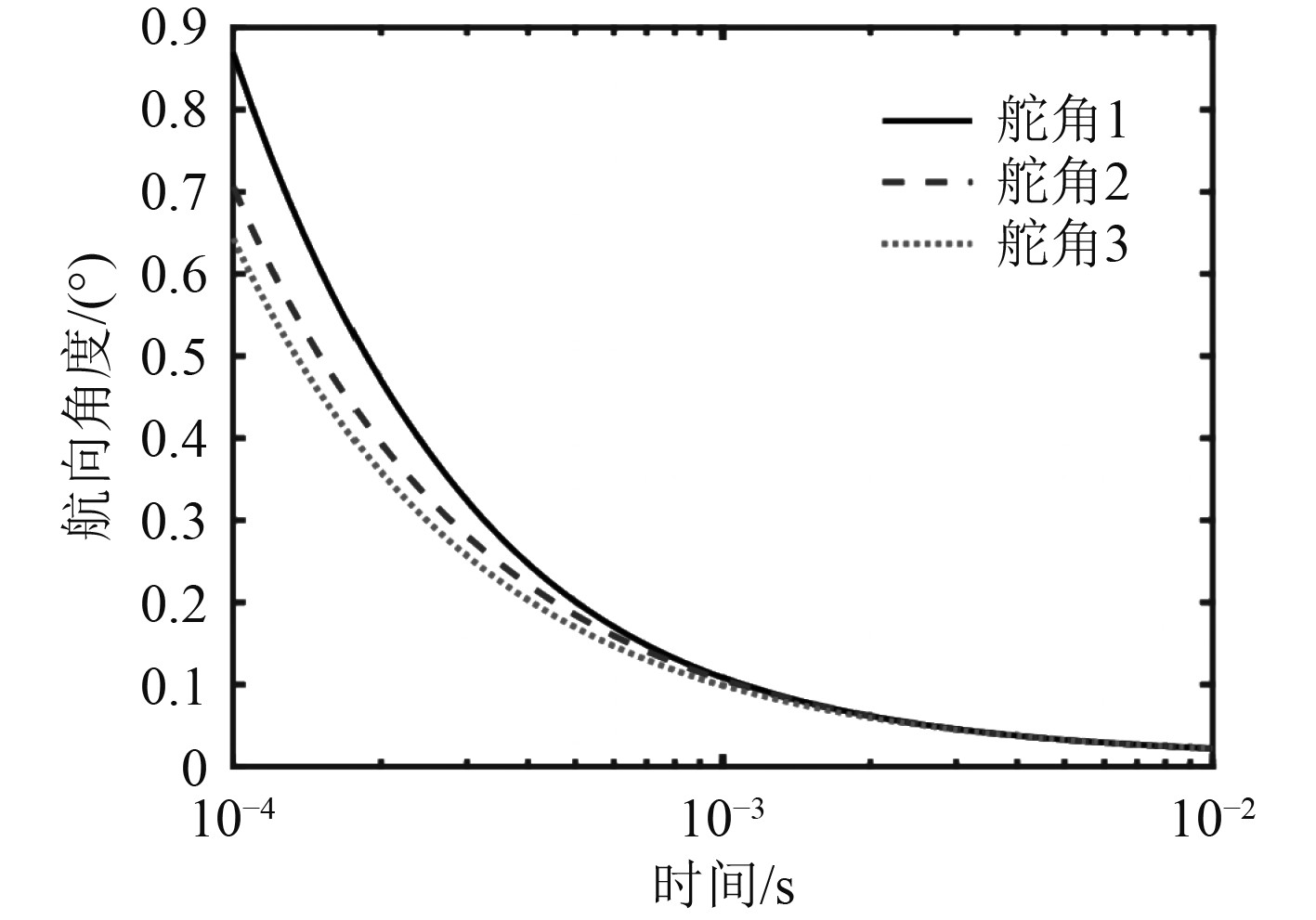
基于SVM逆系统,对船舶模型仿真,将仿真时间设定为50 s,重点研究船舶在25 s时,航向从10°变为5°的历时变化曲线、控制舵角变化曲线以及航向误差变化曲线。为使仿真结果更加趋近于现实,分别在海面上无风浪干扰和有风浪干扰的情况下仿真,其中无风浪的仿真结果如图2~图4所示。有风浪时的系统仿真结果如图5~图7所示。
|
图 2 无风浪状态下船舶航向变化曲线示意图 Fig. 2 Schematic diagram of ship course change curve under no wind and wave condition |
|
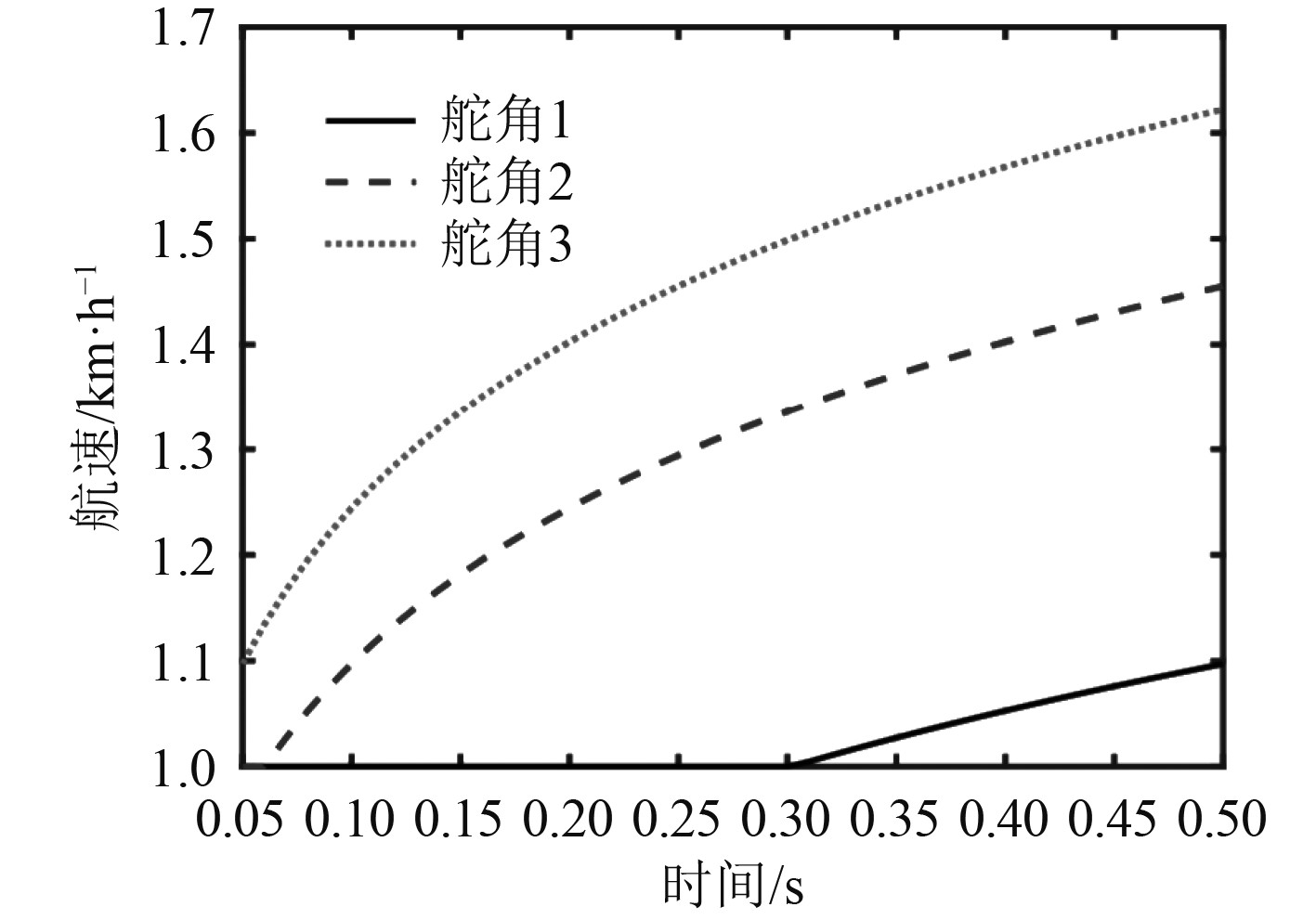
图 3 无风浪状态下控制舵角变化曲线示意图 Fig. 3 Schematic diagram of control rudder angle change curve under no wind and wave condition |
|
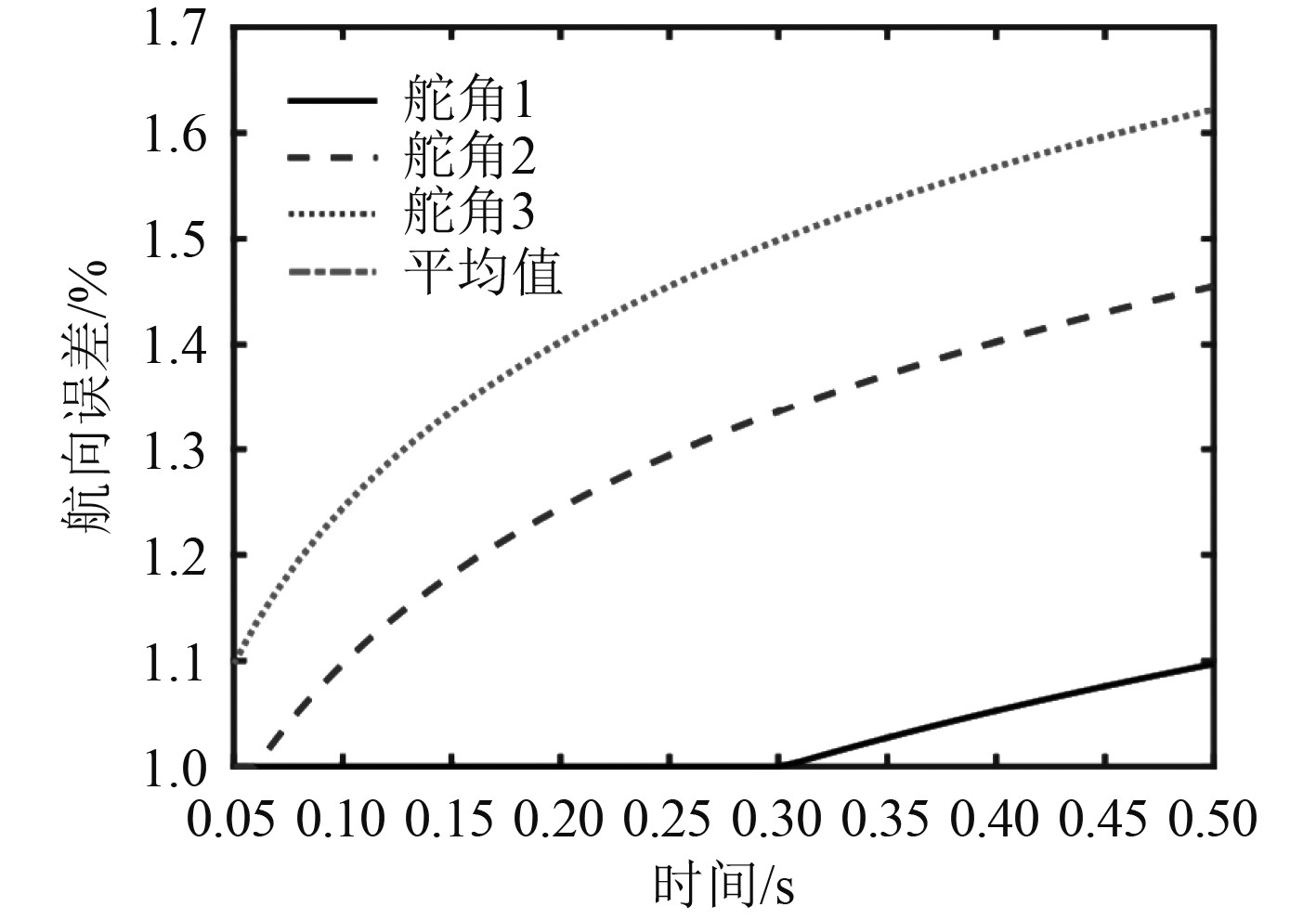
图 4 无风浪状态下航向误差变化曲线示意图 Fig. 4 Schematic diagram of course error change curve under no wind and wave condition |
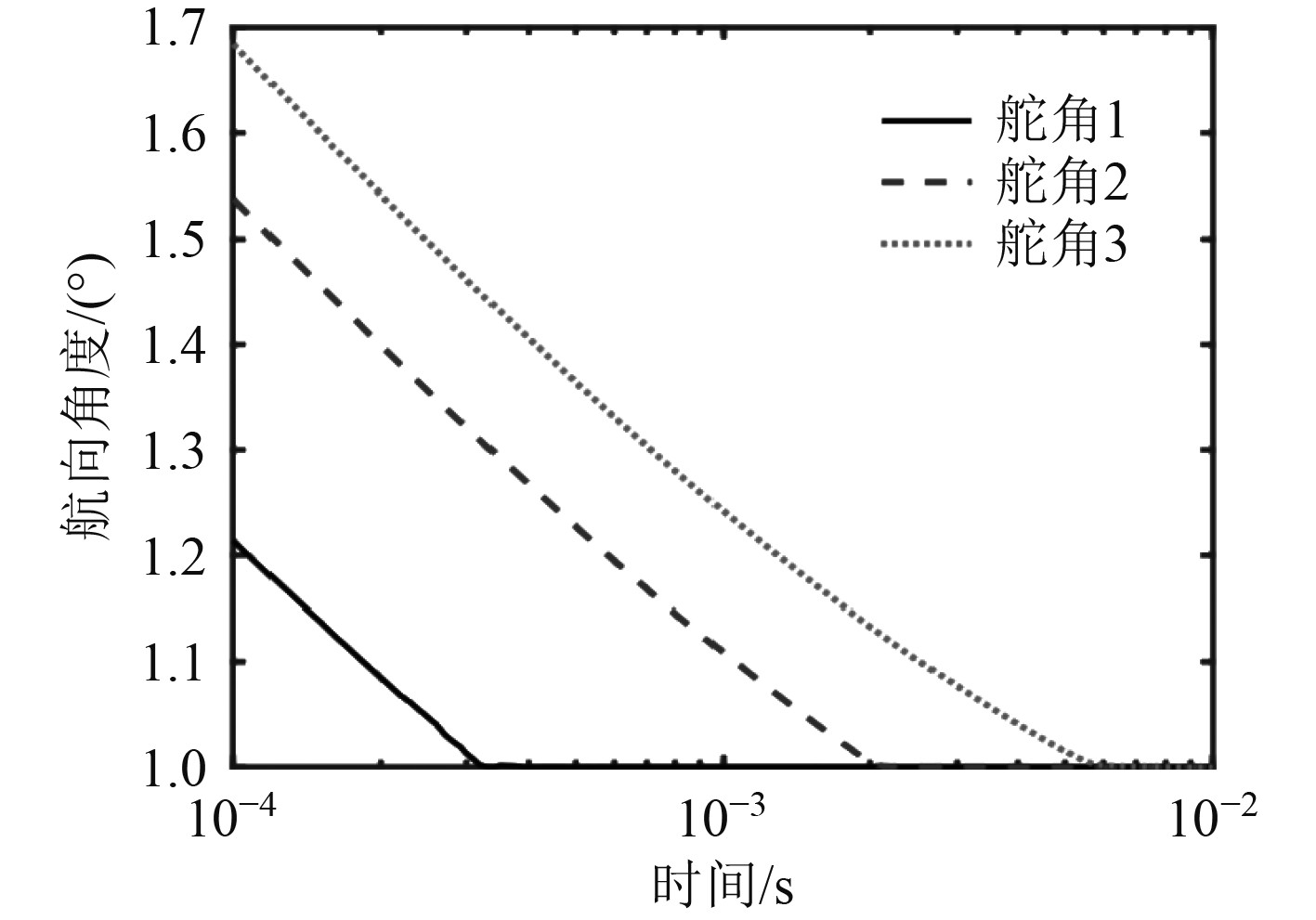
|
图 5 海面有风浪的条件下船舶航向变化曲线示意图 Fig. 5 Schematic diagram of ship course change curve under the condition of wind and waves on the sea surface |
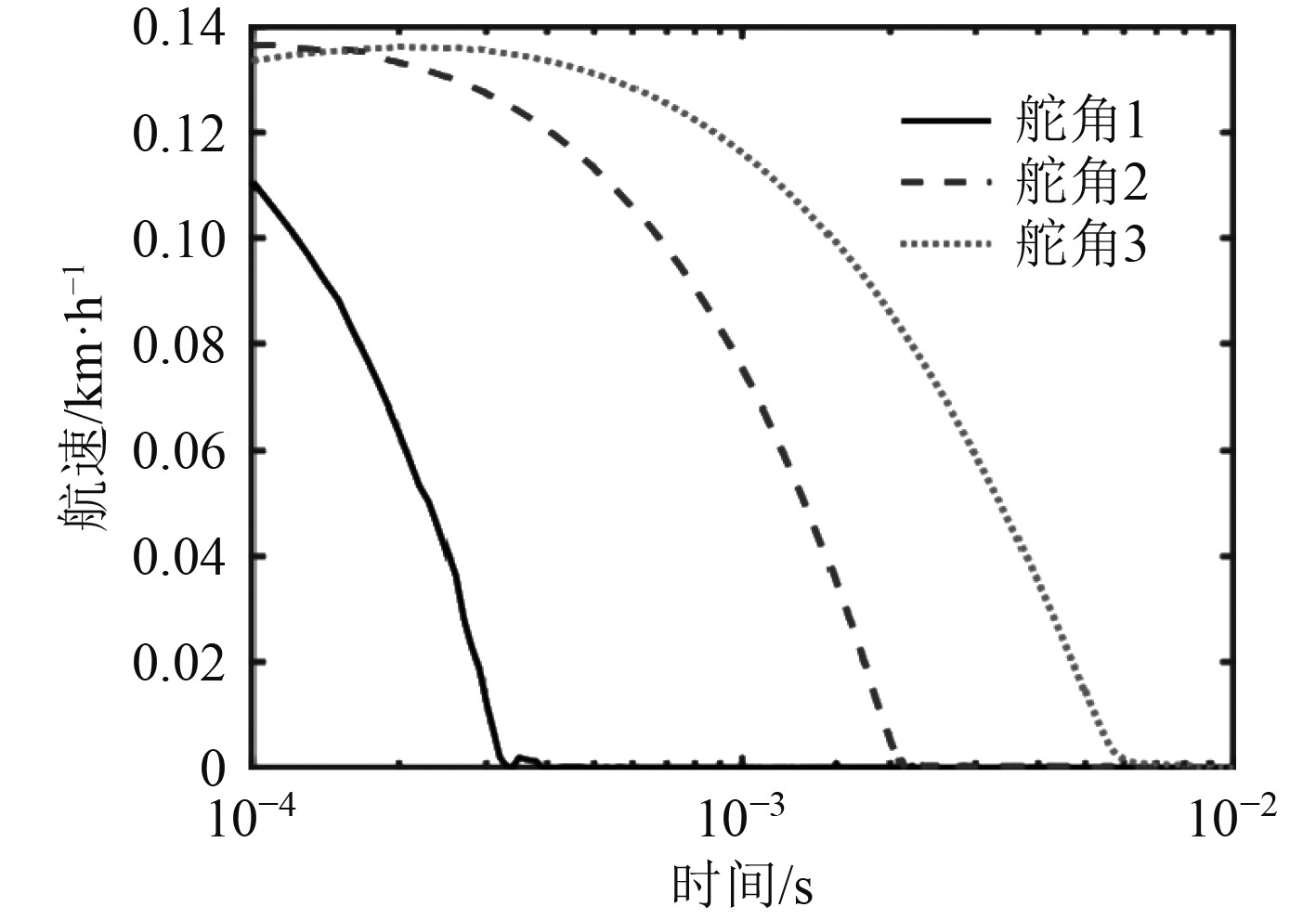
|
图 6 海面有风浪的条件下控制舵角变化曲线示意图 Fig. 6 Schematic diagram of control rudder angle change curve under the condition of wind and waves on the sea |

|
图 7 海面有风浪下船舶航向误差变化曲线示意图 Fig. 7 Schematic diagram of variation curve of ship heading error under wind and waves on the sea |
可以看出,无论海面是否存在风浪干扰,基于SVM逆系统的广义预测控制,具备更加优秀的跟踪预测效果。由此说明基于SVM逆系统的广义预测控制,除了响应速度快外,跟踪效果也比较好,并且误差非常小,所以在船舶航向广义预测控制中,可对SVM逆系统加以合理应用,由此能够达到预期中的控制效果,系统的鲁棒性和稳定性良好。
4 结 语为保证船舶的航行安全性和稳定性,采取有效的方法对船舶航向加以控制。SVM在非线性控制中的效果比较好,可将其应用于船舶航向的广义预测与控制中。通过研究发现,SVM逆系统在船舶航向的广义预测与控制中,具有良好的鲁棒性。
| [1] |
杨忠凯, 仲伟波, 冯友兵, 等. 基于改进的视线导引算法与自抗扰航向控制器的无人艇航迹控制[J]. 中国舰船研究, 2021(1): 121-127,135. |
| [2] |
陆潇杨, 刘志全, 褚振忠. 漂角修正的欠驱动船舶航向鲁棒自适应控制[J]. 上海海事大学学报, 2020(1): 15-19. |
| [3] |
李伟, 宁君, 李悦琪. 基于自抗扰的反步非奇异终端滑模船舶航向控制器设计[J]. 船舶工程, 2019(11): 83-88. |
| [4] |
肖剑波, 陆爱杰, 胡大斌. 基于模糊自整定PID的气垫登陆艇航向控制器研究[J]. 计算机测量与控制, 2019(12): 79-82. |
| [5] |
夏云鹏, 杨田田. 基于预测函数控制的水面无人船航向控制器设计[J]. 舰船电子工程, 2019(7): 54-59. DOI:10.3969/j.issn.1672-9730.2019.07.014 |
| [6] |
秦可, 卜仁祥, 方鹏飞. 基于优化PSO-BP神经网络的船舶航向预测[C]//第十四届中国智能交通年会论文集. 2019(11): 56-58.
|
| [7] |
景富盛. 基于Lyapunov稳定性的欠驱动船舶运动自适应迭代滑模控制研究[D]. 大连: 大连海事大学, 2019.
|
| [8] |
华艺欣, 肖奔. 基于舰船运动预测的无人机着舰航向指令修正方法[J]. 航空科学技术, 2018(11): 55-59. |
| [9] |
周浩. 基于广义预测控制算法的水面无人船航向控制器设计[D]. 武汉: 武汉理工大学, 2018.
|
| [10] |
赵蕊, 许建, 王淼, 等. 基于遗传算法和分数阶技术的水下机器人航向控制[J]. 中国舰船研究, 2018(6): 87-93. |
 2001, Vol. 44
2001, Vol. 44
