0 引　言

随着计算机技术与大数据技术的进步，人工智能技术逐渐崛起，在此背景下，船舶建造与控制技术逐渐向智能化、专业化、科学化方向发展，船舶航行路径规划能够从船舶自身状态与海洋环境状态2个角度出发，设计生成最适合船舶航行的路线，实现船舶航行的安全性与环保性提升^[1-3]。对于船舶航行路线或者航迹点生成已经有众多研究成果，王维刚等^[4]提出使用加权朴素贝叶斯算法规划船舶航行路线，该算法能够准确生成船舶航迹点，但是该算法规划后的航迹点成本较高，不适合长期使用；姜佰辰等^[5]使用多项式卡尔曼滤波算法生成船舶航线的轨迹点，该算法生成后的路线能够准确识别水下障碍物，保证船舶航行的安全性，但是该算法不能缩短船舶航行距离，导致船舶航行过程中需要消耗更多时间，使用效果也不够理想。本文使用人工智能技术作为基础，尝试获得一种全新的船舶航迹点生成算法，使用该算法提升船舶航行的安全性。

1 人工智能技术的船舶航迹点生成算法构建 1.1 船舶航行环境模型构建

自然环境中，船舶航行的水下区域可能存在浅滩和礁石等潜在危险区域，所以需要对海洋环境构建模型，提取环境信息，以便后续使用数学模型生成航迹点，本文构建环境模型时使用栅格法。该方法起源于20世纪中期，广泛应用于处理地图问题^[6-8]。栅格法的原理是使用网格单元(单元中包含二值信息)分解地图环境，网格划分时真实呈现环境中实际存在的障碍区域。针对二维的环境空间，划分时通过相同大小的栅格实现，可以根据自己的需求随意设置栅格尺寸，是否存在障碍物的栅格分别被称为障碍栅格与自由栅格。

海洋环境栅格构建过程中需要考虑海洋环境中实际存在的障碍区域，将这些障碍区域稍作扩展，划分区域中的安全距离。安全区域的存在保证生成船舶航迹点时，即使靠近障碍区域时，航迹点线路仍旧符合航线安全规划需求^[9]。

构建海洋环境数据模型如下：

$ E = \left\{ {{g_{ij}}\left| {{g_{ij}} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} or{\kern 1pt} {\kern 1pt} {\kern 1pt} 1} \right.,i \in \frac{L}{b},j \in \frac{W}{b}} \right\}\text{。} $

(1)

式中： $ L $ 与 $ W $ 分别代表海洋环境图的极限长度与宽度；栅格尺寸则使用 $ b $ 表示； $ {g_{ij}} $ 可以分别取值1或者0，假如取值为0则表示该区域属于无障碍区域，如果取值为1则表示该区域为障碍区域。

栅格划分完成后，使用Matlab仿真平台仿真生成海洋环境栅格化模型，在模型上通常情况使用阴影区域表示障碍区域，使用空白区域表示可航行区域，也就是轨迹点可生成区域。

1.2 船舶航迹点生成算法数学模型

在海洋环境栅格化模型上进一步构建船舶航迹点生成算法数学模型，构建数学模型时有2个目标，分别为航线最短与障碍物最少^[10-11]。假设船舶航行时生成的航线是由多个序列点(航迹点)组成： $\left( S,{p_1},{p_2}, \cdots \right. $ $ \left. {p_i},T \right)$ ， $ S $ 与 $ T $ 分别表示船舶航行的起点与终点， $ p $ 代表除了起点与终点之外的所有航迹点， $ i = 1,2, \cdots ,n $ ，其中任何一个航迹点都有可能成为传播转向的点，所以构建数学模型时需要充分考虑船舶转向造成的约束，可以使用θ_pi代表船舶在航迹点p_i时的转向角，φ_max代表θ_pi极限度数。船舶航行转向时的转弯半径也是影响船舶航行与航迹点生成的重要约束之一，根据已有研究，如果船舶的转向角大于60°时，控制船舶航行时难度较大，航行姿态以及转向速率多会超出船员的掌控；假如船舶的转向角接近90°时，船舶转向时已经出现严重操作困难，如果此时遭遇极端天气，船舶转向时很容易发生转弯失误的情况。为保证船舶航行时足够稳定，且工作人员操作足够便捷，在航速确定的情况下，船舶航行时各个航迹点与转向点上，转向角必须不超过90°。船舶航行时除了约束航线距离与转向角大小以外，还需要确保障碍物最少。

数学模型的约束条件如下：

$ {l_{\max }} \geqslant {l_i} \geqslant {l_{\min }} \text{，}$

(3)

$ \forall l\left( {{p_i},{p_{i + 1}}} \right) \cap {S_j} = \emptyset \text{，}$

(4)

$ \forall \theta {p_j}_{ \in \left( {1, \cdots ,k} \right)} \leqslant {\varphi _{\max }} \text{，}$

(5)

$ {R_{{P_{j \in \left( {1, \cdots ,k} \right)}}}} \geqslant \lambda L \text{，}$

(6)

$ D \geqslant {D_{\min }} \text{。}$

(7)

式中：l_min与l_max分别为最短与最长航行线路。式(3)表示船舶所航行的区域与存在障碍海洋环境之间为空集，l(p_i,p_i+1)用于描述从p_i到p_i+1之间全部航迹点集，S_j用于描述障碍水域障碍物点集。式(4)用于表达航速确定情况下，第 $ j $ 个点的转向角为保证安全不能超过 $ {\varphi _{\max }} $ 。式(5)是对船舶航行过程中对于转弯半径的约束， $ L $ 与 $ \lambda $ 分别代表长波长度与船长与极小转弯半径之间的比值。式(6)用于描述海洋中障碍区域与船舶航行路线之间的极小距离的约束，D_min与 ${{D}}$ 分别表示船舶和障碍区域最小安全距离以及障碍区域和航迹点之间的最小距离。

1.3 基于优化鱼群算法的模型求解

在鱼群算法基础上使用优化算法，因此具有更加良好的稳定性与收敛性。优化鱼群算法的方式是在基础鱼群算法的基础上添加自适应交叉概率与变异概率，优化后预期群算法的变异概率Q_m与较差概率Q_c：

$ {Q_m} = \left\{ \begin{gathered} {q_{m1}},f \leqslant {f_{avg}} \text{，}\hfill \\ {q_{m1}} - \left[ {\left( {{q_{m1}} - {q_{m2}}} \right)*\left( {{f_{\max }} - f} \right)/\left( {{f_{\max }} - {f_{avg}}} \right)} \right] \text{，}\hfill \\ \end{gathered} \right. $

(8)

$ {Q_c} = \left\{ \begin{gathered} {q_{c1}},f' \leqslant {f_{avg}}\text{，} \hfill \\ {q_{c1}} - \left[ {\left( {{q_{c1}} - {q_{c2}}} \right)*\left( {f' - {f_{avg}}} \right)/\left( {{f_{\max }} - {f_{avg}}} \right)} \right]\text{。} \hfill \\ \end{gathered} \right. $

(9)

式中：q_c1与q_m1分别用于描述第一次迭代的交叉率与变异产生值；q_c2与q_m2分别用于描述第二次迭代的交叉率与变异产生值； $ f' $ 与 $ {f_{avg}} $ 分别用来表示适应值与初始适应值。船舶航迹点规划步骤如下：

1）构建符合航行状态参数，将迭代次数确定，航迹点生成过程中需要利用迭代次数；

2）从迭代参数角度出发，设置求解船舶航迹点生成数学模型算法中的适应度函数；

3）构建原始计划，各船舶航迹点生成计划与各个个体对应；

4）从适应度函数角度出发，实现适应度值计算，通过计算结果确定航迹点优劣；

5）根据步骤4的结果，确定下一步的最佳个体；

6）随机选择个体实现异变与交叉，选取最好的个体输入到下一代种群之中；

7）比较对数，如果对比结果中，大于最大值就可以结束求解，输出最优解，如果小于最大值就重新返回步骤4。

根据以上步骤，构建船舶航迹点生成数学模型求解函数：

$ {f_s} = \frac{1}{{\displaystyle\sum\limits_{i = 1}^N {\left( {{\omega _1}{l_i} + {\omega _2}{f_{TAi}}} \right)} *\sum\limits_{i = 1}^N {d\left( {{p_i},{p_{i + 1}}} \right)} }} \text{，}$

(10)

利用式(10)与优化鱼群算法中的变异、交叉概率相结合，由此获得目标函数最优解：

$ {E_s} = \frac{{\displaystyle\sum\limits_{i = 1}^N {\left( {{\omega _1}{l_i} - {\omega _2}{f_{TAi}}} \right)} *\sum\limits_{i = 1}^N {d\left( {{p_i},{p_{i + 1}}} \right)} }}{{{q_c}{q_m}\sqrt {{f_s}} }} \text{。}$

(11)

通过式(10)获得船舶航迹点生成数学模型的最终解。

2 实验结果与分析

选取某具有研究意义的具体海域，收集该区域的水下环境数据。选取10万吨级的LNG船作为研究对象，将海域及船舶相关数据输入到模拟实验平台，开展实验验证。所截取的海洋区域平均水深约为19 m，面积约1.2万平方千米，主要沉积物为粉砂，但是近海区域存在大量浅滩与暗礁，浅滩水深仅为2.5 m，若船舶操纵不当，或者偏离既定航线，很容易发生航行风险。（吃水量约为3 m，富余水深约为0.6 m。）

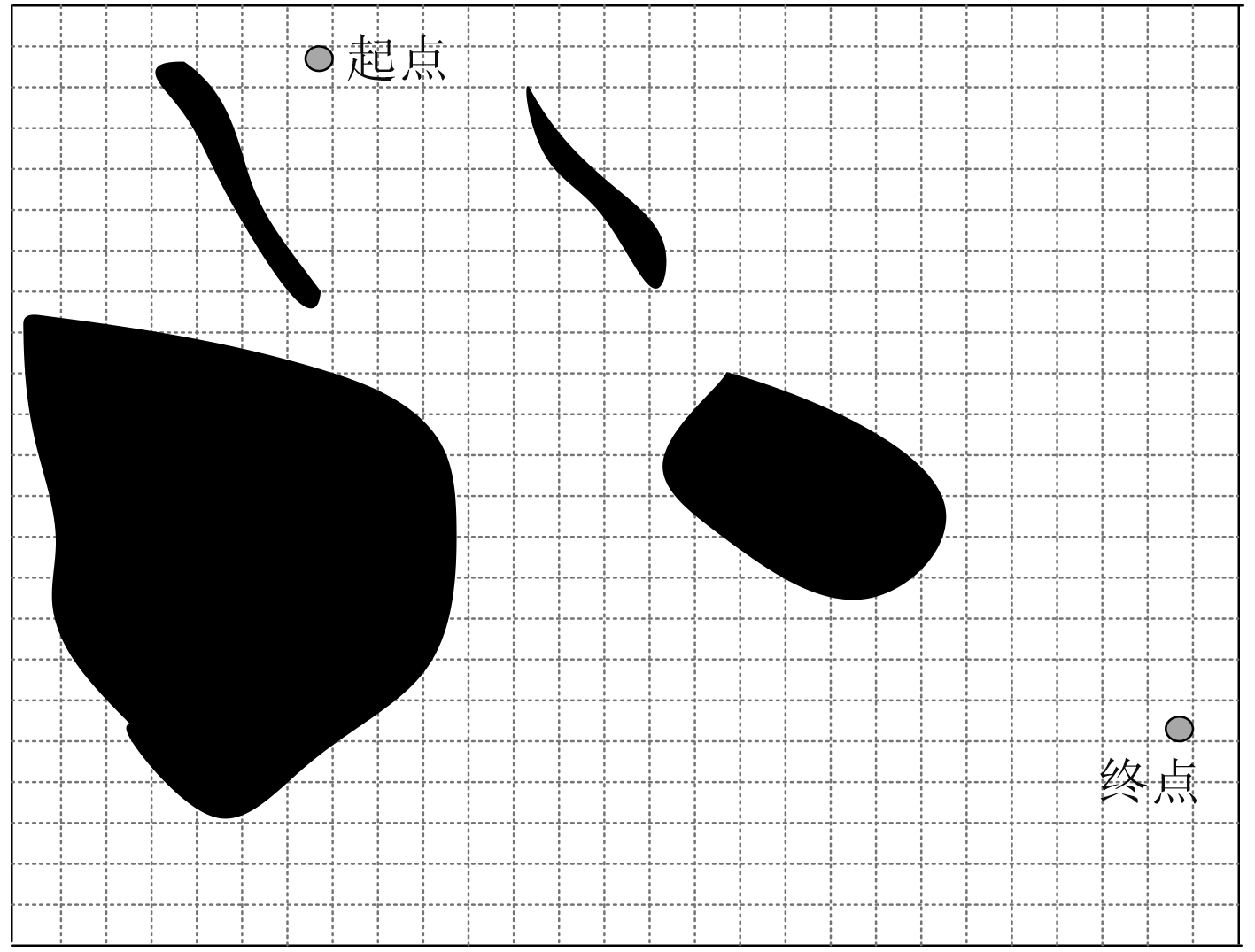
2.1 海洋环境数据栅格模型构建

根据收集的海洋环境信息，结合Matlab仿真平台仿真生成海洋环境栅格化模型。生成结果见图1。从图中能够明显看出，船舶航行规定的起点与终点，其中黑色区域是使用本文算法扩展安全距离之后存在障碍的海洋区域，该区域也是经过栅格化划分后的区域，栅格划分过程中为了提高计算的准确度与速度，选择50*50规格作为栅格尺寸。

2.2 船舶航迹点生成

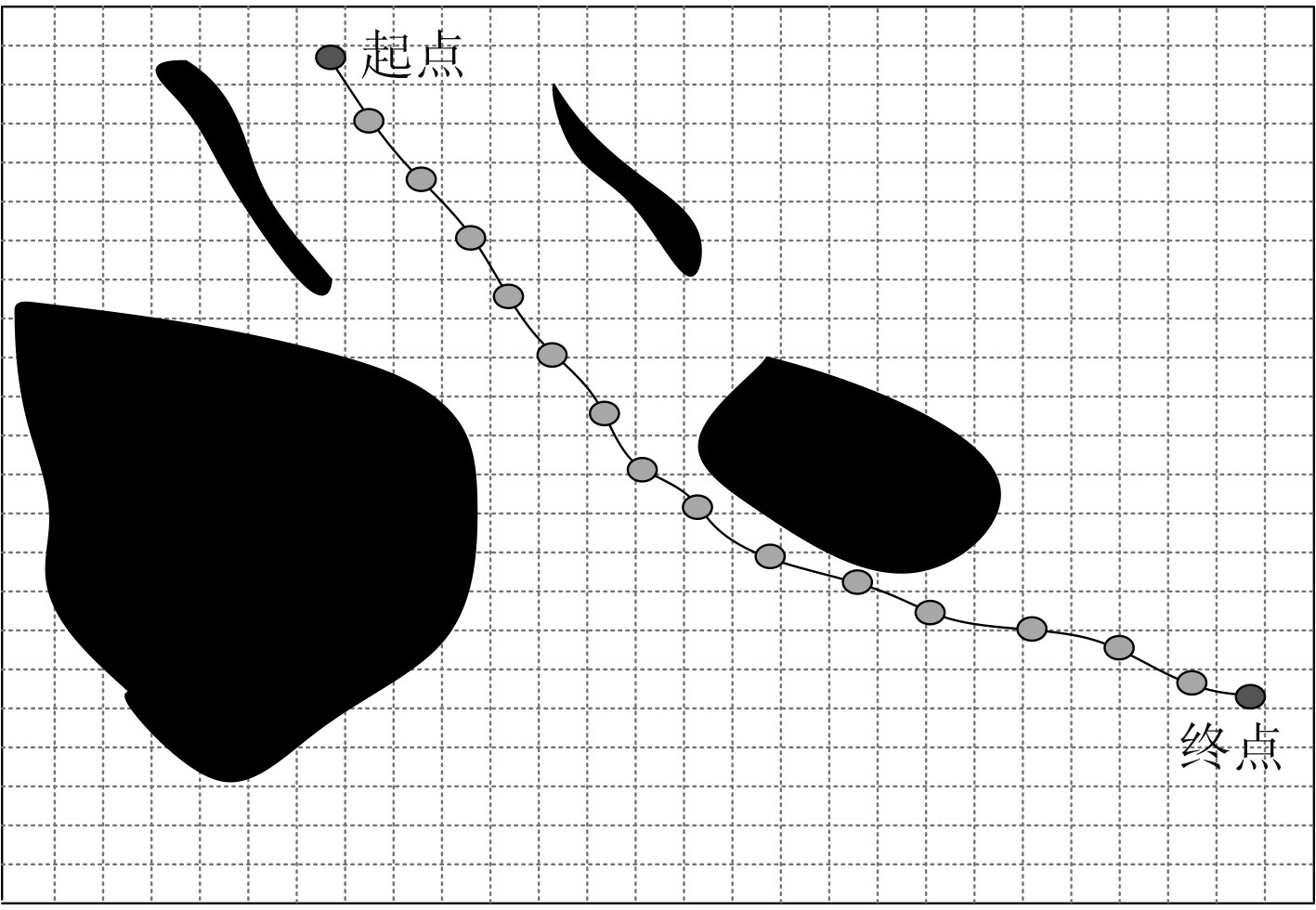
在海洋环境栅格模型基础上，使用本文算法实现船舶航迹点规划生成，规划结果见图2。从图中能够看出，使用本文算法能够合理生成航线最短，障碍物最短的航迹点，该航迹点生成后也保持转向角与转弯半径较为合理，不会出现在转弯操作中发生意外失控情况。

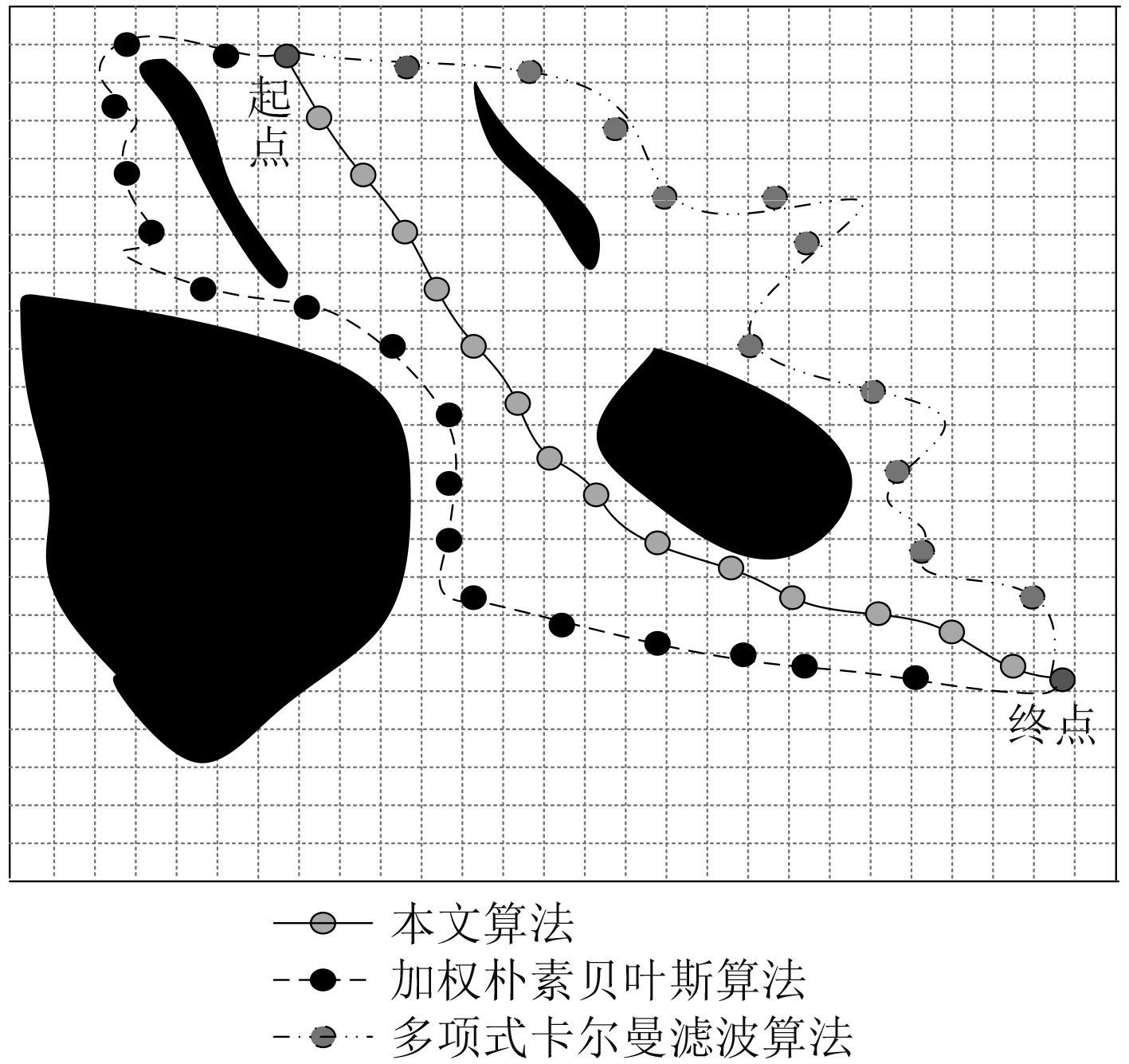
为验证本文算法的优势，分别使用加权朴素贝叶斯算法^[5]与多项式卡尔曼滤波算法^[6]规划船舶航行。使用这2种对比算法分别生成研究区域的航迹点，生成结果见图3。从图3能够较为直观看出，使用本文算法生成的航迹点能够相比于2种对比算法，航行路程更短，与海底障碍物的距离更加合适。经过数据分析发现，本文算法生成的航迹点距离约为2538 km，2种对比算法所生成的航迹点距离分别为3690 km（加权朴素贝叶斯算法）与3875 km（多项式卡尔曼滤波算法）。经过对比可以看出，本文算法在规划船舶航行轨迹方面更加具有优势。

2.3 外部环境干扰下航迹点生成情况

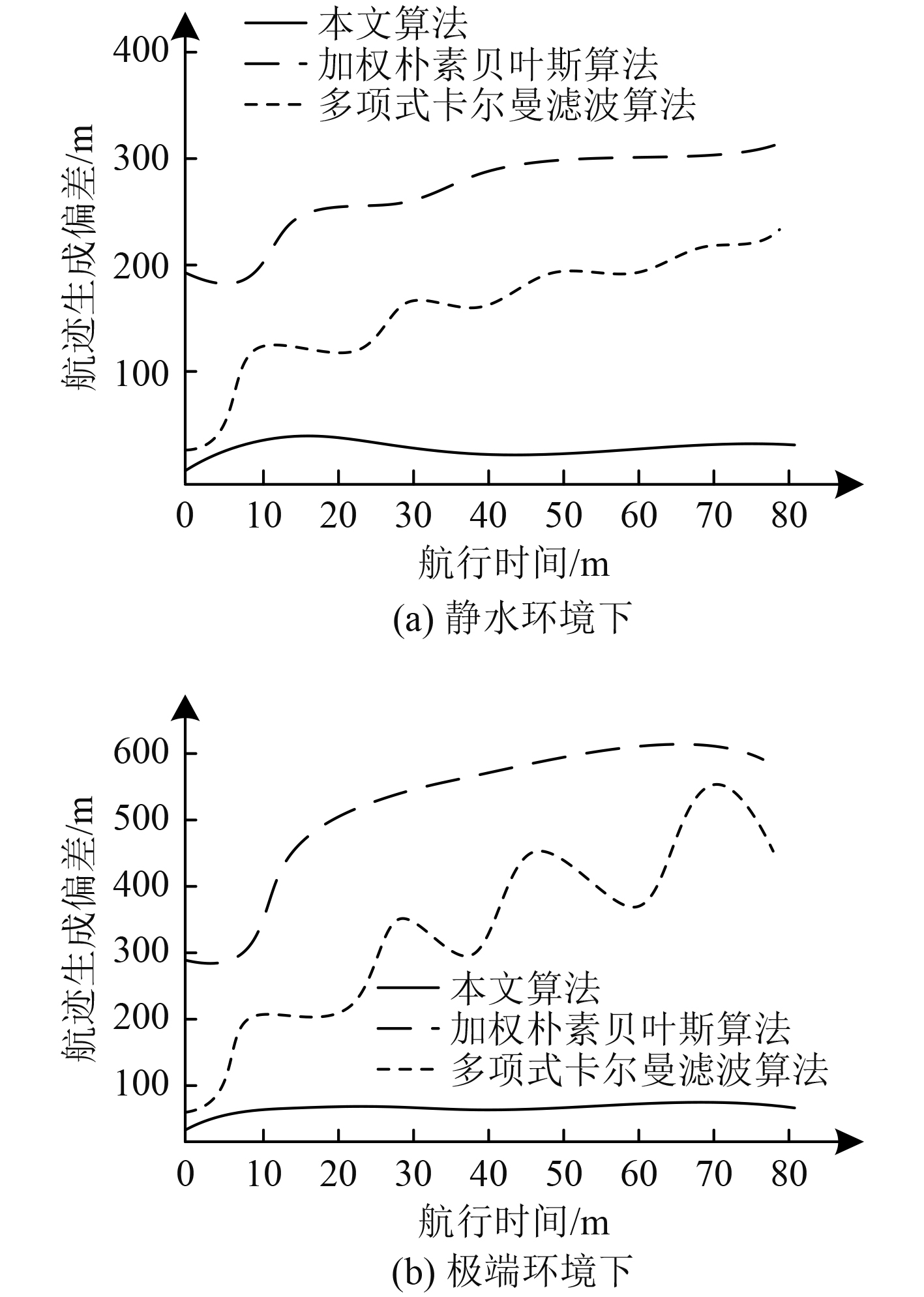
自然环境中，海洋环境较为复杂，除了正常静水环境以外，还会出现强风、暴雨异常天气，因此本文研究过程中，在模拟实验平台中模拟静水环境与极端环境2种工况下，航迹点生成偏差情况，对比结果见图4。从图中能够看出，无论是净水环境之下还是极端环境之下，本文算法生成后的航迹点受到影响后偏航的可能性均更小，由此证明本文算法具有更加良好的航迹生成效果。通过研究分析，使用本文算法生成航迹点后，由于转弯半径与转向角均控制在较为合理的范围中，所以能够间接降低舵角响应幅度，降低船舶的机械损耗，提升船舶转向的速度，获得更加良好的船舶航行效果。

2.4 算法性能验证

分析观察优化后鱼群算法在寻求模型最优解时算法的收敛情况，该收敛过程的实验结果见图5。可知，使用优化鱼群算法能够在迭代初期迅速实现收敛，迭代150次以后几乎已经实现平稳收敛，说明只需要迭代150次便能求解出最优解，但是趋于平稳之后，仍旧出现小幅度波动。分析这种情况可能是由于寻求最优解的过程中，部分种群会向外延伸探索未知区域，但该算法的整体收敛情况较好。

3 结　语

本文研究人工智能技术作为基础的船舶航迹点生成算法，合理规划船舶航行路线。对于环境较为复杂的海洋区域，使用栅格法构建模型，扩展出安全距离，确定目标函数与约束条件，利用优化鱼群算法，实现模型求解，生成船舶航行的航迹点。经过实验分析，本文算法能够生成较为合理的船舶航迹点，为船舶航行创造良好、安全条件。