未来海洋战争将是高新技术条件下的战争,随着信息技术的发展和武器装备性能的不断提高,潜艇数量越来越多,机动性越来越强,战场环境越来越复杂。因此,海洋作战对潜艇目标跟踪的稳定性和跟踪精度提出了更高的要求。
跟踪机动目标时,关键在于建立准确的系统模型[1]。自适应高斯模型[2]较符合水下目标的运动特性,对水下目标的跟踪具有较强的稳定性。该模型由党建武在Singer模型的基础上提出,模型假定,在对目标加速度的统计特性无先验知识的前提下,目标加速度的概率密度服从非零均值的高斯分布,且加速度的均值取当前时刻加速度的最佳估计值,加速度的标准差由加速度最佳估计值的倒数和一个自适应系数构成。
在该模型中,机动频率[3]的取值是预先设定的,对水下目标的运动状态的切换,其跟踪的实时性和跟踪精度的协调较为困难。目前,针对机动频率自适应的研究多基于LMS滤波理论,文献[4]利用滤波新息和假设检验理论来实现机动频率的自适应调整;文献[5]利用位移扰动增量和加速度增量之间的关系来实现机动频率的自适应调整;文献[6]运用模糊理论进一步完善了机动频率的自适应调整。然而,这些方法多存在计算复杂度高的问题,限制了水下目标跟踪的实时性。为降低模型对机动频率经验值的依赖性,提高模型的鲁棒能力,在自适应高斯模型的研究基础上,提出了基于航向变化率的机动检测理论,并通过自适应调节模型的机动频率的方式,实现了对水下非机动目标、转向机动目标的精确跟踪。
1 自适应高斯模型及其局限性分析相比于Singer模型,自适应高斯模型的改进点在利用加速度最佳估计值来修正加速度方差,进而修正误差协方差,以提升对机动目标的跟踪精度。
1.1 目标运动模型基于自适应高斯模型,机动目标的离散时间状态方程为:
| $ {x_{k + 1}} = {\varPhi _{k + 1,k}}{x_k} + {U_k}{\bar a_k} + {w_k},$ | (1) |
式中:
| $ {x}_{k}={({x}_{k},{\dot{x}}_{k},{\ddot{x}}_{k})}^{{\rm{T}}}\text{,}{\overline{a}}_{k}={({\overline{a}}_{k},{\dot{\overline{a}}}_{k})}^{{\rm{T}}},$ | (2) |
| $ {\varPhi _{k + 1,k}} = \left( {\begin{array}{*{20}{c}} 1&T&{(\alpha T - 1 + {e^{ - \alpha T}})/{\alpha ^2}} \\ 0&1&{(1 - {e^{ - \alpha T}})/\alpha } \\ 0&0&{{e^{ - \alpha T}}} \end{array}} \right),$ | (3) |
| $ {U_k}{\text{ = }}\left( {\begin{array}{*{20}{c}} { - T + \displaystyle\frac{{\alpha {T^2}}}{2} + \displaystyle\frac{{1 + {e^{ - \alpha T}}}}{\alpha }}&{( - T + \displaystyle\frac{{\alpha {T^2}}}{2} + \displaystyle\frac{{1 + {e^{ - \alpha T}}}}{\alpha })/\alpha } \\ {\alpha T - 1 + {e^{ - \alpha T}}}&{T - \displaystyle\frac{{1 - {e^{ - \alpha T}}}}{\alpha }} \\ {\alpha (1 - {e^{ - \alpha T}})}&{1 - {e^{ - \alpha T}}} \end{array}} \right)。$ | (4) |
式中:
系统误差协方差矩阵的取值为:
| $ {{\boldsymbol{Q_k}}}{\text{ = 2}}\alpha {\sigma _a}^2\left( {\begin{array}{*{20}{c}} {{q_{11}}}&{{q_{12}}}&{{q_{13}}} \\ {{q_{21}}}&{{q_{22}}}&{{q_{23}}} \\ {{q_{31}}}&{{q_{32}}}&{{q_{33}}} \end{array}} \right)。$ | (5) |
其中:
假定目标的观测方程为
| $ {z_k} = {{\boldsymbol{H_k}}}{x_k} + {v_k}, $ | (6) |
其中:
在滤波过程中,目标机动时最显著的变化量为滤波新息[7]
| $ {{\text{v}}_k}{\text{ = }}{{\text{z}}_k} - {{\boldsymbol{H_k}}}[{\Phi _{k + 1,k}}{x_k} + {U_k}{\bar a_k}]。$ | (7) |
归一化的新息平方
| $ {\tau _k}{\text{ = v}}_k^{\text T}{\boldsymbol{S_k}}^{ - 1}{v_k}, $ | (8) |
其中,
依据估值理论,加速度的均值
| $ \left\{ \begin{split} &{\bar a}_k = {{\hat {\ddot x}}}_k \hfill, \\ &{\dot {\bar a}}_k = {{\dot {\hat {\ddot x}}}}_k = ({{{{\hat {\ddot x}}}}_k} - {{{\hat {\ddot x}}}}_{k {\text{- 1}}})/T \hfill。\\ \end{split} \right. $ | (9) |
其中:
加速度的标准差
| $ {\sigma _a}= \frac{{{{{{\dot {\hat {\ddot x}}}}}_k}}}{b},$ | (10) |
其中,
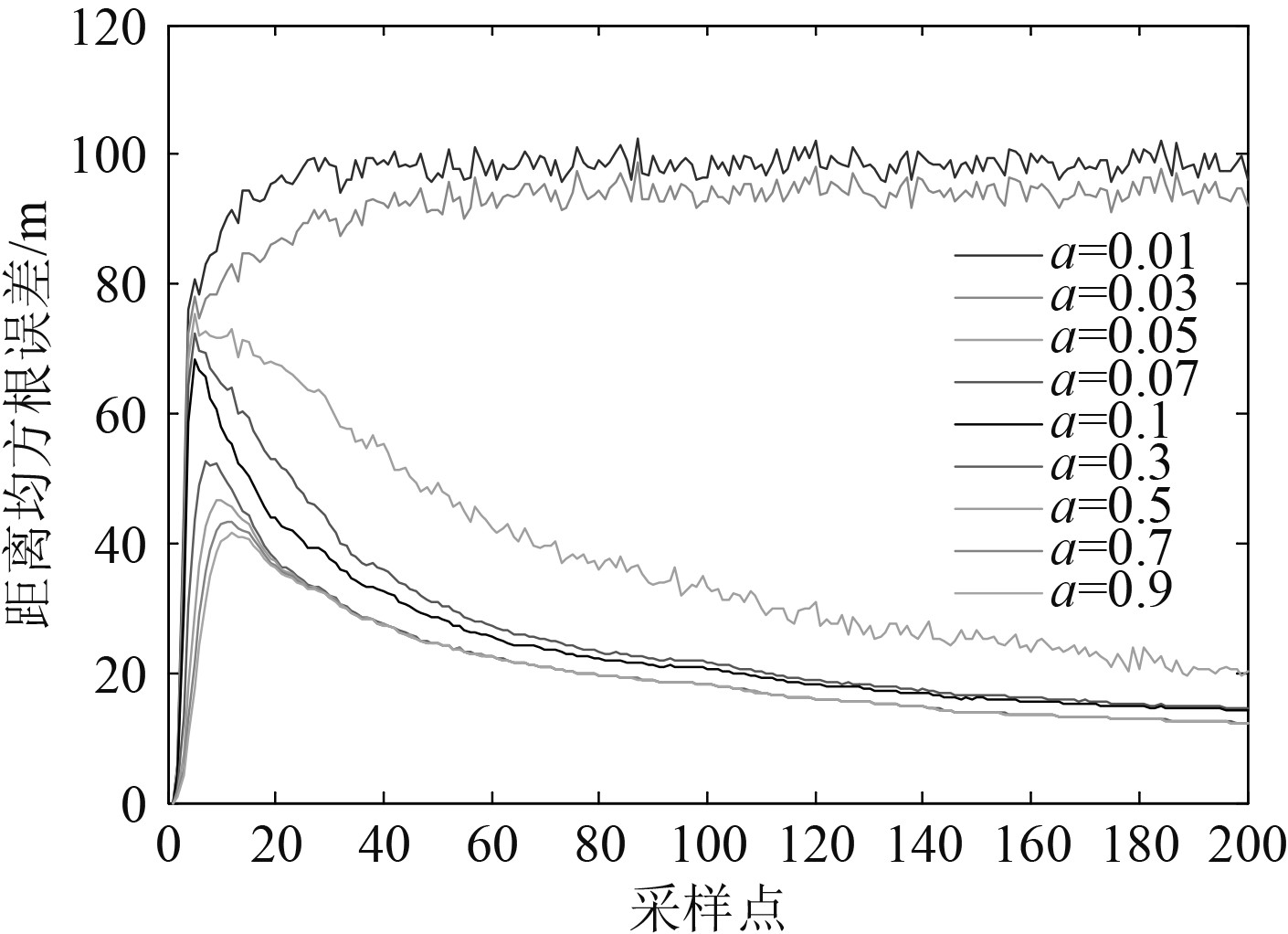
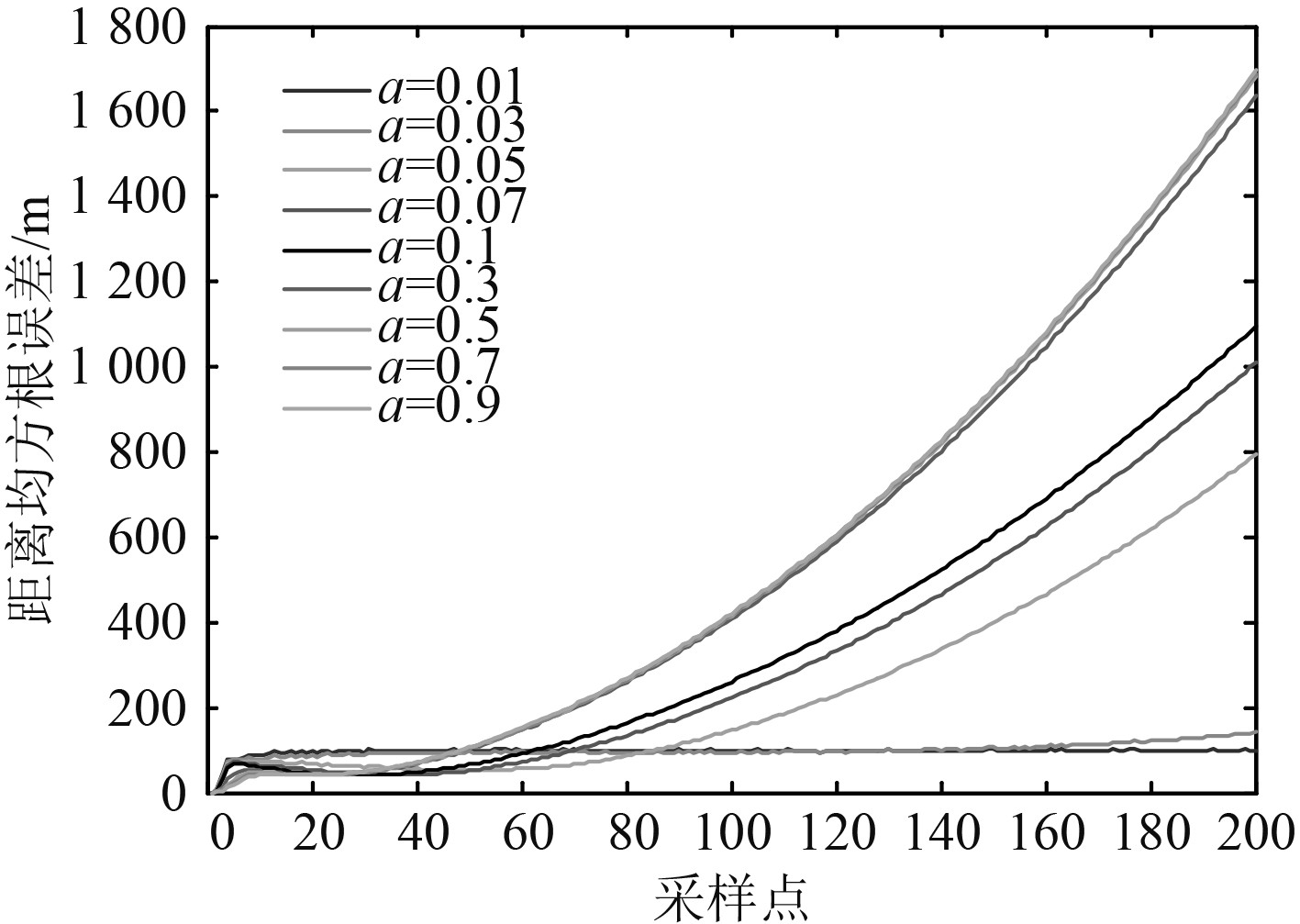
如图1和图2所示,对不同的机动频率,利用该模型对距离为5 km的机动目标(以0.1 m/s2做匀加速运动)和非机动目标(以4 m/s做匀速运动)分别进行仿真跟踪,可发现,机动频率
|
图 1 不同机动频率下,原模型对非机动目标的跟踪误差 Fig. 1 The tracking error of the model to non-maneuvering targets under different maneuvering frequencies |
|
图 2 不同机动频率下,原模型对机动目标的跟踪误差 Fig. 2 The tracking error of the model to the maneuvering target under different maneuvering frequencies |
综上所述,机动频率设置过小,会导致对非机动目标跟踪性能的下降,反之,又会导致对机动目标的跟踪延迟,甚至导致目标丢失。
因此,在对目标机动特性不存在较完备的先验知识情况下,实现机动频率的自适应调整对于提升系统的跟踪精度和稳定性尤为重要。
2 基于机动检测的自适应高斯模型 2.1 机动检测算法在目标跟踪过程中,目标的转向机动主要体现在速度的变化,尤其是航向角
由运动学定律,直角坐标系下目标航向角
| $ {\theta _v}= \arctan \left( {{{\hat {\dot y}}_k}/{{\hat {\dot x}}_k}} \right),$ | (11) |
其中,
由于外部输入的存在,目标发生机动时,其速度的变化值将不再是上一时刻加速度的最佳估计值。为更加准确地描述目标航向角的变化趋势,采用单位时间内速度变化的差值来近似表示当前时刻速度的导数:
| $ \left\{ \begin{array}{*{20}{c}} {\dot{ \hat {\dot x}}}_k = ({\hat {\dot x}}_{k +1} - {\hat {\dot x}}_k)/T,\\ {\dot {\hat {\dot y}}}_k = ({\hat {\dot y}}_{k + 1} - {\hat {\dot y}}_k)/T。\end{array} \right. $ | (12) |
其中,
在一个采样周期内,目标航向角的变化率
| $ \dot \theta _{\rm v} = \frac{{\hat {\dot y}}_k{\dot {\hat {\dot x}}}_k - {\hat {\dot x}}_k{{\dot {\hat {\dot y}}}_k}}{\sqrt {\hat {\dot x}_k^2 + \hat {\dot y}_k^2} } = \frac{{{{\hat {\dot y}}_k}({{\hat {\dot x}}_{k +1}}} - {{\hat {\dot x}}_k}) - {{\hat {\dot x}}_k}({{\hat {\dot y}}_{k + 1}} - {{\hat {\dot y}}_k})}{\sqrt {\hat{ \dot x}_k^2 + \hat {\dot y}_k^2} }。$ | (13) |
假设检测窗口宽度为N,目标在持续转向机动的时段内,其航向角将会持续发生同向偏移,即目标航向变化的方向将保持一致。取检测窗口内航向变化方向一致的观测点所占的比例作为统计量,以降低噪声带来的“伪随机效应”。
基于统计学知识,检测窗口内航向变化方向一致的观测点所占的比例
| $ {\varepsilon _k} = \frac{\left|{\displaystyle\sum\limits_{i = 1}^N {{{\dot \theta }_{\text{v}}}} }\right|}{{\displaystyle\sum\limits_{i = 1}^N {|{{\dot \theta }_{\text{v}}}|} }}。$ | (14) |
分析可知,若目标未发生机动,
在实际检测过程中,由于Kalman滤波器具有无限增长的记忆特性[9],其状态滤波值
为降低检测虚警率,可利用式(8)计算归一化的滤波新息平方,并依据其
| $ P\left\{ {{\tau _k} \leqslant {\tau _{\max }}} \right\} = 1 - \alpha。$ | (15) |
因此,在机动检测过程中,可引入机动阈值
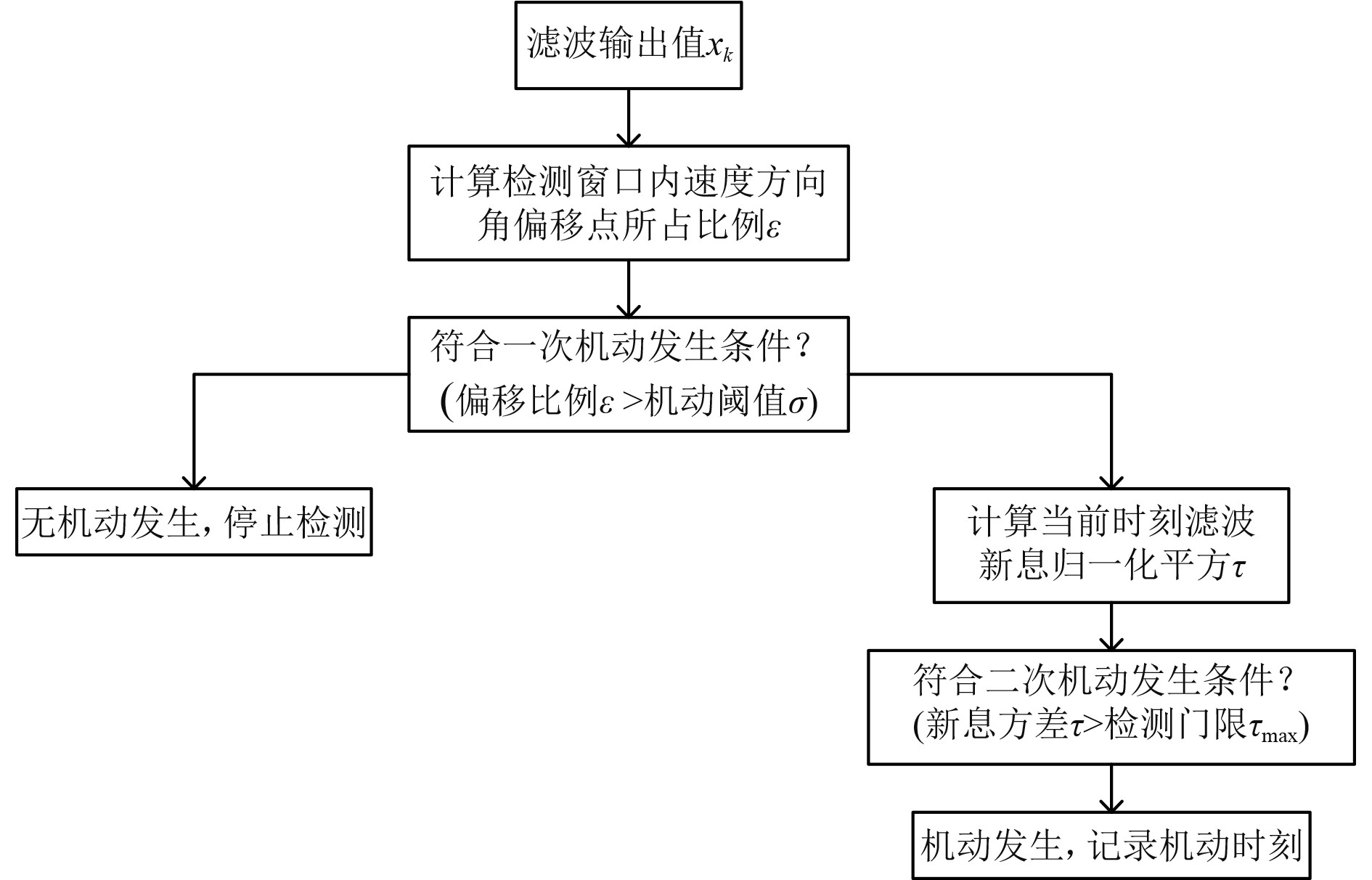
基于航向变化率的机动检测算法流程如图3所示。
|
图 3 机动检测算法流程图 Fig. 3 Flow chart of maneuver detection algorithm |
针对自适应高斯模型中机动频率无法准确描述导致跟踪不稳定的问题,利用机动检测算法来估计目标的机动点和非机动点,依据机动存在与否来自适应调整模型中机动频率的取值,从而减小跟踪误差。
基于机动检测理论,改进模型包含如下步骤:
步骤1 计算先验预测值
| $ {\hat x_{k + 1,k}} = {\varPhi _{k + 1,k}}{\hat x_{k,k}} + {U_k}{\bar a_k};$ | (16) |
步骤2 计算预测误差协方差矩阵
| $ {P_{k + 1,k}} = {\varPhi _{k + 1,k}}{P_{k,k}}\varPhi _{k + 1,k}^{\rm{T}} + {U_k}{\bar a_k} + {Q_k};$ | (17) |
步骤3 计算Kalman滤波增益
| $ {K_{k + 1}} = {P_{k + 1,k}}H_{k{\text{ + 1}}}^{\text {T}}{\left[ {{H_{k + 1}}{P_{k + 1,k}}H_{k{\text{ + 1}}}^{\text {T}} + {R_{k + 1}}} \right]^{ - 1}};$ | (18) |
步骤4 计算最佳估计值
| $ {\hat x_{k + 1,k + 1}} = {\hat x_{k + 1,k}} + {K_{k + 1}}\left[ {{z_{k + 1}} - H{{\hat x}_{k + 1,k}}} \right];$ | (19) |
步骤5 计算状态误差协方差
| $ {P_{k + 1,k + 1}} = \left[ {I - {K_{k + 1}}{H_{k + 1}}} \right]{P_{k + 1,k}};$ | (20) |
步骤6 更新加速度均值
| $ \left\{ \begin{split} &{\bar a}_{k+1} = {\hat {\ddot x}}_{k + 1,k + 1} \hfill,\\ &{\dot {\bar a}}_{k + 1} = ({\hat {\ddot x}}_{k + 1,k + 1} - {\hat {\ddot x}}_{k,k})/T \hfill;\\ \end{split} \right. $ | (21) |
步骤7 计算机动检测统计量
步骤8 更新机动频率
| $ {a}_{k+1}\text=\left\{\begin{split}&{a}_{1},({\epsilon }_{k}\geqslant \delta )\&({\tau }_{k} > {\tau }_{\rm{max}}),\\ &{a}_{2},{\rm{others}};\end{split} \right.$ | (22) |
步骤9 更新机动加速度方差
| $ \sigma _a^2= ({{{\hat {\ddot x}}}_{{{k + 1,k + 1}}}}/b{)^2};$ | (23) |
步骤10 更新过程噪声协方差
| $ {Q_{k{\text{ + }}1}} = 2\alpha \sigma _a^2\cdot{Q_i};$ | (24) |
步骤11 初始化滤波器
| $ k\text=\left\{\begin{split}&{c}k-n,{\scriptsize{机动发生或机动停止}},\\& k+1,{{\rm{others}}}。\end{split} \right.$ | (25) |
在实际情况下,水下目标通常分为常规潜艇和特殊潜艇,常规潜艇的最大航向速度为6~8 kn,特殊潜艇的最大速度为20~30 kn。声呐对潜艇的量测误差与两者间的距离有关,通常情况下,量测误差为两者距离的2%~3%。
以距离5 km的潜艇目标为例,其航向速度通常为3~4 m/s,而量测误差通常能达到100 m。此时,滤波新息中机动行为易被噪声覆盖,这给机动检测算法的稳定性带来了很大的挑战。
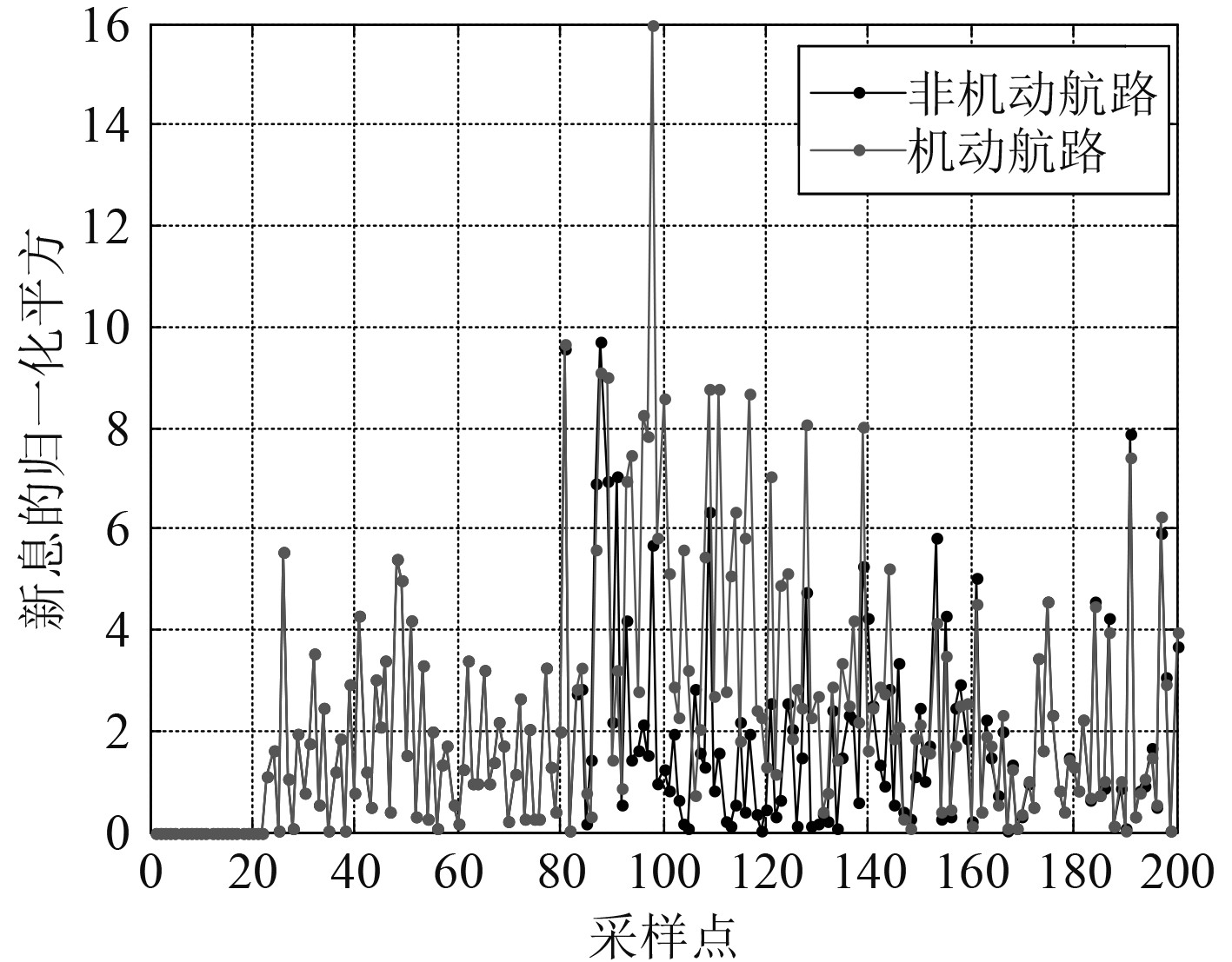
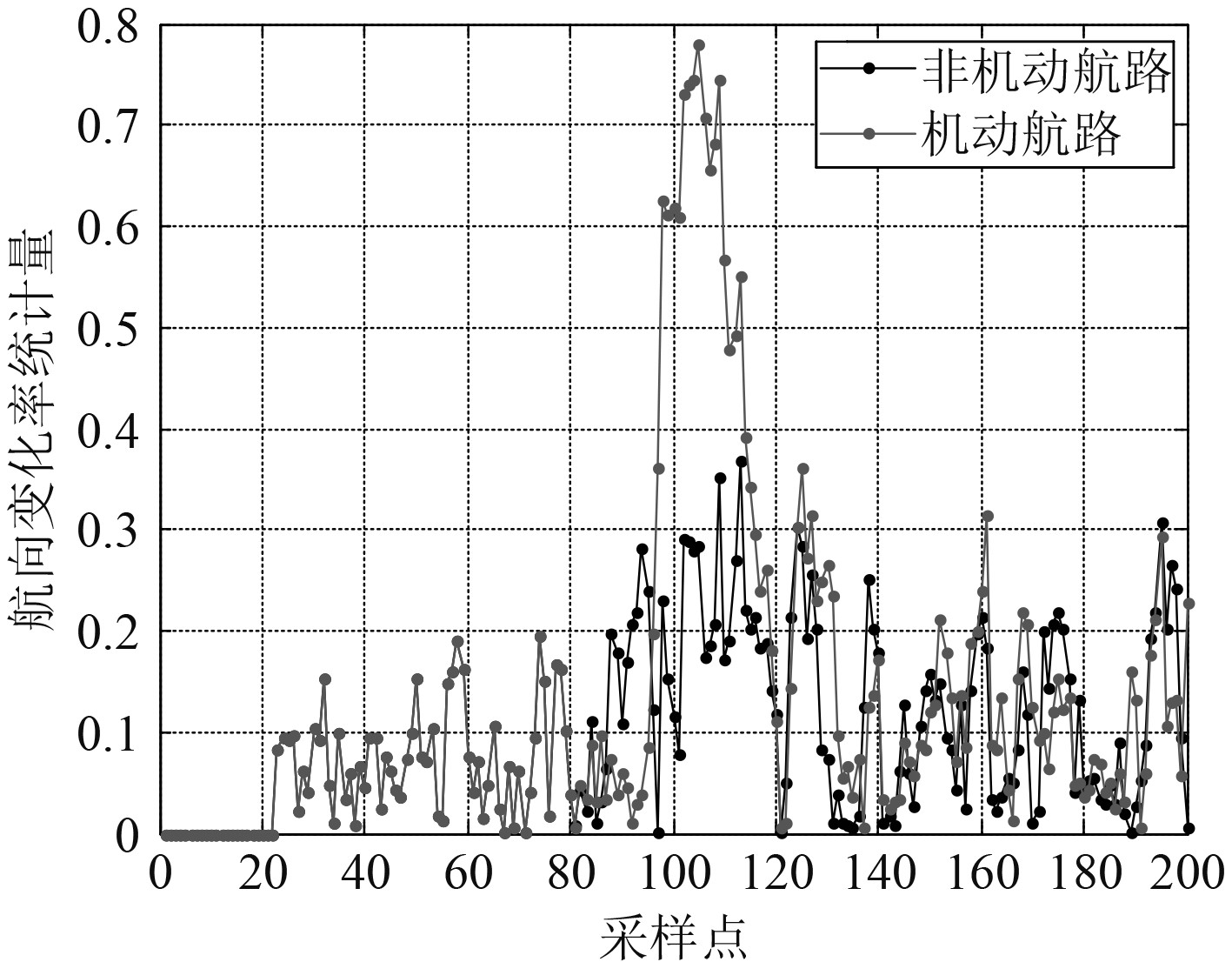
为检验检测效果,分别使用传统算法和改进算法对总时间为200个采样周期的非机动航路(匀速直线运动)和机动航路(目标在采样点为80时开始转向机动,持续5个采样周期)进行机动检测,检测结果如图4和图5所示。
|
图 4 传统算法对水下目标的机动检测效果 Fig. 4 Maneuvering detection effect of traditional algorithms on underwater targets |
|
图 5 改进算法对水下目标的机动检测效果 Fig. 5 Maneuvering detection effect of improved algorithms on underwater targets |
对比分析发现,改进算法相对于传统算法,对水下目标机动的敏感程度有显著提升,提升了机动检测的准确性和稳定性,但对目标机动的检测实时性仍然欠佳。
为分析目标速度、量测误差、检测窗口宽度等因素对基于航向变化率的机动检测算法检测延迟的影响,总结提升算法实时性的有效途径,分别设定两类目标的起始状态,如表1所示。
|
|
表 1 目标起始状态设置 Tab.1 Target initial state setting |
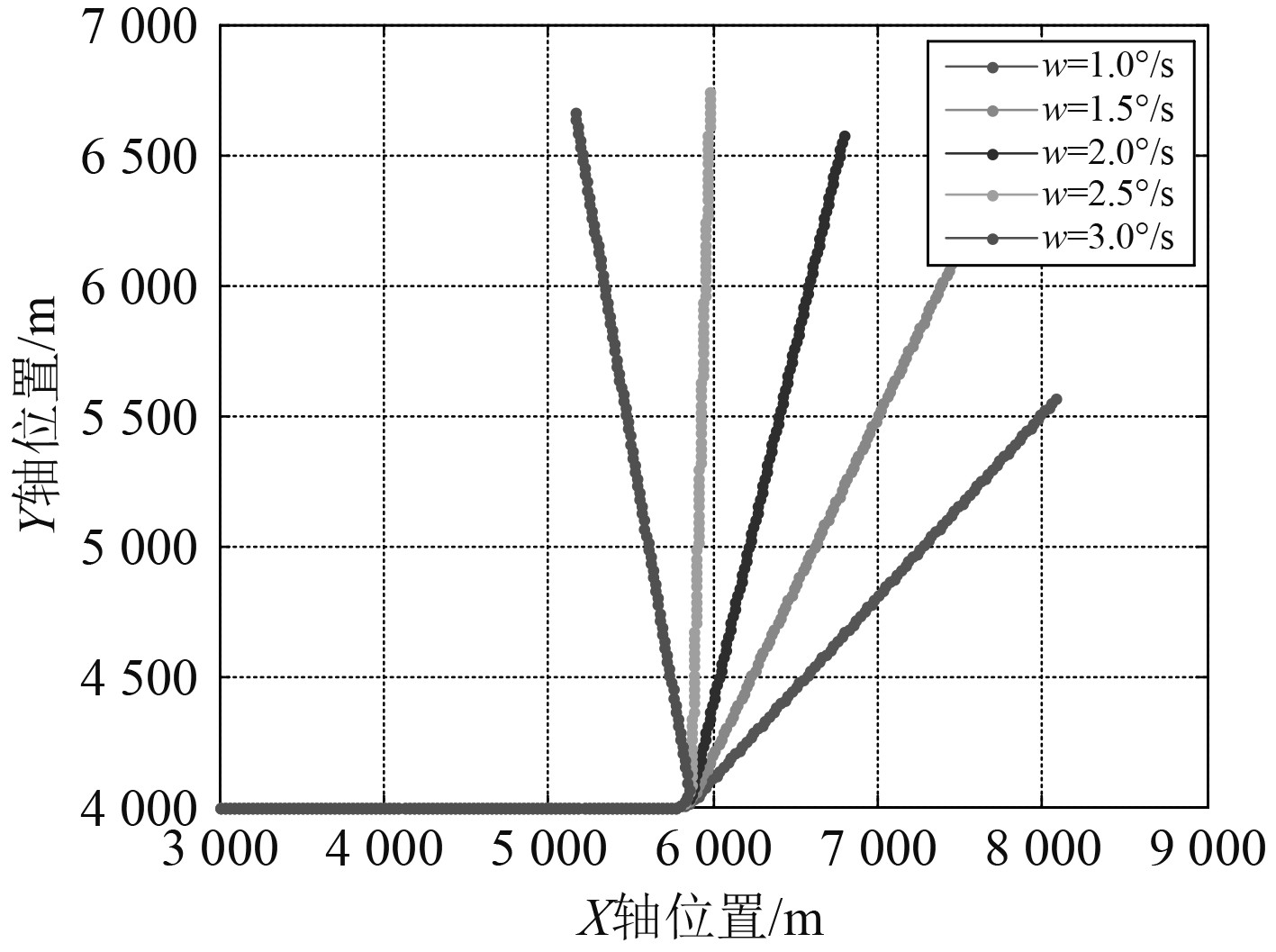
采样周期设置为7 s,目标仿真航路(见图6)是从0~700 s作匀速直线运动,700~735 s以固定角速度作匀速转弯运动,735 s~1 400 s作匀速直线运动,共仿真5条目标航路,目标转向角速度ω最小为1 °/s,阶梯递进量为0.5 °/s。
|
图 6 目标机动检测仿真航路 Fig. 6 Simulation route for target maneuver detection |
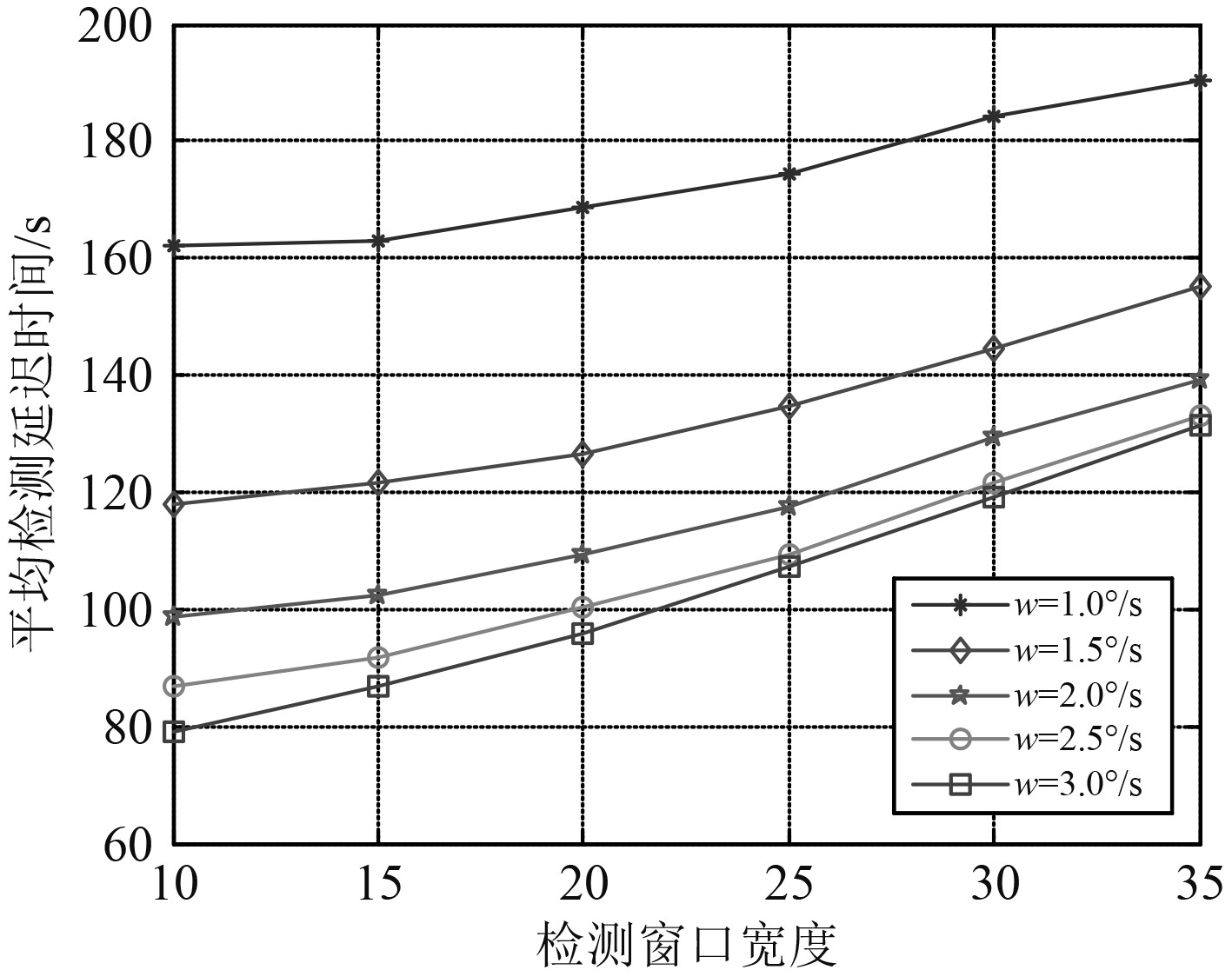
对各航路设置检测窗口宽度从10~35不等。在不同机动强度下,进行1000次仿真检测,平均检测延迟时间、检测虚警率与检测窗口宽度的关系分别如图7~图10所示。
|
图 7 对不同转弯率的低速目标,检测延迟与滑窗宽度的关系 Fig. 7 For low-speed targets with different turning rates, the relationship between detection delay and sliding window width |
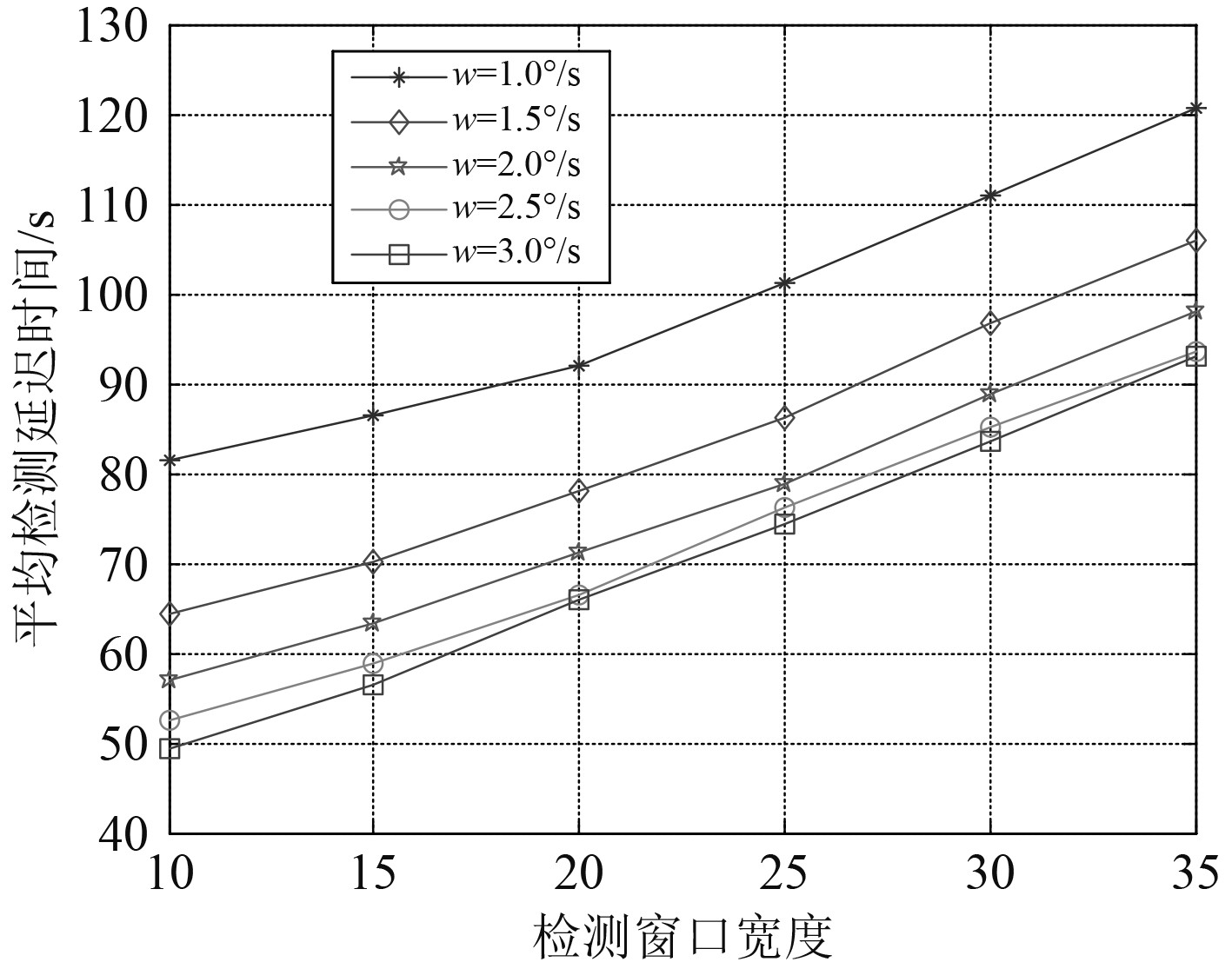
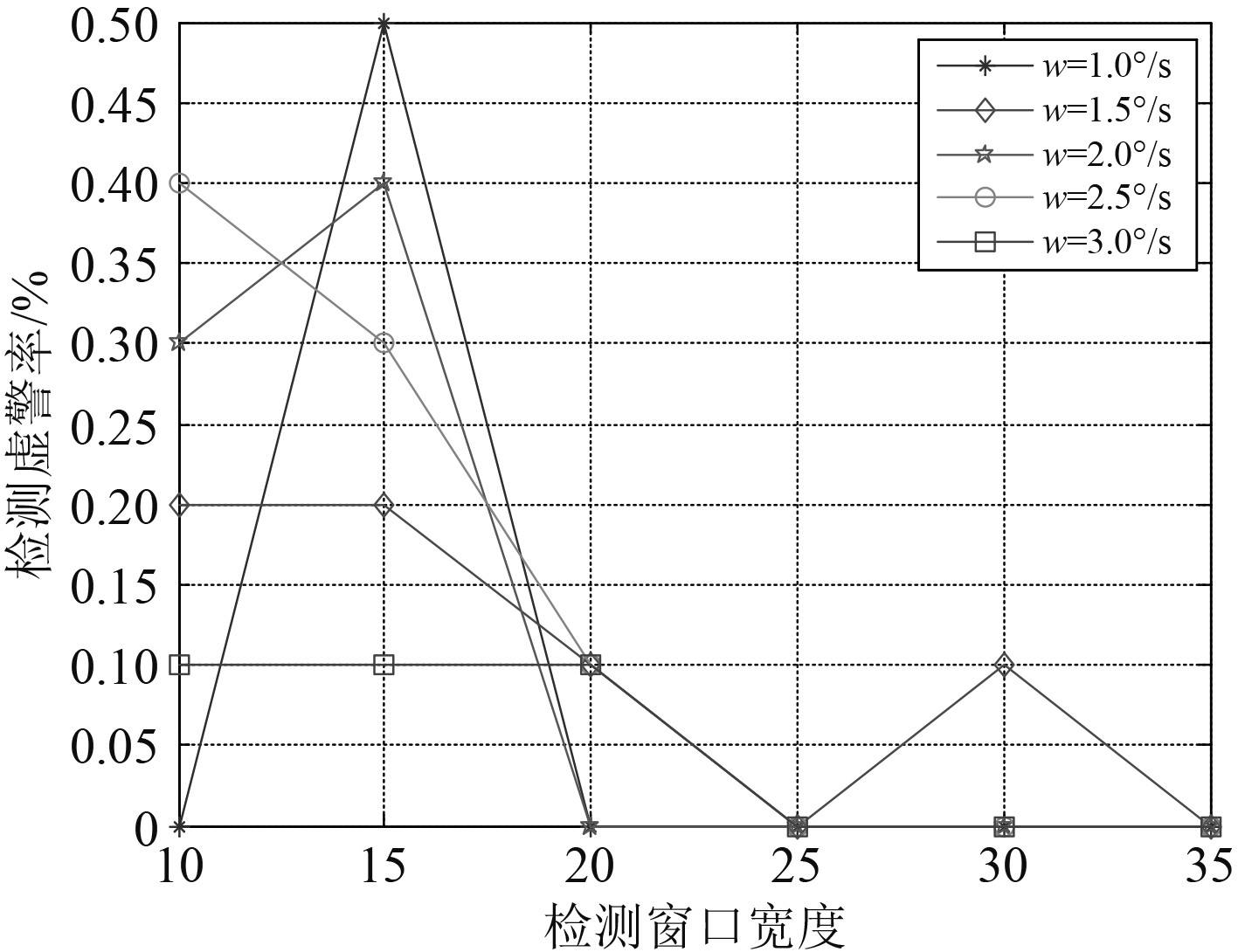
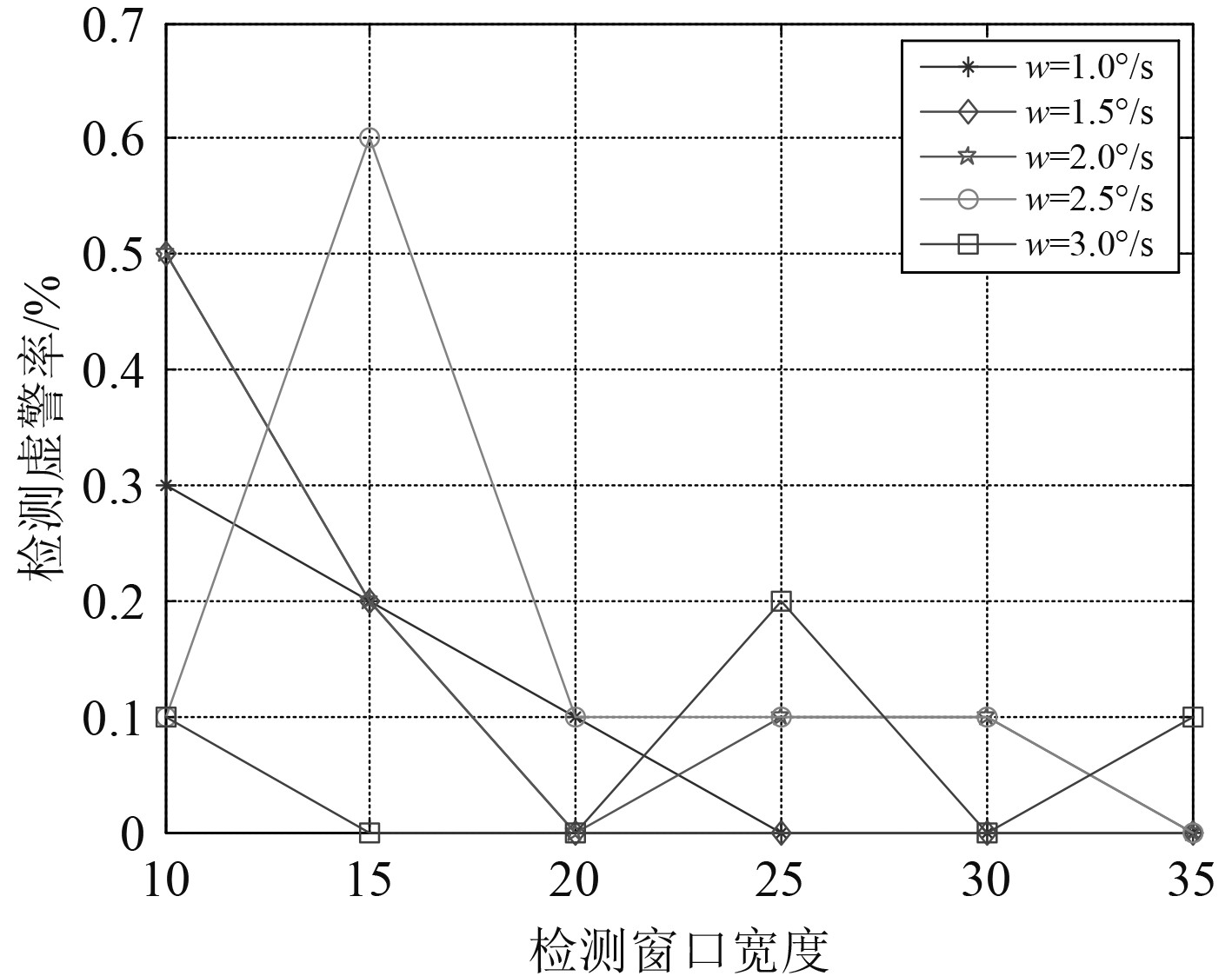
由图7和图8可看出,在目标转弯率固定时,滑窗宽度越长,检测延迟越大;目标速度越快,检测延迟越小。由图9和图10可看出,滑窗宽度小于20时,其检测虚警率总体偏高,检测稳定性不佳。因此,可依据实际需求选用合适的窗口宽度来完成机动检测任务。
|
图 8 对不同转弯率的高速目标,检测延迟与滑窗宽度的关系 Fig. 8 For high-speed targets with different turning rates, the relationship between detection delay and sliding window width |
|
图 9 对不同转弯率的低速目标,虚警率与滑窗宽度的关系 Fig. 9 For low-speed targets with different turning rates, detect the relationship between the false alarm rate and the width of the sliding window |
对以上5条航路在固定窗口宽度为20时,在不同量测误差下,进行1000次仿真检测,平均机动检测延迟时间与目标转弯率的关系如图11和图12所示。
|
图 10 对不同转弯率的高速目标,虚警率与滑窗长度的关系 Fig. 10 For high-speed targets with different turning rates, detect the relationship between the false alarm rate and the length of the sliding window |
|
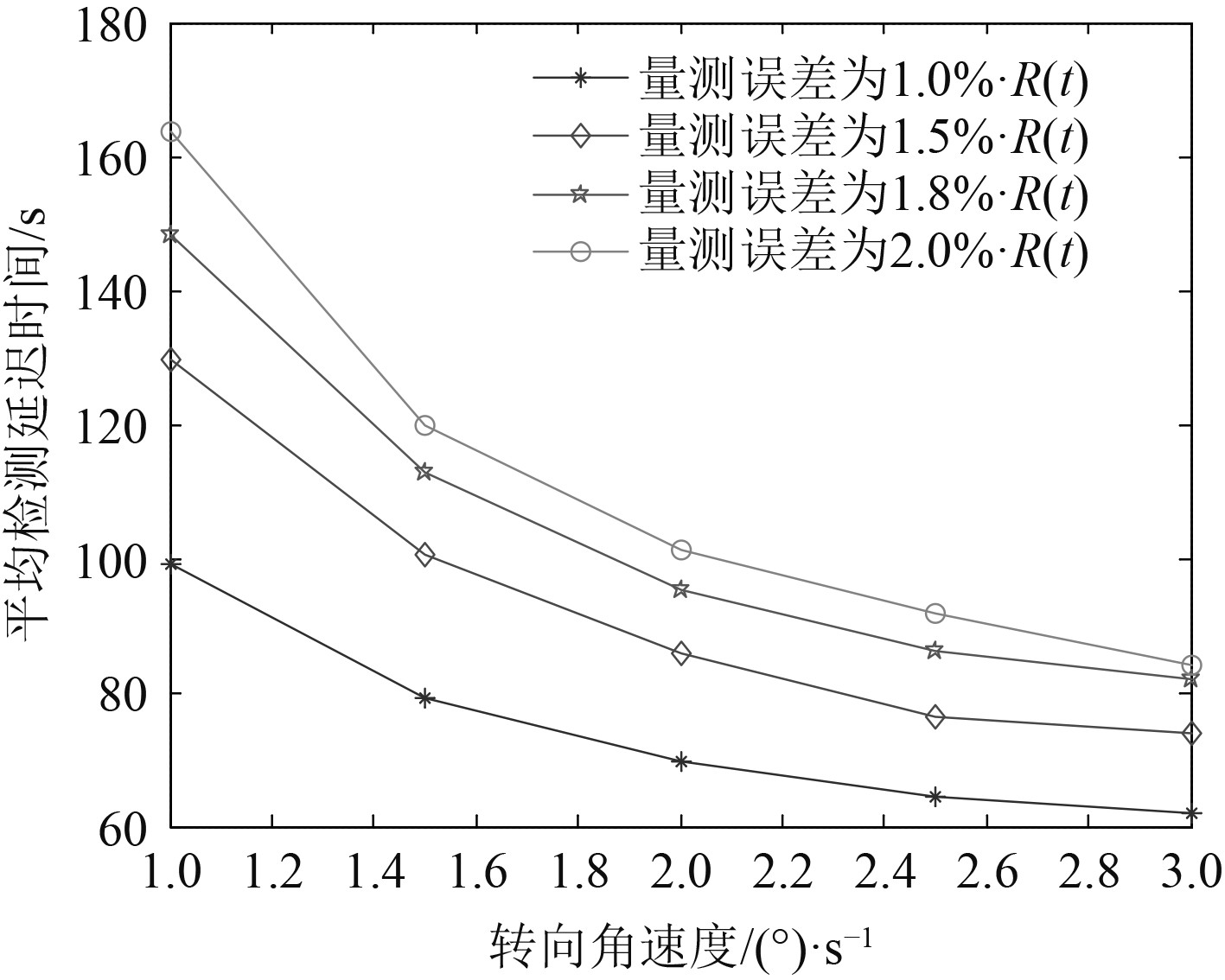
图 11 对不同量测误差的低速目标,检测延迟与转弯率的关系 Fig. 11 For low-speed targets with different measurement errors, detect the relationship between delay and turning rate |
|
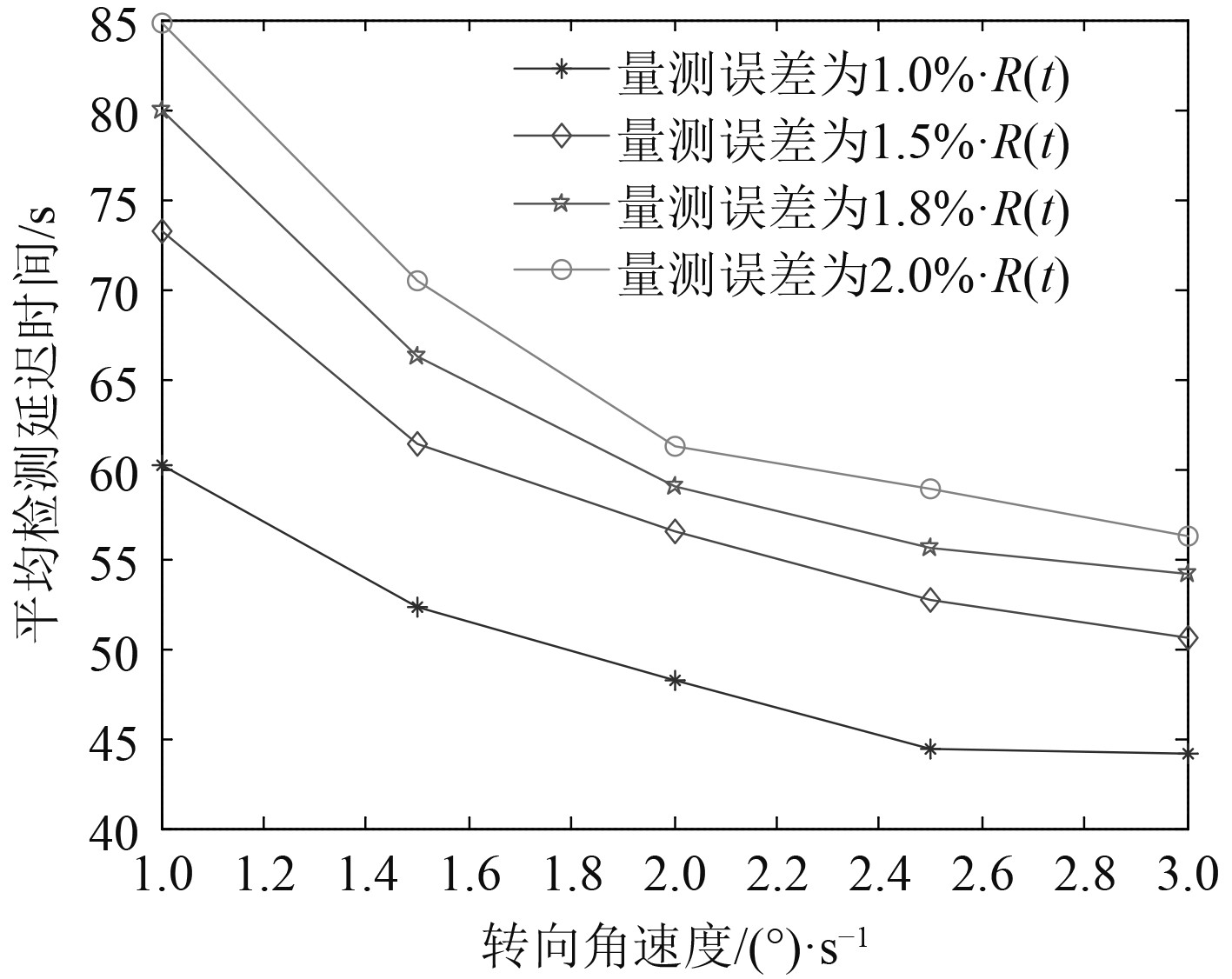
图 12 对不同量测误差的高速目标,检测延迟与转弯率的关系 Fig. 12 For high-speed targets with different measurement errors, detect the relationship between delay and turning rate |
由图11和图12可看出,量测误差越小,检测延迟越小;目标机动强度越大,检测延迟越小。因此,提升传感器的量测精度,可有效提升算法的实时性。
3.2 自适应跟踪算法性能验证假设目标在XY平面上运动,采样周期为7 s,仿真总时间为1 750 s(250个采样周期),目标(以低速潜艇目标为例)初始位置X(0)位于(3 000 m,4 000 m)处,其X轴初始速度为4 m/s,Y轴初始速度为0。
基于水下目标的运动特性,仿真时设定目标机动行为如表2所示。
|
|
表 2 目标机动参数设置 Tab.2 Target maneuvering parameter settings |
基于水下目标的运动特性,仿真时设定距离量测误差为量测距离的2%,自适应高斯模型中设置方差自适应系数b=0.8。
在仿真研究中,设定原模型非机动起始的机动频率
以量测误差100 m为例,目标的理想运动轨迹和量测轨迹如图13所示。
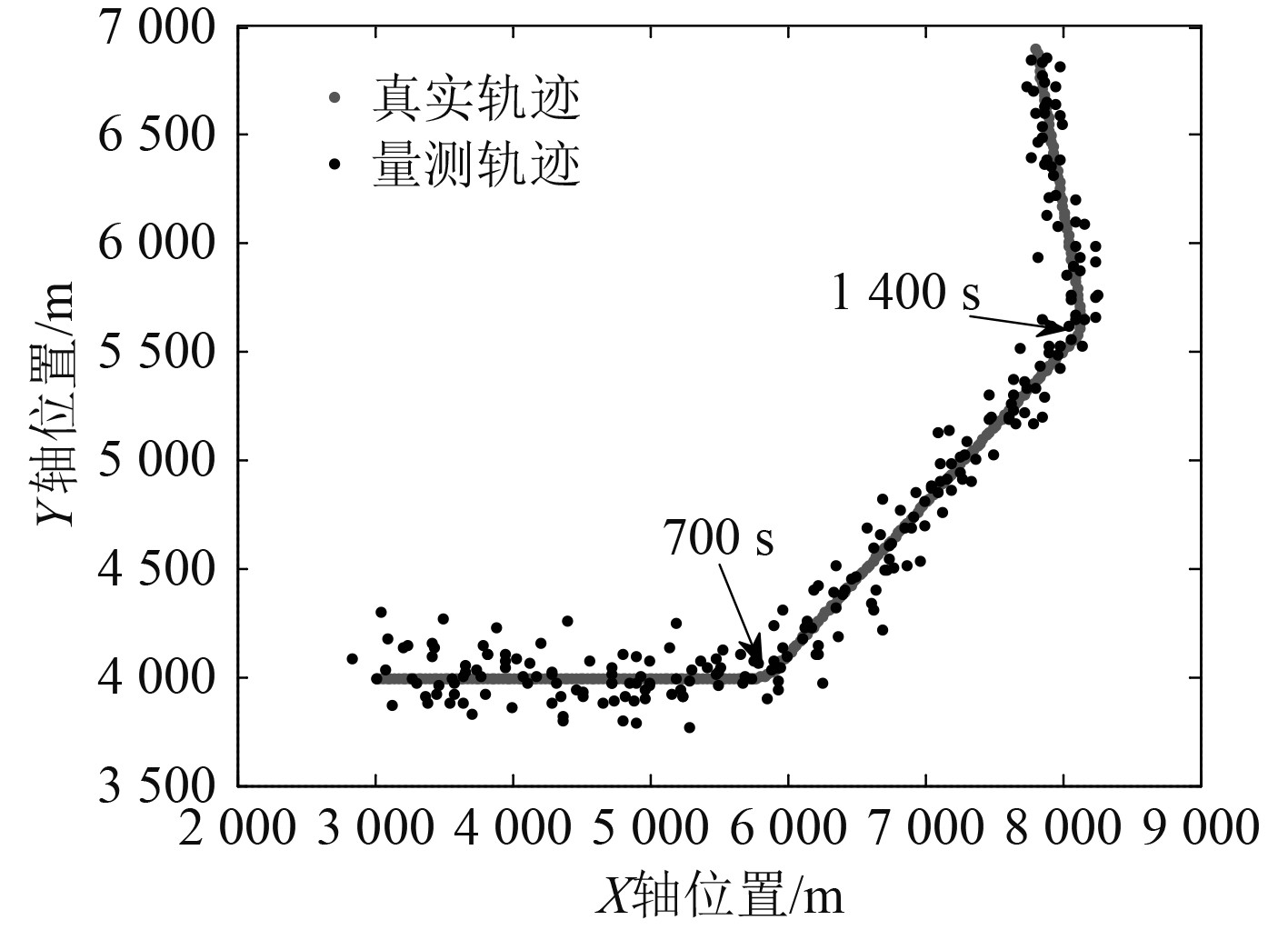
|
图 13 目标理想轨迹和量测轨迹 Fig. 13 Ideal trajectory and measurement trajectory of the target |
以某次机动检测结果为例,机动检测效果如图14所示。可知,基于航向变化率的机动统计量与目标机动行为的相关度很强,然而,噪声带来的虚警现象依然存在,在使用新息的归一化平方进行二次检测后,检测性能获得明显提升。
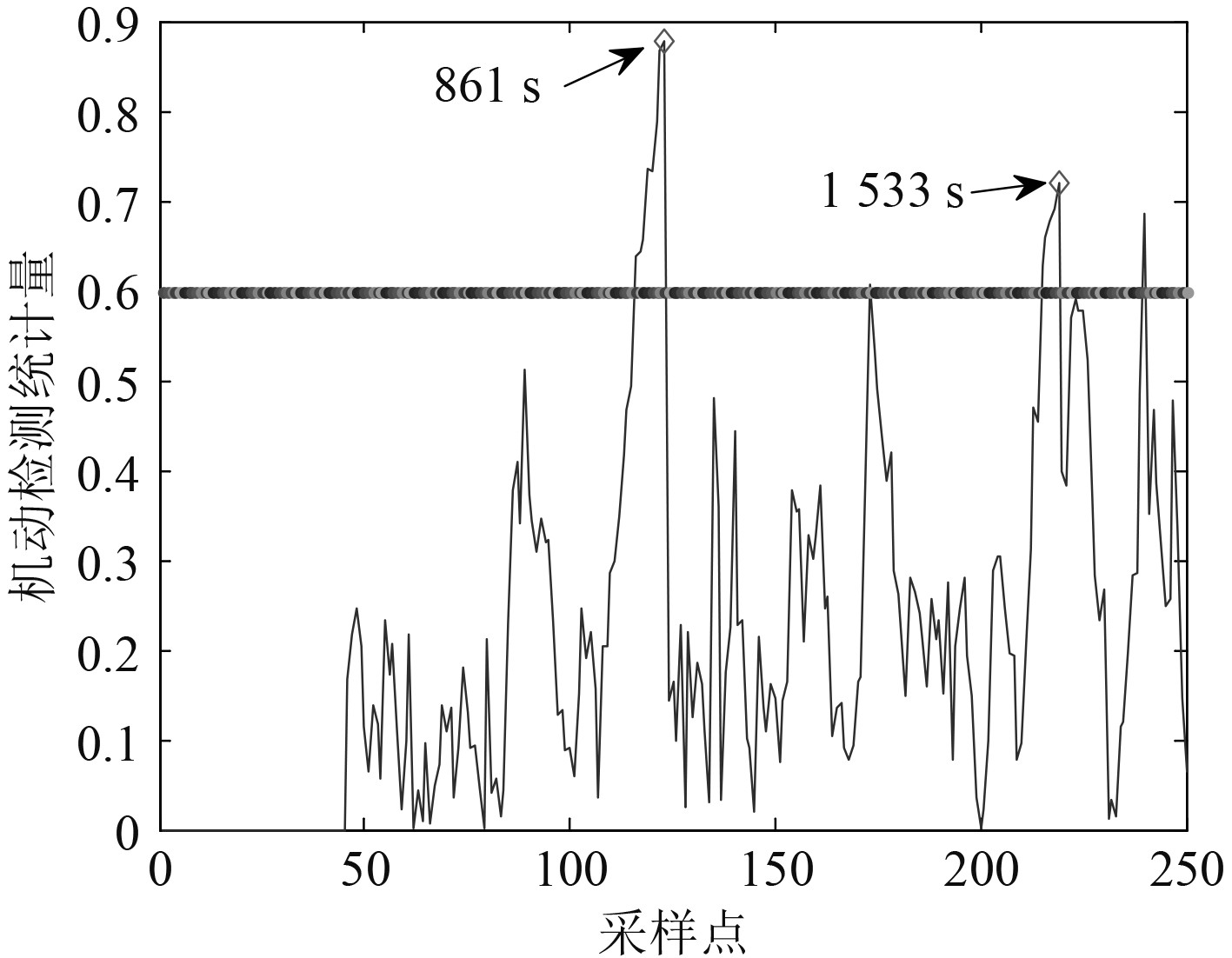
|
图 14 机动检测效果图 Fig. 14 Maneuvering inspection renderings |
改进模型同原模型的仿真对比结果(Monte Carlo仿真结果)如图15和图16所示。
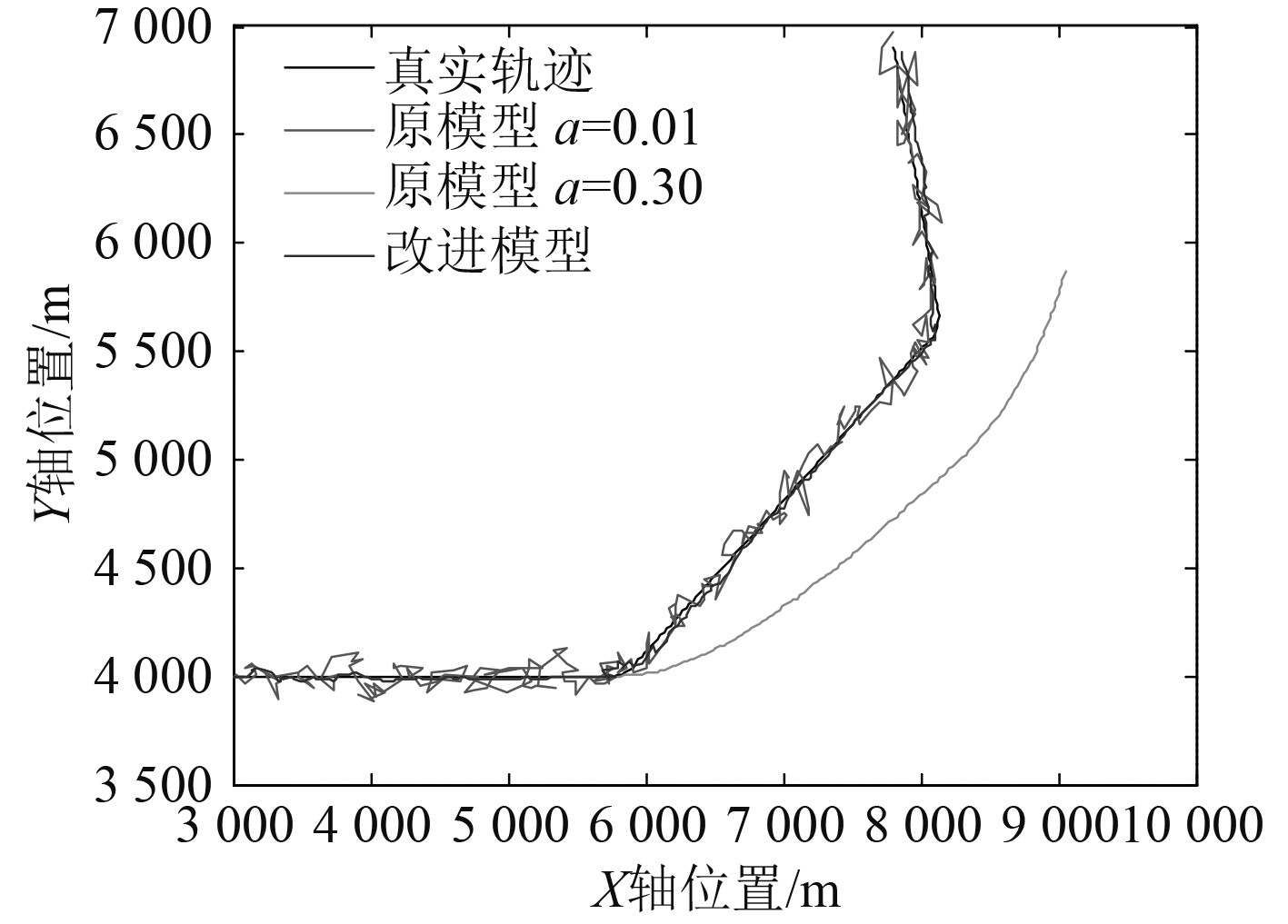
|
图 15 改进算法前后目标运动轨迹对比图 Fig. 15 Comparison chart of target trajectory before and after the improved algorithm |
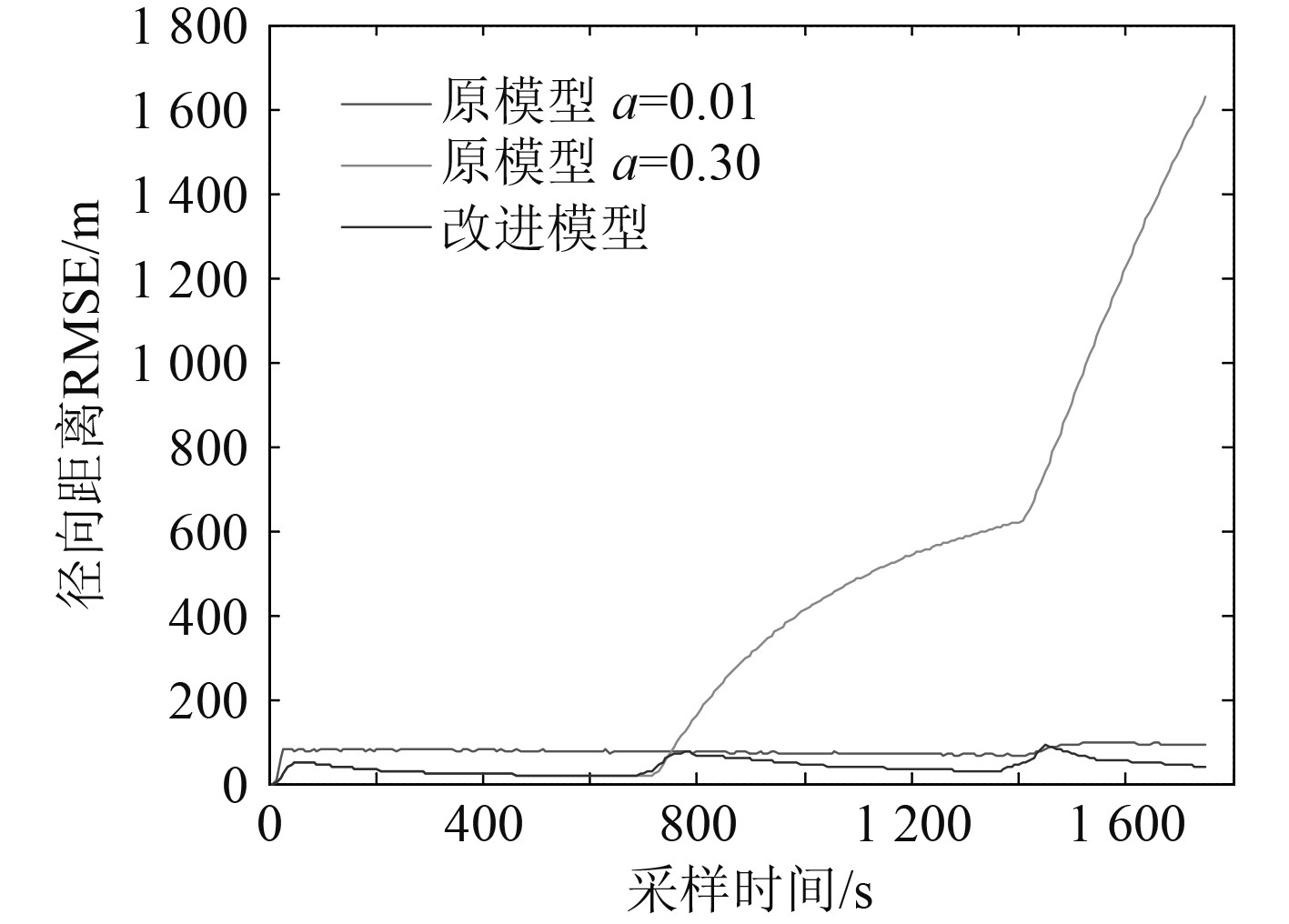
|
图 16 改进算法前后距离均方根误差对比图 Fig. 16 Comparison of distance root mean square error before and after the improved algorithm |
通过实验结果得出各模型在各阶段的平均位置误差如表3所示。
|
|
表 3 各运动阶段的平均位置误差 Tab.3 Average position error in the movement phase |
依据仿真对比结果,在“非机动起始”条件(
针对自适应高斯模型及算法对水下目标跟踪时对机动频率依赖性较强的缺陷,基于航向变化率的机动检测理论,估计目标的机动点和非机动点,以实现自适应高斯模型中机动频率的自适应调整,从而克服模型对机动频率的依赖,提升模型对非机动目标的跟踪精度以及在目标发生机动时的收敛速度,使自适应高斯模型更加便于工程应用。
| [1] |
徐国亮. 机动目标跟踪算法[J]. 情报指挥控制系统与仿真技术, 2002, (8): 42-56.
|
| [2] |
党建武, 黄建国. 机动目标自适应高斯模型与跟踪算法[J]. 电讯技术, 2003, 43(2): 109-113,119. DOI:10.3969/j.issn.1001-893X.2003.02.026 |
| [3] |
董霓, 徐俊艳. 目标机动频率自适应估计的UKF滤波算法研究[J]. 现代防御技术, 2016, 44(6): 72-79. DOI:10.3969/j.issn.1009-086x.2016.06.013 |
| [4] |
刘昌云, 刘进忙, 陈长兴, 等. 机动目标跟踪的机动频率自适应算法[J]. 控制理论与应用, 2004, 21(6): 961-965. DOI:10.3969/j.issn.1000-8152.2004.06.029 |
| [5] |
钱广华, 李颖, 骆荣剑. 机动目标跟踪中一种机动频率和方差自适应滤波算法[J]. 雷达学报, 2013(2): 257-264. |
| [6] |
陈佳俊, 刘高峰, 辛晋生, 等. 机动频率模糊自适应目标跟踪算法研究[J]. 弹箭与制导学报, 2010, 30(2): 259-262. DOI:10.3969/j.issn.1673-9728.2010.02.077 |
| [7] |
徐定杰, 贺瑞, 沈锋, 等. 基于新息协方差的自适应渐消卡尔曼滤波器[J]. 系统工程与电子技术, 2011, 33(12): 2696-2699. DOI:10.3969/j.issn.1001-506X.2011.12.23 |
| [8] |
曹静, 周茜, 冯燕来, 等. 基于机动检测的目标轨迹快速提取算法[J]. 指挥信息系统与技术, 2018, 9(3): 70-74. |
| [9] |
高伟, 李敬春, 奔粤阳, 等. 基于多重渐消因子的自适应卡尔曼滤波器[J]. 系统工程与电子技术, 2014, 36(7): 1405-1409. |
| [10] |
姚洪利, 高效, 田科钰. 基于衰减记忆n次新息的目标机动检测和排飞点[J]. 情报指挥控制系统与仿真技术, 2004(5): 25-29+41. |
 2001, Vol. 44
2001, Vol. 44
