0 引　言

近年来，磁感应通信作为一种新兴水下无线通信技术，得到了国内外研究人员的重视^[1-8]。研究表明，无线磁感应通信具有信道稳定，路径损耗低，天线尺寸小等优点，在地下和水下等挑战环境下具有良好的应用前景，有利于水面舰船与水下航行器、无人潜航器之间的数据传送与通信联络。

由于传统的点对点通信方式传输距离有限^[3]，中继波导对中继线圈的位置要求非常高^[1]，故协作式阵列天线受到越来越多研究人员的关注，其不仅可以实现多波段，使整体带宽得以提高，还可以提供更好的信号强度。虽然在无线磁感应通信系统领域中，对阵列天线的组阵方式和信道特性等研究有一定基础^[9-12]，但是对于阵列天线中各线圈之间的间隔距离分布及其电流加载方式等情况下磁场分布特点的研究还比较少。

本文以常见的空心圆环线圈作为分析对象，针对不同的线圈间隔、空间位置和电流激励方式等情况对阵列天线的磁场分布分别进行了建模仿真，总结了不同条件下各类阵列天线的特点及规律，对舰船无线磁感应通信系统中发射天线阵列的优化与设计具有重要的参考意义。

1 数学模型

针对不同的发射天线阵列对接收端的影响，本文依次对单线圈，双线圈和四线圈阵列天线搭建了数学模型以方便研究其磁场分布。

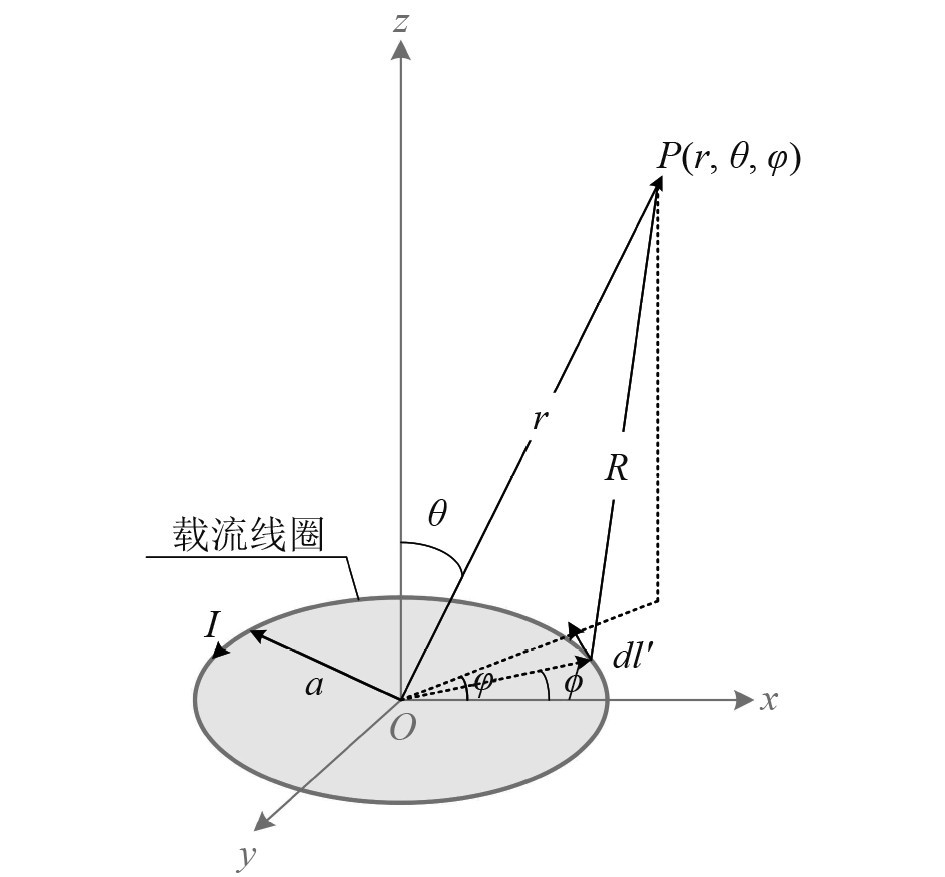
1.1 单线圈

如图1所示，载流线圈可以看作是一个磁偶极子，会在其周围产生变化的电磁场，为了研究磁偶极子在空间中任意一点P的磁场大小，就需要对线圈在空间中所产生的磁感应强度（记为B）进行分析。由于磁感应通信是基于电磁场的近区场特性，利用非辐射交变磁场作为传输介质来进行信息交互，假设r≥a，故半径为a的载流圆环线圈在空间中任意一点P（ $r, \theta, \varphi $ ）处产生的B为^[13]：

$ {\boldsymbol{B}} = \frac{{{\mu _0}NIS}}{{4\text{π} {r^3}}}(2\cos \theta {{\boldsymbol{e}}_r} + \sin\theta {{\boldsymbol{e}}_\theta })，$

(1)

式中： ${\mu _0} $ 为真空磁导率；N，Ｓ分别为线圈的匝数和面积，I为其上加载的交变电流；r为OP之间的距离； $ \theta $ 为OP与Z轴的夹角； $ {{\boldsymbol{e}}_r} $ 和 $ {{\boldsymbol{e}}_\theta } $ 分别是在球坐标系下沿着距离r和角度 $ \theta $ 增加方向的单位向量。

为方便在直角坐标系内计算与分析，根据球坐标与直角坐标之间的关系，可将式（1）用直角坐标系表示，即载流圆环线圈在空间中任意一点P（x，y，z）处的磁感应强度为：

$ {\boldsymbol{B}} = \frac{{{\mu _0}N{I_1}S}}{{4\text{π} {r^5}}}[3xz{{\boldsymbol{e}}_x} + 3yz{{\boldsymbol{e}}_y} + (2{z^2} - {x^2} - {y^2}){{\boldsymbol{e}}_z}]。$

(2)

式中： $ {{\boldsymbol{e}}_x} $ ， $ {{\boldsymbol{e}}_y} $ ， $ {{\boldsymbol{e}}_z} $ 分别是在直角坐标系下X轴、Y轴、Z轴的单位向量。

1.2 双线圈阵列

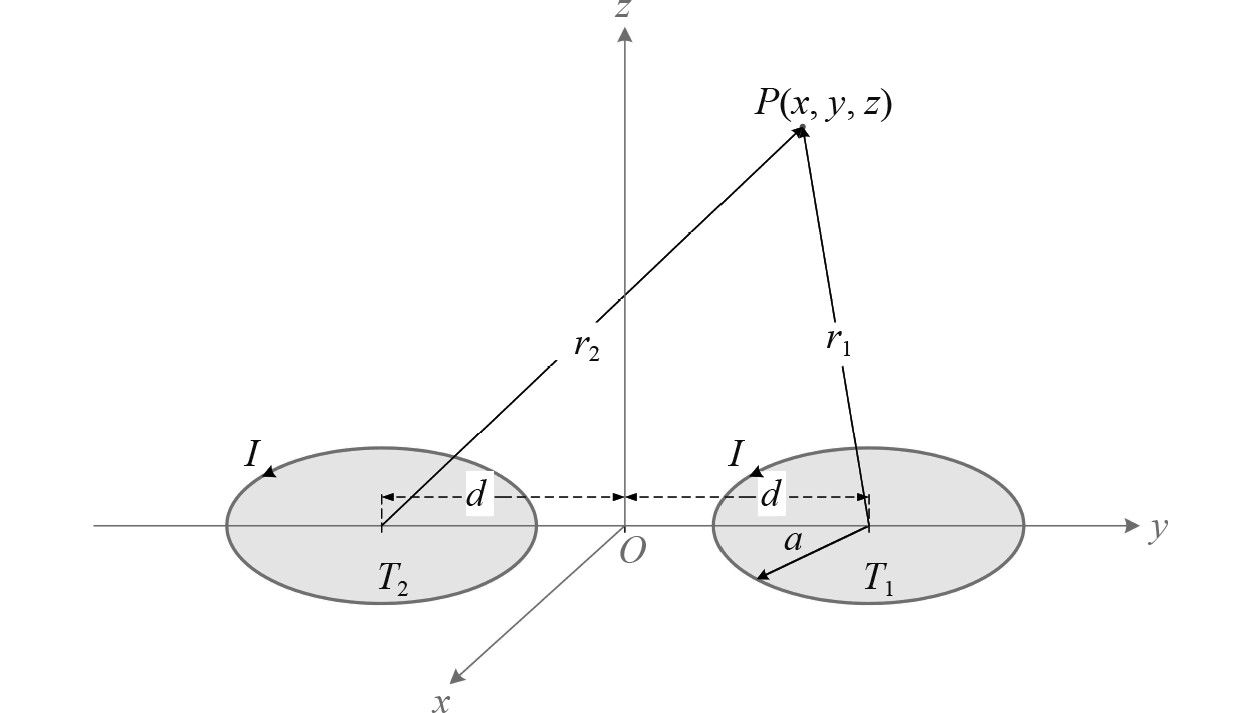
如图2所示，双线圈阵列天线T₁，T₂水平放置在XOY平面内，其圆心分别在Y轴正负半轴两侧，且距原点O的偏移量均为d。则双线圈阵列天线在空间中任意一点P（x,y,z）处的磁感应强度为：

$ {{\boldsymbol B}_{{\text{two}}}} = {{\boldsymbol{B}}_{{\text{T1}}}} + {{\boldsymbol{B}}_{{\text{T2}}}} ，$

(3)

式中： $ {{\boldsymbol{B}}_{{\text{T1}}}} $ ， $ {{\boldsymbol{B}}_{{\text{T2}}}} $ 分别是发射线圈T₁，T₂在点P处产生的磁感应强度。

$ \begin{split} {{\boldsymbol{B}}_{{\boldsymbol{T1}}}} = &\frac{{{\mu _0}N{I_2}S}}{{4\text{π} {{\left[ {{x^2} + {{(y - d)}^2} + {z^2}} \right]}^{\frac{5}{2}}}}}\{ 3xz{{\boldsymbol{e}}_x} + 3(y - d)z{{\boldsymbol{e}}_y} +\\ & [2{z^2} - {x^2} - {(y - d)^2}]{{\boldsymbol{e}}_z}\}，\end{split} $

(4)

$ \begin{split} {{\boldsymbol{B}}_{{\text{T2}}}} =& \frac{{{\mu _0}N{I_2}S}}{{4\text{π} {{\left[ {{x^2} + {{(y{\text{ + }}d)}^2} + {z^2}} \right]}^{\frac{5}{2}}}}}\{ 3xz{{\boldsymbol{e}}_x} + 3(y{\text{ + }}d)z{{\boldsymbol{e}}_y} + \\ & [2{z^2} - {x^2} - {(y{\text{ + }}d)^2}]{{\boldsymbol{e}}_z}\} 。\end{split} $

(5)

1.3 四线圈阵列

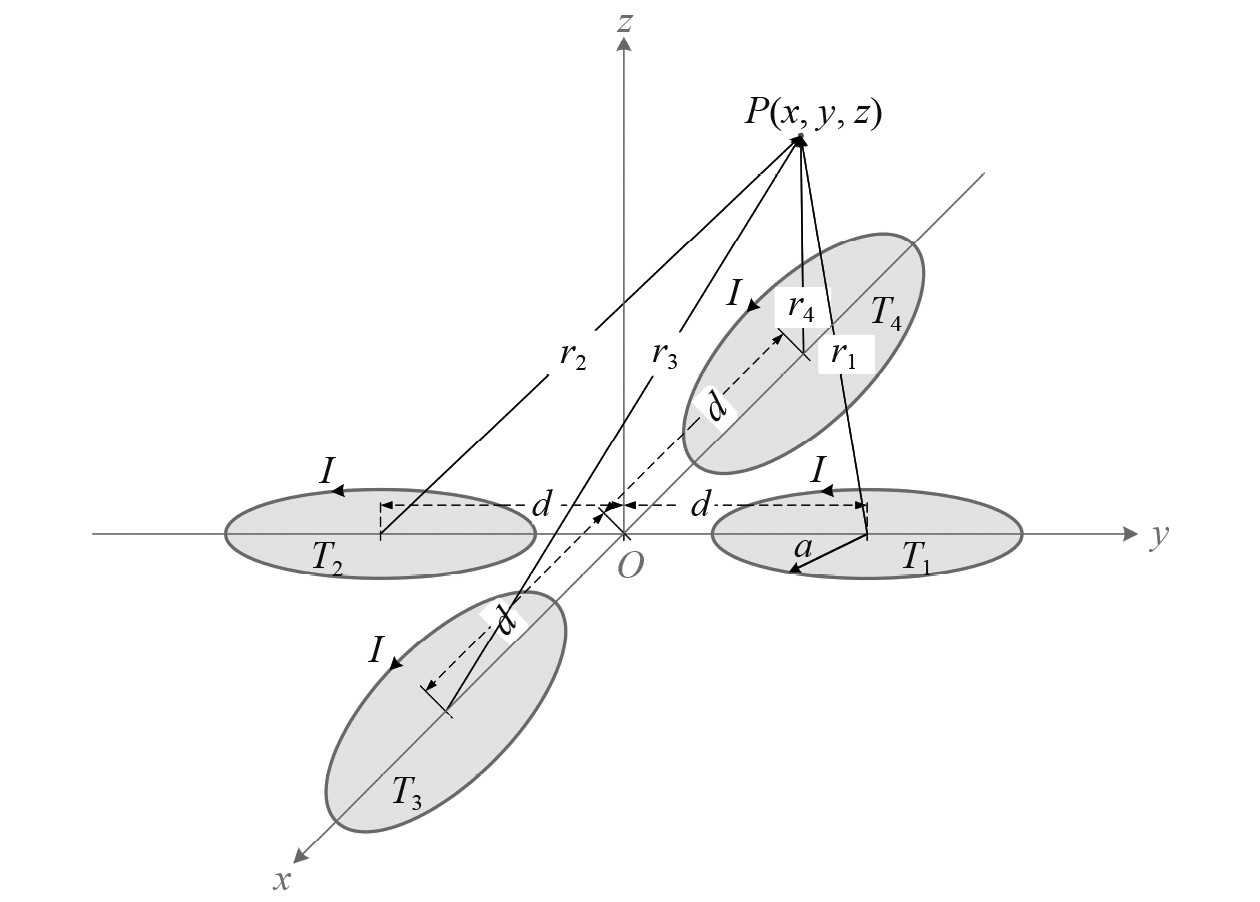
如图3所示，四线圈阵列天线T₁，T₂，T₃，T₄水平放置在XOY平面内，其圆心分别在X，Y轴的正负半轴上，且距原点O的偏移量均为d。则四线圈阵列天线在空间中任意一点P（x,y,z）处的磁感应强度为：

$ {{\boldsymbol{B}}_{{\text{four}}}} = {{\boldsymbol{B}}_{{\boldsymbol{T1}}}} + {{\boldsymbol{B}}_{{\boldsymbol{T2}}}}{\text{ + }}{{\boldsymbol{B}}_{{\boldsymbol{T3}}}} + {{\boldsymbol{B}}_{{\boldsymbol{T4}}}}，$

(6)

式中： $ {{\boldsymbol{B}}_{{\boldsymbol{T3}}}} $ ， $ {{\boldsymbol{B}}_{{\boldsymbol{T4}}}} $ 分别是发射线圈T₃，T₄在点P处产生的磁感应强度。

$ \begin{split} {{\boldsymbol{B}}_{{\text{T3}}}} =& \frac{{{\mu _0}N{I_3}S}}{{4\text{π} {{\left[ {{{(x - d)}^2} + {y^2} + {z^2}} \right]}^{\frac{5}{2}}}}}\{ 3(x - d)z{{\boldsymbol{e}}_x} + 3yz{{\boldsymbol{e}}_y} + \\ & [2{z^2} - {(x - d)^2} - {y^2}]{{\boldsymbol{e}}_z}\} ，\end{split} $

(9)

$ \begin{split} {{\boldsymbol{B}}_{{\text{T4}}}} =& \frac{{{\mu _0}N{I_3}S}}{{4\text{π} {{\left[ {{{(x{\text{ + }}d)}^2} + {y^2} + {z^2}} \right]}^{\frac{5}{2}}}}}\{ 3(x{\text{ + }}d)z{{\boldsymbol{e}}_x} + 3yz{{\boldsymbol{e}}_y} + \\ & [2{z^2} - {(x{\text{ + }}d)^2} - {y^2}]{{\boldsymbol{e}}_z}\} 。\end{split} $

(10)

2 建模与仿真

为了研究不同线圈间隔和空间位置下阵列天线所产生B的分布特点，根据理论公式进行建模仿真，同时针对不同的线圈激励方式下各类阵列天线所产生B的分布情况，总结一些特点与规律。

假设线圈参数完全相同，令线圈半径 $ a = $ $ 0.25\;{\text{m}} $ ，匝数 $ N = 100 $ 。单线圈、双线圈和四线圈模型中每个线圈的激励电流分别为I₁、I₂、I₃，同时为使发射功率保持恒定，存在关系 $ {I_1} = \sqrt 2 {I_2} = 2{I_3} $ 。在本文中，针对不同线圈间隔d，均位于轴向距离z=2.0 m处的XOY平面内来建模观察分析各线圈模型的磁感应强度模（记作|B| ）的分布；而针对不同z，固定d=1.0 m时来建模观察分析各线圈模型|B| 的分布。

2.1 单线圈模型

在z=2.0 m的XOY平面内，对于不同大小的激励电流I，单线圈|B| 的分布如图4所示。随着电流的减小，单线圈的|B| 在逐渐线性减小，较高值的覆盖面积也越来越小，|B| 的峰值（记为|B| max）具体大小及所在位置如表1所示。

2.2 双线圈模型

为保证输入功率恒定不变，令单线圈的激励电流 $ {I_1} = 1 $ A，则双线圈的激励电流 $ {I_2} = 1/\sqrt 2 $ A。为确保线圈之间不重叠，线圈圆心距坐标原点的最小间隔是一个线圈半径的长度，即0.25 m。

2.2.1 双线圈电流同向

1）轴向距离一定时，改变线圈间隔

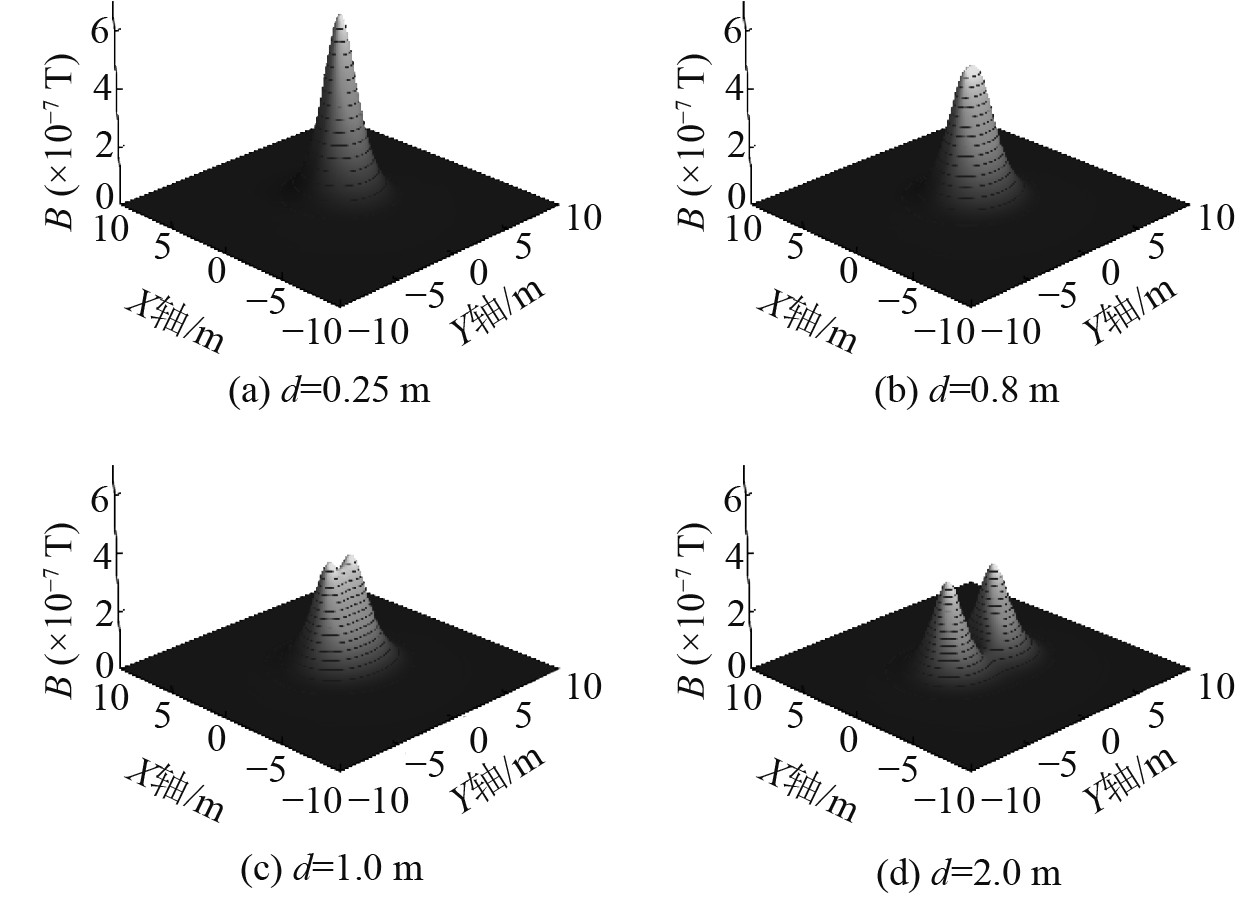
在z=2.0 m的XOY平面内，对于不同的线圈间隔d，双线圈|B| 的分布如图5所示，图中|B| max具体大小及所在位置如表2所示。从d=0.8 m开始，峰值点由原点处的单个分裂为Y轴上对称的2个。

2）线圈间隔一定时，改变轴向距离

当线圈间隔d=1.0 m时，对于不同的轴向距离z，在XOY平面内同功率的单线圈和双线圈|B| 的分布如图6所示，图中|B| max具体大小及所在位置如表3所示。随着z的增加，较高值覆盖面积比单线圈大，且z=1.8 m开始2个峰值点开始向原点处合拢，到2.7 m时合拢为1个峰值点。

2.2.2 双线圈电流反向

1）轴向距离一定时，改变线圈间隔

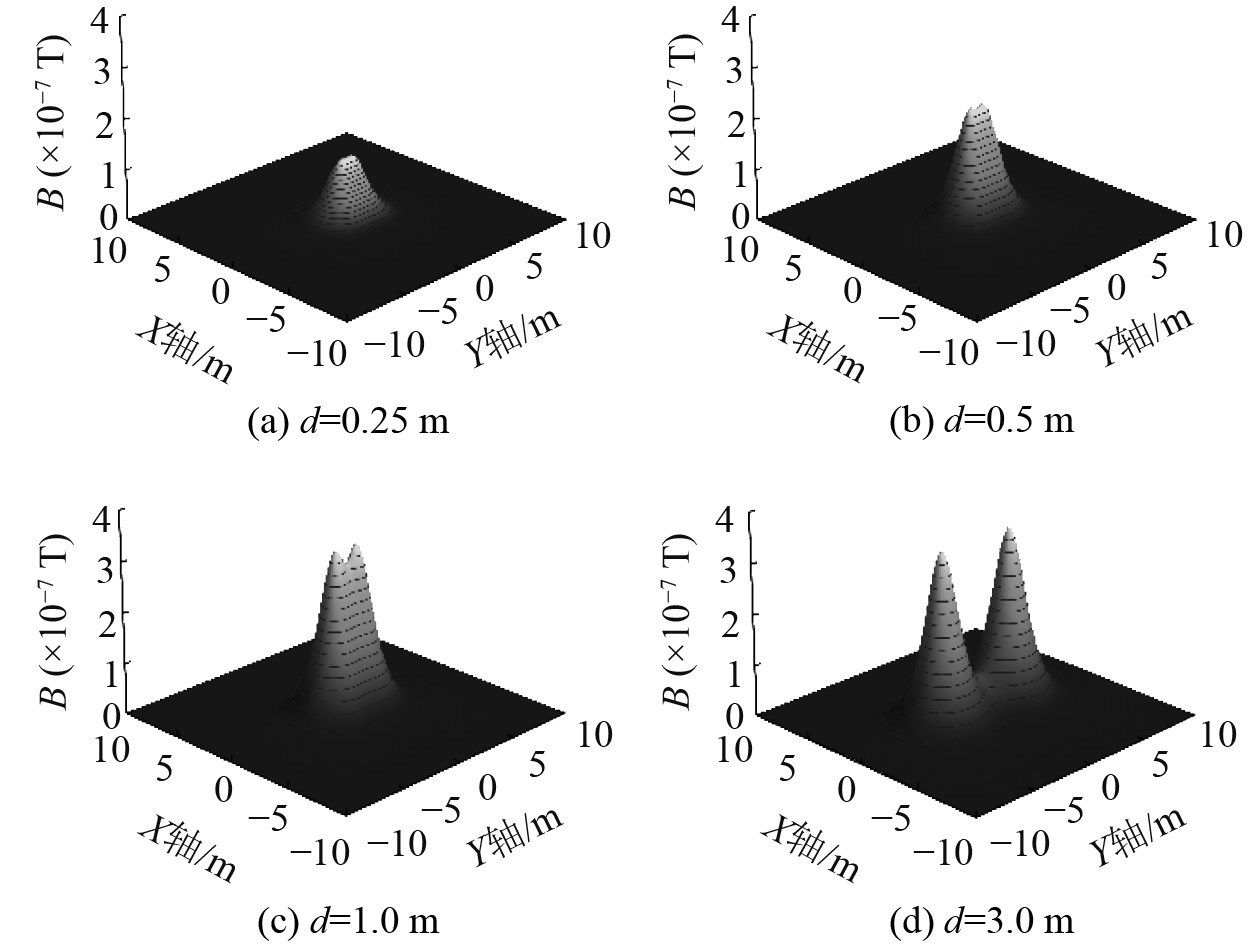
在z=2.0 m的XOY平面内，对于不同的线圈间隔d，双线圈|B| 的分布如图7所示，图中|B| max具体大小及所在位置如表4所示。随着d的变化，始终处于Y轴上对称两峰值点的状态。

2）线圈间隔一定时，改变轴向距离

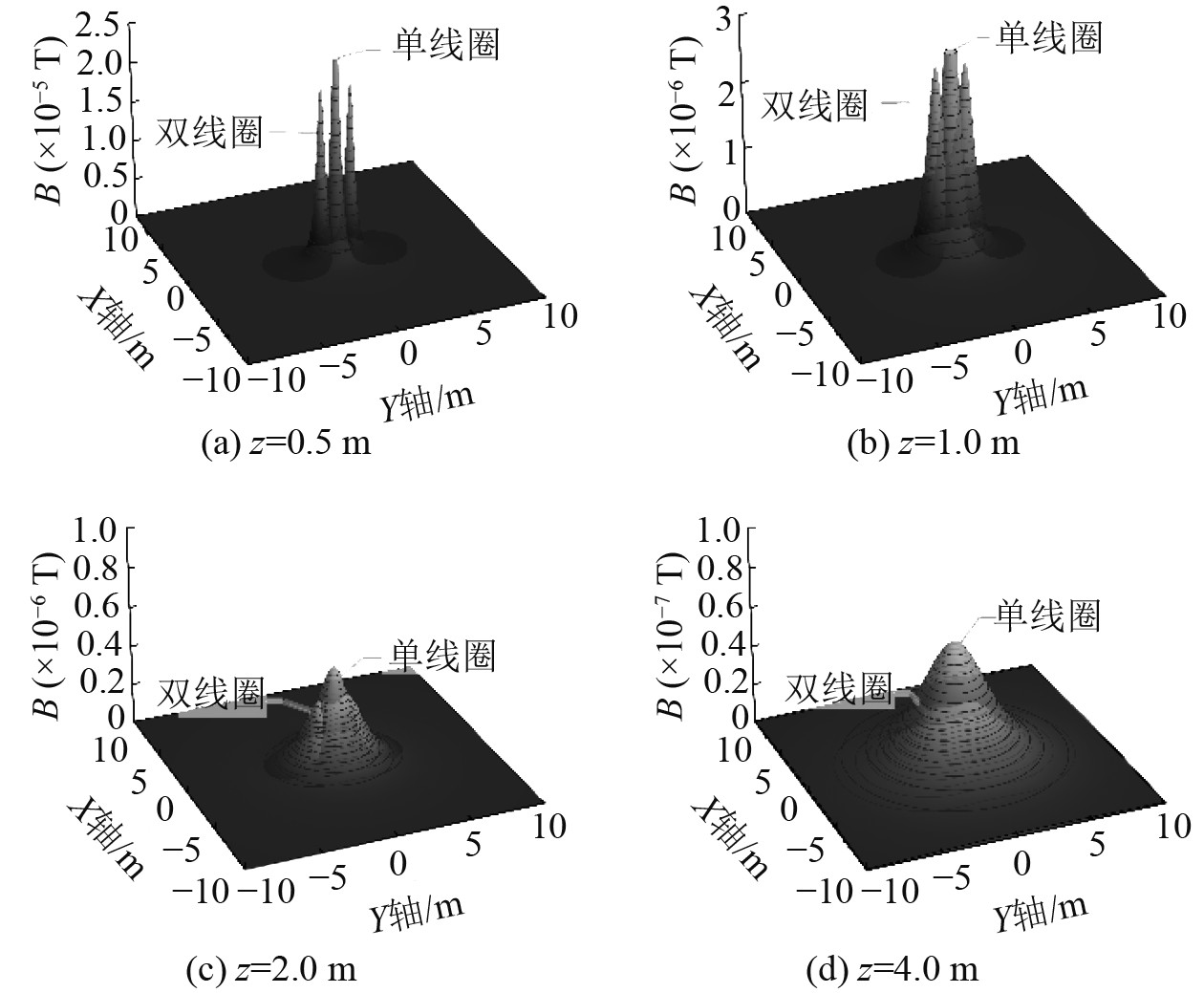
当线圈间隔d=1.0 m时，对于不同的轴向距离z，在XOY平面内同功率的单线圈和双线圈|B| 的分布如图8所示，图中|B| max具体大小及所在位置如表5所示。随着z的增加，较高值覆盖面积比单线圈小；相对于线圈所在坐标轴位置，两峰值点先向原点处靠近，然后一直向Y轴两侧扩散，且在z较大处双线圈|B| max与其对应的点（0,0,Z）的|B| 值相差不大。

2.3 四线圈模型

为保证输入功率恒定不变，当单线圈的激励电流 $ {I_1} = 1 $ A时，则四线圈的激励电流 $ {I_3} = 0.5 $ A。为确保线圈之间不重叠，线圈圆心距坐标原点的最小间隔是 $ \sqrt 2 $ 倍的线圈半径长度，约为0.36 m。

2.3.1 四线圈电流同向

1）轴向距离一定时，改变线圈间隔

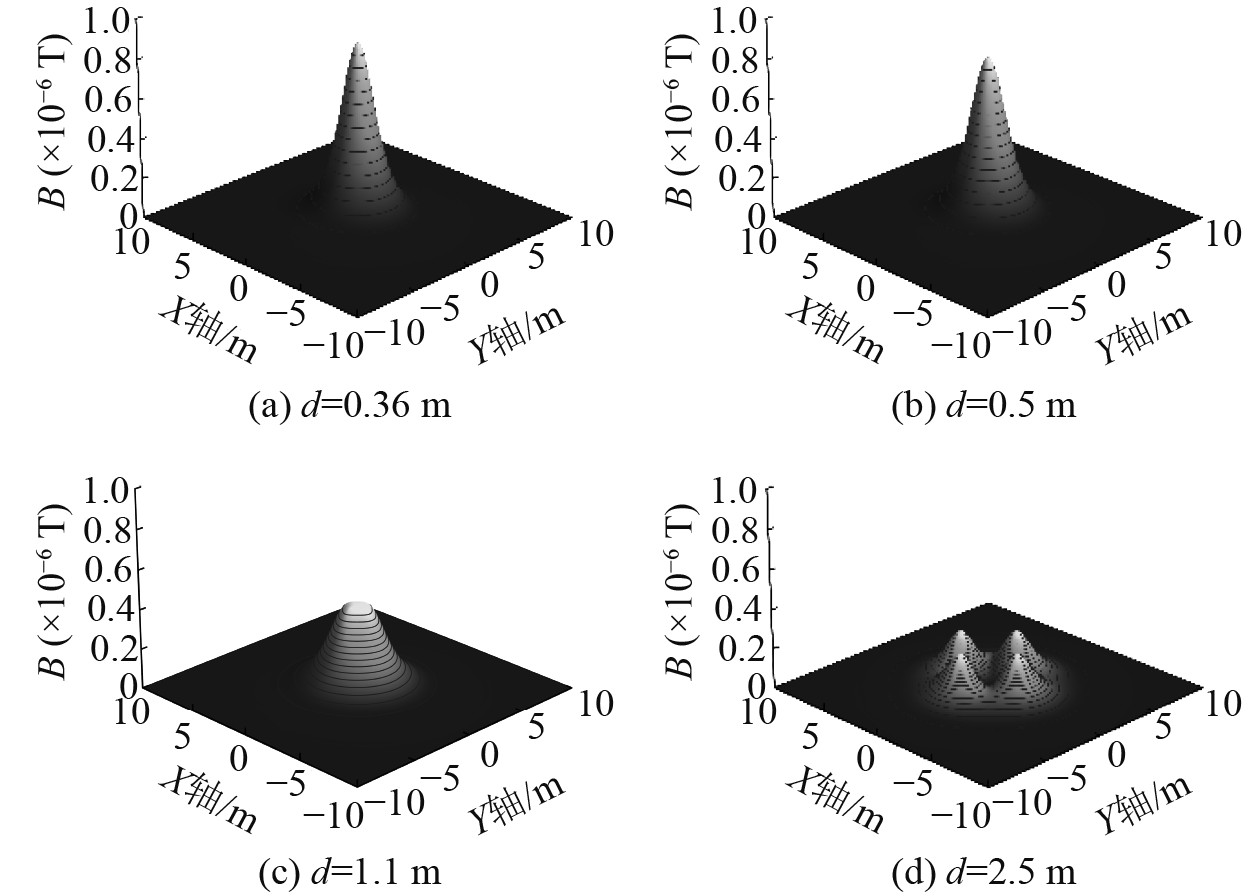
在z=2.0 m的XOY平面内，对于不同的线圈间隔d，四线圈|B| 的分布如图9所示，图中|B| max具体大小及所在位置如表6所示。从d=1.1 m开始，峰值点由原点处的单个分裂为X，Y轴上对称的4个。

2）线圈间隔一定时，改变轴向距离

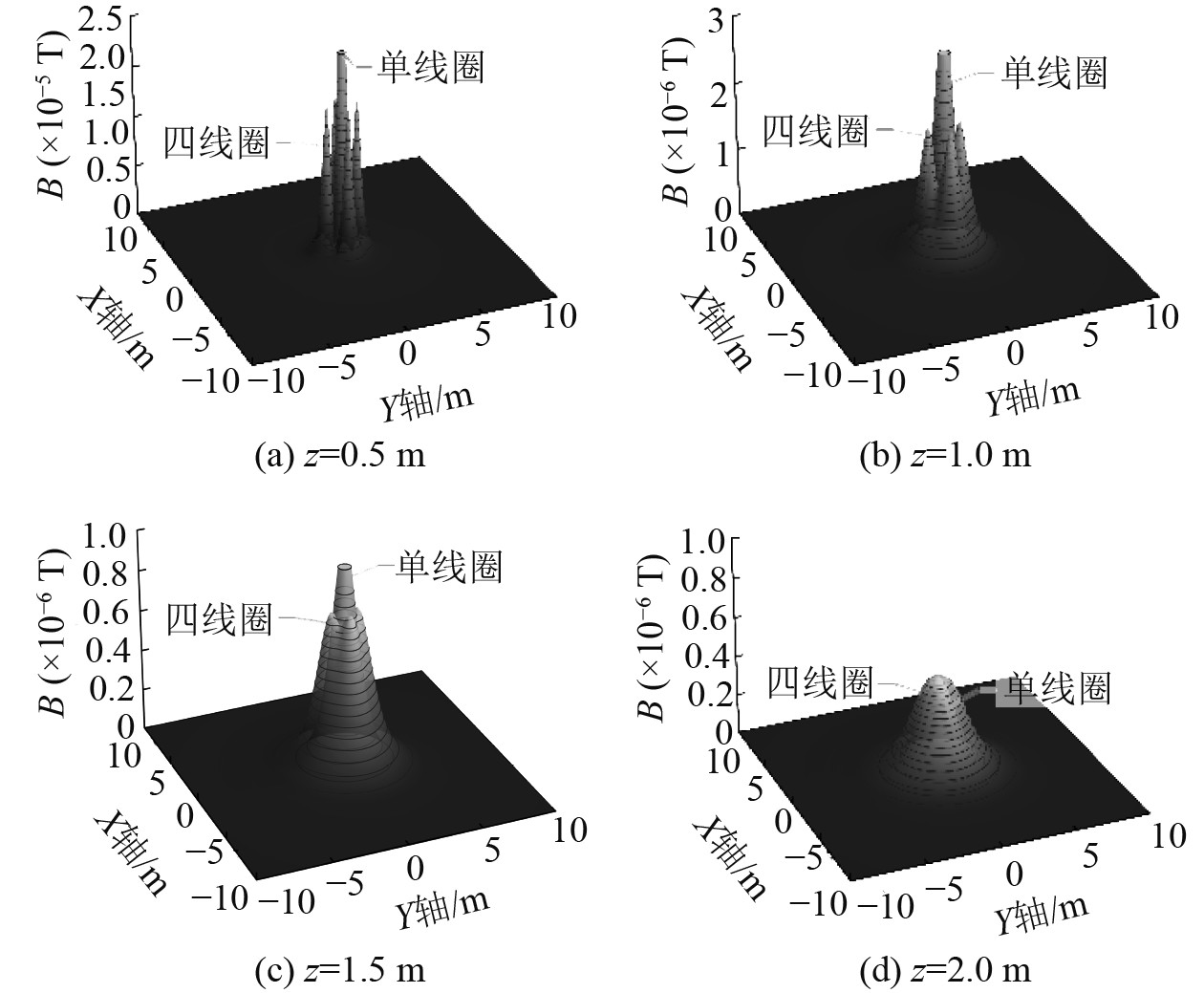
当线圈间隔d=1.0 m时，对于不同的轴向距离z，四线圈|B| 的分布如图10所示，图中|B| max具体大小及所在位置如表7所示。随着z的增加，较高值覆盖面积比单线圈大，且从z=1.3 m开始，4个峰值点向原点处合拢，到1.9 m时合拢为1个峰值点。

2.3.2 负半轴线圈电流反向

1）轴向距离一定时，改变线圈间隔

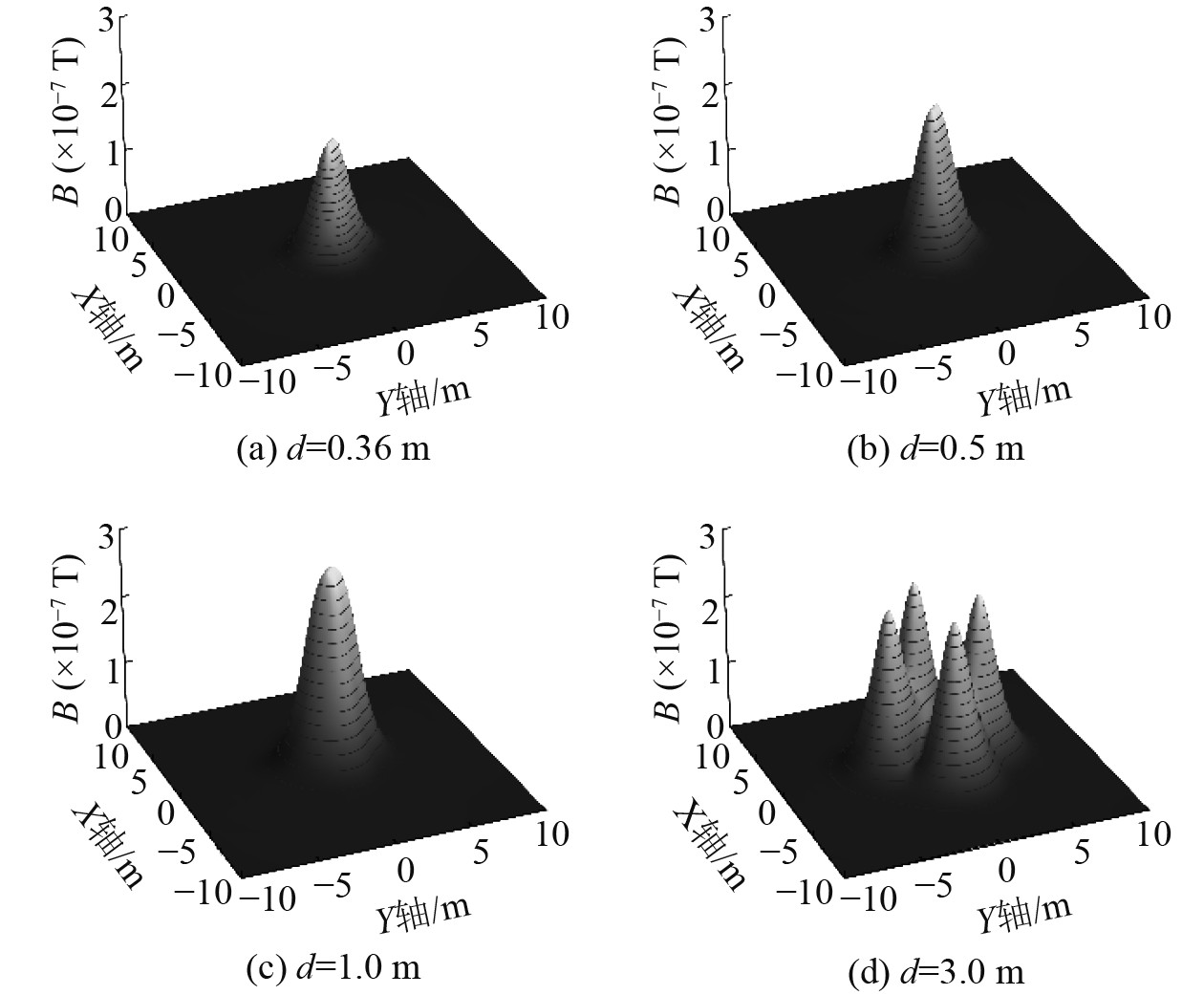
在z=2 m的XOY平面内，对于不同的线圈间隔d，四线圈|B| 的分布如图11所示，图中|B| max具体大小及所在位置如表8所示。随着d的增加，峰值点首先由一、三象限的2个合拢为原点处的一个，之后又继续分裂成二、四象限的2个，最终分裂为X，Y轴上对称的4个。

2）线圈间隔一定时，改变轴向距离

当线圈间隔d=1.0 m时，对于不同的轴向距离z，四线圈磁感应强度模|B| 的分布如图12所示。图中|B| 的峰值具体大小及所在位置如表9所示。随着z的增加，较高值覆盖面积比单线圈小，且峰值点由一开始的4个合拢为2个，之后又继续合拢为一个，最终固定成为2个，是分裂的逆过程。

2.3.3 X轴线圈电流反向

1）轴向距离一定时，改变线圈间隔

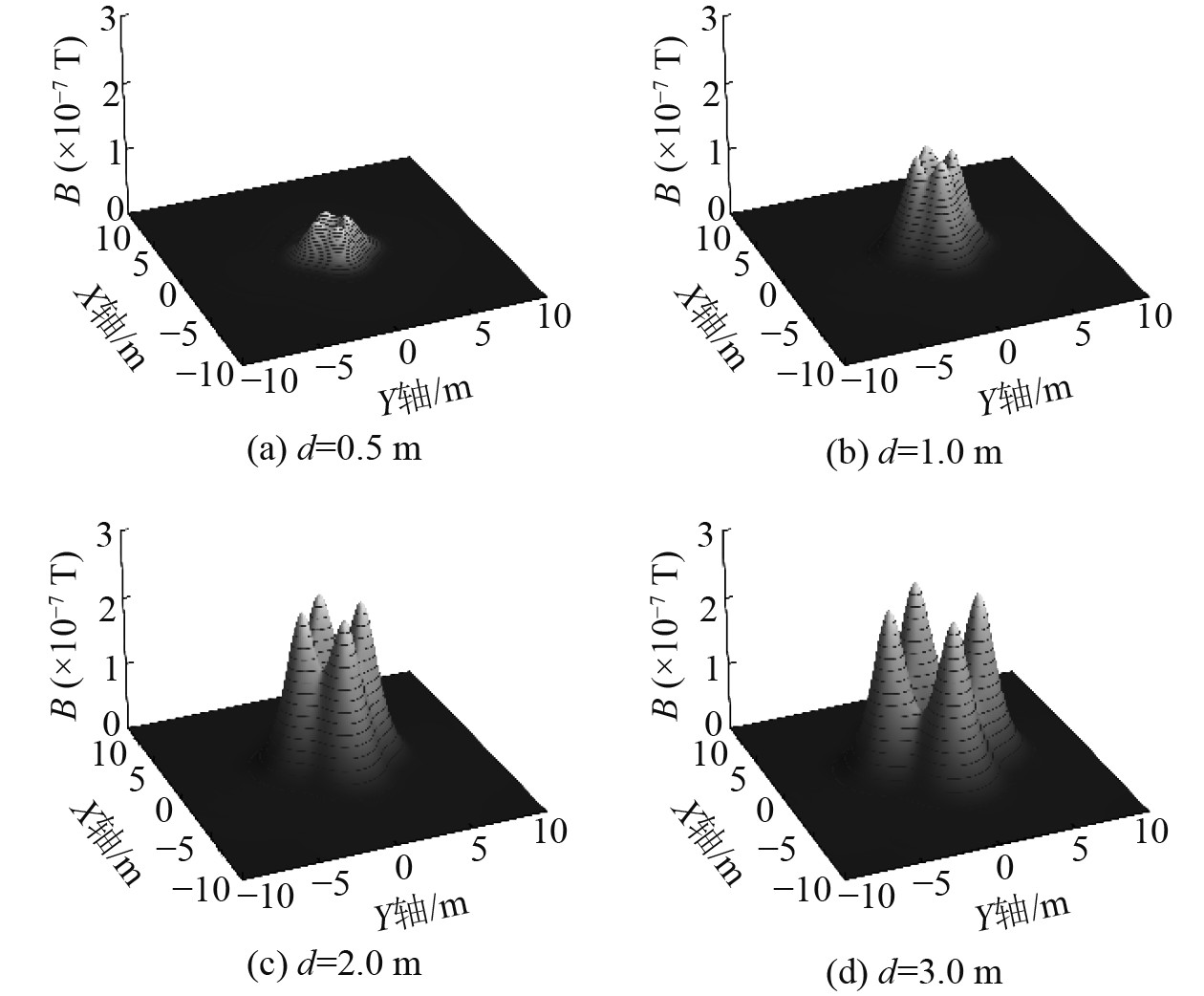
在z=2.0 m的XOY平面内，对于不同的线圈间隔d，四线圈|B| 的分布图13所示，图中|B| max具体大小及所在位置如表10所示。随着d的增加，一直处于X，Y轴上对称的４个峰值点的状态，而(0,0,2)处的B值始终为0。

（2）线圈间隔一定时，改变轴向距离

当线圈间隔d=1.0 m时，对于不同的轴向距离z，四线圈磁感应强度模|B| 的分布如图14所示，图中|B| 的峰值具体大小及所在位置如表11所示。随着z的增加，较高值覆盖面积比单线圈小；相对于线圈所在坐标轴位置，4个峰值点先向原点处靠近，然后一直向X，Y轴两侧扩散，但（0,0,Z）处的B值始终为0。

3 结果与分析 3.1 双线圈

在z=2.0 m的XOY平面内，当线圈间隔 $ d \leqslant 1.4\;{\text{m}} $ 时，同向激励的磁感应强度模|B| max比较高；随着d的继续增大，反向激励|B| max超过同向激励；在d=4.0 m之后，同向、反向2种激励方式对|B| max的大小影响不大，最终均收敛于相同条件下激励电流I= $ 1/\sqrt 2 $ A的单线圈|B| 的峰值，即 $ 3.471 \times $ $ {10^{ - 7}} $ T，如图15所示。

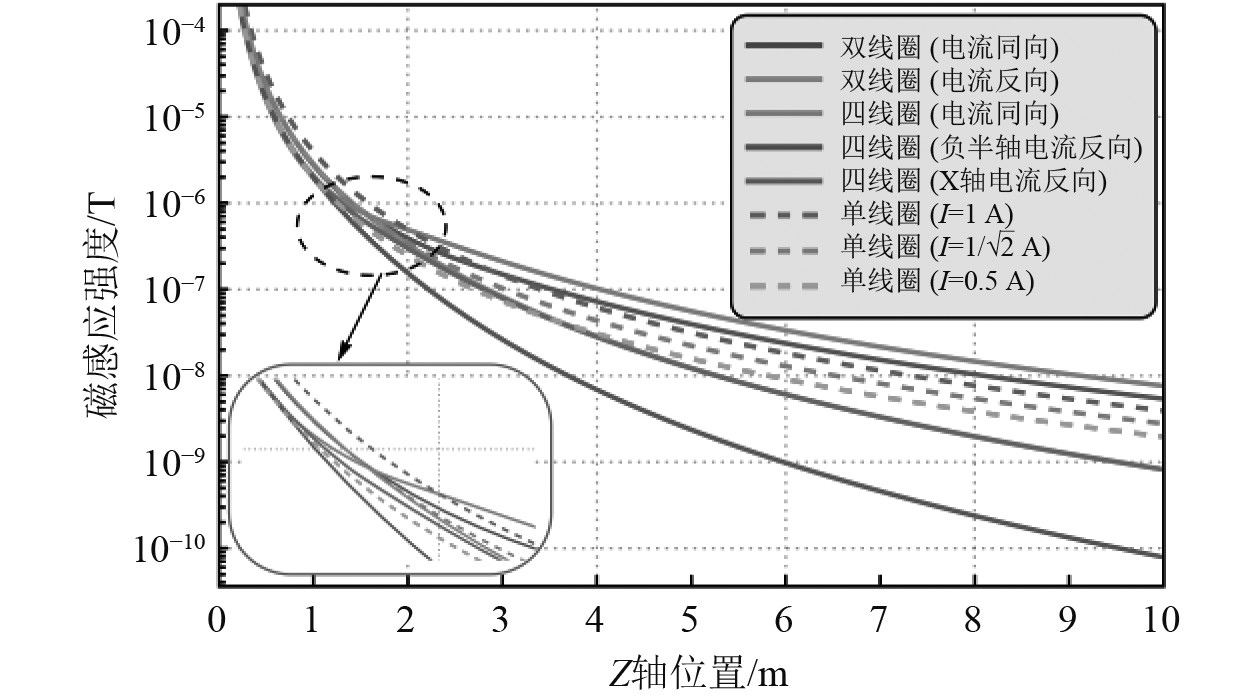
固定线圈间隔d为1.0 m，对于不同的轴向距离z所在的XOY平面内，当 $ z \leqslant 1.5\;{\text{m}} $ 时，同向、反向2种激励方式所产生的|B| max比较接近，相差不大；随着z的继续增大，由于反向激励|B| 的峰值下降速度较快，使得同向激励|B| max与反向激励相比越来越大；当z=10.0 m时，同向激励|B| max是反向激励的6.58倍，如图16所示。

3.2 四线圈

在z=2.0 m的XOY平面内，当线圈间隔d<2 m时，同向激励|B| max较高；随着d的继续增大，负半轴、X轴线圈反向激励方式|B| max超过同向激励；在d=6.0 m之后，同向、反向激励方式对|B| max的影响不大，最终3种激励方式|B| max均收敛于相同条件下激励电流I=0.5 A的单线圈|B| max，即 $ 2.45437 \times {10^{ - 7}} $ T（见图15）。

固定线圈间隔d为1.0 m，在不同的轴向距离z所处的XOY平面内，当 $ z \leqslant 1.0\;{\text{m}} $ 时，同向、负半轴反向，X轴反向这3种激励方式所产生的|B| max比较接近，相差不大；随着z的继续增大，3种激励方式|B| max出现不同程度的下降，其下降速度的大小为：X轴线圈反向激励>负半轴线圈反向激励>同向激励；当z=10.0 m时，同向激励比负半轴线圈反向激励、负半轴线圈反向激励比X轴线圈反向激励的|B| max分别大9.32倍和10.37倍，约高出1个数量级的大小（见图16）。

3.3 不同阵列天线的特性分析

结合磁场仿真模型与图15和图16分析可得：

当电流同向时，d取最小值时|B| max，最大时双线圈、四线圈比同功率单线圈高约35%，82%；随着z的增大，|B| max超过同功率单线圈且较高值覆盖面积比单线圈大，在z=10 m时双线圈、四线圈的|B| max分别是同功率单线圈的1.37倍、1.94倍。

当电流反向时，随着d的增大，|B| max始终比同功率单线圈小，且当d的改变使|B| max最大时，双线圈、四线圈负半轴反向、四线圈X轴反向的|B| max仍比同功率单线圈小28%，39.3%，48.7%；随着z的增大，|B| max始终比同功率单线圈小，双线圈和四线圈负半轴反向两条曲线几乎重合，且当z=10 m时双线圈、四线圈负半轴反向、四线圈X轴反向的|B| max分别只有同功率单线圈的20.9%，20.8%，2%。

当发射线圈的输入功率一定时，可通过调节发射阵列线圈之间的间隔和激励电流相位，使接收线圈在其接收平面处的信号强度和有效覆盖面积最大限度地得以提高，有利于接收线圈有更大的收信区域，提高通信的可靠性。

4 结　语

本文以空心圆环线圈为例，针对不同的线圈间隔、空间位置和电流激励方式，对单线圈、双线圈阵列和四线圈阵列的磁感应强度分布逐一进行建模仿真与特性分析。结合本文线圈模型，总结了以下规律：

电流同向时，磁感应强度在空间中正向叠加效果明显，双线圈、四线圈的|B| 最大可比同功率单线圈高约35%，82%。随着d的增大，最佳接收点由一个分裂成与阵列线圈数目相等的数量；随着z的增大，|B| max超过同功率单线圈且较高值覆盖面积比单线圈大，且在z=10.0 m时双线圈、四线圈|B| max分别是同功率单线圈的1.37倍、1.94倍，最佳接收点最终合拢为原点处的一个；

电流反向时，随着d或z的变化，|B| max始终比同功率单线圈小，其大小为双线圈>四线圈负半轴反向>四线圈X轴反向，且较高值覆盖面积随着z的增大最终比单线圈小；随着d或z的增大，双线圈和四线圈X轴反向的最佳接收点始终与阵列线圈数目相等，而对四线圈负半轴反向而言，随着d的增大，最佳接收点由一、三象限的2个汇聚为原点处1个，再分裂为二、四象限的2个，最终处于各坐标轴正负半轴上关于原点对称的4个，随着z的增大，最佳接收点的分布是其逆过程。