2. 哈尔滨工程大学 核科学与技术学院,黑龙江 哈尔滨 150001
2. College of Nuclear Science and Technology, Harbin Engineering University, Harbin 150001, China
海洋核动力平台由于远离大陆,发生全船断电(含可靠电源丧失)事故以及能动余热排出系统失效时,难以及时得到陆地资源支持,属于事实上的“孤岛”。核安全法规HAF102(2004)《核动力厂设计安全规定》规定:“必须充分考虑事故条件下丧失厂外电源情况下的堆芯余热导出能力”,因此我国海洋核动力平台设计采用非能动余热排出系统(PRHR)将停堆后的余热输送到最终热阱,以防止燃料包壳烧毁和堆芯熔化[1-4]。PRHR HX是海洋核动力平台PRHR的关键设备,由于海洋核动力平台和大型核动力舰艇蒸汽发生器液位高于海面,无法利用舷外侧海水冷却,因此其采用换热器浸没在水箱方案,PRHR系统投运后,水箱温度逐渐升高到饱和温度,换热器管外传热机制为池沸腾换热,PRHR HX池沸腾换热特性对PRHR运行能力有重要影响。
王开元等[5-6]通过实验研究表明,竖直管束池沸腾换热不均匀,管束旁管换热能力相对于中心管提高了约7%。Gupta等[7]通过实验发现,显示沿气泡流动方向沸腾换热系数有增大的趋势。Yonomoto[8-9]实验模拟了ROSA-V装置小破口事故发生时,PRHR启动后堆芯余热排出过程,并验证了Cooper公式计算PRHR HX换热系数的可行性。我国海洋核动力平台PRHR HX采用C型换热器,一方面传统的理论计算公式往往误差较大;另一方面,已有的研究不满足其工作条件,目前国内尚未有非能动余热排出工况下相关实验研究,故目前没有可靠的换热计算式用来计算海洋核动力平台PRHR HX池沸腾换热系数。
为了分析实际运行工况下海洋核动力平台PRHR HX池沸腾传热特性,为PRHR HX传热设计提供依据。采用实验研究的方法,分析非能动余热排出工况下海洋核动力平台PRHR HX池沸腾换热特性,探究热负荷其池沸腾换热系数的影响,参照Rohsenow公式结构,通过拟合实验数据,提出了适用于海洋核动力平台PRHR HX池沸腾换热系数计算式,为进一步研究海洋核动力平台非能动安全系统提供参考。
1 实验装置设计 1.1 实验装置实验装置主要由补水箱、补水泵、实验水箱、U型电加热器、蒸汽发生器、非能动余热排出换热器、测量仪器和采集系统等组成。测量仪表有K型热电偶、功率表、液位计、涡街流量计、质量流量计、压力变送器、压差传感器等,测量系统为NI采集系统。实验装置如图1所示。
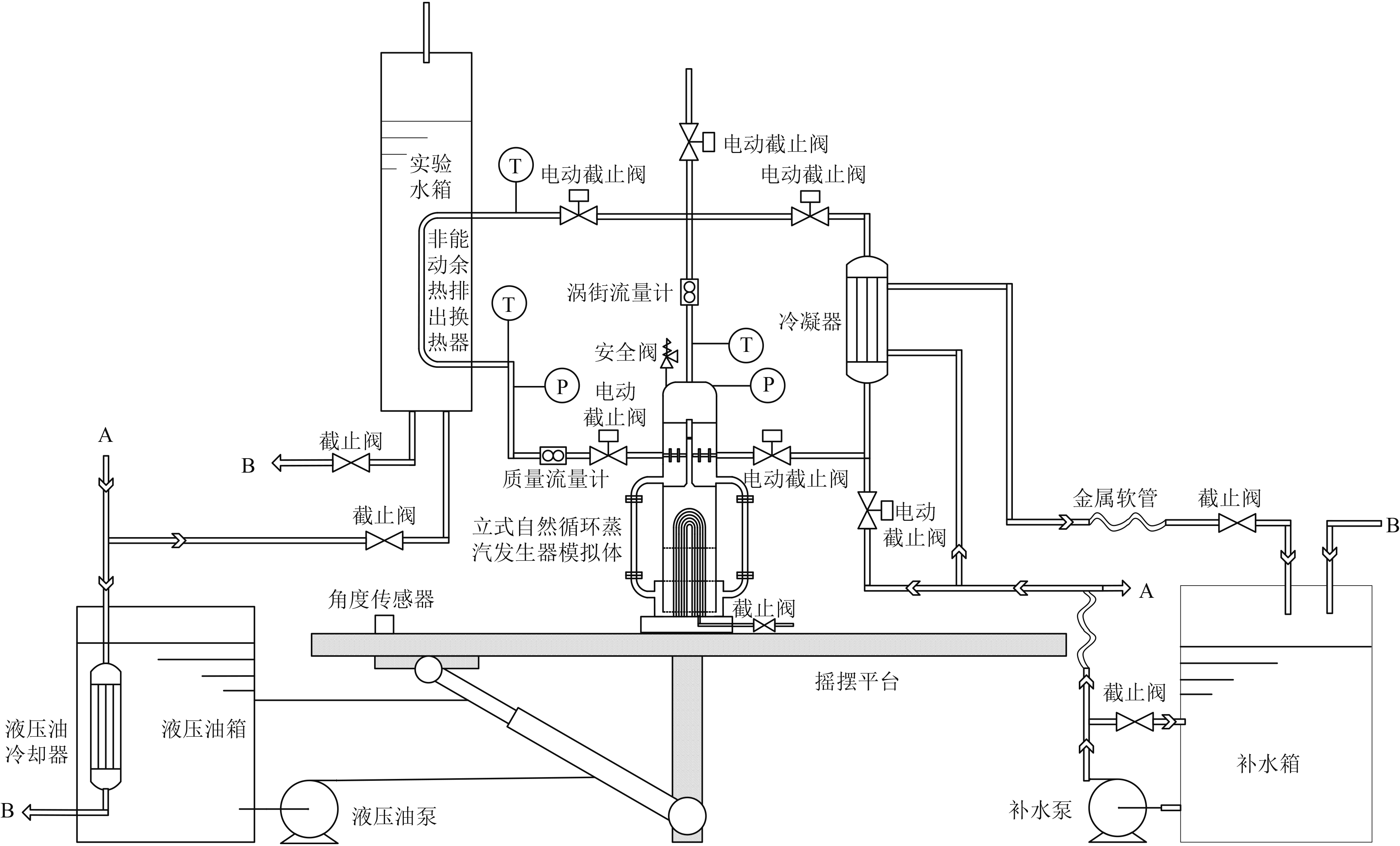
|
图 1 实验装置原理图 Fig. 1 Schematic diagram of experimental device |
PRHR HX的C型传热管采用经磨光并抛光的304不锈钢管,蒸汽发生器模拟立式自然循环蒸汽发生器,其功率由模化分析确定。第三代反应堆中PRHR HX放置在专设的水箱之中,由于海洋核动力平台和大型核动力舰船空间紧凑,故其PRHR HX放置在低压安注箱中,使用带有可视化窗口的实验水箱代替低压安注箱。实验水箱内装有常压下冷却水,其液位远高于PRHR HX上部管段。整个实验装置均使用硅酸铝保温棉包裹,以减少装置散热对实验结果的影响。
1.2 实验参数测量实验水箱冷却水测温点和PRHR HX外壁测温点布置如图2所示,通过2个铠装热电偶测量换热器入口处蒸汽温度和回水管段凝水温度。同时在蒸汽管路和回水管路布置涡街流量计和质量流量计测量蒸汽流量和凝水流量。实验装置主要参数如表1所示。

|
图 2 温度测点布置示意图 Fig. 2 Arrangement of temperature measurement points |
|
|
表 1 实验装置参数表 Tab.1 Experimental device parameter table |
完成实验装置排气后,具体流程如下:
步骤1 开启电加热器,隔离PRHR HX上下游阀门,控制回路温度上升速率小于2 ℃/min;
步骤2 向实验水箱注水至预定水位;
步骤3 当压力到达设定值后,调节电加热器功率至预定值,控制冷凝器7冷却水流量,使系统稳定运行30 min(模拟船上二回路运行);
步骤4 关闭冷凝器7上下游阀门(模拟隔离二回路侧),打开PRHR HX上下游阀门(模拟投运PRHR);
步骤5 当水箱8内冷却水达到饱和温度,且系统压力长时间稳定后,打开采集系统记录数据,完成后开始下个工况;
步骤6 调整电加热器功率,当系统压力到达下一个稳定压力后,记录数据,直至完成所有工况。
1.4 实验原理蒸汽发生器产生的饱和蒸汽进入非能动余热排出换热器,PRHR HX内纯蒸气被水箱中冷却水冷却冷凝为单相水,然后经PRHR HX管外池沸腾换热将电加热器产生的热量(模拟一回路输入能量)传递至热阱(即实验水箱)依靠PRHR冷、热段密度差形成的自然循环持续的排出热量。
1.5 实验数据处理当达到完全冷凝(即系统压力恒定)的状态下即可基于热平衡方程计算出换热量,进而确定平均热流密度。对于PRHR HX而言,热流密度变化只与系统压力有关,可以通过调节电加热器功率来分析不同压力下PRHR HX冷凝换热特性。实验压力范围在0.24~1.78 MPa,热负荷范围在59~340 kW/m2。
在本实验中,PRHR HX外壁面平均热流密度计算式为:
| $ q=\frac{M\left({h}_{{\rm{in}}}-{h}_{{\rm{out}}}\right)}{A}。$ |
式中:M为管内凝液的质量流量,kg/s;
换热管池沸腾换热系数计算式为:
| $ h=\frac{q}{{T}_{w}-{T}_{f}} 。$ |
式中:
不同热负荷下PRHR HX换热系数如图3所示。PRHR HX热负荷对其池沸腾换热系数有较大影响;PRHR HX热负荷范围在59~340 kW/m2时,其池沸腾换热系数范围在11.5~53.4 kW/(m2∙K)。当PRHR处于长期运行阶段时,堆芯余热逐渐降低,换热器热负荷降低,此时管外池沸腾换热系数将减小。
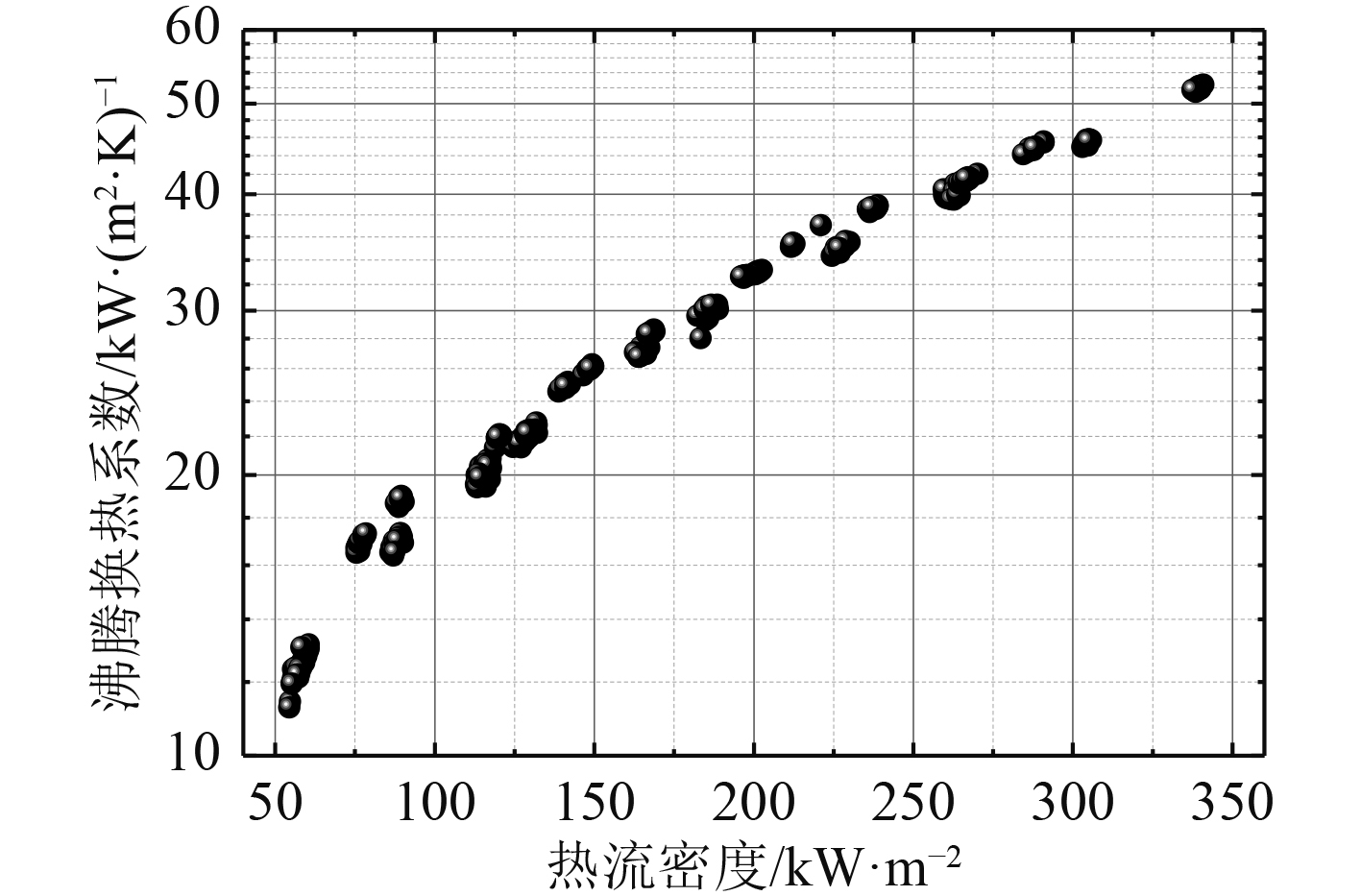
|
图 3 不同热流密度下池沸腾换热系数 Fig. 3 Pool boiling heat transfer coefficient of different heat flux |
由图4可知,PRHR HX沸腾产生的气泡在竖直管段外持续向上聚集,周期性冲刷换热器上部;PRHR HX各管段沸腾剧烈程度不同,说明换热器换热并不均匀;较低热流密度下,换热器上部气泡尺寸较小,气泡在壁面产生后迅速脱离,换热器下部气泡尺寸小于上部;较高热流密度下,PRHR HX整体发生剧烈的沸腾现象,换热器下部产生的气泡聚集成大气弹冲刷换热器竖直段,加大了换热器周围流体搅动。综合分析实验现象可知,热流密度越大,换热器池沸腾换热越均匀。

|
图 4 换热器池沸腾现象 Fig. 4 Photos of heat exchanger pool boiling phenomenon |
不同热负荷下PRHR HX管壁平均过热度如图5所示。PRHR HX平均壁面过热度随热负荷增大而逐渐增大,在本实验工况内,PRHR HX仍在核态沸腾区域;在热流密度59~340 kW/m2变化范围内,平均壁面过热度变化范围为4.4℃~6.6℃。

|
图 5 不同热流密度下管壁平均过热度 Fig. 5 Average superheat of the tube wall under different heat flux |
不同热负荷下PRHR HX管壁温度分布如图6所示。PRHR HX外壁温度沿管程总体呈上升趋势,换热器底部温度明显高于上部温度。由图4实验现场可知,换热器换热并不均匀,上部沸腾更剧烈,换热效果最好,所以换热器上部壁面温度较低,换热器下部与此相反。随着热负荷逐渐增大,换热器外壁面温度逐渐均匀,说明随热负荷增加,PRHR HX池沸腾换热不均匀程度会降低,而这与图4中实验现场观察到的结果一致。
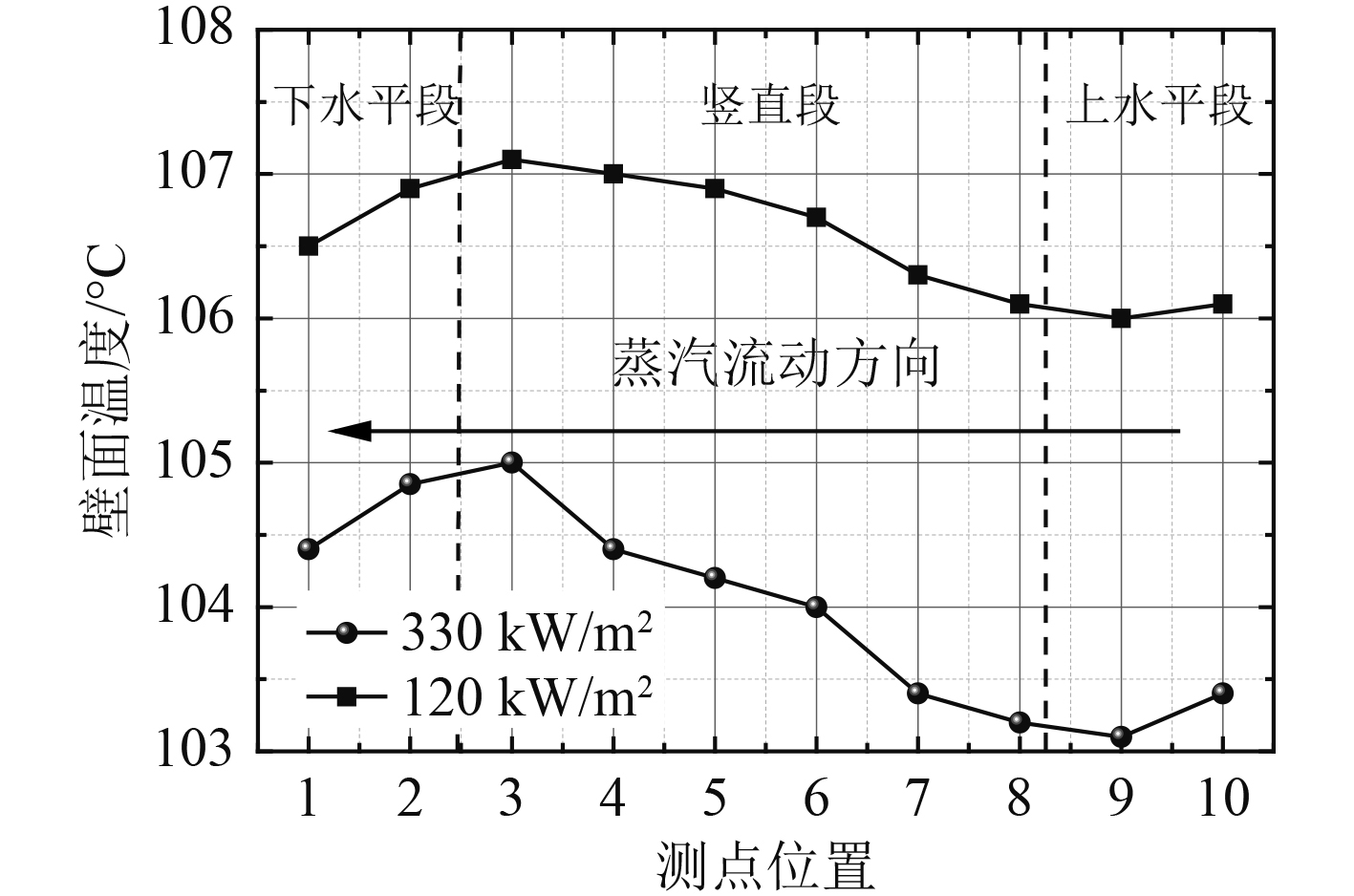
|
图 6 不同热流密度下管外壁温度 Fig. 6 Temperature of the tube wall under different heat flux |
目前常用的计算PRHR HX池沸腾换热系数的关系式有Rohsenow关系式[1],Jens-Lottes关系式[8-9],Kutateladze关系式[10]。将其与实验数据对比,结果如图7~图9所示。
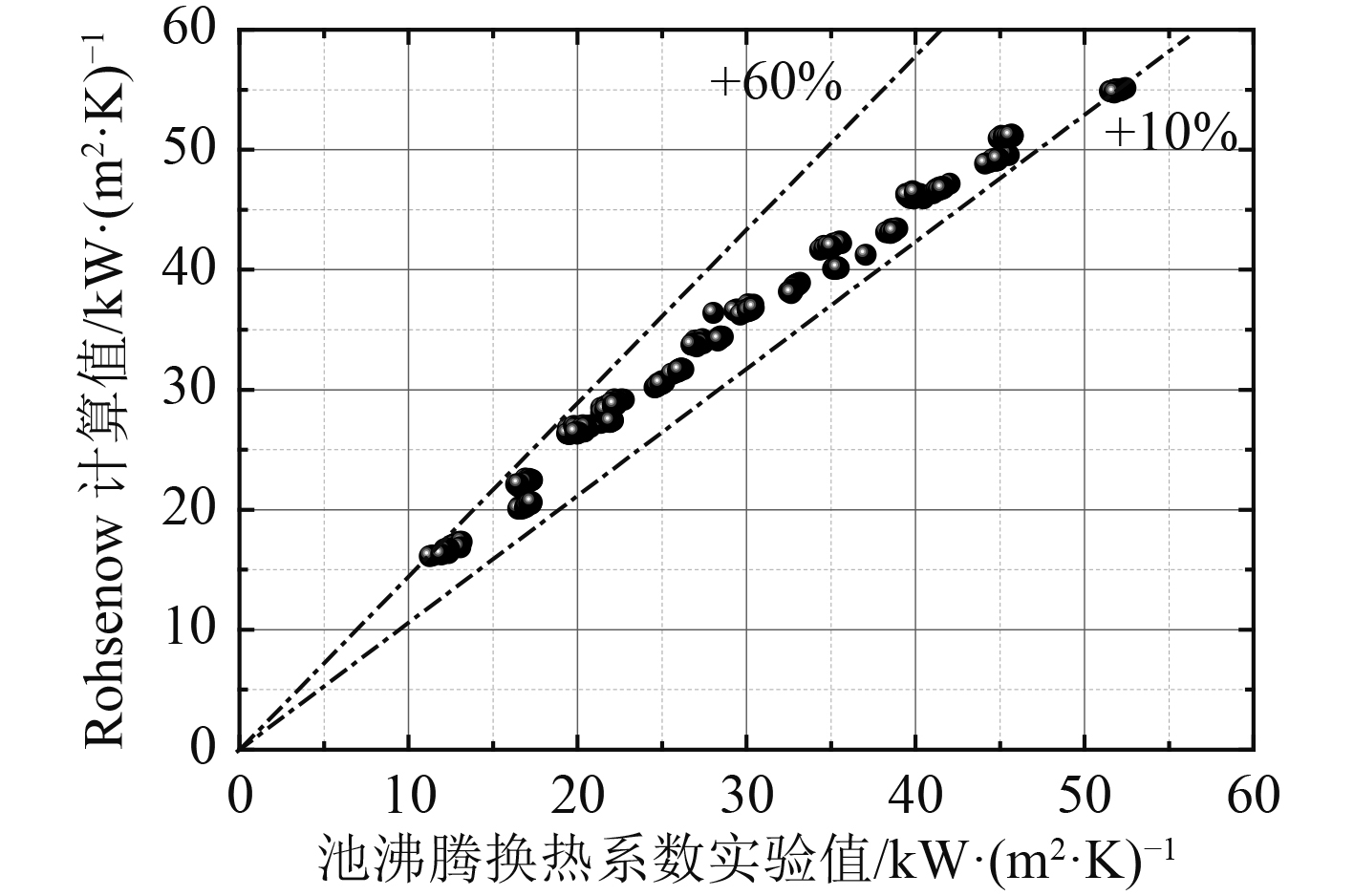
|
图 7 Rohsenow计算式与实验值对比 Fig. 7 Comparison of experimental results and predicted results using Rohsenow correlations |
|
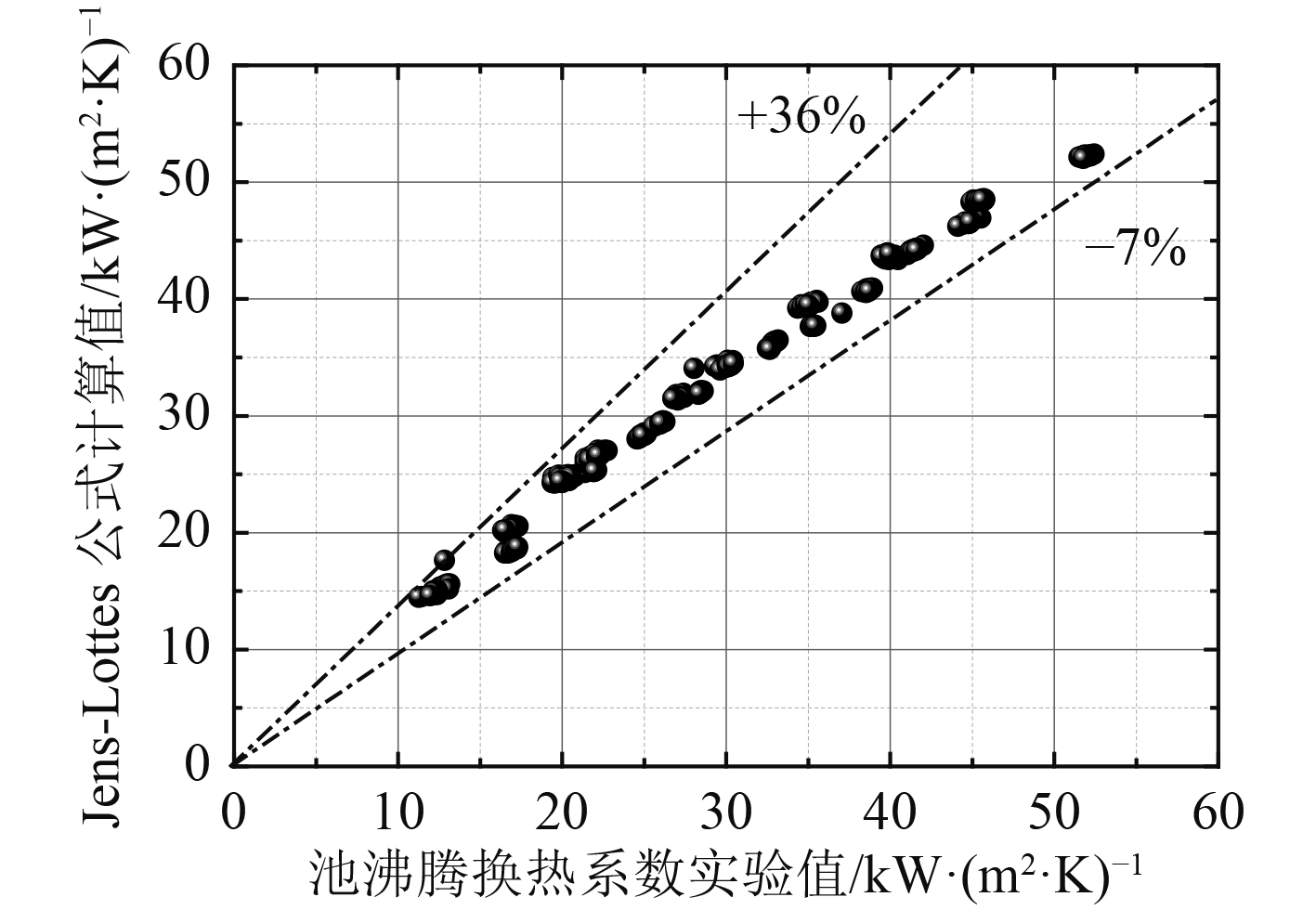
图 9 Jens-Lottes计算式与实验值对比 Fig. 9 Comparison of experimental results and predicted results using Jens-Lottes correlations |
由图7可知,低热负荷下,Rohsenow关系式计算值较实验值偏高约60%,随着热负荷升高,其与实验值相对误差减少,原因是Rohsenow关系式中的经验常数
|
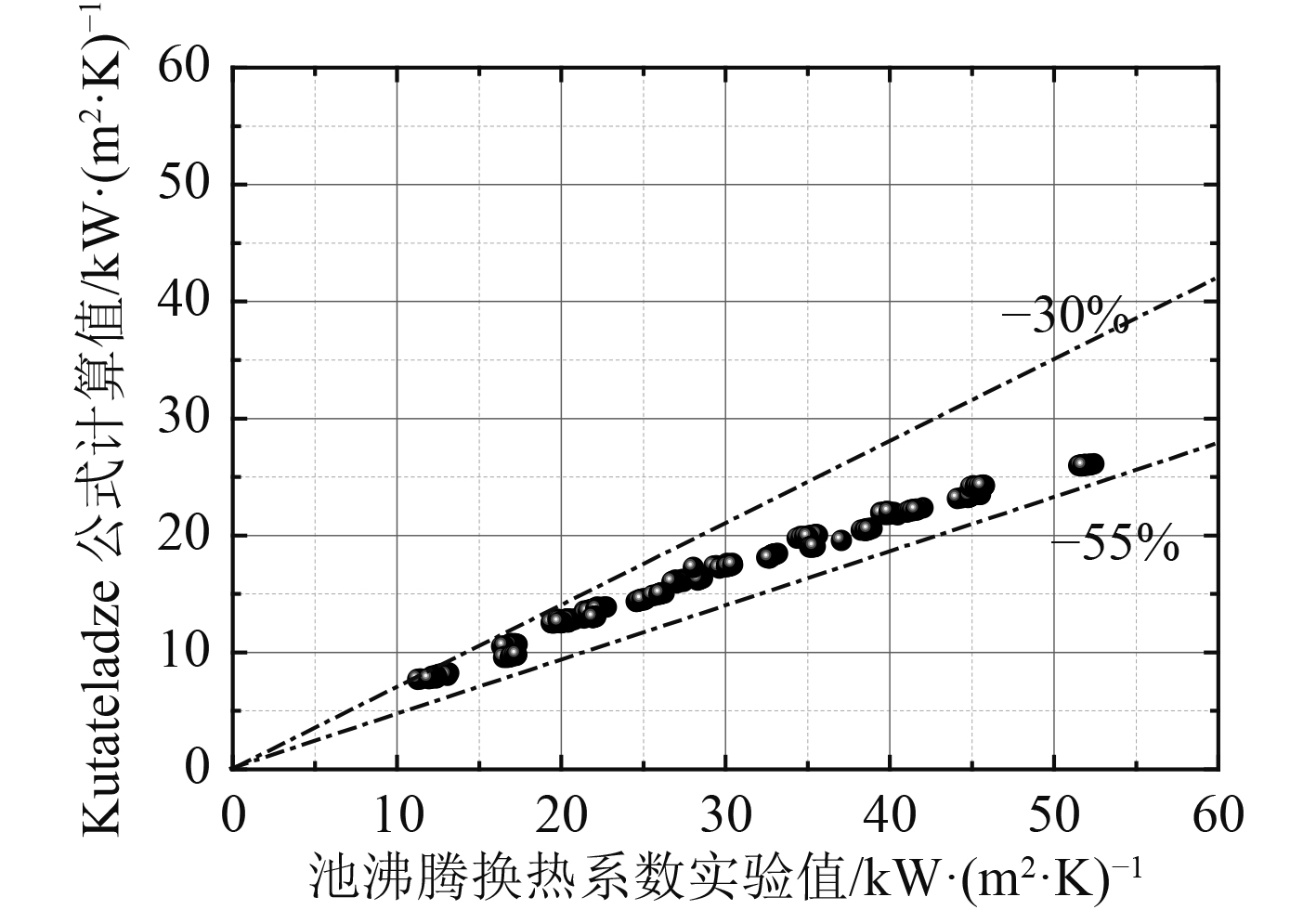
图 8 Kutateladze计算式与实验值对比 Fig. 8 Comparison of experimental results and predicted results using Kutateladze correlations |
Kutateladze关系式计算值较实验值偏低,原因是Kutateladze关系式没有考虑所使用流体种类和沸腾表面特性导致其误差偏大。
相较于前2个半经验关联式,Jens-Lottes关系式计算精度较高,相对误差在±30%以内。原因是Jens-Lottes公式是Yonomto在其PRHR HX池沸腾实验中[8-9],使用的用于计算非PRHR HX池沸腾传热系数的经验公式,这与换热器实验关联度非常高,但受限于管径、结构、材料和加工精度等原因,其计算值偏差仍然较大。同时需要注意的是其公式为实验数据拟合而来,属于纯经验关联式。
2.3 换热准则式提出池沸腾传热过程极为复杂,迄今尚不能像处理某些特定传热问题那样,根据传热机理及其数学模型得到严格的换热解析式,而主要采用半经验或纯经验的关系式。为了得到更高精度、具有一定推广意义的PRHR HX池沸腾换热系数计算模型,参考Rohsenow关系式方法,依据沸腾传热机理结合实验数据总结出非能动余热排出换热器沸腾传热计算的半经验关系式。
为了简化模型,提出与单相强迫对流相类似的池沸腾传热关系式[12]:
| $ {Nu}_{b}=f\left({Re}_{b},{Pr}_{f}\right)。$ |
式中:
Rohsenow等认为气泡逃离壁面的运动是关键的传热因素,原因是气泡搅动换热壁面附近过热液膜,提高了其对流传热效果,定义气泡运动的雷诺数为:
| $ {Re}_{b}=\frac{{G}_{b}{D}_{b}}{{\mu }_{f}}。$ |
式中:
定义气泡的脱离频率为f,则单位传热面逃离气泡的质量流速为:
| $ {G}_{b}=\frac{\text{π} }{6}{{D}_{b}}^{3}{\rho }_{g}fn。$ |
式中:n为换热器壁面汽化核心数,与热流密度相关。
换热器外壁面热流密度通过能量守恒方程可以表示为:
| $ {q}_{b}={h}_{fg}\frac{\text{π} }{6}{{D}_{b}}^{3}{\rho }_{g}fn。$ |
式中:
故池沸腾时气泡努赛尔数和普朗特数可以表示为:
| $ {Nu}_{b}=\frac{{q}_{b}{D}_{b}}{\left({T}_{wo}-{T}_{s}\right){k}_{f}}, $ |
| $ {Pr}_{f}=\frac{{C}_{pf}{\mu }_{f}}{{k}_{f}}。$ |
式中:
气泡的直径采用Fritz经验关系式确定,具体推导可见文献[12]:
| $ {D}_{b}={C}_{d}\beta {\left(\frac{2\sigma }{g\left({\rho }_{f}-{\rho }_{g}\right)}\right)}^{0.5}。$ |
式中:
可以得出:
| $ \frac{{Re}_{b}{Pr}_{f}}{{Nu}_{b}}=\frac{{C}_{pf}\Delta t}{{h}_{fg}}, $ |
| $ {Nu}_{b}=C{{Re}_{b}}^{n}{{Pr}_{f}}^{m}。$ |
根据实验研究结果将上式代入到初始经验关系式中,可得:
| $ \begin{split}\frac{{Re}_{b}{Pr}_{f}}{{Nu}_{b}}=& \frac{{Re}_{b}{Pr}_{f}}{f\left({Re}_{b},{Pr}_{f}\right)}=\frac{{Re}_{b}{Pr}_{f}}{C{{Re}_{b}}^{n}{{Pr}_{f}}^{m}}=\\& C{{Re}_{b}}^{n}{{Pr}_{f}}^{m}=\frac{{C}_{pf}\Delta t}{{h}_{fg}} ,\end{split} $ |
最后可得实验拟合的关系式:
| $ \frac{{C}_{pf}\Delta t}{{h}_{fg}}=C{\left[\frac{q}{{\mu }_{f}{h}_{fg}}\sqrt{\frac{\sigma }{g\left({\rho }_{l}-{\rho }_{v}\right)}}\right]}^{n}{\left(\frac{{c}_{pf}{\mu }_{f}}{{k}_{f}}\right)}^{m} 。$ |
经过非线性最小二乘法拟合多组实验数据,确定系数C和幂指数n和m,最后得到适用于非能动余热排出换热器池沸腾换热系数计算关系式为:
| $ \frac{{C}_{pf}\Delta t}{{h}_{fg}}=0.010\;9{\left[\frac{q}{{\mu }_{f}{h}_{fg}}\sqrt{\frac{\sigma }{g\left({\rho }_{l}-{\rho }_{v}\right)}}\right]}^{0.211}{\left(\frac{{c}_{pf}{\mu }_{f}}{{k}_{f}}\right)}^{1}。$ |
新公式的适用范围:热流密度范围是59~340 kW/m2;管径D=0.019 m。
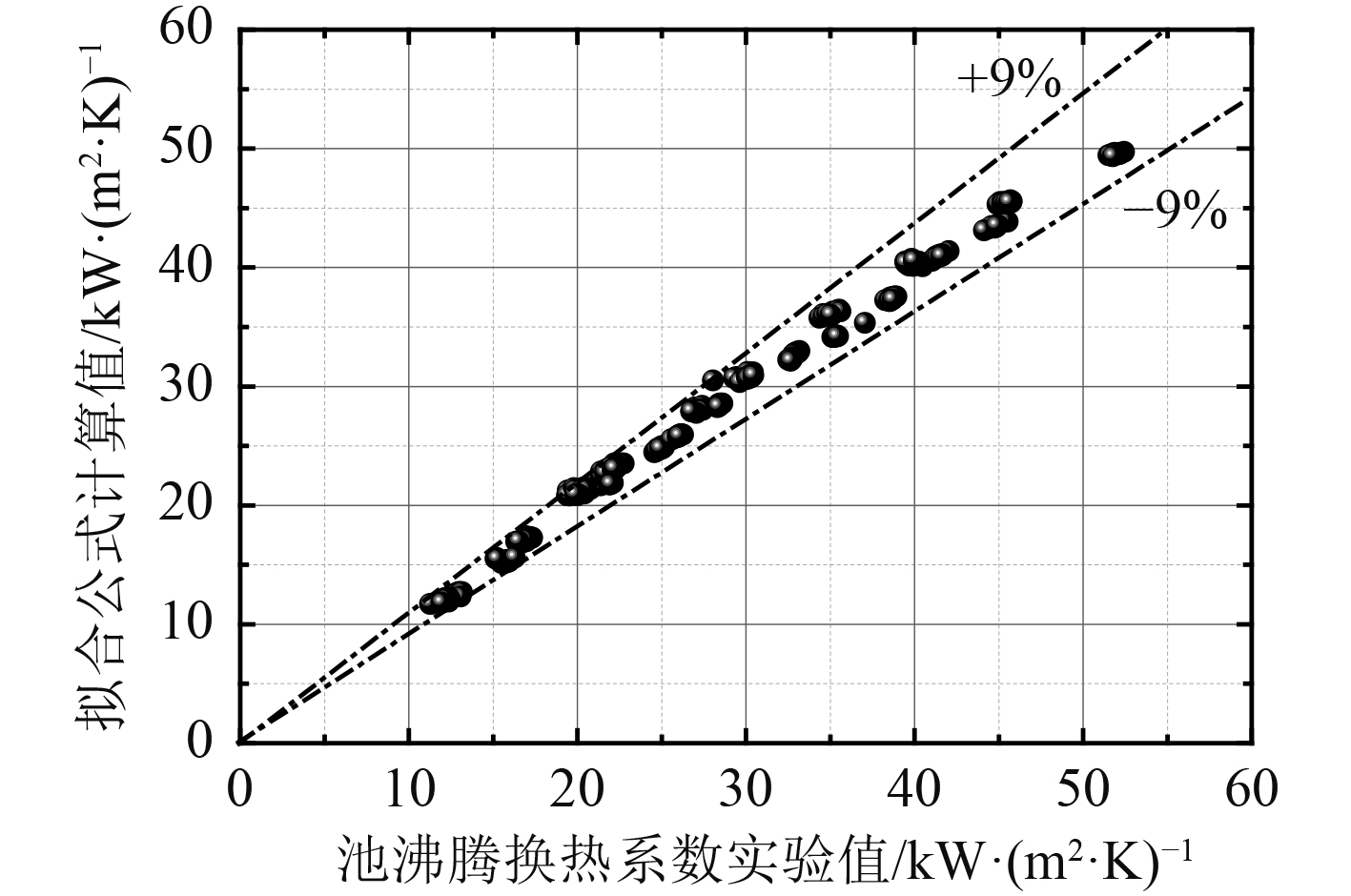
如图10所示,将纯蒸汽冷凝换热系数的实验值与新公式的计算值对比,两者偏差在±9%以内,可见二者符合良好。
|
图 10 本文提出的换热准则式与实验数据对比 Fig. 10 Comparison of experimental results and predicted results using new correlations |
针对海洋核动力平台PRHR HX池沸腾换热特性,通过实验得到如下结论:
1)PRHR HX池沸腾换热不均匀,其下部池沸腾强度弱于上部,热负荷越大,换热器池沸腾换热越均匀;
2)PRHR HX外壁温度沿管程总体呈上升趋势,换热器底部温度明显高于上部温度;
3)参考Rohsenow关系式方法,依据沸腾传热机理结合实验数据,提出了非能动余热排出换热器沸腾传热计算的半经验关系式,计算精度在±9%以内。
| [1] |
孙中宁, 范广铭, 王建军. 反应堆热工水力学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2017.
|
| [2] |
李佳佳, 刘峰, 赵芳. 国外海上浮动核电站的产业发展现状[J]. 船舶工程, 2017, 39(4): 7−11.
|
| [3] |
程坤, 谭思超. 海洋条件下反应堆热工水力特性研究进展 [J]. 哈尔滨工程大学学报, 2019, 40(4): 655−662.
|
| [4] |
ZHANG Yuhao, Lu Daogang, Du Zheng, et al. Numerical and experimental investigation on the transient heat transfer characteristics of C-shape rod bundles used in Passive Residual Heat Remove Heat Exchangers[J]. Annals of Nuclear Energy, 2015, 83: 147-160. DOI:10.1016/j.anucene.2015.04.022 |
| [5] |
王开元, 曹夏昕, 李亚. 非能动余热排出换热器池沸腾换热性能研究[J]. 原子能科学技术, 2014, 48(12): 2263-2268. DOI:10.7538/yzk.2014.48.12.2263 |
| [6] |
李亚, 曹夏昕, 王开元. RELAP5/MOD3.2竖直管束外大容积沸腾换热模型适用性分析[J]. 原子能科学技术, 2014, 48(12): 2269-2273. LI Ya, WANG Kai-yuan, CAO Xia-xin. Validation of RELAP5/MOD3.2 code for simulating pool boiling heat transfer outside vertical tube bundle[J]. Atomic Energy Science and Technology, 2014, 48(12): 2269-2273. DOI:10.7538/yzk.2014.48.12.2269 |
| [7] |
GUPTA A, KUMAR R, UMAR, V. Nucleate pool boiling heat transfer over a bundle of vertical tubes[J]. International Communications in Heat and Mass Transfer, 2010, 37(2): 178-181. DOI:10.1016/j.icheatmasstransfer.2009.06.023 |
| [8] |
YONOMOTO T, KONDO M, KUKITA Y, et al. Core makeup tank behavior observed during ROSA-AP600 experiments[J]. Nuclear Technology, 1997, 119(2): 112-122. DOI:10.13182/NT97-A35380 |
| [9] |
YONOMOTO T, KUKITA Y, Schultz R. Heat transfer analysis of the passive residual heat removal system in ROSA/AP600 experiments[J]. Nuclear Technology, 1998, 124(1): 18-30. DOI:10.13182/NT98-A2906 |
| [10] |
KUTATELADZE S S. Heat transfer and hydeodynamic resistance: handbook[M]. Moscow: Energoatomizdat Publishing Hose, 1990.
|
| [11] |
MIKIC B B, ROHSENOW W M. A new correlation of pool-boiling data including the effect of heating surface charccteristics[J]. Journal of Heat Transfer, 1969, 91(2): 245-250. DOI:10.1115/1.3580136 |
| [12] |
朱光昱. 气泡微细化沸腾现象可视化实验研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
 2001, Vol. 44
2001, Vol. 44
