对水下航行体而言,冷却水在浮升过程中,会有部分热水上升到海面上,在海面上形成一定的热尾迹,不利于水下航行体隐藏踪迹,增加暴露的风险;同样滨海地区的火/核电站为释放废热,需将大量的冷却水释放到附近海域,产生热污染问题,以上都存在排放附近海域水温升高的现象,均涉及到静止状态下热射流的浮升扩散问题。
在热射流的研究方面,国内外学者已经做出了大量研究,Yasuhiro[1]通过实验发现射流速度和温度轨迹主要由动量比决定;Guo[2]将射流的密度差、速度和倾角作为影响射流扩散的主要因素,找出了射流稀释的最佳方案;槐文信等[3]建立了横流中单圆孔紊动射流的数学模型,对不同流速比的流动进行了仿真计算,得到了该类流动的特性;张健[4]在进行水平热射流的相关研究中,探究了流速比和不同射流出口温度对热射流的影响;戴天奇[5]则对比研究了环境流速和排放口角度对热射流的影响。Bemporad[6]进行了稳定分层环境中浮力圆形射流的数值模拟,探究了环境速度和环境分层对热射流特性的综合影响;Chen[7]考虑了相对水深、波高与水深之比和浮力对射流扩散的影响,在所考虑的条件下,波高与水深之比是射流扩散过程中最重要的因素。
在静止环境中的浮力射流相关研究中,槐文信[8]通过仿真计算对静止分层环境中浮力射流全场进行了预报;曾玉红等[9]对静止环境中有限水深的水平圆形浮力射流进行了数值模拟,研究证明了基于RNG方法的k-ε模型建立的数学模型的有效性;杨中华[10]基于RNG方法的k-ε湍流模型,建立了静止环境中圆形负浮力射流的数学计算模型,仿真计算结果与试验资料吻合良好;袁丽蓉[11]针对静止浅水环境中垂向射流的水面会有明显突起的情况,建立了相关的二维数学模型,对不同入射速度、水深、入射口宽度组合进行了数值模拟实验,发现自由面的分布特点和速度场的分布特点相对应。尽管以往在热射流方面已经有了大量研究,但是在单体热射流水团的浮升扩散方面,目前还没有研究涉及。单体热射流水团本文定义为具有一定初始动量的圆形脉冲射流,可将其具象化为水下航行体在一瞬间排出的冷却水,或是所排出的冷却水中取其部分作为研究对象,研究对比初始动量的大小、方向与背景水域的温差等影响因素对单体热射流水团浮升扩散的影响,得到了热射流水团在几种影响因素下的温度分布规律及其运动轨迹,可以作为水下热射流相关研究的补充。
1 数学模型及计算方法假设在无限大水域中,根据流体运动的基本控制方程和数值传热学的理论,采用SSTk-omega湍流模型,建立流动环境中的二维数学模型如下:
连续性方程为
| $ \frac{{\partial p}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}} \right)}}{{\left( {\partial {x_i}} \right)}} = 0 。$ | (1) |
动量方程(N-S)方程为
| $\begin{split} \rho \frac{{\partial {u_i}}}{{\partial t}} +& \rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial p}}{{\partial {x_i}}} - \left( {{\rho _0} - \rho } \right){g_i} =\\ &\frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {u_j}}} + \frac{{\partial {u_j}}}{{\partial {u_i}}}} \right)} \right] - \frac{2}{3}\frac{\partial }{{\partial {x_i}}}\left( {\mu \frac{{\partial {u_j}}}{{\partial {x_j}}}} \right) \end{split}。$ | (2) |
式中:ρ0为环境流体密度。
能量方程为
| $ \rho {c_p}\frac{{\partial T}}{{\partial t}} + \rho {c_p}{u_j}\frac{{\partial T}}{{\partial {x_j}}} = {u_j}\frac{{\partial p}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_j}}}\left( {\lambda \frac{{\partial T}}{{\partial {x_j}}}} \right) 。$ | (3) |
式中:
湍动能方程为
| $ \rho \frac{{{\rm{D}}k}}{{{\rm{D}}t}} + \rho \frac{{\partial \left( {k{u_i}} \right)}}{{\partial {x_f}}} = \frac{\partial }{{\partial {x_f}}}\left( {{T_k}\frac{{\partial k}}{{\partial {x_f}}}} \right) + {G_k} - {Y_k}。$ | (4) |
比耗散率方程为
| $ \rho \frac{{{\rm{D}}\omega }}{{{\rm{D}}t}} + \rho \frac{{\partial \left( {\omega {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_f}}}\left( {{T_\omega }\frac{{\partial \omega }}{{\partial {x_f}}}} \right) + {G_\omega } - {T_\omega } + {D_\omega }。$ | (5) |
式中:
利用Fluent软件,采用Simple算法,考虑重力影响,重力加速度为9.81 m/s2。将计算域水体的密度和温度拟合成多项式,实现密度随温度的变化而变化。计算过程中对各项残差进行监控,当能量残差小于10−6,其余项小于10−4且流场分布合理,认为计算收敛。
2 网格及边界条件计算域为长20 m高10 m的矩形,单体热射流水团半径为0.3 m圆形热水团。热水团的圆心位于平面的中心,距离底面2 m的位置。整个计算域采用结构网格划分,经过独立性检验,网格量达到50万后,继续增加网格密度,计算结果变化不明显,最终网格数量为49.5万。计算域边界条件底部设置为对称边界,顶部为压力出口,两侧为壁面边界。
计算过程中,将背景水域温度初始化为T1=290 K,并设置了以下4种工况见表1,速度方向以X正方向为0°,顺时针为正。
|
|
表 1 计算工况参数 Tab.1 Calculate working condition parameters |
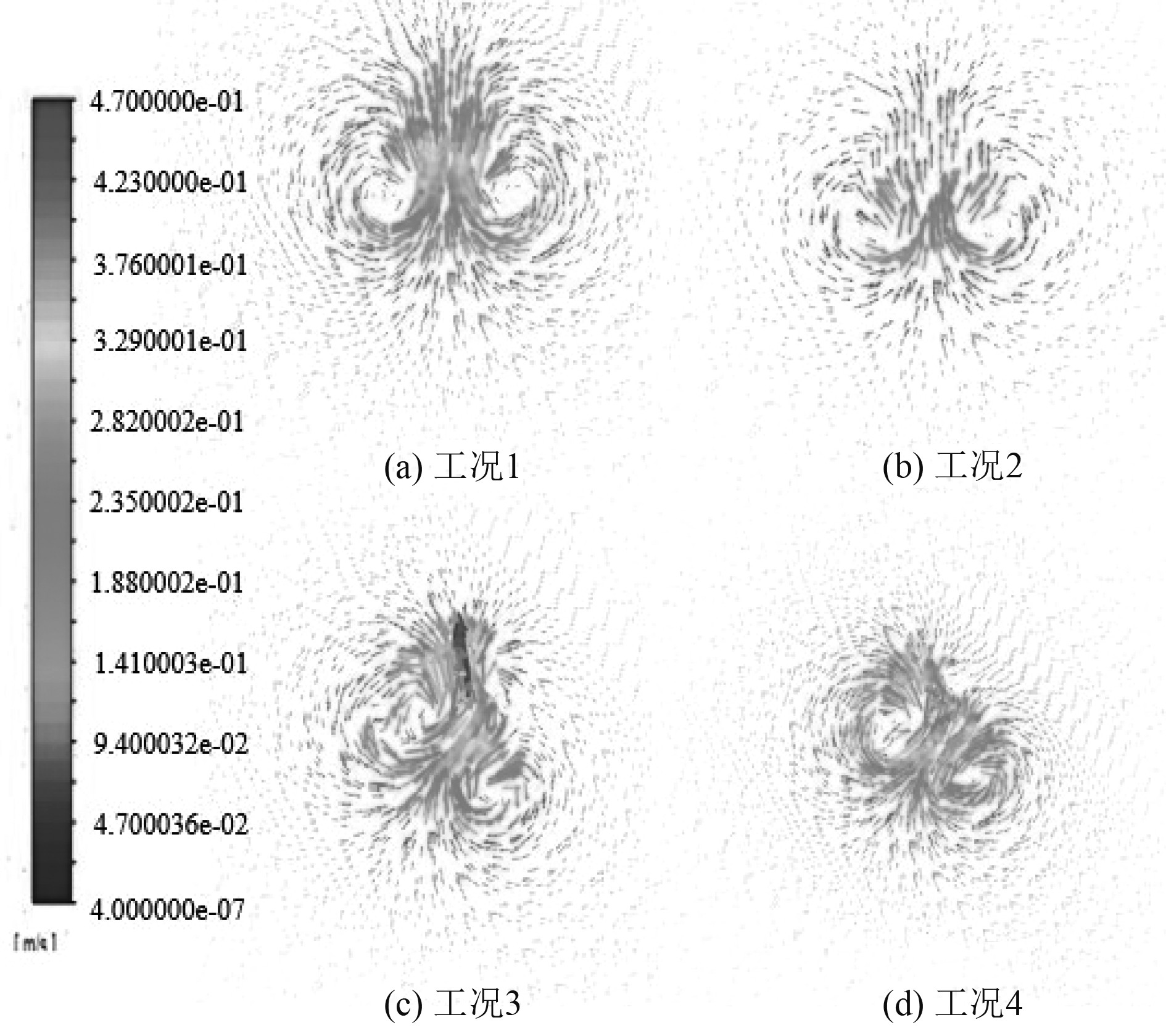
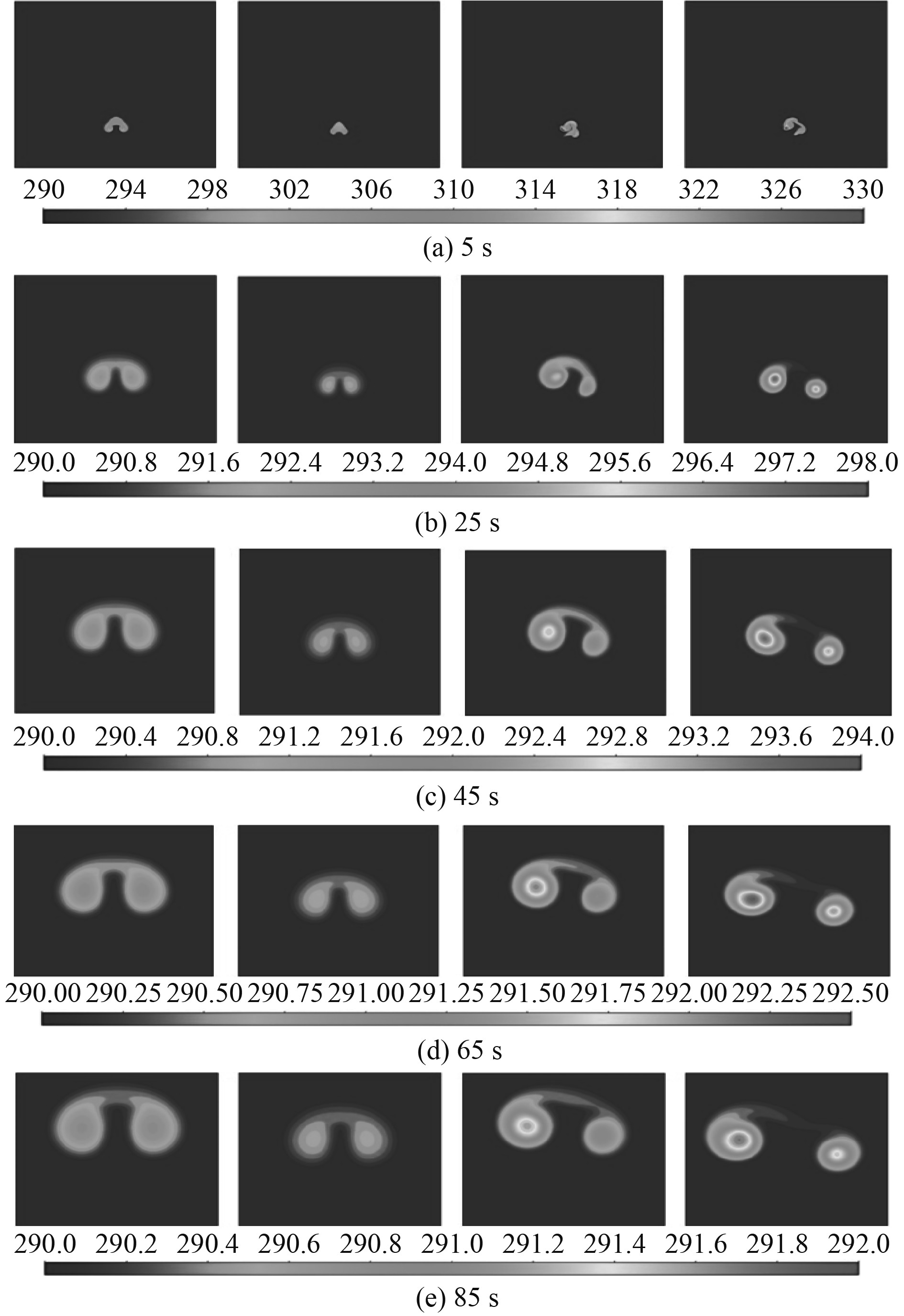
进行仿真模拟计算,5 s时的速度矢量图如图1 所示,从第5 s开始每隔20 s取工况1~工况4前90 s的温度云图如图2所示,从左至右依次为4种工况。
|
图 1 5 s时的速度矢量图 Fig. 1 Velocity vector diagram at 5 seconds |
|
图 2 前85 s的温度云图 Fig. 2 Temperature cloud image of the first 85 seconds |
从图1和图2可以看出,在浮升过程中,工况1和工况2均产生了一对对称的旋转涡对,进行了一次旋转后,不再有明显的旋转,大致呈直线浮升;工况3和工况4受到初始动量的影响,产生了一对不对称的旋转涡对,且在较长的一段时间内始终保持着旋转的趋势,增加了其在X方向上的扩散距离。另外,工况3和工况4相对于工况1和工况3在X方向的扩散范围更大,但是温度分布并不均匀,这是由于在浮升扩散初期,工况3和工况4在初始动量的影响下,分成了不对称的两部分,且由于其自身的旋转,进一步阻碍了旋转涡对中心与背景水域的换热,导致工况3和工况4旋转涡对中心温度偏高。
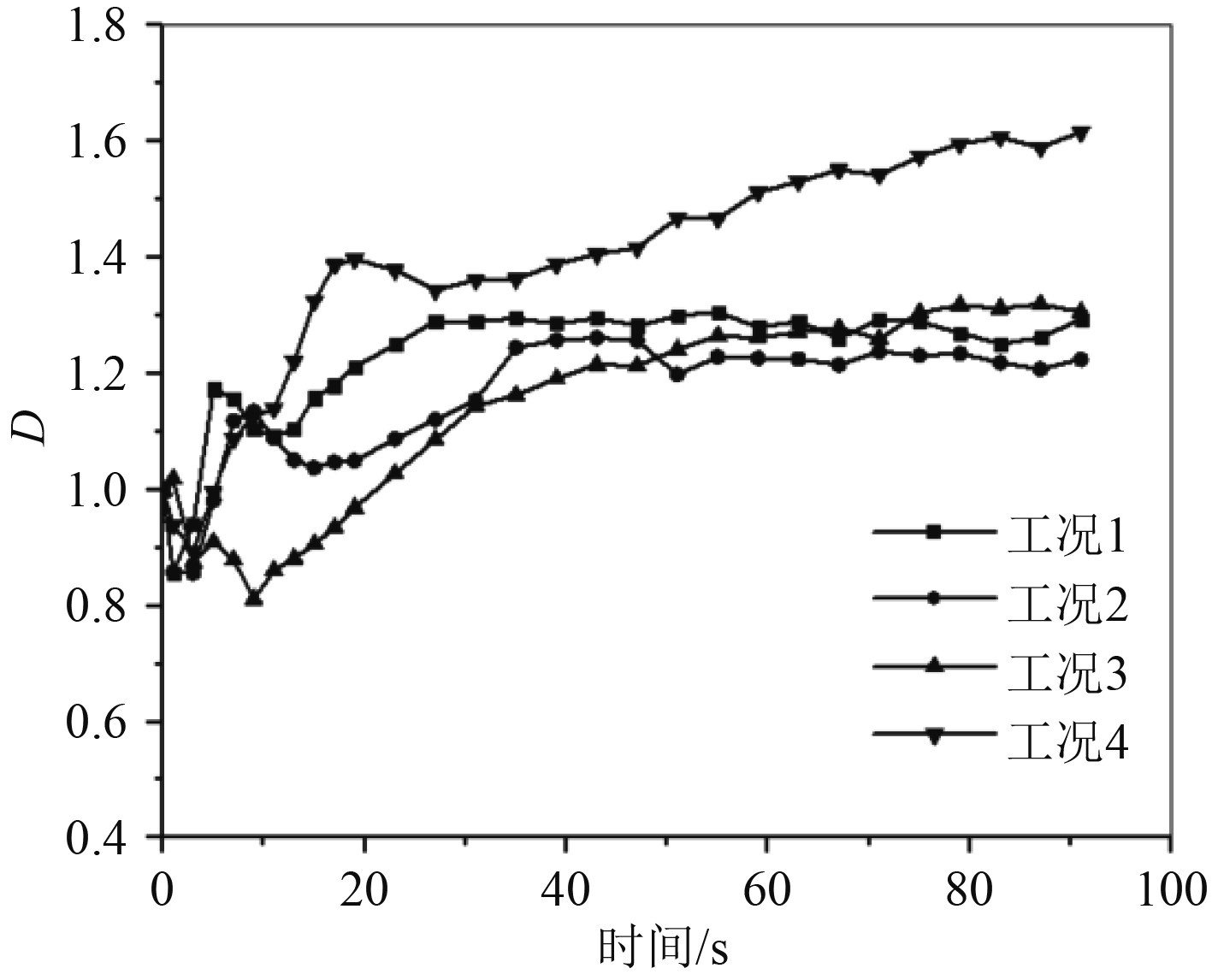
3.2 横向与纵向的浮升扩散对比定义D=X/Y用于表征单体热射流在X方向和Y方向上的扩散距离的比值,D值大于1说明其在X方向上扩散的距离大于Y方向上扩散的距离。为提高数据的准确性,取290.002−290.001 K的边界作为X和Y方向上扩散距离的具体数值,4种工况的D值变化规律如图3所示。
|
图 3 4种工况D值变化曲线 Fig. 3 Variation curve of D value under four working conditions |
可以看出,4种工况在浮升扩散初期,D均小于1,这说明此时Y方向上的浮升扩散距离要大于X方向的扩散距离,这是由于在初始阶段,单体热射流与背景水域的温差最大,热射流在Y方向上的浮升比较明显,因而Y方向上的扩散距离更大。工况3的D值在前20 s内始终小于1,是由于工况3在Y负方向上存在初始动量,40 s后D值和工况1相差不大。工况4的D值在4种工况中最大。究其原因,主要是其具有X正方向上的初始动量,形成了一对保持较长旋转趋势的不对称旋转涡对,拉长了其X方向上的扩散距离。另外,从工况1和工况2的D值上可以看出,温差对X和Y方向上扩散距离的影响并不明显。
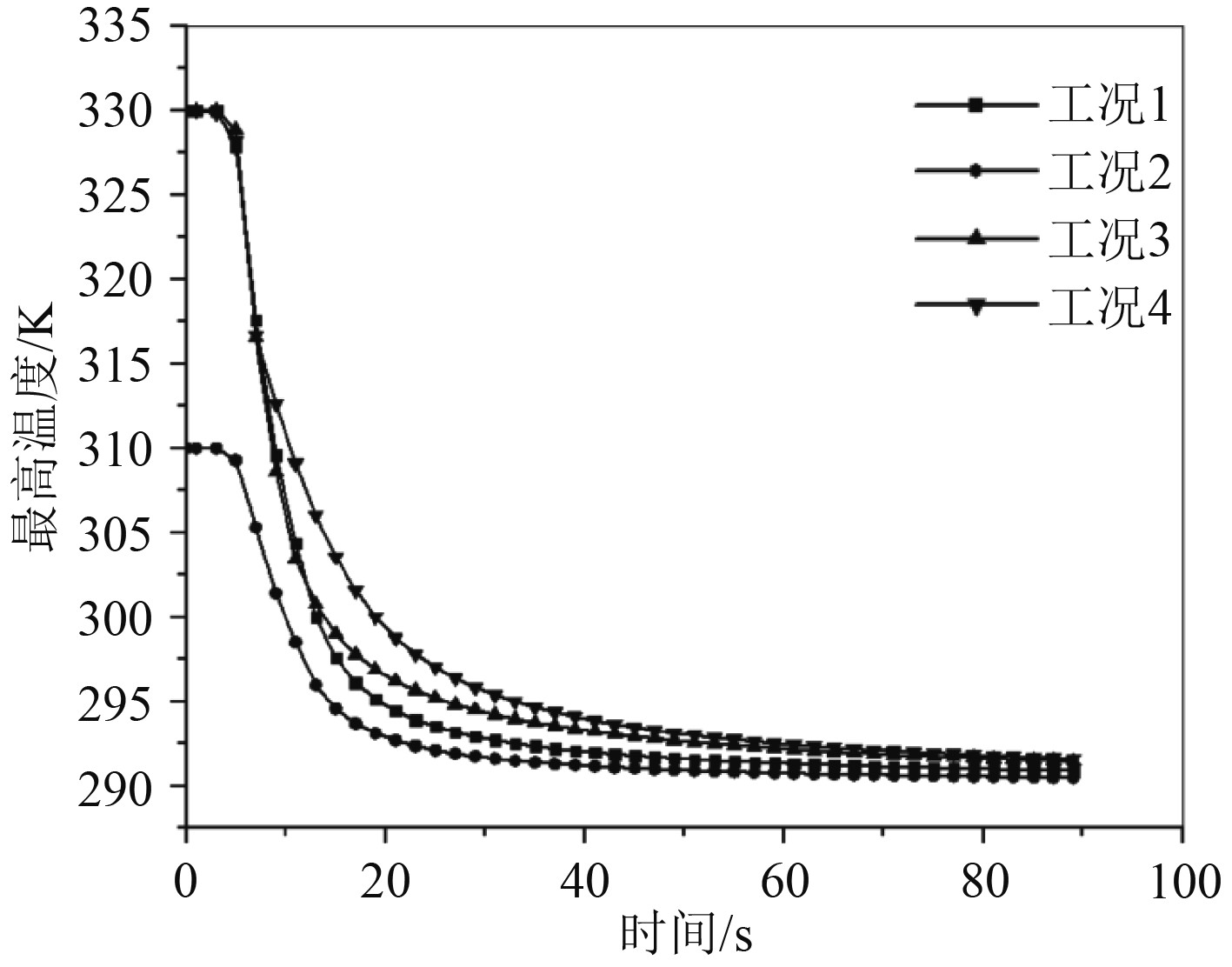
3.3 浮升速度及温度变化规律4种工况在前90 s内的的最大速度、最高温度及Y方向浮升距离变化如图4~图6所示。
|
图 4 最高温度变化曲线 Fig. 4 Maximum temperature curve |
|
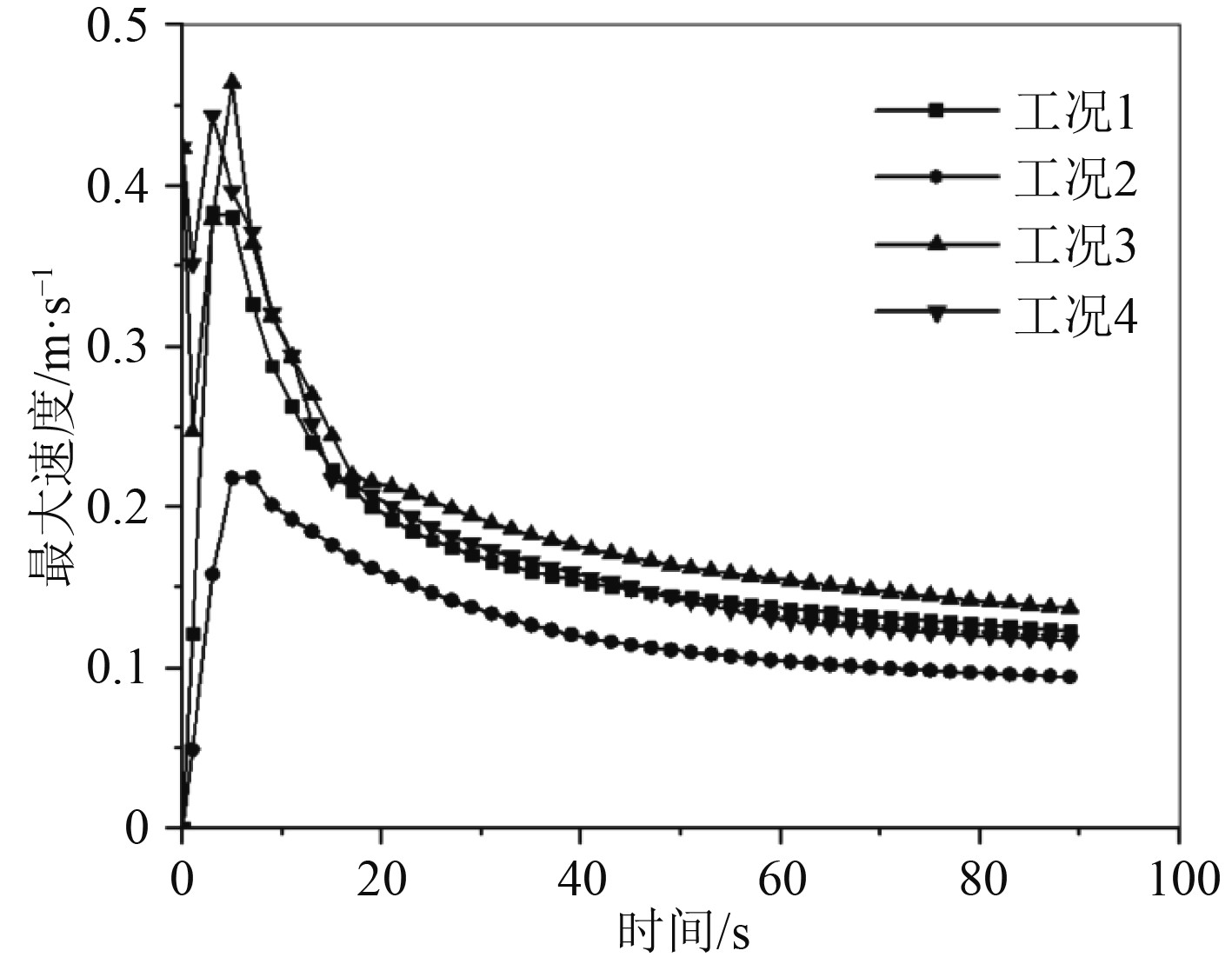
图 5 最大速度变化曲线 Fig. 5 Maximum speed curve |
|
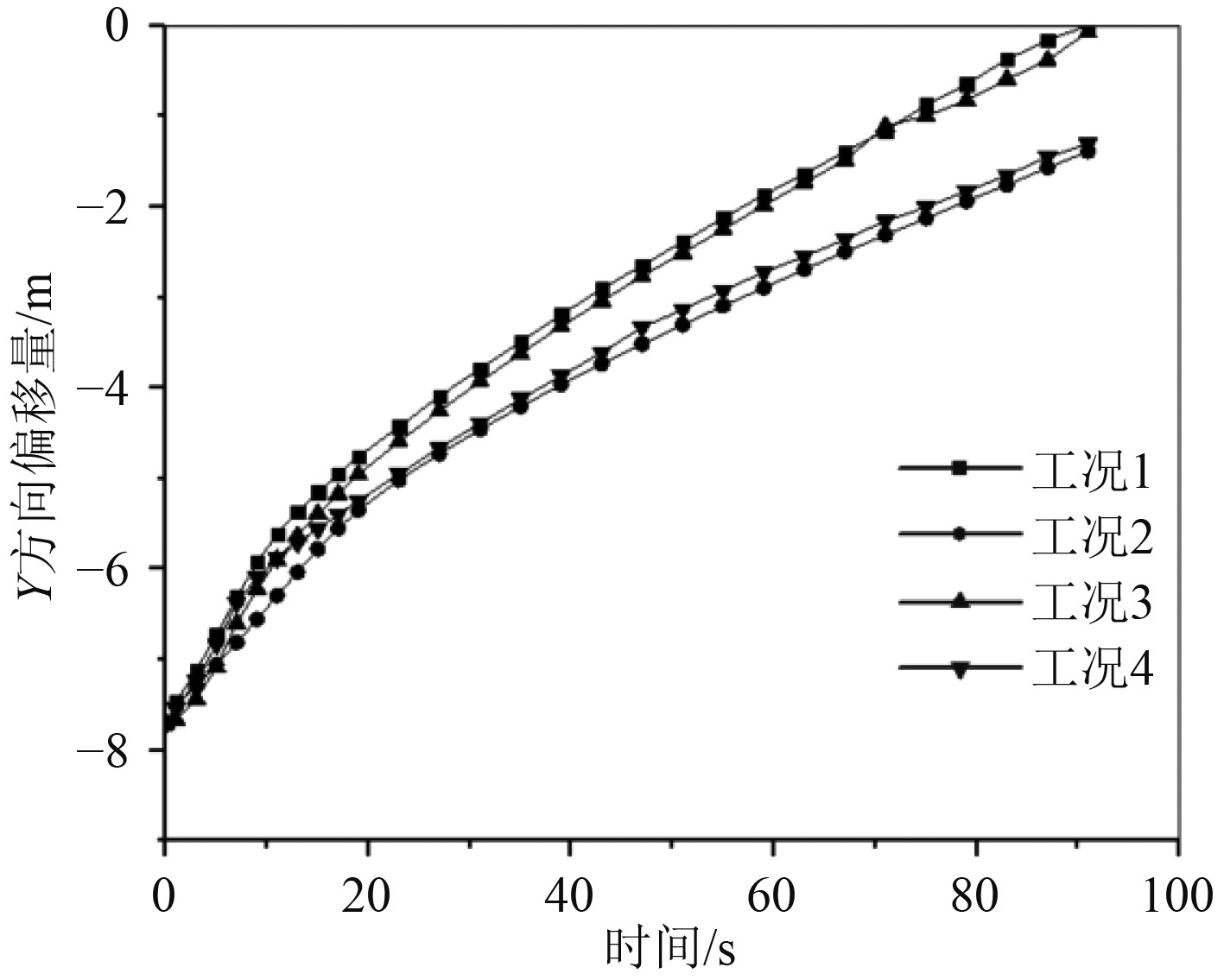
图 6 Y方向偏移变化曲线 Fig. 6 Y-direction offset curve |
由图4可以看出,就最高温度衰减情况而言,在10~50 s的时间段,工况1、工况3、工况4区别较大,无初速度的工况1温度衰减更快,工况4衰减的最慢,且工况4的最高温度在整个浮升过程中都始终高于另外3种工况。另外,由图6可以看出,工况1到达顶面时间最短,工况3仅次于工况1,工况2和工况4时间最长。4种工况大致在6 s时达到最大浮升速度,这其中工况3的最大,可达0.46 m/s,且有初始动量的工况3和工况4均出现了速度先减小再增大再逐渐减小的过程。
对于上述现象,主要是工况4在初始阶段分成了一大一小不对称的两部分,大的部分温度高,且自身在进行一定的旋转,导致整体而言掺混散热不均匀,在90 s时最高温度仍高于其他另外工况,但其产生的不对称旋转涡对也令其在Y方向上的浮升减慢,降低了其浮升速度;工况3的表现介于工况1和工况4之间,是其在X正方向和Y负方向上的初始动量共同作用的结果,降低了达到顶面时的最高温度及时间,但是相比于工况1改变不大;工况2相比工况1有更小的温差,这使其浮升更慢,到达顶面的温度更低,可见适当降低温差可以有效降低水面的红外特征。
4 结 语对单体热射流水团的浮升扩散规律进行仿真模拟计算,探究了单体热射流的速度大小、方向及温差对其浮升扩散规律的影响,主要结论如下:
1)单体热射流水团在浮升过程中会产生旋转涡对,不同的是无初始动量的热水团产生一对对称的旋转涡对,而具有初始动量的热水团则产生一对不对称的旋转涡对,且旋转将会持续较长的时间。
2)具有水平初始动量的单体热射流水团因其产生的旋转涡对使其在X方向的扩散更强,但也因此,其各个时刻的最高温度始终略高于其他工况。
3)温差对静止状态下射流的浮升扩散有一定影响,适当降低温差能降低热射流的浮升速率,延迟热射流浮升到水面的时间,增强水下热射流与背景水域的掺混换热。
| [1] |
YASUHIRO K, ISAAC G. Experiments on a turbulent Jet in a Cross Flow[J]. AIAA Journal, 1972. 10(11): 1425-1425.
|
| [2] |
GUO Y. Experimental and numerical study of submerged inclined buoyant jet discharges into stagnant saline ambient water[D]. University of Ottawa, 2020.
|
| [3] |
槐文信, 李炜, 彭文启. 横流中单圆孔紊动射流计算与特性分析[J]. 水利学报, 1998(4): 7-14. DOI:10.3321/j.issn:0559-9350.1998.04.002 |
| [4] |
张健, 杨立, 张士成, 等. 流动环境中圆孔水平热射流三维数值模拟[J]. 水科学进展, 2011, 22(5): 668-673. |
| [5] |
戴天奇, 姚世伟, 李永全, 等. 横流环境中冷却水排放浮升规律[J]. 舰船科学技术, 2015, 37(4): 112-116. DAI Tian-qi, YAO Shi-wei, LI Yong-quan, et al. Study of buoyant rule of cooling waterdischarged in cross flow[J]. Ship Science and Technology, 2005, 37(4): 112-116. |
| [6] |
BEMPORAD A G. Simulation of round buoyant jet in stratified flowing environment[J]. Journal of Hydraulic Engineering, 1994. 120(5): 529-543.
|
| [7] |
Chen Y L, HSIAO S C, Numerical modeling of a buoyant round jet under regular waves[J]. Ocean Engineering, 2018. 161: 154−167.
|
| [8] |
槐文信, 李炜. 静止分层环境中圆形浮力射流全场特性的数值模拟[J]. 水动力学研究与进展, 1993(12): 595−600.
|
| [9] |
曾玉红, 槐文信. 静止环境中水平圆形浮力射流流动特性研究[J]. 华中科技大学学报(自然科学版), 2005, 33(11): 90-92. |
| [10] |
杨中华, 槐文信, 等. 采用RNG紊流模型计算静止环境中圆形负浮力射流[J]. 水科学进展, 2004, 15(6): 760-764. DOI:10.3321/j.issn:1001-6791.2004.06.013 |
| [11] |
袁丽蓉, 沈永明, 郑永红. 用VOF方法模拟静止浅水环境中的垂向紊动射流[J]. 水科学进展, 2004(5): 566-570. DOI:10.3321/j.issn:1001-6791.2004.05.005 |
 2001, Vol. 44
2001, Vol. 44
