当船舶在航行过程中处于轻载甚至空载的时候,船舶携带压载水可以提高自身的操作性、增强抵御风浪的能力,最大化地提升船舶螺旋桨的工作效率,同时船舶通过控制压载水在船舱中的分布,来动态调整船舶的航行姿态以控制船舶稳定航行,降低船舶弯矩以及剪力,最大化地确保船体安全,因此船舶的压载水对船舶的安全航行起到了十分重要的作用,但是船舶的压载水带来的生态环境的影响也很大。船舶的压载水中存在很多船舶起点地的微生物以及海洋动植物,这些生物被船舶的压载水带到目的地之后,由于在目的地没有天敌,因此这些动植物的数量会急速增长,严重威胁到当地其他动植物的生存空间,有些外来物种可能会携带一些病原体,这会严重威胁当地居民的健康安全。目前全球很多国家都面临船舶压载水所带来的生物入侵问题,在我国社会经济的飞速发展的过程中,海运起到了十分重要的作用,我国也面临着压载水对环境的威胁,通过船舶的压载水是我国生物入侵的主要方式之一,例如我国沿海的赤潮。为了解决船舶压载水给社会经济、人类健康带来的影响,可以通过立法、提升压载水处理技术、改善船舶设计等方面来综合治理,其中无压载水船舶由于可以从根本上消除压载水带来的环境问题从而成为研究热点。本文基于3D打印技术,研究无压载水船体型线设计系统,对船舶技术的发展起积极的推动作用。
1 3D打印技术 1.1 3D打印方法设计3D打印是一种通过逐层递加选择性材料,然后按照物体的CAD三维模型直接对实体物质进行制造的技术,在打印过程中,先从物体的CAD 模型中提取设计信息,接着利用切片技术将物体的信息切割成含有零件信息的切片,同时将这些切片信息转换成3D打印机能够识别的文件格式,最后一层一层地打印,最终完成单个零件的打印。3D打印的能力包括形状自由、零件合并、零件分割、无装配机构、填充控制、拓扑优化等。具备3D打印能力之后,则需要与之相匹配的3D打印设计方法,只有同时具备了合适的设计方法,工程师才能设计出合格的产品。本文的3D设计借助公理化设计方法,根据船舶的结构特性以及需求,基于当前3D打印的生产能力,提出一种适合无压载水船舶生成制造的3D打印设计方法。
用户、功能、物理、工艺是公理化设计方法的4个域。用来表示需求特征的是用户域;用来表示零件功能特征的是功能域;用来表示功能要求以及几何特征的是物理域;用来表示生产工艺的是工艺域。信息和独立性是公理化设计的两大公理,公理化设计的独立性公理是指在各个功能之间的设计需要保持独立性,即其中一个功能模块的功能需要调整时,不会影响到其他模块;公理化设计的信息公理要求在满足功能需求以及设计约束的所有方案中,信息量最少的方案是最优的设计方案。公理化的设计过程是将产品的需求、结构参数以及工艺参数联系在一起的过程,即将产品的设计流程切分成4个域的映射过程,映射过程如图1所示。

|
图 1 公理化设计过程 Fig. 1 Axiomatic design process |
从图1可以看出,根据功能要求将用户域的产品需求映射到功能域的产品功能,接着根据结构参数将功能域的产品功能映射至物理域的产品几何结构,然后根据工艺参数将物理域的几何结构映射至工艺域的生产工艺。由于公理化设计容易受到传统工业制造能力的限制,因此物理域中的一些结构无法实现,即某些零件无法通过传统工业技术生产,虽然间接地通过其他结构实现,但是不是最优的设计,同时在公理化设计方法中功能域到物理域之间的映射过程,在很大程度上是基于设计人员的经验,通过不断地尝试,最终找到满足要求的结构。但是3D打印是基于增材制造原理的,可以不受制造环境的限制,按照需求直接加工处理成各种几何结构,因此3D打印的设计方法可以灵活多样。
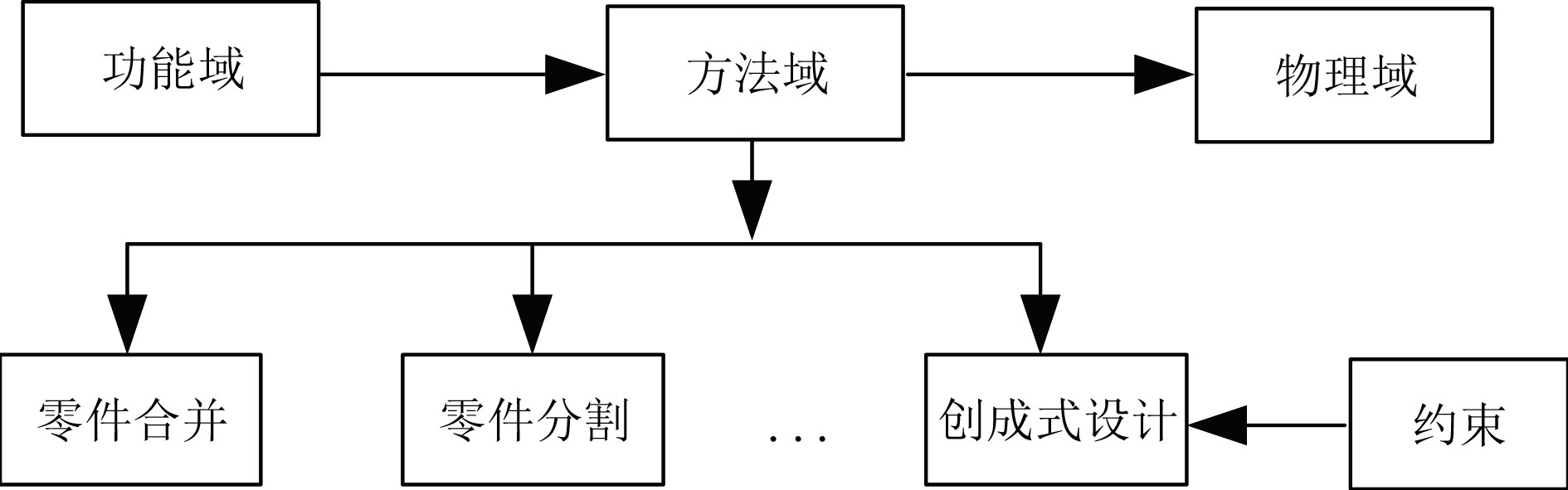
本文提出的无压载水船舶3D打印设计方法以公理化设计方法为基础,结合船舶设计需求,增加了方法域这一概念,该方法域是3D打印设计所支持方法的统称,如图2所示。
|
图 2 3D打印设计过程 Fig. 2 3D printing design process |
可以看出,船舶设计工程师按照这种3D打印设计方法进行3D打印设计的时候,首先通过功能域映射至方法域中,接着对所打印的物体的功能以及特点进行分析,并找到合适的零件设计方法,如零件分割等,最后再从方法域中映射至物理域中。本文设计的3D打印的设计方法虽然和公理化设计在流程上有所区别,但是该设计方法的流程依旧是根据域和域之间的映射关系逐一进行的,并且也是以产品的功能需求为基础,利用结构设计来实现,也需要遵循信息和独立性这两大公理,本文提出的3D打印的设计方法是对公理化设计方法的补充。
1.2 3D打印设计约束及目标3D打印技术的增材制造原理和传统制造业的减材制造原理不同,因此3D打印技术可以不受传统制造技术的瓶颈限制,能够对各种复杂结构进行加工处理,所以传统制造业的设计约束无法完全用于3D打印技术,但是这并不是说3D打印可以脱离设计约束而随便打印,相反的是3D打印由于成型质量因素多,例如材料种类、设备类型、成型技术等,因此3D打印技术存在特有的设计约束方案。
按照本文提出的船舶3D打印设计进行3D设计打印过程中需要遵循3D打印约束,有精度约束、尺寸约束、支撑约束、残余应力约束、后处理约束、打印路径约束、壁厚约束以及尺寸公差约束等,其中船舶3D打印设计成型的精度影响因素比较多。
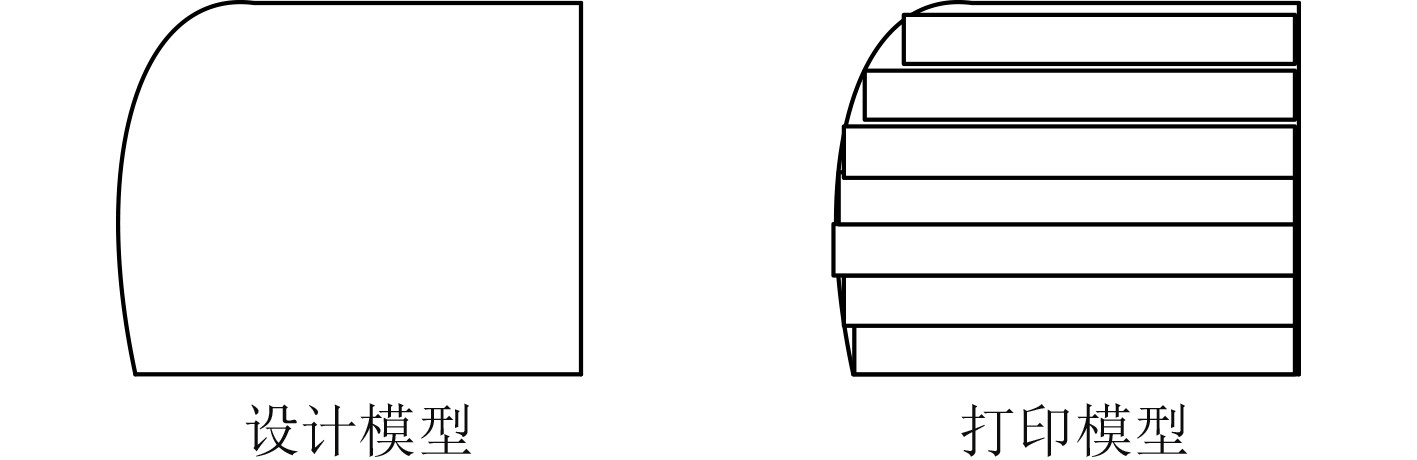
一方面3D打印的成型机理导致3D打印成型过程中必定会产生一定的偏差,如图3所示。从图3可以看出,船舶3D打印的过程就是将3维的物体拆分成多个2维的物体进行加工的过程,接着将所有的2维零件逐一叠加成一个完整的3维零件,因此在船舶3D打印过程中必定会由于台阶现象而导致相应的误差。
|
图 3 3D打印成型模型 Fig. 3 3D printing molding model |
在3D打印设计加工过程中,待打印的物体模型用T来表示,假设物体T被分割成n层,并且任意第i层的实物模型用Xi来表示(
| $ T \approx \sum\limits_{i = 1}^n {{X_i}} \text{。} $ | (1) |
当单层物体的厚度无限接近于0的时候,即n向∞不断接近的时候,实物的成型模型就会和设计模型完全一样,但是在3D打印实际加工生成过程中,单层的厚度不可能无限接近于0,这就导致3D打印出来的实物模型一定会出现失真现象,因此只能使用尽可能降低厚度的方式来降低误差。
另一方面,船舶3D打印出来的模型精度也和打印设备以及打印参数有关,不同的3D打印设备的打印精度不一样,此外打印设备的打印速度、温度、路径等参数对最终成型的模型精度也存在一定的影响。
2 船体型线设计 2.1 非均匀有理B样条曲线船舶外形设计和其他机械模型设计一样,会遇到由二次曲线弧以及二次曲面表示的结构。例如船身截面曲线通常由圆、椭圆以及抛物线等二次曲线和直线共同构成,这些曲线结构在设计上都可以十分精确地给出,但是在加工处理上需要极高的精度。B样条曲线只能用来表示抛物线构成的曲面,无法对二次曲线构成的曲面进行处理,因此需要扩展B样条曲线描述二次曲线以及二次曲面的功能,这种扩展方式就是有理B样条曲线,由于在实际生产中,遇到的大多数曲线或者曲面都是非均匀,因此又被叫做非均匀有理B样条曲线。有理分式、其次坐标、有理基函数是非均匀有理B样条曲线3种表示方式。
K次非均匀有理B样条曲线的有理分式如下式:
| $ p\left( u \right) = \frac{{\displaystyle\sum\limits_{i = 0}^n {{\omega _i}{d_i}{N_{i,k}}\left( u \right)} }}{{\displaystyle\sum\limits_{i = 0}^n {{\omega _i}{N_{i,k}}\left( u \right)} }}\text{。} $ | (2) |
式中:ωi(i=
式(2)所表示NURBS曲线方程可以换成式(3)和式(4)的等价形式。
| $ P\left( u \right) = \sum\limits_{i = 0}^n {{d_i}{R_{i,k}}\left( u \right)} \text{,} $ | (3) |
| $ {R_{i,k}}\left( u \right) = \frac{{{\omega _i}{N_{i,k}}\left( u \right)}}{{\displaystyle\sum\limits_{i = 0}^n {{\omega _j}{N_{i,k}}\left( u \right)} }}\text{。} $ | (4) |
式中:Ri,k(u)为K次有理基函数,该函数的特性在于分母不为0的时候在区间内无限可微。如果所有的权重系数ωi=1(
| $ {R_{i,k}}\left( u \right) = \frac{{{B_{i,k}}\left( u \right),\left( {u = [0,\cdots,1,\cdots,1]} \right)}}{{{N_{i,k}}\left( u \right),{\rm{others}}}}\text{。} $ | (5) |
非均匀有理B样条曲线可以将自由曲线和二次曲线进行统一描述,因此非均匀有理B样条曲线设计技术被广泛地用于船舶曲面设计中。
2.2 船体数学型线设计方法船体的数学型线设计是指根据需要设计的船舶的尺寸以及相关系数,使用数学的方法构造出船舶的曲面。船体型线的数学设计方法主要有曲线方法和曲面方法2种,曲线方法一般存在横剖线和水线2种方程。
当x为一恒定值的时候,则y-z平面相当于船舶横剖面,因此船舶横剖线方程可以用式(6)来表示,利用横剖线的不同参数,则可以得到不同的横剖线方程,根据这些横剖线方程最终可以得到船体的曲面。
| $ y = f\left( z \right)\text{。} $ | (6) |
当z为一恒定值时,y-x平面相当于船舶的水线面,则船舶的水线方程可以用式(7)来表示,通过每条水线各自的水线参数,则可以获得不同的水线方程,最终可以得到船体曲面。
| $ y = f\left( x \right)\text{。} $ | (7) |
通过不同的曲面方程求解船体曲面的方法称为曲面方法,曲面方法是将船体曲面看成是由多个曲面片构成的,接着再次按照位置的先后顺序将所有的曲面片再连接起来,然后获得船体线型。船舶的曲面方法是通过不同参数曲面的拼接得到最终的船舶曲面。
本文主要使用纵向函数法进行无压载水船体曲面的设计。纵向函数法首先得到船舶的横剖线方程,然后根据船舶的横剖线参数,得到船舶的船体曲面,因此对纵向函数的求解就是对船舶横剖面面积曲线、剖面轮廓线、龙骨半宽以及设计水线半宽的求解,最后生成横剖线方程。横剖面面积曲线可以由下式求解:
| $ \omega = {T^2}\int_0^1 {v{\rm{d}}u} \text{,} $ | (8) |
| $ v = {a_{\frac{1}{m}}}{u^{\frac{1}{m}}} + \sum\limits_{i = 0}^n {{a_i}{u^i}} \text{。} $ | (9) |
设计水线半宽求解如下式:
| $ y\left( x \right) = \left( {B - {B_f}} \right)\left( {1 - {{\bar x}^n}} \right){e^{ - {{\bar x}^m}}} + {B_f}\text{,} $ | (10) |
剖面轮廓线由轮廓线以及龙骨线共同构成,表达式如下式:
| $ {z_s}\left( x \right) = x{\rm{tg}}{\alpha _3}\text{,} $ | (11) |
式中α3为原始倾角。
龙骨半宽由直线以及抛物线共同构成,公式如下:
| $ y\left( x \right) = {B_k} + \left( {{y_k} - {B_k}} \right){\bar x^n}\text{。} $ | (12) |
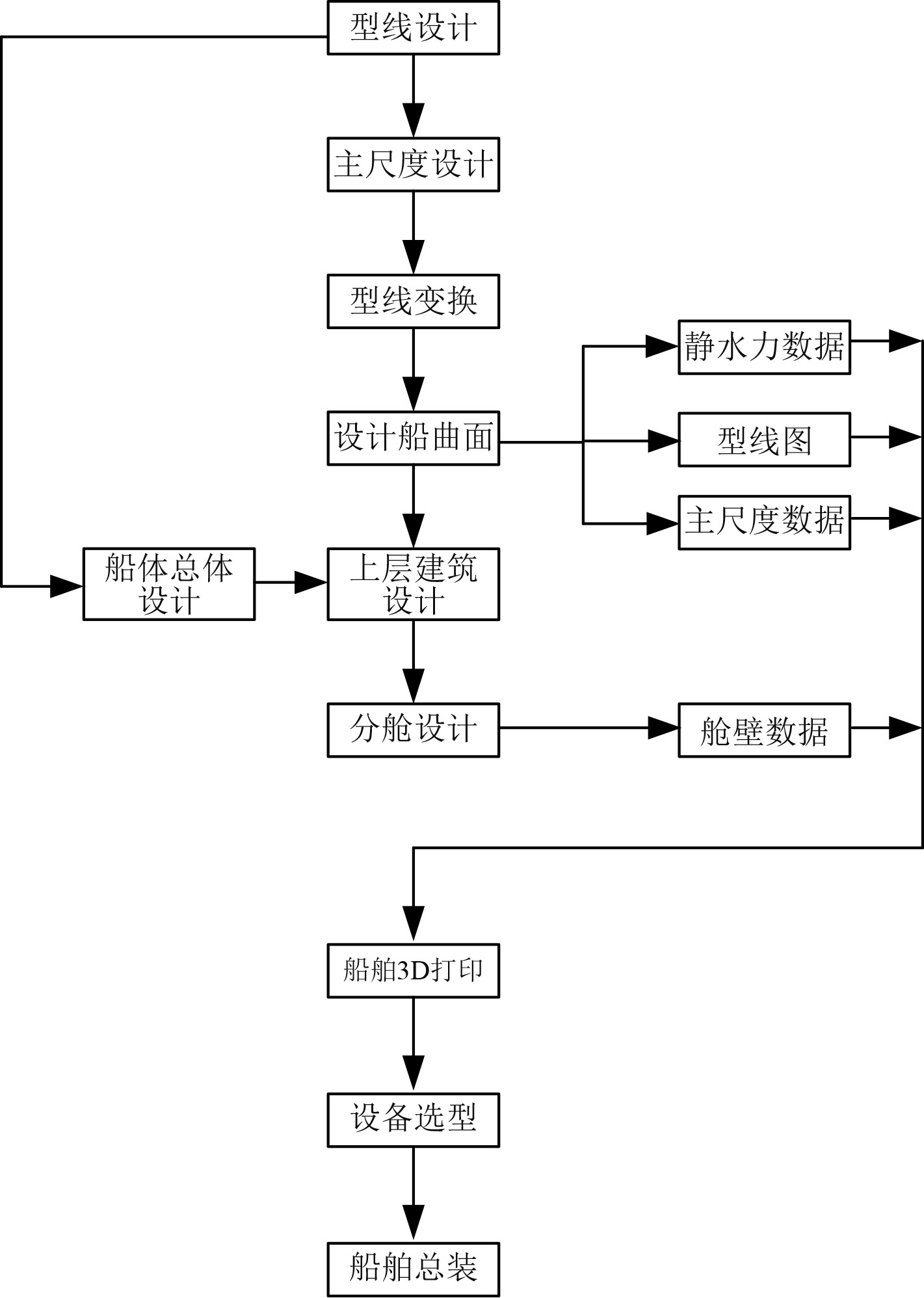
本文提出的基于3D打印技术的无压载水船体型线设计系统如图4所示。根据待设计无压载水船体的尺度数据以及船舶参数进行型线设计,然后基于母型船选用型线库进一步进行船舶的主尺度设计。通过等比例变换以及“1-Cp”变换进行船舶的型线变换设计,利用船舶曲面设计方法设计船曲面,同时获得无压载水船舶的静水力数据、型线图以及主尺度数据。基于船体曲面以及船体总体设计进行上层建筑设计,并得到舱壁数据。船舶3D打印系统根据无压载水船舶的静水力数据、型线图、主尺度数据以及舱壁数据进行3D打印设计,最后根据无压载水船体的设计需求进行设备选型以及船体总体结构的装配。
|
图 4 无压载水船体型线设计系统 Fig. 4 Design system of hull line of non ballast ship |
作为海上最主要的运输工具,船舶所携带的压载水会给目的地水域的生态产生很大的影响,因此对船舶压载水的管理变得逐渐严格,但是在严格的管理下依旧存在压载水的加工处理技术无法达到指定要求,同时目前的部分压载水处理技术无法根除压载水带来的环境问题。我国作为一个海运大国,通过船舶压载水已经成为入侵我国水域的主要方式之一。作为一种新型的船舶,无压载水船可以从源头消除压载水所产生的环境问题,因此对无压载水船舶的研究有着重大意义。本文研究了基于3D打印技术的无压载水船体型线设计系统,对我国无压载水船舶的发展起推动作用。
| [1] |
卢宝胜, 程东霞. 3D打印砂芯技术在铸件开发中的应用[J]. 铸造技术, 2021(42): 1026-1029. |
| [2] |
杨彦晨, 白斌, 程云章. 3D打印在颅内动脉肿瘤血管内治疗中的应用[J]. 北京生物医学工程, 2021(49): 642-646. |
| [3] |
韦俊凯, 林焰. V型无压载水船舶型线设计变换研究[J]. 中国舰船研究, 2010(5): 24-27. |
| [4] |
胡庆华, 刘建朔. V型无压载水小型LNG运输船设计研究[J]. 煤气与热力, 2019(39): 39-44. |
| [5] |
姜文英, 林焰, 陈明, 等. 变量化船舶型线表达与设计方法[J]. 上海交通大学学报, 2013(47): 323-328. |
| [6] |
张明霞, 李岗, 赵正彬, 等. 基于CAD二次开发的V型无压载水船[J]. 造船技术, 2019(3): 8-13. DOI:10.3969/j.issn.1000-3878.2019.03.003 |
| [7] |
王永青, 邓建辉, 李特, 等. 软体机器人3D打印制造技术研究综述[J]. 机械工程学报, 2021(57): 186-198. |
| [8] |
王鹏晖, 洪碧光, 于洋, 等. 一种无压载水船船型参数探讨[J]. 船海工程, 2016(45): 40-44. |
| [9] |
汪敏, 吴静萍. 一种无压载水船船型与阻力性能优化[J]. 船海工程, 2013(42): 28-31. |
 2001, Vol. 44
2001, Vol. 44
