2. 武汉工程大学 机电工程学院 湖北 武汉 430000;
3. 武汉交通职业学院 汽车学院,湖北 武汉 430000;
4. 武汉理工大学 能源与动力工程学院,湖北 武汉 430000
2. School of Mechanical and Electrical Engineering, Wuhan Institute of Technology, Wuhan 430000, China;
3. School of Automobile, Wuhan Technical College of Communications, Wuhan 430000, China;
4. School of Energy and Power Engineering, Wuhan University of Technology, Wuhan 430000, China
伴流[1]是船舶航行中不可避免的流体,由于伴流的不均匀特性,螺旋桨在工作时周围区域的流体运动会变得更加不均匀,如果在设计螺旋桨时,不考虑伴流对螺旋桨的影响,就会使设计出的螺旋桨和周围的伴流场不吻合,从而产生不合规范的振动,因此研究伴流对螺旋桨的影响非常重要。王文全[2]和侯立勋[3]开展了船舶螺旋桨适伴流设计方面的研究。
在20世纪中后期,伴流问题引起了国外学者的关注,而且成为了船舶流体力学研究方面的重点研究问题之一。高秋新[4]将RNG k-ε模型应用到DTMB5415驱逐舰的仿真中;姚震球[5]在进行潜艇尾流场模拟时,运用了滑移网格来仿真对比有/无螺旋桨的尾流场;吴琼等[6]在研究船舶阻力与推进时,同样运用滑移网格,且对比实验数据达到了高度的一致;Bennaya[7]运用RANS湍流模型、滑移网格以及流固耦合,对某一散货船进行船桨一体化仿真,研究船桨的振动特性。
本文采用双向流固耦合的方法对螺旋桨进行仿真,选取瞬态模型并启用动网格,使仿真过程呈现一种动态的变化。选择湍流模型来模拟船舶航行中错综复杂的流体运动,并将有/无伴流时的仿真结果进行对比,揭示不均匀的伴流对螺旋桨的影响特征。
1 理论方法与仿真模型 1.1 理论方法航行中的螺旋桨在运转时,其船舶尾部伴流的状态会呈现不均匀分布,考虑到螺旋桨处旋流的复杂流动,拟采用RNG k-ε[8-9]湍流模型进行仿真,因为该模型对湍流漩涡的计算精度更高[10]。利用N-S方程[11-12]进行运算,其方程描述如下:
湍流动能方程k为
| $ \frac{\partial}{\partial t}+\frac{\partial}{\partial x_j}(\rho ku_i)=\frac{\partial}{\partial x_j}\left(\alpha_k \mu_{eff}\frac{\partial k}{\partial x_j} \right)+G_k+G_b-\rho \varepsilon -Y_M+S_k,$ | (1) |
扩散方程为
| $\begin{split}\frac{\partial}{\partial t}(\rho \varepsilon)+\frac{\partial}{\partial x_i}(\rho \varepsilon u_i)=& \frac{\partial}{\partial x_j}\left(\alpha_{\varepsilon} \mu_{eff}\frac{\partial\varepsilon}{\partial x_j}\right)+C_{1\varepsilon}\frac{\varepsilon}{k}(G_k+G_{3\varepsilon}G_b)-\\& C{2\varepsilon}\rho \frac{\varepsilon^2}{k}-R_{\varepsilon}+S_{\varepsilon}。\end{split} $ | (2) |
式中:
利用RNGk-ε湍流模型对某中小型散货船的螺旋桨进行分析,其主尺度如表1所示,螺旋桨的主要参数如表2所示。
|
|
表 1 船舶主要参数 Tab.1 Main parameters of ship |
|
|
表 2 螺旋桨主要参数 Tab.2 Main parameters of propeller |
船尾螺旋桨为仿真对象,以该船的设计水线面为草图基准面一个尺寸为120 m×32 m×14 m的静止域,然后以螺旋桨盘面的中心为圆心画一个尺寸为3.2 m×3 m的圆柱体旋转域。
流体域内部的介质设置为液态水,其密度为1000 kg/m2,粘度为0.001 kg/(m·s)。将静止域的入口来流速度设置为10 m/s来模拟船舶在水中的航速,出口表压设置为0;由于在进行Fluent分析前已经将螺旋桨实体压缩,所以无法直接设置螺旋桨的转速,因此可以改为设置旋转域的角速度来仿真其转速,为300 r/min,且螺旋桨与旋转域的耦合面设置为跟随旋转域转动,相对转速为0。
采用Hybrid方法进行初始化,并设置迭代步数为1 000步。其中,在仿真敞水螺旋桨时,实体模型只有螺旋桨,在仿真船后螺旋桨时,实体模型包含整船和螺旋桨。
1.3 网格划分 1.3.1 流体网格在Fluent中进行流体部分的网格划分。将固体螺旋桨抑制掉,由于整个流体域区域的结构比较复杂,所以采用曲率和狭缝控制函数,如图1所示,在螺旋桨区域的流体网格密度非常精细。

|
图 1 流体网格 Fig. 1 Fluid mesh |
如表3所示,设置收敛标准,将连续性、xyz方向速度、湍动能和湍动能耗散率的最大残差收敛值设置为10−6,对仿真结果进行评估,得出最佳的单元尺寸限制为2 000 mm。共得到298164个节点,1 574 291个单元。
|
|
表 3 网格质量 Tab.3 Mesh quality |
在Transient Structural中进行固体部分的网格划分。将流体区域抑制掉,采用曲率和狭缝控制函数。将最大单元尺寸限制在100 mm,共得到617 872个节点,403 899个单元,且平均单元质量为0.820,平均正交质量为0.738。
添加螺旋桨总变形和等效应力为求解对象,并在其中一片桨叶的边缘设置一个变形监测点以获取该点在2 s内的位移变化作为分析螺旋桨桨叶振动[13]的依据。
2 仿真结果及对比分析 2.1 流线分析研究选取低速肥大型船舶,自由液面对伴流的影响很小,可以忽略不计,所以只需要对比局部流线状态,采用螺旋桨尾流[14-15]对比的方式更加直观。
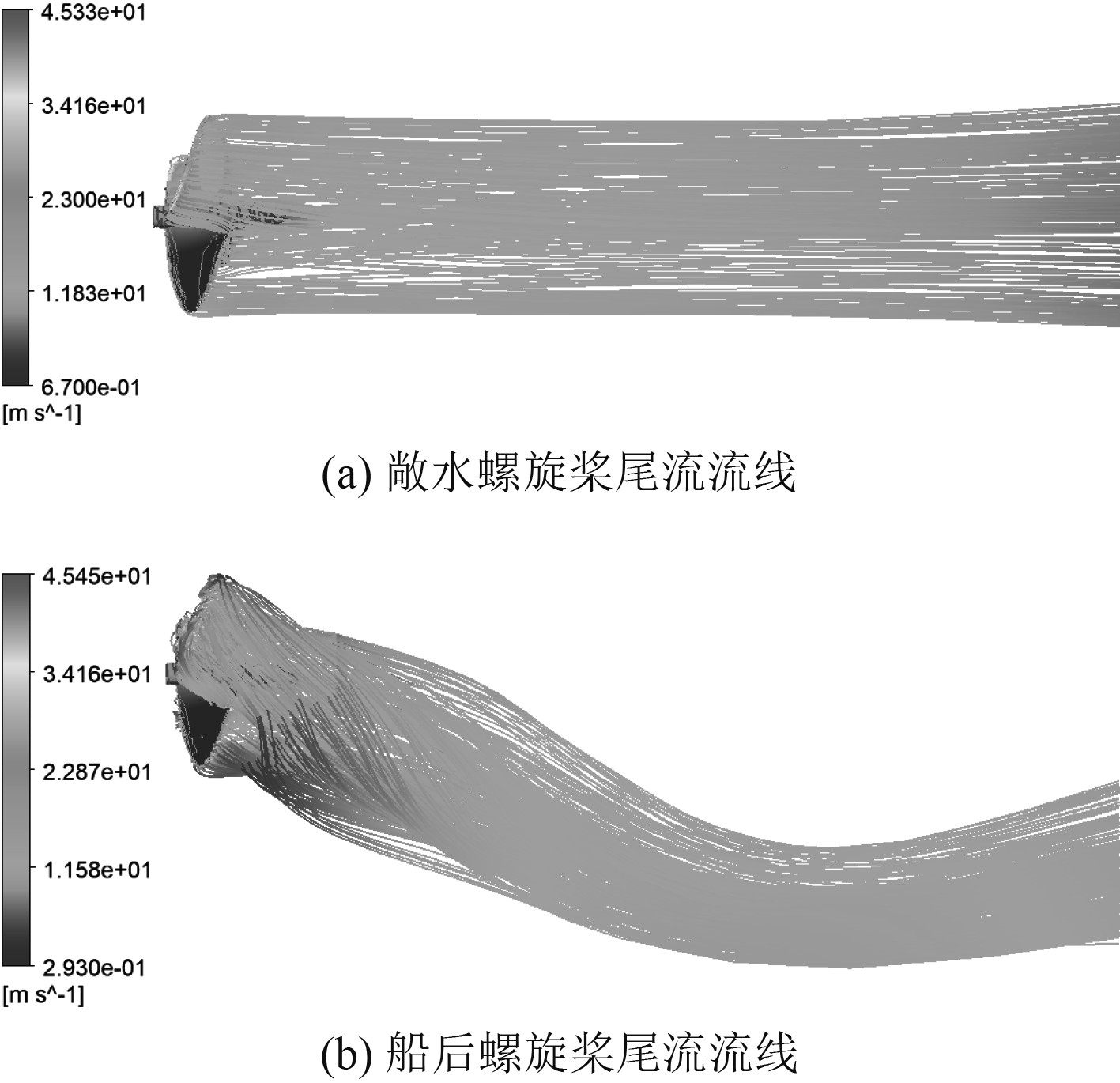
由CFD-Post仿真得出的螺旋桨尾部流线图如图2所示。图2(a)为敞水螺旋桨,当水流经过螺旋桨区域时,其绕流在后方形成了交叉聚拢的轨迹,最后向后流去。图2(b)为船后螺旋桨,其绕流部分在聚拢部分有明显的转向和加速的现象,这股流体的速度在扭转的极限位置达到最大值(除螺旋桨层流位置)。
|
图 2 螺旋桨尾流流线图 Fig. 2 Propeller wake streamline |
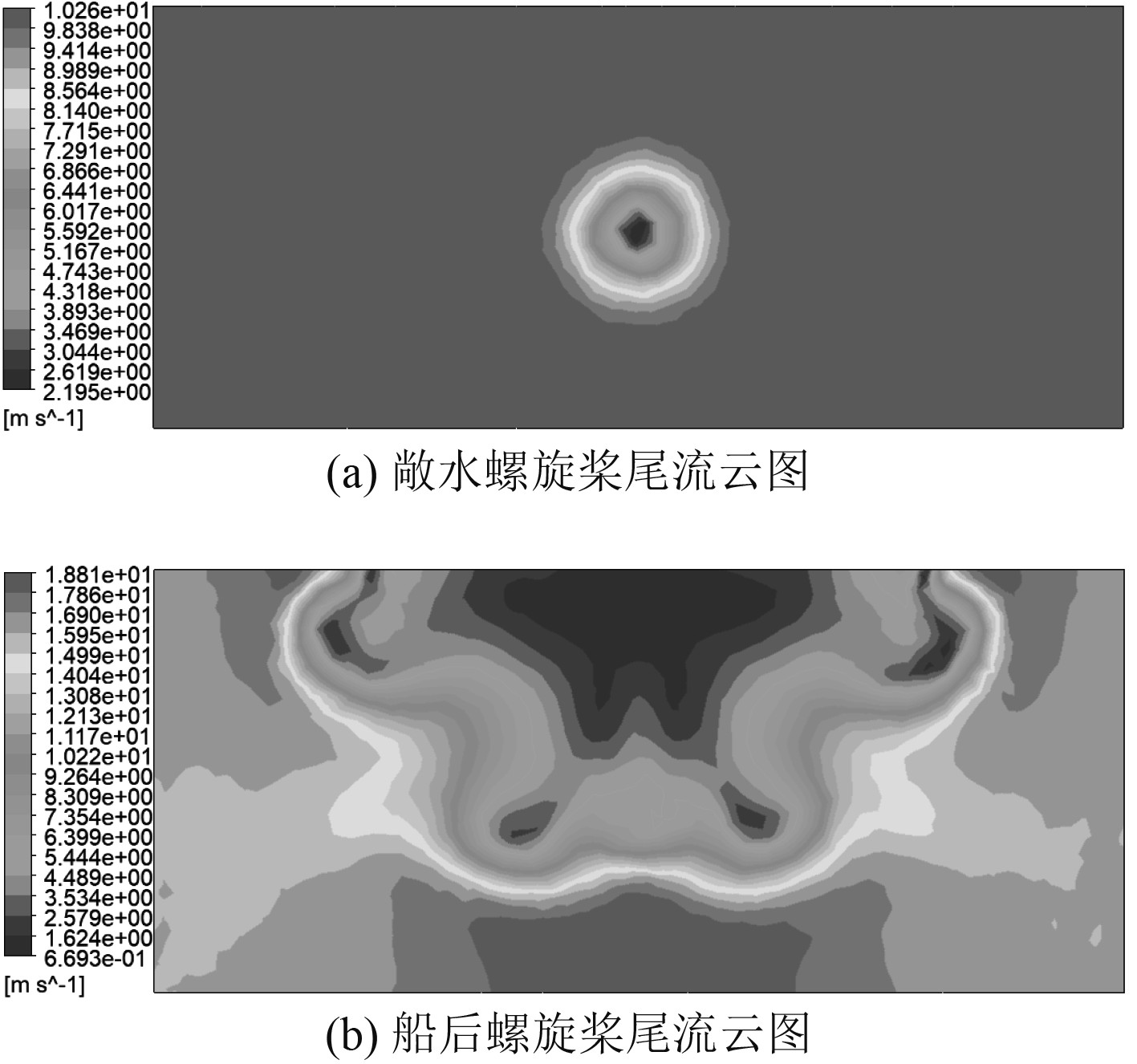
图3为螺旋桨桨盘后方5 m处的截面尾流速度云图。
|
图 3 螺旋桨桨盘后方5 m处的截面尾流速度云图 Fig. 3 Cross-sectional wake velocity cloud at 5 m behind the propeller disc |
没有伴流的情况下,即使流体经过螺旋桨被带动旋转,也能在之后很快恢复原来的流动状态,流线运动更加平稳一些。有伴流情况下,流体在经过船体的分流之后,到达船尾的流体不再是垂直于螺旋桨盘面的速度方向,而是以一种从船体外侧向螺旋桨聚拢的方向运动,引起伴流的不均匀性,使流体在经过螺旋桨后产生转向,不能快速恢复原来的流向,甚至在尾流处还有比较明显的加速。由于力的作用是相互的,此时螺旋桨的排出流向下倾斜,则螺旋桨相对受到一种倾斜上升的作用,使得其受力变形更加复杂化。
2.2 螺旋桨受力分析由于仿真采用的是0~2 s内的瞬态仿真,可以观察2 s内间隔0.005 s的每一时刻状态,以第2 s的状态为研究对象。
图4为2种工况下叶面叶背压力分布图。水压力自桨轴向叶梢扩散呈现出一种先增大后减小的趋势。在桨叶的导边和随边处的受力更加复杂,既有最大正向应力,又有最大反向应力,这对桨叶的抗冲击疲劳强度是一种很大的考验。

|
图 4 螺旋桨叶面叶背水压力分布图 Fig. 4 Propeller blade surface and back water pressure distribution |
无伴流状态下,最大的正向水压力为7.386×105Pa,反向水压力9.826×105 Pa;有伴流状态下,最大的正向水压力为1.415×106Pa,反向水压力为1.707×106Pa。很显然,不均匀的伴流加大了这一时刻螺旋桨所受的水压力梯度。
水的正向压力作用可以间接看作螺旋桨前进的推力,反向压力可以看作其阻力,这表明不均匀的伴流不仅削弱了螺旋桨的推力,还增加了其所受的阻力。
如图5所示,桨叶的最大受力点在叶根与桨轴的连接位置,2 s时刻敞水螺旋桨最大受力为108.39 MPa,船后螺旋桨最大受力为341.75 MPa,均从叶根到叶梢应力逐渐减小且梯度变化很平缓。船后螺旋桨因为在2 s内没有达到稳定工况,不同叶片的应力也不一样。

|
图 5 螺旋桨等效应力图 Fig. 5 Propeller equivalent stress diagram |
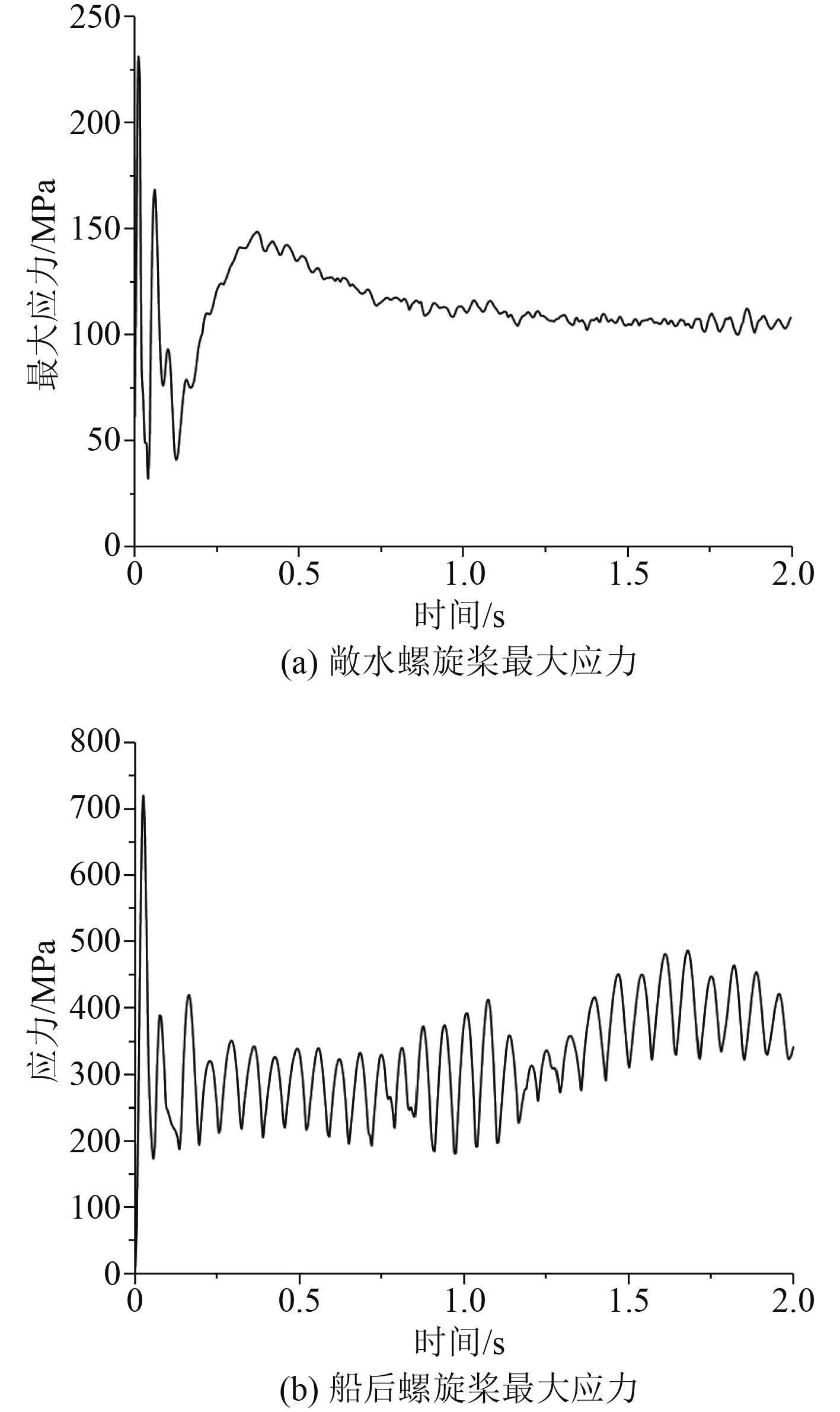
如图6所示,敞水螺旋桨在0 ~ 0.5 s内所受的最大应力波动较大,最低在0.04 s时刻,为32.437 MPa,最高在0.01 s时刻,达到了230.06 MPa;在0.5 ~ 2 s时间段内,逐渐开始趋向于稳定状态,约为105 MPa;整段时间内的最大应力都在材料的拉伸屈服强度250 MPa内,对结构的强度影响较小。船后螺旋桨最大应力在0~0.1 s内波动较大,最低在0.05 s时刻,为173.59 MPa,最高在0.02 s时刻,达到了721.48 MPa,超过了材料的抗拉极限强度460 MPa,说明产生了一定程度的塑性变形;在0.1~2 s时间段内,最大应力处于一种近似的简谐波动状态,均值约为300 MPa,超过了材料的拉伸屈服强度250 MPa,对结构的强度影响较大,而且波动的振幅较大,约为200 MPa。
|
图 6 螺旋桨所受应力随时间变化图 Fig. 6 Variation of propeller stress with time |
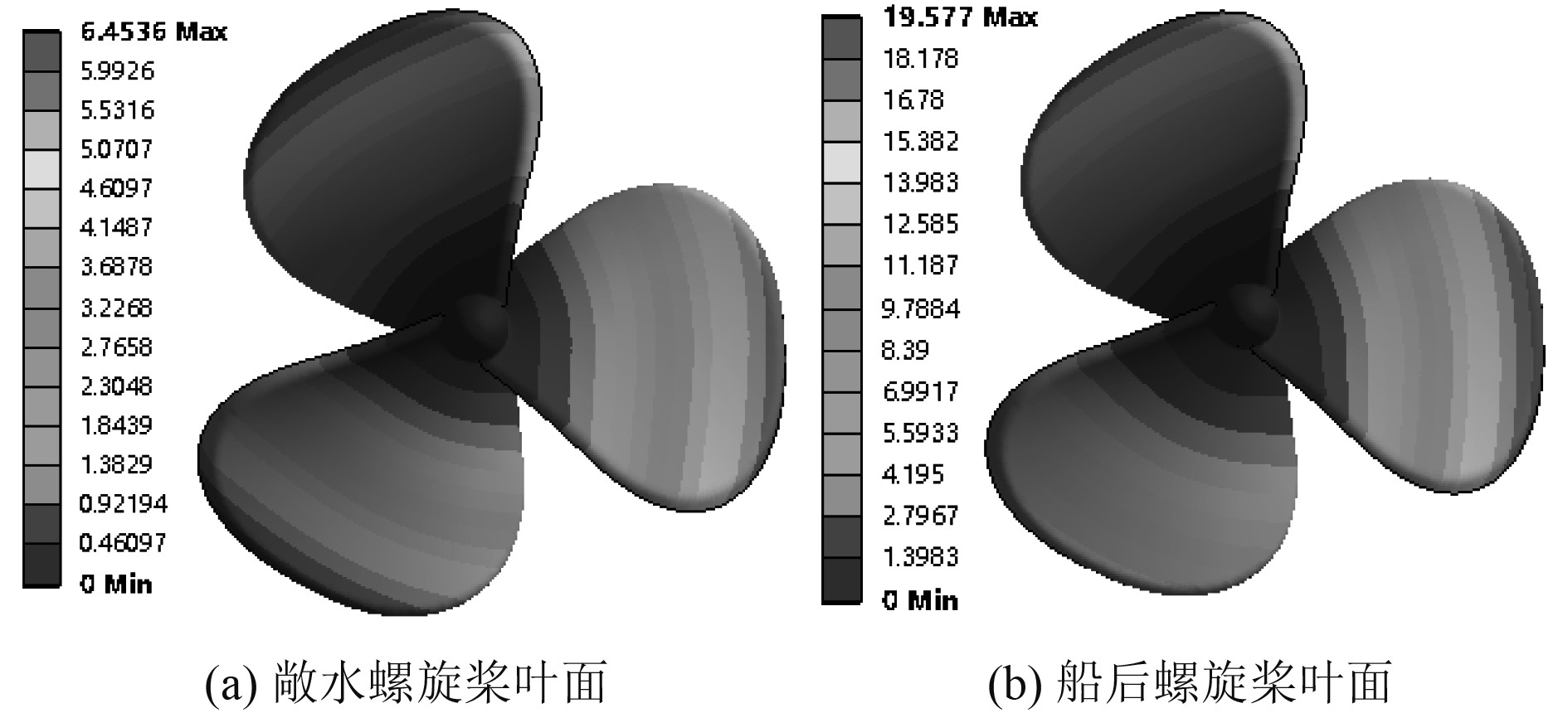
如图7所示,2种情况下螺旋桨的整体变形趋势相同,都是自桨轴向桨叶外缘逐渐增加,在每个叶片的最大圆盘位置变形最大。但是敞水螺旋桨显然在第2 s已经达到了稳定变形状态,3片螺旋桨叶片的变形几乎一致,最大的变形为6.4536 mm。而船后螺旋桨在第2 s并没有达到稳定变形状态,每一片桨叶的变形程度不一样,最大变形高达19.577 mm。这与桨叶在这一时刻的不同位置有很大的关系,由于螺旋桨此刻还没有达到稳定工作状态,且由图2可以看出相对在上方的桨叶处流体的转向程度加大。
|
图 7 螺旋桨2 s时刻总变形图 Fig. 7 Total deformation diagram of propeller at 2 s |
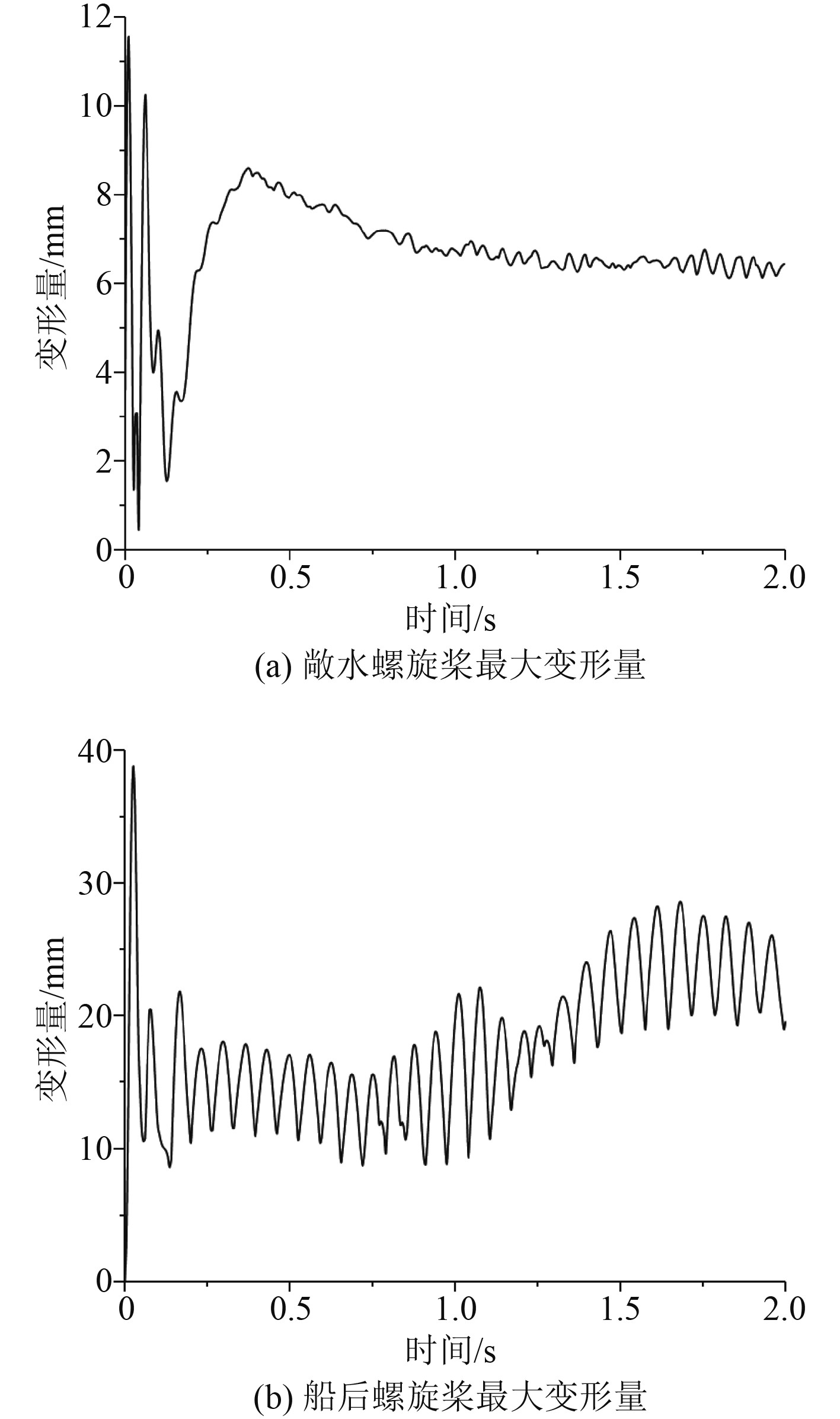
如图8所示,没有伴流时,前0.5 s内螺旋桨的最大变形量波动很大,在0.04 s时最小,为0.45159 mm,在0.01 s时最大,为11.578 mm,产生了强烈的振动趋势,后1.5 s就趋于一种稳定的变形状态,约为6.4 mm。有伴流时,前0.1 s内其最大变形量的波动更陡,在0.05 s时最小,为10.599 mm,在0.02 s时最大,为38.834 mm。说明伴流的不均匀性,影响了螺旋桨随时间变形的趋势。
|
图 8 螺旋桨变形量随时间变化图 Fig. 8 Variation of propeller deformation with time |
将图8中2种工况的瞬态最大变形状态与图6中的瞬态最大应力变化对比发现两者保持一致,说明本文采用的双向流固耦合仿真准确度很高。
3 振动分析 3.1 监测点振动状态为了提取螺旋桨桨叶连续地振动变形情况,需要在桨叶上设置监测点。由于叶片的振动沿桨毂的轴向上更加明显,所以分析轴向振动更优。由图7可知,叶片变形自叶根向叶梢逐渐增大,那么轴向位移的幅度也越明显,且每一片叶片完全相同,所以将监测点设置在螺旋桨梢圆与其中一片叶片的交点位置即可。
将2种状态下的螺旋桨桨叶上设置的监测点在0~2 s内轴向的位移变化进行对比,为了便于观察结果,采用折线图的形式。
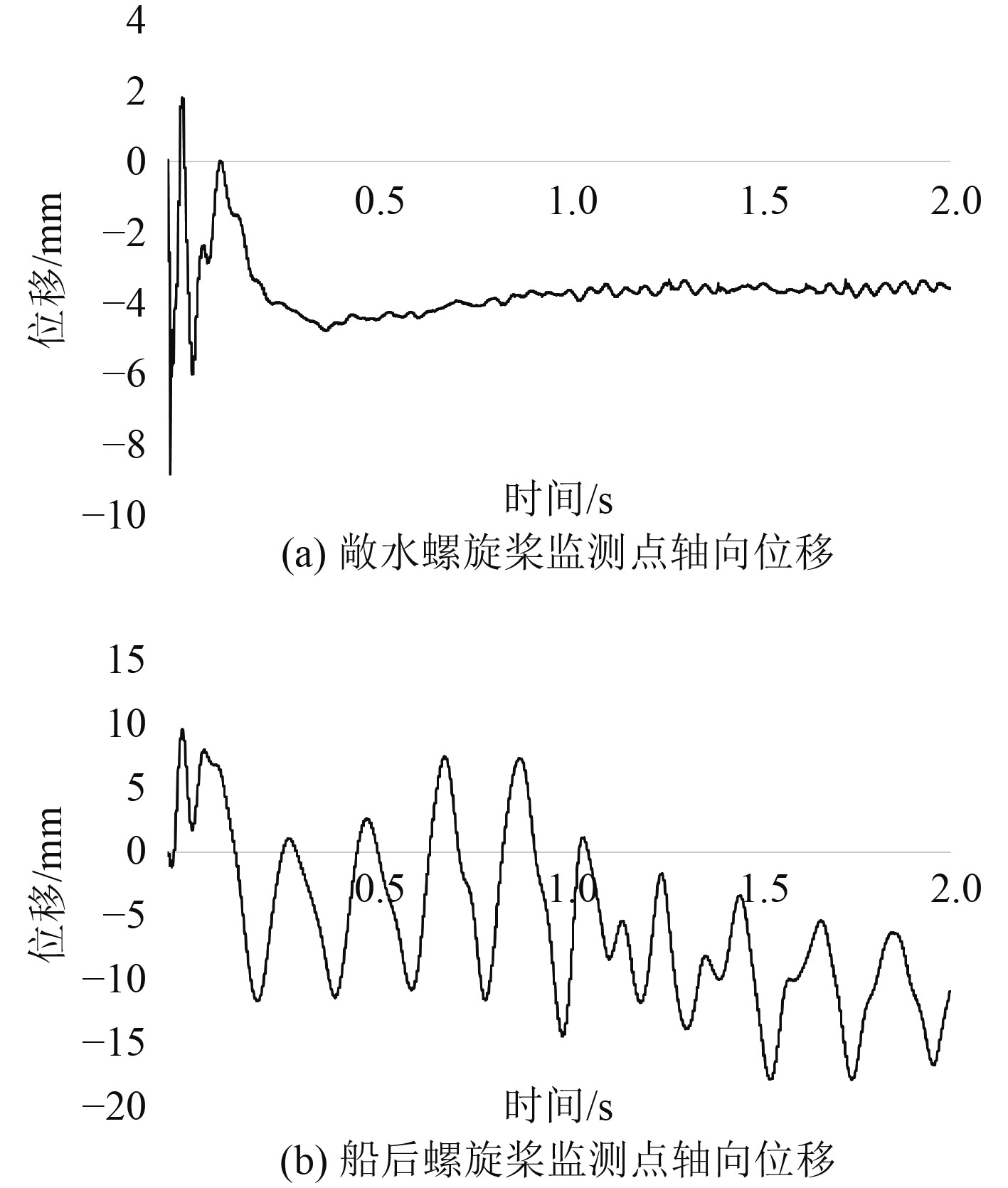
如图9所示,将监测点的初始静止位置设为0,来流方向设为正向,则敞水螺旋桨上的监测点在前0.5 s内先向负向摆动至最大位移处,再向正向摆回至最大位移处,在−10~2 mm的范围内摆动,在1.5 s内趋于平稳,最终在−4 mm处达到一种相对稳定的小振动状态。船后螺旋桨上的监测点先是沿负向小幅度摆动,再沿正向大幅度摆动至最大位移处,然后继续来回地大摆动至1 s末,最后只在负向较大地摆动。显然在2 s内还没有达到一种相对稳定的振动状态,直到1.5 s末才有相对较小的振动趋势。
|
图 9 监测点轴向位移图 Fig. 9 Axial displacement of monitoring points |
模态分析可以用于研究各种结构的振动特性。在仿真过程中,由于前6阶的频率常为0或近似为0,属于刚体运动,所以采用后6阶的求解结果作为螺旋桨1~6阶模态的振动频率。
将2种状态下的螺旋桨的模态进行对比。
由表4可以看出,1阶振型为横向扭转振动,螺旋桨的2片叶片沿周向扭转变形;2阶振型为纵向扭转振动,螺旋桨的1片叶片沿轴向扭转变形;3阶振型为纵向弯曲振动,螺旋桨的3片叶片沿轴向弯曲变形;4阶振型为横向弯曲振动,螺旋桨的1片叶片沿周向弯曲变形;5阶振型为纵向弯扭振动,螺旋桨1片叶片沿轴向弯曲变形、1片叶片沿轴向扭转变形;6阶振型为纵向弯扭振动,螺旋桨3片叶片沿轴向扭转变形。2种情况下螺旋桨的固有振动频率没有发生变化。
|
|
表 4 螺旋桨模态对比 Tab.4 Comparison of propeller modes |
基于有限元分析,采用控制变量法,通过螺旋桨双向流固耦合的瞬态仿真分析,研究伴流对螺旋桨的影响。仿真结果表明,不均匀的伴流对螺旋桨受力变形的影响很显著,结论如下:
1)不均匀的伴流会对螺旋桨区域的流体产生一定程度的扭转作用,改变其原来的流线轨迹,使之不能快速恢复原始的流向,引发螺旋桨尤其是桨叶区域的结构大变形。
2)不均匀的伴流在一定程度上,增加了来流对螺旋桨的冲击梯度变化,使桨叶上所受的冲击更加不均匀,也增加了其所受等效应力的梯度变化,使其抗弯扭疲劳强度要求更高。
3)在不均匀的伴流作用下,船后螺旋桨在0~2 s内所受应力的变化趋势远比敞水螺旋桨大,最大应力达到了721.48 MPa,超过了材料的抗拉极限强度460 MPa,说明产生了一定程度的塑性变形,且产生的变形也随应力而波动更陡,达到了38.834 mm,是敞水螺旋桨最大变形量的3倍多。
4)伴流的存在会使螺旋桨结构的振动变得更复杂,尤其是桨叶部分的振动变形更加明显,而且使之不能快速达到一种稳定的振动状态,对船舶启航时螺旋桨的稳定性影响较大。
| [1] |
盛振邦, 刘应中. 船舶原理(下)[M]. 上海: 上海交通大学出版社, 2016: 41−45.
|
| [2] |
王文全, 马开放, 王诗洋, 等. 螺旋桨适伴流理论设计及参数优化设计[J]. 应用科技, 2019, 46(5): 1-9. |
| [3] |
侯立勋, 汪春辉, 胡安康. 对转桨适伴流设计方法研究[J]. 中国造船, 2015, 56(4): 1-7. DOI:10.3969/j.issn.1000-4882.2015.04.001 |
| [4] |
GAO Qiu- xin. Numerical simulation of free surface flow around ship hull[J]. Journal of Ship Mechanics. 2002, 6(3) : 1−13.
|
| [5] |
姚震球, 高慧, 杨春蕾. 基于滑移网格的带螺旋桨体尾流场数值分析方法艇[J]. 江苏科技大学学报(自然科学版), 2008, 22(2): 15-20. |
| [6] |
WU Q, FENG X M, YU H, et al. Prediction of ship resistance and propulsion performance using multi-block structural grid[C]//Proceedings of Gothenburg 2010 Workshop on Numerical Ship Hydrodynamics. Gothenburg, Sweden, 2010: 483−487.
|
| [7] |
MOHAMED B. Vibration and sound radiation of ship structure by propulsion system[D]. Harbin: Harbin Engineering University, 2015.
|
| [8] |
黄政, 熊鹰, 杨光. 基于ANSYS ACP的复合材料螺旋桨流固耦合计算方法[J]. 计算力学学报, 2017, 34(4): 501-506. DOI:10.7511/jslx201704016 |
| [9] |
黄鑫, 朱汉华, 安邦. 基于滑移网格的螺旋桨性能分析[J]. 舰船科学技术, 2018, 40(4): 6-11. DOI:10.3404/j.issn.1672-7649.2018.04.002 |
| [10] |
王丹. 复合材料螺旋桨流固耦合分析研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
|
| [11] |
齐冠鸣. 基于Ansys的水下潜体螺旋桨对环境声速场的影响研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [12] |
沈煜. 船舶尾部伴流场的数值预报及尺度效应研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
| [13] |
Ivo Senjanović, Ivica Ančić, Gojko Magazinović, et al. Validation of analytical methods for the estimation of the torsional vibrations of ship power transmission systems[J]. Ocean Engineering, 2019, 184: 107-120. DOI:10.1016/j.oceaneng.2019.04.016 |
| [14] |
GUILMINEAU E, DENG G B, Leroyer A, et al . Wake simulationof a marine propeller[C]//Joint 11th World Congress on Computational Mechanics, WCCM 2014, the 5th European Conference on Computational Mechanics, ECCM 2014 and the 6th European Conference on Computational Fluid Dynamics, ECFD 2014, 2015.
|
| [15] |
刘恬. 伴流场的尺度效应研究及其短波中特性分析[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
 2001, Vol. 44
2001, Vol. 44