0 引　言

货物载荷通过运输装置底部的搁置脚作用在甲板上，对比传统轮胎载荷而言，搁置脚载荷结构更复杂、材料刚度更大，所以与甲板的非线性接触也更为复杂。曾鸣^[1]对比分析了均布载荷作用下的线弹性计算与搁置脚载荷作用下的非线性接触计算的结构响应，发现两者载荷分配有着很大的区别，考虑到搁置脚和甲板之间的接触区域刚度具有一定的不均匀性，所以不能直接将搁置脚载荷作为线弹性的均布载荷来处理。熊群飞^[2]通过实验的方法直接获得搁置脚载荷作用下甲板的接触压力分布，通过应力等效提出了搁置脚载荷简化模型，将搁置脚载荷转化为板格局部均布载荷。郑朝斌^[3-4]讨论了在搁置脚与甲板的非线性接触计算时的结构建模、接触面选取以及载荷施加等问题，通过计算甲板板、甲板纵骨、甲板横梁不同工况下的非线性接触，总结各结构接触力分布规律，提出对应的载荷计算公式。

但是，目前的研究均假定甲板为平整的理想状态，未考虑甲板初始变形对搁置脚接触问题的影响，但是在实际材料加工时，由于焊接等工艺条件，实际甲板并非理想状态，存在初始变形，而初始变形在研究加筋板极限强度等^[5-8]领域已经进行过大量的研究。本文将通过Abaqus软件建立甲板与搁置脚的非线性接触模型，分析甲板板Mises应力与接触压力分布特征，探究甲板初始变形对搁置脚非线性接触问题的影响。

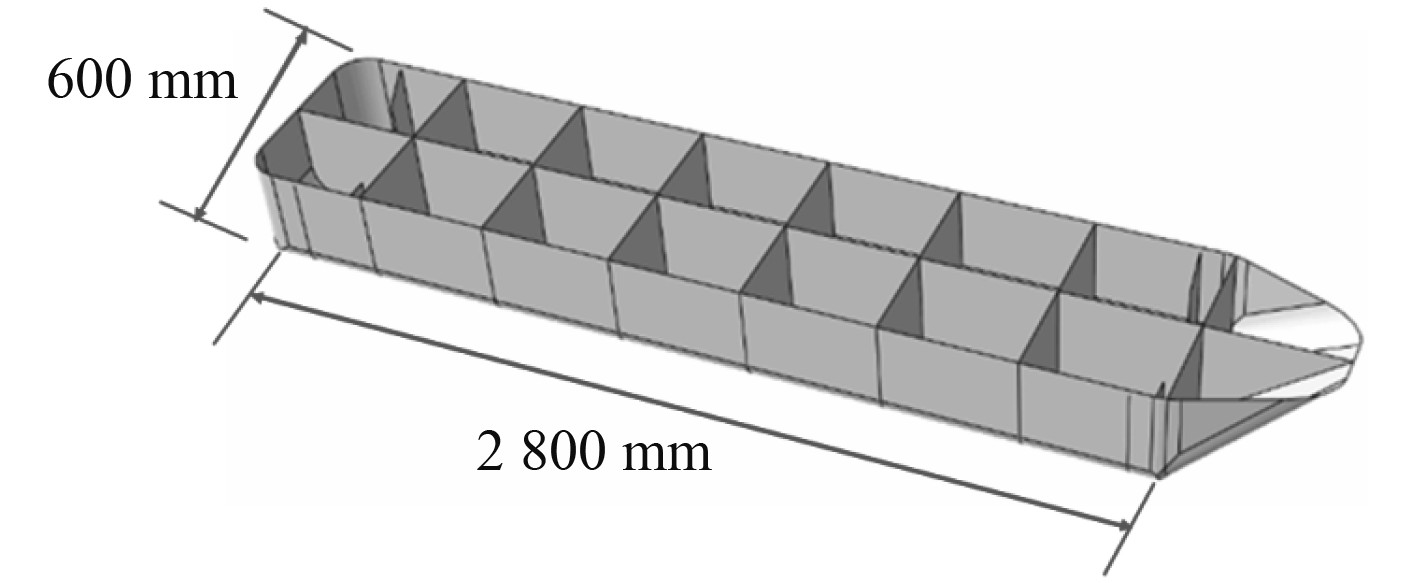
1 有限元计算模型

本文非线性接触计算中有限元模型由甲板模型和搁置脚模型组成。甲板模型由纵骨、横梁以及甲板板组成，纵骨间距为600 mm，横梁间距为2 400 mm。甲板材料采用普通船用钢，弹性模量 $E{\text{ = }}206\;{\rm{GPa }}$ ，密度 $\, \rho = 7.85{\rm{E}} - 9\;{\rm{t}}/{\rm{m{m^3}}}$ ，泊松比 $ \, \mu {\text{ = }}0.3$ 。甲板计算模型如图1所示。搁置脚模型为铝合金箱型结构，内部结构主要包含底板、侧板、纵横隔板、横梁以及纵骨。搁置脚结构底部长为2 800 mm，宽为600 mm，几何尺寸如图2所示。搁置脚材料的弹性模量 $E{\text{ = }}72\;\,{\rm{GPa}}$ ，密度 $\rho = 2.7{\rm{E}} - 9\,\;{\rm{t}}/{\rm{m{m^3}}}$ ，泊松比 $\mu {\text{ = }}0.3$ 。

接触计算在Abaqus软件中进行，Abaqus软件中关于接触属性的定义包括接触主从面的定义以及摩擦系数的定义。在计算中，将甲板模型与搁置脚模型如图3所示进行装配。接触对建立在甲板板与搁置脚底板之间，其中以甲板板作为接触主面，以搁置脚底板作为接触从面。接触对的属性定义如下：法向硬接触，切向库伦摩擦模型。本文计算中定义的普通船用钢和铝合金之间的摩擦系数为0.45^[2]。

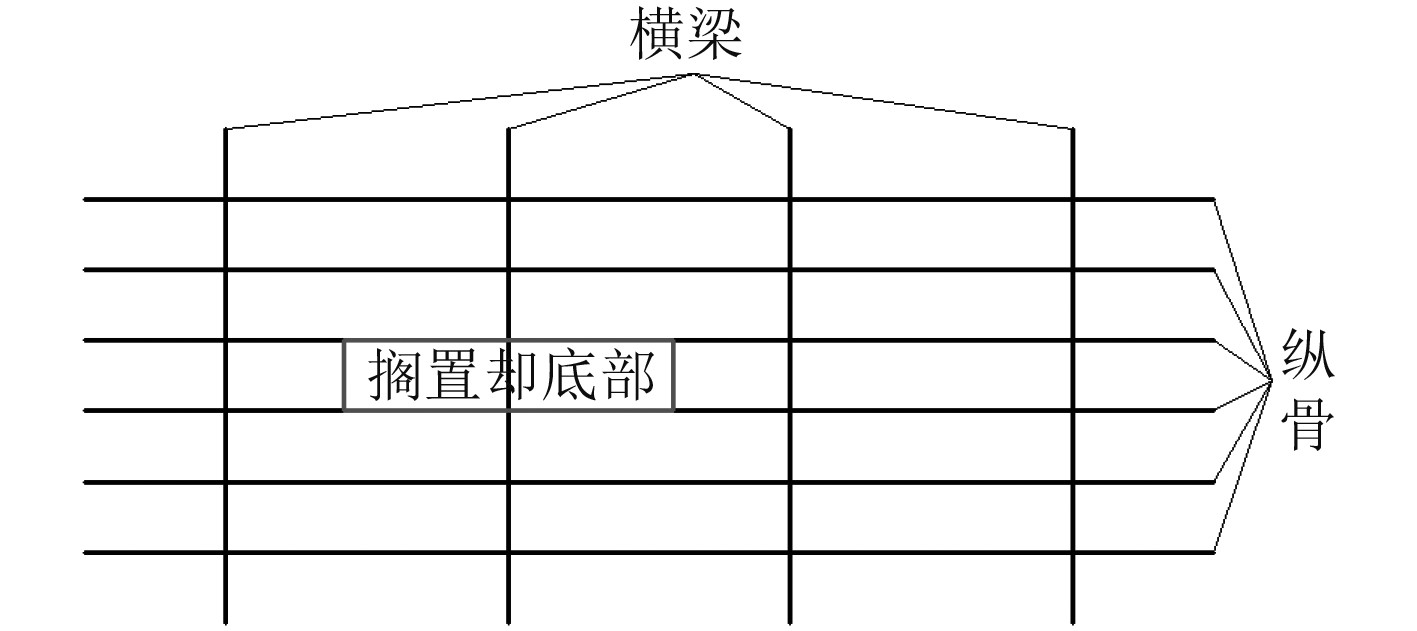
搁置脚位于运输装置下端，且与运输装置底部刚性连接。因此，在搁置脚顶部增加顶板是为了模拟搁置脚顶部的大刚度，同时便于在计算过程中施加载荷以及设置约束。载荷的施加方式为在搁置脚底部中心对应的搁置脚顶板位置建立参考点，顶板所有单元节点与参考点之间建立Coupling耦合。如图4所示，关联自由度为z，并将力作用在该参考点上，如此顶板这些点的合力就通过了底部中心，考虑单个搁置脚承受载荷为10 t。甲板模型边界条件设置为四边固支，搁置脚顶部参考点的边界条件设置为x=0，y=0，Rx=0，Ry=0，Rz=0，约束搁置脚不能朝任意方向偏转。典型计算工况如图5所示，搁置脚底部横跨在一根横梁上。

2 无初始变形工况分析

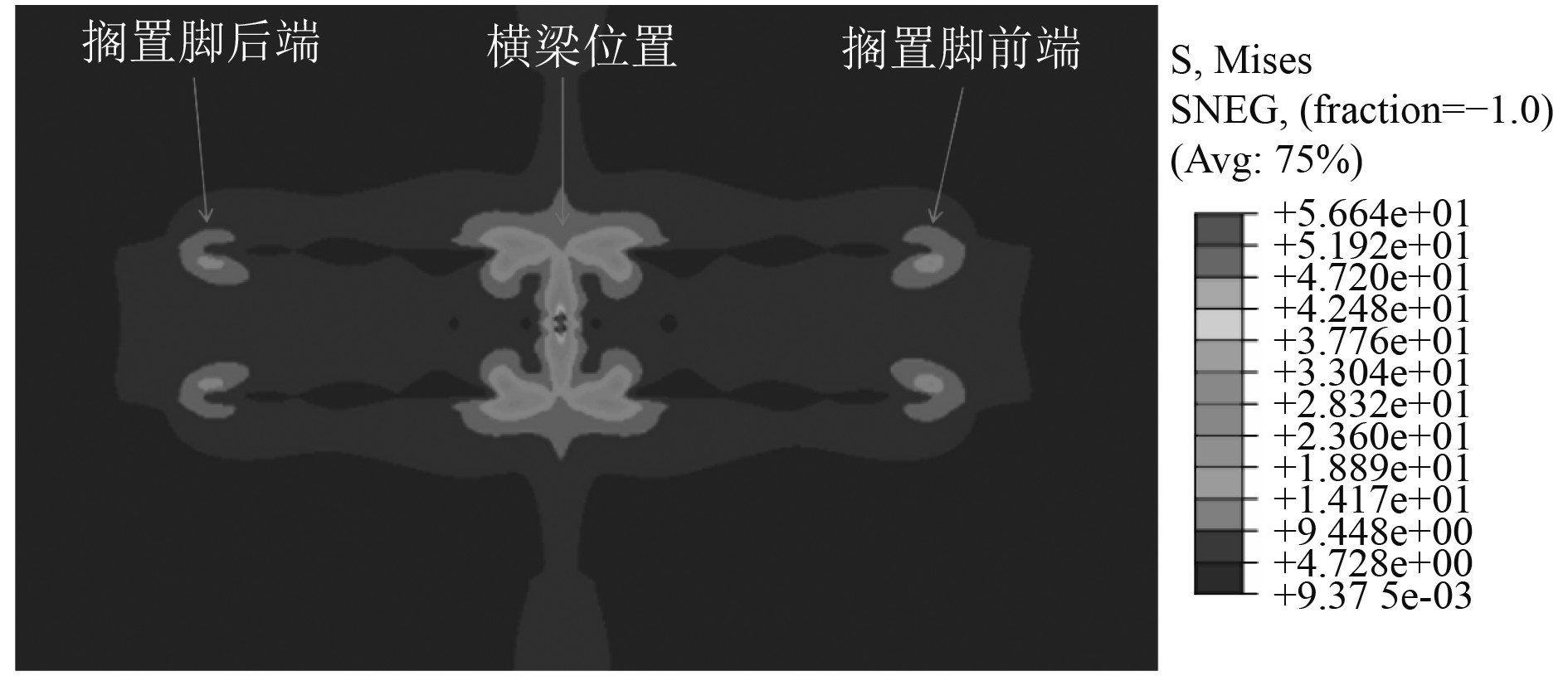
通过非线性接触计算得到最大甲板Mises应力为56.64 MPa，位于甲板横梁处，搁置脚前后端位置处应力也较为明显，应力分布如图6所示。最大接触压力为21.73 MPa，也位于甲板横梁处，压力分布如图7所示，除横梁外其他位置的接触压力分布不是很明显。由于搁置脚放置位置底部关于横梁位置对称，所以各云图也关于横梁位置对称。

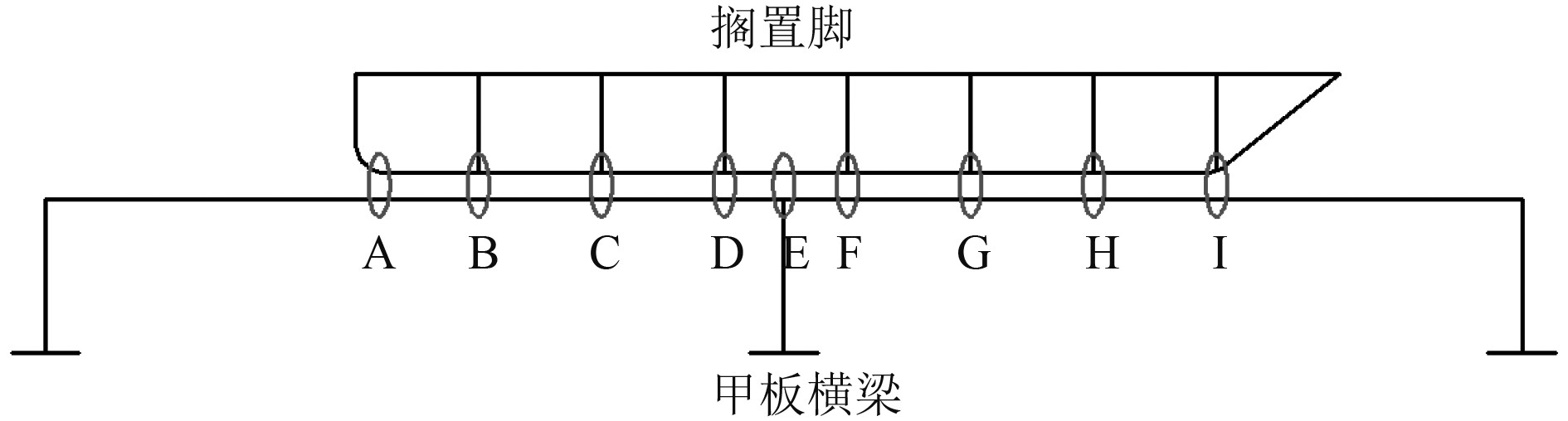
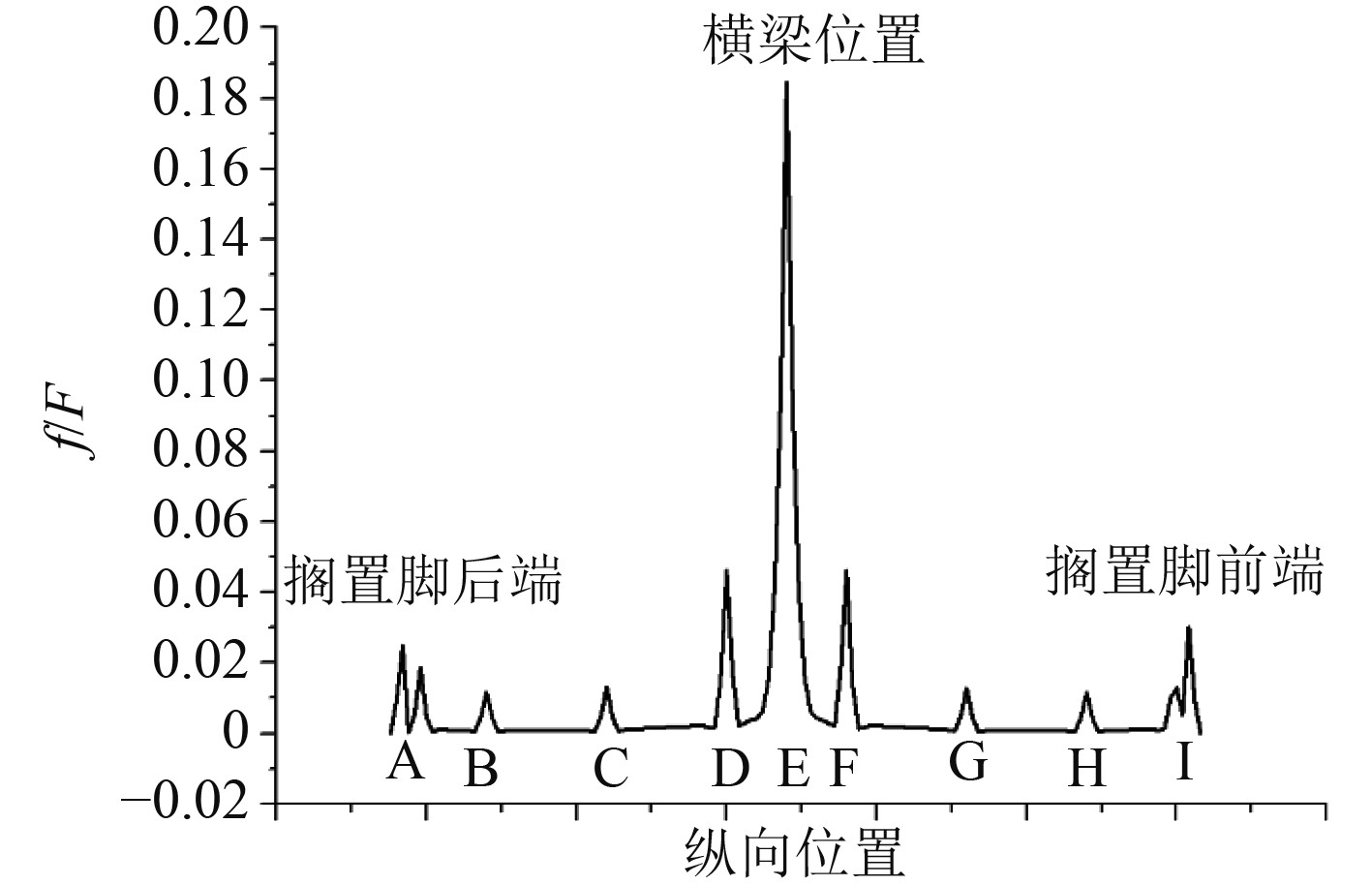
图8为无初始变形工况下主要接触位置示意图，是沿图1甲板中Line3截面。为了研究接触力在纵向上的分布规律，在对应的每个纵向单元节点位置，将甲板板上横向各单元节点接触力进行求和，求和结果记为f，再除以搁置脚上作用的总力F，本文工况下总力F为10 t，最终得到接触力在纵向上的分布比例曲线，如图9所示。可知，甲板接触力主要集中在甲板横梁、搁置脚横隔板以及搁置脚前后端（包含搁置脚横梁）对应甲板位置处。且其中甲板横梁处接触力比例最大，说明接触力主要由甲板横梁承担。进一步对横梁左右各40 mm范围内的节点接触力求和，得到横梁接触合力记为F₁，可得横梁接触合力占比，即F₁/F，为45.72%。

3 考虑初始变形工况分析

以结构的弹性屈曲模态作为初始变形假定，初始变形表现为板的初始变形、加强筋的梁柱型初始变形以及加强筋的侧倾初始变形，其对应的计算公式^[6]如下：

$ 板的初始变形{\omega _{opl}} = {A_0}\sin \frac{{m{\pi} x}}{a}\sin \frac{{{\pi} y}}{b}，$

(1)

$ 加强筋的梁柱型初始变形{\omega _{oc}} = {B_0}\sin \frac{{\pi x}}{a}\sin \frac{{\pi y}}{B}, $

(2)

$ 加强筋的侧倾初始变形{\omega _{os}} = {C_0}\frac{z}{{{h_w}}}\sin \frac{{\pi x}}{a}。$

(3)

式中： $a$ ， $b$ 为板格的长度和宽度； $B$ 为加筋板总宽度； ${A_0},{B_0},{C_0}$ 分别为各种初始变形的幅值，板的初始变形幅值分为3种水平。

$ {A}_{0}=\left\{\begin{array}{*{20}{l}} 0.025{\beta }^{2}t，& {\scriptsize{轻微水平}}，\\ 0.1{\beta }^{2}t，&{\scriptsize{平均水平}}，\\ 0.3{\beta }^{2}t，&{\scriptsize{严重水平}}。\end{array}\right. $

$ {B_0}{\text{ = }}{C_0}{\text{ = }}0.001a。$

其中： $\beta $ 为板格的柔度， $\beta {\text{ = }}\dfrac{b}{t}\sqrt {\dfrac{{{\sigma _y}}}{E}}$ ，t为板厚；m为板的纵向屈曲半波数，为满足不等式 $a/b \leqslant \sqrt {m(m + 1)} $ 的最小整数。

采用平均水平板的初始变形进行研究， ${\sigma _y}$ =235 MPa，根据上述公式，得到 ${A_0}{\text{ = }}3.4{\rm{mm}}$ ， $m = 4$ ， ${B_0}{\text{ = }} {C_0}{\text{ = }} $ $ 2.4\;\,{\rm{mm}}$ 。采用MSC Patran软件，对有限元模型中的节点坐标进行修改，模拟甲板的初始变形。表1为各初始变形示意图，每种初始变形又根据变形方向分为2种，共6种。其中板的初始变形示意图是沿图1甲板中Line1截面，梁柱型初始变形与侧倾初始变形为沿图1甲板中Line2截面。

以典型加筋板结构为研究对象，分析板的初始变形、梁柱型初始变形以及侧倾初始变形对搁置脚非线性接触的影响。表2为3种初始变形单独作用以及无初始变形情况下甲板最大Mises应力以及最大接触压力的计算结果。可知，板的初始变形对接触的影响最大，加强筋的梁柱型初始变形对接触的影响次之，加强筋的侧倾初始变形对接触的影响最小。

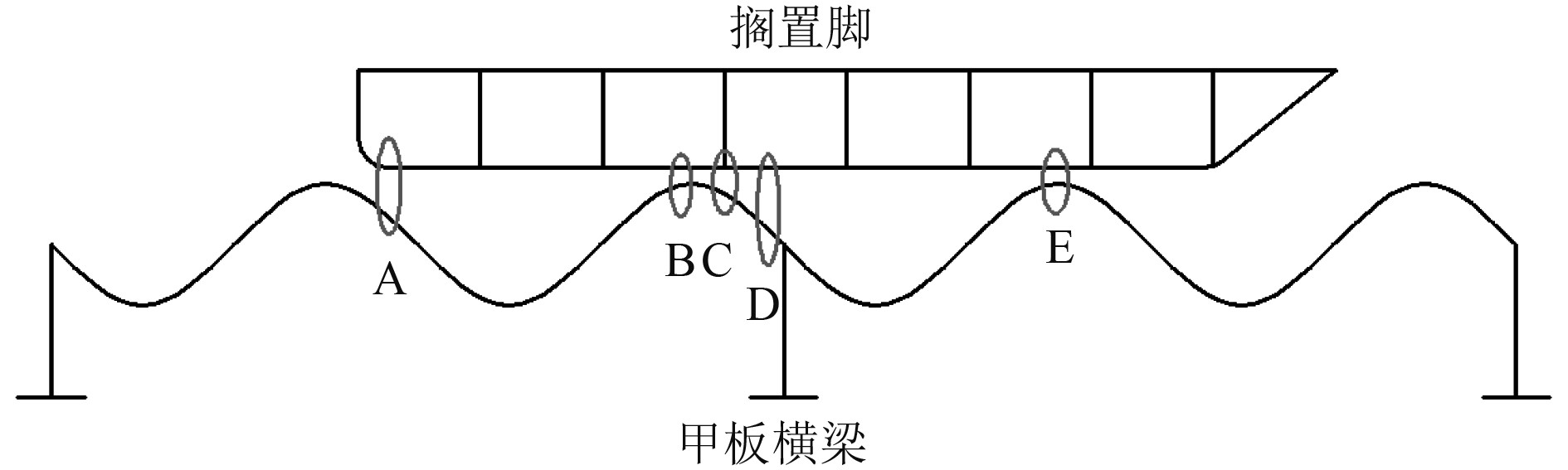
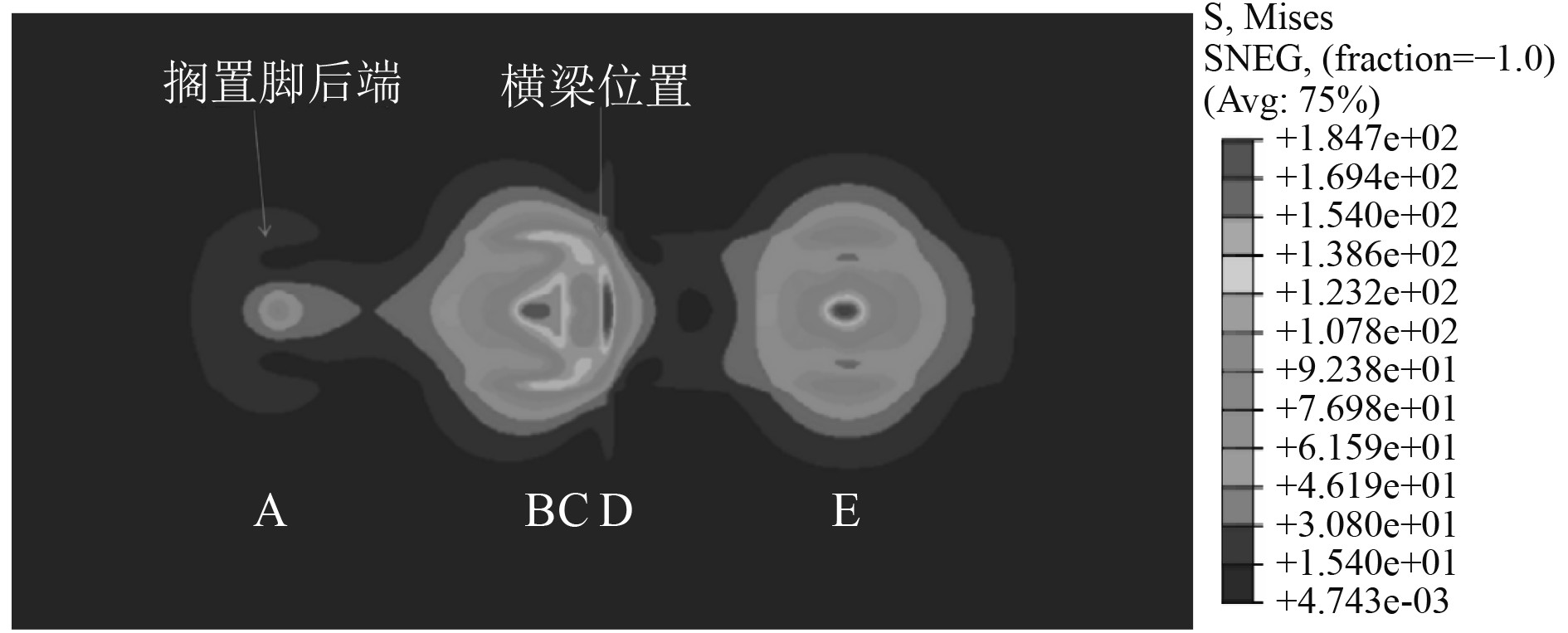
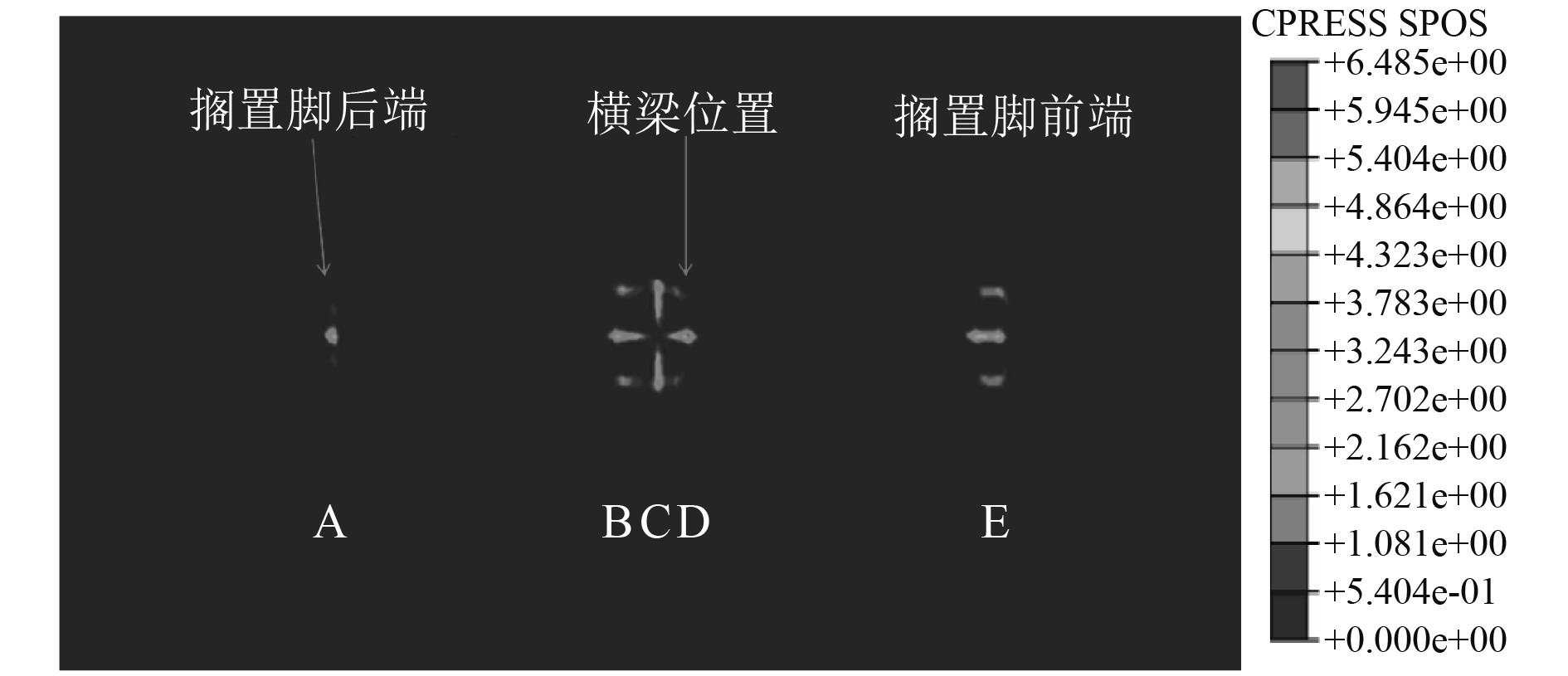
取板的初始变形2工况进一步分析，根据板的初始变形与搁置脚放置位置，并结合接触力分布云图，得到5个主要接触位置如图10所示。A点为搁置脚后端与甲板接触位置，B点和E点是搁置脚与甲板拱起部分接触位置，C点为搁置脚横隔板对应位置，D点为甲板横梁位置。甲板Mises应力如图11所示，最大应力出现在甲板板对应横梁位置D点附近。甲板接触压力如图12所示，最大接触压力减小明显，且最大接触压力位置始终在横梁位置处，压力分布变化明显，由于甲板板的不平整，搁置脚对横梁的接触作用减弱，甲板的局部拱起分担了部分接触压力。同样方法得到接触力在纵向上的分布比例曲线，如图13所示。可以发现，此时横梁位置不再是最主要的承载位置，由于甲板板局部拱起，在纵向位置处横隔板接触占比占比高于横梁位置。此时搁置脚后端A点接触合力占比8.83%，搁置脚与甲板拱起部分接触位置B点接触合力占比14.48%，搁置脚横隔板C点接触合力占比22.17%，横梁D点接触合力占比10.38%，搁置脚与甲板拱起部分接触位置E点接触合力占比28.95%，5个主要接触位置接触力总占比为84.81%。

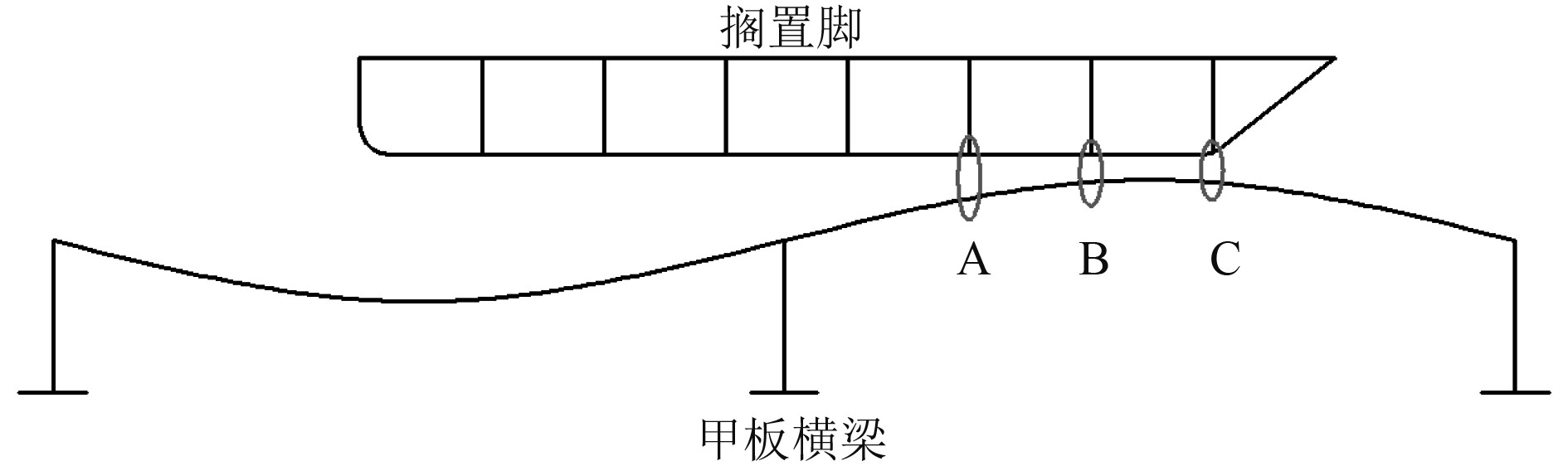
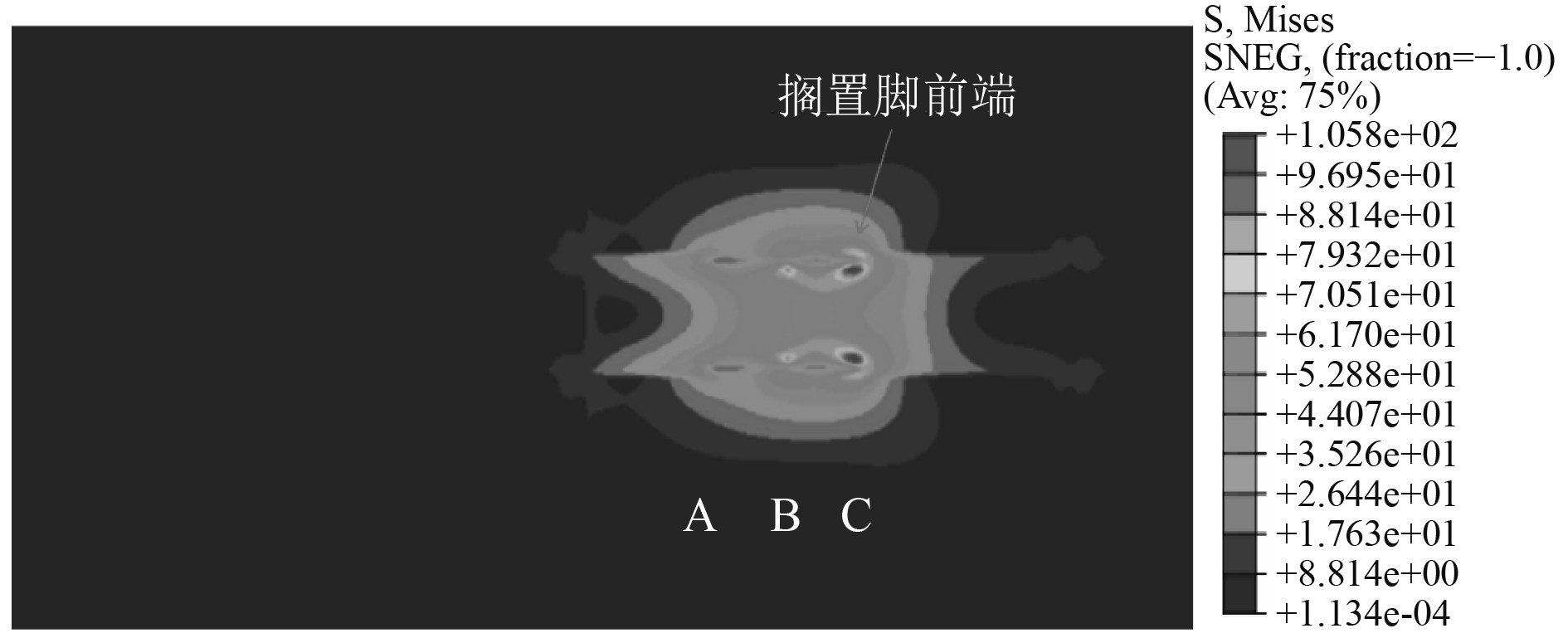
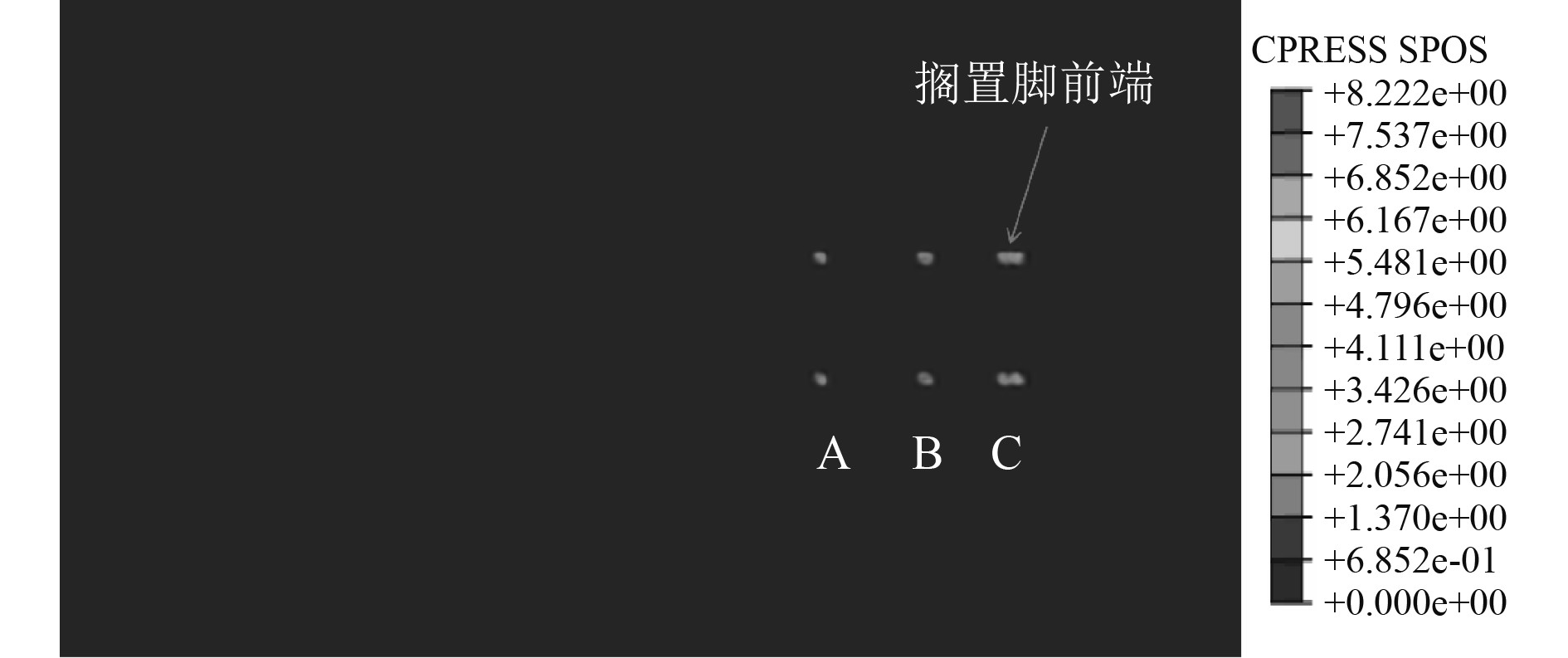
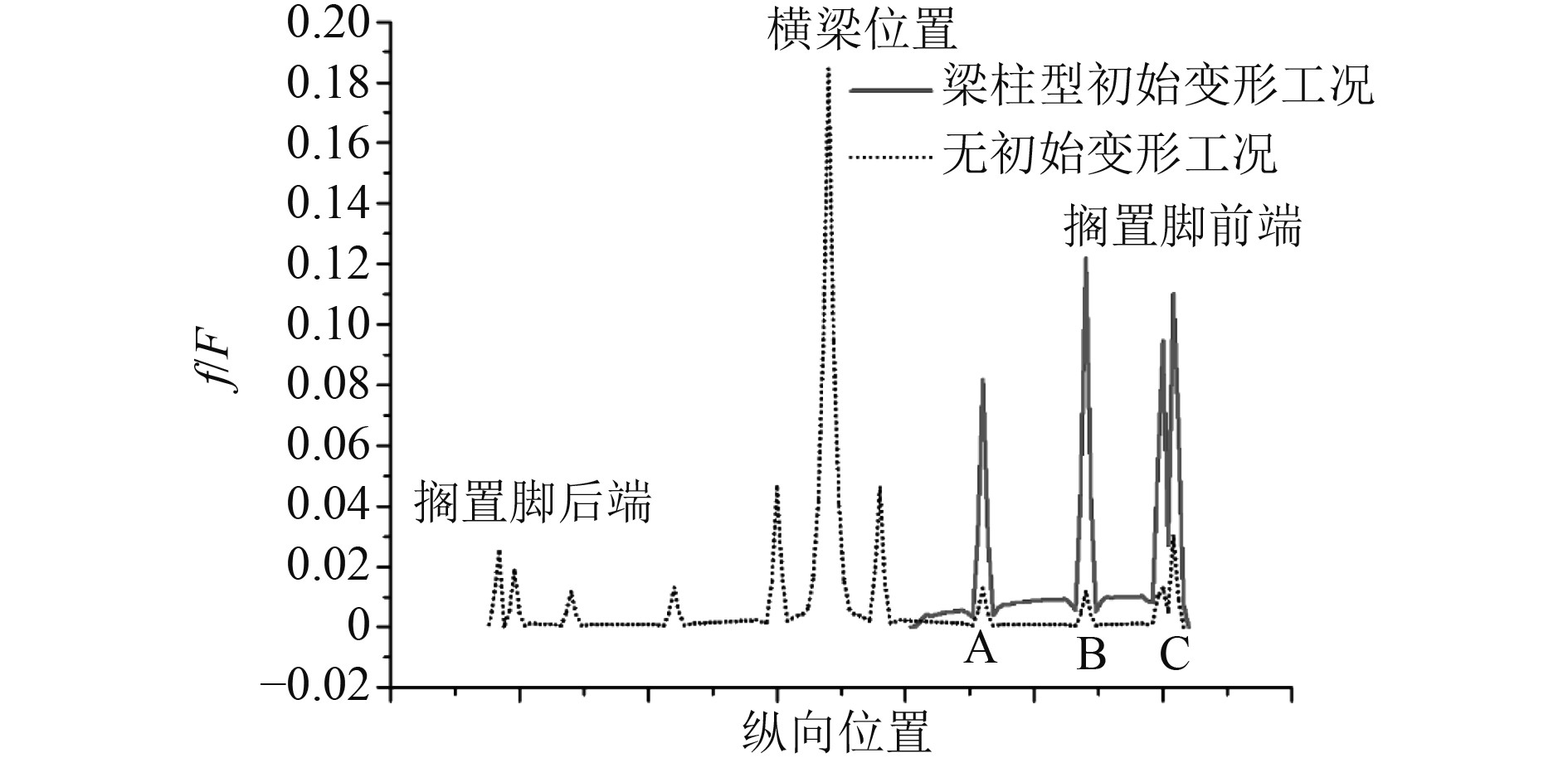
取梁柱型初始变形2工况进行进一步分析，根据甲板板初始变形与搁置脚放置位置，并结合接触力分布云图，得到3个主要接触位置如图14所示。A和B为搁置脚横隔板对应位置，C点为搁置脚前端与甲板接触位置。甲板Mises应力分布如图15所示，最大Mises应力出现在甲板板与搁置脚前端接触位置。应力分布主要集中在横梁关于搁置脚前端一侧。这是由于搁置脚后端与甲板存在间隙，并未接触上，接触力分布同理也集中在横梁关于搁置脚前端一侧，甲板接触力分布力如图16所示。同样方法得到接触力在纵向上的分布比例曲线，如图17所示。可以发现，搁置脚前端位置接触力占比最大，甲板横梁位置处与搁置脚并未接触上。此时搁置脚横隔板A点接触合力占比13.98%，搁置脚横隔板B点接触合力占比20.89%，搁置脚前端C点接触合力占比35.03%，3个主要接触位置接触力总占比为69.9%。

由于加强筋的侧倾初始变形的影响很小，几乎为0，所以在考虑初始变形叠加时，仅考虑板的初始变形与加强筋的梁柱型初始变形同时作用，又因为板的初始变形与加强筋的梁柱型初始变形各分别有2种，根据排列组合，得到叠加后的组合初始变形则共有4种，如表3所示。同样采用非线性接触计算，得到计算结果如表4所示。

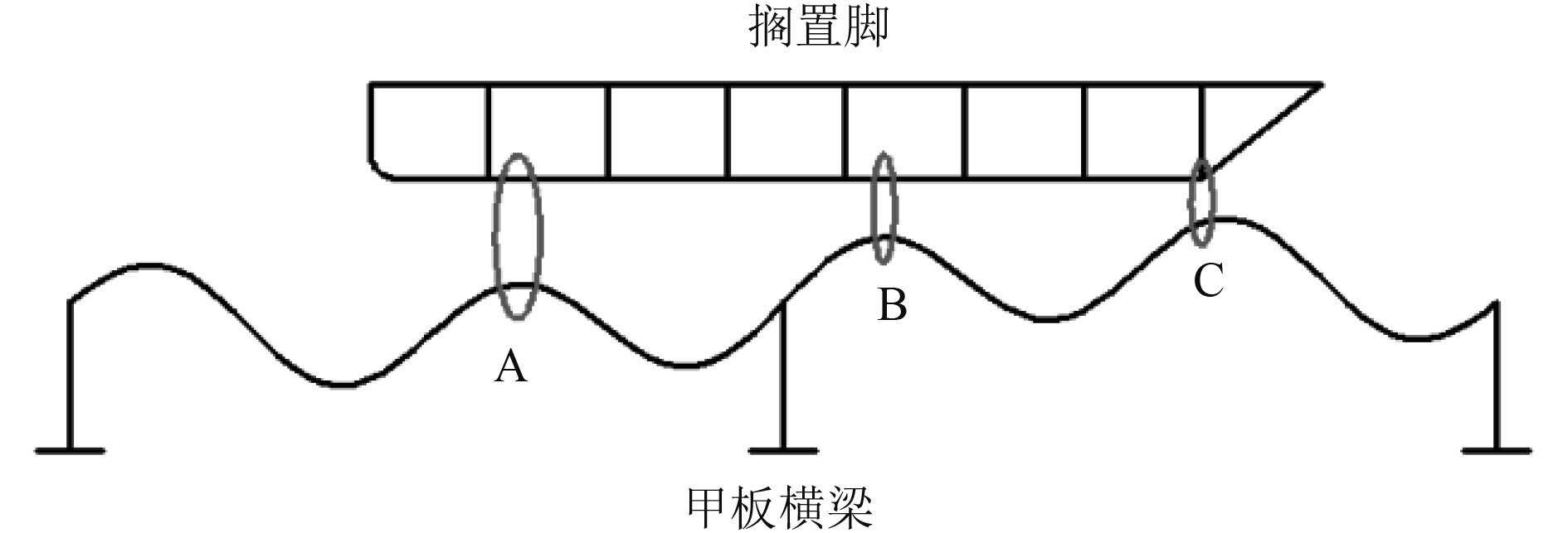
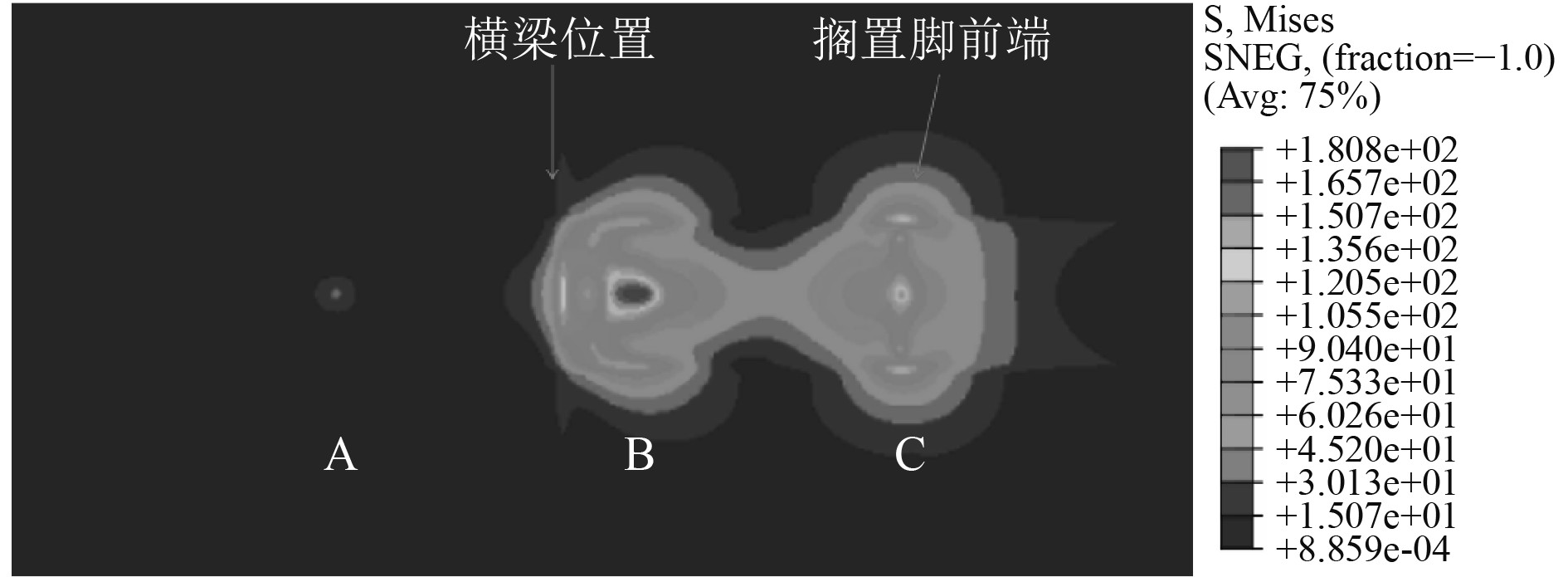
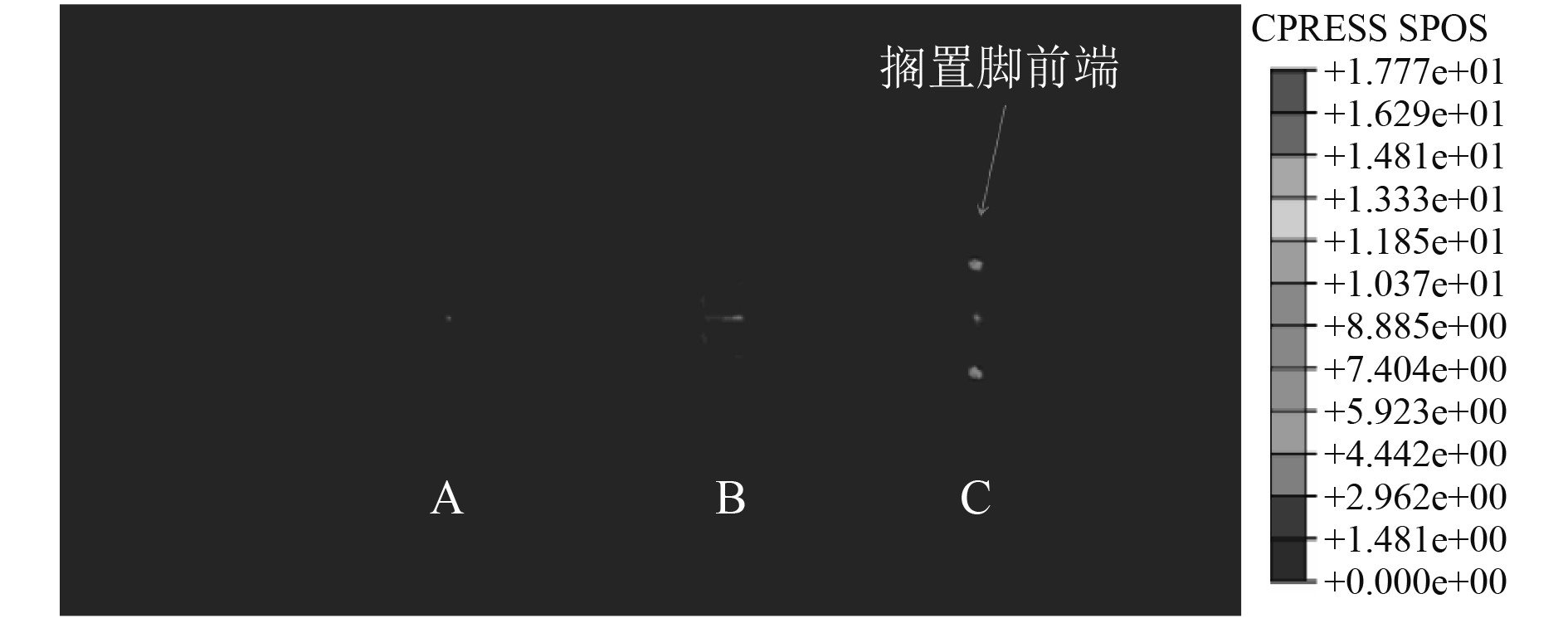
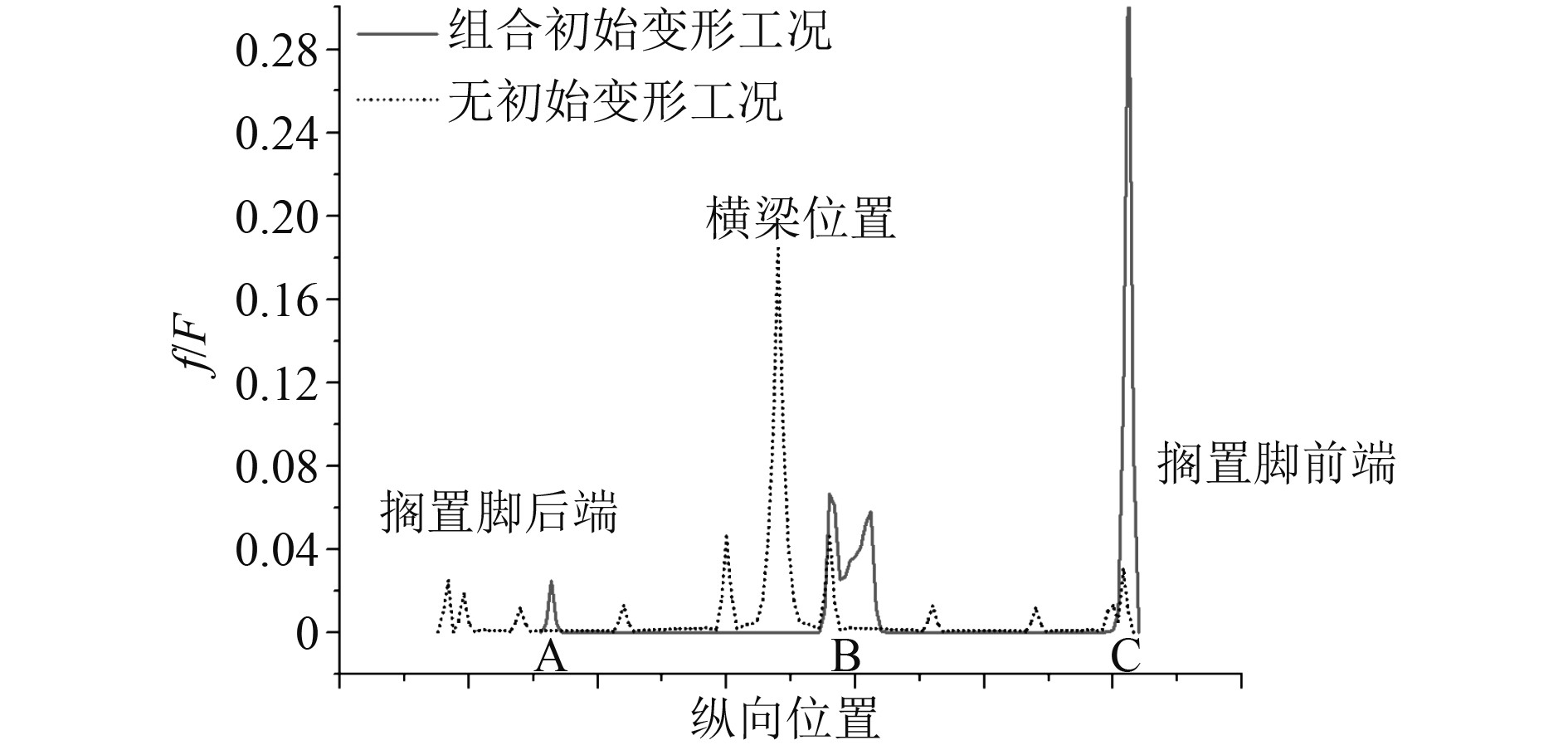
取组合初始变形2工况进行进一步分析，根据甲板板初始变形与搁置脚放置位置，并结合接触力分布云图，得到3个主要接触位置如图18所示。A和B为搁置脚与甲板拱起部分接触位置，C点为搁置脚前端与甲板接触位置。甲板Mises应力分布如图19所示，甲板最大应力依旧增大明显，但此时甲板最大应力不在横梁位置处，而是出现在甲板板局部拱起位置B处。甲板接触力分布力如图20所示，最大接触压力位置位于搁置脚前端与甲板接触位置。同样方法得到接触力在纵向上的分布比例曲线，如图21所示。可以发现，搁置脚前端位置接触力占比最大，甲板横梁位置处与搁置脚并未接触上。此时搁置脚与甲板拱起部分接触位置A点接触合力占比3.32%，搁置脚与甲板拱起部分接触位置B点接触合力占比34.29%，搁置脚前端C点接触合力占比53.19%，3个主要接触位置接触力总占比为90.8%。

4 结　语

1）将各种初始变形单独作用以及组合作用，发现板的初始变形对接触的影响最大，加强筋的梁柱型初始变形对接触的影响次之，加强筋的侧倾初始变形对接触影响很小。应力分布与接触力分布变化明显，说明初始变形对搁置脚接触的影响较大，不能忽略，且这种影响是由甲板板局部拱起所导致的，而甲板局部凹陷处与搁置脚并未接触上，所以影响较小。这对甲板加工精度提出了更高的要求。

2）无初始变形工况计算时，最大Mises应力位置出现在甲板板横梁处，而考虑初始变形后，应力分布也变得复杂，最大应力增大明显，且最大应力位置随着初始变形形式的变化可能出现在甲板板局部拱起位置或搁置脚前端与甲板接触位置。那么在甲板结构设计时对于甲板板的校核需要预留一定的安全余量。

3）得到各工况下接触力在纵向上的分布占比。在无初始变形时，接触力主要由横梁承担，主要接触位置为甲板横梁、搁置脚横隔板以及搁置脚前后端位置；在考虑初始变形后接触力分布复杂，横梁处接触合力占比降低，甲板拱起部分接触合力占比升高。