2. 中国船级社舟山办事处,浙江 舟山 316000
2. Zhoushan Office, CCS, Zhoushan 316000, China
船舶在制造过程中,需考虑船舶的承载应用性,需满足大吨位货物的承载[1-2]。为提升其行驶速度,会对船舶结构实行轻量化设计,但这种结构会导致船舶结构的强度和刚度受到影响[3],在不同载荷情况下,船体结构的承载性能会受到一定影响。因此,如果在保证船舶较大载荷下的承载性能的同时,提升船舶的行驶速度,成为船舶结构设计的核心问题[4,5]。
文献[6]和文献[7]针对船舶结构设计展开相关研究后,分别基于直接计算和基于空腹桁架理论,提出相应的结构强度分析方法,上述方法分别基于不同的角度完成船舶结构的强度分析,但是其在分析过程中,对于船舶在不同荷载情况下的船舶结构的强度变化仍需进一步研究。本文为分析船舶制造结构的强度,提出了基于有限元分析的船舶制造结构设计方法,对船舶结构承载强度实行分析,并且依据有限元分析结果,提出船舶制造结构的优化。
1 基于有限元分析的船舶制造结构设计方法 1.1 船舶制造结构分析的有限元模型采用Ansys有限元分析平台完成船舶制造结构分析,利用该软件对船舶制造结构的抗损程度以及承载强度实行模拟和校核,在对全船实行建模过程中,船舱区域采用的单元尺寸为肋距或者纵骨间距;机舱以及甲板室等区域的建模采用强框架间距尺寸完成,结合建模后载荷的施加[8],仍将肋距或者纵骨作为实际单元的间距尺寸;板应的模拟则采用Shell单元完成,并且在高应力等范围以及位置处,不能够采用三角形单元;通过梁单元完成全船加强筋的模拟[9]。
在全船模型构建过程中,为保证模型的仿真精度,采用插值和网格划分2种方法完成全船形状模拟以及网格划分[10]。
1)数据插值算法:为提升全船形状的模拟精度,采用Akima 插值算法完成模型的数据插值处理,
| $ \left\{ {\begin{array}{l} {{y_k} = f\left( {{x_k}} \right),} \\ {{y_{k + 1}} = f\left( {{y_{k + 1}}} \right)},\end{array}} \right. $ | (1) |
| $ \left\{ {\begin{array}{l} {{g_k} = \dfrac{{{\rm{d}}{y_k}}}{{{\rm{d}}t}}} ,\\ {{g_{k + 1}} = \dfrac{{{\rm{d}}{y_{k + 1}}}}{{{\rm{d}}t}}} 。\end{array}} \right. $ | (2) |
式中:gk表示曲率,且对应当前曲线位置。
2)确定模型表面型线二次多项式,完成全船有限元模型表面网格划分,获取的全船有限元网格划分模型如图1所示。获取的船舶制造结构有限元模型结构主要包含全电焊、纵骨架和横骨架结构[11]。其中纵向结构的船舶部位包含两侧对称的船舶货仓壁、甲板等;横向结构的船舶部分主要包含水密舱壁等。

|
图 1 船舶制造整体有限元网格划分模型 Fig. 1 The overall finite element meshing model of shipbuilding |
模型的主要尺寸和相关参数如表1所示。
|
|
表 1 船舶制造结构有限元模型尺寸和参数 Tab.1 Dimensions and parameters of finite element model of shipbuilding structure |
有限元软件在对船舶制造结构实行抗损程度以及承载强度分析时,主要通过弹性力学[12]、几何和物理3种方程完成。
| $ \left\{ {\begin{array}{*{20}{c}} {\dfrac{{\delta {\sigma _x}}}{{\delta x}} + \dfrac{{\delta {\tau _x}}}{{\delta y}} + \dfrac{{\delta {\tau _z}}}{{\delta z}} + {q_x} = 0}, \\ {\dfrac{{\delta {\tau _x}}}{{\delta x}} + \frac{{\delta {\sigma _y}}}{{\delta y}} + \dfrac{{\delta {\tau _y}}}{{\delta z}} + {q_y} = 0}, \\ {\dfrac{{\delta {\tau _x}}}{{\delta x}} + \frac{{\delta {\tau _y}}}{{\delta y}} + \dfrac{{\delta {\tau _z}}}{{\delta z}} + {q_z} = 0} 。\end{array}} \right. $ | (3) |
几何方程则包含弹性体形变和位移两部分,其公式分别为:
| $ {\varepsilon _x} = \frac{{{{\delta}} u}}{{{{\delta}} x}},{\varepsilon _y} = \frac{{{{\delta}} v}}{{{{\delta}} y}},{\varepsilon _z} = \frac{{{{\delta}} w}}{{{{\delta}} z}} ,$ | (4) |
| $ {\kappa _x} = \frac{{{{\delta}} u}}{{{{\delta}} x}} + \frac{{{{\delta}} v}}{{{{\delta}} y}},{\kappa _y} = \frac{{{{\delta}} w}}{{{{\delta}} x}} + \frac{{{{\delta}} v}}{{{{\delta}} y}},{\kappa _z} = \frac{{{{\delta}} u}}{{{{\delta}} y}} + \frac{{{{\delta}} v}}{{{{\delta}} z}} 。$ | (5) |
物理方程矩阵为:[σ]= [D] [ε],[D]表示弹性矩阵。
1.3 载荷分析主要从海水浮力、空船、满载、波浪扭矩、货物扭矩载荷、静态、动态载荷情况下,分析船舶制造结构。
1)海水浮力载荷:Pw表示海水压力,其加载于船体甲板上,计算公式为:
| $ {P_w} = {\rho _w}g{h_z}。$ | (6) |
式中:Pw,g,hz分别表示密度、加速度、垂直距离,以此分别对应海水、重力、计算点和水线之间。
2)船舶在满载情况下,向模型湿表面每个单元上分布施加压力,其载荷取中垂波面;空载情况下取中拱波面。
3)波浪扭矩等效分布载荷计算公式为:
| $ {p_t}\left( x \right) = \frac{{{m_{{{{T}}}}}\left( x \right)}}{{b\left( x \right)}}。$ | (7) |
式中:b(x)表示等效力偶臂;mT(x)表示分布扭矩。
4)货物扭矩载荷计算公式为:
| $ {p_{tc}}\left( x \right) = \frac{{{m_{tc}}\left( x \right)}}{{b\left( x \right)}}。$ | (8) |
式中:mtc(x)表示分布扭矩,对应货物扭矩。
5)满载时,静态状态下,计算点的载荷计算公式为:
| $ {P_{{\rm{still}}}} = {\rho _c}g{h_z} + {P_0}。$ | (9) |
6)满载时,动态状态下,计算点的垂向、垂向和纵向、横载荷分,具体为:
| $ {P_v} = {\rho _c}g{h_z}\left( {1{\text{ + }}{a_z}} \right) + {P_0},$ | (10) |
| $ {P_{v + l}} = {\rho _c}g{h_z}\left( {1{\text{ + }}{a_z}} \right) + {\rho _c}g{h_x}{a_x} + {P_0},$ | (11) |
| $ {P_t} = {\rho _c}g{h_z} + {\rho _c}g{h_y}{a_y} + {P_0}。$ | (12) |
式中:P0为蒸汽压力;hx和hy均表示纵向的水平距离;ax,ay,az分别表示纵、横、垂3个方向加速度分量。
1.4 船体制造结构尺寸优化采用Ansys有限元分析平台完成船舶模型结构尺寸优化。优化的目标函数W(x)为保证优化后船舶制造结构在满载静态情况下,结构的最大应力不超过应力的上限值。约束条件为:
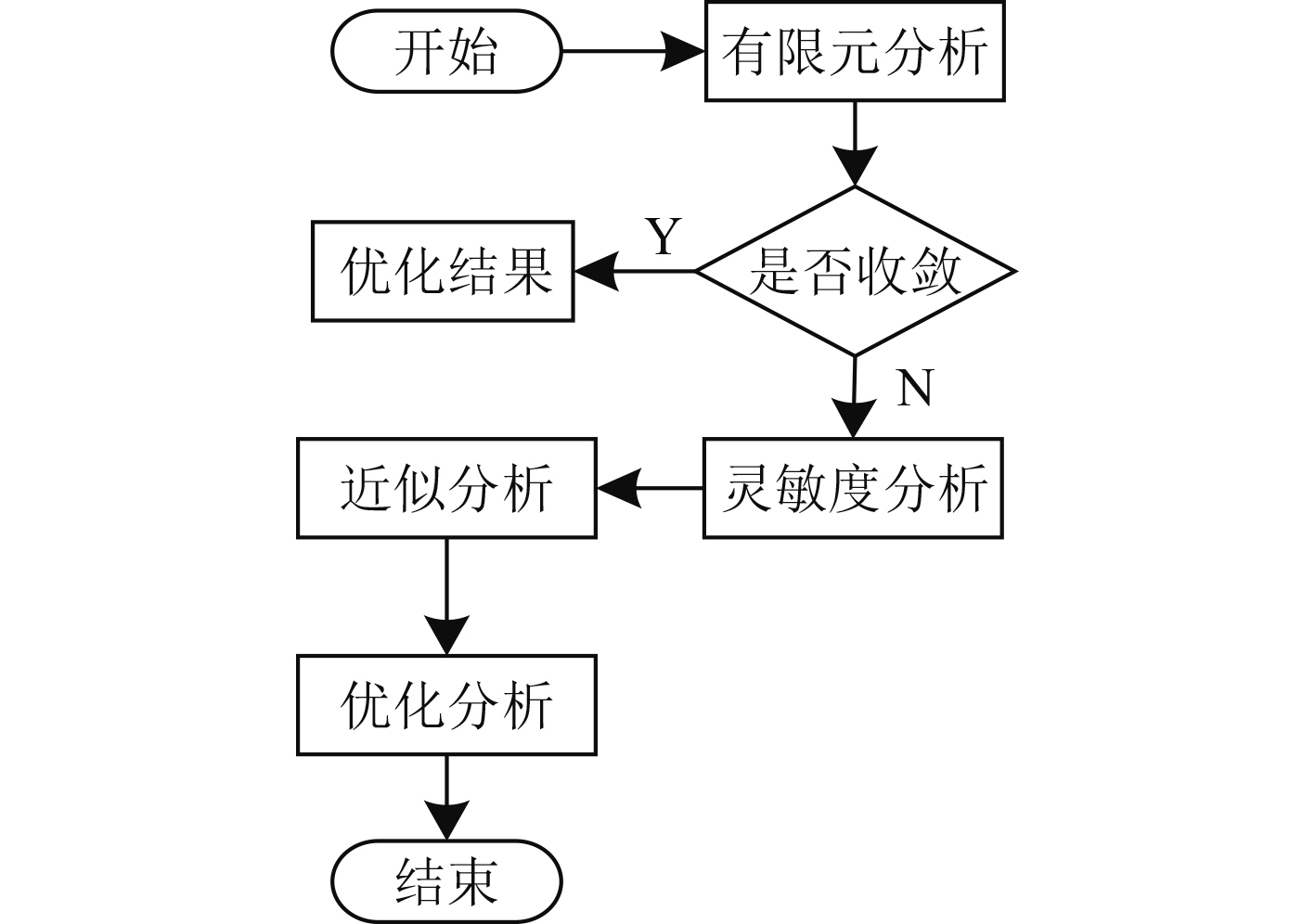
|
图 2 船舶制造模型结构优化流程 Fig. 2 Structure optimization process of ship manufacturing model |
对船舶结构部位的最大应力测试结果进行分析,结果仅呈现载荷分析中的满载和空载2种载荷在动态情况下的船舶5个部位的应力结果,如表2所示。按照本文方法以及船舶模拟的相关数据尺度要素,完成全船模拟,并且获取船舶在空载静态状态下,船舶结构的应力分布结果如图3所示。依据表2结果可知:本文方法能够获取不同载荷下总体船舶不同结构部位的应力分布结果,并且可得出最大应力值的位置,表明本文的方法适用于船舶制造结构应力分析中,能够提供船舶制造结构的分析结果。依据图3结果可知:船舶在空载静态状态下,船舶整体结构中,在船体下方中心位置,发生小范围应力分布,其载荷分布相对较为均匀,因此本文方法具备船舶制造结构应力分析功能,可模拟船舶的应力分布结果。
|
|
表 2 船舶5个部位的应力结果 Tab.2 Stress results of five parts of the ship |
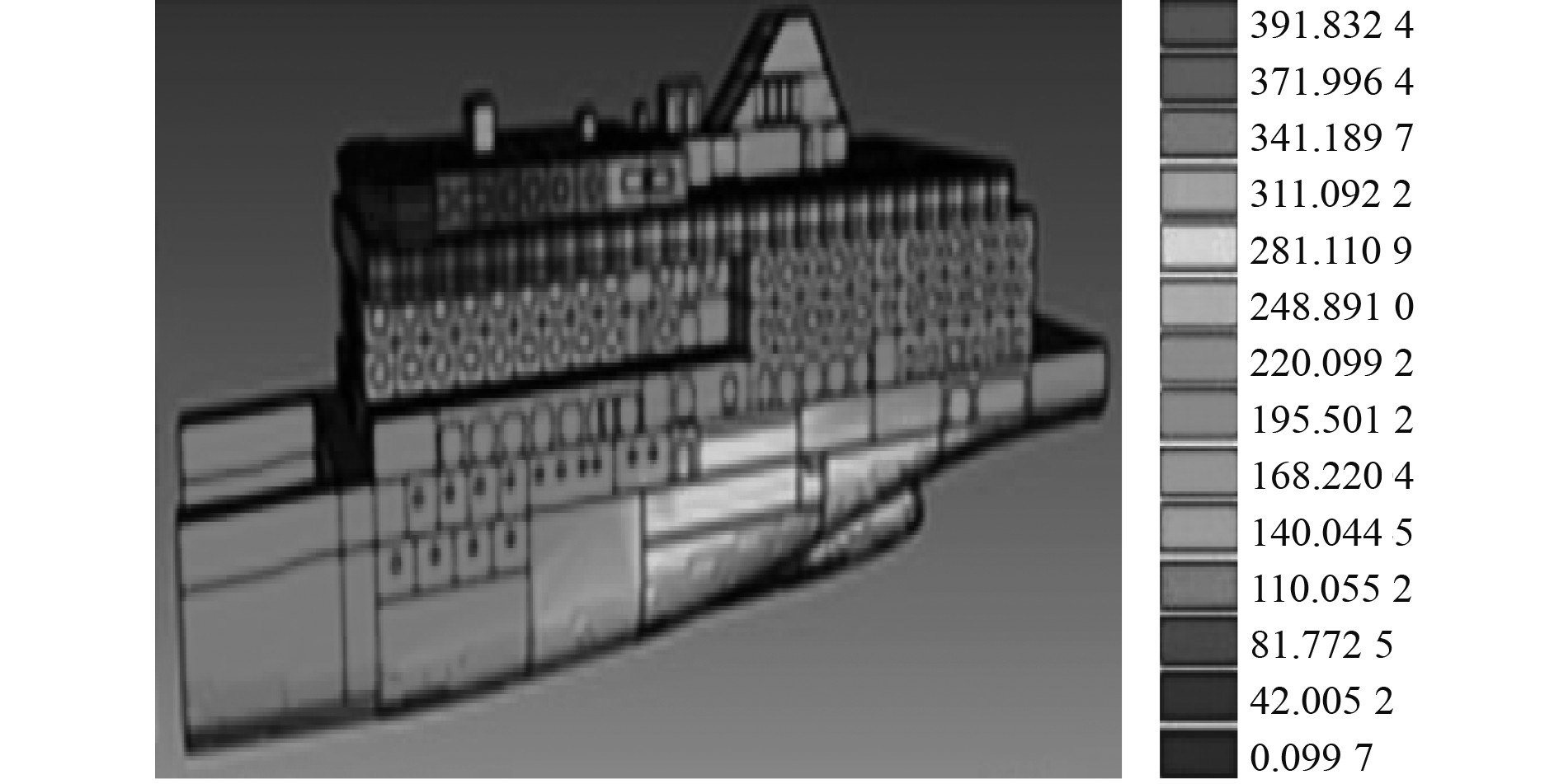
|
图 3 空载静态状态下总体船舶结构应力分布结果 Fig. 3 Stress distribution results of the overall ship structure in the no-load static state |
甲板支撑结构在货物扭矩载荷下,其纵向加筋板结构的扭转焊接变形结果如图4和图5所示。分析可知:甲板支撑结构纵向加筋板在货物扭矩载荷下,会随着货物的扭矩发生焊缝失稳形变,最大发生接近8 cm的变形,导致焊缝产生纵向应力,导致焊接板发生焊接处失稳现象,以此会极大程度引发焊缝裂纹。因此,船舶制造结构会在不同的载荷下,发生不同的应力分布结果。
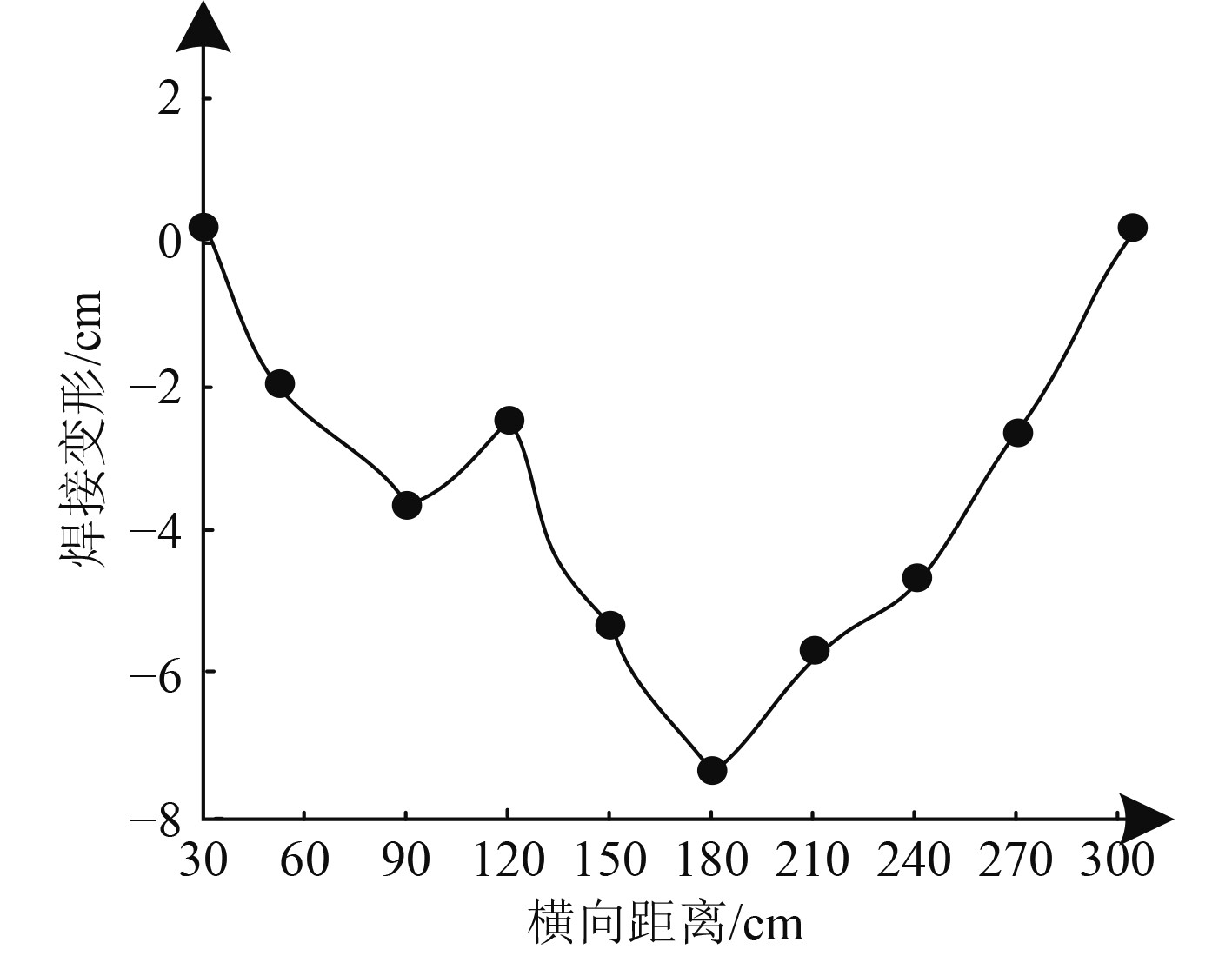
|
图 4 纵向加筋板结构的扭转焊接变形结果 Fig. 4 Torsion welding deformation results of longitudinal stiffened plate structure |

|
图 5 纵向加筋板结构的扭转焊接变形应力分布 Fig. 5 Distribution of deformation stress during torsional welding of longitudinal stiffened plate structure |
采用优化方法对船舶模型结构的尺寸实行优化,优化的目标函数为保证优化后船舶制造结构在满载静态情况下,结构的最大应力不超过应力的上限值,获取优化结果如表3和图6所示。尺寸优化结果仅呈现船舶6个结构部位的优化结果。分析可知:本文方法对船舶制造结构尺寸实行后,不改变约束条件的前提下,目标函数值显著降低,优化后,船舶的6个结构部位的最大应力均不超过上限值,并且完成船舶结构尺寸优化后,随着优化部位结构数量的增加,整体船舶质量也逐渐发生轻量化。
|
|
表 3 船舶模型结构的尺寸优化结果(mm) Tab.3 Size optimization results of ship model structure (mm) |
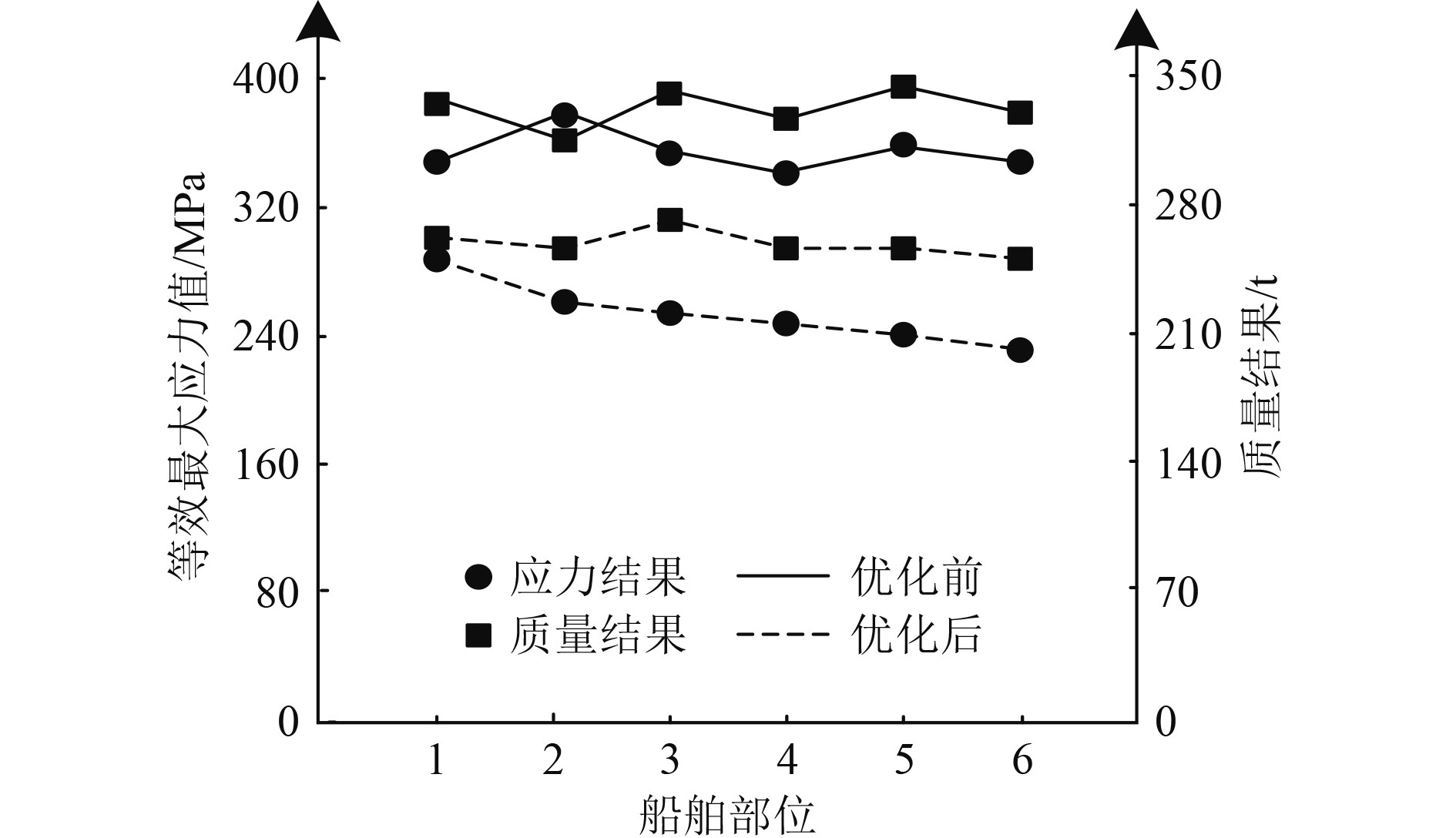
|
图 6 船舶制造结构优化结果 Fig. 6 Optimization results of ship manufacturing structure |
为分析船舶制造结构的性能,本文研究基于有限元分析的船舶制造结构设计方法,采用有限元分析平台,按照船舶数据对其实行全船建模,并计算分析其结构应力结果,分析船舶的结构性能,提出结构尺寸优化方法。分析结果表明:本文方法能够全面完成船舶制造结构模拟分析,且分析结果可靠。同时,依据分析结果确定船舶结构的应力情况,并针对性给出结构优化方法,提升船舶结构的承载性能,为船舶制造提供可靠依据。
| [1] |
张帆, 李瑞, 刘玉君, 等. 基于参数化方法的船体分段吊装快速有限元分析技术[J]. 大连理工大学学报, 2020, 60(1): 22-29. |
| [2] |
于兴鹏, 管义锋, 赵铁军, 等. 双体铝合金风电运维船结构强度有限元分析[J]. 舰船科学技术, 2021, 43(15): 42-46. |
| [3] |
潘文秀. 基于有限元分析的散货船横向强度计算[J]. 舰船科学技术, 2020, 42(2): 1-3. DOI:10.3404/j.issn.1672-7649.2020.02.001 |
| [4] |
李坤宏, 陈峥. 有限元分析在船舶复杂结构强度计算与优化中的应用[J]. 舰船科学技术, 2020, 42(20): 4-6. |
| [5] |
田阿利, 姚鹏, 傅梓轩, 等. SPS覆层船艏局部加强结构的抗砰击性能仿真分析[J]. 中国舰船研究, 2020, 15(4): 59-65. |
| [6] |
甄春博, 王天霖, 于鹏垚. 基于直接计算的三体船结构疲劳强度影响因素分析[J]. 中国舰船研究, 2017, 12(3): 86-90. DOI:10.3969/j.issn.1673-3185.2017.03.012 |
| [7] |
乔鹏远, 袁昱超, 薛鸿祥, 等. 基于空腹桁架理论的船体结构腹板开孔强度简化分析方法[J]. 舰船科学技术, 2020, 42(7): 31-35+55. |
| [8] |
李荣, 李毓洲, 张笛, 等. 基于多因素耦合的超大型风电安装船设计参数有限元计算与实船参数验证[J]. 船海工程, 2020, 49(4): 60-65. DOI:10.3963/j.issn.1671-7953.2020.04.016 |
| [9] |
殷小琪, 刘亚东. 大开口深拖母船全船强度有限元分析[J]. 船舶工程, 2020, 42(9): 44-48+92. |
| [10] |
赵杰, 赵丁辉, 熊伟, 等. 不同扶正方案下的破损舱段强度有限元分析[J]. 船舶力学, 2020, 24(5): 618-625. DOI:10.3969/j.issn.1007-7294.2020.05.007 |
| [11] |
邱吉廷, 李文华, 郑文青. VLGC舱段结构强度有限元分析方法[J]. 船海工程, 2020, 49(1): 61-66+71. DOI:10.3963/j.issn.1671-7953.2020.01.015 |
| [12] |
张庆亚, 卓子超, 周宏, 等. 厚板多层多道对接焊残余应力轮廓法测量及热-弹-塑性有限元分析[J]. 船舶力学, 2021, 25(5): 627-636. DOI:10.3969/j.issn.1007-7294.2021.05.011 |
 2001, Vol. 44
2001, Vol. 44
