0 引　言

流体与结构砰击是船舶与海洋工程领域的一个重要研究问题。砰击发生的时间非常短暂，此时压力和流体质点加速度非常大并且在短时间内快速变化，这一物理过程极其复杂，若进一步考虑内部液体运动的影响，此类问题的研究将更具挑战性。

瓦格纳理论是解决入水砰击问题的重要方法之一。基于这个方法，Howison等^[1] 给出了一个小底升角物体入水问题的显式解，Korobkin ^[2]采用2阶瓦格纳理论研究砰击问题。而非线性边界元法在砰击问题的求解中更加精确，一方面采用此方法可以捕捉到物面与自由面交线的精确位置，另一方面拉伸坐标系技术的引入可使物面砰击压力的求解更加精确^[3]。基于边界法的代表性工作包括Dobrovol^[4]以及Zhao等^[5]关于对称楔形体的垂向入水问题研究。在边界元基础上，考虑拉伸坐标系的工作包括，Xu等^[6]非对称楔形体斜向入水，和Wu ^[7]双楔形体入水问题。然而这些工作均是针对匀速情况。Wu等考虑了楔形体单自由度自由入水问题，Xu等^[8]研究了楔形体三自由度自由入水，Sun等^[9]考虑了楔形体在波浪中的斜向入水。

张书谊等^[10]基于CFD软件Fluent探索了二维情况下矩形液舱内液体水动力特性。朱仁庆等^[11]对船舱内液体的三维晃荡特性进行分析，揭示了三维情况下液舱晃荡机理。甄长文等^[12]对于三维共振频率下油船液舱舱内液体晃荡情况进行模拟研究，发现当晃荡稳定后舱内液体以驻波与行波组合的方式运动。李裕龙等^[13]基于OpenFOAM对载液船舶在波浪中的运动进行研究，揭示了船舶在发生液舱晃荡时的横摇特性。还有一些其他典型的工作，包括骆阳等^[14]研究了两船体靠近时运动与液舱晃荡的耦合效应，朱仁庆等^[15]研究了弹性舱壁与液体晃荡的相互耦合作用，龚少军等^[16]基于粒子法研究了液舱共振现象。

本文基于不可压缩势流理论，采用边界元方法，求解楔形液舱入水问题。建立2个独立计算域，第一个计算域用于计算内部流场，第二个计算域用于计算外部流场。前者在物理坐标系下求解，后者在拉伸坐标系下求解。2个计算域内流体运动以及液舱壳之间的耦合通过辅助函数方法实现。本文将展开液舱内相同质量水和冰的对比性研究，以深入分析当液舱内流体质点发生运动对整个耦合系统的影响。

1 数学模型和数值过程 1.1 物理参数的定义和笛卡尔坐标系

图1描述了一个二维楔形液舱在给定初始速度条件下自由入水问题。物体的旋转中心固定在楔形体尖端，以 $O$ 表示，建立一个笛卡尔坐标系 $O - xy$ ，随物体平动， $x$ 轴水平向右， $y$ 轴竖直向上。关于 $O$ 的水平速度、垂向速度和旋转速度分别表示为 $U$ ， $W$ 和 $\varOmega$ ， $W$ 向下为正。 $t = 0$ 时刻，用 ${U_0}$ ， ${V_0}$ 和 $\varOmega _0$ 表示初始速度。 $\theta $ 为楔形体对称轴旋转角度， ${\theta _0}$ 为入水时刻初始角度， ${\gamma _0}$ 为楔形体内半角。基于以上定义，楔形体左右底升角 ${\gamma _1}$ 和 ${\gamma _2}$ 采用以下关系式求解。

$ {\gamma _1} = \frac{\text{π} }{2} + \theta - {\gamma _{\text{0}}},{\gamma _2} = \frac{\text{π} }{2} - \theta - {\gamma _{\text{0}}}。$

(1)

楔形体运动的垂向位移 $s$ ，水平位移 $l$ 以及旋转角度 $\theta $ 与相应速度关系式为

$ \dot{s}(t)=W(t)\text{，}\dot{l}(t)=U(t)\text{，}\dot{\theta }(t)=\varOmega (t)。$

(2)

1.2 数学模型

采用完全非线性边界元方法对以下数学模型进行求解。在流体域内满足拉普拉斯方程，引入其梯度等于流体质点速度的速度势 $ {\phi _i} $ 分析流场，因此有

$ {\nabla ^2}{\phi _i}{\text{ = 0}},\begin{array}{*{20}{c}} {} \end{array}(i = 1,2)，$

(3)

其中，下标1和 2分别代表液舱内部流体域和液舱外部流体域，简称内域和外域。在动坐标系下满足的其他边界条件为：

$ \frac{{{\rm{D}}{\phi _i}}}{{{\rm{D}}t}} = \frac{1}{2}{\left| {\nabla {\phi _i}} \right|^2} - g(y - s) \text{，}自由面，$

(4)

$ \frac{{{\rm{D}}x}}{{{\rm{D}}t}} = \frac{{{\partial} {\phi _i}}}{{\partial x}} - U,\begin{array}{*{20}{c}} \end{array}\frac{{{\rm{D}}y}}{{{\rm{D}}t}} = \frac{{\partial {\phi _i}}}{{\partial y}} + W \text{，}自由面，$

(5)

$ \frac{{{{\partial}} {\phi _i}}}{{{{\partial}} n}} = (U - \Omega y){n_x} + ( - W + \Omega x){n_y} \text{，}物面，$

(6)

$ \nabla {\phi _{\text{2}}}{\text{ = }}0 \text{，}外域远场。$

(7)

$ {y_i}(x,t = 0) = {H_i},\begin{array}{*{20}{c}} {} \end{array}{\phi _i}(x,{H_i},t = 0) = 0\text{，}初始时刻 。$

(8)

其中， $ {H_1} $ 为初始时刻内域液面深度，外域初始时刻为静水，且坐标系原点在静水面上，因此有 $ {H_2} = 0 $ 。

由于在初始入水时刻，楔形体只有极其微小的部分进入到水中。为保证外域的计算精度，将针对外域采用拉伸坐标系技术^[3]。定义一个拉伸坐标系 $ O - \alpha \beta $。

$ {\phi _2}(x,y,t) = s\varphi (\alpha ,\beta ,t),\alpha = x/s,\beta = y/s，$

(9)

其中， $s$ 为采用式（2）计算的垂向位移。在拉伸坐标系下，物面与自由面边界条件为：

$ \frac{{{{\partial}} \varphi }}{{{{\partial}} n}} = (U - s\Omega \beta ){n_\alpha } + ( - W + s\Omega \alpha ){n_\beta }\text{，}物面, $

(10)

$ \frac{{{\rm{D}}(s\varphi )}}{{{\rm{D}}t}} = \frac{1}{2}(\varphi _\alpha ^2 + \varphi _\beta ^2) - g(s\beta - s)\text{，}自由面, $

(11)

$ \frac{{\rm{D}}(s\alpha )}{{\rm{D}}t}={\phi }_{\alpha }-U\text{，}\begin{array}{c}\end{array}\frac{{\rm{D}}(s\beta )}{{\rm{D}}t}={\phi }_{\beta }+W \text{，}自由面。$

(12)

2个计算域的控制方程和边界条件确立以后，均可以采用边界积分公式进行求解，可参考文献[17]。

1.3 压力求解

基于伯努利方程和自由面零压条件，流场压力可表达为：

$ {p_i} = - {\rho _i}\left[ {{\phi _{it}} + \frac{1}{2}{{\left| {\nabla {\phi _i}} \right|}^2} + g(y - s)} \right]，$

(13)

其中， $ {\rho _i}(i = 1,2) $ 分别为内域和外域流体密度。通过前面的边界积分公式可以求解出 ${\phi _i}$ ，速度势梯度 $ \nabla {\phi _i} $ 可以通过数值方法求解。然而式（13）中 $ {\phi _{it}} $ 是未知的。为处理这一问题，采用辅助函数方法。 $ {\phi _{it}} $ 满足的物面边界条件为^[18]：

$ \frac{{{\partial} {\phi _{it}}}}{{{\partial} n}} = \left( {{{\dot {\boldsymbol{U}}}} + {{\dot {{\varOmega}} }} \times {\boldsymbol{{{x}}}}} \right) \cdot {\boldsymbol{{{n}}}} - {\boldsymbol{{{U}}}} \cdot \frac{{{{\partial}} \nabla {\phi _i}}}{{{{\partial}} n}} + {{{{\varOmega}} }} \cdot \frac{{{\partial}} }{{{{\partial}} n}}\left[ {{\boldsymbol{{x}}} \times \left( {{\boldsymbol{{U}}} - \nabla {\phi _i}} \right)} \right]。$

(14)

需要注意式（14）中加速度是未知的，所以无法通过这个公式直接求解压力，因此建立多个辅助函数，以实现物体运动和流体压力的解耦。

$ {\phi _{it}} = {\chi _{i0}} + \dot U{\chi _{i1}} + \dot W{\chi _{i2}} + \dot \Omega {\chi _{i3}} - {\boldsymbol{{U}}} \cdot \nabla {\phi _i} + {\varOmega} \cdot \left[ {{\boldsymbol{{x}}} \times \left( {{\boldsymbol{{U}}} - \nabla {\phi _i}} \right)} \right]。$

(15)

流体域内辅助函数 $ {\chi _{ij}}(i = 1,2;j = 0 \cdots 3) $ 满足拉普拉斯方程。其他边界条件可分别表达为：

$ \begin{split}\frac{{{{\partial}} {\chi _{ij}}}}{{{{\partial}} n}} =& {n_j},{n_0} = 0,{n_1} = {n_x},{n_2} = {n_y},{n_3} = (x{n_y} - y{n_x}),\\ &(i = 1,2,j = 0, \cdots, 3)\text{，}物面，\end{split} $

(16)

$ \begin{split}{\chi _{i0}} = & - \left[ {\frac{1}{2}{{\left| {\nabla {\phi _i}} \right|}^2} + g(y - s)} \right] + U{\phi _{ix}} - W{\phi _{iy}} - \\& {\varOmega} \left[ {x( - W - {\phi _{iy}}) - y(U - {\phi _{ix}})} \right] \text{，}自由面，\end{split}$

(17)

$ {\chi _{ij}} = 0,(i = 1,2,j = 1,2,3) \text{，}自由面，$

(18)

$ \frac{{{{\partial}} {\chi _{20}}}}{{{{\partial}} n}} = \Omega ({n_x}W + {n_y}U) \text{，}远场，$

(19)

$ \frac{{{\partial} {\chi _{2i}}}}{{{\partial}} n} = 0,(i = 1,2,3) \text{，}远场。$

(20)

所有辅助函数均可以采用边界积分公式求解。

1.4 运动方程

楔形液舱入水的运动方程可表达为

$ \left[ {{{\boldsymbol{M}}_0}} \right]\left[ {\boldsymbol{A}} \right] = \left[ {{{\boldsymbol{F}}_1}} \right] + \left[ {{{\boldsymbol{F}}_2}} \right] + \left[ {{{\boldsymbol{F}}_{\text{G}}}} \right]。$

(21)

其中：

$ \left[ {{{\boldsymbol{M}}_0}} \right] = \left[ {\begin{array}{*{20}{c}} {{m_0}}&0&{ - {m_0}{l_{c0}}\cos \theta } \\ 0&{{m_0}}&{ - {m_0}{l_{c0}}\sin \theta } \\ { - {m_0}{l_{c0}}\cos \theta }&{ - {m_0}{l_{c0}}\sin \theta }&{{I_0}} \end{array}} \right]，$

(22)

为液舱壳的质量矩阵。其中 $ {m_0} $ 为液舱壳质量， $ {I_0} $ 为转动惯量， $ {l_{c0}} $ 为质心和旋转中心距离。式（21）中 $\left[ {\boldsymbol{A}} \right]$ 为加速度向量， $\left[ {{{\boldsymbol{F}}_1}} \right]$ ， $\left[ {{{\boldsymbol{F}}_2}} \right]$ 和 $\left[ {{{\boldsymbol{F}}_{\text{G}}}} \right]$ 分别为内部水动力，外部水动力和物体重力向量。 $\left[ {{{\boldsymbol{F}}_1}} \right]$ 和 $\left[ {{{\boldsymbol{F}}_2}} \right]$ 可通过沿内湿表面 $ {S_1} $ 和外湿表面 $ {S_2} $ 进行压力积分求解。因此有：

$\begin{split} {{\boldsymbol{F}}_i} = & - {\rho _i}\int_{{S_i}} \Biggr\{ {\chi _{i0}} + \dot U{\chi _{i1}} + \dot W{\chi _{i2}} + \dot \Omega {\chi _{i3}} - {\boldsymbol{U}} \cdot \nabla {\phi _i} + \\& {{\varOmega }} \cdot \left[ {{\boldsymbol{x}} \times \left( {{\boldsymbol{U}} - \nabla {\phi _i}} \right)} \right] + \frac{1}{2}{{\left| {\nabla {\phi _i}} \right|}^2} + g(y - s) \Biggr\}{\boldsymbol{n}}{\rm{d}}s \end{split}。$

(23)

将式(23) 代入式 (21)，并且把加速度项移动到左端，可以得到

$ (\left[ {{{\boldsymbol{M}}_0}} \right] + \left[ {{{\boldsymbol{C}}_1}} \right] + \left[ {{{\boldsymbol{C}}_2}} \right])\left[ {\boldsymbol{A}} \right] = \left[ {{{{\boldsymbol{F'}}}_1}} \right] + \left[ {{{{\boldsymbol{F'}}}_2}} \right] + \left[ {{{\boldsymbol{F}}_{\text{G}}}} \right]。$

(24)

其中：

$ {C_{ijk}} = {\rho _i}\int\limits_{{S_i}} {{\chi _{ij}}{n_k}{\rm{d}}s}，$

为内部流体和外部流体的附加质量。

$\begin{split} {{\boldsymbol{F'}}_i} = & - {\rho _i}\int_{{S_i}} \Biggr\{ {\chi _{i0}} - {\boldsymbol{U}} \cdot \nabla {\phi _i} + {{\varOmega }} \cdot \left[ {{\boldsymbol{x}} \times \left( {{\boldsymbol{U}} - \nabla {\phi _i}} \right)} \right] +\\ &\frac{1}{2}{{\left| {\nabla {\phi _i}} \right|}^2} + g(y - s) \Biggr\}{\mathbf{n}}{\rm{d}}s。\end{split} $

当液舱内部的水被冻成冰时，液舱内部流体的附加质量和水动力均为0。

2 数值结果与讨论

分别对内半角 ${\gamma _0}$ 分别为45°和60°的楔形液舱进行讨论， ${\theta _0}$ 取为0，见图1。液舱内部流体高度 ${H_1} = {\text{1}}\;{\rm{{m}}}$ ，内外部流体密度均为 ${\rho _{\text{1}}}{\text{ = }}{\rho _{\text{2}}}{\text{ = 1\;025}}\;{\rm{kg\cdot{m^{ - 3}}}}$ 。假设液舱壳没有厚度和体积，因此液舱壳的质量和转动惯量均为0，相当于式（21）中矩阵 $\left[ {{{\boldsymbol{M}}_0}} \right] = 0$ 。将旋转中心设置在楔形体尖端，即强迫液舱绕楔形体尖端旋转，设置初始速度为 $W = 5\;{\rm{m}}\cdot{{\rm{s}}^{ - 1}}$ ， ${{\varOmega}} {\text{ = }}1\;{{\rm{s}}^{ - 1}}$ ， $U = 0$ 。本文将分别对内半角 ${\gamma _0}$ 为45°和60°的楔形液舱进行运动特性研究。

2.1 内半角 ${\gamma _0}$ 为45°的楔形液舱入水

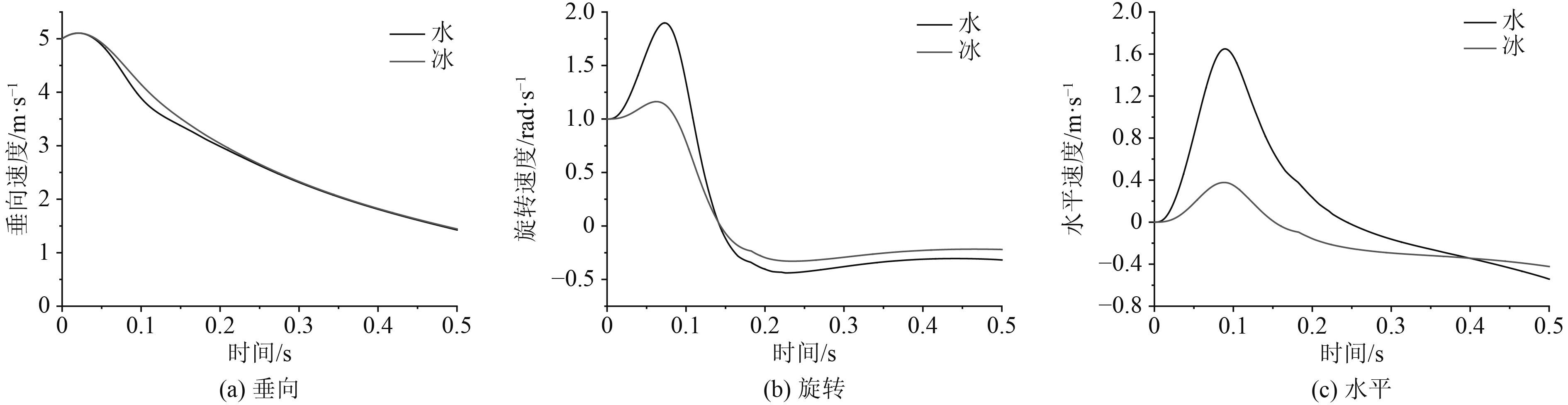
图2给出了内半角 ${\gamma _0}$ 为45°时水舱和冰舱的运动时历图，液舱内水与冰质量、体积和高度相等。如图2（a）所示，在初始阶段，水舱和冰舱的垂向速度略有增加，然后很快达到峰值。这主要取决于流体载荷和物体重力之间的平衡。与一般水面水动力问题不同，在开始的一段时间内，大部分楔形体都暴露在空气中，并未与水接触，此时水动力小于楔形体本身的重力，基于牛顿定律，楔形体在初始阶段将经历一段加速。随着楔形体进一步进入到水中，物面湿面积增加显著，物体受到的水动力也显著增加。当向上的水动力大于重力时，物体的加速将变为减速，因此垂向速度也随之降低。由图2（a）可见，水舱与冰舱的垂向运动时历曲线基本重合，由此可以推断，舱内流体质点的运动对垂向运动影响较小。

如图2（b）所示，入水过程中，水舱和冰舱旋转速度都呈现出先增加，再快速降低，然后达到平稳的变化过程。这是由于旋转中心位于楔形体尖端，而物体重心位于旋转中心之上，当物体发生旋转时，将产生与旋转方向相同的力矩，使物体旋转运动加速。随着旋转角度的增加，顺旋转方向一侧的底升角 ${\gamma _1}$ 变小，对应侧面的水动力或砰击力增加；与此同时，反面的底升角增加并且水动力变小，水动力在楔形体两侧作用面的差别将导致形成一个逆物体旋转方向的力矩。当逆旋转方向的水动力力矩与重力力矩平衡时，角速度达到峰值。此后，水动力力矩继续增大，物体开始减速。水舱的运动幅度明显大于冰舱的运动幅度，这主要是两点原因造成的。首先，与同等质量冰相比，每个流体质点的加速度都不同，这将导致液舱内流体的附加质量小于冰的质量，使液舱既容易加速，也容易减速。其次，液舱内水的流动性将导致水的质心比冰的质心移动更快，物体将获得更大的作用力合力，这是导致液舱运动幅度较大的另外一个重要原因。

图2（c）中的水平速度开始增加，然后减小。水平速度增加主要是由于水舱或冰舱在旋转中，顺旋转方向物面底升角变小，逆旋转方向物面底升角增加，导致前者表面压力增加，后者表面压力降低。两侧压力差形成的水平方向合力将导致物体向水平方向加速度运动。在物体水平加速运动过程中，顺水平运动方向的流体质点与物面相对运动速度增加，逆水平运动方向的流体质点与物面相对运动速度降低，这将导致前者压力增加，后者压力降低，此时形成的水平方向合力的作用是使物体水平减速。还可以发现，图2（c）中，仍然是水舱运动幅度较大，原因与图2（b）类似。

2.2 内半角 ${\gamma _0}$ 为60°的楔形液舱入水

图3给出了内半角 ${\gamma _0}$ 为60°时水舱和冰舱的运动时历图，液舱内水与冰质量、体积和高度相等。对于内半角 ${\gamma _0}$ 为60°时水舱和冰舱入水时的垂向速度、旋转速度和水平速度变化的原因与上文内半角 ${\gamma _0}$ 为45°时一样。讨论当内半角 ${\gamma _0}$ 由45°变到60°时，液舱垂向速度、旋转速度和水平速度的变化情况。

当内半角 ${\gamma _0}$ 由45°变到60°时，垂向运动时历曲线变化趋势基本保持不变，但是内半角 ${\gamma _0}$ 为60°时，垂向速度减小的更快。这是由于内半角 ${\gamma _0}$ 增大导致左右底升角变小，在楔形体入水过程中，相同时刻下物面湿面积更大，物体受到的水动力也更大。因此内半角 ${\gamma _0}$ 为60°时，垂向速度的峰值到来的更早且峰值较小，随时间减小的更快。

内半角的增加同样影响旋转速度和水平速度。当内半角 ${\gamma _0}$ 为60°时，两侧的底升角小于内半角 ${\gamma _0}$ 为45°时的底升角。在入水过程中，由于旋转速度增加导致的顺旋转方向一侧的底升角 ${\gamma _1}$ 比相同时刻内半角 ${\gamma _0}$ 为45°时的底升角 ${\gamma _1}$ 更小，对应侧面的水动力或砰击力更大。与此同时，反面的底升角虽然由于底升角减小导致水动力增大，但是顺旋转方向一侧的水动力增加的更大，因此水动力在楔形体两侧作用面更大的差别导致的逆物体旋转方向的力矩更大。因此，内半角 ${\gamma _0}$ 为60°时液舱的旋转速度峰值更早到来，并且小于内半角 ${\gamma _0}$ 为45°时的峰值。

对于水平速度，两侧压力差形成的水平方向合力是物体向水平方向加速运动或减速运动的原因。与旋转速度一样，内半角的增加会导致顺水平运动方向的流体质点与物面相对运动速度增加的更快，逆水平运动方向的流体质点与物面相对运动速度降低的更快。由此引起两侧压力差的增大，使得内半角 ${\gamma _0}$ 为60°时液舱的水平速度的峰值更早的到来，并且小于内半角 ${\gamma _0}$ 为45°时的峰值。

3 结　语

基于完全非线性边界条件的势流理论，用边界元法求解了自由下落的楔形液舱入水问题。研究了液舱内部载有等质量水或冰入水时的楔形液舱运动特性，通过对比不同内半角的楔形液舱入水，得到以下结论：

1）舱内液体的运动对垂向速度影响较小，对旋转速度和水平速度影响较大。垂向速度主要由楔形液舱的重力和垂直方向的水动力决定，垂向水动力对于液舱内液体的流动并不敏感，舱内流体质点的运动对垂向运动影响较小。而对于旋转速度和水平速度，随着液舱内流体的运动，不同的流体质点会以不同的加速度运动，这会导致附加质量不同于相同重量的冰，此时液舱更容易加速和减速。除此之外，舱内液体的流动会使楔形液舱的质心更快的移动，液舱将获得更大的合力或力矩。所以当液舱装有水时，旋转速度和水平速度的幅值更大。

2）楔形液舱内半角的增大会使垂向速度、旋转速度和水平速度随时间减小的更快且峰值更小。内半角增大会导致两侧的底升角减小，从而导致相同时刻下物面湿面积更大、逆物体旋转方向的力矩更大以及楔形体两侧压力差更大。因此速度峰值更早的到来，液舱的垂向速度、旋转速度和水平速度减小的更快。