船舶阻力预报是船舶设计中一项极为重要的指标,在船舶设计之初就需要进行船舶阻力预报,船舶阻力预报的精度直接影响船舶快速性及航速指标的完成进而影响交船等重大节点的成败。船舶阻力预报现行有试验方法、一维方法和三维方法3种[1]。在工程界,船舶设计是一个呈螺旋上升并不断更新迭代的过程。在不同的阶段,限于已知和未知信息的权重,迫使设计师不得不选择不同的计算方法。因此,本文提出3种方法用于在不同阶段进行船舶阻力计算,以满足工程项目的实际需求。
在船舶设计之初,船体三维模型还未成型,但此时又需要进行船舶快速性分析以求初定主机功率并据此确定为主机服务的辅机设备规格,这时只能运用一维方法,该方法在仅知道一些很少的船舶主参数(如船长、型宽、方形系数CB和水线面系数CW等)的基础就能进行船舶阻力计算。比较著名的一维计算方法包括1957ITTC船舶摩擦阻力系数计算公式和Holtrop实船总阻力系数计算公式等[2]。这种类似的一维计算公式非常多,在开发这些公式的过程中,运用统计学方法分析并融入了大量船模和实船阻力数据。这些公式大多被开发成了程序,以便于使用,比较典型的程序比如NavCad[3]。这些一维计算公式都有一定的适应范围,在使用过程中,需要特别注意。如果目标船型的船型参数落在所用的一维计算公式所要求的范围之内,再辅以计算师的经验,一般来说其计算精度可以满足工程精度要求。
待船型基本确定有了完整的船体三维模型后就可以进行基于三维方法的船舶阻力计算,以研究一些更丰富的信息(比如伴流场、耐波性等)。三维方法也称为虚拟水池方法,运用STAR-CCM+[4],Fluent或Numeca等CFD软件进行船舶阻力数值计算。三维方法由于其不受一维计算方法的船型限制,相比水池试验成本较低,因此在船型优化中应用很多。数值计算的精度主要取决于网格和湍流模型的逼真度[5]。一位有经验的设计师会根据目标船型的特点调整其网格方案和物理模型,能取得可比拟试验方法的满足工程要求的计算精度。
对于重点工程项目尤其是大型远洋轮船,为了降低技术风险,一般在一维和三维方法之后还会基于真实物理水池试验进行船舶阻力分析。
本文针对具有大量对照数据的KCS船[6],计算中所用的船模参数和实船参数如表1所示。运用一维计算方法和三维方法分别计算KCS船模阻力和实船阻力,并通过与文献[7]中所述的试验结果或者ITTC换算结果进行对比以验证计算精度。
|
|
表 1 KCS船模参数和实船参数 Tab.1 KCS model-scale parameters and full-scale ship parameters |
基于NavCad软件进行KCS船模和实船阻力计算,船模和实船阻力计算中输入的各参数设置见表1。
1 基于一维方法的船舶阻力计算 1.1 一维方法简介鉴于KCS船型参数特征,基于NavCad软件使用Holtrop方法[8-9]进行基于一维方法的船模阻力计算和实船阻力计算。Holtrop方法是荷兰MARIN水池在1978−1984年发表的根据船模试验和实船试航资料基于统计学方法分析而得的实船阻力计算公式,该公式是非系列船的,适应范围比较广。Holtrop实船阻力计算公式为:
| $ {R_T}{\text{ = }}{R_F}(1 + k) + {R_w} + {R_A} + {R_{APP}} + {R_B} + {R_{TR}} 。$ | (1) |
式中:RF为按1957ITTC计算公式计算的摩擦阻力;Rw为兴波和破波阻力;RA为实船与船模相关的修正阻力;RAPP为船舶的附体阻力;RB为球首引起的附加压阻力;RTR为浸水的方尾引起的附加压阻力。关于该方法的详细论述参考文献[2,8-9]。
1.2 计算过程在NavCad的阻力计算模块中,设置如表2所示参数以便进行船模阻力和实船阻力计算。在选择阻力计算公式的时候,必须保证目标船型主参数以及设计航速位于所选用方法的母型船主参数范围以及使用航速范围之内。NavCad针对不同的船型一共有40多种阻力预报方法,因此要想真正算准船舶阻力,需要知道这40多种阻力预报方法创建时所依据的母型船及其使用航速。针对KCS船,推荐使用Holtrop法[3]。
|
|
表 2 基于NavCad的船舶阻力计算 Tab.2 Ship resistance calculation based on NavCad |
在进行船模阻力计算的时候不需要考虑实船与船模相关的阻力修正系数,但在进行实船阻力计算的时候则需要考虑。另外在进行实船阻力计算的时候,经常需要考虑船体表面粗糙度,这里没有考虑是因为便于与三维计算结果进行对比。
1.3 计算结果及分析基于NavCad运用Holtrop方法计算的KCS船模阻力和实船阻力结果如表3所示。注意NavCad在进行船模阻力和实船阻力计算的时候,对于新造船默认统一考虑了0.00015的粗糙度补贴因子。为便于与三维计算结果和船模试验结果进行对比,将原由粗糙度补贴因子引起的这一部分阻力扣除掉。在运用NavCad软件计算的同时,基于ITTC-57公式采用手工计算了摩擦阻力系数。同时,为了验证基于NavCad的总阻力系数计算值,基于ITTC推荐的公式[10]利用Excel编辑了船模阻力到实船阻力的换算小程序,取船模总阻力系数为0.00355(试验值),采用二因次法换算得到了实船总阻力系数。
|
|
表 3 基于一维方法计算的KCS船舶阻力 Tab.3 Resistance of KCS ship calculated by 1D method |
将基于一维方法的手工计算结果和NavCad软件计算结果与水池试验结果进行对比,对比结果如表4所示。
|
|
表 4 基于一维方法计算KCS船舶阻力误差分析 Tab.4 Resistance error analysis of KCS Ship based on 1D method |
针对KCS船,计算域为船头1倍Lpp,船尾2倍Lpp,水线以上1倍Lpp,水线以下2倍Lpp。
2.2 网格划分及边界条件网格类型流体域为切割体网格并在船体表面具有棱柱层网格。模型尺度阻力计算域基本尺寸为145.574 mm,在船体表面设置棱柱层,棱柱层层数为7,棱柱层厚度为20 mm,船体表面细化网格为25%基本尺寸,出入口和外墙网格设置为800倍基本网格。在船首、船尾、自由面、伴流区、卡尔文波区域进行体网格加密,体网格大小分别为8%基本尺寸、8%基本尺寸、8%基本尺寸、100%基本尺寸、50%基本尺寸,划分的网格如图1所示。

|
图 1 网格划分方案 Fig. 1 Grid division scheme |
实船尺度阻力计算域基本尺寸为230 m,在船体表面设置棱柱层,棱柱层层数为16,棱柱层厚度为225 mm,船体表面细化网格为4%基本尺寸,出入口和外墙网格设置为16倍基本网格。在船首、船尾、自由面、伴流区、卡尔文波区域进行体网格加密,体网格大小分别为0.15%基本尺寸、0.15%基本尺寸、0.15%基本尺寸、1.5625%基本尺寸、3.125%基本尺寸。
2.3 边界条件及求解器设置为节省资源,沿中纵面剖开只计算半体阻力。湍流模型选择SST k-ω模型,在池底、池顶、入口为速度入口,出口为压力出口,侧面和中纵面为对称平面。速度入口为平波,速度大小见表3,打开升沉和纵倾自由度。模型尺度阻力计算求解器时间步长为0.04 s,实船尺度阻力计算求解器时间步长为0.02 s。
2.4 计算结果及分析基于STAR-CCM+三维方法计算的模型尺度船舶阻力及实船尺度的自由液面分别如图2和图3所示。在计算模型尺度的KCS船舶阻力时通过调节网格尤其是棱柱层网格使得Y+值在60左右,可以获得很高的计算精度;在计算实船尺度的KCS船舶阻力通过同样的方法使得Y+值在300左右,可以获得很高的计算精度。基于STAR-CCM+计算的模型尺度和实船尺度的船舶阻力如表5所示。
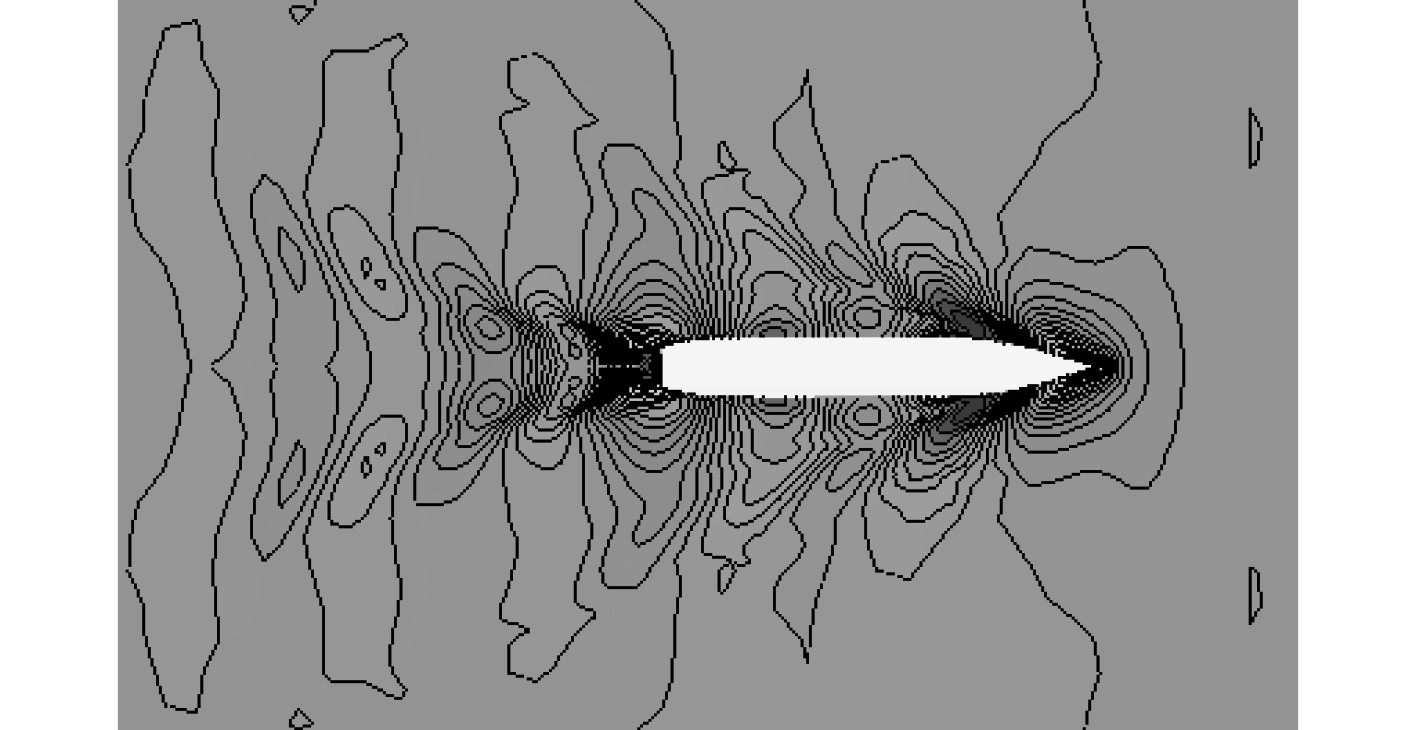
|
图 2 基于STAR-CCM+计算的KCS船模尺度自由液面 Fig. 2 The free surface of KCS model-scale based on STAR-CCM + calculation |

|
图 3 基于STAR-CCM+计算的KCS实尺度自由液面 Fig. 3 The free surface of KCS full-scale based on STAR-CCM + calculation |
|
|
表 5 基于三维方法计算的KCS船舶阻力 Tab.5 Resistance of KCS ship calculated by 3D method |
将基于三维软件计算的船模阻力计算结果通过ITTC换算公式进行手工换算后的结果和三维软件直接计算的实尺度结果与ITTC换算结果进行对比,对比结果如表6所示。
|
|
表 6 基于三维方法计算KCS船舶阻力误差分析 Tab.6 Resistance error analysis of KCS ship based on 3D method |
本文基于一维方法或三维方法对KCS船模尺度总阻力和实船尺度总阻力进行了分析研究,研究结果表明其计算误差均在2%以内,满足工程精度要求,并通过研究形成如下结论:1)只要设置得当,不管是一维方法还是三维方法计算船舶阻力均能得到满足工程精度要求的船舶阻力结果;2)在进行船舶阻力计算时,船舶设计初始阶段一维方法为首选方法;待船型确定后一维方法仍然为首选,再辅以三维方法加以对比分析;对于重点工程项目或者一维方法与三维方法差距较大时,建议进行水池试验;3)基于NavCad计算船模阻力或实船阻力时,其默认统一考虑了系数为0.00015的粗糙度补贴,该粗糙度补贴只能增加不能减少;4)基于三维方法计算船模尺度或者实船尺度船舶阻力时,在打开升沉和纵摇的前提下,如果摩擦阻力与基于ITTC-57公式手工计算值基本吻合,则总阻力计算结果一般都能满足工程精度要求;5)基于三维方法计算实尺度船舶阻力的时候,由于雷诺数较大,很容易导致计算发散,这时需要采用较小的松弛因子和较小的时间步,并关闭升沉和纵摇,待迭代稳定后再逐步增大松弛因子并开启升沉和纵摇以算得真实的船舶阻力;6)Y+值对实尺度船舶阻力影响很大,通过调整棱柱层方案尤其是第一层网格厚度可以调整船舶阻力计算精度,船舶尺度Y+值建议在60左右,实尺度船舶建议Y+值在300左右;7)湍流模型对船舶阻力影响不大,推荐采用SST k-ω模型计算船舶阻力。
| [1] |
刘应中, 张怀新, 李谊乐, 等. 21世纪的船舶性能计算和RANS方程[J]. 船舶力学, 2001, 5(5): 66-84. DOI:10.3969/j.issn.1007-7294.2001.05.009 |
| [2] |
陈京普, 朱德祥, 刘晓东. 兴波阻力数值预报方法研究及其在集装箱船船型优化中的应用[J]. 水动力学研究与进展, 2006, 21(5): 113-121. |
| [3] |
NavCad users guide, Hydrocomp Co., USA. 2015.
|
| [4] |
Star-CCM+ users guide, Siemens Co., Germany. 2019.
|
| [5] |
MILOVAN P. Full-scale simulation for marine design. Siemens PLM Software White paper. 2019.
|
| [6] |
李晓植. 螺旋桨盘面比对KCS船自航性能的影响研究[D]. 武汉: 华中科技大学, 2019.
|
| [7] |
李亮, 王超, 孙帅, 孙盛夏. 实船自航试验数值模拟及尺度效应分析[J]. 哈尔滨工程大学学报, 2016(7): 901–907.
|
| [8] |
HOLTROP J, MENNEN G G J. An approximate power prediction method[J]. International Shipbuilding Process, 1982, 29(335): 166–170.
|
| [9] |
HOLTROP J. A statistical re-analysis of resistance and propulsion data[J]. International Shipbuilding Process, 1984, 31(363): 272–276.
|
| [10] |
ITTC. 7.5-02 -02-01. ITTC Recommended Procedure and Guidelines for Resistance Test[S].
|
 2001, Vol. 44
2001, Vol. 44
