0 引　言

电子装备作为舰船的重要组成部分，特别是随着计算机技术和海军武器装备的迅猛发展，电子装备在舰船任务执行和作战中发挥的作用越来越大^[1,2]。电子装备性能主要由其自身质量和有效的备件管理工作所决定，但由于海洋环境复杂多变，电子装备极容易发生故障，加之舰船吨位和经济等多种因素的影响，电子装备库存备件数量必须控制在合理范围内^[3]。因此研究科学的舰船电子装备备件优化模型，为备件管理人员提供可靠的决策依据甚为重要。

张怀强等、杨建华等^[4,5]分别利用故障率与延迟时间理论，实现舰船电子装备备件优化。这2种方法的求解精度和收敛速度较高，对提升舰船电子装备保障率具有显著效果，但计算过程较为复杂，且忽略了舰船电子装备使用特点分析。

极限学习机作为单隐层前向网络，具有极高的训练速度和泛化性能，将其与具备强大的全局寻优能力的蚁群算法相结合，提出蚁群算法和极限学习机的舰船电子装备备件优化模型，实现舰船电子装备备件的合理配置，从而保证舰船航行期间的高可靠性。

1 蚁群算法和极限学习机的舰船电子装备备件优化模型 1.1 舰船电子装备备件优化模型构建 1.1.1 舰船电子装备使用特点分析

分析舰船电子装备使用特点是创建舰船电子装备备件优化模型的重要环节，为此做出以下假设：

1）舰船电子装备能够循环利用，每次利用后若想使其恢复到规定状态^[6]，仅需进行适当的维护保养即可。

2）对舰船电子装备的使用频率进行约束，是因为各电子装备均具有有限的使用寿命，假设各舰船电子装备最大使用次数用 $ {N_0} $ 描述，当超过该值时，则停止使用对应的舰船电子装备。

3）舰船电子装备故障率用 $ \lambda $ 描述，在一次使用时电子装备的寿命满足 $ \lambda $ 的指数分布^[7]。N为舰船电子装备使用次数用，N的分布率表示为 $ {p^n} = \Pr \left\{ {N = n} \right\} $ 。一般情况下，N满足以下概率分布：

$ P\left( {N = n\left| {N \leqslant {N_0}} \right.} \right) = \frac{{{\rho ^n} - {\rho ^{n + 1}}}}{{1 - {\rho ^{{N_0} + 1}}}} ，$

(1)

在N₀取较大值的条件下，使用舰船电子装备的概率可以近似为 $ \rho $ 。

1.1.2 舰船电子装备备件优化模型

根据舰船电子装备使用特点分析，构建包含定可靠度备件优化和定费用备件优化两部分的舰船电子装备备件优化模型。对于舰船电子装备，其次序为i的零部件可靠度用 $ {R_i} $ 描述，依据可靠性工程理论^[8-9]，得到 $ {R_i} $ 的计算过程：

$ \begin{split} {R_i} =& \sum\limits_{j = 0}^{{x_i}} {{e^{ - {\lambda _i}T}}\frac{1}{{j!}}\lambda _i^j{T^j}} = \\ &{e^{ - {\lambda _i}T}} \left[ {1 + {\lambda _i}T + \left( {\frac{1}{{2!}} + \cdots + \frac{1}{{{x_i}!}}} \right)\left( {\lambda _i^2{T^2} + \cdots + \lambda _i^{{x_i}}{T^{{x_i}}}} \right)} \right] 。\end{split} $

(2)

式中：x_i为次序为i的舰船电子装备零部件数量总和，其由库存备件与使用中零部件两部分组成；舰船电子装备每个零部件执行任务时间的平均值用T描述；对于次序为i的零部件， $ {\lambda _i} $ 为其失效系数， $ {a_i} $ 为使用中的数量，b_i为失效的概率，三者之间的关系满足 $ {\lambda _i} = {a_i}{b_i} $ 。

$ {R_s} $ 为整个舰船系统的可靠度，计算公式为：

$ {R_s} = \prod\limits_{i = 1}^n {{R_i}} = \prod\limits_{i = 1}^n {\sum\limits_{j = 0}^{{x_i}} {{e^{ - {\lambda _i}T}}\frac{1}{{j!}}\lambda _i^j{T^j}} }，$

(3)

式中，舰船电子装备零部件的总类别数用n描述。

1）定可靠度备件优化模型

在符合提前设置的R_S的条件下，通过尽可能少的费用实现舰船库存内电子装备备件类型与数量的合理配置^[10]，即

$ \begin{gathered} \min {C_s} = \sum\limits_{i = 1}^n {{c_i}{x_i}} ，\hfill \\ {\rm{ s.t.}}\mathop {}\limits_{} {R_s} \geqslant {R_0} ，\hfill \\ \end{gathered} $

(4)

式中：x_i的值大于0，且为整数；minC_s为舰船电子装备需要的库存备件的总费用最小值；R₀为提前设置的舰船系统可靠度；c_i描述舰船电子装备的次序为i的零部件价格。

2）定费用备件优化模型

在舰船电子装备库存备件费用满足预设费用的条件下，通过库存内电子装备备件类型与数量的合理配置，最大化舰船系统运行可靠度，具体如下所示：

$ \max {R_s}\mathop {}\limits_{} {\rm{s.t.}}\mathop {}\limits_{} \sum\limits_{i = 1}^n {{c_i}{x_i} \leqslant {C_0}}，$

(5)

式中，C₀为提前设置舰船电子装备库存备件经费总额。

通常需要依据专家经验设置R₀和C₀的值，利用费效分析原则能得到公式(6)所示以可靠度与费用的比当作目标函数的表达式：

$ \begin{split} &\max \frac{{{R_s}}}{{{C_s}}}，\hfill \\ & {\rm{s.t}}\mathop {}\limits_{} {C_s} = \sum\limits_{i = 1}^n {{c_i}{x_i}}，\hfill \\ &{R_s} = \prod\limits_{i = 1}^n {\prod\limits_{j = 0}^{{x_i}} {{e^{ - {\lambda _i}T}}\frac{1}{{j!}}\lambda _i^j{T^j}} } 。\hfill \end{split} $

(6)

1.2 基于蚁群算法和极限学习机的模型求解 1.2.1 基于极限学习机的模型求解

将采集的舰船电子装备备件优化模型所需数据当作训练集为 $ \left\{ {{x_j},{t_j}} \right\}_{j = 1}^k $ ，其中 $ {x_j} $ 和 $ {t_j} $ 分别表示为 $ {x_j} = $ $ {\left[ {{x_j},{x_{j + 1}},\cdots ,{x_{j + n - 1}}} \right]^{\rm{T}}} $ ， $ {t_j} = {x_{j + n}},{x_j} $ ，嵌入维数与训练样本数分别用n，k描述，则训练集的回归约束表达式如下：

$ \begin{split} &\min \left( {\frac{{\beta _L^T{\beta _L} + \gamma {\varepsilon ^T}\varepsilon }}{2}} \right)，\hfill \\ & {\rm{s.t.}}\mathop {}\limits_{} {t_j} = \sum\limits_{i = 1}^L {{\beta _i}f\left( {{a_i}{x_j} + {c_i}} \right) - {\varepsilon _i}}。\hfill \end{split} $

(7)

式中：隐层i的神经元偏差为 $ {c_i} $ ；隐层神经元个数为L；隐层神经元函数为f()；隐层神经元输入权值为 $ {a_i} $ ；隐层神经元输出权值为 $ {\beta _i} $ ；回归误差为 $ {\varepsilon _i} $ 。

创建公式(8)所示拉格朗日函数，以求解上式描述的回归约束问题：

$ L\left( {w,\varepsilon ,{\beta _L}} \right) = \frac{{\beta _L^T{\beta _L} + \gamma {\varepsilon ^{\rm{T}}}\varepsilon }}{2} - w{H_L}{\beta _L} + T + \varepsilon。$

(8)

式中：w为拉格朗日权值；T为输出向量；H_L为神经元矩阵； $ \varepsilon $ 为设定的阈值。

采用式(9)描述求解上式每个变量的偏导，并将偏导数设置成零所得结果：

$ \left\{ \begin{gathered} L/{\beta _L} \to \beta _L^T = w{H_L} ，\hfill \\ L/\varepsilon \to \gamma {\varepsilon ^{\rm{T}}} + w = 0，\hfill \\ L/w \to {H_L}{\beta _L} - \left( {T + \varepsilon } \right) = 0。\hfill \\ \end{gathered} \right. $

(9)

求解上式可得到式(10)所示结果：

$ {\beta _L} = \frac{{\gamma H_L^TT}}{{\gamma H_L^T{H_L} + {I_L}}}。$

(10)

式中，I为单位矩阵。

依据上式结果即可实现舰船电子装备备件优化模型求解，具体求解过程用式(11)描述：

$ t = \sum\limits_{i = 1}^L {{\beta _i}f\left( {{a_i}x + {c_i}} \right)}。$

(11)

式中：x为模型的输入用；t为模型的输出。

1.2.2 基于蚁群算法优化的极限学习机

蚁群算法内各蚂蚁的爬行路径节点，可选择极限学习机的阈值和权值，通过最佳路径搜索获得全局最优解，即利用蚁群算法优化极限学习机的基本思想。

1）参数初始化

Y(0)为初始种群，其内包含的蚂蚁数量为M。mg、n分别为进化代数和节点数；fit_i为路径i的适应度；两节点i，j的启发度代表启发因子 $ {\eta _{ij}} $ ，其求解过程表示为 $ {\eta _{ij}} = \dfrac{1}{{{d_{ij}}}} $ ；针对边(i,j)，其中的信息素量和蚂蚁k残留的信息素量分别用 $ {\tau _{ij}} $ ， $ \Delta \tau _{ij}^k $ 描述； $ \rho $ 为信息素量蒸发系数； $ P_{ij}^k\left( t \right) $ 为第k只蚂蚁在t时刻从节点i爬行到节点j的几率。

2）适应度计算

通过适应度函数获得如下所示蚂蚁的适应度fit(y)评价过程：

$ \begin{split} &fit\left( y \right) = {\left[ {{y_1},{y_2},\cdots,{y_M}} \right]^{\rm{T}}}，\hfill \\ & {y_i} = \frac{1}{m}\sum\limits_{j = 1}^m {O_j^2 - 2{O_j}{T_j} + T_j^2} 。\hfill \end{split} $

(12)

式中：m为输入样本总数；O_j为次序为j的输出值；T_j为次序为j的实际值。

3）利用适应度完成信息素的释放

蚁群爬行后各路径的信息素计算过程为：

$ \begin{split} &{\tau }_{ij}\left(t+n\right)={\tau }_{ij}\left(t\right)-\rho {\tau }_{ij}\left(t\right)+\Delta {\tau }_{ij}，\\ & \Delta {\tau }_{ij}={\displaystyle \sum _{k=1}^{m}\Delta {\tau }_{ij}^{k}}，\\ & \Delta {\tau }_{ij}^{k}=\left\{\begin{array}{l}Q/fi{t}_{k},{{\displaystyle }}^{}蚂蚁k行走经过\left(i,j\right)，\\ 0,{{\displaystyle }}^{}{{\displaystyle }}^{}{{\displaystyle }}^{}蚂蚁k行走不经过\left(i,j\right)。\end{array}\right.\end{split} $

(13)

式中：fit_k为第k只蚂蚁的适应度，Q为常数；将 $ \Delta {\tau _{ij}}\left( 0 \right) $ 和 $ \Delta {\tau _{ij}}\left( 0 \right) $ 的值均初始化为Q。

4）蚁群移动可通过信息素完成

使用式(14)描述转移概率 $ P_{ij}^k\left( t \right) $ 的计算过程：

$ P_{ij}^k = \frac{{{{\left[ {{\tau _{ij}}\left( t \right){\eta _{ij}}\left( t \right)} \right]}^{\alpha \beta }}}}{{\beta \displaystyle \sum\limits_{s \in {J_k}\left( i \right)} {{{\left[ {{\tau _{is}}\left( t \right)} \right]}^\alpha }\left[ {{\eta _{is}}\left( t \right)} \right]} }} 。$

(14)

式中： $ \alpha $ 和 $\ \beta $ 为信息素和启发因子的重要度；J_k(i)为供第k只蚂蚁选择的节点集合用。

5）将当前迭代的路径及最佳路径保存

若达到设置的迭代次数最大值，则将目前最优路径输出，若不满足上述条件，则跳转到步骤2。

通过最优路径即可获得极限学习机优化后的阈值和权值，进而得到更精确的舰船电子装备备件优化模型的解。

2 结果分析

将某执行2个月护航任务的舰船作为实验对象，从中选择具有代表性的9个电子装备进行研究，分别为雷达、声呐、光电潜望镜、舰载通信侦察设备、高低频噪声干扰器、舰船数据链系统、重力仪、计程仪以及鱼雷火控。各电子装备在舰船航行期间平均每日运作18 h，舰船可靠度为0.952，库存备件经费为26万元，在上述背景下，使用本文方法完成舰船电子装备备件优化。

选择舰载通信侦察设备的4种备件作为测试对象，各备件单价分别为0.05万元，0.02万元，0.17万元，0.03万元，使用本文方法完成该电子装备备件优化，所得8组优化结果用表1描述。可以看出，使用本文方法获取的舰船电子装备备件优化结果中，仅有A7和A8结果的舰船可靠度达到规定标准，但A8结果的库存备件费用比A7结果的库存备件费用少0.24万元，且舰船可靠度能达到更高数值，因此选择A8结果作为舰载通信侦察设备4种备件的优化方案。以上结果表明，本文方法能够有效实现舰船电子装备备件优化。

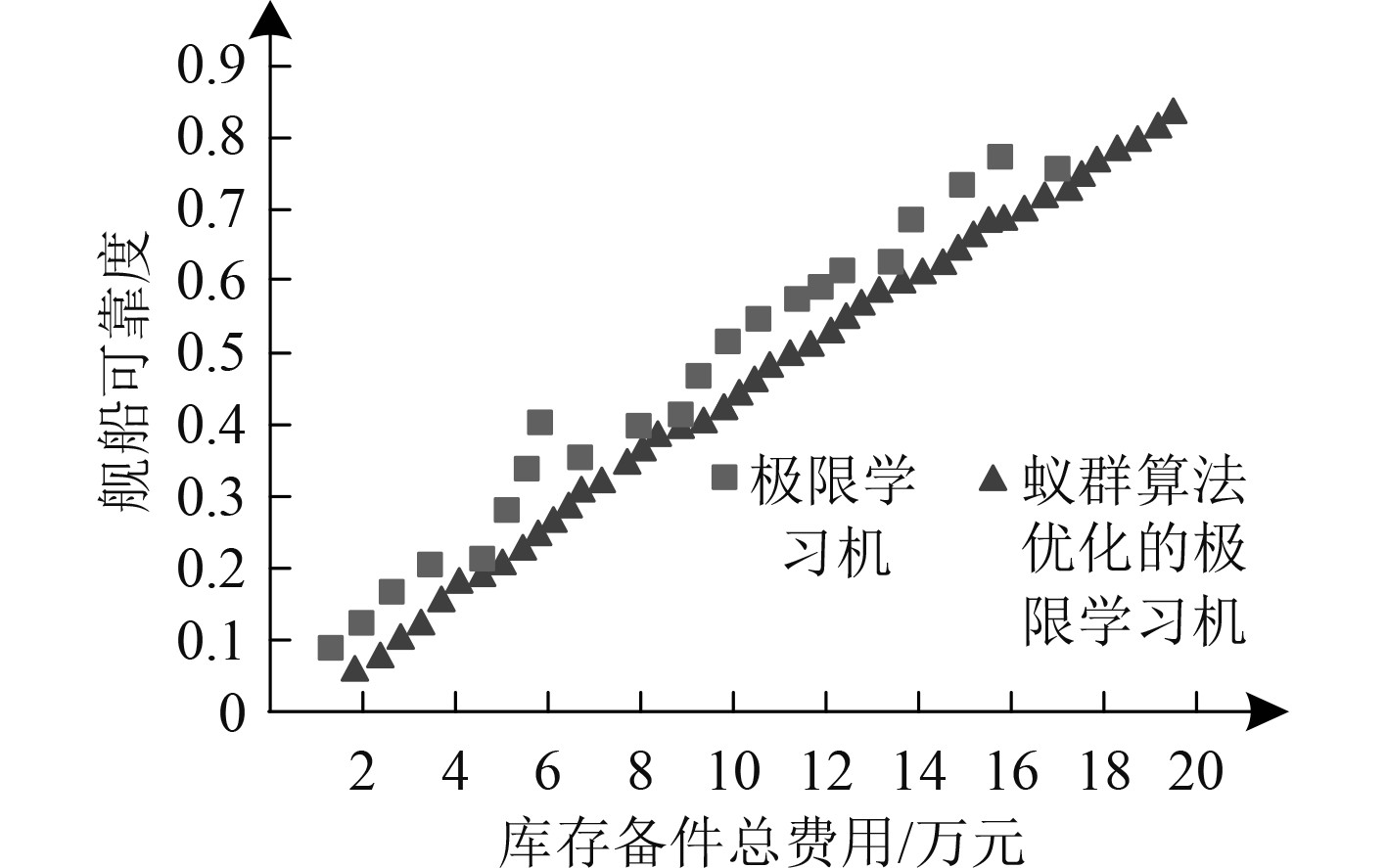
分别使用极限学习机和蚁群算法优化的极限学习机求解舰船电子装备备件优化模型，所得舰船电子装备需要的库存备件总费用和舰船可靠度优化结果如图1所示。可以发现，使用极限学习机求解舰船电子装备备件优化模型时，解的数量较少，且分布较为分散；使用蚁群算法优化的极限学习机求解优化模型时，解的数量明显增加，且分布较为均匀、密集；在舰船可靠度相同的条件下，蚁群算法优化的极限学习机所得解的库存备件总费用始终保持最低。以上结果表明，本文方法的舰船电子装备备件优化效果较优异，并能有效提升解的多样性。

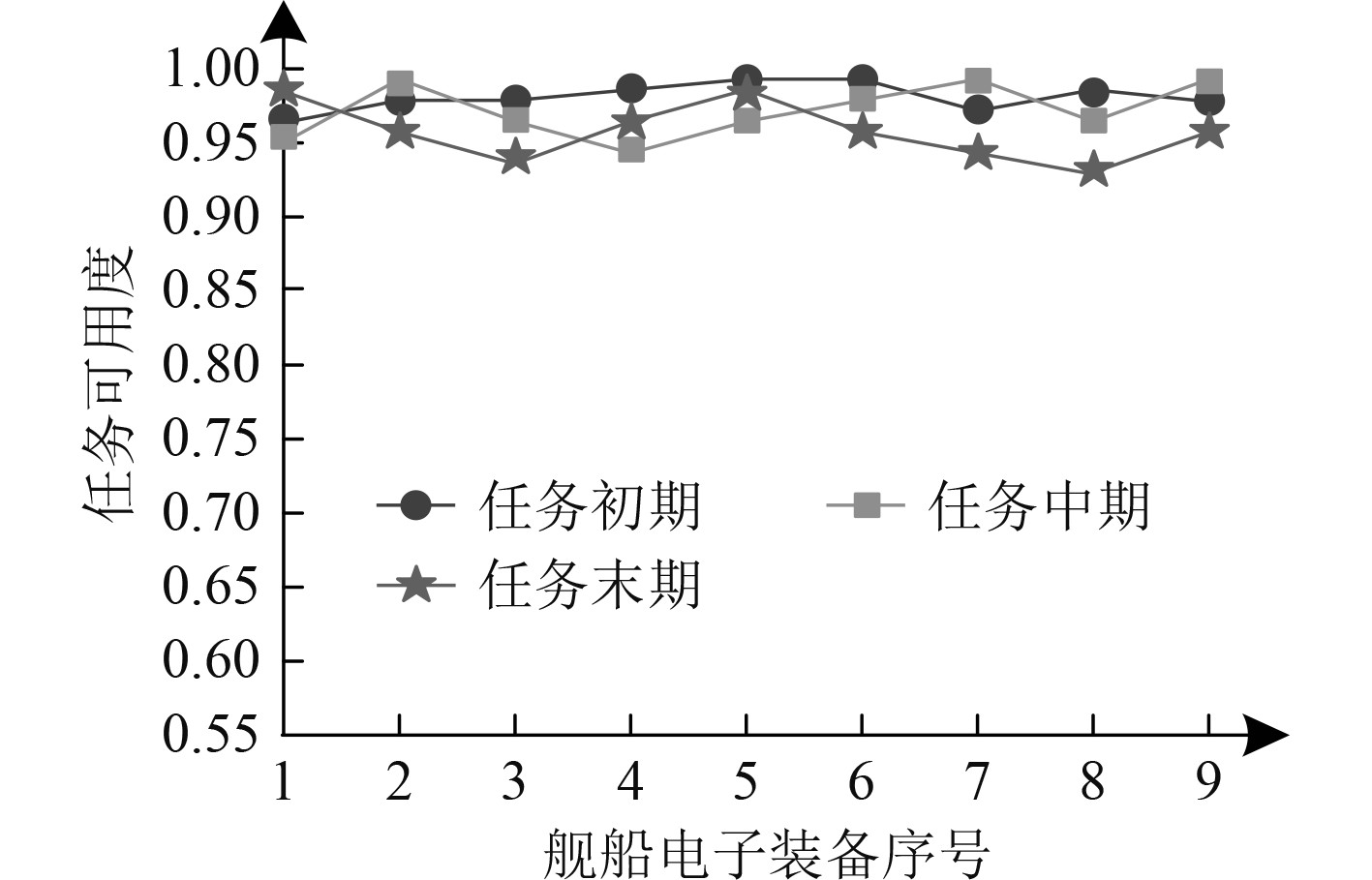
通过舰船电子装备的任务可用度衡量舰船执行护航任务时，电子装备的随时可用程度，将为期2个月的护航任务划分为初期、中期、末期3个阶段，不同任务阶段的各舰船电子装备的任务可用度结果，如图2所示。可以看出，在舰船护航任务初期阶段，各电子装备的任务可用度整体水平最高，最低阶段为舰船护航任务末期，但该阶段电子装备的任务可用度仍保持在0.93以上。因此表明本文方法具有较理想的舰船电子装备备件优化效果，对保证电子装备在整个舰船航行期间的随时可用程度具有显著作用。

3 结　语

舰船电子装备备件优化是确保各电子装备正常运行和舰船顺利完成既定任务的重要手段，因此本文提出蚁群算法和极限学习机的舰船电子装备备件优化模型。在极限学习机的基础上，利用蚁群算法优化极限学习机完成模型求解，实现舰船电子装备备件合理配置。该方法能获得较理想的舰船可靠度和库存备件总费用优化结果，不仅可以保证电子装备在整个舰船航行期间的随时可用程度，还可以尽可能避免由于电子装备故障导致的延误出航或无法出航情况。