2. 大连东软信息学院 智能与电子工程学院,辽宁 大连 116023
2. School of Intelligence and Electrical Engineering, Dalian Neusoft University of Information, Dalian 116023, China
在复杂的海洋环境下,船舶6个自由度的运动给船载设备的正常工作带来严重影响。而船舶的升沉、横摇和纵摇运动船载设备的影响较大,且需要通过稳定平台进行补偿。三自由度船载稳定平台可以保证船载设备相对惯性空间保持稳定,不但具有更高的性价比和实用性,还具有高承载、高刚度、稳定精度高等优点。目前三自由度并联稳定平台机构形式有多种,应用场景也不尽相同。文献[1]研发的基于4TPS-1PS机构的稳定平台,可补偿船舶升沉、横摇、纵摇和首摇4个自由度。文献[2]针对3-UPS/S型并联三自由度船载稳定平台的性能进行研究,搭建了稳定平台的实验系统。文献[3]设计了一种三自由度并联复合驱动的船载稳定平台,并进行了理论与实验研究。文献[4]对三自由度并联机构进行了详细的运动学分析,并通过ADAMS进行了仿真。以上研究的仿真大都没有加入扰动平台加以观测。本文设计了一种适用于船吊起重机的三自由度稳定平台,同时利用Matlab/Simulink的Simscape将稳定平台和扰动平台相结合组成虚拟样机仿真系统,并进行了样机制作和实验测试。
1 机构设计与约束分析三自由度并联稳定平台示意图如图1所示,由基座平台、动平台、3个驱动支路和3个约束支路构成。

|
图 1 并联稳定平台示意图 Fig. 1 Structure diagram of parallel stabilization platform |
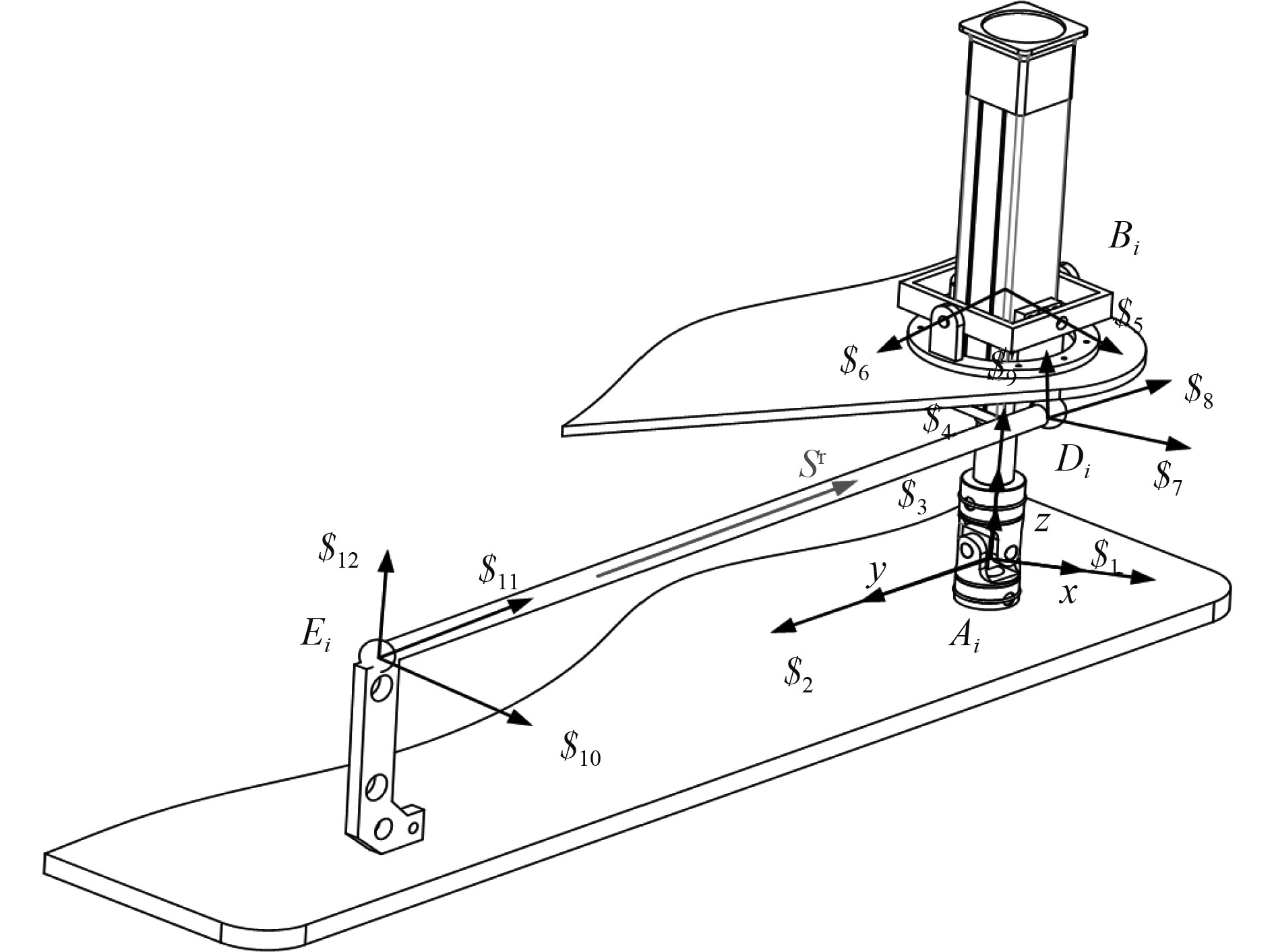
并联机构的约束支路如图2所示。约束支路坐标系建立规则如下:以分支球副中心Ai为坐标原点,令z轴方向沿移动副轴线Pi方向,x轴平行于约束杆DiEi轴线方向,则y轴方向可以由右手法则确定。基于螺旋理论,每个分支的运动螺旋系统包含12个运动螺旋,每个球副可以看成3个转动轴线交于一点的转动副组成。
|
图 2 约束支路示意图 Fig. 2 Structure diagram of constraint branch |
定义CiDi的长度为n,为球副Di相对于移动副AiBi的偏置,DiEi的长度为m。因此Ei和Di约束分支的运动螺旋如下式:
| $ \left\{ {\begin{array}{*{20}{l}} {{{S/ }_{{\text{i7}}}} = \left( {\begin{array}{*{20}{c}} 1&0&{0;}&0&h&0 \end{array}} \right)} ,\\ {{{{S/ }}_{{\text{i8}}}} = \left( {\begin{array}{*{20}{c}} 0&1&{0;}&{ - h}&0&0 \end{array}} \right)} ,\\ {{{{S/ }}_{{\text{i9}}}} = \left( {\begin{array}{*{20}{c}} 0&0&{1;}&0&0&0 \end{array}} \right)} ,\\ {{{{S/ }}_{{\text{i10}}}} = \left( {\begin{array}{*{20}{c}} 1&0&{0;}&0&h&{ - m} \end{array}} \right)} ,\\ {{{{S/ }}_{{\text{i11}}}} = \left( {\begin{array}{*{20}{c}} 0&1&{0;}&{ - h}&0&0 \end{array}} \right)} ,\\ {{{{S/ }}_{{\text{i12}}}} = \left( {\begin{array}{*{20}{c}} 0&0&{1;}&m&0&0 \end{array}} \right)} 。\end{array}} \right. $ | (1) |
其中,运动螺旋
| $ {S/}_{i}^{\prime \prime}=\left(\begin{array}{llllll} 0 & 1 & 0 ; & -h & 0 & 0 \end{array}\right) 。$ | (2) |
由于并联平台机构相对复杂,正运动学求解过程难度较大,且存在多个解的可能性。三自由度并联稳定平台的作用是补偿舰船运动对船载设备的扰动,在海浪的作用下保持动平台的位姿不变,因此需采用逆运动学进行分析。根据上所述的坐标系定义,动坐标系P-xyz相对于定坐标系O-XYZ的姿态矩阵R表示如下式:
| $\begin{split} & {\boldsymbol{R}} =\\ & \left[{\begin{array}{*{20}{c}} {{\text{c}}{{\text{θ }}_{\text{z}}}{\text{c}}{{\text{θ }}_{\text{y}}}}&{{\text{c}}{{\text{θ }}_{\text{z}}}{\text{s}}{{\text{θ }}_{\text{y}}}{\text{s}}{{\text{θ }}_{\text{x}}}{\text{ - s}}{{\text{θ }}_{\text{z}}}{\text{c}}{{\text{θ }}_{\text{x}}}}&{{\text{c}}{{\text{θ }}_{\text{z}}}{\text{s}}{{\text{θ }}_{\text{y}}}{\text{c}}{{\text{θ }}_{\text{x}}}{\text{ + s}}{{\text{θ }}_{\text{z}}}{\text{s}}{{\text{θ }}_{\text{x}}}} \\ {{\text{s}}{{\text{θ }}_{\text{z}}}{\text{c}}{{\text{θ }}_{\text{y}}}}|&{{\text{s}}{{\text{θ }}_{\text{z}}}{\text{s}}{{\text{θ }}_{\text{y}}}{\text{s}}{{\text{θ }}_{\text{x}}}{\text{ + c}}{{\text{θ }}_{\text{z}}}{\text{c}}{{\text{θ }}_{\text{x}}}}&{{\text{s}}{{\text{θ }}_{\text{z}}}{\text{s}}{{\text{θ }}_{\text{y}}}{\text{c}}{{\text{θ }}_{\text{x}}}{\text{ - c}}{{\text{θ }}_{\text{z}}}{\text{s}}{{\text{θ }}_{\text{x}}}} \\ {{\text{ - s}}{{\text{θ }}_{\text{y}}}}&{{\text{c}}{{\text{θ }}_{\text{y}}}{\text{s}}{{\text{θ }}_{\text{x}}}}&{{\text{c}}{{\text{θ }}_{\text{y}}}{\text{c}}{{\text{θ }}_{\text{x}}}} \end{array}} \right] 。\end{split}$ | (3) |
式中:动平台相对于底部平台绕X轴运动为角为θx,绕Y轴旋转角为θy,绕Z轴旋转角为θz,
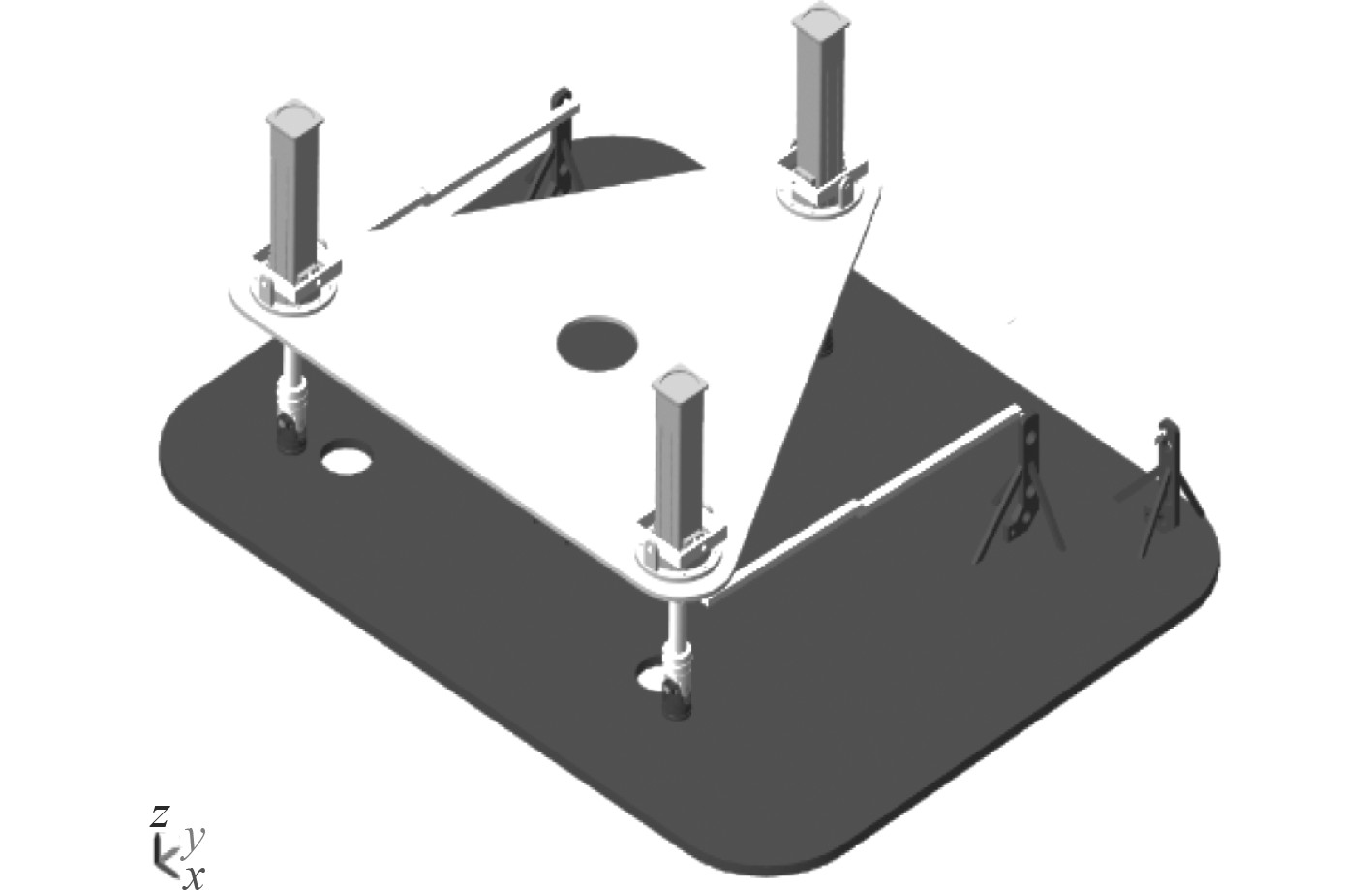
为了验证三自由度并联稳定平台的补偿效果,通过Solidworks建立样机的三维几何模型,并在Solidworks中预先定各零部件的材料、装配好各零部件,使用与Simscape/Multibody的接口插件,将装配体模型保存成xml格式的文件,导入到Simulink模块中生成物理模型。xml文件不仅包括装配体模型中各零部件的质量、密度、惯性张量等动力学属性,还包含装配体中各运动关节的运动副类型及运动副的位置和方向。三自由度并联模拟平台的机械结构系统在Simulink模块中将几何模型转化为物理模型。物理模型由扰动平台、基座、电动缸等几何模型和球铰、移动副关节组合而成,其中每个球铰由一个万向节和一个转动副组成,如图3所示。
|
图 3 虚拟样机物理模型 Fig. 3 Physical model of virtual prototype |
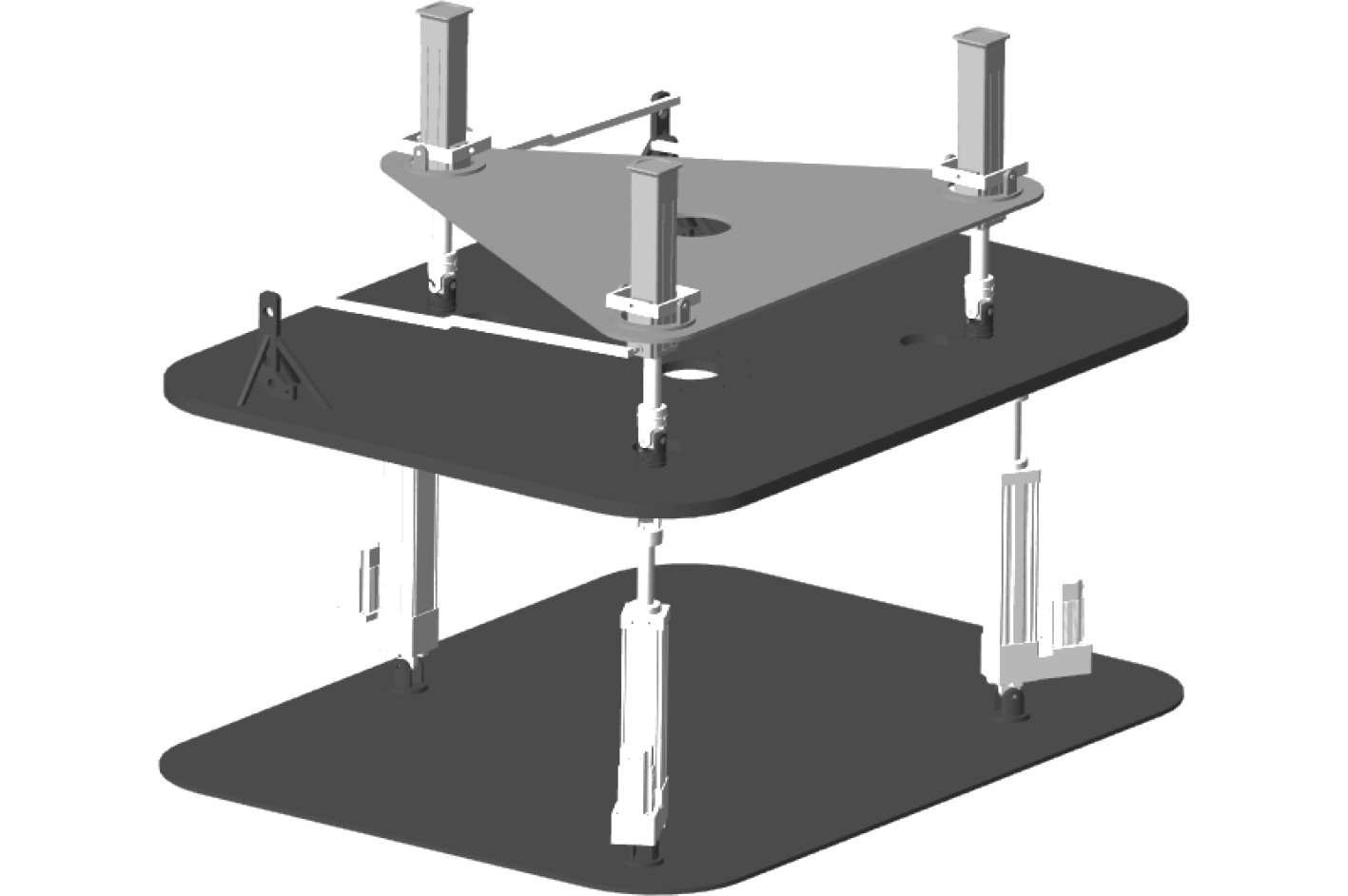
为了更直观地验证三自由度并联平台的补偿特性,设计一种3-UPS型并联平台作为扰动平台,且放置在三自由度并联稳定平台下方,模拟海浪干扰等运动。将扰动平台并安装在补偿平台的正下方,构成完整的海浪补偿测试系统如图4所示,并将表1参数添加到模型中。同时给3-UPS扰动平台添加驱动函数,使其产生模拟舰船在海浪中的横摇、纵摇和升沉运动。
|
图 4 虚拟样机仿真系统模型 Fig. 4 Physical model of virtual prototype simulation system |
|
|
表 1 虚拟样机仿真系统参数 Tab.1 Parameters of virtual prototype simulation system |
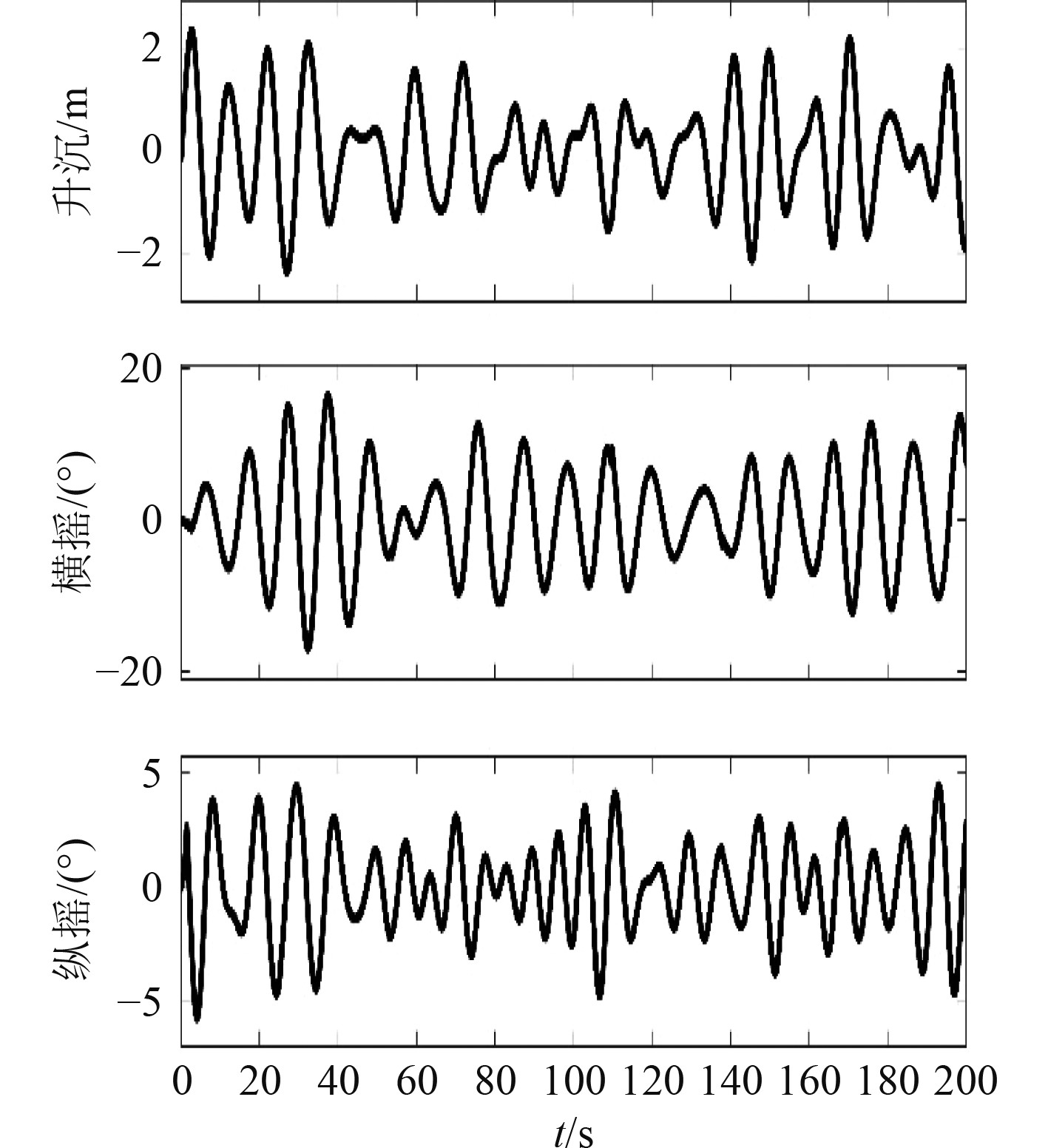
为了更真实地模拟海浪运动,采用挪威科技大学开发的Marine System Simulator(MSS)工具箱来产生海浪运动,使用Wave模块产生海浪波形,海浪谱类型为ITTC型。设置3级海况作为扰动环境。产生的横摇、纵摇和升沉运动如图5所示。
|
图 5 3级海况下扰动平台的三自由度变化曲线 Fig. 5 Three degrees of freedom variation of disturbed platform under three-level oceanic condition |
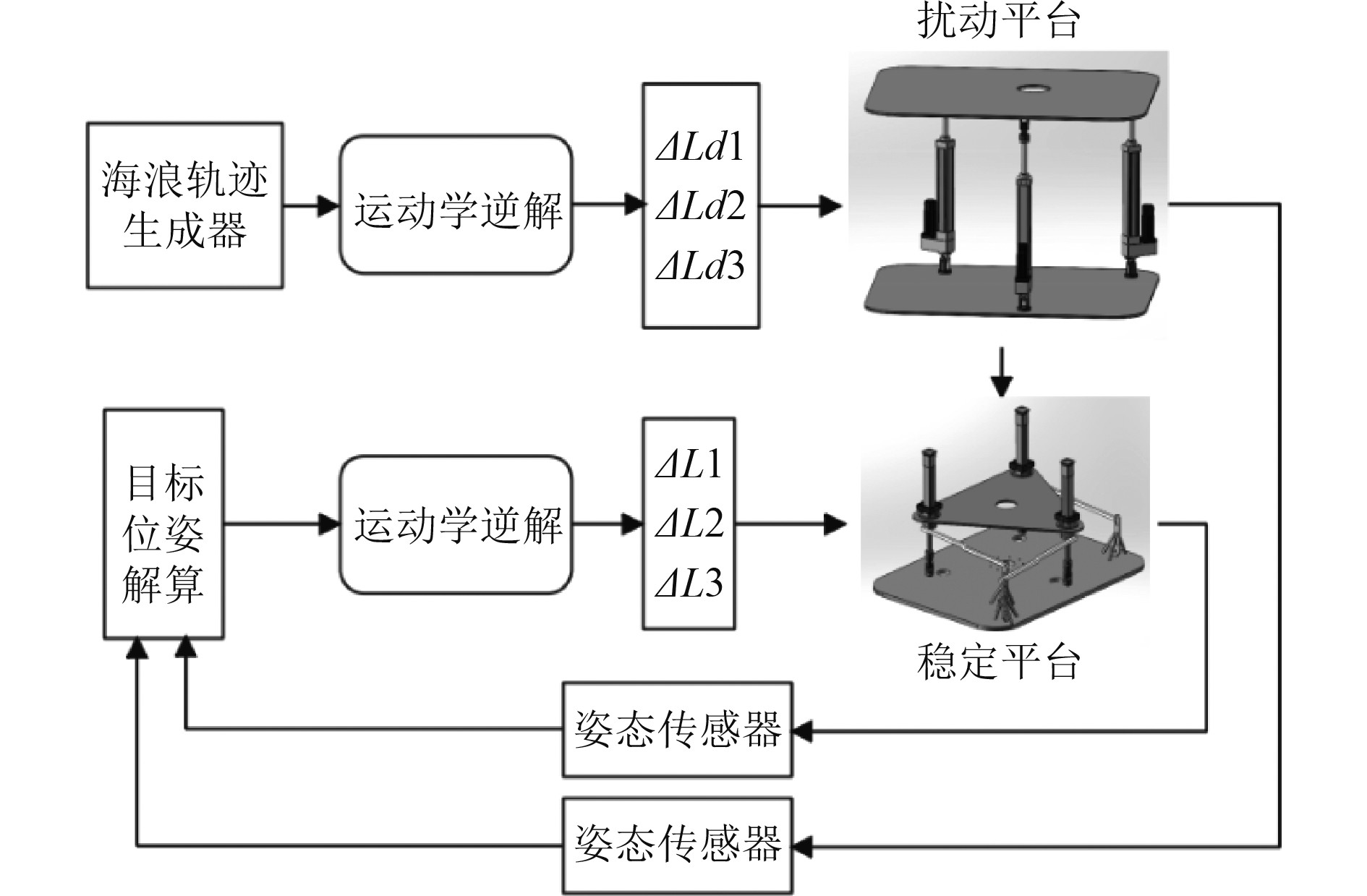
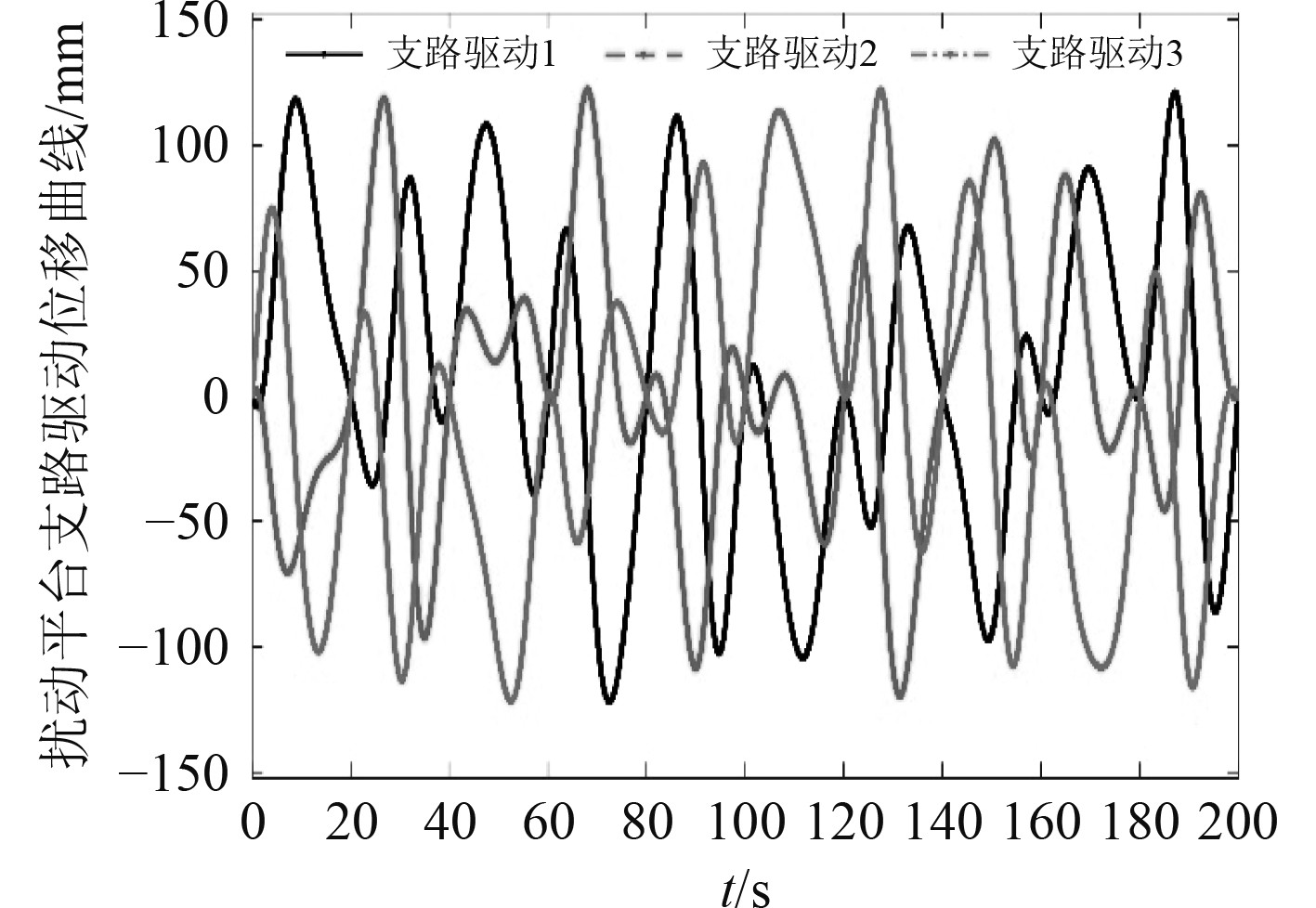
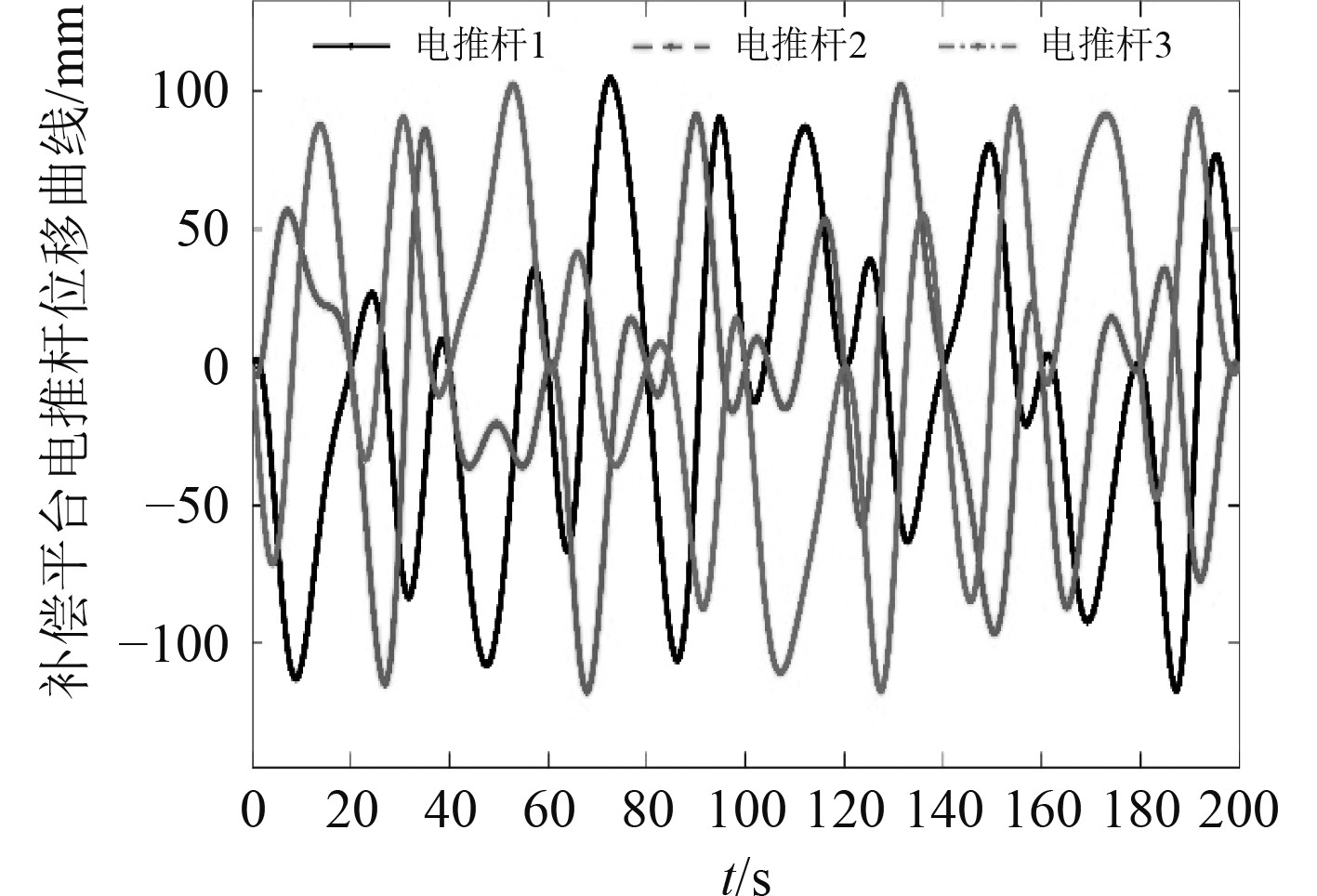
完整的三自由度并联稳定平台虚拟样机仿真系统框图如图6所示。在稳定平台的基座和动平台分别添加姿态传感器用于测量出横摇、纵摇和升沉三个姿态。通过3-UPS扰动平台的几何参数,计算出扰动平台3个驱动支路的位移,用来模拟海浪运动。在3级海况下扰动平台各支路驱动的位移变化曲线如图7所示。在理想情况下认为动平台是空载的,利用稳定平台基座和动平台的姿态传感器测量出横摇、纵摇和升沉3个参数,通过目标位姿解算模块得出3个电推杆的伸缩量,其变化曲线如图8所示。
|
图 6 虚拟样机测试系统框图 Fig. 6 Structure diagram of virtual prototype simulation system |
|
图 7 三级海况下扰动平台各支路位移变化 Fig. 7 Displacement variation of each branch of disturbance platform under three-level oceanic condition |
|
图 8 稳定平台电推杆位移变化 Fig. 8 Displacement variation of electric putter of stabilization platform |
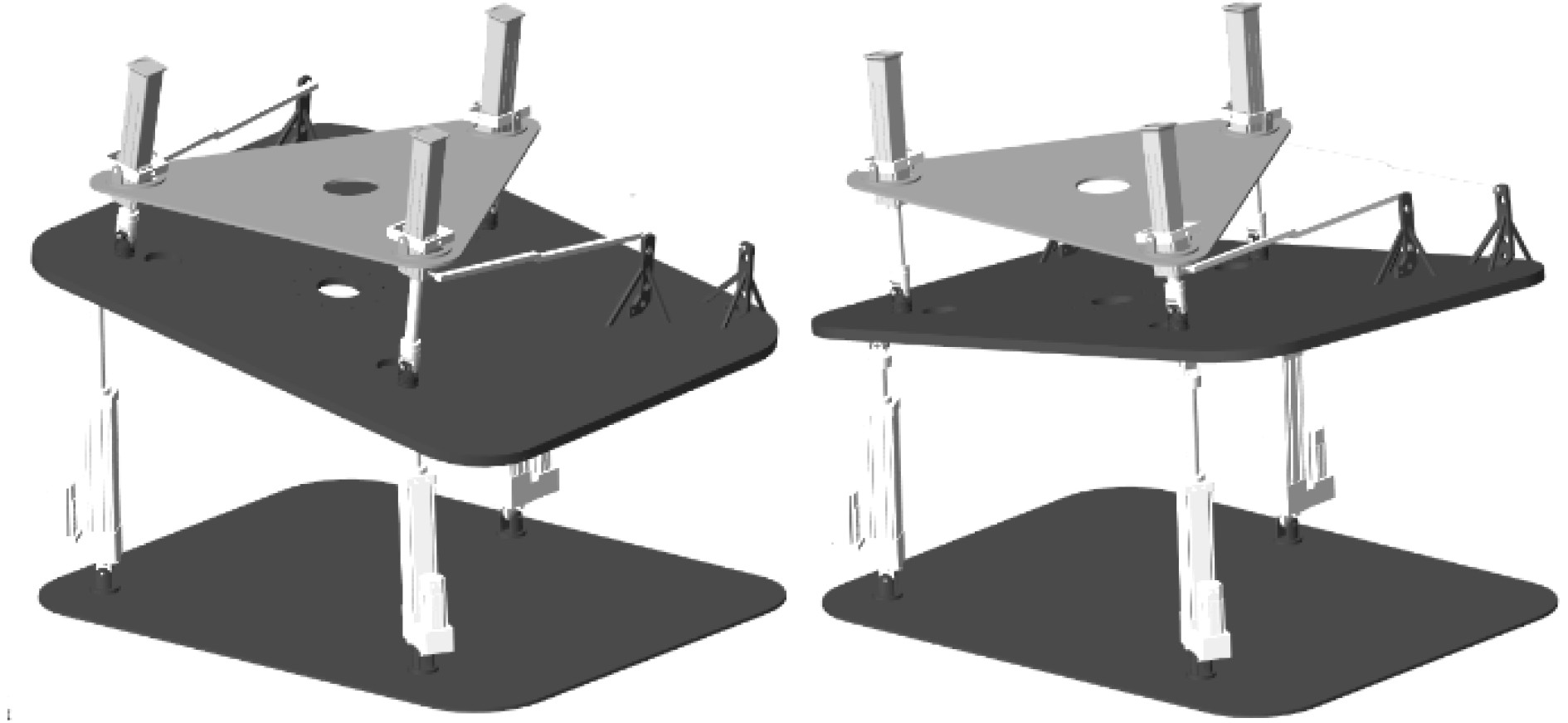
由于三自由度并联稳定平台的运动学控制不需要位姿控制算法,且在无负载变化、摩擦力等外界干扰等情况下,因此可以实现横摇、纵摇和升沉3个自由度的补偿,补偿误差取决于参数是否精确。另外补偿平台由于机构中存在约束,因此只能在一定自由度范围内实现海浪补偿,如果超过海浪超过补偿范围则补偿效果欠佳,虚拟测试系统的海浪补偿效果如图9所示。
|
图 9 稳定平台的波浪补偿效果 Fig. 9 Wave compensation effect of stabilization platform |
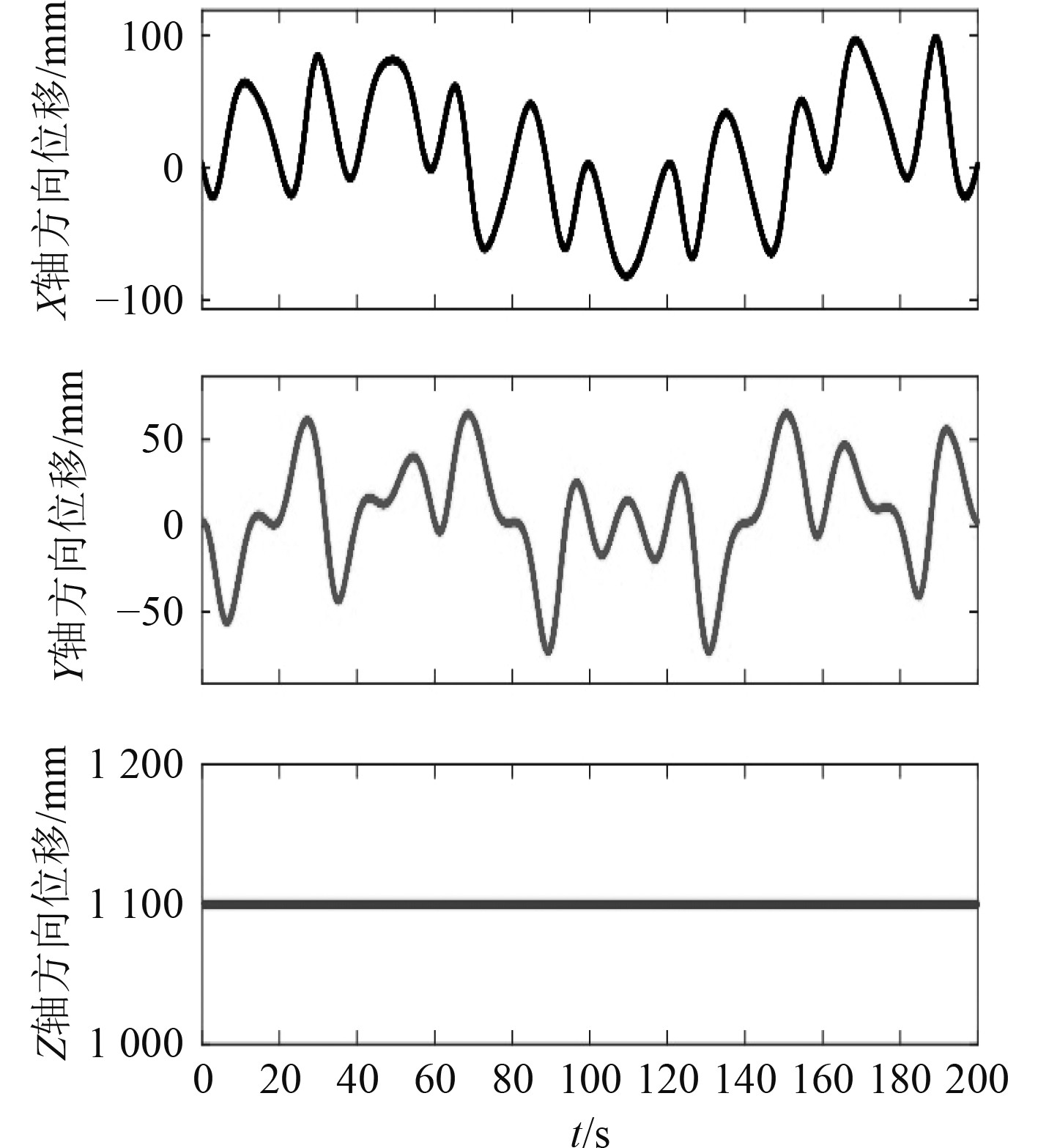
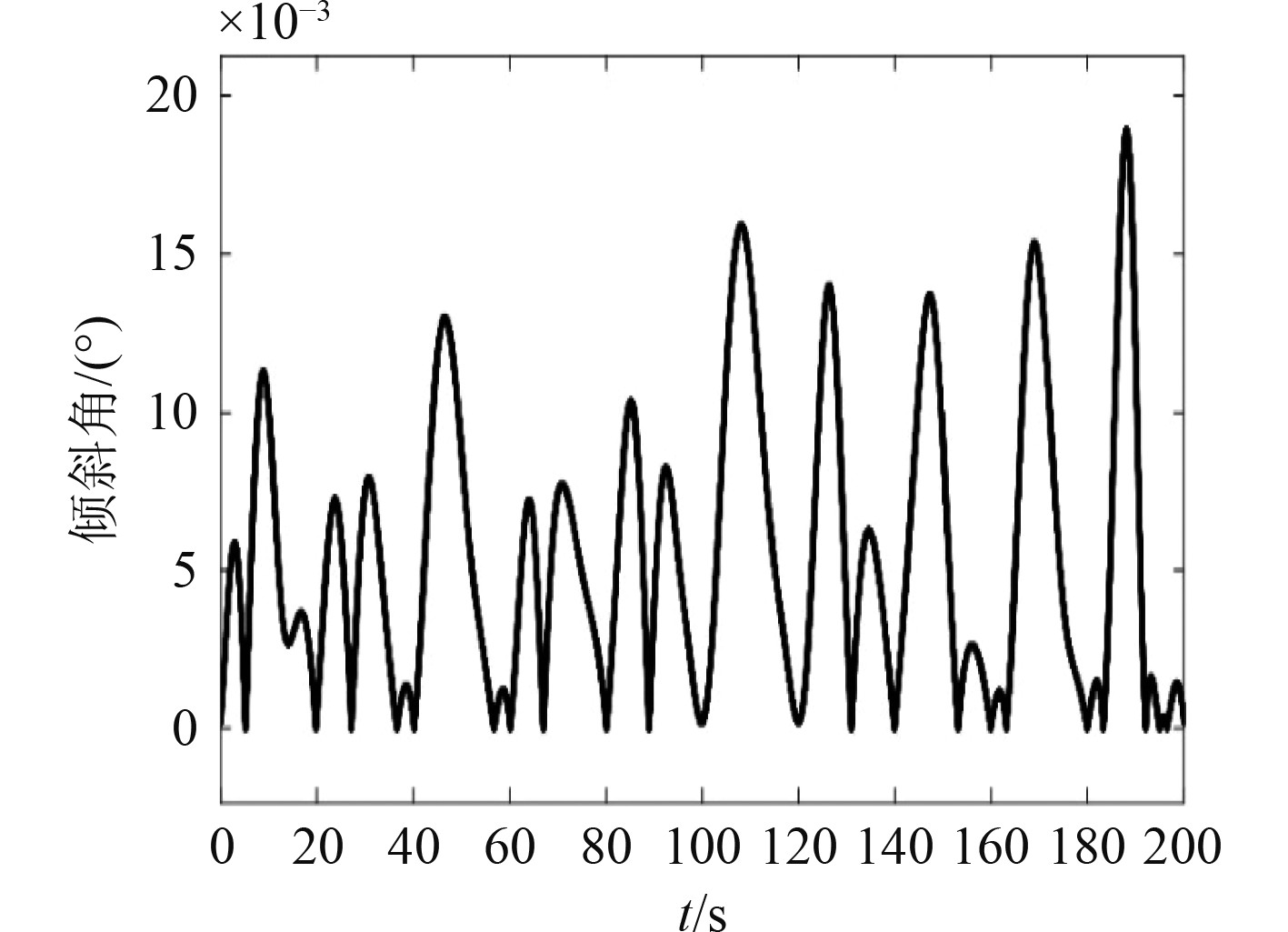
在三自由度并联稳定平台的动平台添加姿态传感器,输出的X,Y和Z轴的运动位移曲线变化如图10所示,倾角角度变化曲线如图11所示。根据运行结果可知,稳定平台的横摇、纵摇和升沉3个姿态均保持平稳。尽管在X轴和Y轴方向受到约束杆作用后有一定的位移变化,但是不影响稳定平台的横摇、纵摇和升沉3个自由度的补偿。在3级海况下补偿平台的电推杆位移曲线平滑,补偿性能良好,在运动学上满足设计要求。
|
图 10 稳定平台X轴、Y轴和Z轴方向位移变化 Fig. 10 Displacement variation of X axis, Y axis and Z axis of stabilization platform |
|
图 11 稳定平台倾斜角变化 Fig. 11 Tilt Angle variation of stabilization platform |
本文设计的三自由度并联稳定平台采用西门子S1500系列PLC作为核心控制器,通过伺服驱动器控制3个伺服电推杆。利用惯性导航模块采集并联平台的横摇和纵摇角度。而升沉数据通过位移传感器测得。通过上位机实现位置逆解算法,将3个伺服的位置数据实时共享给PLC,最终由伺服驱动器控制3个电推杆位置实现期望的姿态,经过测试该平台能够有效补偿海浪的三自由度扰动。
5 结 语针对船舶三自由度并联稳定平台进行了机构设计、虚拟样机的物理建模与3D仿真以及样机的制作和测试。该三自由度并联稳定平台具有承载能力较强、低重心和稳定性强等特点,适合于船载吊装起重机等设备,具备升沉、纵摇和横摇的补偿能力。电推杆由于受到约束杆的作用,会发生部分水平偏移,但是不影响3个自由度的姿态补偿。
| [1] |
王宣银, 4TPS-1PS四自由度并联电动平台动力学建模与位姿闭环鲁棒控制[J], 浙江大学学报, 2009, 43(8): 1492−1496.
|
| [2] |
李玉昆. 3-UPS/S并联稳定平台的性能分析与稳定补偿实验研究[C]// 秦皇岛: 燕山大学, 2018.
|
| [3] |
ZHAO Xing-yu, ZHAO Tie-shi, WANG Chang, et. al. Type synthesis and analysis of parallel mechanisms with sub-closed-loops, Mechanism and Machine Theory, 2018, 120: 140−165.
|
| [4] |
冯志坚, 王桂莲, 吕秉锐, 等, 三自由度并联机构的设计与运动学分析[J]. 组合机床与自动化加工技术, 2020(6): 1−4.
|
 2022, Vol. 44
2022, Vol. 44
