0 引　言

舰船分段装载是当前舰船装配的主要技术，该技术的应用在很大程度上降低了舰船组装的周期和成本。但舰船装配是一个大型且复杂的工程，在舰船分段装载过程中，零件装载位置不同其应用到的相关工具也不尽相同^[1-2]，因此在其装载过程中难免出现零件干涉情况和频繁更换装载工具情况。为降低分段装载难度，国内很多学者对其分段装载顺序进行优化。如袁福帅等^[3]提出了基于改进遗传算法装载优化方法，该方法引入指导进化因子对遗传算法进行改进后，利用遗传算法对配件顺序因子进行交叉变异操作，输出其顺序优化结果。李国杰等^[4]研究了装卸顺序优化方法，该方法通过建立零件信息库，以距离作为指标，利用机器学习算法输出其优化结果。但上述2种方法在应用过程中均存在收敛性不足问题。遗传模拟退火算法则是在遗传算法内引入了模拟退火算法，利用模拟退火算法抑制遗传算法内因子陷入局部极值情况^[5]，以提升遗传算法的收敛性。本文设计遗传模拟退火算法舰船分段装载的顺序优化方法，提高舰船分段装载效果。

1 舰船分段装载的顺序优化方法 1.1 分段装载顺序优化数学模型建立

船舶装载序列的合理性前提是各个装载零件之间互相独立的同时，存在关联联系的装置零件可以相互协作^[6]。在已知舰船装配零件的尺寸前提下，建立舰船分段装载数学模型，通过求解该模型实现舰船装载顺序的优化。构建舰船分段装载数学模型如下：

$ \mathrm{min}S=({\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}+{\sigma }_{4})\cdot({f}_{1}+{f}_{2}+{f}_{3}+{f}_{4}) 。$

(1)

式中：f₁表示循环次数；f₂表示舰船分段装载过程中更换吊装设备的次数；f₃表示舰船分段装载的组装效率；f₄表示装载程序实时监测衡量； $ {\sigma _1} $ ， $ {\sigma _2} $ ， $ {\sigma _3} $ ， $ {\sigma _4} $ 均表示舰船分段装载零件。

1.2 装配顺序可行性条件设置

设置式(1)的舰船分段装配顺序可行性条件，依据该条件对式(1)进行求解。Q_i表示舰船装配组，在该装配组内已完成的装载零件为 $ m $ 个，则此时该检测分段装载顺序表达式如下：

$ A{S_m} = \left\{ {{Q_1},{Q_2}, \cdots ,{Q_m}} \right\} 。$

(2)

式中：Q_j为舰船分段装载顺序内任意零件，若获得该零件在其装载顺序内是否可行，则需从以下2个可行性对其进行设置。

1）装载顺序零件接触关系可行性设置

第 $ i $ 个分段零件装载之初，先考虑与该分段零件其他存在关联关系分段零件是否已经装载，若是，则第 $ i $ 个分段零件在该装载顺序较为合理。反之则认为第 $ i $ 个分段零件在其装载顺序内不可行^[7]。舰船在分段装载时，其第一个分段零件无须考虑上述接触关系^[8]，但其后续的每个零件均需考虑与之存在关联关系的是否已经装载。在判断舰船分段零件之间的关联关系时，利用矩阵形式描述，其表达式如下：

$ {M_A} = {\left[ {{M_{ij}}} \right]_{N\cdot N}} 。$

(3)

式中： $ {M_A} $ 表示分段零件和之前的关联关系； $ N\cdot N $ 表示矩阵规格。

依据式(3)，第 $ i $ 个零件的装载顺序的关联关系表达公式如下：

$ {M_i} = {M_i}{Q_1} \cup {M_i}{Q_2} \cup {M_i}{Q_3} \cup \cdots \cup {M_i}{Q_m}。$

(4)

式中：分段装载零件 $ i $ 和舰船装配组Q₁之间的关联关系由M_iQ ₁表示，后续依此类推。当分段装载零件 $ i $ 和舰船装配组Q₁之间数值为1时，说明二者之间存在关联关系。若分段装载零件 $ i $ 和舰船装配组Q₁之间数值为0，则说明二者之间无关联关系。当式(4)数值为1时，则说明此时舰船分段装载的顺序可行。

2）装载顺序干涉可行性设置

令舰船装配组Q_i和零件Q_j之间的干涉向量为 $ Y $ ，表达式如下：

$ Y = \left\{ {{b_{ijX}},{b_{ijY}},{b_{ijZ}},{b_{jiX}},{b_{jiY}},{b_{jiZ}}} \right\} 。$

(5)

式中： $ X $ ， $ Y $ ， $ Z $ 表示舰船分段零件装载三维坐标轴方向。按照运动相互相理论可知，舰船分段零件 $ i $ 在三维坐标轴的正方向上和分段零件 $ j $ 在三维坐标轴反方向上的干涉情况相同。因此通过构建干涉矩阵 $ b $ ，即可计算公式(5)内各个元素数值，其表达式如下：

$ {b_{dk}} = {\left[ {{b_{ij{d_k}}}} \right]_{N*N}} 。$

(6)

式中： $ {b_{ij{d_k}}} $ 表示第 $ j $ 个装载零件顺着 $ {d_k} $ 方向装载时，其与装载零件 $ i $ 之间的干涉关系；当第 $ j $ 个装载零件和第 $ i $ 个装载零件存在干涉关系时，则数值为1，反之则为0。

将式(6)结果代入到式(5)内后，以舰船装配组Q_i为例，当的干涉向量内存在一个元素数值为0的情况时，说明第 $ i $ 个分段装载零件在该装配组内的顺序较为合理。此时，在舰船装载方向上 $ \pm {d_k} $ ，对Q_i和与之存在关联关系的其他组件实施与运算，其表达式如下：

$ \left\{ \begin{gathered} + {b_{i{d_k}}} = {b_{i{Q_1}{d_k}}} \cup {b_{i{Q_2}{d_k}}} \cup \cdots {b_{i{Q_m}{d_k}}}，\hfill \\ - {b_{i{d_k}}} = {b_{{Q_1}i{d_k}}} \cup {b_{{Q_2}i{d_k}}} \cup \cdots {b_{{Q_m}i{d_k}}} 。\hfill \\ \end{gathered} \right. $

(7)

式中： $ + {b_{i{d_k}}} $ ， $ - {b_{i{d_k}}} $ 分别表示正方向和反方向与运算结果。当 $ + {b_{i{d_k}}} $ 和 $ - {b_{i{d_k}}} $ 的内元素最低有一项为0时，则舰船装配组Q_i为在该方向上和已经装载好的零件不存在干涉关系。

1.3 基于遗传模拟退火算法的分段装载顺序优化数学模型求解

使用遗传算法和模拟退火算法相结合的遗传模拟退火算法对舰船分段装载的顺序实施优化，其详细步骤如下：

1）适应度函数选取

舰船分段装载装配顺序以其装配效率最快作为可行顺序^[9-10]。定义分段装载顺序优化数学模型适应度函数时，需考虑舰船分段装载时装配工具、夹具等变化对其整体装载效率的影响。依据舰船分段装载难度描述其装载效率，其总装载难度表达式如下：

$ AU = \sum\limits_{i = 1}^n {({U_{{x_{i - 1}},{x_i}}})}，$

(8)

$ {U_{{x_{i - 1}},{x_i}}} = {\alpha _i} + {\beta _i} + {\gamma _i} + {\omega _i} 。$

(9)

式中： $ AU $ 表示舰船分段装载的总难度； $ {x_i} $ 表示第 $ i $ 个装载零件； $ {U_{{x_{i - 1}},{x_i}}} $ 表示在第 $ {x_{i - 1}} $ 个零件装载后，再对第 $ {x_i} $ 个零件装载时的难度； $ \alpha $ ， $ \beta $ ， $ \gamma $ ， $ \omega $ 均表示难度因子。

在任意一个零件装载过程中，当 $ {U_{{x_{i - 1}},{x_i}}} $ 数值为0时，分段装载顺序优化数学模型的适应度函数表达式如下：

$ Fitness({Q_i}) = \sum\limits_{i = 1}^N {4i - \sum\limits_{i = 1}^N {({\alpha _i} + {\beta _i} + {\gamma _i} + {\omega _i})} }。$

(10)

式中： $ N $ 表示舰船分段装载零件总数量； $ Fitness({Q_i}) $ 表示第 $ {Q_i} $ 个装配组的分段装载顺序优化适应度数值。

2）分段装载因子选择

选择舰船分段装载因子，以保障舰船分段装载顺序的最优顺序个体。在此利用数学计算方式选取舰船分段装载最优因子。当舰船分段装载顺序内单个零件适应度数值最大时^[11]，可将其作为下一代的父代概率，E_i表示舰船装载顺序内单个零件被选择的概率，即

$ {E_i} = \frac{{{h_i}}}{{\displaystyle\sum\limits_{j = 1}^N {{h_j}} }}。$

(11)

式中：h_i，h_j分别表示舰船分段装载的安装方式。

在0～1内选择任意常数 $ r $ ，当该常数符合条件式(13)时，舰船装载顺序选择零件 $ i $ 将其遗传到下一代。

$ \sum\limits_{j = 0}^{i - 1} {{E_j}} \leqslant r \leqslant \sum\limits_{j = 0}^i {{E_j}} 。$

(12)

3）交叉与变异操作

使用单位置顺序交叉方式对舰船分段装配顺序进行调整，首先将E_i和E_j看做2个父代因子，利用二者生成属于区间[1,n-1]的随机数r_c；其次选取父代因子E_i和随机数r_c之间的因子片段，并从父代因子E_j内删除属于E_i的因子，然后以r_c为起始点，将E_j内剩余因子按照顺序放置在E_i内，得到子代因子V_i。再次依据上述步骤获得子代因子V_j。

4）模拟退火处理

对舰船装载顺序交叉和变异结果进行模拟退火处理，抑制遗传算法因子早熟情况。O、O_min分别表示舰船装载顺序交叉和变异结果的当前温度和阈值温度，当O>v时，则对舰船装载顺序交叉和变异结果进行基本变换，并依据Metropolis接受原则计算舰船装载顺序被接受的概率，其表达式如下：

$ {E_a} = \left\{ \begin{gathered} 1,{F_i}(O) < {F_i}(O)，\hfill \\ \exp \left[ {\frac{{{F_i}(O)}}{T} - \frac{{{F_j}(O)}}{T}} \right],{F_i}(O) \geqslant {F_i}(O)。\hfill \\ \end{gathered} \right. $

(13)

式中： $ {F_i}(O) $ 和 $ {F_j}(O) $ 分别表示对舰船装载顺序交叉和变异基本变化前的适应度数值。

利用随机数生成函数生成区间[0,1]内任意随机数R_d，当R_d小于公式(14)数值时，则接受新的舰船装置顺序内零件个体并更新 $ T $ 数值，即

$ O = O\cdot \xi，$

(14)

式中， $ \xi $ 表示温度衰减系数。

5）建立初始因子群并设置迭代终止条件。利用优先级函数和随机数函数各生成一半初始因子群，其中将随机数生成的因子作为优先级，其计算公式如下：

$ {E_i} =\left (\frac{{{l_i}{p_r}}}{{{w_i}}} + \frac{{{l_i}\cdot {w_i}\cdot {E_a}}}{{{w_i}}}\right)。$

(16)

式中：E_i表示第 $ i $ 个分段装载零件的优先级；l_i，w_i，p_r分别表示分段装载零件的长、宽和长宽比重数值；E_a表示分段装载零件所占面积；R_i表示属于0～1的随机常数。

因子群更新迭代完成后，即可输出最优个体位置，从而实现舰船分段装载的顺序优化。

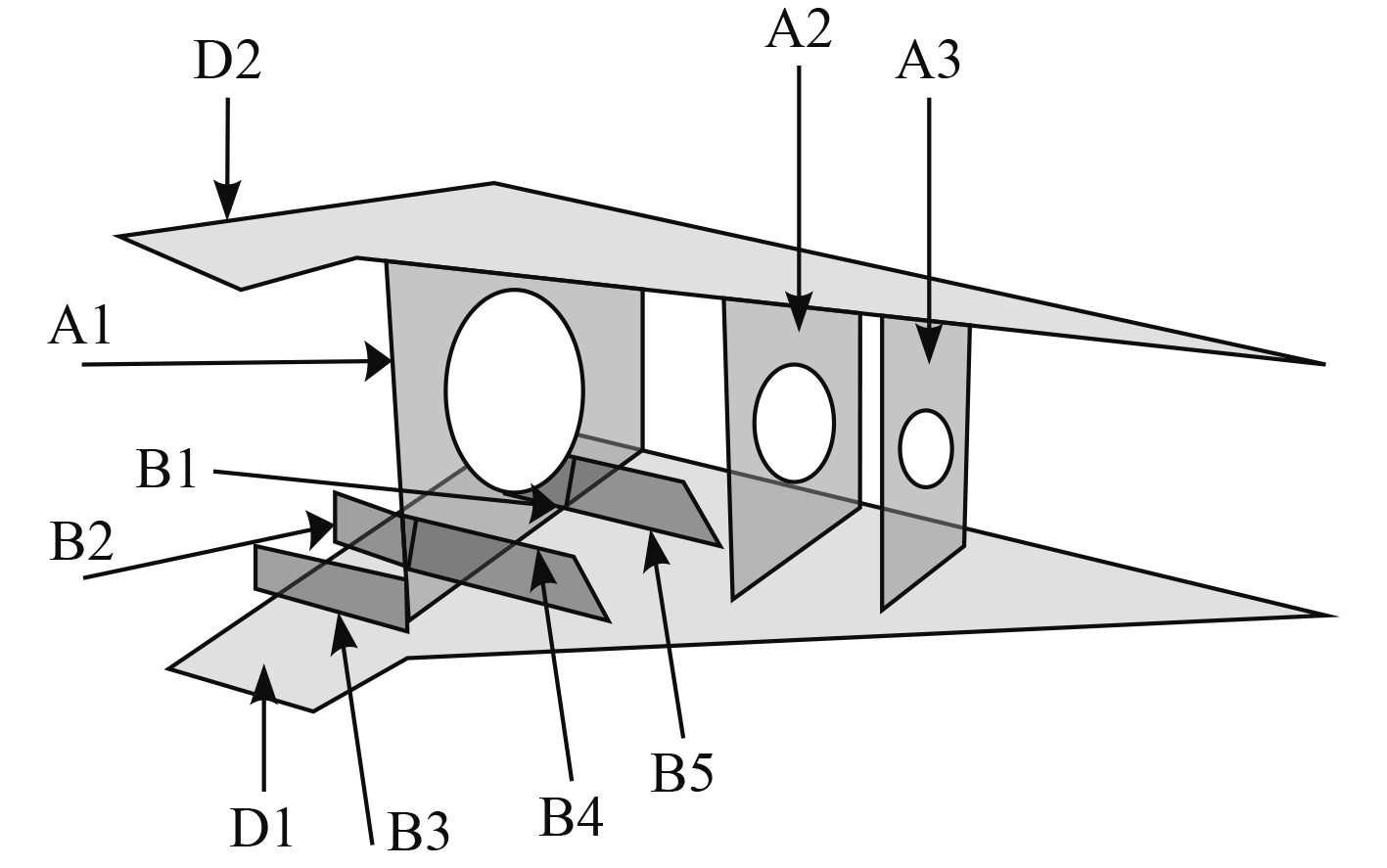
2 实验结果分析

以某自升式起重船船底边仓组件为实验对象，为方便呈现该边仓组件结构，对其进行局部简化处理，其整体结构如图1所示。在自升式起重船船底边仓组件结构内，由若干零件共同组成一整个分段装配组，且各个零件之间存在关联的同时，也互相独立。

2.1 交叉与变异概率确定

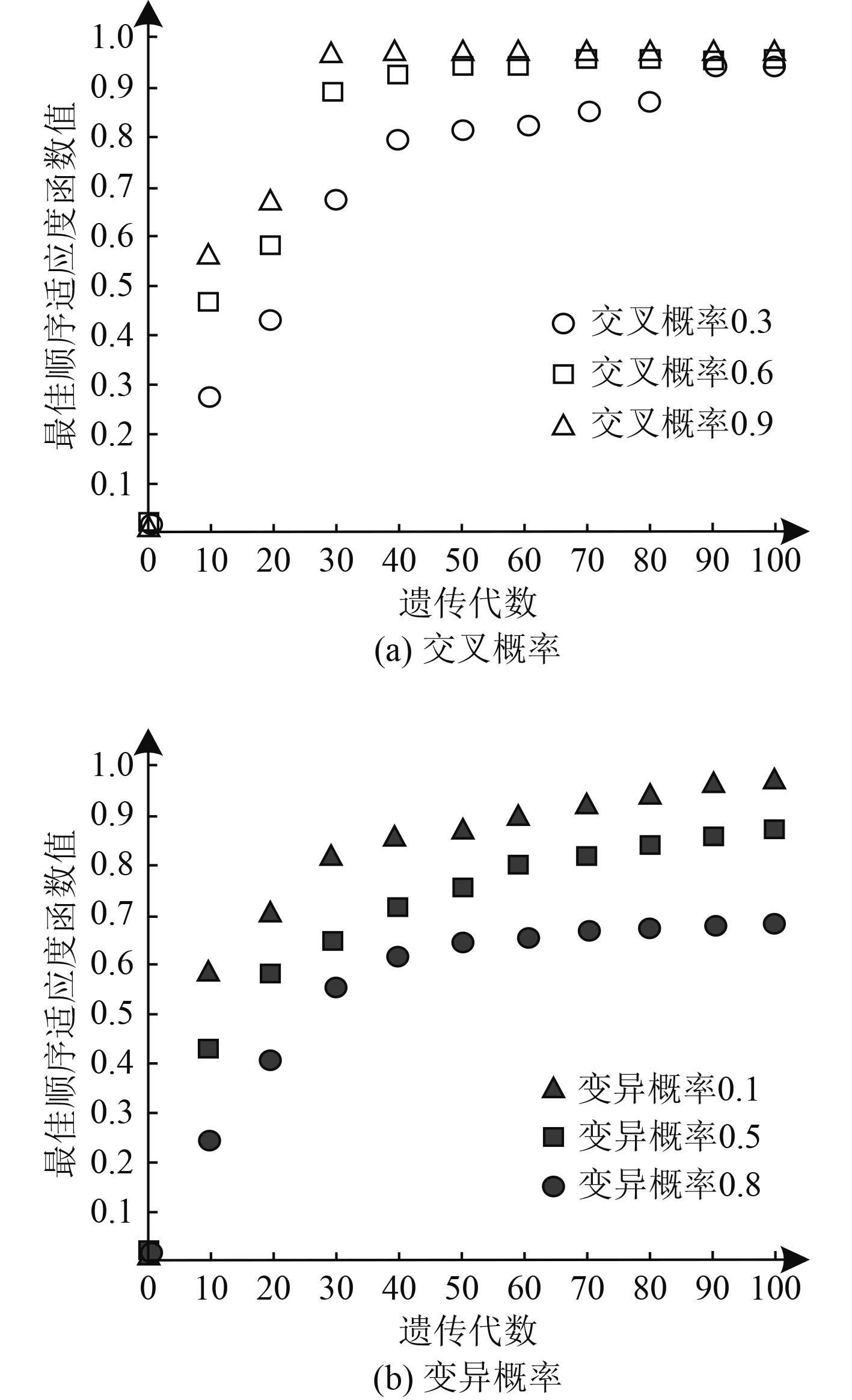
在对舰船分段装载顺序进行优化前，需确定分段装载因子的交叉与变异系数，作为后续优化舰船分段装载顺序优化时交叉与变异操作的输入。交叉与变异概率确定结果如图2所示。由图2(a)可知，不同交叉概率情况下，本文方法的最佳顺序适应度函数值随着遗传代数的增加而上升，但当遗传代数超过30后，交叉概率为0.6和0.9时的最佳顺序适应度函数数值达到稳定状态，不受遗传代数的增加而变化。其中交叉概率为0.9时，本文方法在不同遗传代数情况下的最佳顺序适应度函数数值接近1.0，因此交叉概率设置为0.9。分析图2(b)可知，变异概率数值越大，则本文方法的最佳顺序适应度函数数值越小，因此本文方法的变异概率数值选择0.1。

2.2 分段装载的顺序优化测试

以装载工具更换次数和发生干涉次数为衡量本文方法对舰船分段装载顺序优化指标，测试其在不同装配组数量情况下，装载工具更换次数和发生干涉次数，分析可知，该舰船船底边仓组件的初始分段装载顺序和优化后的装载顺序仅D1、D2两个零件的顺序相同，说明本文方法对其进行装载顺序进行优化后，变更了部分零件的装载顺序。从累计发生干涉次数和累计更换工具次数角度分析，经过本文方法对该边仓组件进行优化后，累计发生干涉次数和更换工具次数分别降低3次和4次。综上所述，本文方法可有效对舰船分段装载顺序进行优化的同时，也降低了其分段装载时发生的干涉次数和更换工具次数，应用效果良好。

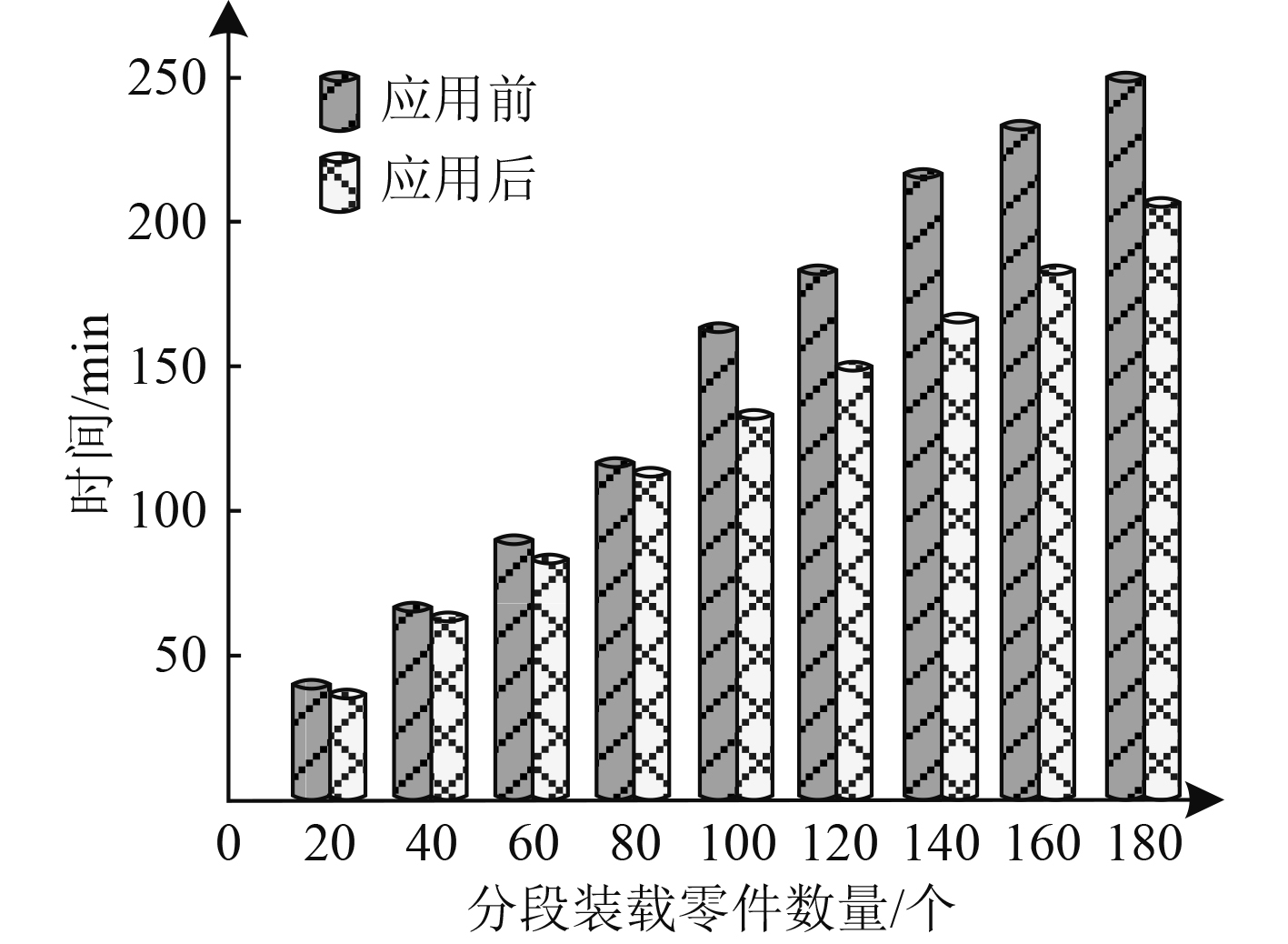
测试在装载零件数量不同情况下，应用本文方法前后舰船分段装载完成时间，结果如图3所示。分析可知，舰船分段装载所用时间与其零件数量成正比例关系。但在分段装载零件数量为40个之前时，本文方法优化后其装载所需时间与应用前相差不大。而当分段装载零件超过60个后，本文方法应用前后分段装载所用时间差距逐渐拉大。在分段装载零件数量为180个时，二者之间所用时间差值约为50 min。综上结果，本文方法较适用于装载零件较多的舰船组件，且其应用后分段装载所需时间得到有效降低。

3 结　语

本文设计遗传模拟退火算法舰船分段装载的顺序优化方法，在其中运用了遗传算法和模拟退火算法，有效地提升舰船分段装载顺序优化使适应度数值的收敛效果。经过实验验证：该方法运用后，在分段装载零件数量为180个时，降低其装载耗时接近50 min；且优化后的分段装载顺序发生的更换工具次数和发生干涉次数均得到有效降低。