2. 浙江广厦建设职业技术大学,浙江 东阳 322100
2. Zhejiang Guangsha Construction Vocational and Technical University, Dongyang 322100, China
由于在舰船网络通信过程中,因通信环境与通信介质等的影响,导致网络信号存在干扰噪声而变得微弱,造成整体舰船网络通信质量不佳[1]。因而,为保障舰船网络的通信质量,需实现对舰船网络通信中微弱信号增强[2-3]。
聚类属于一种数据挖掘方法,能够由相应集合内挖掘出所需信息数据[4]。基于密度法的聚类方法应用较为广泛,其应用中可由存在噪声干扰的相应数据集合内挖掘出随机形态与数目的簇,无须提前将聚类簇的数量指定,目前已被大量应用于模式识别、信号检测及生物智能等领域内[5-6]。经验模态分解(EMD)法可有效划分繁琐信号为数个具备初始信号各尺度细节特征信号的本征模态函数(IMF),其分解过程是以初始信号的序列时间尺度细节特征为基础而实现的,自适应性较强,尤其针对非线性与非稳定信号的分解更具优势[7]。小波变换法能够随机设定阈值预估标准及阈值函数,并依据相关阈值设定结果实现信号的去噪处理,增强信号的信噪比[8]。奇异谱分析(SSA)法是基于矩阵求奇异值分解而实现的一类主成分分析法,其特点为时效性高、便于运算等,在预测与去噪等领域内应用广泛[9]。
本文结合稠密度聚类、EMD、小波变换及SSA方法,实现对舰船网络内微弱信号的自适应增强处理,有效去除舰船网络微弱信号噪声干扰,提升信号的强度,保障舰船网络航行过程中的整体通信质量。
1 稠密度聚类的舰船网络微弱信号自适应增强方法 1.1 基于稠密度聚类的舰船网络微弱信号检测在实现舰船网络微弱信号增强前,需先检测微弱信号,选用稠密度聚类方法。稠密度聚类是指依靠稠密度聚类的密度可达理论,为舰船网络内传输的各个微弱信号创建稠密度区域[10-11]微弱信号x与y二者之间的近似性量化表示以l(x,y)呈现,在此选用欧几里得间距预估l(x,y)值。m个舰船网络微弱信号中每2个微弱信号间的l(x,y)通过相异度矩阵储存,通过一个m×m维的上三角矩阵呈现,该矩阵可表示为:
| $ {\boldsymbol{l}}\left( {x,y} \right) = \left[ \begin{gathered} 0\mathop {}\nolimits_{} l\left( {0,1} \right)\mathop {}\nolimits_{} l\left( {0,2} \right)\mathop {}\nolimits_{} \cdots l\left( {0,m - 1} \right) \hfill \\ \mathop {}\nolimits_{} \mathop {}\nolimits_{} 0\mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\limits_{} l\left( {1,2} \right)\mathop {}\nolimits_{} \cdots l\left( {1,m - 1} \right) \hfill \\ \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \vdots \mathop {}\nolimits_{} \mathop {}\nolimits_{} \hfill \\ \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} 0\mathop {}\nolimits_{} l\left( {m - 2,m - 1} \right) \hfill \\ \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} \mathop {}\nolimits_{} 0\mathop {}\nolimits_{} \mathop {}\nolimits_{} \end{gathered} \right]。$ | (1) |
设定舰船网络B的核心微弱信号b和微弱信号a之间的间距以l(b,a)呈现,在具备N个微弱信号a的r0-邻近区域内,核心微弱信号b和微弱信号a之间的最短间距即为r0,其可表示为:
| $ {r_0} = \min \left\{ {l\left( {b,a} \right),N} \right\},$ | (2) |
设定在r-邻近区域中,当邻近区域的层数提升,半径r的值也随之提升,此关系的表达式为:
| $ {r_M} = \left\{ \begin{gathered} {r_0},M = 1 ,\\ {r_{M - 1}} + 2{r_0}/\left( {1 + M} \right),M \geqslant 2 。\end{gathered} \right. $ | (3) |
式中:邻近区域的层数以M呈现,设核心微弱信号位于第0层。
设定在整体舰船网络B上所构建的微弱信号稠密度区域以{D1, D2,…, Dm}呈现,则各个稠密度区域的密度ρ可表示为:
| $ \rho = \frac{{\left| {{D_i}} \right|}}{{\left| B \right|}} 。$ | (4) |
式中:整体舰船网络内微弱信号数量以|B|
| $ \bar \rho = \frac{1}{m}\sum\limits_{i = 1}^m {\rho \left( {{D_i}} \right)}。$ | (5) |
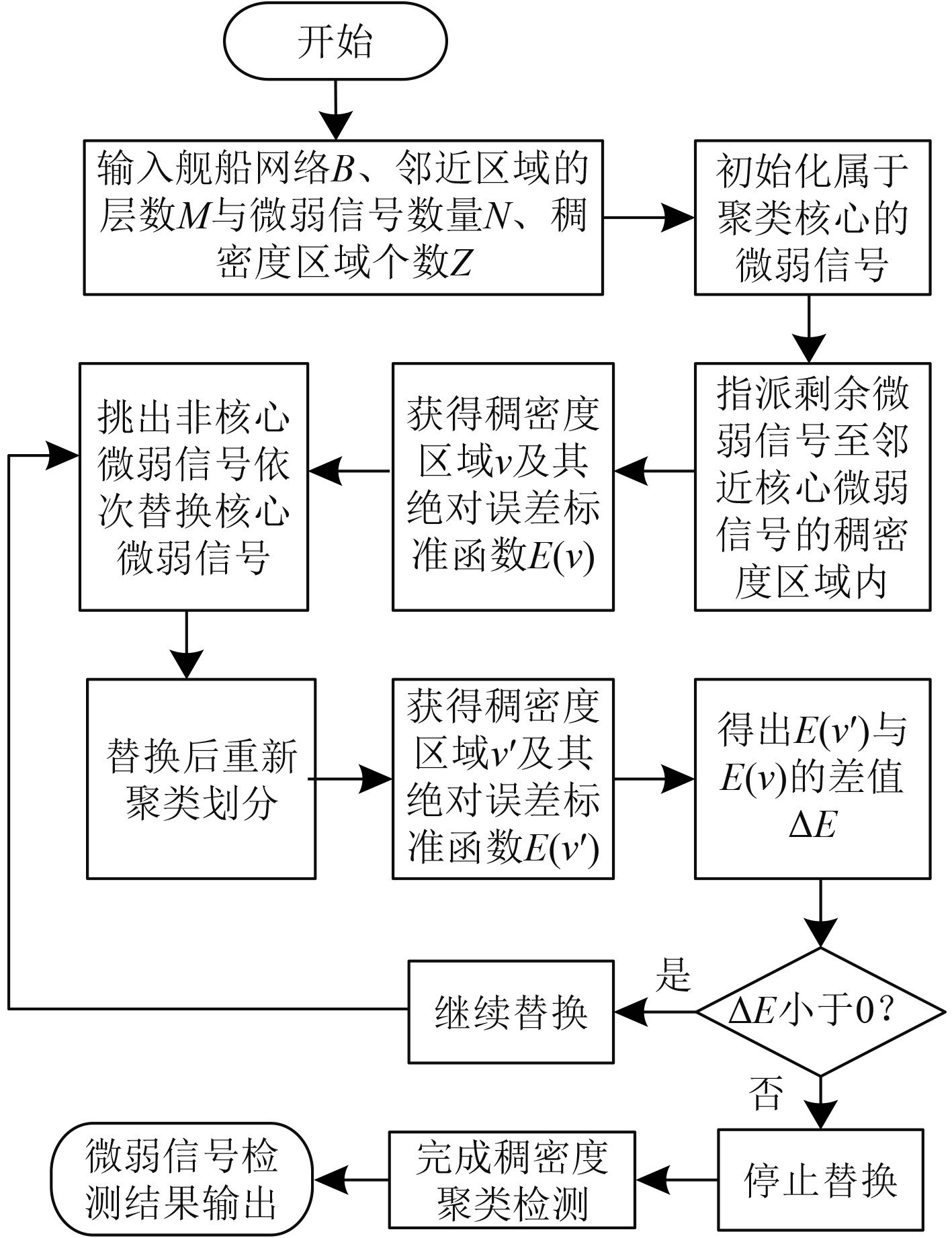
稠密度聚类的舰船网络微弱信号检测整体过程如图1所示。
|
图 1 稠密度聚类的舰船网络微弱信号整体检测过程图 Fig. 1 Overall detection process diagram of weak signals in ship network based on density clustering |
以所检测出的舰船网络内微弱信号a为例,设该微弱信号中包含白噪声信号与纯净信号,二者分别以d与c表示,则舰船网络内微弱信号a的表达式为:
| $ a = d + c ,$ | (6) |
通过EMD分解微弱信号a为数个IMF分量与残余分量,其表达式为:
| $ a = \sum\limits_{i = 1}^J {IM{F_i} + {f_J}}。$ | (7) |
式中:微弱信号a所分解出的IMF分量以IMFi表示,其个数以J表示;残余分量以fJ表示。在此基础上,结合能量阈值判别法区分各个IMF分量IMFi中的信号IMF分量与噪声IMF分量,该能量阈值的表达式为:
| $ S = \arg \max \left[ {{F_p}} \right],1 \leqslant p \leqslant J。$ | (8) |
式中:S表示能量最高的IMF分量索引值,也就是第S个IMF分量的能量值Fp最高。IMF分量的能量值Fp的运算公式为:
| $ {F_p} \cong \frac{1}{J}\sum\limits_{j = 1}^J {{{\left[ {IM{F_p}} \right]}^2}},$ | (9) |
当确定了S后,即可将i小于S的IMF分量IMFi挑出,重构后即为噪声IMF分量g,表达式为:
| $ g = \sum\limits_{i = 1}^S {IM{F_i}},$ | (10) |
对于此部分噪声IMF分量,需结合小波变换法对其实施去噪处理。对于i大于或等于S的IMF分量,重构后即为信号IMF分量h,其表达式为:
| $ h = \sum\limits_{i = s}^J {IM{F_i}} 。$ | (11) |
对于此部分信号IMF分量,需运用SSA算法对其实施去噪处理。
1.2.2 小波变换的舰船网络微弱信号噪声IMF分量去噪针对EMD分解得出的舰船网络微弱信号的噪声IMF分量部分,采取小波变换法实现去噪处理[12],去噪处理过程为:
1)选取恰当的小波基函数,对微弱信号的噪声IMF分量g实施小波变换,获取到一组小波系数,以σj,k表示;
2)依据相应规则设置阈值函数W,采用阈值函数W处理不同尺度上的小波系数,将其中比该阈值函数小的小波系数置为0,并收缩或者保存比该阈值函数大的小波系数,获得预估小波系数σ′j,k;
3)运用预估小波系数σ′j,k实施小波重构,获得预估IMF分量g′,此即为小波去噪后的微弱信号部分IMF分量。
1.2.3 SSA的舰船网络微弱信号IMF分量去噪运用SSA算法对EMD分解得出的舰船网络微弱信号的IMF分量部分实施去噪处理。对于SSA算法而言,其对信号IMF分量实施去噪后重构的关键即为重构阶次的选取[13]。若重构阶次不恰当,易造成信号IMF分量的剩余噪声较多或失真,而恰当的重构阶次能够将信号IMF分量的有用部分更好地保留。在此通过奇异谱创建三角形运算余弦值的方式,将去噪后重构信号IMF分量的重构阶次确定。通过奇异谱创建的三角形如图2所示。

|
图 2 奇异谱创建三角形 Fig. 2 Singular spectra create triangles |
余弦定理方程式为:
| $ {a'^2} = {b'^2} + {c'^2} - 2b'c'\cos A'。$ | (12) |
式中:奇异谱创建三角形的3个边长依次以a′,b′,c′表示;与边长a′相对应的角以A′表示。式(12)变形后为:
| $ \cos C' ={{{a'}^2} + {{b'}^2} - {{c'}^2}}/{2a'b'},$ | (13) |
通常信号分量中噪声部分的奇异值较低,有用部分的奇异值较高。由于位于0~π之间的余弦函数属于单调递减趋势,故与最小角相对应的余弦值最高。故而,最高余弦值位置与拐点处相对应,也就是重构阶次q值。通过SSA分解求得信号IMF分量h的奇异值,以降序的方式依次排序后,剔除掉其中奇异值较低部分,保留奇异值较高部分,并将其重构阶次q确定,利用所确定的重构阶次q重构所保留部分后,获得去噪重构后的信号IMF分量h′。重构信号IMF分量h’的表达式为:
| $ h' = \sum\limits_{w = 1}^q {{\delta ^w}{H^w}} ,1 \leqslant w \leqslant T 。$ | (14) |
式中:信号IMF分量的嵌入维数以T表示;分解奇异值后所得的第w个特征向量以Hw表示,同时其也代表经验正交函数;信号IMF分量在向量上的正交投影系数以δw表示。
将此部分重构后得到的信号IMF分量h′、上一小节中重构后得到的IMF分量g′及EMD分解后的残余分量fJ重构,获取到最终的舰船网络微弱信号a的增强信号
| $ \hat a = {f_J} + h' + g'。$ | (15) |
以某舰船网络为实验对象,应用本文方法对其微弱信号实施自适应增强处理,通过分析整个增强处理过程中各个步骤的应用结果,检验本文方法的实际应用效果。首先通过本文方法对实验舰船网络微弱信号实施稠密度聚类检测,检测结果见图3。由图3可看出,本文方法能够以不同核心微弱信号作为聚类核心,将实验舰船网络内全部微弱信号聚集为5个稠密度区域,实现对实验舰船网络微弱信号的检测。

|
图 3 实验舰船网络微弱信号稠密度聚类检测结果 Fig. 3 Clustering detection results of weak signal density of experimental ship network |
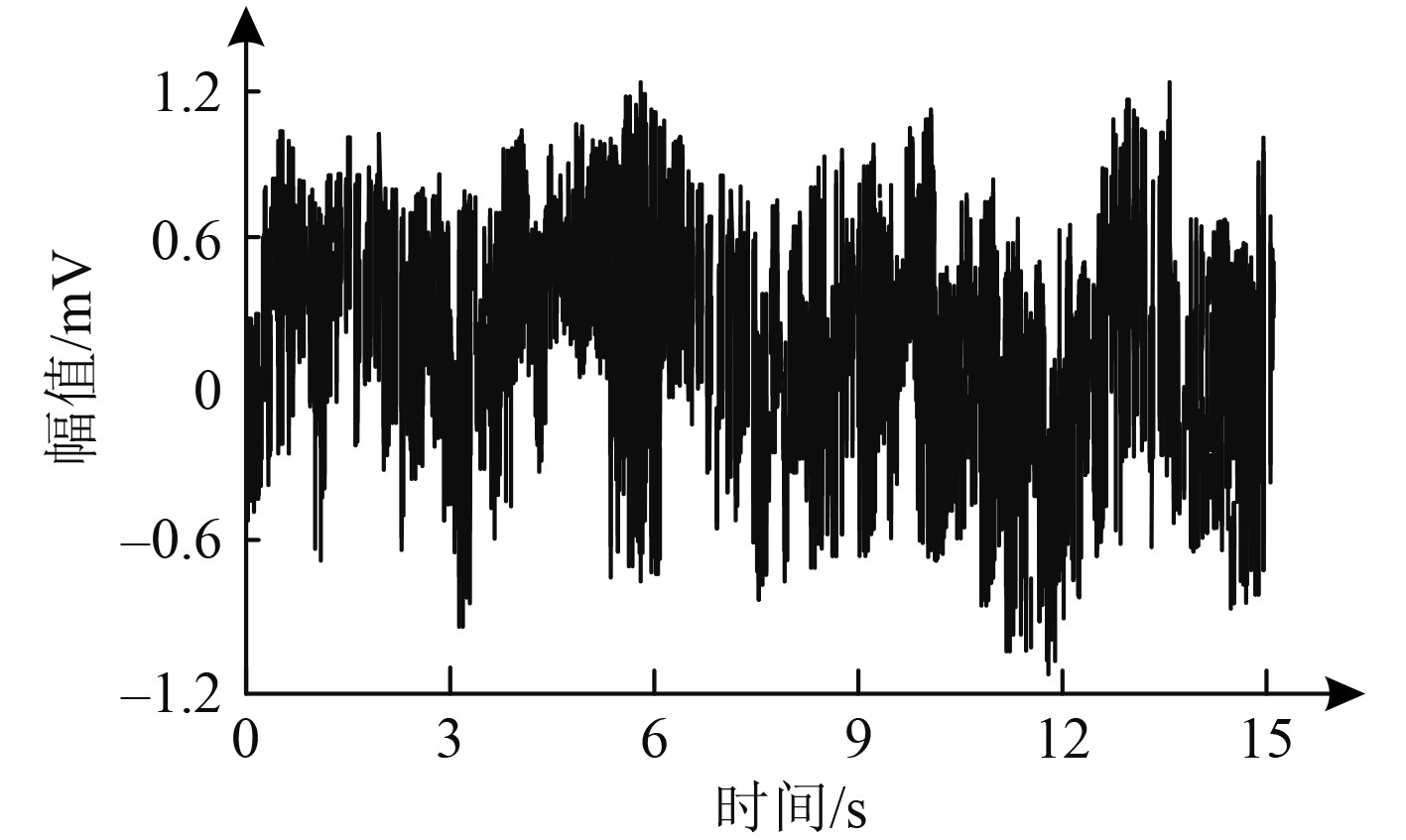
由所检测出的实验舰船网络微弱信号中随机抽取一组初始微弱信号a,通过本文方法对其实施自适应增强处理,检验本文方法的增强效果。所抽取的初始微弱信号如图4所示。
|
图 4 舰船网络初始微弱信号 Fig. 4 Initial weak signal in ship network |
通过本文方法分解该初始微弱信号,获得分解后的3个IMF分量与1个残余分量。
经由本文方法分别对分解后的3个IMF分量实施去噪处理,所获得的3个去噪后IMF分量在保留原有特征的前提下,去除了多余噪声,整体去噪效果十分理想。
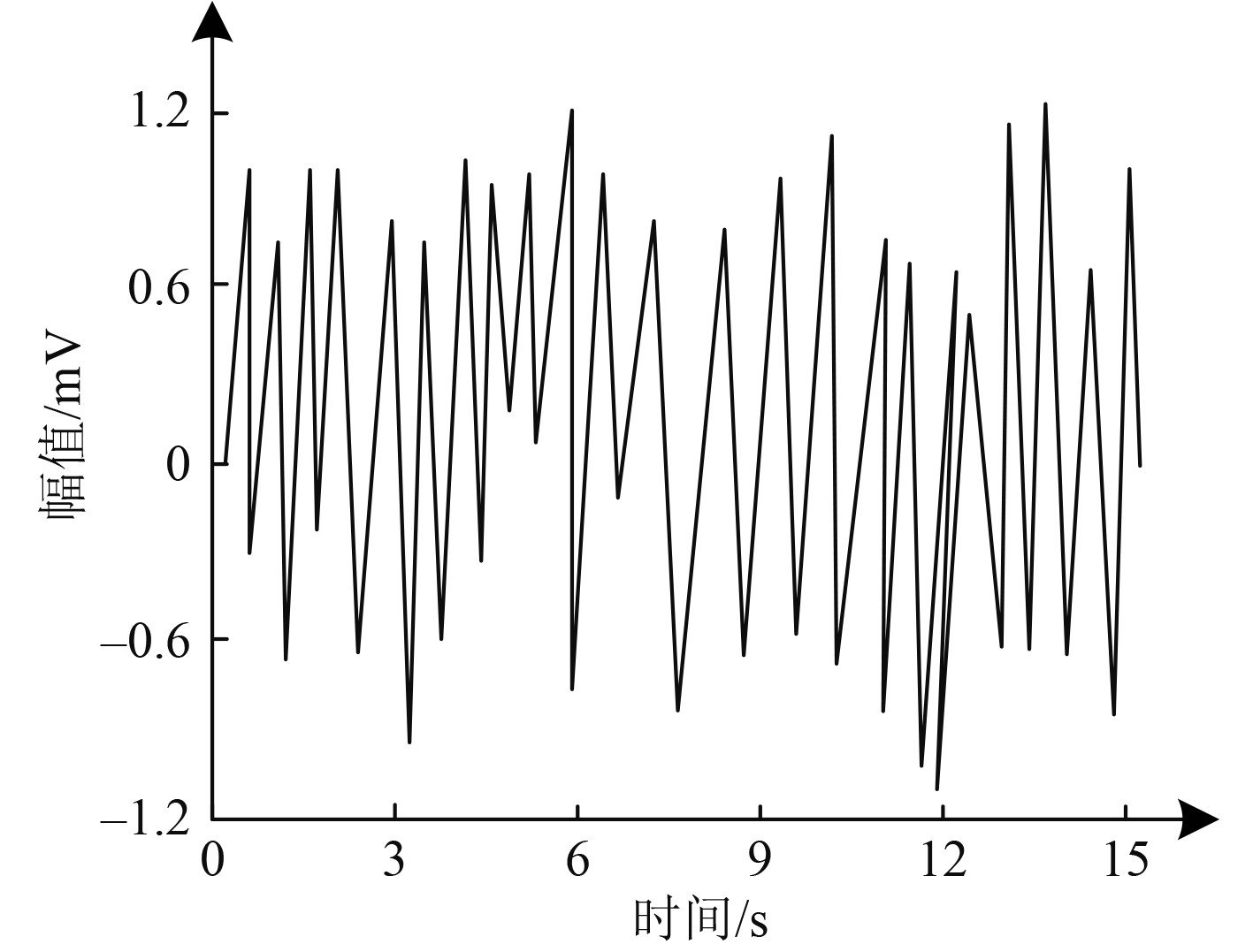
获得实验舰船网络初始微弱信号
|
图 5 舰船网络微弱信号a的增强信号 Fig. 5 Enhancement signal of weak signal A in ship network |
针对稠密度聚类在舰船网络微弱信号自适应增强中的应用方式与效果展开研究,通过应用稠密度聚类算法检测出舰船网络内全部微弱信号。在此基础上,结合小波变换法与EMD-SSA算法实现对所检出微弱信号的分解与去噪处理,重构去噪后各分量获得舰船网络微弱信号的增强信号。实际应用结果表明,本文方法能够实现对舰船网络全部微弱信号的稠密度聚类检测,可针对所检测微弱信号实施分解与去噪处理,去噪后各信号分量中的干扰噪声被有效消除掉,同时能够完整地保留各原始信号分量的细节特征,重构去噪后各信号分量后,得到高清晰度、高质量的增强信号,保障舰船网络通信的整体质量。
| [1] |
时培明, 袁丹真, 张文跃, 等. 基于时延反馈多稳随机共振的微弱信号检测方法[J]. 计量学报, 2020, 41(7): 868-872. |
| [2] |
于希明, 洪硕, 于金祥, 等. 可见光遥感图像船舶目标数据增强方法研究[J]. 仪器仪表学报, 2020, 41(11): 261-269. |
| [3] |
刘刚, 行鸿彦, 张金玉. 一种优化的微弱信号检测方法[J]. 现代雷达, 2019, 41(6): 23-30. |
| [4] |
王骞, 何培宇, 徐自励. 利用奇异谱分析的深度神经网络语音增强方法[J]. 信号处理, 2020, 36(6): 902-910. |
| [5] |
张鑫涛, 马福民, 曹杰, 等. 基于混合度量与类簇自适应调整的粗糙模糊K-means聚类算法[J]. 模式识别与人工智能, 2019, 32(12): 1141-1150. |
| [6] |
黄钢, 瞿伟斌, 许卉莹. 基于改进密度聚类算法的交通事故地点聚类研究[J]. 交通运输系统工程与信息, 2020, 20(5): 169-176. |
| [7] |
王飞宇, 胡志祥, 黄潇. 基于密度峰值聚类算法的模态参数识别[J]. 振动与冲击, 2019, 38(2): 172-178. |
| [8] |
崔彩霞, 曹付元, 梁吉业. 基于密度峰值聚类的自适应欠采样方法[J]. 模式识别与人工智能, 2020, 33(9): 811-819. |
| [9] |
徐丽丽, 董一鸿, 王雄, 等. 基于K-sup稠密子图的大规模复杂网络概要算法及可视化[J]. 计算机辅助设计与图形学学报, 2019, 31(3): 400-411. |
| [10] |
杨璐, 李醒飞, 纪越, 等. 基于EMD-DFA-NLM的电涡流传感器信号去噪方法[J]. 传感技术学报, 2019, 32(9): 1318-1323. DOI:10.3969/j.issn.1004-1699.2019.09.007 |
| [11] |
罗红梅, 宋维琪, 邢漪冉, 等. 基于改进经验模态分解的地震弱信号增强处理方法[J]. 地球物理学进展, 2019, 34(1): 167-173. DOI:10.6038/pg2019BB0402 |
| [12] |
李敏, 刘岩, 马然, 等. 一种用于海水DOC微弱信号去噪处理的小波多阈值算法研究[J]. 传感技术学报, 2021, 34(1): 75-79. DOI:10.3969/j.issn.1004-1699.2021.01.012 |
| [13] |
徐博, 刘斌, 刘德政, 等. 基于小波理论的舰船IMU加速度计信号处理算法[J]. 中国舰船研究, 2020, 15(2): 151-158+164. |
 2022, Vol. 44
2022, Vol. 44
