0 引　言

作为无人操作控制的水面船，无人船以其高自主性、高环境适应性以及高安全性等特征广泛用于替代民用与军用等不同领域^[1]，用于执行一些特殊环境以及对人类产生危险的任务中。无人船的路径规划问题是无人船应用问题中的主要研究方向^[2]，路径规划的本质即为在相应的环境下获取科学的、安全的、简洁的路径^[3]。

刘蔚与谈果戈等^[4]针对无人船路径规划问题，基于路径评价函数得到初步路径规划结果，在此基础上采用快速行进平方法优化路径规划过程，由此获取高精度的路径规划结果。但该方法所规划的路径内包含大量节点，造成无人船航迹路径规划结果所占内存较大。乔双虎等^[5]针对传统的支持向量机路径规划方法，设定约束条件，并以此为基础拓展支持向量机，以此获取无人船路径规划结果。但该方法所规划的路径中，在障碍物与目标点距离较近的条件下，有较大概率生成“死区”限制了该方法的应用性能。胡锟与张亮^[6]针对无人船路径规划构建以非线性系统为基础的控制模型，并采用罚函数凸优化迭代算法求解该模型，获取无人船路径规划结果。但该方法在实际应用过程中需耗费大量时间，规划效率较差。

本文研究基于改进A*算法的无人船路径规划方法，针对A*算法中的实际代价函数与启发函数进行优化，完成无人船路径规划需求的同时，提升规划性能。

1 改进A^*算法的无人船路径规划方法 1.1 基于栅格法的无人船行驶环境模型构建

由于栅格法在环境建模过程中具有结构简单、易于实现等优势^[7]，因此选取栅格法构建无人船行驶环境模型，通过栅格描述无人船行驶环境地图，通过1和0分别表示存在障碍物的栅格和自由栅格，由此生成无人船路径规划的基础。由于无人船的实际大小与水面行驶环境相比过于微小，因此可分别将水面行驶环境和无人船视为一个二维平面和一个具有移动性能的质点，由此可将无人船在水面环境执行任务控制过程理解为二维平面内质点的移动过程。利用栅格法构建无人船行驶环境模型过程中，栅格尺寸设定具有重要意义，直接影响无人船行驶环境模型构建的性能^[8]。在实际构建过程中，以边长为 $ d $ 的正方形作为单一栅格， $ d $ 值的设定如下式：

$ d{\text{ = }}1.5 \times \max \left\{ {{W_c},{W_k}} \right\} 。$

(1)

式中， $ {W_c} $ 和 $ {W_k} $ 分别表示无人船长度与宽度。

由此可将水面环境空间设定为100×100的栅格图，即为无人船行驶环境地图，在该地图内采用改进A*算法规划无人船航行路径。

1.2 基于A^*算法的路径规划 1.2.1 A*算法的改进

以Dijstar算法为基础引入的启发式函数即为A^*算法^[9]，利用该算法规划无人船行驶路径的过程就是经由确定代价函数判断代价大小，由此确定最优无人船行驶路径。

为提升无人船路径规划的性能，需对A*算法进行改进，改进过程从实际代价函数与启发函数两方面出发。实际代价函数的改进需考虑无人船转弯半径下限、路径长度下限和行驶速度条件约束等内容。

1）无人船转弯半径下限

无人船在水平面上转弯过程中的转弯半径下限 $ {R_{\min }} $ 就是无人船在符合自身性能条件下的边界运动半径，一般情况下可通过下式描述：

$ {R_{\min }} = \frac{v}{u} \times \frac{v}{{\tan {\phi _{\max }}}}。$

(4)

式中： $ v $ ， $ u $ 和 $ {\phi _{\max }} $ 分别表示无人船行驶速度、重力加速度与最大滚转角。

无人船路径规划过程中通常利用下式描述转弯半径的路径代价函数：

$ {s_R} = \left\{ \begin{gathered} \sum\limits_{k = 1}^n {\frac{1}{{{r_k}}},{r_k} \geqslant {R_{\min }}} , \hfill \\ \infty ,\mathop {}\nolimits_{} {r_k} < {R_{\min }}。\hfill \\ \end{gathered} \right. $

(5)

2）路径长度下限

无人船由 $ {X_0}\left( {{x_0},{y_0}} \right) $ 行驶至 $ {X_N}\left( {{x_n},{y_n}} \right) $ 的过程中，以 $ {X_0}\left( {{x_0},{y_0}} \right) $ 至 $ {X_N}\left( {{x_n},{y_n}} \right) $ 的直线距离 $ {L_{\min }} $ 表示无人船行驶距离下限值，由此可通下式表示无人船的行驶距离下限值：

$ {L_{\min }} = \sqrt {{{\left( {sum{X_0}} \right)}^2} - {{\left( {sum{X_1}} \right)}^2}}，$

(6)

基于式(6)能够得到路径长度代价函数为：

$ {s_L} = \frac{{{L_n}}}{{{L_{\min }}}} \times \varepsilon 。$

(7)

式中， $ {L_n} $ 和 $ \varepsilon $ 分别表示无人船行驶路径长度和长度修正值。

3）行驶速度条件约束

无人船在路径过程中行驶速度 $ v $ 的约束条件为：

$ 0 \leqslant v \leqslant {v_{\max }}。$

(8)

无人船在实际运行过程中需达到相应的时速要求，即需在设定时间T内达到 $ {X_N}\left( {{x_n},{y_n}} \right) $ ，由此在无人船行驶过程中的理论速度 $ {v_l} $ 和速度代价值可通过下式描述：

$ \left\{ \begin{gathered} {v_l} = \frac{L}{T} ,\hfill \\ {s_v} = \left| {{v_l} - v} \right|。\hfill \\ \end{gathered} \right. $

(9)

以 $ s\left( x \right) $ 表示考虑无人船转弯半径下限、路径长度下限和行驶速度条件约束的代价函数，其公式描述如下：

$ s\left( {x,y} \right) = \left( {{k_1} \times {s_R} + {k_2} \times {s_L} + {k_3} \times {s_v}} \right) \times \sigma 。$

(10)

式中： $ {k_1} $ ， $ {k_2} $ 和 $ {k_3} $ 分别表示转弯半径下限代价函数、路径长度下限代价函数和速度代价函数的权重系数， $ \sigma $ 表示代价函数修正值。

普遍使用的启发函数通常同实际代价函数存在一定差异，通常情况下， $ {X_0}\left( {{x_0},{y_0}} \right) $ 到 $ {X_N}\left( {{x_n},{y_n}} \right) $ 之间存在障碍物，在障碍物分别位于 $ {X_0}\left( {{x_0},{y_0}} \right) $ 的周边和 $ {X_N}\left( {{x_n},{y_n}} \right) $ 的周边时，通过欧几里得距离获取的 $ b\left( {x,y} \right) $ 相较于实际代价 $ s\left( {x,y} \right) $ 更小，由此造成搜索效率较差，若选用Manhattan距离获取 $ b\left( {x,y} \right) $ ，则与 $ s\left( {x,y} \right) $ 相比较大，由此造成搜索得到的路径不是最优路径。因此需改进启发函数，在 $ {X_0}\left( {{x_0},{y_0}} \right) $ 到 $ {X_N}\left( {{x_n},{y_n}} \right) $ 之间不存在障碍物的条件下，利用欧几里得距离获取 $ h\left( {x,y} \right) $ ；在 $ {X_0}\left( {{x_0},{y_0}} \right) $ 到 $ {X_N}\left( {{x_n},{y_n}} \right) $ 之间存在障碍物的条件下，利用欧几里得距离与曼哈顿距离的线性组合获取 $ b\left( {x,y} \right) $ 。改进后的 $ b\left( {x,y} \right) $ 公式描述如下：

$ b\left( {x,y} \right) = m \times \sqrt {{{\left( {N - {X_1}} \right)}^2}} + \left( {1{{ - }}m} \right) \times \left( {\left| {N - {X_1}} \right|} \right)。$

(11)

式中， $ m $ 表示权重。

1.2.2 路径规划流程

利用栅格法将二维空间分成若干个正方形，正方形边长为 $ d $ ，通过栅格划分得到当前节点附近存在八个节点，采用改进后的A*算法在其中依照代价函数确定代价最小的节点，并将其作为下一个轨迹点，判断该轨迹点是否为终止点，若是终止点则输出无人船路径规划结果，相反则返回确定代价最小的节点的过程迭代进行。

1.3 路径规划结果的简化处理

利用改进后的A*算法规划无人船航行路径具有较好的实时性与较好的规划效率，但考虑无人船实际工作环境具有一定的复杂性与不确定性，所以通过改进后的A*算法规划出了无人船航行路径并非最优路径，同时A*算法所需的内存空间同搜索空间之间呈正比例相关，若搜索空间较为广泛，则无人船路径规划过程所需的内存空间也较大。因此需要对A*算法所规划出的无人船路径实施处理，在短时间内清除无人船路径内的额外节点，令其达到最优。 $ {X_l} $ 和 $ \left( {{x_0},{x_1},{x_2}, \cdots ,{x_N}} \right) $ 分别表示A*算法所规划出的无人船路径和路径上的航迹节点， $ {x_0} $ 和 $ {x_N} $ 分别表示无人船的初始点与目标点， $ {X_p} $ 为清除额外节点后的无人船航迹路径，设置初始状态下的 $ {X_p} $ 为空。额外节点清除的具体过程如下：

1）设定 $ i = 1 $ ，在 $ {X_p} $ 内添加 $ {x_i} $ ；

2）针对各 $ j \in \left( {i + 1, \cdots ,N} \right) $ ，确定在点 $ {x_i} $ 与 $ {x_j} $ 构成的线段 $ {x_i}{x_j} $ 间不存在障碍物，在发现第一个障碍物的条件下暂停搜索，同时设定 $ i = j - 1 $ ，在 $ {X_p} $ 内添加 $ {x_i} $ ；

3）循环步骤过程至 $ i = N $ 为止，由此获取简化后的无人船航迹路径。

2 实验结果与分析

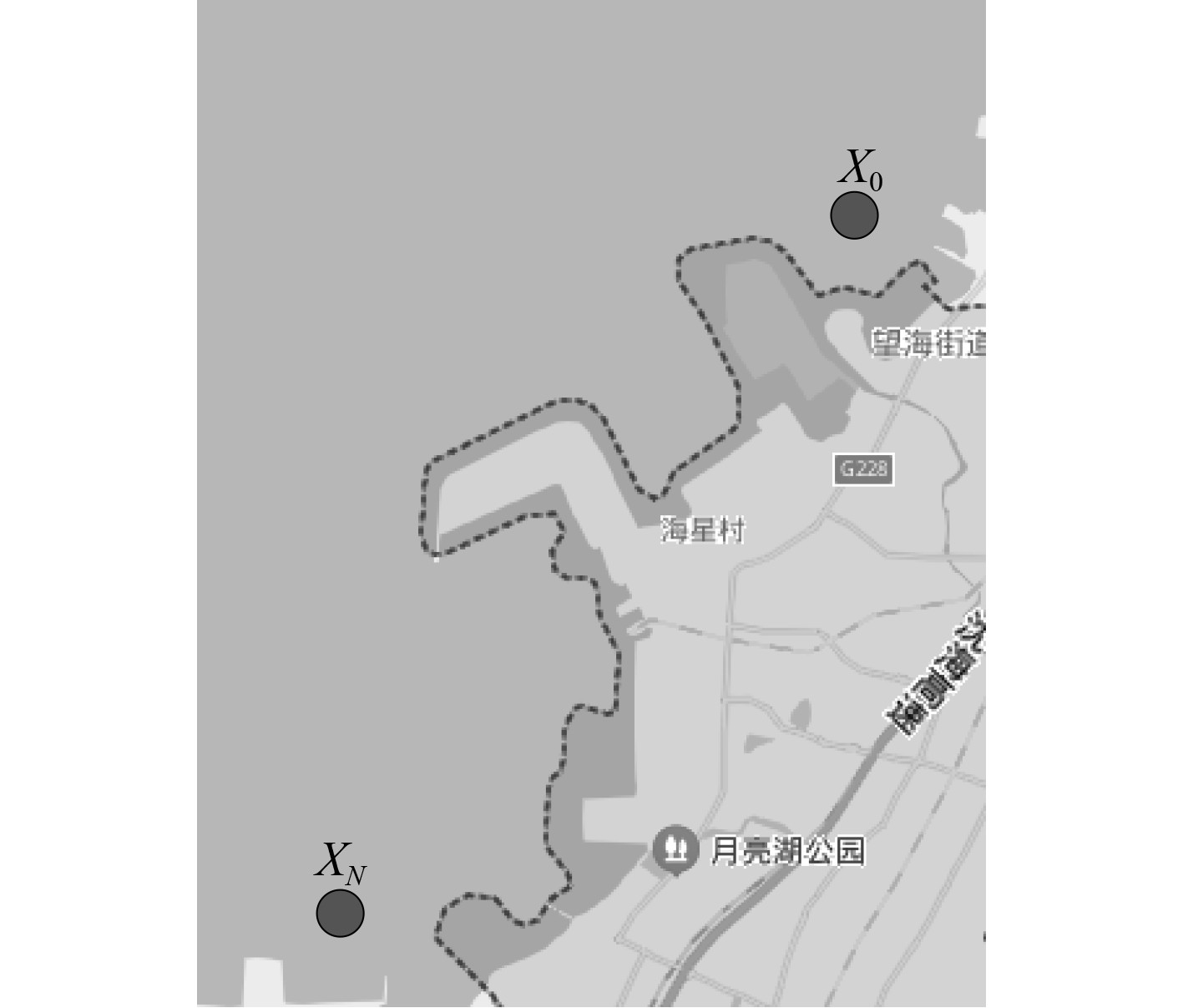
实验为验证本文所研究的基于改进A*算法的无人船路径规划方法在实际无人船路径规划中的应用效果，以某型号无人船为实验对象，实验对象航行区域如图1所示，其中X₀号节点和X_N号节点分别为初始点和目标点。

2.1 有效性验证

为验证本文方法的有效性，采用计算机仿真实验对象航行区域，其中白色区域与黑色区域分别表示可行区域与障碍物。采用本文方法规划实验对象航行路径。本文方法实际应用过程中启发函数内的权重m值需根据经验确定，一般条件下m值的确定标准如下：

1）在实验对象处于图2(a)所示的仿真环境内，实验对象航行区域内的障碍物较多，同时实验对象由X₀至X_N的转弯行驶次数高于直行次数，m的取值范围为[0,0.35]；

2）在实验对象处于图2(b)所示的仿真环境内，实验对象航行区域内的障碍物数量适中，同时实验对象由X₀至X_N的转弯行驶次数与直行次数约一致，m的取值范围为[0.35,0.70]；

3）在实验对象处于图2(c)所示的仿真环境内，实验对象航行区域内的障碍物数量较少，同时实验对象由X₀至X_N的转弯行驶次数低于直行次数，m的取值范围为[0.70,1.00]。

分析图2得到，在设定相应参数后，采用本文方法规划实验对象航行路径，在不同的仿真环境下均能够有效实现障碍物躲避的目的，由此说明采用本文方法规划研究对象航行路径具有较高的可应用性。

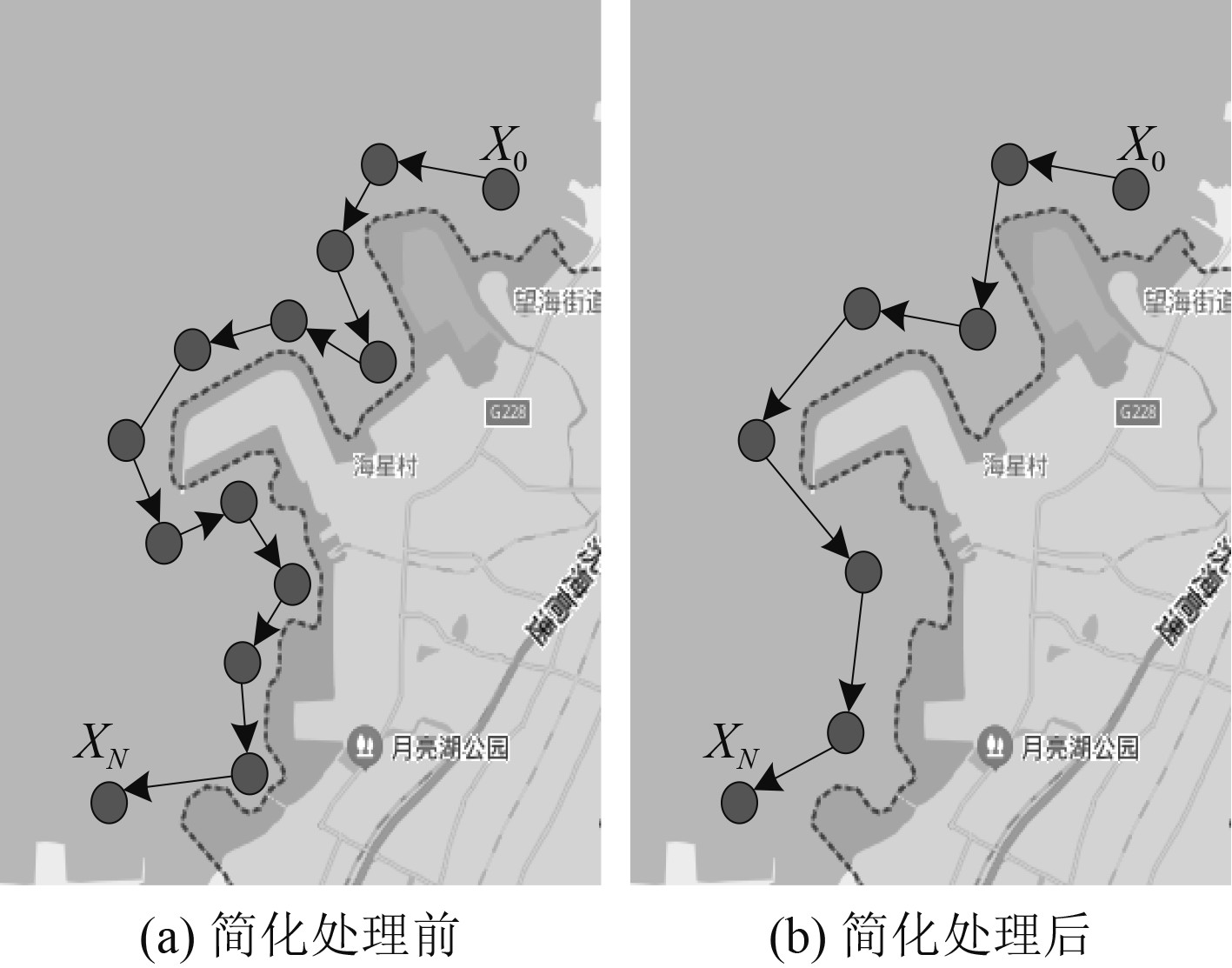
2.2 实际路径规划结果

实验对象采用本文方法进行路径规划，所得结果如图3所示。可知，采用本文方法对实验对象航迹路径进行规划，能够获取一条有效的航行路径，并且通过简化处理后可清除额外节点。通过本文方法所规划的路径能够有效巡查航行区域。

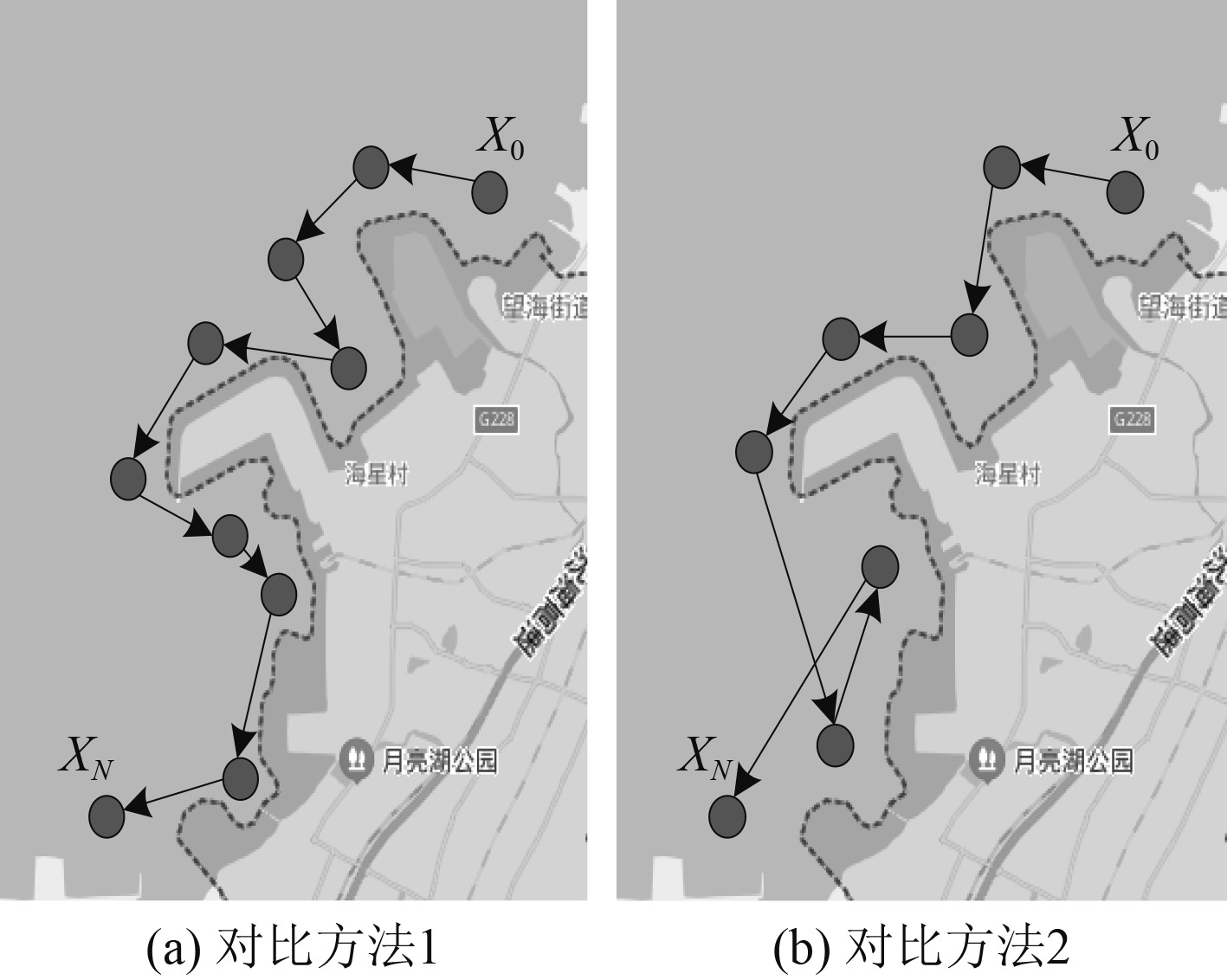
为进一步验证本文方法的路径规划性能，以文献[4]中基于快速行进平方法的规划方法和文献[5]中基于拓展支持向量机的规划方法为对比方法，分别定义为对比方法1和对比方法2。采用2种对比方法规划实验对象航迹路径，所得结果如图4所示。可知，对比方法1所规划的路径内节点数量较多，这样将占用较大内存；而对比方法2所规划的路径内节点数量与本文方法一致，但在后期产生路径重叠现象。

对比本文方法与2种对比方法所规划的路径，所得结果如表1所示。分析得到，3种不同的路径规划方法中，本文方法的规划时间与2种对比方法相比更少，规划结果的总航程与2种对比方法相比也更少，在规划步数上也具有一定优势性。

3 结　语

本文基于改进A*算法的无人船路径规划方法，通过改进A*算法的实际代价函数与启发函数提升无人船路径规划性能。实验结果显示，本文方法在不同环境下均能够有效躲避障碍物，并获取更优的无人船路径规划结果。