0 引　言

永磁同步电机磁场由永磁体产生，不需要励磁电源和励磁绕组，且电机通过逆变器供电，可省去电刷结构，因此永磁同步电机具有结构简单、可靠性高、功率密度大等显著优点。随着永磁材料性能的发展进步，永磁同步电机在汽车、高铁、舰船、飞机等领域应用越来越广泛，考虑到舒适性、隐蔽性等指标，这些领域对电机的振动噪声要求也在不断提高^[1]。

国内外对电机的振动噪声进行了大量研究。诸自强等^[2]研究了电机的噪声机理；Leleu等^[3]分析了变频器供电对电机振动的影响；Fodorean等^[4]对永磁同步电机振动噪声进行了仿真和试验分析；于慎波^[5]提出了降低永磁同步电机的振动噪声的方法；刘和平^[6]对电动汽车用电机电磁振动噪声进行了研究；崔淑梅^[7]对电机模态进行仿真计算并通过实验验证；卢兆刚^[8]研究了电机转子结构刚度对其振动性能的影响。

目前，大多数电机的振动噪声研究偏重于理论分析计算，本文针对科考船船推进系统永磁同步电机振动过大的问题进行振动测试，得到主要转速下的振动响应。通过对振动数据分析，找到电机振动能量分布的主要频率，并对振动产生机理进行了阐述。根据分析结果，后续设计改进时，可选择合适的极槽配合和磁极布置来降低电机振动。

1 电机振动理论及测试方法 1.1 径向电磁力波

铁芯的磁导率远大于空气，磁力线垂直进入铁芯，所以磁通密度的径向分量远大于切向分量，忽略切向分量，电机径向电磁力 $ {p_r}\left( {\theta ,t} \right) $ 可表示为：

$ {p_r}\left( {\theta ,t} \right) \approx \frac{1}{{2{\mu _0}}}{b^2}\left( {\theta ,t} \right) {\text{。}}$

(1)

式中： $ b\left( {\theta ,t} \right) $ 为永磁电机气隙磁密； $ {\ \mu _0} $ 为磁导率； $ \theta $ 为空间角度； $ t $ 为时间。

气隙磁密表达式如下：

$ b\left( {\theta ,t} \right) = f\left( {\theta ,t} \right)\lambda \left( {\theta ,t} \right) $

(2)

式中： $ \lambda \left( {\theta ,t} \right) $ 为气隙比磁导，可近似表达为：

$ \lambda \left( {\theta ,t} \right) = {\lambda _0} + {\lambda _1}\cos \left( {z\theta } \right){\text{。}} $

(3)

式中： $ {\lambda _0} $ 为常数项； $ {\lambda _1} $ 为1谐次下的幅值系数； $ z $ 为电枢槽数。

根据麦克斯韦定律，在PWM变频器供电情况下，三相永磁同步电机的气隙磁势 $ f\left( {\theta ,t} \right) $ 由定子基波磁势 $ {f_0}\left( {\theta ,t} \right) $ 、定子谐波磁势 $ \sum {{f_v}\left( {\theta ,t} \right)} $ 、转子谐波磁势 $ \sum {{f_u}\left( {\theta ,t} \right)} $ 和变频器时间谐波磁势 $ \sum {{f_k}\left( {\theta ,t} \right)} $ 构成，即

$ f\left( {\theta ,t} \right) = {f_0}\left( {\theta ,t} \right) + \sum {{f_v}\left( {\theta ,t} \right)} + \sum {{f_u}\left( {\theta ,t} \right)} + \sum {{f_k}\left( {\theta ,t} \right)} {\text{。}}$

(4)

分项表达式如下：

$ \begin{gathered} {f_0}\left( {\theta ,t} \right) = {F_0}\cos \left( {p\theta - {\omega _0}t - {\varphi _0}} \right), \hfill \\ \sum {{f_v}\left( {\theta ,t} \right)} = \sum\limits_v {{F_v}\cos \left( {vp\theta - {\omega _0}t - {\varphi _v}} \right)}, \hfill \\ \sum {{f_u}\left( {\theta ,t} \right)} = \sum\limits_u {{F_u}\cos \left( {up\theta - u{\omega _0}t - {\varphi _u}} \right)}, \hfill \\ \sum {{f_k}\left( {\theta ,t} \right)} = \sum\limits_k {{F_k}\cos \left( {p\theta \pm {\omega _k}t - {\varphi _k}} \right)}{\text{。}} \hfill \\ \end{gathered} $

(5)

式中： $ v $ =5,7,11,…； $ u $ =3,5,7,9,11,…； $ k $ =1,2,3,…； $ p $ 为电机极对数； $ {\omega _0} $ 为基波频率； $ {\omega _k} $ 为变频器的第 $ k $ 次谐波电流角频率； $ {F_0} $ ， $ {F_v} $ ， $ {F_u} $ ， $ {F_k} $ 为对应谐次下的幅值系数； $ {\varphi _0} $ ， $ {\varphi _v} $ ， $ {\varphi _u} $ ， $ {\varphi _k} $ 为对应谐次下相角。

将各项表达式代入式（1），去除振动幅值小和阶数高的分项，可得对振动影响较大的径向电磁力波表达式。

2倍基波频率项（力波幅值大）：

$ \frac{1}{2}F_0^2\lambda _0^2[\cos \left( {2p\theta - 2{\omega _0}t - 2{\varphi _0}} \right) + 1] ,$

(6)

6倍基波频率项（力波阶数为0）：

$ \frac{1}{2}\lambda _0^2\sum\limits_v {{F_v}\sum\limits_u {{F_u}} } \cos \left[ {\left( {vp - up} \right))\theta + \left( {u \pm 1} \right){\omega _0}t + \left( {{\varphi _u} - {\varphi _v}} \right)} \right] ,$

(7)

与变频器相关的项（力波阶数为0）：

$ \frac{1}{2}F_0^2{\lambda _0}\sum\limits_k {{F_k}} \cos [\left( {{\omega _0} \pm {\omega _k}} \right)t - \left( {{\varphi _k} - {\varphi _0}} \right)] {\text{。}}$

(8)

1.2 齿槽转矩

齿槽转矩 $ {T_{cog}} $ 傅里叶表达式如下：

$ {T_{cog}} = \sum\nolimits_{n = 1}^\infty {{T_n}} \sin \left( {n{N_s}\alpha } \right) {\text{。}}$

(9)

式中： $ {T_n} $ 为齿槽转矩的傅里叶系数； $ n $ =1,2,3 ； $ {N_s} $ 为齿槽转矩的周期数； $ \alpha $ 为定转子相对位置角。

$ {N_s} $ 由电枢槽数 $ z $ 和极对数 $ p $ 的最小公倍数确定：

$ {N_s} = LCM\left( {2p,z} \right) {\text{。}}$

(10)

1.3 振动测试

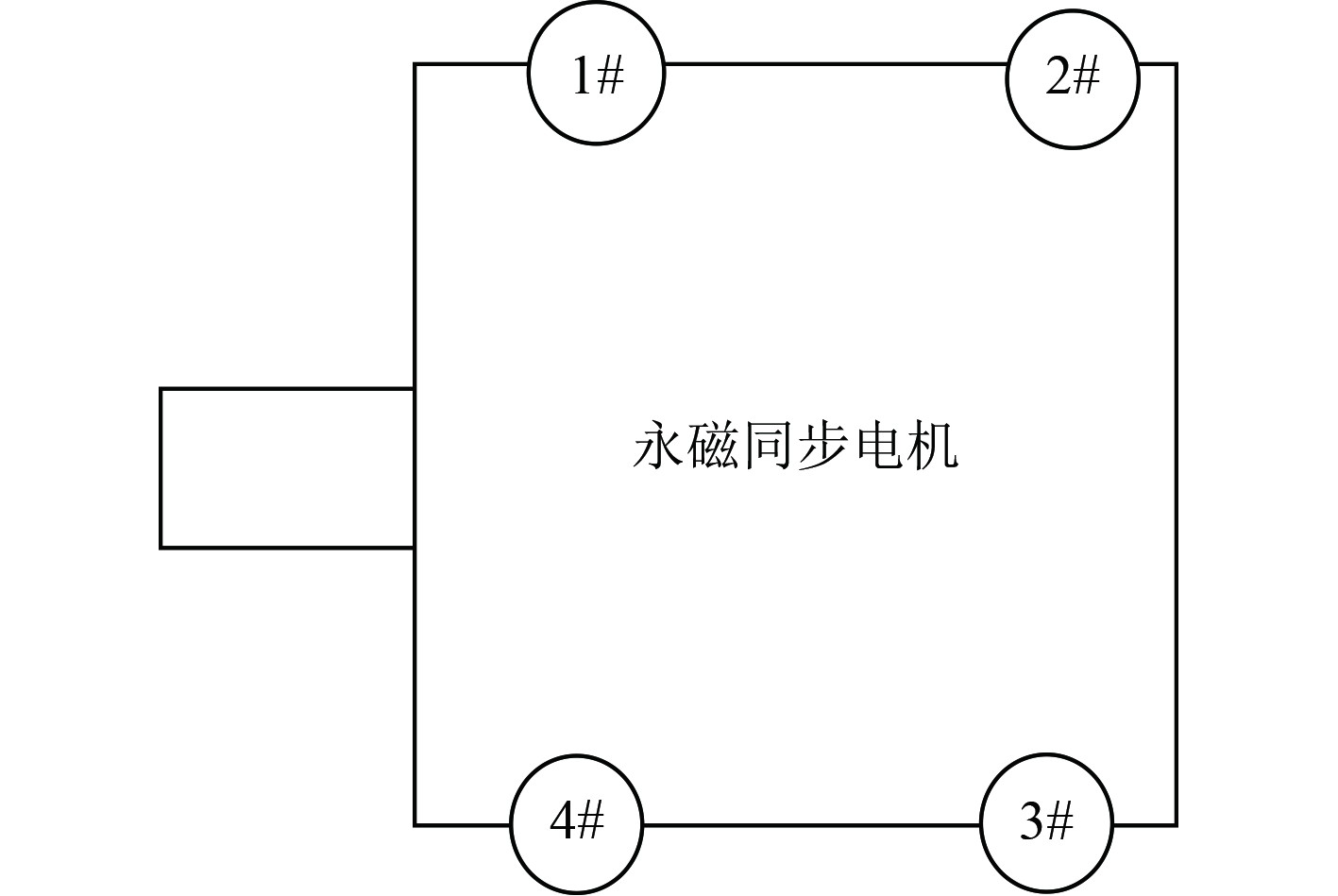
永磁同步电机4个机脚通过螺栓固定在基座上，振动测试系统由B&K加速度传感器、B&K振动噪声数据采集系统及测试计算机组成，如图1所示。振动加速度测量传感器用粘结剂安装在电机4个机脚上。安装部位已清除油迹、油漆、污垢和其它影响测量的杂质，安装表面与被测表面垂直，如图2所示。其中x向为电机轴向，y向为电机轴左右方向，z向为垂直电机向上方向。测试频率范围为10～8 000 Hz，选取转速65 r/min和98 r/min两个主要推进工况进行测试，推进电机的主要技术参数如表1所示。

2 测试结果分析 2.1 振动特征分析

表2为电机2个额定工况振动测试结果汇总，振动参考值为1 μm/s²，分析测试数据可知：

a）65 r/min工况下推进电机3个方向振动总级分别为137 dB，133 dB，135 dB，5～315 Hz低频段量级为114 dB，108 dB，110 dB。

b） 98 r/min工况下推进电机3个方向振动总级分别为149 dB，146 dB，148 dB（x/y/z,下同），5～315 Hz低频段量级为126 dB，120 dB，127 dB。65 r/min工况下推进电机振动量级小于98 r/min工况振动量级。

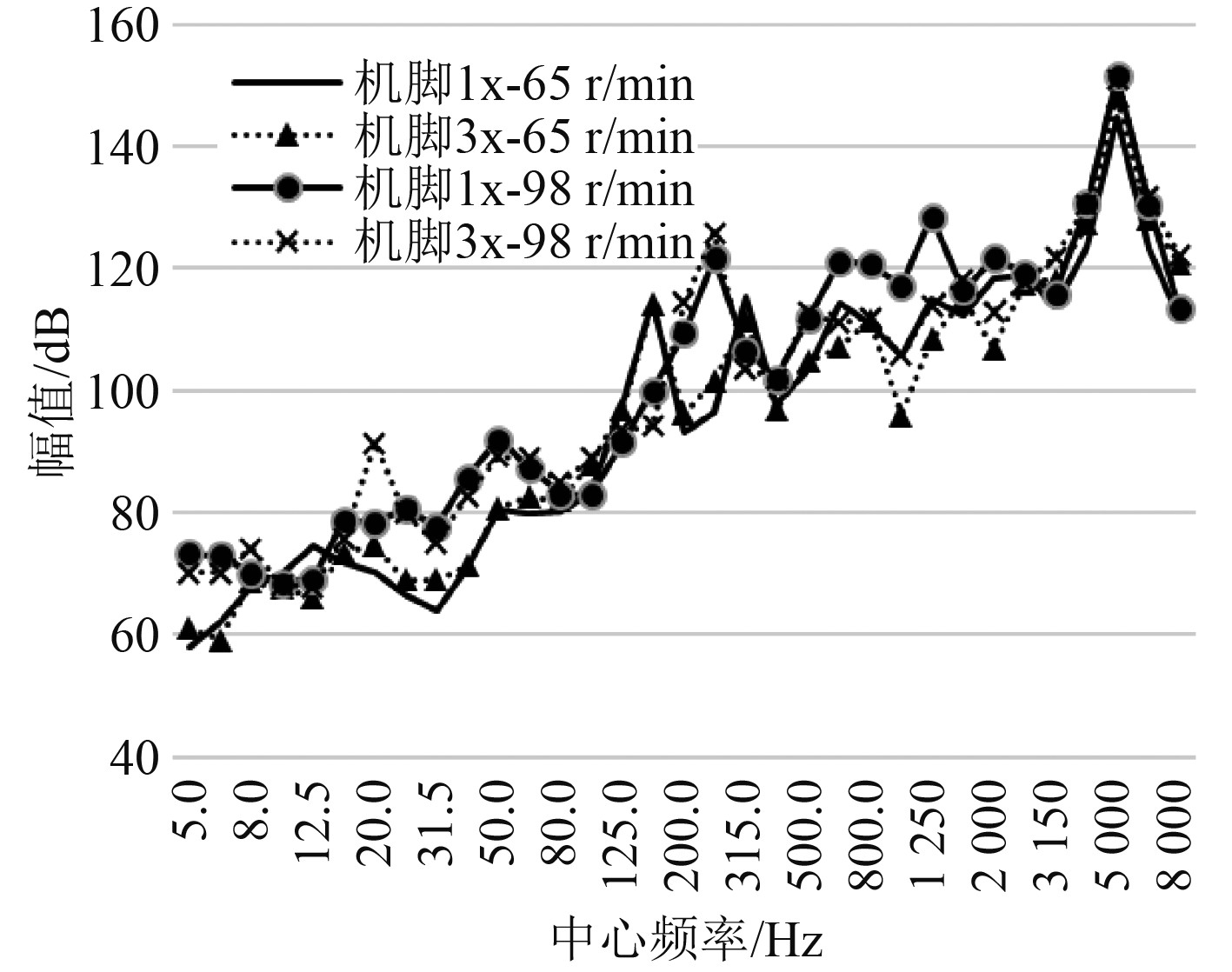
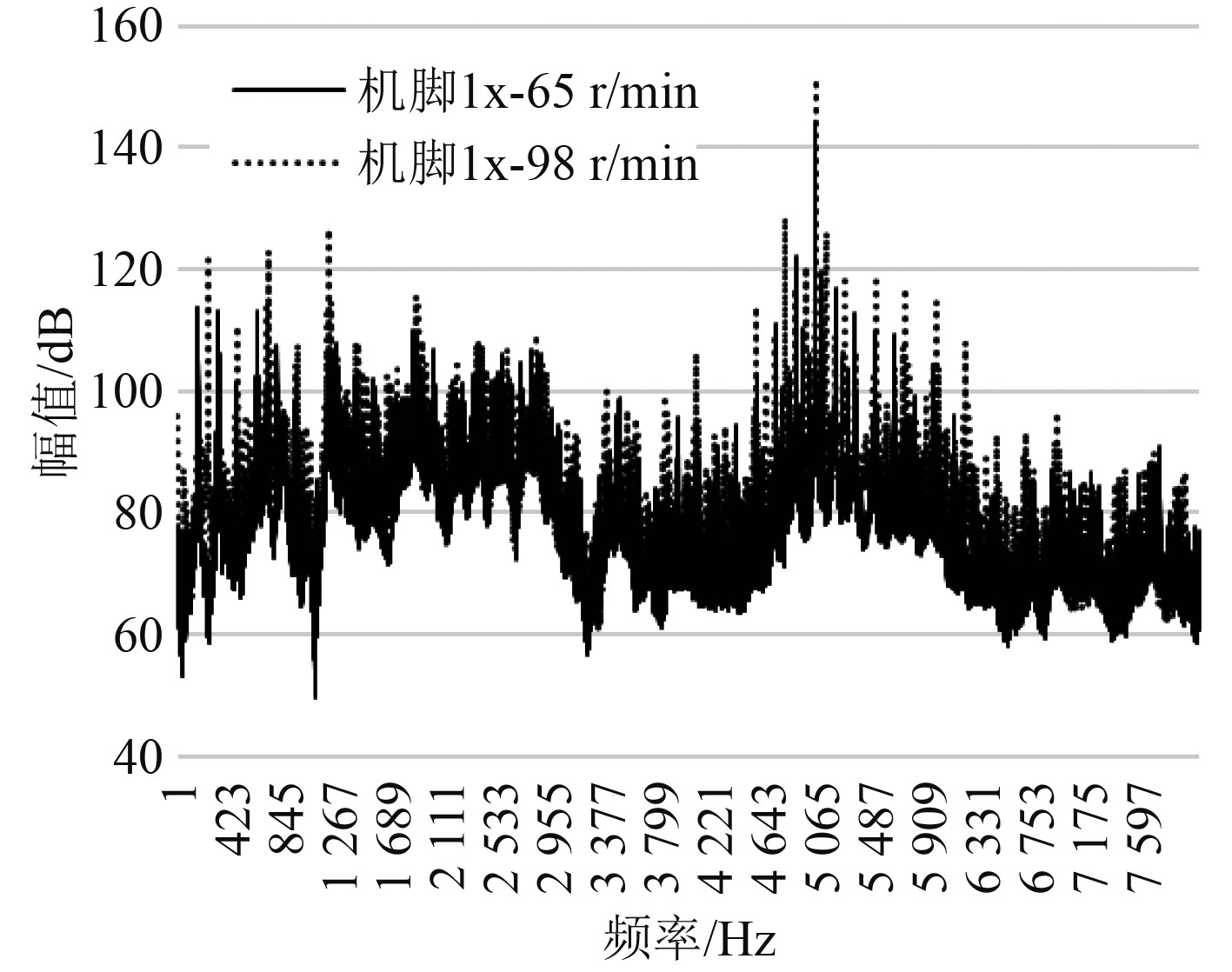
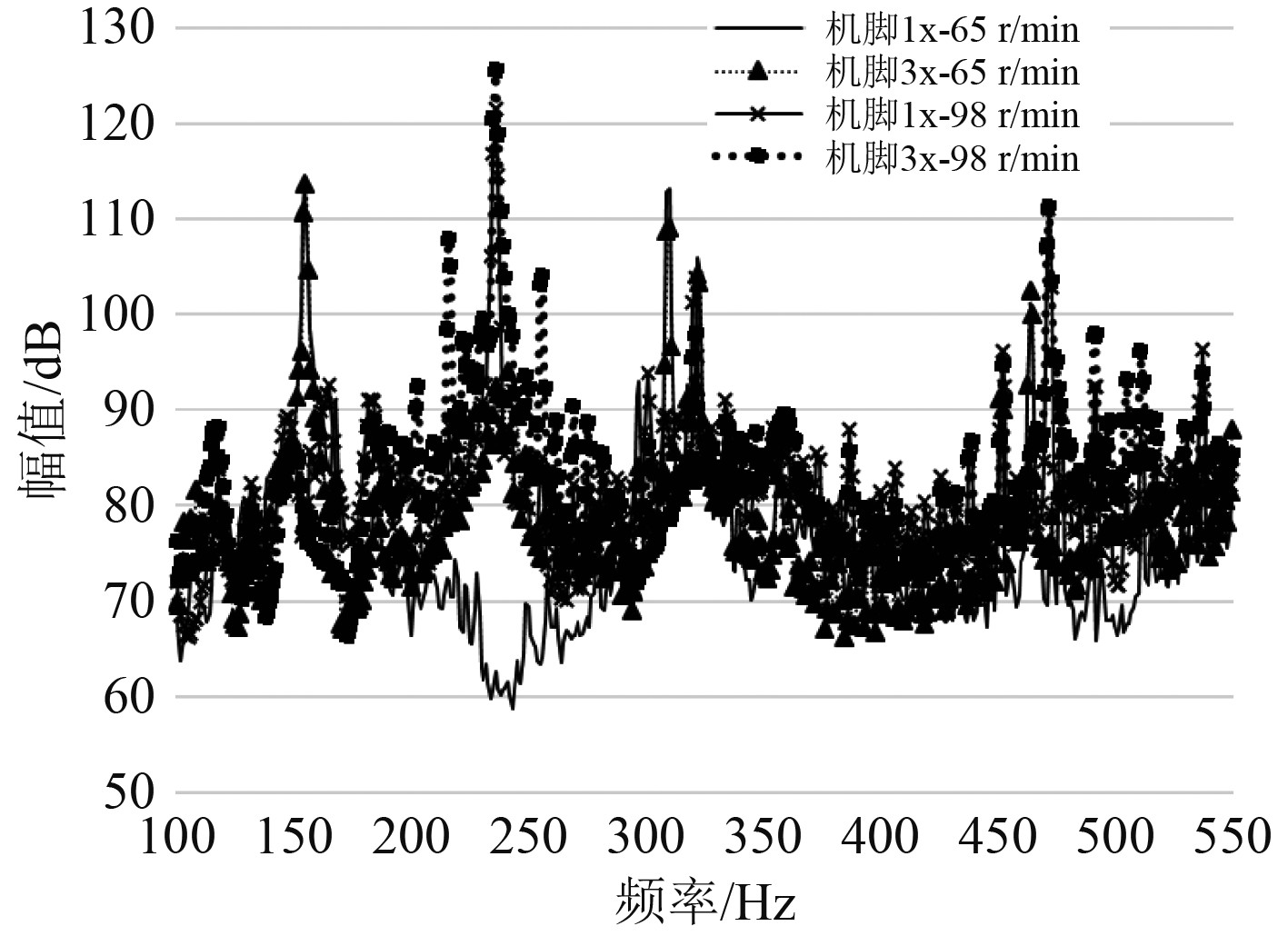
c）不同工况下电机振动能量均分布在高频段，选取2个工况下振动量级相对较大的2个典型通道（机脚1x、机脚3x）数据进行细化分析，如图3～图5所示。

可以看出，65 r/min工况下，电机振动量级在155 Hz及其倍频处有明显突出，155 Hz频率处幅值114 dB，2倍频处幅值为113 dB；98 r/min工况下，电机振动量级在236 Hz及其倍频处有明显突出，236 Hz频率处幅值125 dB，2倍频处幅值为111 dB；2工况幅值最大处频率均在5 000 Hz，且单根线谱幅值超过140 dB。

2.2 振动原因分析

电机的基波频率 ${\omega _0} = \dfrac{{pn}}{{60}}$ ， $ n $ 为电机转速， $ p $ 为电机极对数，根据式（7），则65 r/min工况和98 r/min工况对应的6倍基波频率分别为155 Hz和236 Hz，与3.1节中描述的低频段电机振动量级分布相吻合。

变频器的开关频率为5 000 Hz，根据式（8）可知，电机在5000 Hz附近将有强振动发生，且振动主频率特征不随转速变化，与测试数据一致。

电机齿槽为144个，极对数24个，根据式（9）和式（10）可知，电机在144倍转动频率及倍频处将有振动发生，这一特征与径向力波6倍基波频率分布一致，二者共同作用，导致电机在低频发生强振动。

除电磁力直接作用产生的强迫振动，还应排查激振力与结构是否发生共振。

2.3 模态分析

对电机进行模态仿真计算，为了模拟实际安装条件，对电机4个机脚位移约束，提取前2阶主要模态振型及对应频率，如图6所示。电机的1阶模态频率为203.9 Hz，振型为端盖沿轴向方向振动；2阶模态频率为485.6 Hz，振型为定子及机壳在外径处摆振。

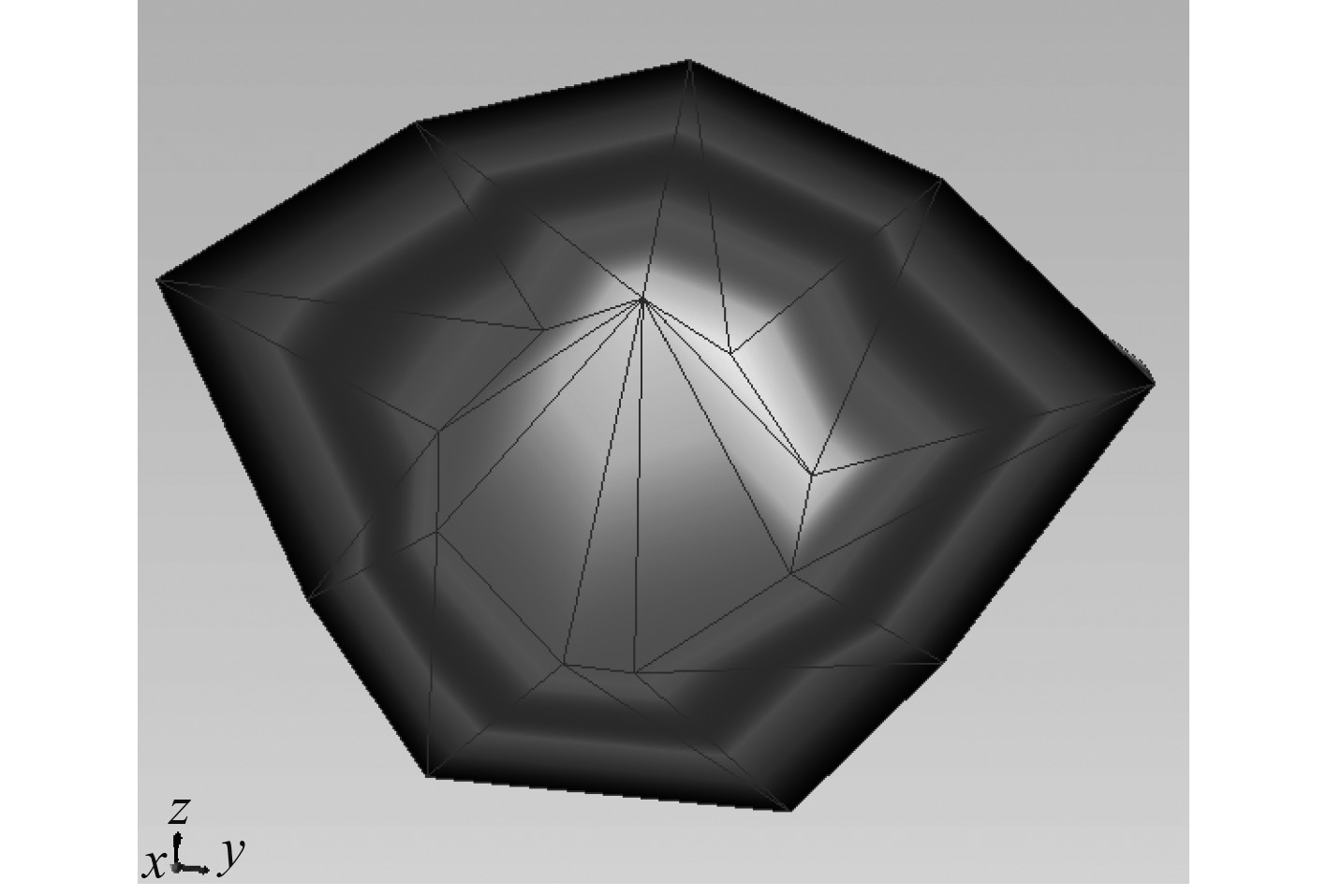
考虑到2阶频率已经很高，因此模态试验时，仅考虑识别1阶模态，模态测试结果如图7所示，频率为209.4 Hz，振型与计算结果一致，频率误差不到2.7%。

电机98 r/min工况运转时，主要激励频率为236 Hz，与一阶模态的错开率大于10%，不存在共振风险，因此可以判断电机振动过大不是由机械共振引起。

3 结　语

本文经过研究，得出以下结论：

1）电机振动能量主要分布在逆变器开关频率5000 Hz附近；

2）电机齿槽转矩和6倍基波电磁激励频率重合造成电机在此频率段振动幅值较大；

3）模态分析结果表明电机振动过大不是由机械共振引起。

根据上述结论，后续设计改进时，可选择合适的极槽配合和磁极布置来降低电机振动。