0 引　言

我国海洋面积广阔，浅水域（0～20 m）的水下任务繁重，水下环境未知多变，长时间的水下作业不仅效率低下，也极大程度的威胁着作业人员的生命安全。于是水下机器人就成为了人类开发海洋的最重要的设备。耐压舱与水下机器人的安全性、稳定性、灵活性以及智能化程度密切相关，是AUV研发中非常重要的一环。但是，理论计算具有局限性、试验成本难度大、成本高，导致耐压舱的结构设计不合理，周期长，所以如何设计出结构合理的耐压舱体成为当前研究的热点问题。文献[6]给出了大浅深耐压舱的快速优化设计方法，提高了设计效率，得到了可靠的尺寸结果，但是文中响应面的类型为克里金响应面，适合大规模样本空间的求解，并不适合可以参照薄壳理论的小浅深耐压舱的优化设计，同时没有考虑到结果的嘈杂性。文献[9]提出了基于遗传算法的优化过程，结果可靠，但是未结合有限元仿真，计算规模大，不适用于快速优化设计。本文对水下自治机器人AUV的耐压舱进行初步设计和受力分析，并基于Ansys Workbench中优化设计模块，探索利用响应面法和多目标遗传算法（MOGA）求解耐压舱优化尺寸的方法，并且进行静力学仿真验证，证明该优化设计方法的合理性。

1 耐压舱的设计与建模

通过对AUV功能和工作场景的分析,耐压舱材料选择为亚克力材料（有机玻璃），材料的工程属性见表1。

确定AUV的工作深度为20 m，安全系数为1.5，计算深度为30 m，通过计算得耐压舱收到的均布载荷P=0.3 MPa。耐压筒轴向长度L为200 mm,内径D₁为120 mm；半球形封头的内径为120 mm。通过薄壳理论（式（1））计算，当壁厚t>0.41 mm时，满足强度要求；通过临界长度公式（2）计算可知本文中耐压筒属于短圆筒形式，当壁厚t>3.5 mm时，满足稳定性要求。

$ t=\beta \frac{{P}_{cr}\cdot R}{{\sigma }_{s}} ，$

(1)

$ {L}_{cr}=\frac{2.59\times \left(1-{\vartheta }^{2}\right)\times D}{2}\times \sqrt{\frac{D}{t}} 。$

(2)

参考理论计算值，从安全的角度出发，耐压舱的尺寸为：半球形封头内径为120 mm，外径为135 mm，耐压筒轴向长度L=200 mm，内径D₁=120 mm，外径D₂=135 mm，后盖厚度t=7.5 mm。

观测型AUV内部搭载众多电气电子元件，所以耐压舱的密封尤为重要，设计一种密封效果好且方便拆装的双径耐压舱密封器，将弹性高、恢复变形能力大的O型密封圈安装在套筒密封器的双槽内形成径向静密封，通过挤压塞满密封器的槽口防止液体进入耐压舱内部，经过下水试验发现舱体内无液体，密封效果良好。通过Solidworks对耐压舱进行三维建模，图1为AUV耐压舱结构图。

2 静力学仿真求解

为了验证设计的可靠性，利用Ansys Workbench中的静力学模块对耐压舱的结构进行静力学仿真，验证耐压仓的设计是否满足强度要求。

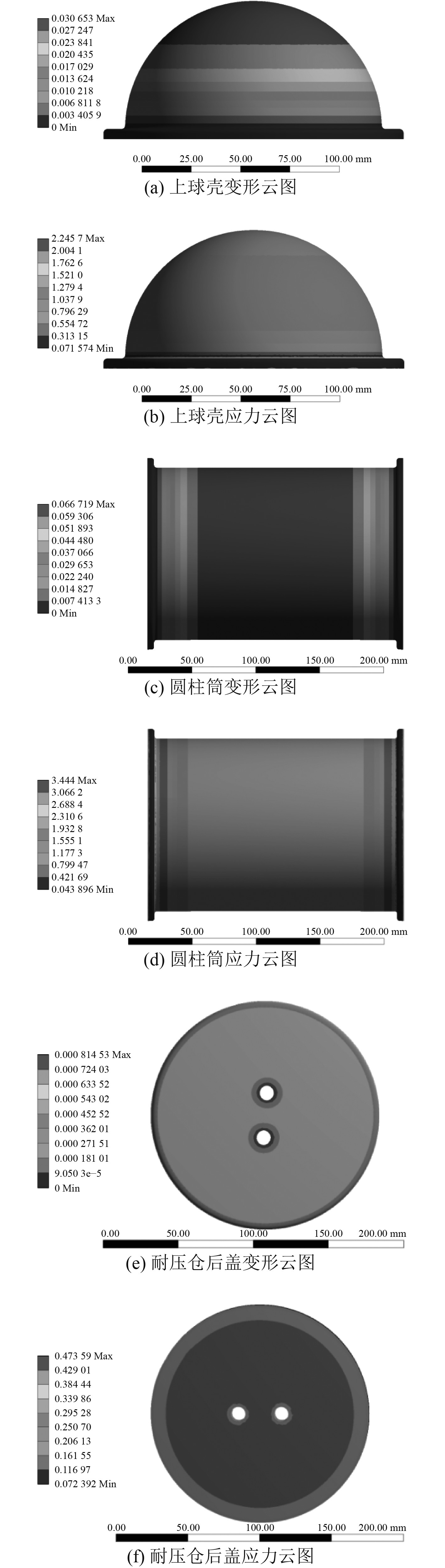
耐压舱模型简化处理后，分别对上球壳、耐压筒以及后盖进行静力学仿真；根据经验对最大应力可能出现的位置进行网格质量加密，确保结果云图深色部分覆盖连续的2层网格，进行求解。图2（a）和图2（b）为对上球壳、耐压筒，后盖进行静力学求解得到的变形量和应力分布云图。

由图2仿真结果可以看到，最大总变形量出现在圆柱耐压筒的中部，变形量约为0.067 mm，最大变形量为壁厚的0.89%，变形量不足1%，且从仿真云图可以观察到变形关于耐压舱轴向对称，稳定性满足要求。耐压圆柱筒与前后接触约束的部位进行圆角设计，可以改善应以集中现象，最大应力值为3.444 MPa，远远小于材料的许用应力32.27 MPa（许用应力=屈服强度/安全系数，表1中亚克力材料的屈服强度为48.4 MPa，安全系数取1.5），强度满足要求；且耐压舱整体质量为1.18 kg，体积为 $ 9.85\times {10}^{5}\;\mathrm{m}{\mathrm{m}}^{3} $ 。

3 基于Workbench的耐压舱多目标优化

由上述静力学仿真可以看出结构受到的最大应力仅为材料许用应力的12%，变形量也不足1%，显然参照理论计算结果的设计尺寸过于保守。

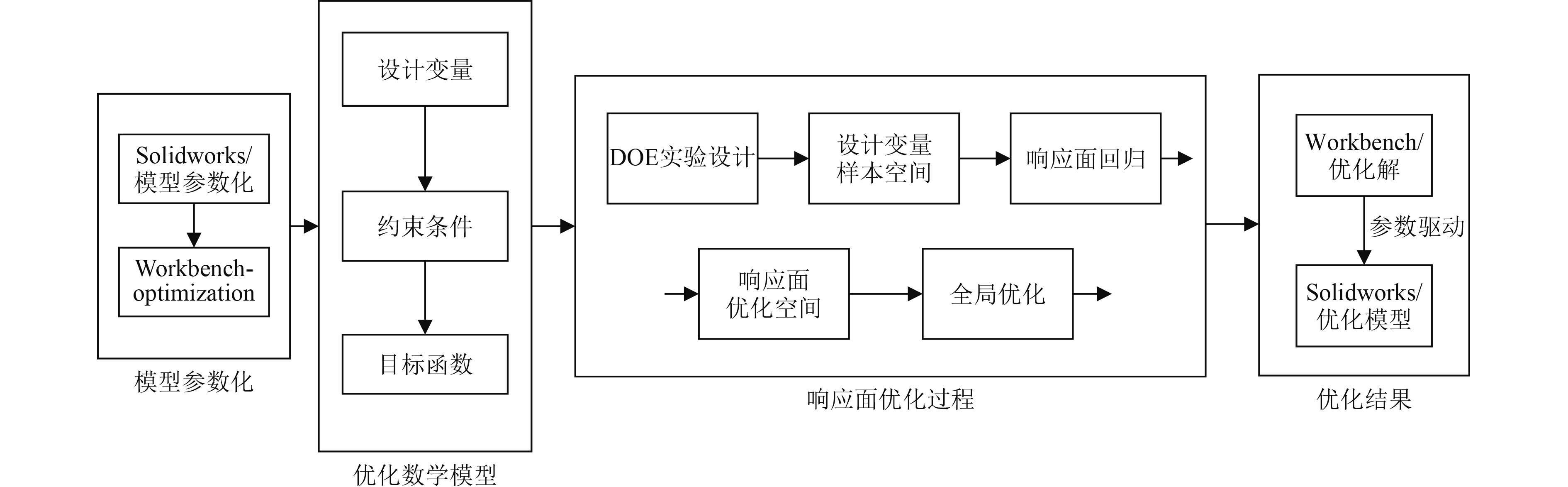
为了降低耐压舱质量，本文利用Workbench的优化设计模块对耐压舱进行优化设计，首先构建优化数学模型（边界条件、优化输入变量与输出变量、优化目标函数等），其次进行DOE设计试验，生成样本空间，利用神经网络拟合响应值与设计变量间的映射关系，构建结构优化的响应面回归模型。最后利用多目标遗传算法（MOGA）根据适应度函数对试验设计得到的样本空间进行最优解的搜索，从而得到帕累托解集，结合数值分析方法和生产装配工艺，并确定最终的优化设计点，完成优化设计过程，多目标优化流程如图3所示。

3.1 耐压筒的多目标优化 3.1.1 优化数学模型与DOE设计试验

由图2可以观察到，最大应力和最大变形都位于耐压筒中间位置，即耐压筒对强度要求最大，即先对耐压筒体进行优化设计。

方法选择响应面法，耐压舱的内径 $ {D}_{1} $ 和轴向长度L由内部搭载的功能模块决定，将其设为固定值，将外径 $ {D}_{2} $ 与压力P作为优化设计的输入变量，将耐压圆筒的质量m、体积v、等效应力 $ \tau $ 、总变形量 $ \delta $ 作为优化输出变形量，则输入变量： $ X=\left[{D}_{2}P\right] $ ，输出变量： $ Y= $ $ \left[mv\tau \delta \right] $ ，优化目标函数： $ {f=\left\{{m}_{\mathrm{m}\mathrm{i}\mathrm{n}},{\tau }_{\mathrm{m}\mathrm{i}\mathrm{n}},{\delta }_{\mathrm{m}\mathrm{i}\mathrm{n}}\right\}}^{\mathrm{T}} $ ，压力值P： $0.27\;\mathrm{M}\mathrm{P}\mathrm{a}\ll P\ll 0.3\;\mathrm{MPa}$ ，外径 ${{D}}_{2}：121.5\;\mathrm{m}\mathrm{m}\ll $ $ D_{2}\ll 140\;\mathrm{m}\mathrm{m}$ 。

由于初始条件下变形量与最大应力值均较小，不再对质量m、等效应力 $ \tau $ 、总变形量设置约束。

在优化设计变量、优化目标函数、约束条件设置之后，进行DOE试验设计。DOE设计试验可以进行多元输入输出的试验，并且能够真实反映出多元输入之间的交互关系，DOE方法选择样本分布最均匀的最佳填充空间设计实验法来最大程度的表征样本空间的数量特征，这样避免了最优解的缺漏，本文设置样本空间中向量数为50个进行DOE试验。

3.1.2 利用神经网络构建响应面模型

由于研究问题的输入输出映射关系不明确，非线性化程度高，同时考虑到结果嘈杂性，借助神经网络构建样本空间的优化响应面模型，拟合度如表2所示，拟合度均大于75%，证明响应面类型选择的合理性。

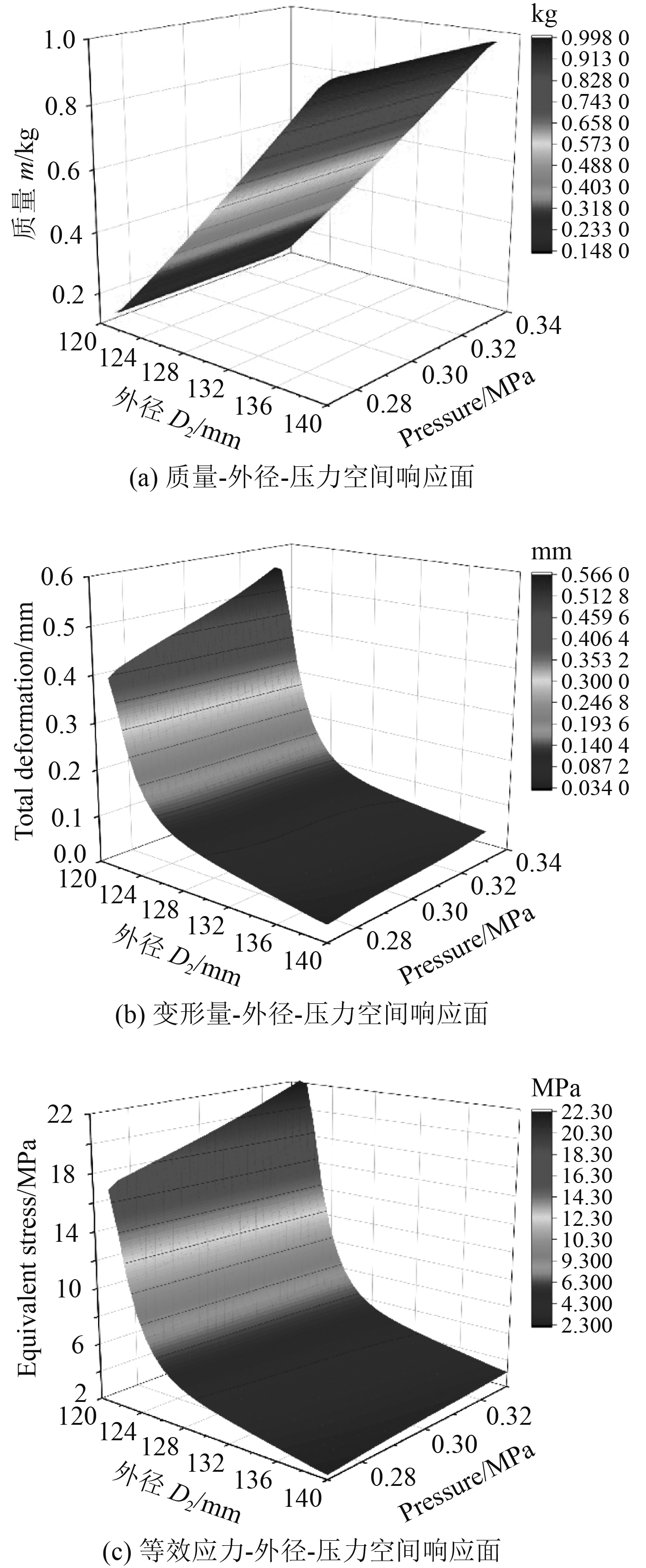
响应面模型是对样本空间的优化拟合，反映了多元输入输出之间回归关系，同时为多目标遗传优化提供初始种群。图4（a）和图4（c）分别为优化输入变量压力P、外径D₂与目标变量质量m、等效应力 $ \tau $ 、总变形量 $ \delta $ 之间的响应面，反映了输入变量与目标变量的空间分布关系。

图4（a）的响应面均匀分布在坐标空间内，不难看出耐压筒的质量m与外径D₂是存在线性关系的，与压力P无明显相关性。

图4（b）响应面为光滑的曲面，表示总变形量 $ \delta $ 与外径D₂、均布载荷P的样本关系，可以用响应面切平面的法向量表示总变形量的变化情况，切平面的法向量沿着外径D₂由大到小的移动过程中，其斜率变化明显，且在D₂=124 mm左右发生明显变化；而切平面的法向量沿着压力P由大到小的过程中，其斜率发生变化，但是并不明显。

由此可以得到，总变形量受外径D₂的影响更大，且在D₂=124 mm左右发生突变，外径一旦小于该值，不管均布载荷P取坐标轴内的任何值，总变形量瞬时增加，则D₂在124 mm处的取值对于耐压舱的设计与优化有重要的参考意义。而在D₂大于124 mm时，压力值的变化对总变形量的变化均在较小的范围内波动。

图4（c）中等效应力 $ \delta $ 与压力P、外径D₂的响应面与图4（b）中响应面的空间分布相似，因此关于等效应力 $ \tau $ 的结论与总变形量的结论相似。

相比于耐压舱所受的均布载荷P，总变形量与等效应力的大小受外径D₂影响更大，对外径D₂的变化也更为敏感，在求优化解的过程中，应该更加注重外径的取值。

3.1.3 利用多目标遗传算法求优化解

与传统算法相比，遗传算法能够有效解决较为复杂的非线性问题，针对全局最优解的搜寻问题，能快速得到可靠的结果。

多目标遗传算法（MOGA）在遗传算法的基础上改进了编码方法和插值方法，这样有助于子代继承到分布更加均匀的优秀基因，避免搜索陷入局部最优。通过帕累托最优、共享函数（个体之间的密切程度）和适应度函数值三者来评估子代种群解的优劣，从而继续进行遗传繁衍或者得到符合要求的子代个体，得到全局的最优解或者解集。

结合本文的研究内容，即在强度、稳定性满足要求的前提下，获得轻量化的设计，利用Workbench的多目标遗传算法（MOGA）对响应面空间模型进行最优解的搜索，结构尺寸计算出的样本空间即为初始种群，让其不断交叉、变异形成不同于亲代的子代，通过适应度值保留符合要求的子代，进行优化，可得到表3中耐压筒多目标优化分析的候选解。

参考变量间的敏感性分析，对上述参考点进行数值处理，同时考虑生产与装配的便捷性，圆整后取外径D₂=130 mm作为优化后的设计尺寸，重新对总变形量 $ \delta $ 、等效应力 $ \tau $ 、质量m进行求解，云图如图5所示，并与初始设计点（参考点）进行比较，如表4表示。

由表4可知，优化设计后的外径为130 mm，圆柱筒质量减轻31.1%，最大总变向量增加至0.0947，约为此时壁厚（t=5 mm）的1.9%，由于变形量关于耐压筒轴向中心对称，所以该变形不会对耐压筒造成损坏，稳定性良好；最大等效应力值增加至4.4315 MPa，远小于材料的需用应力（32.27 MPa）。可见，多目标优化分析得到的优化尺寸在足够保证耐压圆筒强度和稳定性的前提下，减轻了耐压筒的质量，实现了轻量化。

3.2 半球封头和后盖的优化设计

半球封头的优化设计过程与耐压圆筒的相似，因为密封于螺栓装配的问题，将半球封头的外径作为固定值，内径和均布载荷P作为优化输入变量，同样得到3个候选点，候选点情况如表5所示。

对候选点进行数值处理，且考虑生产的成本与便捷性，圆整后取120 mm为半球壳封头的内径，将该点作为优化后设计点进行仿真后发现，在强度绝对满足要求的基础上，质量减少了27.31%。后盖结构简单，其优化设计过程与上述耐压筒和半球封头的过程与方法类似。

3.3 优化结果

通过Workbench的Design Exploration模块对整个耐压舱进行优化设计后，得到新的设计点，将该点对应的耐压舱结构与初始设计点的耐压舱结构进行静力学求解并比较，比较结果如表6所示。

由表6数据计算可得，优化后质量和体积都减小了30.6%，变化显著。而总变相量的最大值和等效应力最大值变化细微，略有增长，最大变形量为优化后壁厚5 mm的1.9%，且变形量关于耐压舱轴向对称，稳定性良好。最大等效应力远远小于材料的许用应力（32.27 MPa），证明优化后的设计在强度和稳定性良好的情况下，实现了轻量化，并且显著减小耐压舱的体积，优化合理。

4 结　语

1）设计了一种半球壳与圆板球头，通过螺栓与双径密封器连接到圆柱主舱体的AUV耐压舱结构，通过理论计算，确定耐压舱初步的尺寸，建立参数化的三维模型。

2）利用Workbench中的Static structural模块，对基于理论计算的耐压舱结构进行仿真求解，得到总变形量、等效应变、等效应力分布云图，同时满足强度与稳定性要求，但是结果较为保守，可见后续的优化分析十分重要。

3）在强度和稳定性均满足要求的前提下，通过Workbench的Design Exploration模块对耐压舱各个部分进行优化设计，且通过响应面定性分析了变量之间的敏感性关系。利用多目标遗传算法（MOGA）得到优化候选结果，优化后的耐压舱在有足够强度和稳定性的前提下，质量和体积分别减小了30.6%,实现了轻量化设计，降低了生产成本，缩短了设计周期，优化结果弥补了理论计算的不足，验证了本文提出的优化设计方法和理论和合理性和正确性。