0 引　言

在水下声学覆盖层的研究中，粘弹性聚合物由于存在阻尼效应和内摩擦，可以有效消耗入射波的能量，一直是声学覆盖层的主要材料^[1]。为了获得好的吸声效果，粘弹性材料中引入空腔来改进吸声效果，Alberich型声学覆盖层从20世纪50年代延续至今仍然是共振型覆盖层的基本结构形式。研究人员提出了多种理论、数值方法来研究这一结构。而其中粘弹性材料的阻尼很复杂且不易确定，由于其方程的复杂性，理论方法中一般使用一种阻尼模型，这对计算结果产生了一定的影响。因此有必要对其阻尼进行研究。

声学覆盖层的研究开始于Oberst^[2]，之后Meyer^[3]研究了带有短圆柱空腔的橡胶介质中的振动并提出一种将短圆柱等效为带阻尼的振子的离散化方法，其阻尼采用了定值的粘性阻尼。20世纪60年代，Greenspon^[4]得出了厚壁圆柱管中弹性波的精确解。Gaunaurd^[5]基于Kelvin-Voigt线性粘性模型在圆柱坐标系分析了短圆柱的振动。朱蓓丽等^[6]用工程近似的方法等效计算纵波波数，建立了一维粘弹性理论模型，在研究中，一阶拉梅常数（Lamé）不考虑其结构阻尼，二阶考虑结构阻尼。汤渭霖^[7]同样基于Kelvin-Voigt线性粘性模型在圆柱坐标系中给出了有限长圆柱空腔的二维理论模型。

随着计算机和数值方法的飞速发展，边界元方法和有限元方法得到了广泛应用。Hennion^[8]于1991年开发了一种3D有限元方法来分析Alberich涂层。Panigrahi等^[9]基于有限元提出了多焦点的声学覆盖层设计，在有限元方程中使用的是结构阻尼的形式。Sohrabi等^[10]在随频率变化计算中确定单元大小的研究中使用的阻尼也是结构阻尼。王世波等^[11-12]在研究声学覆盖层的性能时在理论部分以及使用Comsol有限元软件分析时使用结构阻尼。

目前主要的研究方法是有限元法^{[10, 12-13]}。对于常用消声瓦材料，杨氏弹性模量、密度、泊松比等相对容易得到且非频散（不随频率变化），但是阻尼通常随温度、频率乃至初始变形等变化明显，且对计算结果影响较大，是计算尤其是频响计算中的关键参数。橡胶属于粘弹性材料，阻尼综合了粘性阻尼和结构阻尼。因此，综合考虑了粘性阻尼与结构阻尼，提出计权的方法对仿真结果进行修正，提高仿真精度。

1 理论分析

典型的声学覆盖层模型如图1所示，其基料主要为橡胶类高分子材料，其内均布有喇叭形空腔结构。入射波由喇叭形空腔的小口端垂直入射到声学覆盖层表面。整体形状为圆柱体，直径为 $\phi $ ，厚度为h，定义孔隙率 $\delta {\text{ = }} {d}/{H}$ 。

建立空腔阵列的精确理论模型并进行求解，存在一定复杂度及困难。因此会选取具有代表性的单个空腔单元进行分析^[14]。同时由于单个腔体亦非同种均匀介质，为简化分析将其考虑成分层的均匀介质的组合^[6]，如图2所示。

每一层等效的均质材料，都有以下方程^[15]：

$ \begin{split} \left( {\begin{array}{*{20}{c}} {{p_i}} \\ {{v_i}} \end{array}} \right) & = \left[ {\begin{array}{*{20}{c}} {\cos (k_{li}^el_i^e)}&{j\rho _i^ec_i^e\sin (k_{li}^el_i^e)} \\ {\dfrac{{j\sin (k_{li}^el_i^e)}}{{\rho _i^ec_i^e}}}&{\cos (k_{li}^el_i^e)} \end{array}} \right]\left( {\begin{array}{*{20}{c}} {{p_{i + 1}}} \\ {{v_{i + 1}}} \end{array}} \right) =\\ & \left[ {{T_i}} \right]\left( {\begin{array}{*{20}{c}} {{p_{i + 1}}} \\ {{v_{i + 1}}} \end{array}} \right)，\end{split} $

(1)

其中的纵波波数 $k_{li}^e$ 可以表示为^[6]：

$ k_{li}^e = {k_{li}}\sqrt {\frac{1}{{1 + 3\delta _i^2}}\left(1 + \frac{\lambda }{\mu }\delta _i^2\right)} 。$

(2)

式中： ${k_{li}} = \omega \sqrt {\dfrac{\rho }{{\lambda + 2\mu }}} $ ，是孔隙率为0时的纵波波数； ${\delta _i}$ 为第i层的穿孔率； $ \lambda $ 和 $\mu $ 分别为一、二阶拉梅常数； $\rho _i^e = \rho (1 - \delta _i^2)$ 为等效密度； $c_i^e = \dfrac{\omega }{{k_i^e}}$ 为等效波速。

总的传递矩阵有：

$ \left[ T \right]{\text{ = }}\left[ {{T_1}} \right]\left[ {{T_2}} \right] \cdots \left[ {{T_n}} \right] ，$

(3)

已知输出端为刚性边界，则 $ {v}_{2}=0 $ ，可以求得声学覆盖层的阻抗为：

$ {Z_r} = \frac{{{T_{11}}}}{{{T_{21}}}}{\text{ = }}\frac{{{p_1}}}{{{v_1}}} ，$

(4)

$ r = \frac{{{Z_r} - {\gamma _i}}}{{{Z_r} + {\gamma _i}}} = \frac{{{T_{11}} + \dfrac{1}{{{\gamma _i}}}{T_{12}} - {\gamma _i}{T_{21}}}}{{{T_{11}} + \dfrac{1}{{{\gamma _i}}}{T_{12}} + {\gamma _i}{T_{21}}}}。$

(5)

声学覆盖层的吸声效率为：

$ \alpha {\text{ = }}1 - {\left| r \right|^2}。$

(6)

2 数值仿真

首先通过有限元计算验证理论中平面波假设在不同频率及开孔率下的情况。在Ansys中对图1中的模型进行谐响应分析。设置材料的弹性模量为165 MPa，泊松比为0.48，阻尼比为0.08。底面固定，在顶面施加单位载荷压力的正弦激励，计算得到频率在1000 ～5000 Hz范围内的速度响应。

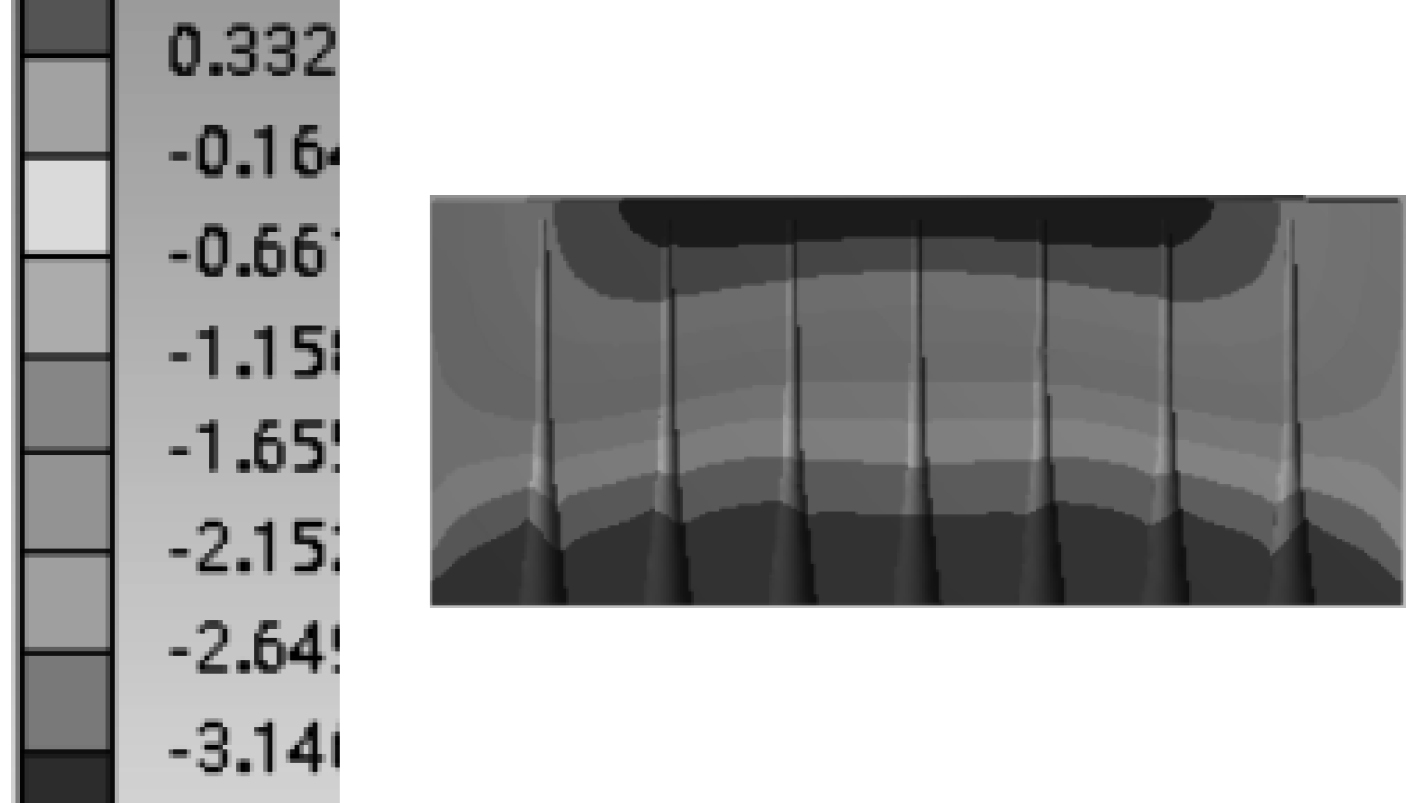
对空腔横向放大2倍的模型进行计算，结果如图3～图5所示。可以看出，频率增高激发了模型的高阶模态，响应不再是平面波形式。结合图6可以看出，大孔隙率更容易使速度响应不再是平面波。因此在小孔隙率、较低频率范围内，可以认为入射波经声学覆盖层反射的过程可以看做一维的平面波过程。

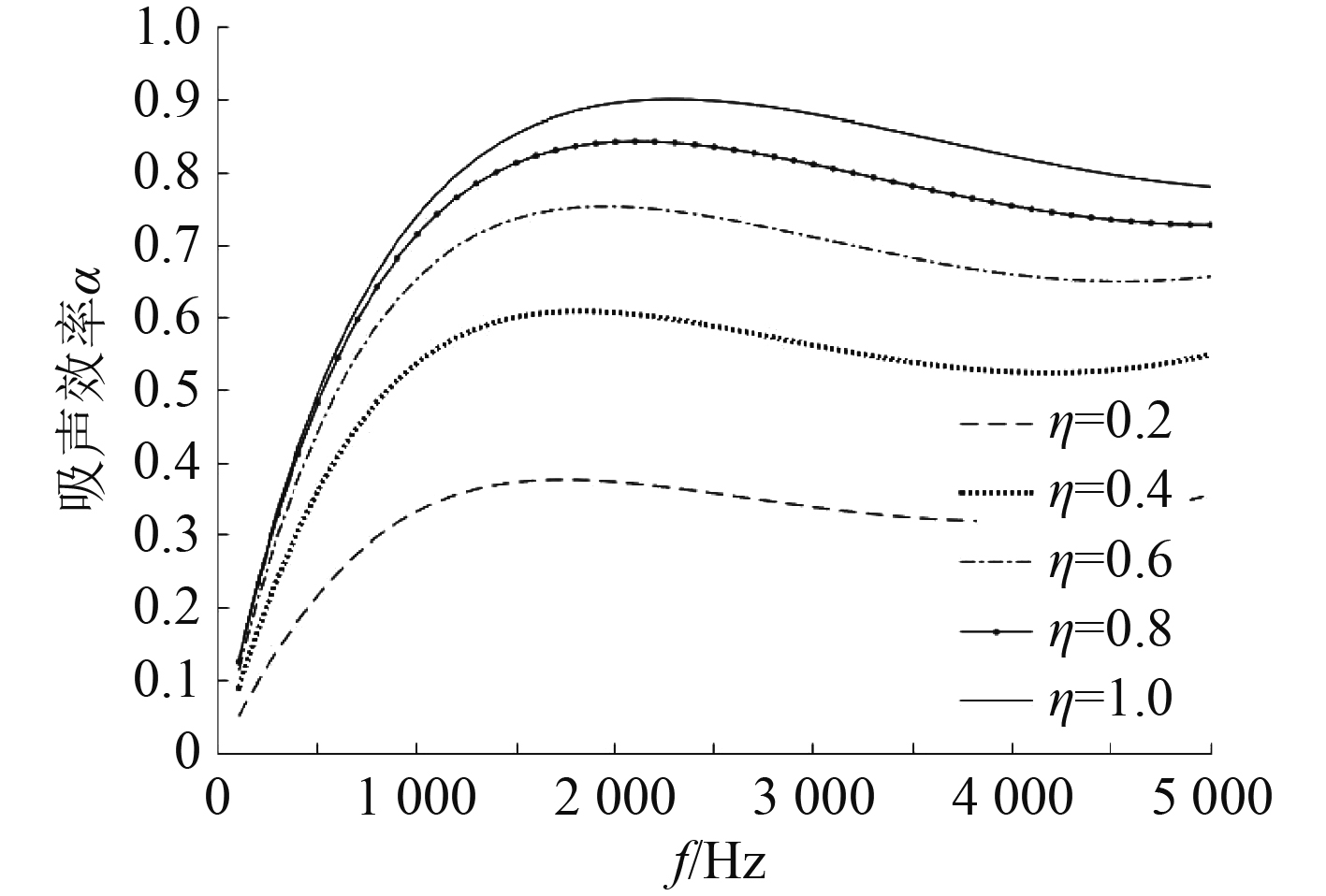
由于理论中对于双周期结构只取其中一个单元，同时边界条件的设定与真实情况并不相同，而且橡胶材料各向异性，所以理论计算的结果会有误差，需要通过有限元进行数值辅助计算。计算时选取材料为165 MPa，泊松比为0.48，利用式(4)～式(6)分别计算图1中模型在结构阻尼 $\eta \text{=}0.05,\;0.10,\;0.20,\;0.40,\;0.80$ 和粘性阻尼阻尼比 $\zeta \text{=}0.05,\;0.10,\;0.20,\;0.30,\;0.40$ 时的吸声效率，得到图7和图8的结果。

可以看出，结构阻尼在0～3000 Hz的频率下起作用，粘性阻尼在1500～5000 Hz的频率下起作用。因此考虑在不同频率段使用不同阻尼，低于1500 Hz时只考虑结构阻尼，高于3000 Hz时只考虑粘性阻尼。在1500～3000 Hz，加入权函数 ${q_\eta }(\omega )$ 和 ${q_\varsigma }(\omega )$ ，分别是结构阻尼和粘性阻尼的权重，且 ${q_\eta }(\omega ) + {q_\varsigma }(\omega ) = 1$ 。考虑到将粘性阻尼等效到结构阻尼上，其大小是随频率线性变化的，因此在两者之间的过渡段采用频率 $\omega $ 的二分之一次方定义权函数：

$ {q_\eta }(\omega ) = \frac{1}{{\sqrt {1\;500} }}\sqrt {3\;000 - w} ，$

(7)

$ {q_\varsigma }(\omega ) = 1 - \frac{1}{{\sqrt {1\;500} }}\sqrt {3\;000 - w} 。$

(8)

3 实验验证

为了验证复合阻尼公式的有效性，对表12块不同孔隙率的声学覆盖层样品进行吸声测试。测试在内径120 mm，壁厚5 cm的声管中进行。实验台架如图9所示，声管垂直放置，注满纯净水（温度23 ${}^ \circ {\text{C}}$ ，密度998 ${\text{kg}}/{{\text{m}}^3}$ ，声速1482.1 ${\text{m/s}}$ ）。测试样品与厚度为20 cm的不锈钢刚性背衬连接安装在声管顶部。信号源产生不同频率的正弦信号并通过功率放大器驱动置于声管底部的换能器产生与声管轴线方向一致、垂直入射到样品表面的入射波。声管中部的2个不同位置的水听器测量声压信号经过适调放大器被数据采集仪收集并传递到计算机。

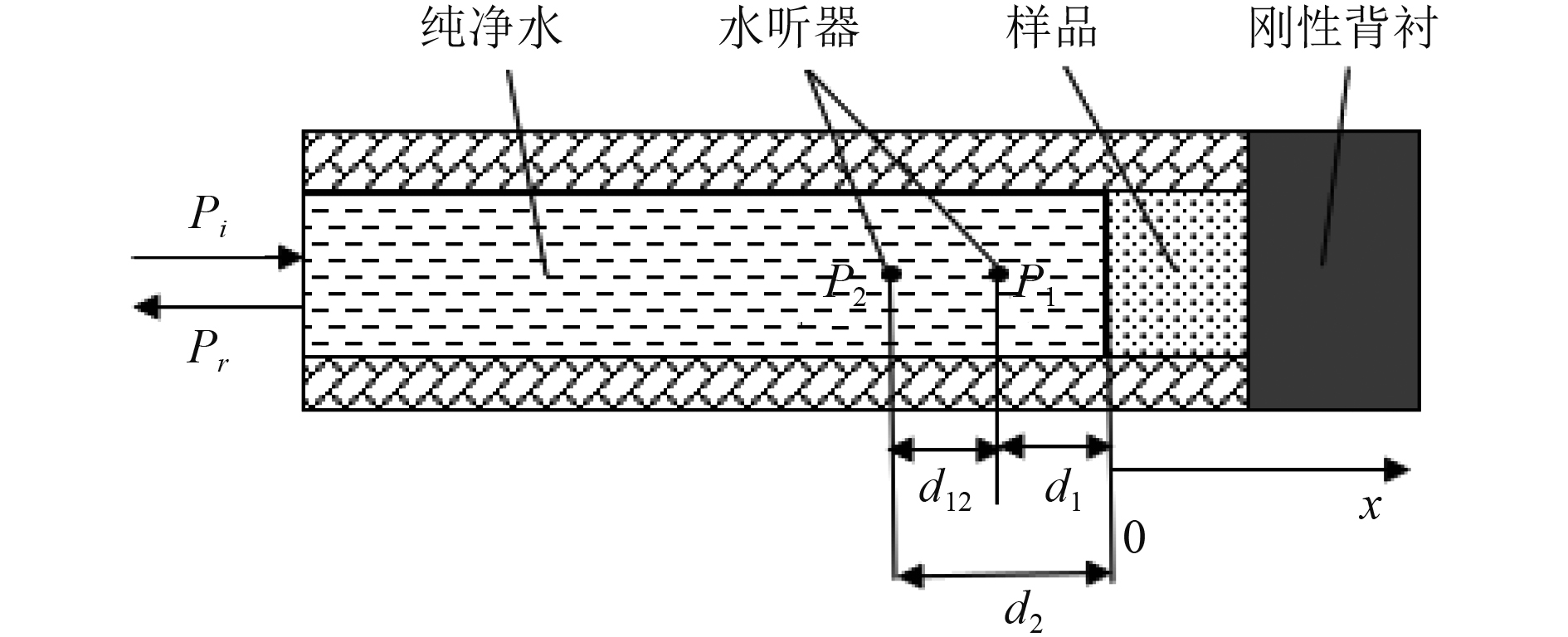
声管中的声波可以看做是入射波与反射波的叠加，根据图10中的坐标系，位置分别为 $x = - {d_1}, x = $ $ - {d_2}$ 的2个水听器在特定频率 $\omega $ 下，测得的声压可以分别表示为：

$ {P_1}(t) = {\text{(}}{\hat P_i}{e^{jk{d_1}}} + {\hat P_r}{e^{ - jk{d_1}}}){e^{j\omega t}} ，$

(9)

$ {P_2}(t) = {\text{(}}{\hat P_i}{e^{jk{d_2}}} + {\hat P_r}{e^{ - jk{d_2}}}){e^{j\omega }} 。$

(10)

其中： ${\hat P_i}$ 为带相位的入射波； ${\hat P_r}$ 为带相位的反射波。

求解上述2个方程，得到：

$ r = \frac{{{{\hat P}_r}}}{{{{\hat P}_i}}}{\text{ = }}\frac{{{P_2}{e^{2jk{d_1}}} - {P_1}{e^{2jk{d_2}}}}}{{{P_1} - {P_2}}} ，$

(11)

$ \alpha {\text{ = 1 - }}{\left| {\frac{{{P_2}{e^{2jk{d_1}}} - {P_1}{e^{2jk{d_2}}}}}{{{P_1} - {P_2}}}} \right|^2} 。$

(12)

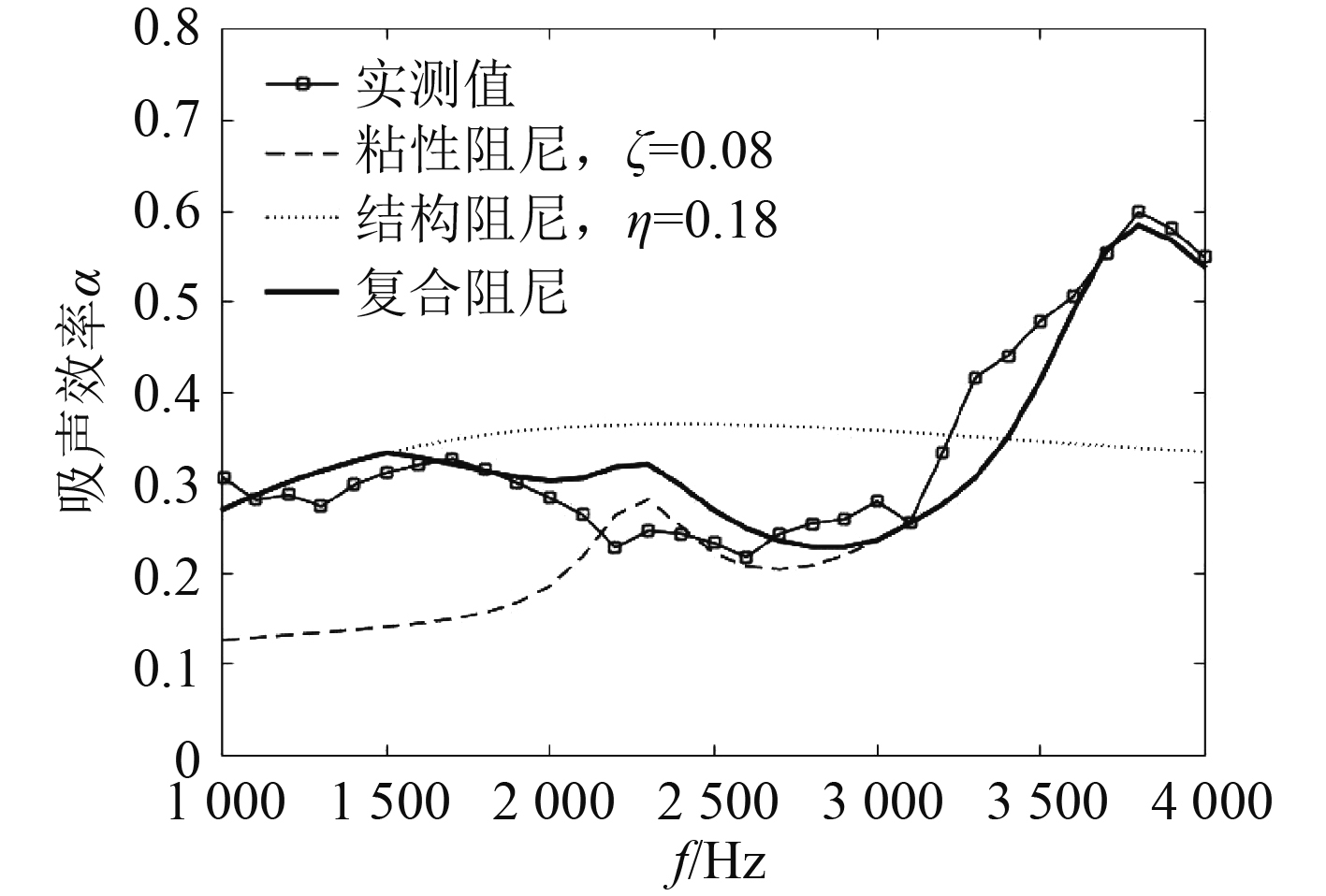
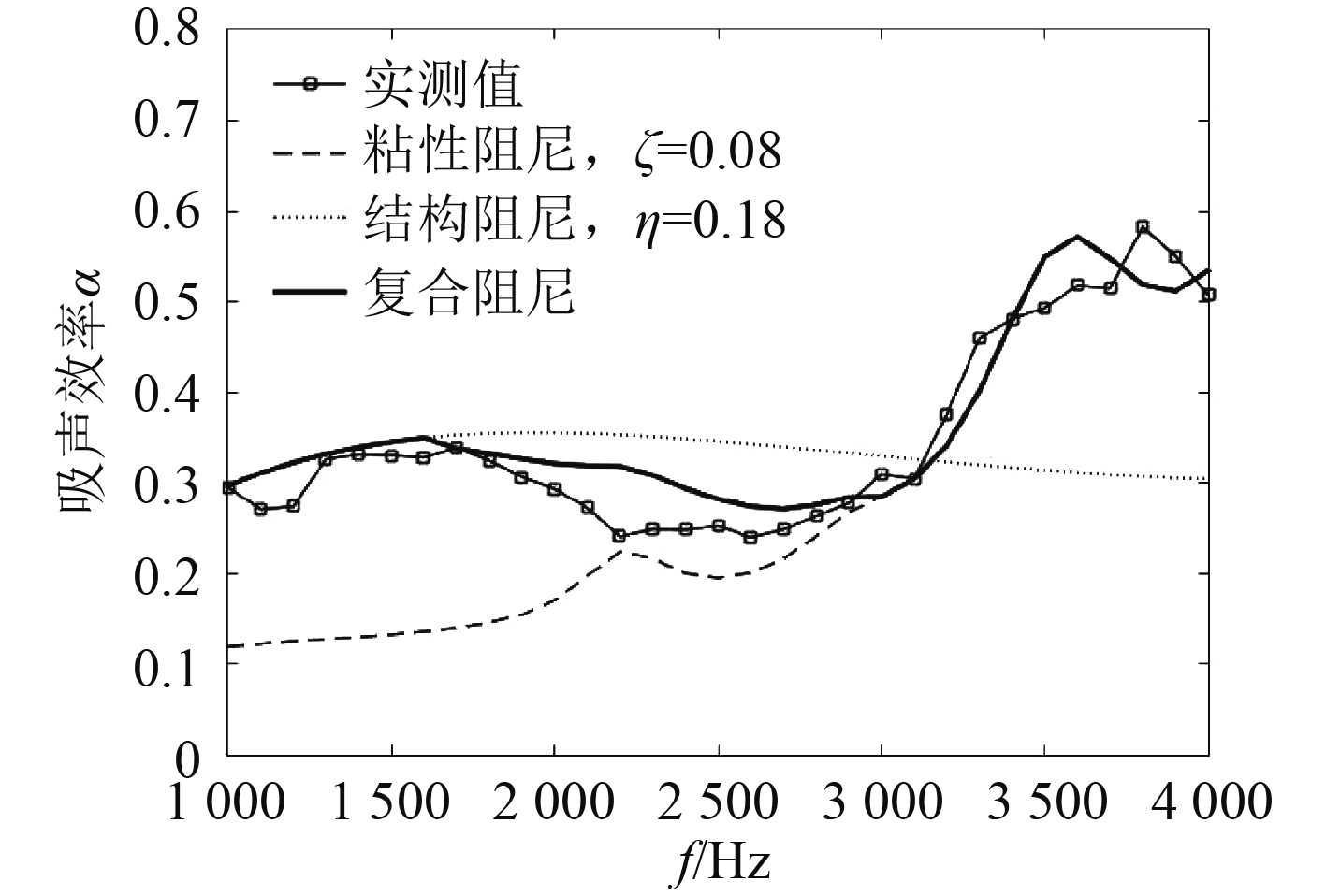
实验频率选取1 000～4 000 Hz，矩形框实线是处理实验数据得到的吸声效率。在数值计算时损失因子取 $\eta $ =0.18、阻尼比 $\varsigma $ 为0.08，分别得到短虚线和长虚线。粗实线为使用权函数得到的吸声效率曲线。

由图11和图12通过对比可以看出：在低频段1000 ～1500 Hz，结构阻尼与实测值更接近，粘性阻尼要明显偏小；在中频段3000 ～4000 Hz，粘性阻尼要比实测值更小，结构阻尼要偏大一点；在高频段3000 ～4000 Hz，粘性阻尼与实测值更接近，结构阻尼要明显偏小；复合阻尼整体的预测效果还是比较好的。分析与实测值产生误差误差的原因有：1）入射波方向与声管轴线方向存在微小夹角，入射波非法向入射；2）换能器发射出的入射波是球面波非平面波，随着频率增加，波长减小使在管径方向产生驻波；3）在高频段，样品激发了高阶模态，反射的波不再是平面波；4）声管不是半无限长结构，入射端也有反射。

4 结　语

结合理论计算与有限元计算，综合考虑粘弹性材料的迟滞阻尼和粘性阻尼，分段处理不同阻尼的主要作用频域，给出了一种声学覆盖层的简单有效的一维计算方法，得到如下结论：

1）这种方法可以通过简便的计算得到较为精确的结果。

2）在低频段（1000～1500 Hz）结构阻尼起到主要作用，在高频段（3000～4000 Hz）粘性阻尼起主要作用。在过渡段（1500～3000 Hz），两者共同起作用，且随频率增加，结构阻尼起到的作用在消退，粘性阻尼的作用逐渐增强。

3）给出粘性阻尼、结构阻尼对吸声性能的影响规律，可以针对不同的需求，进行胶料的调整。在低频段调节材料的结构阻尼更有效，高频段调整材料的粘性阻尼更能起到作用。