2. 南方海洋科学与工程广东省实验室(广州), 广东 广州511458)
2. Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou), Guangzhou 511458, China
近年来大型船舶的事故损伤情况促使国内外学者针对新规范的出台以及新规范对船体结构的影响开展探讨研究[1-5]。研究结果表明,对于超大型船舶来说,船体尺度的增大导致其遭受的总体载荷中波浪载荷的高频成分显著增大,这些高频成分在中低海况下主要是由波激振动引起,在中高海况下时,高频成分往往是由波激振动和砰击颤振叠加产生。波浪载荷高频成分的增加在超大型船舶的疲劳损伤和结构强度评估方面有着重要影响,进而影响着船舶的航行安全。另一方面,实现船舶轻量化成为国际海事界的共识,作为波浪载荷分析中重要的影响因素,船体梁刚度随着轻量化的进行发生改变。研究表明,小刚度的船体梁更容易在波浪中发生波激振动[6],从而导致作用于船体梁上的波浪载荷增大。载荷的变化会对结构的设计评估与优化产生重要影响,进而决定刚度的变化,二者相互耦合。如果忽视这方面的影响,可能会导致优化结果不合理。目前,各国船级社已将这方面的影响考虑到相关的规范[7]中,这也使得超大型船舶的设计面临了更多的挑战。但是,波浪载荷的高频分量在船体结构优化设计中的影响并没有受到应有的关注。本文采用设计波方法理念,给出了民船结构优化模型中非线性波浪载荷的计算方法,分析了船体梁刚度变化对波浪载荷的影响。以优化软件Isight为平台,集成非线性波浪载荷计算程序、截面属性计算程序以及极限强度计算程序,选用多岛遗传算法,自动化、参数化的实现超大型集装箱船的剖面优化计算,并将船体剖面在考虑以及不考虑波浪载荷影响下的优化结果进行了对比。
1 高频波浪载荷计算对于高航速具有大外飘的大型船舶,在海上做大幅运动时,船体诱导的弯矩响应本质上非线性,即中垂弯矩大于中拱弯矩,中垂中拱弯矩与波高的关系非线性,合理的将砰击弯矩与波浪弯矩叠加是棘手问题。为了定量的描述船体梁刚度与波浪载荷之间的关系,采用非线性波浪载荷程序对超大型集装箱船在不同船体梁刚度下垂向波浪载荷响应进行理论计算。该程序在切片理论基础上,从工程应用的角度出发,综合考虑了船体非直壁以及外飘砰击等引起的非线性波浪载荷响应。把船体作为弹性梁,预报其在高浪级下的非线性合成弯矩,并考虑了波浪诱导弯矩与砰击弯矩相互叠加的相位问题。具体方法如下[8]:
将船体简化为两端自由的Timoshenko梁,则其垂向强迫振动方程可表示为:
| $ \mathrm{\mu }\left(x\right)\frac{{\partial }^{2}y\left(x,t\right)}{\partial {t}^{2}}+c\left(x\right)\frac{\partial y\left(x,t\right)}{\partial t}+\frac{\partial V\left(x,t\right)}{\partial t}=F\left(x,t\right),$ | (1) |
| $ \frac{\partial y\left(x,t\right)}{\partial t}=-\frac{V\left(x,t\right)}{k{A}_{S}G}+\mathrm{\gamma }\left(x,t\right)。$ | (2) |
式中:
利用模态迭加法可推得主坐标方程为:
| $ \bar{{\mu }_{i}}{\ddot{q}}_{i}+\bar{{c}_{i}}{\dot{q}}_{i}+{\dot{k}}_{i}={Q}_{i},$ | (3) |
| $ \bar{{\mu }_{i}}=\int _{-\frac{L}{2}}^{\frac{L}{2}}\mu {{X}_{i}}^{2}\left({x}\right){{\rm{d}}}{x},$ | (4) |
| $ \bar{{c}_{i}}={\int _{-\frac{L}{2}}^{\frac{L}{2}}}c{{X}_{i}}^{2}\left({x}\right){{\rm{d}}}{x},$ | (5) |
| $ \bar{{k}_{i}}={{\omega }_{si}}^{2}\bar{{\mu }_{i}},$ | (6) |
| $ {Q}_{i}={\int _{-\frac{L}{2}}^{\frac{L}{2}}}F(x,t){X}_{i}\left({x}\right){{\rm{d}}}{x} ,$ | (7) |
则含砰击弯矩的非线性合成弯矩和剪力可表示为:
| $ {M}_{c}\left(x,t\right)=\sum _{i=1}^{\infty }{q}_{i}\left(t\right){M}_{i}\left(x\right),$ | (8) |
| $ {Q}_{c}\left(x,t\right)=\sum _{i=1}^{\infty }{q}_{i}\left(t\right){Q}_{i}\left(x\right)。$ | (9) |
式中:
由式(8)便可得到弹性船体下,含砰击弯矩的非线性波浪载荷,为结构优化提供迭代载荷。
在目前的民船规范中,对于非线性波浪载荷的直接计算方法没有相关的规定。借鉴军用舰船的设计波方法理念,在计算中首先采用三维线性理论计算求得船舶在单位波幅规则波中的响应,之后再基于谱分析和概率统计的方法对船舶的波浪载荷进行长期预报,得到一定超越概率水平下的波浪载荷做为波浪载荷设计波高确定依据[9]。据此确定设计波的周期、波高、浪向角及航速等参数,获得目标船在该设计波下的含高频成分的波浪载荷。在设计波的原理中,可以用载荷、船体运动响应等载荷参数来表示海浪诱导的船舶波浪载荷。载荷参数的选取应根据船舶结构的特性以及其在海浪中航行时的受力特点来确定,以其中影响最大的载荷参数作为船体结构强度分析的设计载荷[10]。考虑到超大型集装箱船的垂向砰击振动比较明显,因此以船舯横剖面垂向波浪弯矩为主要考虑的载荷参数。
根据目标船舶服役期间经历的海浪情况,选择北大西洋海浪谱。浪向角取为0°~180°,每15°取为一浪向,共13个浪向角。波浪圆频率范围为0.1~ 2 Hz,每隔0.1Hz取一频率,共20个波浪频率。采用线性切片理论计算船舶在单位波幅规则波中的响应和波浪传递函数。基于谱分析和概率统计的方法,以船中横剖面垂向波浪弯矩为标准,对上述计算得到的规则波下的船舶波浪载荷进行短期预报和长期预报。取10−5概率水平的预报值作为设计波浪载荷极值,即得到可能出现的最危险的外部波浪载荷。在所有浪向和波频范围内,对计算的该载荷参数的频率响应函数进行搜索,其中中横剖面垂向波浪弯矩的幅频响应最大值对应的规则波频率即为该工况下设计波浪的波频,最终计算得到的波频ω=0.069 Hz。
设计波波幅h由主要载荷参数的长期预报极值除以该载荷参数对应的幅频响应的最大值得到。即
| $ {h}=\dfrac {\scriptsize{{\mathrm{主}\mathrm{要}\mathrm{载}\mathrm{荷}\mathrm{参}\mathrm{数}\mathrm{的}\mathrm{长}\mathrm{期}\mathrm{预}\mathrm{报}\mathrm{极}\mathrm{值}}}}{\scriptsize{\mathrm{该}\mathrm{参}\mathrm{数}\mathrm{幅}\mathrm{频}\mathrm{响}\mathrm{应}\mathrm{最}\mathrm{大}\mathrm{值}}}=6.68\;{\rm{m}}。$ |
以船体梁垂向惯性矩表示船体梁刚度,给出船体梁在不同垂向惯性矩下,以非线性波浪载荷程序计算得出的合成中垂和中拱波浪载荷值。计算结果如表1所示。
|
|
表 1 不同刚度下波浪载荷计算结果 Tab.1 Calculation results of wave load under different stiffness |
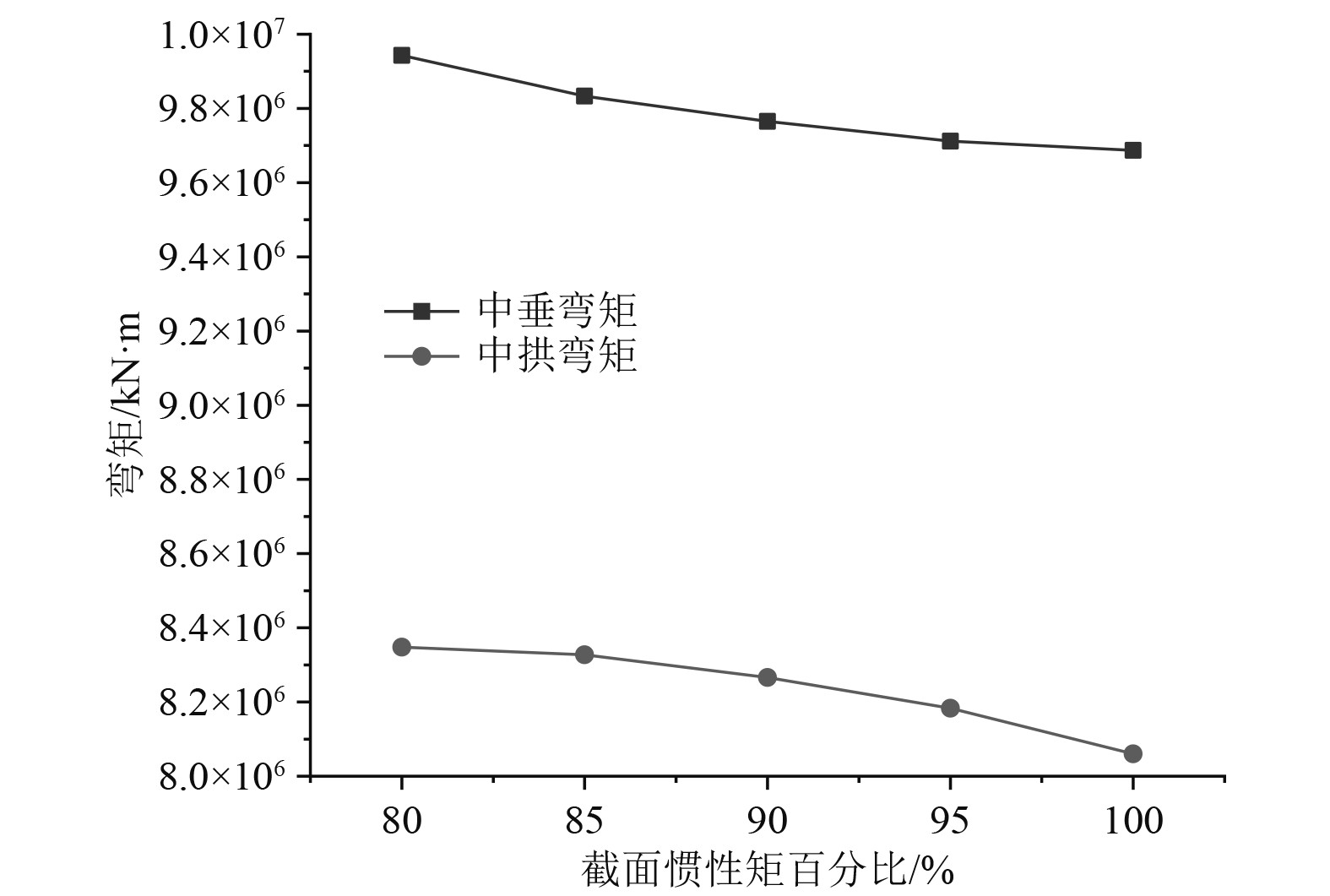
将不同刚度下考虑高频振动的非线性合成弯矩进行处理,得出随刚度变化的波浪载荷曲线如图1所示。
|
图 1 非线性合成弯矩变化曲线 Fig. 1 Nonlinear composite bending moment curve |
从非线性波浪载荷程序的计算结果可以看出:
1) 随着船体垂向截面惯性矩的减小,波浪载荷的波频成分不变,而计及高频成分的非线性合成弯矩则有着随船体垂向截面惯性矩的减小而增大的趋势。船体的高频振动会导致其总体载荷中的高频成分显著增大,该结果与其他文献中的研究结果是相吻合的。
2) 根据计算结果,船体梁垂向惯性矩减小20%,会导致非线性中拱合成弯矩增大3.58%,非线性中垂合成弯矩增大2.65%。该结果表明非线性波浪载荷在船体结构优化中有着不可忽视的影响,把波浪载荷高频成分受刚度影响的变化考虑到船舶结构优化中来十分必要。
2 优化分析 2.1 算例船主尺度及剖面模型本文以一艘13 500 TEU超大型集装箱船为例,该集装箱船的主尺度如表2所示。
|
|
表 2 13 500 TEU集装箱船主尺度 Tab.2 Main dimensions of 13 500 TEU container ship |
目标船舱段有限元模型及待优化剖面如图2所示。

|
图 2 集装箱船舱段及优化剖面 Fig. 2 Container ship cabin and optimized section |
计算中,选取对船体垂向截面惯性矩影响较大的纵向板厚为设计变量。设计变量的取值区间按照《钢制海船入级建造规范》中的规定进行选取,以规范规定的最小尺寸为板厚的下限。此外,考虑到计算效率及工程实用性,对设计变量进行离散化处理,板厚间隔取为0.5 mm。优化计算中板厚设计变量信息如表3所示。
|
|
表 3 剖面板厚设计变量单位(mm) Tab.3 Design variables of sectional panel thickness |
考虑满载出港工况,分别施加考虑以及不考虑非线性波浪载荷影响的总体弯矩以构建优化模型1和优化模型2进行优化计算。以目标船纵向板厚为设计变量,以极限强度、构件尺寸为约束条件,以船中剖面面积为优化目标,应用多岛遗传算法,完成目标船剖面的优化设计。在优化模型中,由Excel组件输入舱段纵向板厚为设计变量,由Simcode组件中的截面属性计算程序和非线性波浪载荷计算程序输出随船体刚度变化的波浪弯矩值,最后由极限强度模块进行船体梁极限强度的计算及校核。
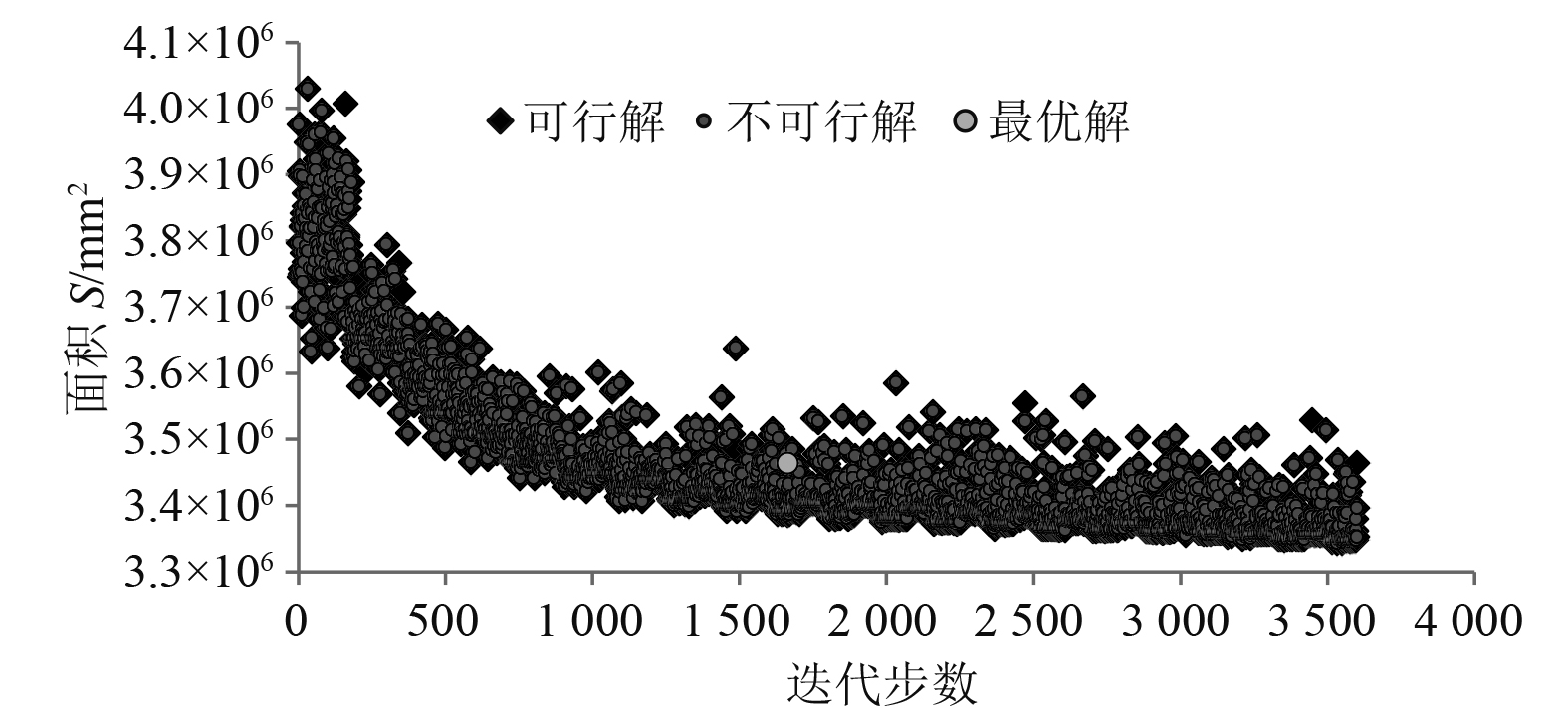
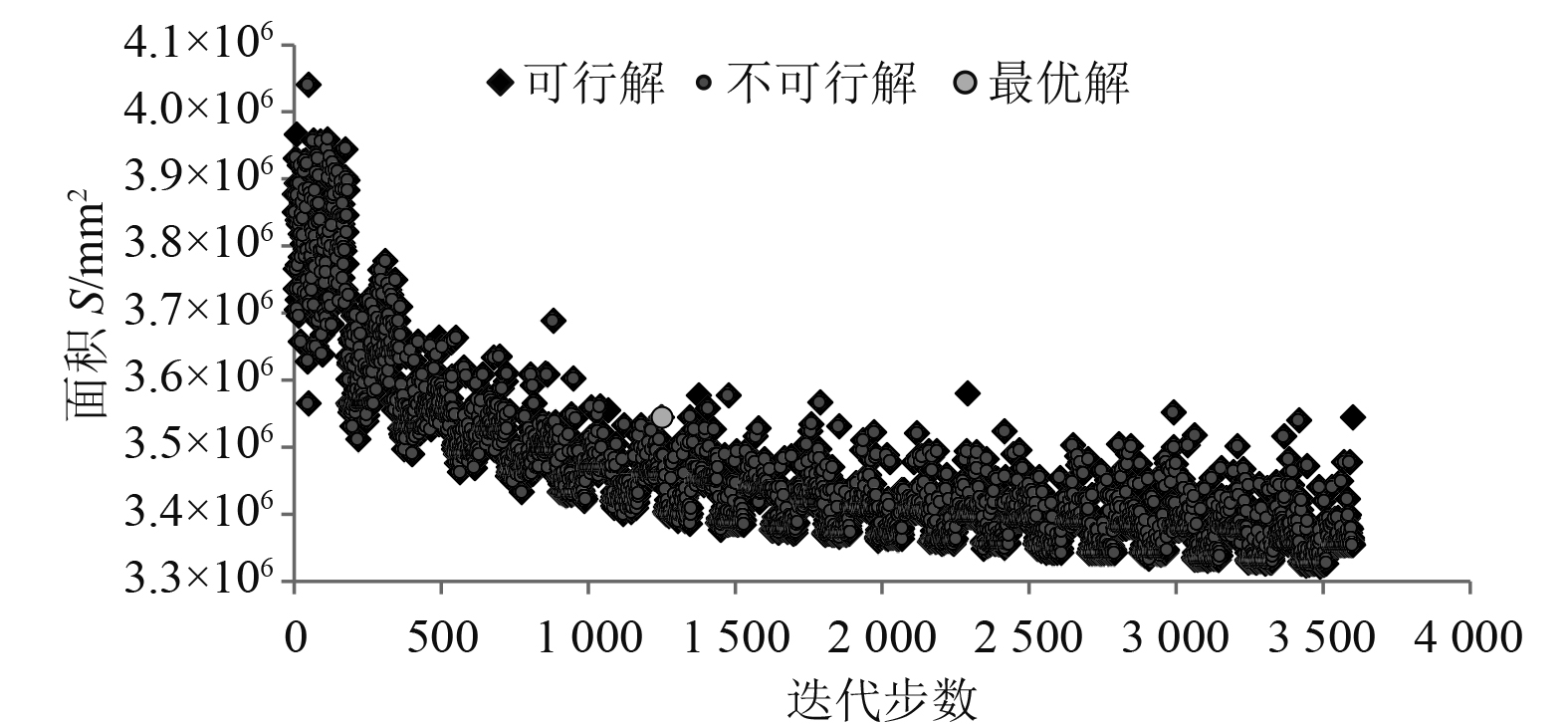
以优化软件Isight为平台,集成上述组件构建优化模型。根据设计变量个数,设置算法参数,经过3600次迭代计算,得出优化结果。两模型的优化历程如图3和图4所示。
|
图 3 不考虑非线性波浪载荷(模型1)优化历程图 Fig. 3 Optimization history chart without considering nonlinear wave load(Model 1) |
|
图 4 考虑非线性波浪载荷(模型2)优化历程图 Fig. 4 Optimization history considering nonlinear wave load(Model 2) |
经过优化计算,船中剖面各位置的板厚如表4所示,剖面面积优化效果如表5所示。
|
|
表 4 优化后剖面板厚对比单位(mm) Tab.4 Comparison of thickness of optimized section panel |
|
|
表 5 剖面面积优化效果 Tab.5 Optimization effect of section area |
由优化历程图可以看出,随着迭代步数的增加,2种优化模型的目标函数可行解趋于平缓,两者均达到收敛。在目标函数、设计变量以及约束条件相同的情况下,不考虑非线性波浪载荷影响的工况模型船中剖面面积减小5.085%,考虑非线性波浪载荷影响的工况模型船中剖面面积减小2.896%。对两模型的优化效果进行对比分析可以得知,随着优化设计的进行,纵向板厚的减小导致船中剖面截面惯性矩减小,进而导致船体梁刚度降低,作用于船体梁上的非线性波浪载荷增大,从而反过来对剖面的优化结果产生影响。因而,考虑非线性波浪载荷影响的优化结果更加安全合理。
分析不考虑非线性波浪载荷影响的船中剖面板厚优化结果,外底板、舭列板、舷侧上部以及边舱水平桁位置的板厚减小,内底板及双层底纵桁位置的板厚增大。由于船底板及舷侧上部板距剖面中和轴距离较远,该位置板厚的变化对截面惯性矩的影响更大。将两模型的优化结果进行对比可以看出,考虑了非线性波浪载荷的影响之后,外底板、舭列板、舷侧上部、内底板、双层底纵桁及边舱水平桁位置的板厚相较于不考虑非线性波浪载荷影响的优化板厚有所增大。由此可见,考虑了非线性波浪载荷影响之后,对船体剖面距中和轴较远位置处的板列有着更高的要求。
3 结 语本文以某超大型集装箱船为研究对象,借鉴设计波方法,采用非线性波浪载荷程序对超大型集装箱船在不同船体梁刚度下的低频和高频垂向波浪载荷响应进行理论计算。对比分析了船中剖面在考虑以及不考虑波浪载荷影响下的优化结果,得到以下结论:
1)船体的高频振动会导致其总体载荷中的高频成分显著增大,随着船体梁刚度的降低,波浪载荷的波频成分不变,而计及高频成分的非线性合成弯矩则有着随船体梁刚度减小而增大的趋势。计算结果显示,船体梁垂向惯性矩减小20%,会导致非线性中拱合成弯矩增大3.58%,非线性中垂合成弯矩增大2.65%。
2)对比船中剖面优化结果,在目标函数、设计变量以及约束条件相同的情况下,不考虑非线性波浪载荷影响的工况模型船中剖面面积减小5.085%,考虑非线性波浪载荷影响的工况模型船中剖面面积减小2.896%。随着优化的进行,船体梁刚度减小,导致波浪载荷不断增大,从而对优化的结果产生影响,因而有必要在船舶结构优化中考虑刚度变化与非线性波浪载荷相互耦合的影响。
3)对比两优化模型各位置板厚的变化趋势,考虑了非线性波浪载荷影响之后,对船体剖面距中和轴较远位置处的板列有着更高的要求。
| [1] |
王知谦, 王佳颖. UR S11A对大型集装箱船结构设计的影响研究[J]. 船舶工程, 2017, 39(2): 1-6. |
| [2] |
郑祖园, 王德禹. UR S11A对集装箱船直接强度的影响[J]. 中国舰船研究, 2016, 11(4): 44-50. DOI:10.3969/j.issn.1673-3185.2016.04.007 |
| [3] |
徐敏, 唐明文. UR S11A和UR S34对超大型集装箱船结构强度直接计算的影响[J]. 船舶工程, 2017, 39(10): 5-7+23. |
| [4] |
任晨辉. 非线性波浪载荷对船体结构强度的影响研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [5] |
KOO J B, JANG, K B, SUH, Y S, et al., Fatigue damage assessment based on full scale measurement data for a large container carrier[C]//Proceedings of the Twenty-First International Offshore and Polar Engineering Conference, 2011, International Society of Offshore and Polar Engineers, Maui, Hawaii, USA.
|
| [6] |
汪雪良. 船体梁刚度对波激振动影响的比较研究[J]. 中国舰船研究, 2016, 11(5): 56-62. |
| [7] |
船体结构波激振动和砰击颤振直接计算评估指南[S]. 中国船级社, 2018.
|
| [8] |
顾学康, 胡嘉骏. 散货船船体大幅运动中的非线性波浪载荷计算总结[R]. 中国船舶科学研究中心研究报告.
|
| [9] |
冯国庆, 任慧龙. 船体结构疲劳评估的设计波法[J]. 哈尔滨工程大学学报, 2005, 26(4): 430-434. DOI:10.3969/j.issn.1006-7043.2005.04.003 |
| [10] |
樊佳. 基于设计波法的舰船整船有限元强度分析[D]. 武汉: 华中科技大学, 2011.
|
 2022, Vol. 44
2022, Vol. 44
