2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China
立管作为将海底油田井口与油气生产勘探平台连接起来的细长结构物,被认为是海上平台系统的重要组成部分。而在一定流速的来流作用下,立管将在横流及顺流方向上同时出现涡激振动(vortex-induced vibration, VIV),引起结构疲劳损伤。
目前,涡激振动的主要研究方法分为实验方法、计算流体力学法(CFD)以及经验模型法。Trim[1]记录并分析了大尺度立管在不同均匀流下的横流、顺流振动实验数据;Chaplin[2]设计了阶梯流作用下立管的一系列涡激振动实验;Baarholm[3]对实尺度立管模型在不同剪切流下立管横流和顺流向振动幅值及振动频率进行了分析;Song[4-5]研究了均匀流下立管模型所受到流体激励力在顺流和横流方向的分布规律。数值模拟方面,Wang[6]则采用CFD方法预报了均匀及线性剪切流下立管双向涡激振动并与实验进行了对比。而基于尾流振子模型方法的立管双向涡激振动响应预报工作也陆续展开[7-8]。但对于常用于工业界的流体力分解模型,相关研究主要针对横流的振动[9],或在仅考虑横流响应对顺流向激励力放大作用进行顺流向振动预报[10-12]。而近年的实验表明横流向与顺流向振动间存在明显的耦合效应[13]。因此,有必要建立能够考虑横流-顺流向耦合效应的立管涡激振动预报模型,以更为准确地进行立管动力响应分析。
本文针对顶张式立管,基于双自由度受迫振动试验数据,采用有限元法和能量平衡方程建立了考虑双向耦合效应的涡激振动频域预报模型,通过与实验结果的对比验证了其合理性,并讨论附加质量系数变化效应对预报结果的影响规律。
1 数学模型 1.1 立管振动方程将顶张式立管简化为受轴向张力作用的简支梁,坐标原点位于立管悬挂点,z轴向下为正,x轴为顺流方向,y轴为横流方向。将简支梁在空间上进行有限元离散,得到单元刚度矩阵
| $ {{\boldsymbol K}_M}{\text{ = }}\frac{{EI}}{{{l^3}}}\left[ \begin{aligned} {12}&{6l}&{ - 12}&{6l} \\ {6l}&{4{l^2}}&{ - 6l}&{2{l^2}} \\ { - 12}&{ - 6l}&{12}&{ - 6l} \\ {6l}&{2{l^2}}&{ - 6l}&{4{l^2}} \end{aligned} \right] ,$ | (1) |
| $ {{\boldsymbol K}_T}{\text{ = }}\frac{T}{{30l}}\left[ \begin{aligned} {36}&{3l}&{ - 36}&{3l} \\ {3l}&{4{l^2}}&{ - 3l}&{{l^2}} \\ { - 36}&{ - 3l}&{36}&{3l} \\ {3l}&{{l^2}}&{3l}&{4{l^2}} \end{aligned} \right] 。$ | (2) |
梁单元集中质量矩阵可写为:
| $ {\boldsymbol M}{\text{ = }}\frac{{({m_0} + {m_a})}}{{420}}\left[ \begin{aligned} {156}&{22l}&{54}&{ - 13l} \\ {22l}&{4{l^2}}&{13l}&{ - 3{l^2}} \\ {54}&{13l}&{156}&{ - 22l} \\ { - 13l}&{ - 3{l^2}}&{ - 22l}&{4{l^2}} \end{aligned} \right]。$ | (3) |
式中:
引入简支梁顶端和底端的约束条件,按照单元节点坐标组装得到总刚度矩阵
| $ \left[ {{{\boldsymbol K}_M}{\text{ + }}{{\boldsymbol K}_T}} \right]\varphi - {\omega ^2}\left[{\boldsymbol M} \right]\varphi = 0 {\text{。}}$ | (4) |
式中:
通过求解矩阵方程即可得到简支梁不同模态的频率和振型。
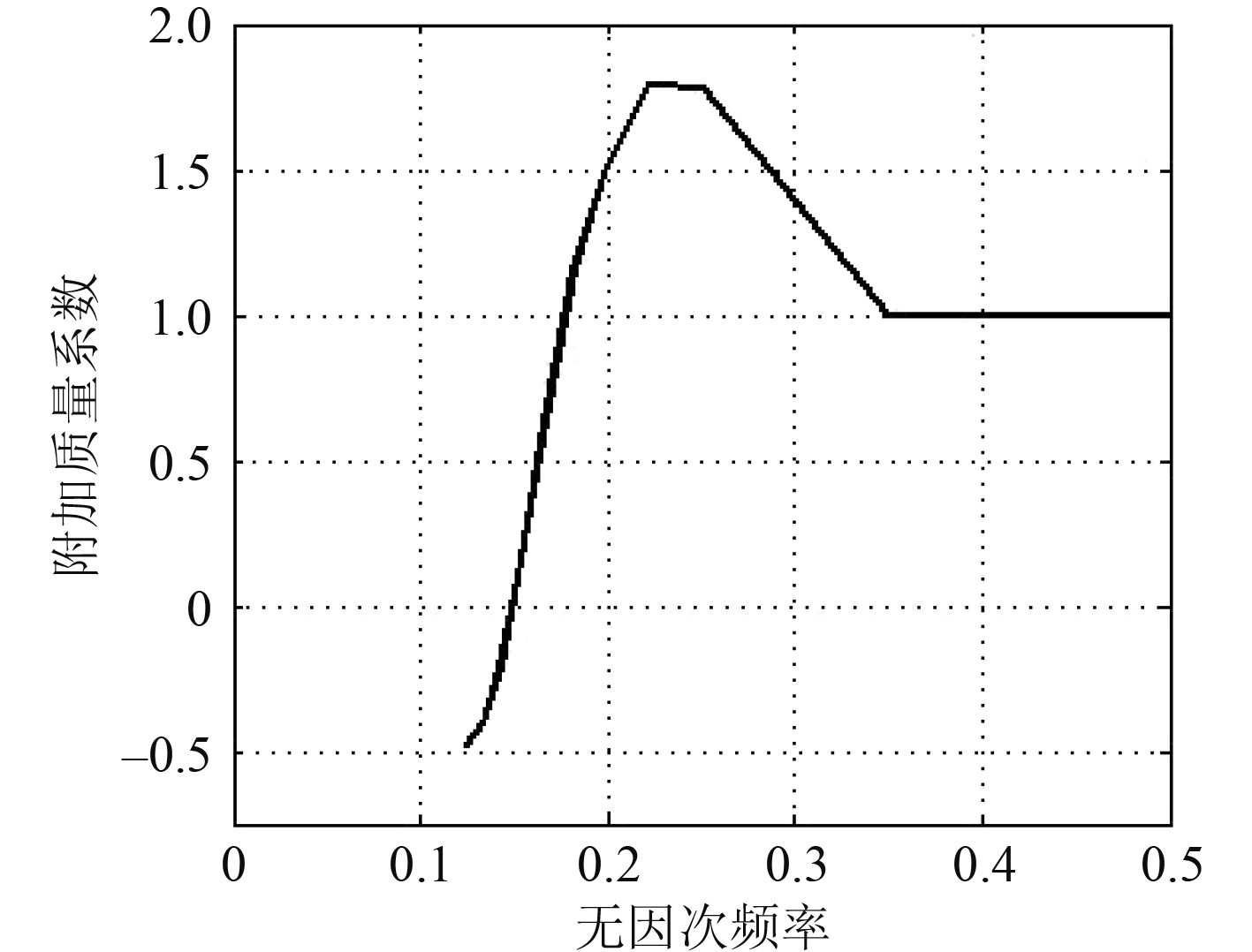
1.2 涡激振动附加质量系数模型研究表明当立管发生涡激振动时,其顺流向响应频率往往为横流向的2倍[13]。Zheng[14]基于此开展了一系列圆柱体横流-顺流双自由度耦合受迫振动实验,得到了不同横流向振幅
|
图 1 横流方向附加质量系数简化曲线 Fig. 1 Simplified curve of added mass coefficient in CF direction |
|
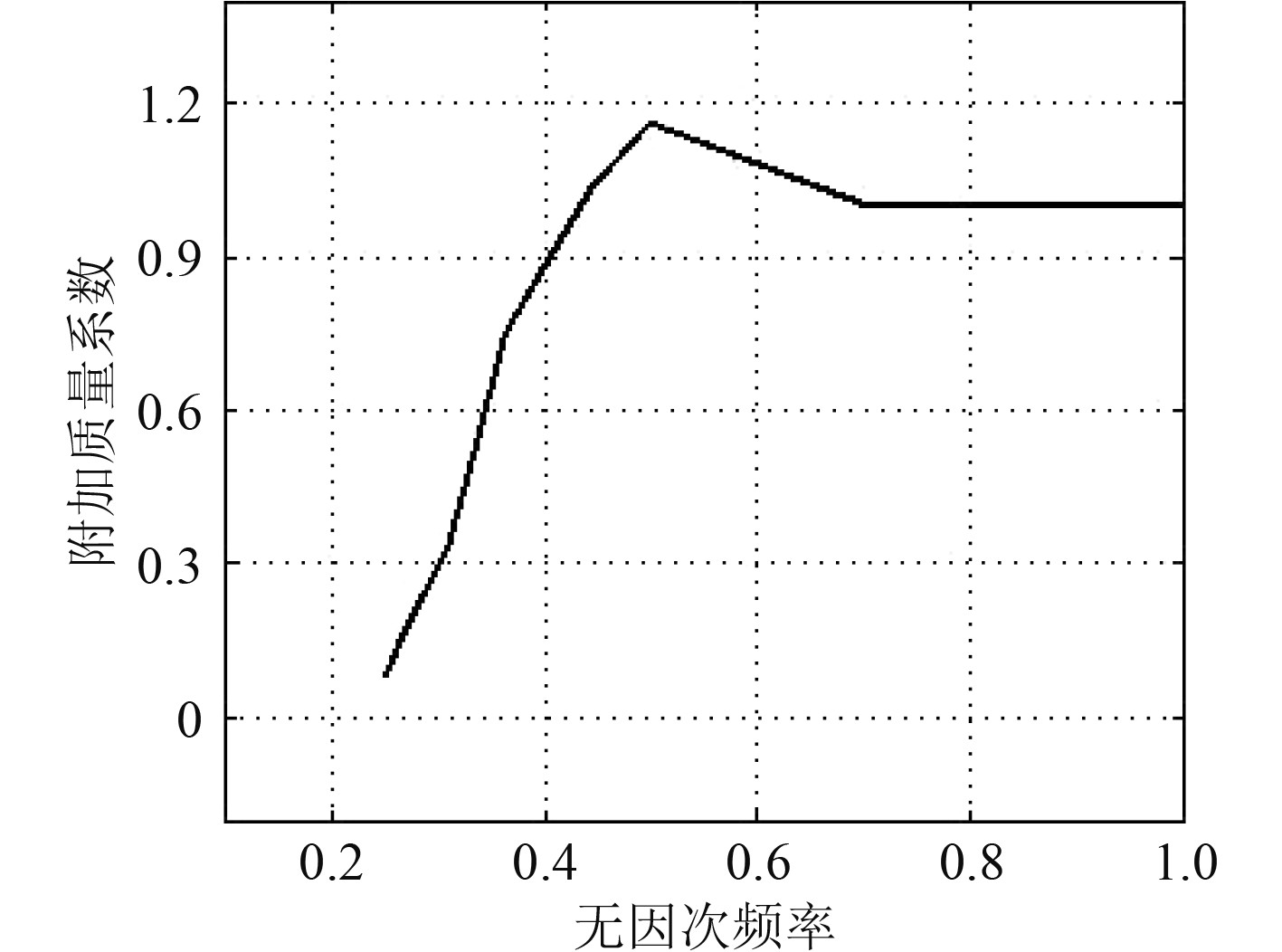
图 2 顺流方向附加质量系数简化曲线 Fig. 2 Simplified curve of added mass coefficient in IL direction |
而考虑到不同工况中附加质量将随流场分布发生变化,立管响应频率及振型可通过迭代计算得到。
在横流方向上,计算步骤为:
1)假设
2)根据流场流速分布,计算立管不同位置无因次频率
3)根据横流方向附加质量系数简化曲线得到附加质量分布,更新振动方程,计算得到新的振动频率
4)重复步骤2和步骤3直至结果收敛,得到横流向实际振动频率
由于基于顺流方向附加质量系数计算得到的振动频率往往并不满足总是横流响应频率的2倍,常出现
1)针对第i阶横流向振动模态,假设其相对应顺流振动频率满足
2)根据附加质量系数分布曲线得到顺流向附加质量分布,建立振动方程,计算第i阶横流向振动模态对应的顺流向模态及频率;
3)对比
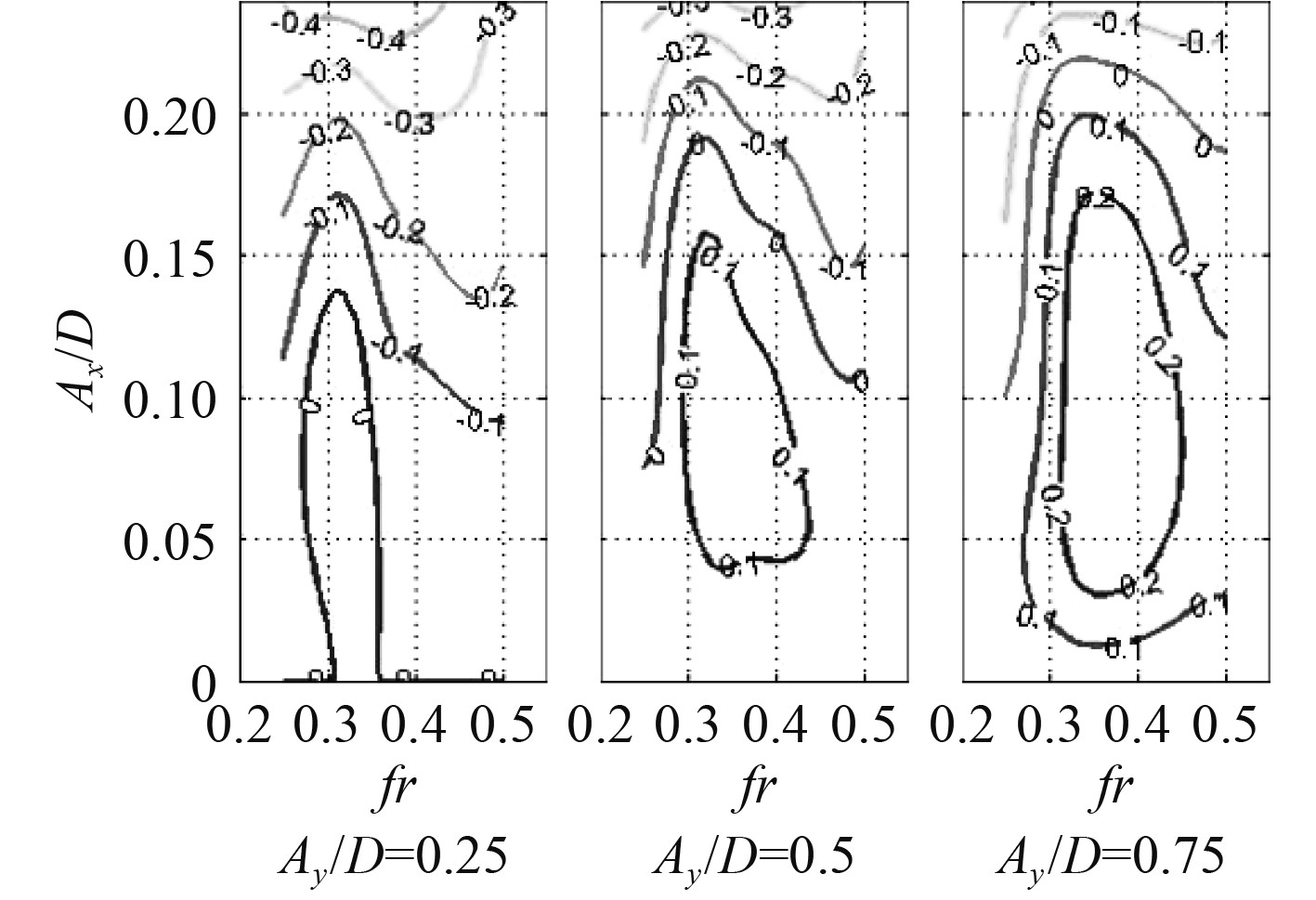
对于流体对立管的激励力,同样采用Zheng[14]实验得到的横流向和顺流向涡激振动激励力系数。与单自由度强迫振动实验不同,Zheng所进行的实验可以反映出横流与顺流振动间存在的耦合效应,并在激励力系数的分布上有所体现。以0°位移相位角情况为例,典型激励力系数分布云图如图3和图4所示。可以发现,随顺流振幅增大,横流向激励力系数激励中心所对应无因次频率减小;而顺流向激励力系数将随横流振幅呈现增大趋势。参考文献[13],将立管横流向无因次频率介于0.125和0.25之间的区域作为能量输入区。计算中根据无因次响应频率及幅值进行插值得到相应的横流及顺流向激励力系数。

|
图 3 典型横流向激励力系数云图[14] Fig. 3 Typical cloud chart of fluid exciting force coefficient in CF direction[14] |
|
图 4 典型顺流向激励力系数云图[14] Fig. 4 Typical cloud chart of fluid exciting force coefficient in IL direction[14] |
当立管结构响应超出能量输入区范围时,认为流体作用力将转变为水动力阻尼。本文使用由 Venugopal[15]针对涡激振动提出的经验阻尼模型。
Venugopal阻尼模型可分为高流速区和低流速区,其中高流速区水动力阻尼系数为:
| $ {r_{hh}} = {{\rho {U^2}(z){C_{vh}}} \mathord{\left/ {\vphantom {{\rho {U^2}(z){C_{vh}}} \omega }} \right. } \omega } ,$ | (5) |
低流速区水动力阻尼系数为:
| $ {r_{hl}} = {r_{sw}}(z) + \rho DU(z){C_{vl}}。$ | (6) |
式中:
参考SHEAR7方法,通过预估能量选取所振动激发模态[7]。针对横流向振动模态i及对应顺流向振动模态j,计算预估能量:
| $ {\varPi _{i\& j}} = {\varPi _{i,CF}} + {\varPi _{j,IL}} = \frac{{{{\left| {{Q_{i,CF}}} \right|}^2}}}{{2{R_{i,CF}}}} + \frac{{{{\left| {{Q_{j,IL}}} \right|}^2}}}{{2{R_{j,IL}}}}。$ | (7) |
其中:
| $ Q{\text{ = }}\int_{Li} {\frac{1}{2}\rho {C_{V,\max }}(\hat f)D{U^2}(z)\left| {\varphi (z)} \right|{\text{dz}}}, $ | (8) |
| $ R{\text{ = }}\int_L {{r_s}(z){\varphi ^2}(z)\omega {\rm{d}}z} + \int_{L - Li} {{r_h}(z){\varphi ^2}(z)\omega {\text{dz}}}{\text{。}} $ | (9) |
式中:
选取激发振动模态时,根据最大预估能量值
当处于涡激振动状态时,在一段时间内立管的能量输入及输出可分别写为
其中,模态激励力为:
| $ \begin{split} & P(t) =\int_0^L {P(z,t)\left| {{\varphi _{CF/IL}}(z)} \right|{\text{dz}}} =\\ &\; \int_0^L {\frac{1}{2}\rho D{U^2}(z){C_V}[\hat f,Y(z),X(z)]\sin (\omega t)\left| {{\varphi _{CF/IL}}(z)} \right|{\text{dz}}} 。\end{split} $ | (10) |
式中:
立管模态速度为:
| $ {V_i}(t) = {A_i}{\omega _i}\sin ({\omega _i}t), $ | (11) |
模态阻尼为:
| $ R(t){\text{ = }}\int_0^L {\left[ {{r_s} + {r_h}(z)} \right]{\varphi ^2}(z){V_i}(t){\text{dz}}} {\text{。}}$ | (12) |
针对涡激振动响应中激发的横流向模态i及顺流向模态j建立能量平衡方程,可得模态振幅:
| $ \begin{gathered} \frac{{{A_{x,i}}}}{D} = \hfill \\ \frac{{\dfrac{1}{2}\int_{Li} {\rho D{U^2}(z){C_{V,CF}}[{{\hat f}_{i,CF}},{Y_i}(z),{X_j}(z)]\left| {{\varphi _{i,CF}}(z)} \right|{\text{dz}}} }}{{\displaystyle\int_L {{r_s}\varphi _{i,CF}^2(z){\omega _{i,CF}}(t){\text{dz}}} + \displaystyle\int_{L - Li} {{r_h}(z)\varphi _{i,CF}^2(z){\omega _{i,CF}}(t){\text{dz}}} }} , \end{gathered} $ | (13) |
| $ \begin{gathered} \frac{{{A_{y,j}}}}{D} = \hfill \\ \frac{{\dfrac{1}{2}\int_{Li} {\rho D{U^2}(z){C_{V,IL}}[{{\hat f}_{j,IL}},{Y_i}(z),{X_j}(z)]\left| {{\varphi _{j,IL}}(z)} \right|{\text{dz}}} }}{{\displaystyle\int_L {{r_s}\varphi _{j,IL}^2(z){\omega _{j,IL}}(t){\text{dz}}} + \displaystyle\int_{L - Li} {{r_h}(z)\varphi _{j,IL}^2(z){\omega _{j,IL}}(t){\text{dz}}} }} {\text{。}} \end{gathered} $ | (14) |
同时,对于柔性立管多阶模态同时被激发这一现象,本文通过模态叠加的方式进行计算处理。
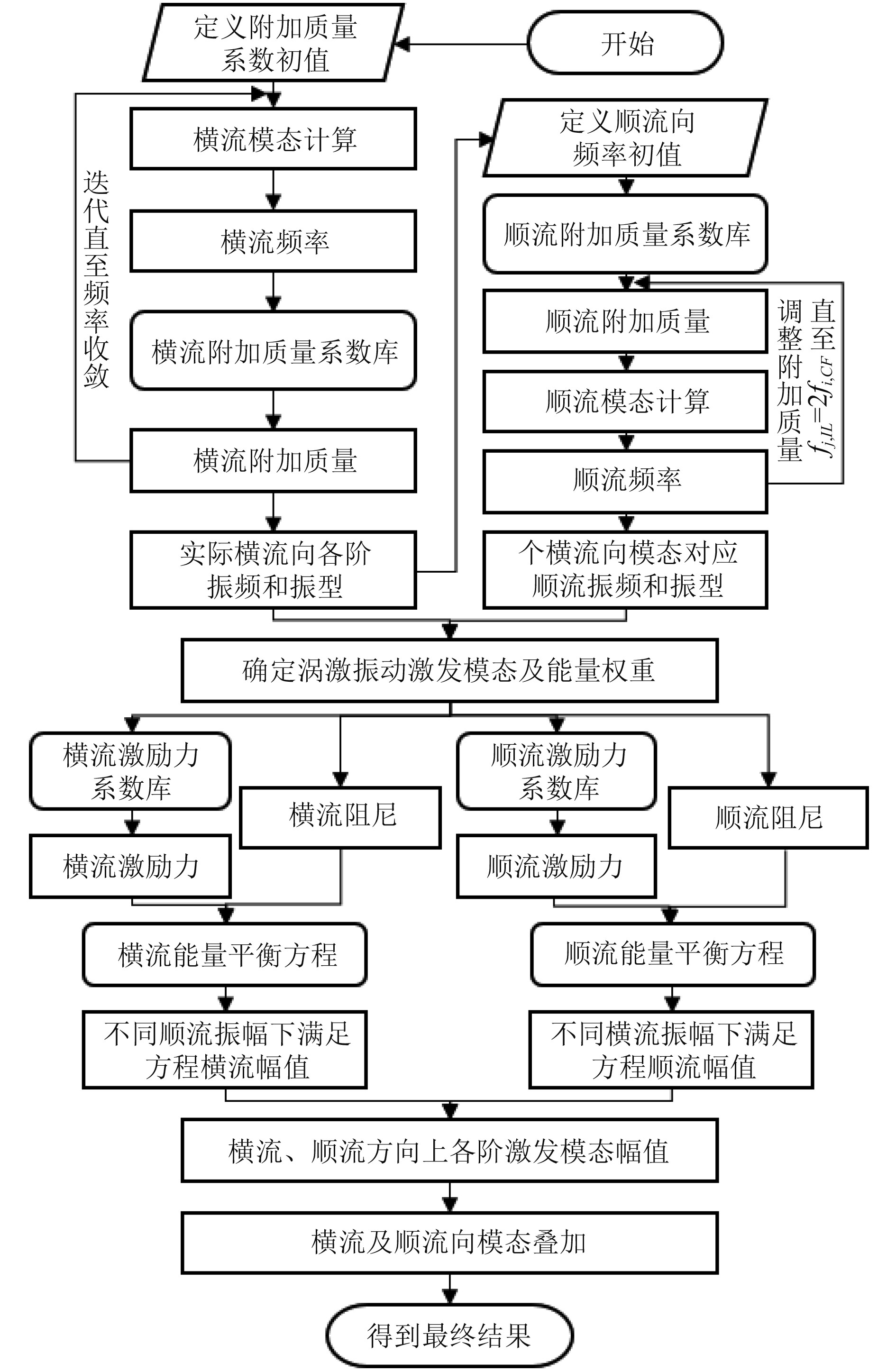
综上,顶张式立管涡激振动响应幅值计算流程如图5所示。
|
图 5 涡激振动预报流程图 Fig. 5 The flow chart of VIV prediction |
选取均匀流、阶梯流、剪切流3种流场工况进行计算,并与实验结果进行对比。为分析附加质量系数的影响,同时计算了附加质量系数固定为1情况下的涡激振动响应。
2.1 均匀流工况对比分析采用Trim 等[1]进行的大尺度立管模型均匀流试验。该试验立管模型长38 m,整体置于拖曳水池中,并在两端施加预张力。模型主要参数如表1所示。
|
|
表 1 Trim试验模型参数 Tab.1 Experimental parameters of Trim’s model |
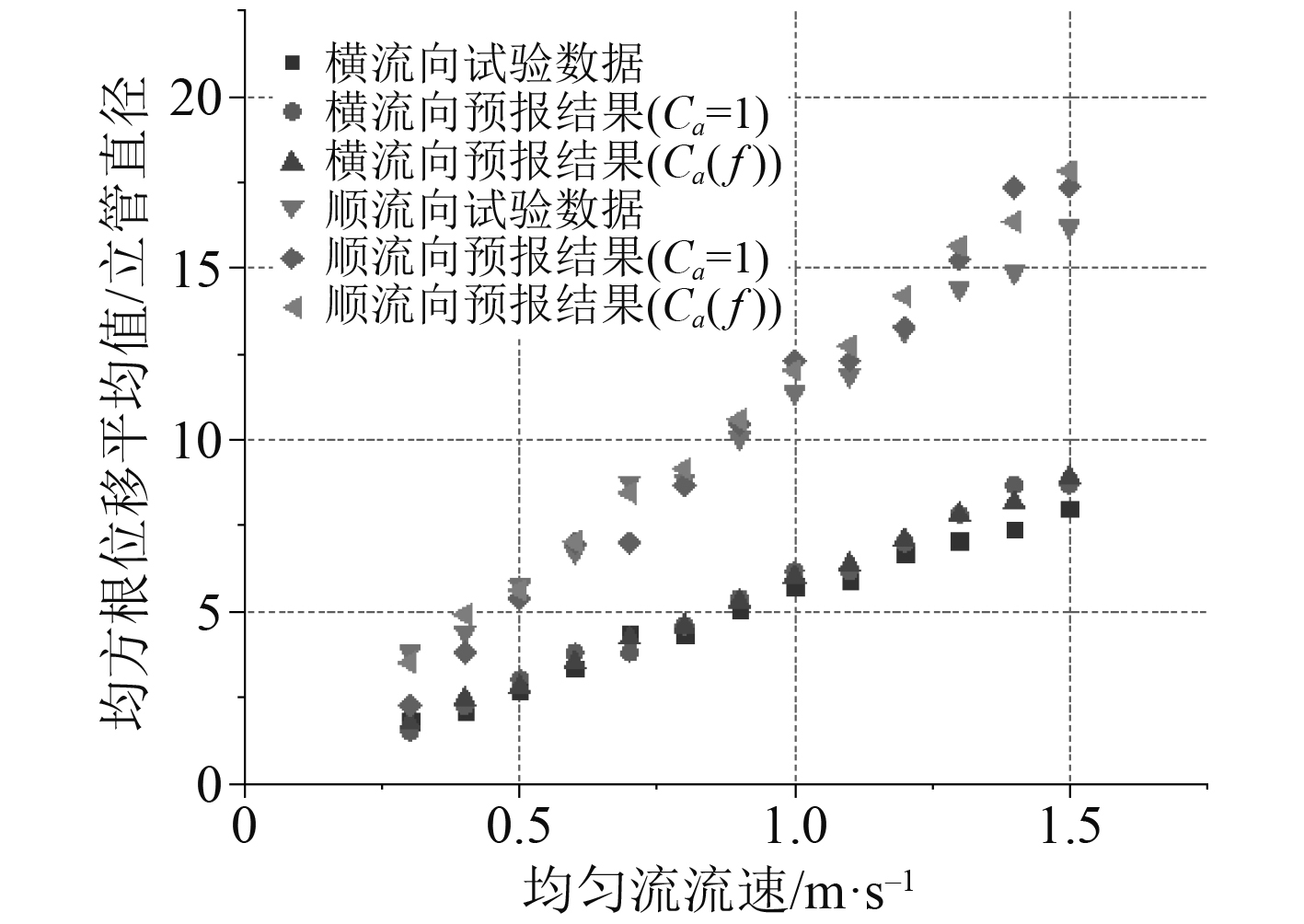
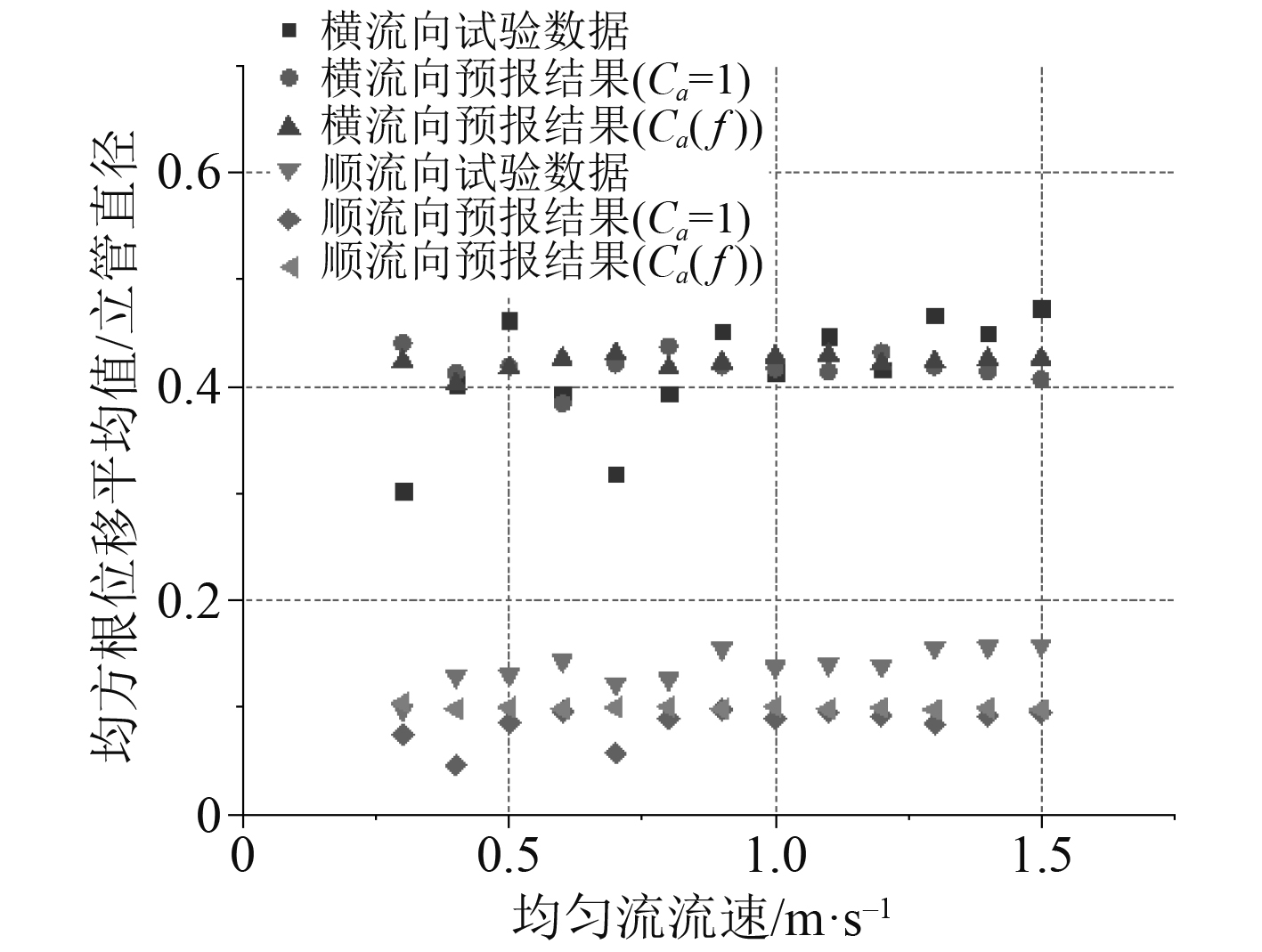
图6与图7对预报所得涡激振动响应与试验数据进行了全面的对比。其中
|
图 6 不同均匀流下响应主导振频对比 Fig. 6 Comparison of response dominant frequency under uniform flow |
|
图 7 不同均匀流下响应均方根位移分布平均值对比 Fig. 7 Comparison of spatial mean of temporal displacement standard deviation under uniform flow |
在振动频率方面,与本文假设相同,试验得到顺流向主导振动频率为横流向的2倍。当来流流速低于1.0 m/s时,预报与试验结果间较为一致,而随着流速增大其间会产生一定的误差,但总体而言模型的预报误差处在可接受的范围内。在振幅方面,
选取流速为0.4 m/s工况作为典型工况对立管响应进行具体的分析,频域预报得到横流向无量纲均方根位移及顺流向无量纲均方根位移沿管长分布如图8所示。结果表明,频域模型在横流及顺流方向上均预测得到的与实验一致的第三阶和第五阶模态。其中在横流向振幅上,2种预报模型的结果较为一致。而在顺流方向上,由于

|
图 8 均匀流工况下响应幅值沿管长分布(U=0.4 m/s) Fig. 8 Response amplitude along the riser under uniform flow (U=0.4 m/s) |
Chaplin等[2]设计了一种特殊的试验装置,立管模型下半部分在拖曳水池中,为阶梯流流速段,高于水池水面部分置于与拖车同时拖动的装水容器中,为静水段,并在立管顶端施加张力。试验参数如表2所示。
|
|
表 2 Chaplin试验模型参数 Tab.2 Experimental parameters of Chaplin’s model |
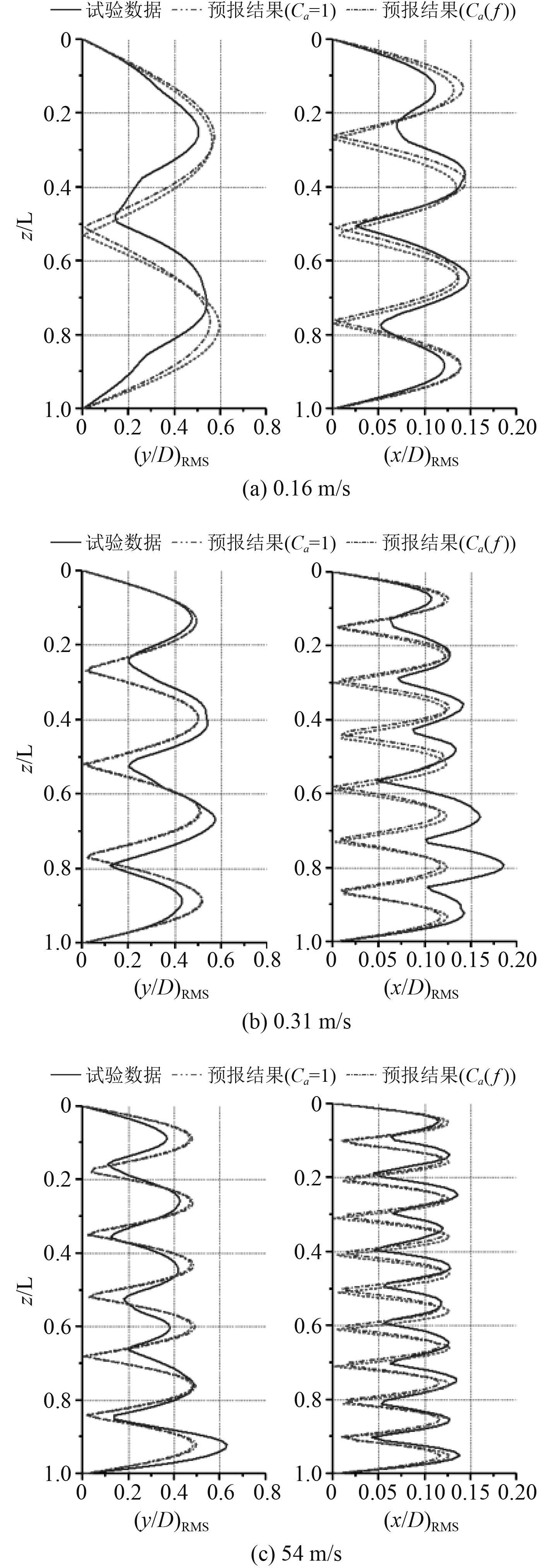
选取3种流速工况进行计算分析,流速段流速分别为0.16 m/s,0.31 m/s,0.54 m/s,对应立管顶张力为405 N,457 N,598 N。响应幅值分布如图9所示。计算结果表明,在该类型阶梯流作用下,立管呈现单一模态主导的响应特性,同时2种附加质量处理方法下预报得到的振型、振幅沿立管分布基本一致。与实验值相比,横流向响应吻合度较好;而顺流向响应除在流速0.31 m/s工况下在0.6L至底端区域内预报结果相对较小,其余均能够较好地吻合试验数据。
|
图 9 阶梯流工况下响应幅值沿管长分布 Fig. 9 Response amplitude condition along the riser under stepped flow |
MARINTE公司于挪威Hanoytangen海域建立了实尺度顶张式立管模型涡激振动试验装置。立管模型的一端与拖车相连,另一端靠浮箱牵引。当拖车运动时,立管将受到线型剪切流作用。试验参数如表3所示。
|
|
表 3 实尺度立管模型参数 Tab.3 Experimental parameters of the real scale riser model |
针对顶部最大流速为0.54 m/s的剪切流工况,模型预报所得激发模态、振动频率、模态振幅及权重如表4,表5所示。由表可见,在剪切流下立管多个振动模态将被激发。而由于附加质量系数取值的不同导致频率预报存在差异,2种方法在横流及顺流向涡激振动激发模态上有明显不同。
|
|
表 4 横流向涡激振动响应信息(U=0.54 m/s) Tab.4 VIV response parameters in CF direction(U=0.54 m/s) |
|
|
表 5 顺流向涡激振动响应信息(U=0.54 m/s) Tab.5 VIV response parameters in IL direction(U=0.54 m/s) |
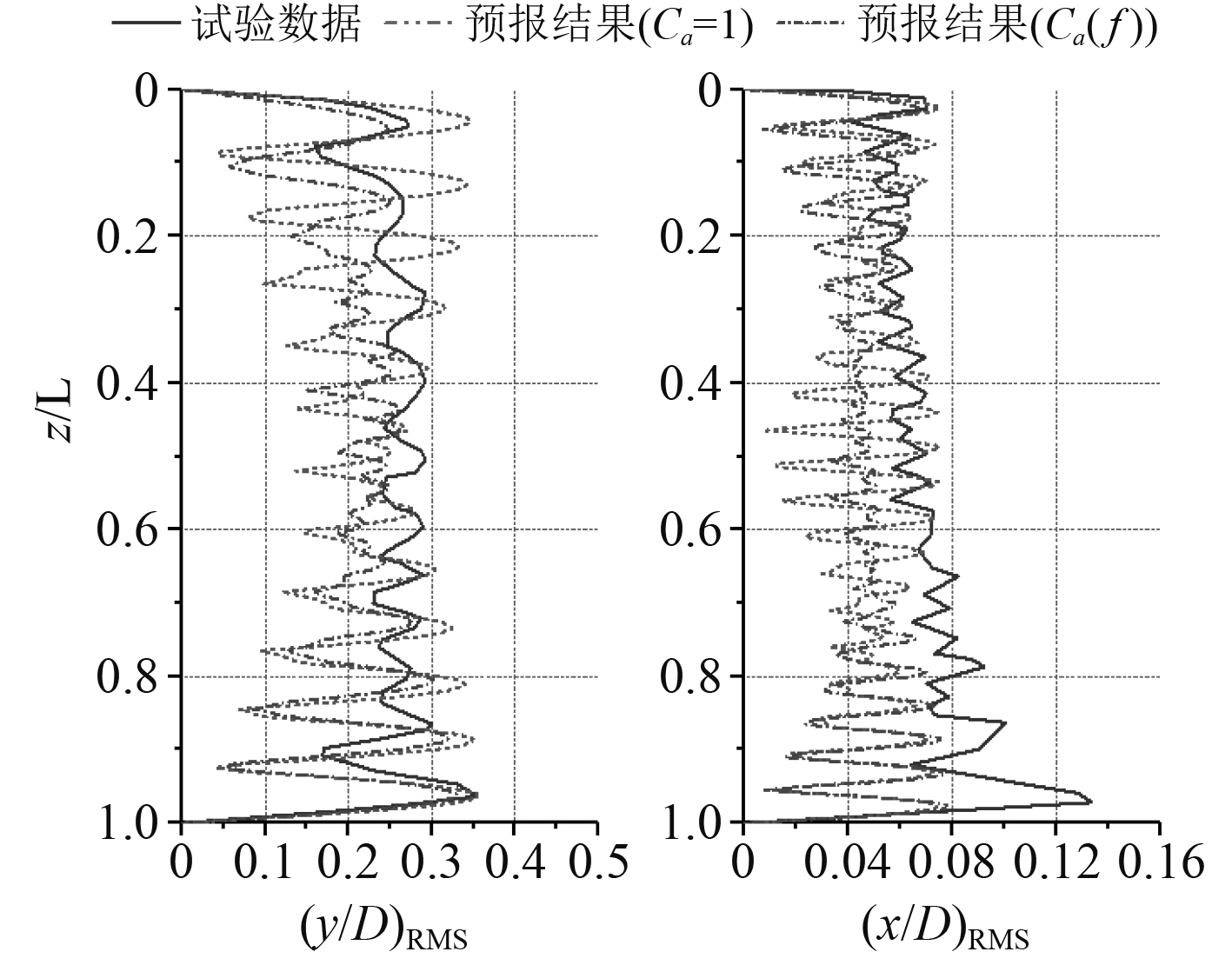
通过模态叠加得到立管涡激振动响应幅值分布如图10所示。Baarholm等[3]给出了该工况下实验得到的涡激振动响应振幅沿立管分布。
|
图 10 剪切流工况下响应幅值沿管长分布(U=0.54m/s) Fig. 10 Response amplitude along the riser under shear flow(U=0.54m/s) |
在横流方向上,试验数据表明立管涡激振动含有明显的第11阶模态成分;而
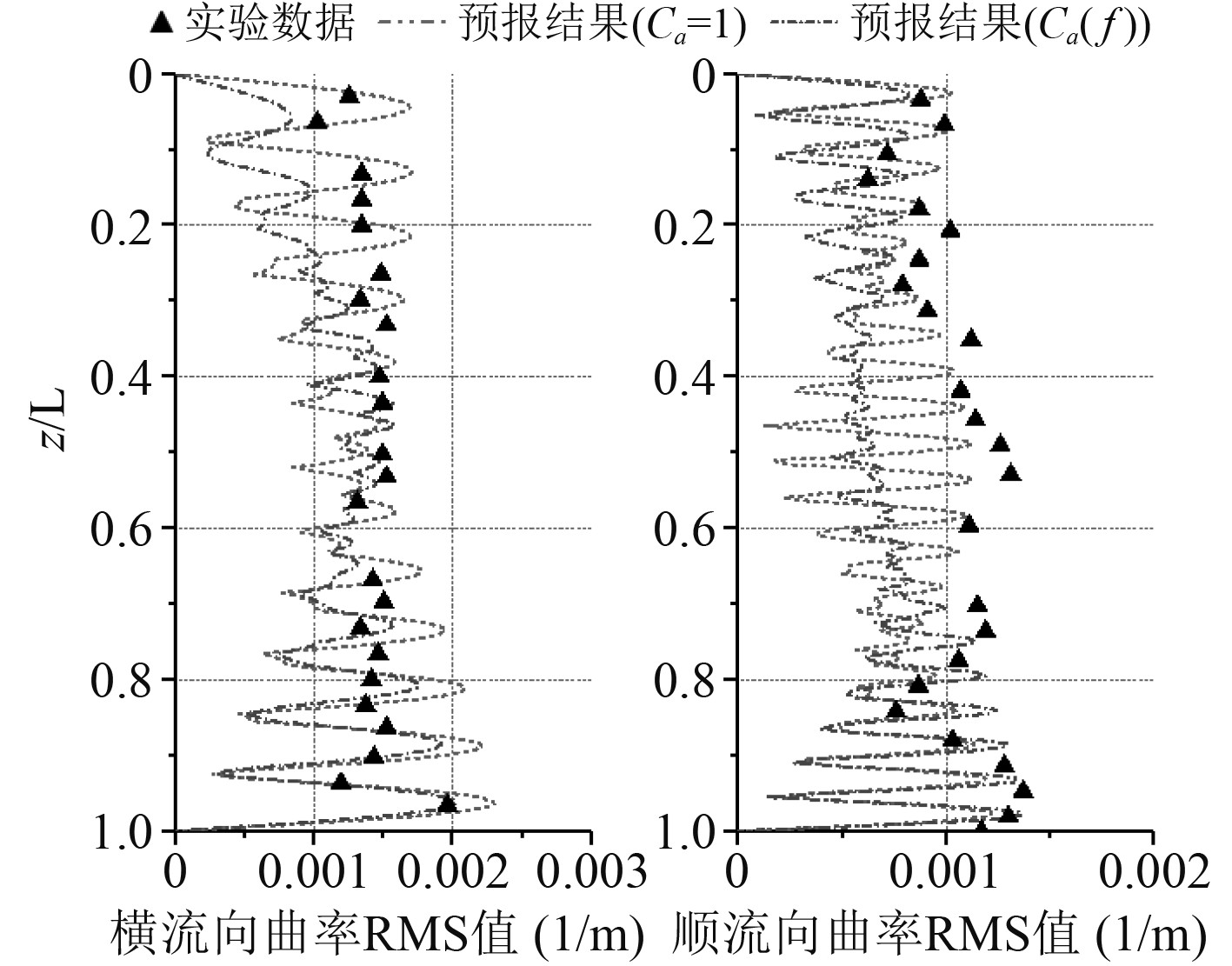
由于立管曲率与其弯曲应力及疲劳损伤密切相关,本文同样针对剪切流工况下横流向和顺流向曲率进行分析,如图11所示。横流方向上,在立管0~0.3L范围内,2种附加质量情况下计算所得曲率与试验数据间存在一定差异,而其余部分均与试验结果较为一致,其中
|
图 11 剪切流工况下曲率沿管长分布(U=0.54 m/s) Fig. 11 Curvature along the riser under shear flow(U=0.54 m/s) |
本文基于双自由强迫振动试验数据,通过有限元方法及能量平衡理论,建立了顶张式立管的双向涡激振动频域预报模型,与不同流场试验观测进行了对比,并讨论了附加质量系数对预报结果的影响。研究结果表明:
1)本文建立的双向耦合涡激振动频域预报方法可较为准确地得到立管在横流向及顺流向涡激振动响应频率及位移分布,计及附加质量的变化效应能够更好地反映出立管在不同流场下的涡激振动响应特性。
2)涡激振动引起的立管顺流向响应幅值虽小于横流向,但由于激发的模态阶数高、振动频率大,顺流向涡激振动引起的疲劳损伤同样应引起足够关注。
| [1] |
TRIM A D, BRAATEN H, LIE H, et al. Experimental investigation of vortex-induced vibration of long marine risers[J]. Journal of Fluids and Structures, 2005, 21(3): 335-361. DOI:10.1016/j.jfluidstructs.2005.07.014 |
| [2] |
CHAPLIN J R, BEARMAN P W, CHENG Y, et al. Blind prediction of laboratory measurements of vortex-induced vibrations of a tension riser[J]. Journal of Fluids and Structures. 2005. 21(1SPEC. ISS. ): 25−40.
|
| [3] |
BAARHOLM G S, LARSEN C M, LIE H. On fatigue damage accumulation from in-line and cross-flow vortex induced vibrations on risers[J]. Journal of Fluids and Structures, 2006, 22(1): 109-127. DOI:10.1016/j.jfluidstructs.2005.07.013 |
| [4] |
SONG L, FU S, ZENG Y, et al. Hydrodynamic forces and coefficients on flexible risers undergoing vortex-induced vibrations in uniform flow[J]. Journal of Waterway Port Coastal & Ocean Engineering, 2016, 142(4). |
| [5] |
SONG L, FU S, CAO J, et al. An investigation into the hydrodynamics of a flexible riser undergoing vortex-induced vibration[J]. Journal of Fluids and Structures, 2016, 63: 325-350. DOI:10.1016/j.jfluidstructs.2016.03.006 |
| [6] |
WANG E, XIAO Q. Numerical simulation of vortex-induced vibration of a vertical riser in uniform and linearly sheared currents[J]. Ocean Engineering, 2016, 121: 492-515. DOI:10.1016/j.oceaneng.2016.06.002 |
| [7] |
秦伟, 康庄, 宋儒鑫, 等. 深水钢悬链立管的双向涡致疲劳损伤时域模型[J]. 哈尔滨工程大学学报, 2013, 34(1): 26-33. |
| [8] |
高云, 张壮壮, 杨斌, 等. 圆柱体横流与顺流方向涡激振动耦合模型研究[J]. 振动与冲击, 2020, 39(11): 22-30. |
| [9] |
VANDIVER J. K, LI L. SHEAR7 V4.4 User Guide[M]. Cambridge, MA, Department of Ocean Engineering, MIT, USA. 2005.
|
| [10] |
曲雪, 薛鸿祥, 唐文勇. 深海顶张式立管顺流涡激振动响应预报方法[J]. 振动与冲击, 2013, 32(15): 32-36. DOI:10.3969/j.issn.1000-3835.2013.15.006 |
| [11] |
LARSEN C M, VIKESTAD K, YTTERVIK R, et al. VIVANA 4.8. 2 Theory Manual[M]. Marintek, Trondheim, Norway. 2016.
|
| [12] |
袁昱超, 薛鸿祥, 唐文勇. 计及附加质量系数变化效应的立管涡激振动时域响应研究[J]. 振动与冲击, 2018, 37(1): 53-59. |
| [13] |
JASON D. Vortex-induced vibration of a circular cylinder with combined in-line and cross-flow motion[D]. Massachusetts Institute of Technology, 2008.
|
| [14] |
ZHENG Haining. The influence of high harmonic force on fatigue life and its prediction via coupled inline-crossflow VIV modeling[D]. Massachusetts Institute of Technology. 2014.
|
| [15] |
VENUGOPAL M. Damping and response of a flexible cylinder in a current[D]. Massachusetts Institute of Technology. 1996.
|
 2022, Vol. 44
2022, Vol. 44
