2. 烟台大学 工程实训中心,山东 烟台 264005
2. Engineering Training Center , Yantai University, Yantai 264005, China
随着人们对船舶的舒适性要求不断提高,船舶振动噪声控制成为越来越多船舶设计人员所关注的问题,而舱室振动带来的对结构的破坏和噪声污染是不可忽略的重要因素[1-2],当舱室的固有频率和外激振频率相同或相近时,舱室会被激发强烈振动,从而产生巨大噪声。因此,为了有效指导舱室的减振降噪,舱室的振动特性分析和响应分析就显得格外重要。
近些年许多国内外学者对舱室的减振降噪进行了研究。吴硕[3]利用Ansys软件对一艘多功能海洋船进行了振动特性分析,并提出了一种建立复杂曲面的建模方法,验证了该方法在工程实际中的可行性。王啸宇等[4]提出等效建模法,并对某实船进行模态分析和试验,结果表明二者结果吻合良好,验证了等效建模法的正确性。李良碧[5]通过优化舰船浮筏的结构参数对浮筏进行振动特性分析,结果表明浮筏的结构参数设置对舰船的振动有较大影响。乔志[6]基于有限元的方法对敷设粘弹性阻尼材料前后的舱室进行了振动特性分析和试验,仿真结果和试验结果吻合较好,证明该阻尼材料具有良好的减振效果。梁炳南[7]通过建立船舶舱室浮动地板的动力学模型,计算了浮动地板动态响应和参数规律,并且提出了抑制板件振动的阻尼技术,对减振控制有一定参考价值。仇远旺[8]采用橡胶阻尼材料对舱室进行减振研究,研究表明该阻尼材料对低频段的减振效果较好,对主机舱的减振效果不如其他舱室的减振效果好。温华兵[9]以复杂薄壳结构为研究对象,提出了一种新型空心阻振结构,通过基座到圆柱壳体的振动特性分析,揭示了该结构对中高频振动具有良好阻振性能,对于船舶等复杂薄壳结构减振降噪设计提供有效参考。王国庆[10]将2种粘弹性阻尼材料应用于舱壁上,分析施加粘弹性阻尼材料前后不同频段的舱室减振量,对比试验数据,验证了粘弹性阻尼材料对舱室减振的可行性。
以船舶舱室模拟件为研究对象,建立舱室的三维几何模型,通过Ansys Workbench平台对舱室进行模态分析,并进行模态测试和阻尼比测试,验证了该模型处理方法的正确性。通过对敷设粘弹性层舱室前后的谐响应分析得到了对舱室动态性能影响最大的模态和减振效果,为舱室的减振设计和优化提供依据。
1 模态分析和半功率带宽法理论| $ {\boldsymbol{M}}\ddot x + {\boldsymbol{K}}x = 0。$ | (1) |
式中:M,K分别为质量矩阵和刚度矩阵;
经变换可得:
| $ ({\boldsymbol{K}} - {\omega ^2}{\boldsymbol{M}}){\rm{X}} = 0 。$ | (2) |
显然自由振动节点振幅不能全为0,因此式(2)的系数行列式必须等于0,即
| $ |{\boldsymbol{K}} - {\omega ^2}{\boldsymbol{M}}| = 0,$ | (3) |
将式(3)展开后可得
| $ {\omega ^{2n}} + {a_1}{\omega ^{2(n - 1)}} + \cdot \cdot \cdot + {a_{n - 1}}{\omega ^2} + {a_n} = 0 。$ | (4) |
这一方程有n个根
将求得的固有频率
半功率带宽法的原理可以概括为:首先获取系统的频响共振峰曲线,然后利用共振频率
| $ \xi = \frac{{{\omega _2} - {\omega _1}}}{{2{\omega _r}}}。$ | (5) |
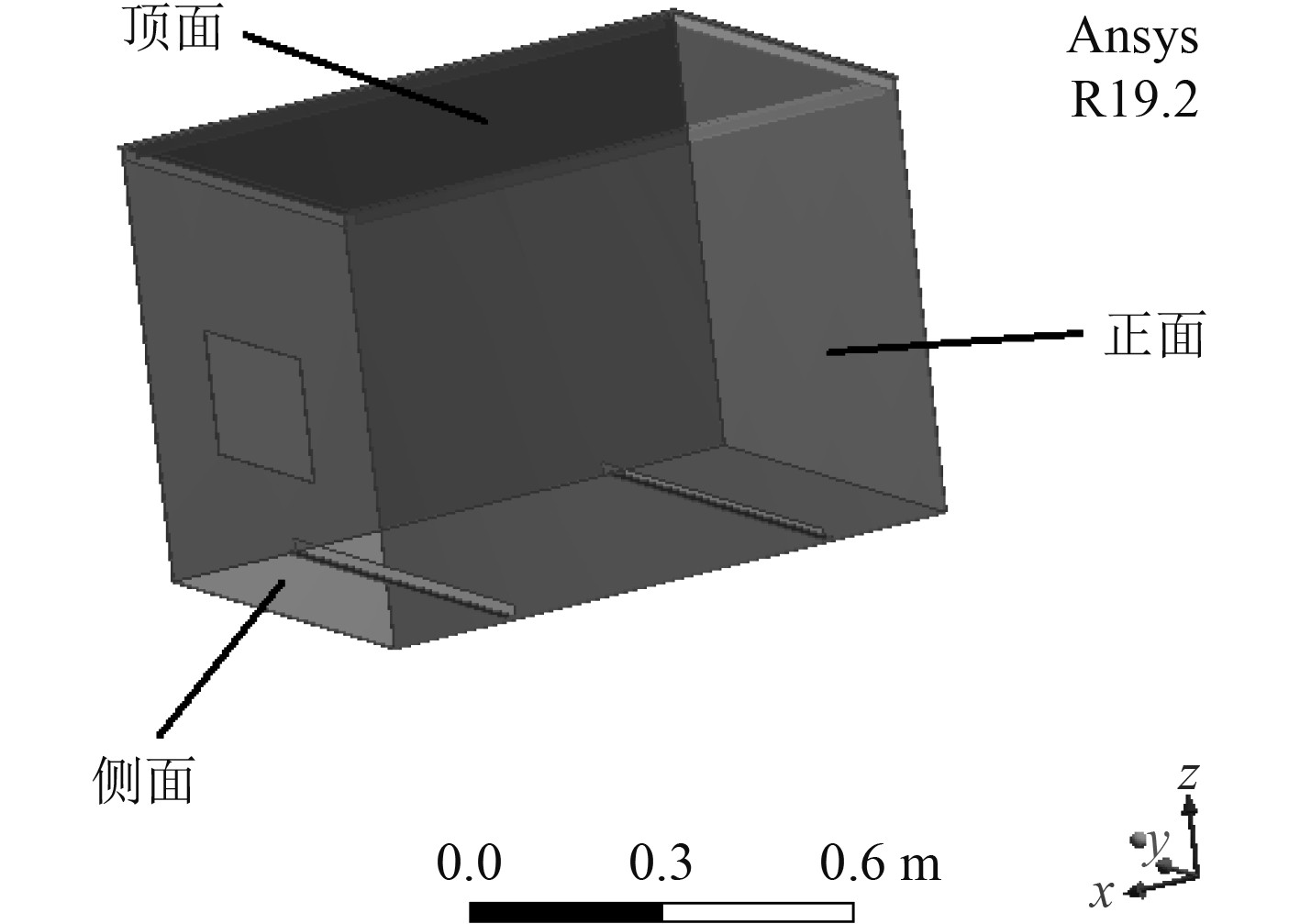
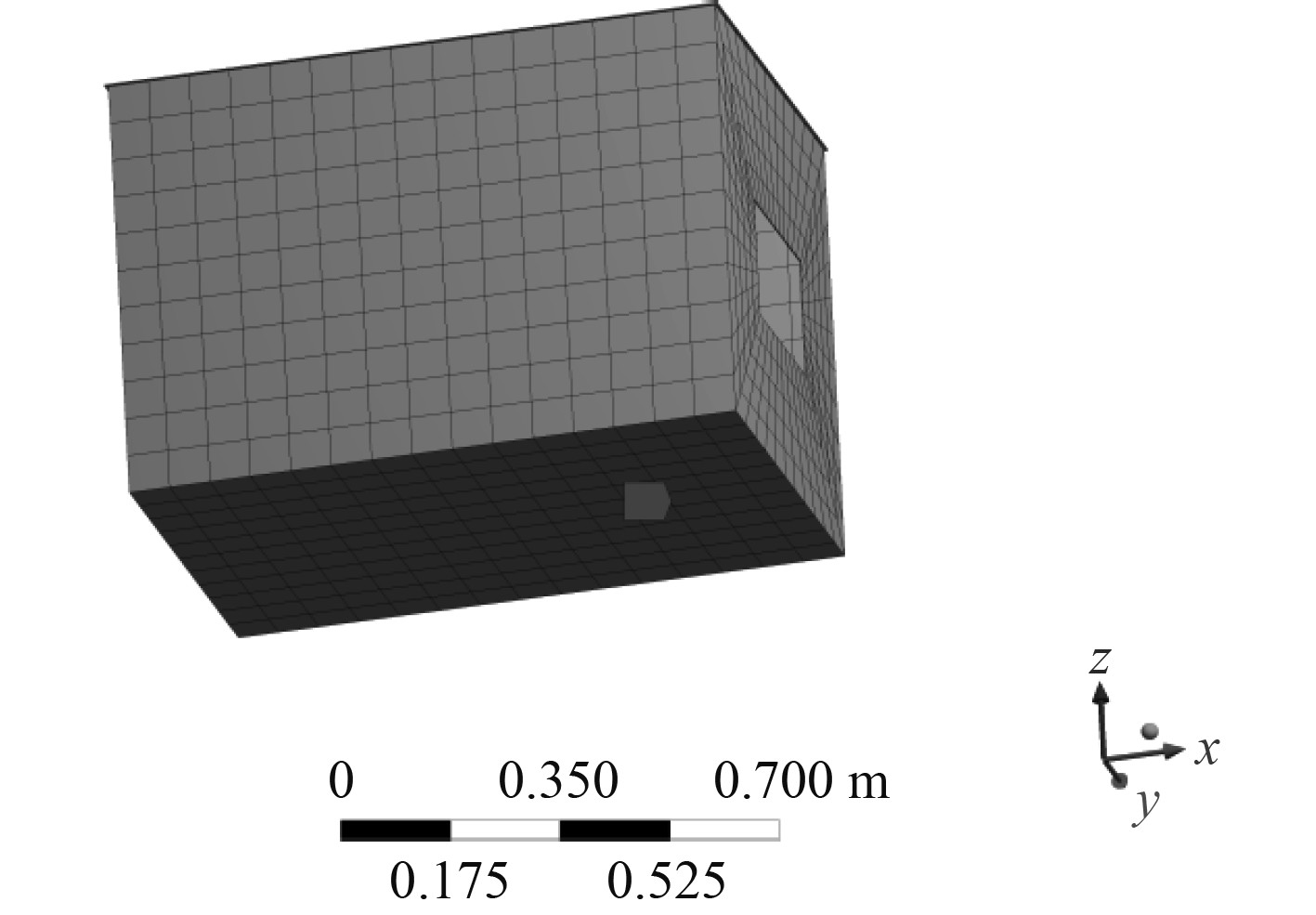
采用Solidworks对舱室建立三维实体模型,如图1所示。由于该模型厚度相对于特征尺寸较小且壳单元专门模拟薄壁结构[12],所以采用壳单元进行有限元建模,利用Ansys Workbench将舱室底部实行固定约束,进行模态分析,舱室有限元模型如图2所示。舱室有限元模型尺寸为1 m × 0.7 m × 0.7 m,围板厚度0.002 m。该舱室的材料为铝合金,其主要参数为:密度2770
|
图 1 舱室三维模型 Fig. 1 3D model of cabin |
|
图 2 舱室有限元模型 Fig. 2 Finite element model of cabin |
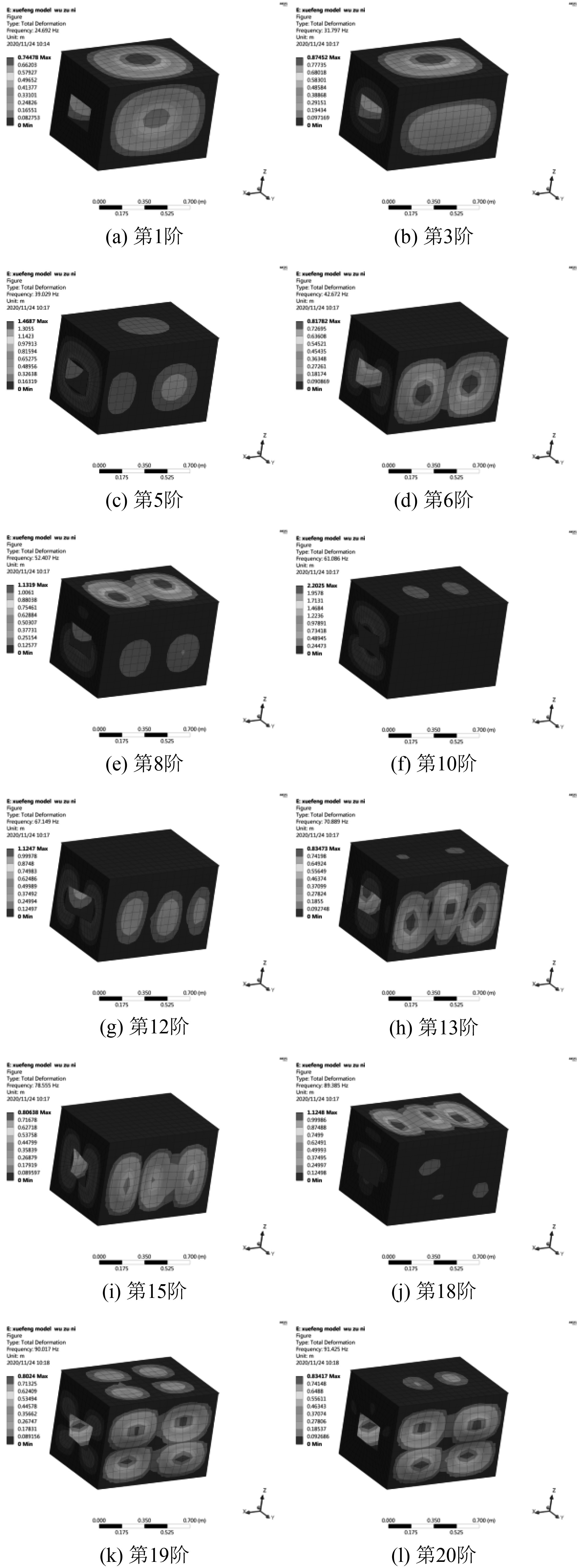
通过Ansys Workbench的模态分析,求得舱室的模态参数,计算得出的前20阶固有频率如表1所示,部分振型如图3所示。
|
|
表 1 舱室固有频率计算结果 Tab.1 Calculation result of cabin natural frequency |
|
图 3 舱室部分振型图 Fig. 3 Cabin vibration mode |
由表1可知,舱室的前20阶固有频率范围在24~92 Hz,除了第8阶和第9阶、第14阶和第15阶、第16阶和第17阶固有频率间隔分别为6.392 Hz,6.922 Hz,6.631 Hz外,其他频率间隔均在6 Hz之内,而且没有出现重根模态,比较符合网壳结构的近频模态特征[13]。从图3振型结果可以看出,舱室的模态振型主要以舱室面的鼓胀为主,第1阶~第5阶舱室的正面、侧面和顶面均有波数为1的鼓胀;第6阶~第12阶主要以舱室各面波数为2的鼓胀且左右鼓胀和上下鼓胀的情况均有出现;从第13阶到第18阶出现正面和顶面波数为3的鼓胀且鼓胀类型为左右鼓胀;第19阶和第20阶为波数为4的正面鼓胀。随着固有频率阶数的增加,对应的振型呈现由简单到复杂的趋势。
3 舱室模态及阻尼比试验对舱室进行扫频试验,振动系统设置参数为:扫频范围15~100 Hz,传感器灵敏度10.14 mV/g,加速度激励1 g,振动系统最大自检电压3 V,获得舱室频响曲线如图4所示。

|
图 4 舱室频响曲线图 Fig. 4 Frequency response curve of cabin |
可以看出,舱室频响函数曲线各个峰值比较清楚,通过试验测得舱室固有频率如表2所示。
|
|
表 2 舱室固有频率试验结果 Tab.2 Test result of cabin natural frequency |
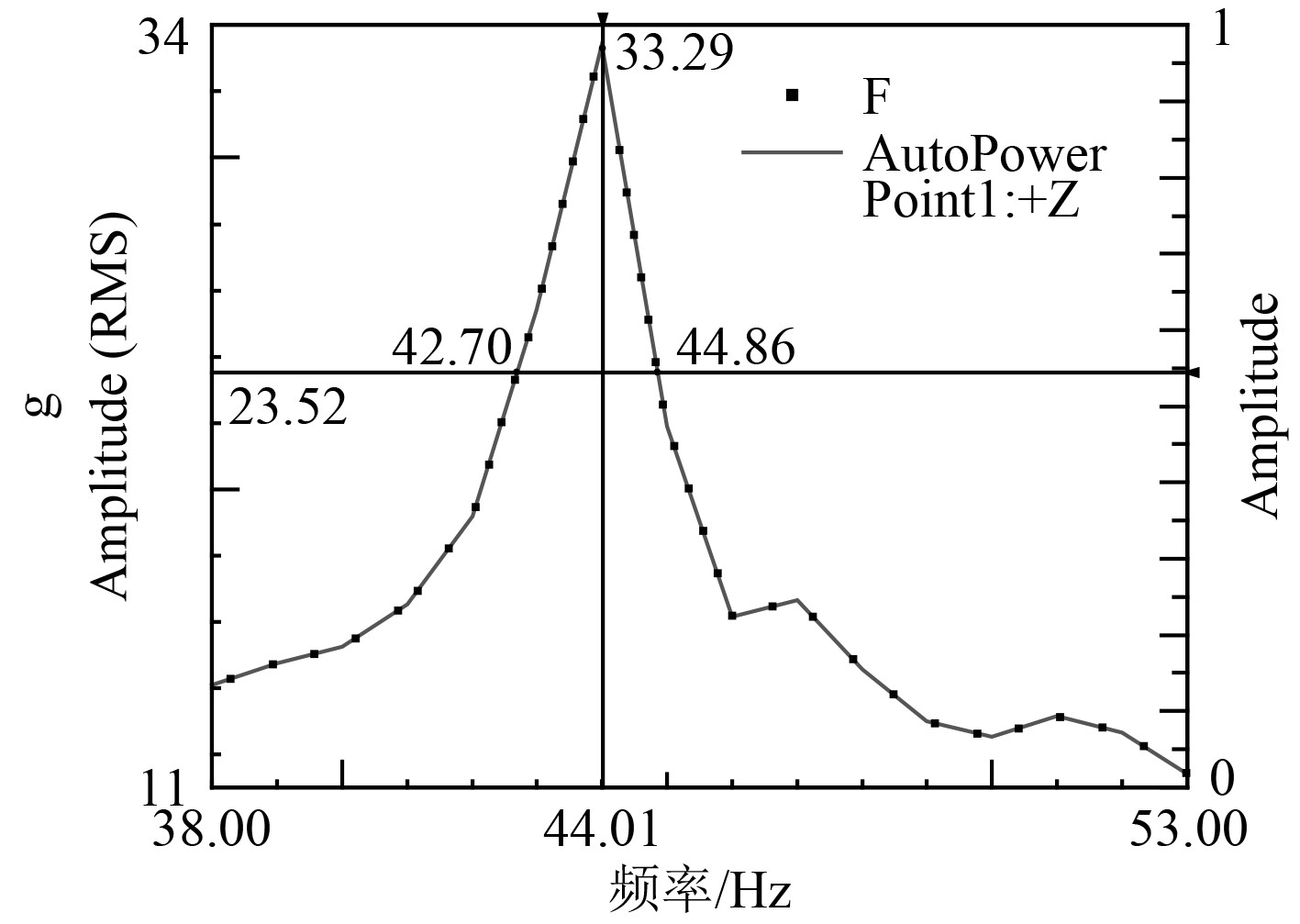
利用图4测得的频响函数曲线图,根据半功率带宽法计算舱室阻尼比。
|
图 5 半功率带宽法计算阻尼比 Fig. 5 Calculation of damping ratio by half power bandwidth method |
分别对舱室进行有限元模态分析和模态试验,将二者的数据进行对比,列出前6阶模态结果如表3所示。
|
|
表 3 有限元结果和仿真结果对比 Tab.3 Comparison of finite element results and simulation results |
可以看出,除了第3阶计算误差在5.84%之外,其余各阶误差均在5%之内,说明有限元仿真计算的固有频率和试验测得的频率吻合良好。一般来说,计算值和试验值的误差在10%范围之内是可以接受的。分析其误差产生的主要原因可能有以下几点:1)有限元建模时忽略了实际舱室结构上的螺栓孔、门把手等一些细节,使得有限元模型和实际情况有细小差别;2)舱室结构焊接部位在有限元分析中采用了共节点的方式,与实际情况略有不同;3)试验中难以避免的测量和分析误差。
5 粘弹性阻尼层对舱室振动特性的影响采用DFM自由阻尼层对舱室的减振特性进行研究。DFM阻尼属性为:厚度3 mm,密度1450
|
|
表 4 DFM阻尼参数(20℃) Tab.4 DFM damping parameters(20℃) |
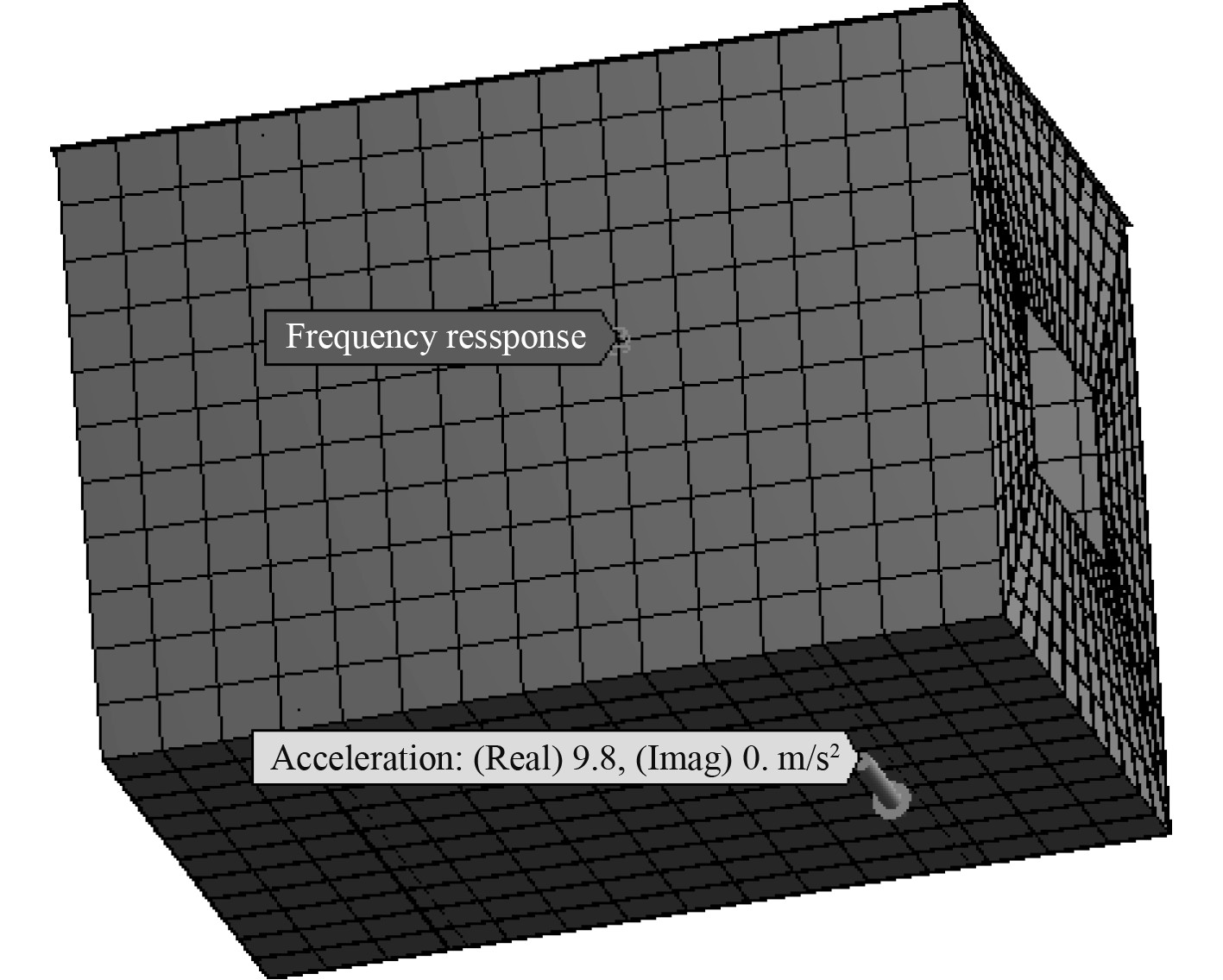
对敷设粘弹性层舱室前后进行谐响应分析。由于前文计算出的舱室固有频率范围在100 Hz以内,因此设置频率范围为0~100 Hz,求解间隔设置为50,在舱室底部施加沿Y方向,大小为1 g的基础激励,由于粘弹性材料属性随频率变化而变化,因此在有限元分析软件中插入命令定义粘弹性材料属性,在舱室正面取一个拾振点,如图6所示。由于Y方向为激励加载方向,故此方向的响应幅值最大,X和Z方向的位移响应可不考虑。通过谐响应分析得出敷设粘弹性层前后Y方向上的频响曲线图,如图7所示。
|
图 6 粘弹性舱室有限元模型 Fig. 6 Finite element model of cabin with viscoelastic layer |
|
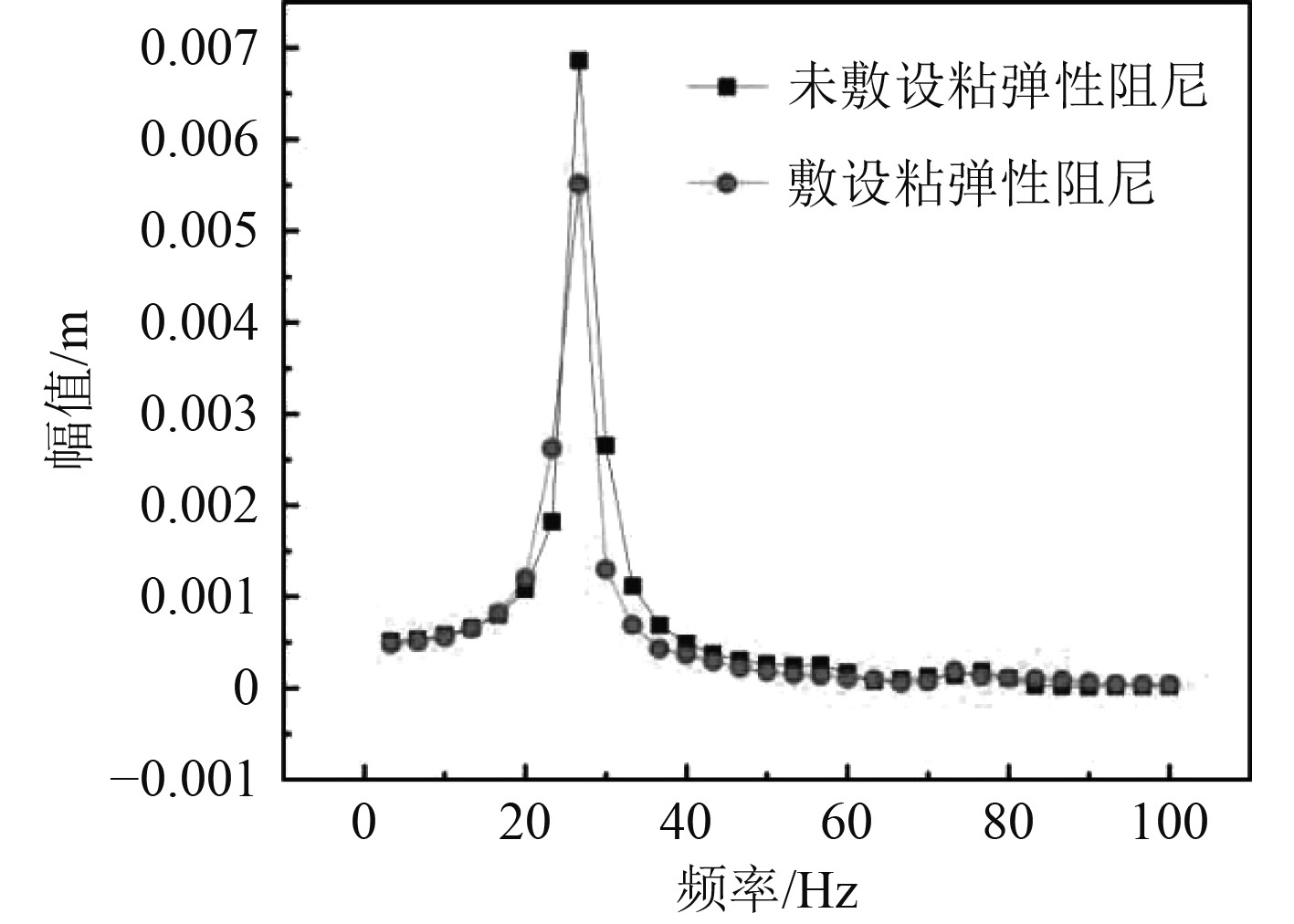
图 7 贴敷粘弹性层前后舱室频响曲线对比 Fig. 7 Comparison of frequency response curves of cabins with or without viscoelastic layer |
可知,当激励频率为28 Hz时,黏贴阻尼层前后舱室的振动响应均达到最大值,既舱室的第2阶固有频率附近容易发生共振,黏贴阻尼前后舱室最大振动响应分别为6.86 mm和5.51 mm,同比下降了19.6%,说明该粘弹性阻尼层对舱室有明显减振效果。
6 结 语本文建立了舱室的有限元仿真模型,从仿真和试验2个方面对舱室进行了振动特性分析,考虑粘弹性材料的频变特性,基于谐响应分析分别对敷设粘弹性层前后进行分析并得出以下结论:1)有限元计算的舱室固有频率和试验测得的固有频率二者吻合良好,验证了有限元模型的正确性;2)舱室的振型主要以舱室面的鼓胀为主,第2阶模态为对舱室振动特性影响最大的模态,最大振幅出现在舱室正面中心区域;3)敷设粘弹性层后舱室减振明显,说明该粘弹性阻尼层能够有效抑制舱室在基础激励下的响应。
| [1] |
陈越澎, 谭林森. 船舶舱室噪声控制技术综述[J]. 武汉造船, 1995: 34−40.
|
| [2] |
宋现国, 赵日定. 海工船舱室噪声控制技术探索[J]. 船舶工程, 2015, 37(12): 82-86. |
| [3] |
吴硕. 46 m海洋工作船振动特性分析[D]. 大连: 大连理工大学, 2012.
|
| [4] |
王啸宇, 成磊. 全船振动分析等效建模方法[J]. 噪声与振动控制, 2020, 40(4): 190−193.
|
| [5] |
李良碧, 王国治, 温华兵. 舰船浮筏隔振特性的有限元分析及试验研究[J]. 华东船舶工业学院学报, 2001, 15(2): 72-76. |
| [6] |
乔志, 褚夫强, 渠鸿飞, 等. 敷设约束阻尼层舱室振动噪声特性的试验与仿真对比[J]. 材料开发与应用, 2014, 29(3): 14-20. |
| [7] |
梁炳南. 船舶浮动舱室振动和声学性能研究[D]. 大连: 大连海事大学, 2016.
|
| [8] |
仇远旺, 章炜, 郑发彬, 等. 船舶模型阻尼减振试验研究[J]. 工程与试验, 2010, 50(4): 22-23,77. DOI:10.3969/j.issn.1674-3407.2010.04.008 |
| [9] |
温华兵. 复杂薄壳结构振动声辐射特性及控制技术研究[D]. 镇江: 江苏大学, 2014.
|
| [10] |
王国庆. 海洋工程舱壁结构减振降噪问题研究[D]. 青岛: 中国海洋大学, 2013.
|
| [11] |
刁杰胜, 刘文慧, 尹杨平. 白车身固有振动特性CAE及试验分析对比[J]. 井冈山大学学报(自然科学版), 2019, 40(2): 72-76. |
| [12] |
周炬, 苏金英. ANSYS Workbench有限元分析实例详解[M]. 北京: 人民邮电出版社, 2017.
|
| [13] |
王卓. 网壳结构的模态局部化现象及其影响[M].北京: 中央广播电视大学出版社, 2015.
|
| [14] |
闫凯, 宋庆军, 孙秋香, 等. 正弦振动试验及其相关参数的计算[J]. 实验室科学, 2013, 16(6): 43-44,47. |
 2022, Vol. 44
2022, Vol. 44

