2. 海军研究院,北京 100161
2. Naval Research Academy, Beijing 100161, China
当前,决策部门对远海方向大型舰船动态情报信息需求迫切,需要实时掌握国外主要大型舰船的位置、活动等情报信息,并能够准确判断其未来的动向。航天侦察信息能够提供大型舰船的当前状态信息,但仅凭航天侦察信息很难推断出其未来的动向。互联网大数据、人工智能技术以及数据挖掘技术的快速发展为侦察情报提供了更多手段。航天侦察信息加上互联网大数据,经过人工智能算法处理以及数据挖掘,可以从大量碎片化、静态数据中挖掘出大型舰船的动态信息,为指挥决策提供辅助。
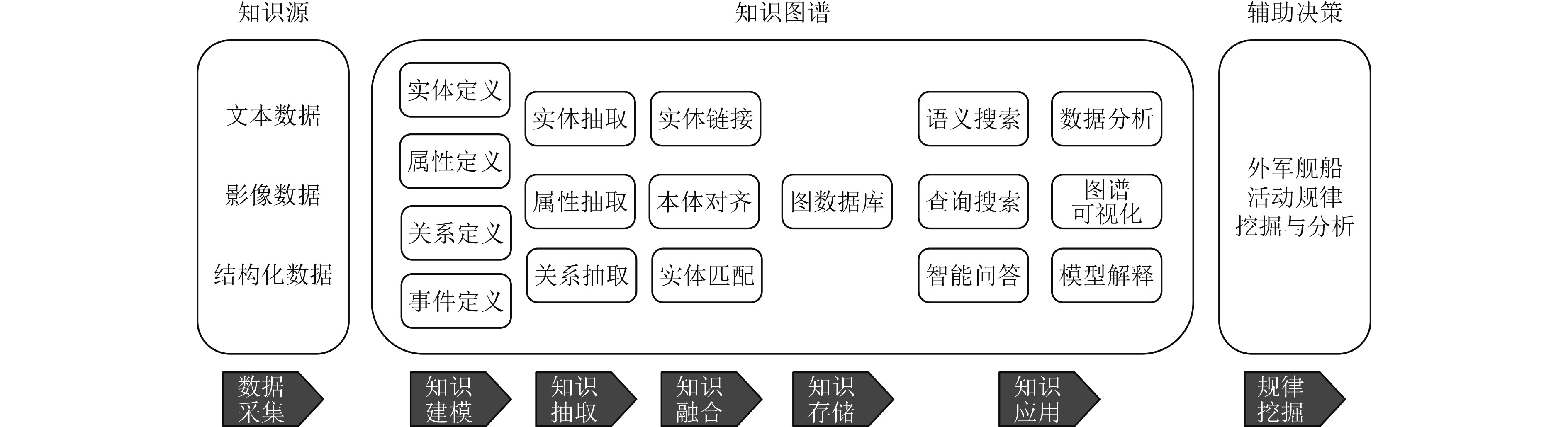
1 舰船活动规律知识图谱分析系统框架舰船活动规律知识图谱系统由3个部分组成:数据采集模块、知识图谱构建模块和规律挖掘模块。数据采集模块采集的数据包括来自互联网和其他渠道的文本数据、结构化数据和来自卫星的影像数据。知识图谱构建模块主要是构建舰船活动知识图谱,包括舰船知识建模、知识抽取、知识融合、知识存储和知识应用[1]。规律挖掘模块主要包括舰船活动规律挖掘与分析及图形化展示。系统框架如图1所示。
|
图 1 舰船活动规律知识图谱分析系统框架图 Fig. 1 The framework diagram of the knowledge map analysis system for the laws of ship activity |
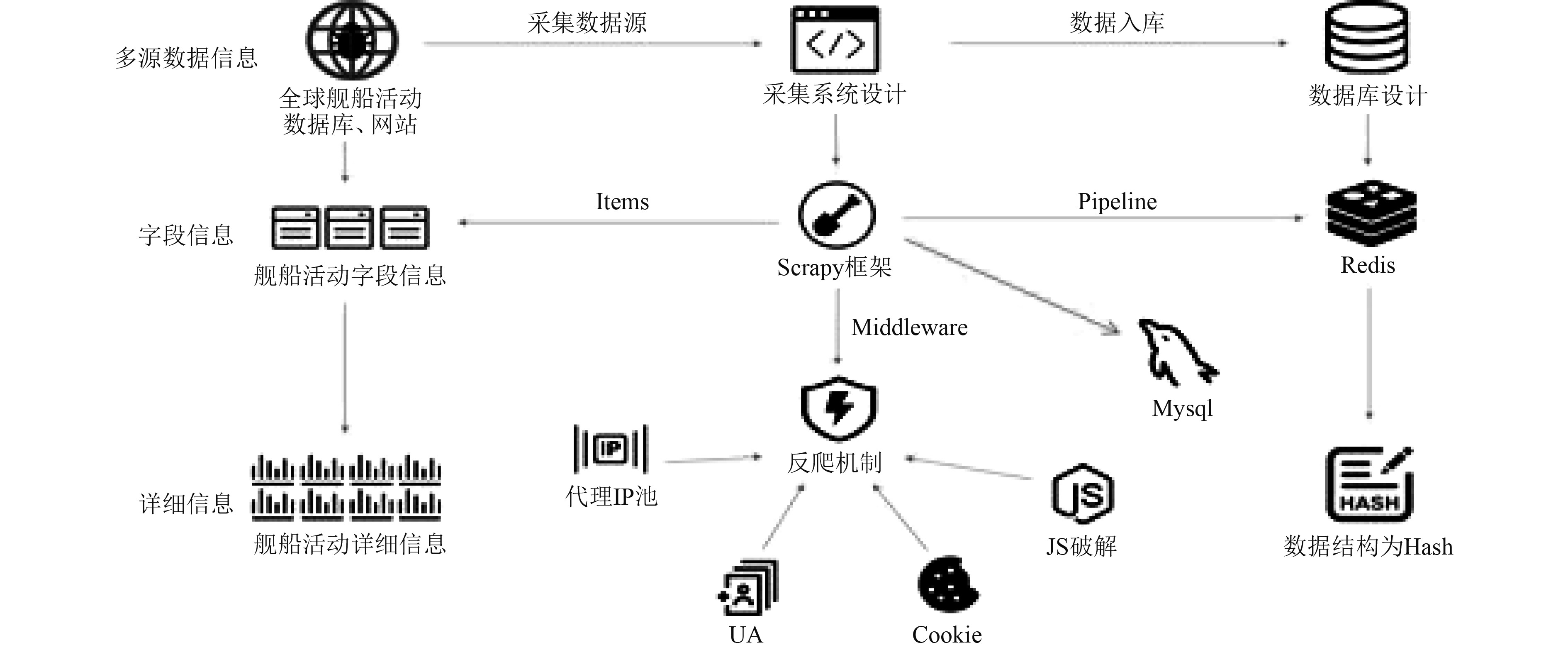
数据采集模块采用模块化、组件化的设计模式设计数据的采集、解析、存储功能单元,利用爬虫框架Scrapy、分布式内存数据库Redis、列式数据库Hbase、文件存储服务FastDFS等,实现文本的采集、存储等功能。数据采集模块示意图如图2所示。
|
图 2 数据采集模块示意图 Fig. 2 Schematic diagram of data acquisition module |
采集器对分布在全球的军事类数据库、舰船活动数据库、网站、社交媒体等进行数据采集。采用分布式集群采集模式对数据进行采集,并对原始数据进行存储。为了获取数据,本文采用一些技术策略抵消“反爬虫”,如设置下载延迟,延迟时间越长则越不容易被阻止;禁止Cookie,防止网站通过Cookie识别用户身份,禁用后使得服务器无法识别爬虫轨迹;使用user agent池,也就是每次发送的时候随机从池中选择不一样的浏览器头信息,防止暴露爬虫身份等。
数据采集主要来自以下数据源:
1)Vessel Database。数据库中不同类型的船共有493720条,军事类的2120条。数据内容包括舰船的特征、位置信息、航行信息、图片、地图、新闻等。
2)Marine Traffic Data。数据库中6种不同类型的船只共500条,数据内容包括船只的图片、活动信息,位置信息以及IMO,name,Vessel Type,MMSI,length,width等特征。
3)Fleetmon Vessels Database。数据库中和军事类型相关的舰船信息共4280条,数据内容包括图片、新闻,以及船只的IMO,name,Vessel Type,MMSI,length,width等基本信息。
4)MyShipTracking Vessel Database。数据库中不同类型船只的记录共30625条,数据内容包括船只的图片、位置信息、航行信息、停靠口岸、活动以及IMO,name,Vessel Type,MMSI,length,width等基本信息。
5)公开数据集:AIS Vessel Traffic Dataset。数据集的数据包含了2009年~2017年沿海水域的船只情况。数据根据月份对不同海域进行记录。数据为csv类型,船只的实体和属性包括了MMSI,BaseDateTime,LAT,LON,SOG,COG,Heading,VesselName,IMO,CallSign,VesselType,Status,Length,Width,Draft,Cargo,TransceiverClass。数据没有提供图像信息。
6)军事类信息网站包括军事新闻类信息。太平洋舰队:
舰船活动规律知识图谱构建是根据舰船领域专业知识,构建一个垂直领域的知识图谱,主要包括知识建模、知识抽取、知识融合、知识存储等步骤。
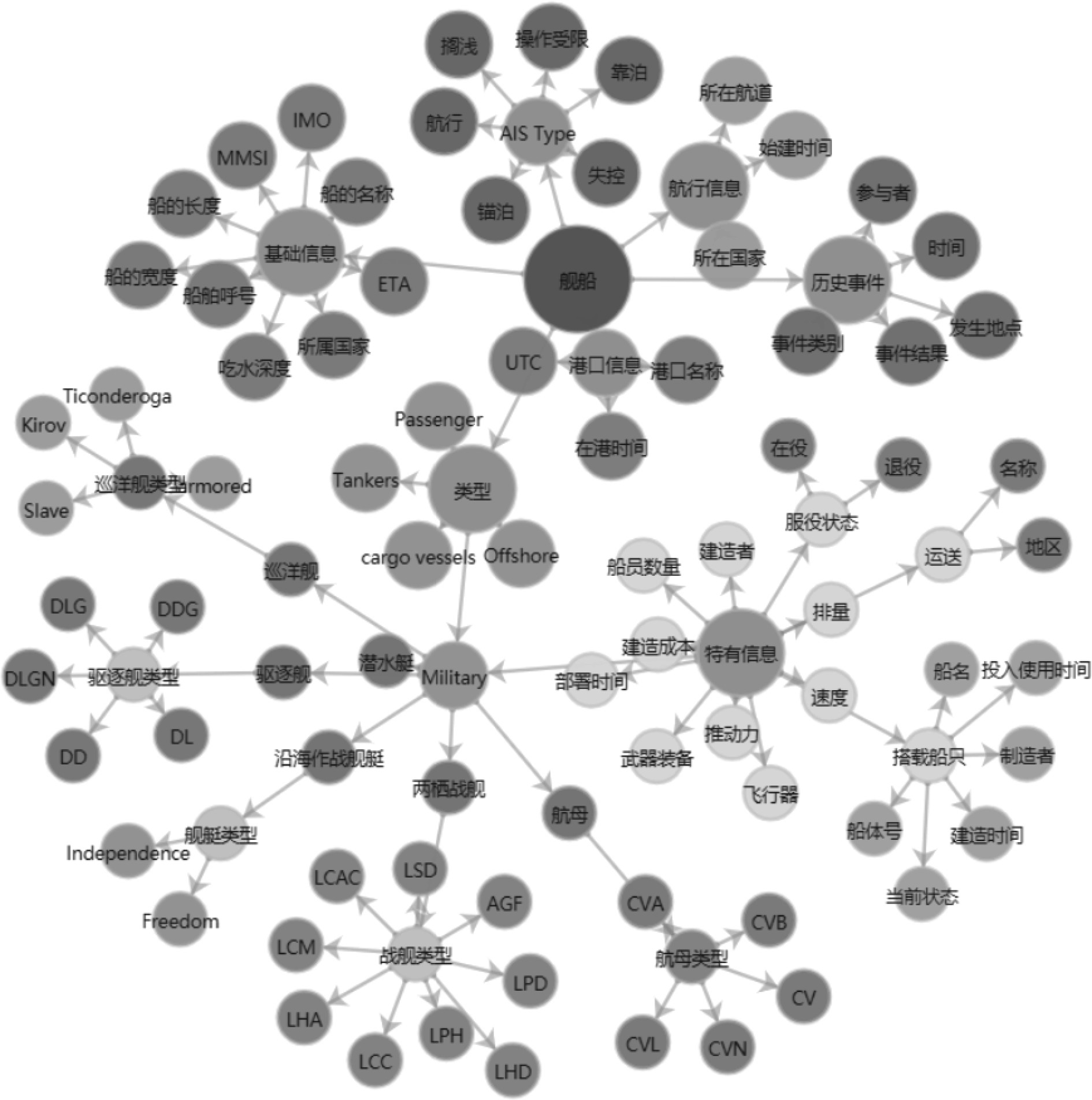
3.1 知识建模知识建模是按照知识图谱约定的一些模式进行业务抽象以及业务建模,在本文中主要是指对外军舰船活动数据中的文本内容进行实体、实体属性、实体属性值类型、实体关系等的定义[2]。构建舰船知识图谱,主要包括以下5个步骤:
1)以节点(概念)为主体目标,实现对不同来源的数据进行映射与合并(确定节点);
2)利用属性来表示不同数据源中针对节点的描述,形成对节点的全方位描述(确定节点属性、标签);
3)利用关系来描述各类抽象建模成节点的数据之间的关联关系,从而支持关联分析(图设计);
4)通过节点链接技术,实现围绕节点的多种类型数据的关联存储(节点链接);
5)使用事件机制描述客观世界中动态发展,体现事件与节点间的关联,并利用时序描述事件的发展状况(动态事件描述)。
舰船图谱的设计如图3所示。
|
图 3 舰船图谱设计 Fig. 3 Ship map design |
知识抽取是指从多种来源及多种结构的数据中提取实体、属性以及实体间的相互关系,并将它们存入到知识图谱数据库。构建出实体、属性及它们之间的关系之后就可以形成本体化的知识表达[3]。针对不同种类的数据,需利用不同的技术。结构化数据可通过采用ETL工具进行重新组织、清洗、检测,最后得到符合使用目的的数据;抽取非结构化文本数据主要包括:实体抽取、关系抽取和属性抽取[4]。
3.3 知识融合知识融合指的在不同的数据集中找出同一个实体的描述记录,实现对不同数据源中的信息整合,形成更加全面的实体信息。知识融合过程指的是对舰船信息抽取获得的实体/关系/属性数据进行清洗与整理,以减少冗余和错误,并构建数据间的逻辑与层次[5]。知识融合包括实体对齐和实体消歧两部分。
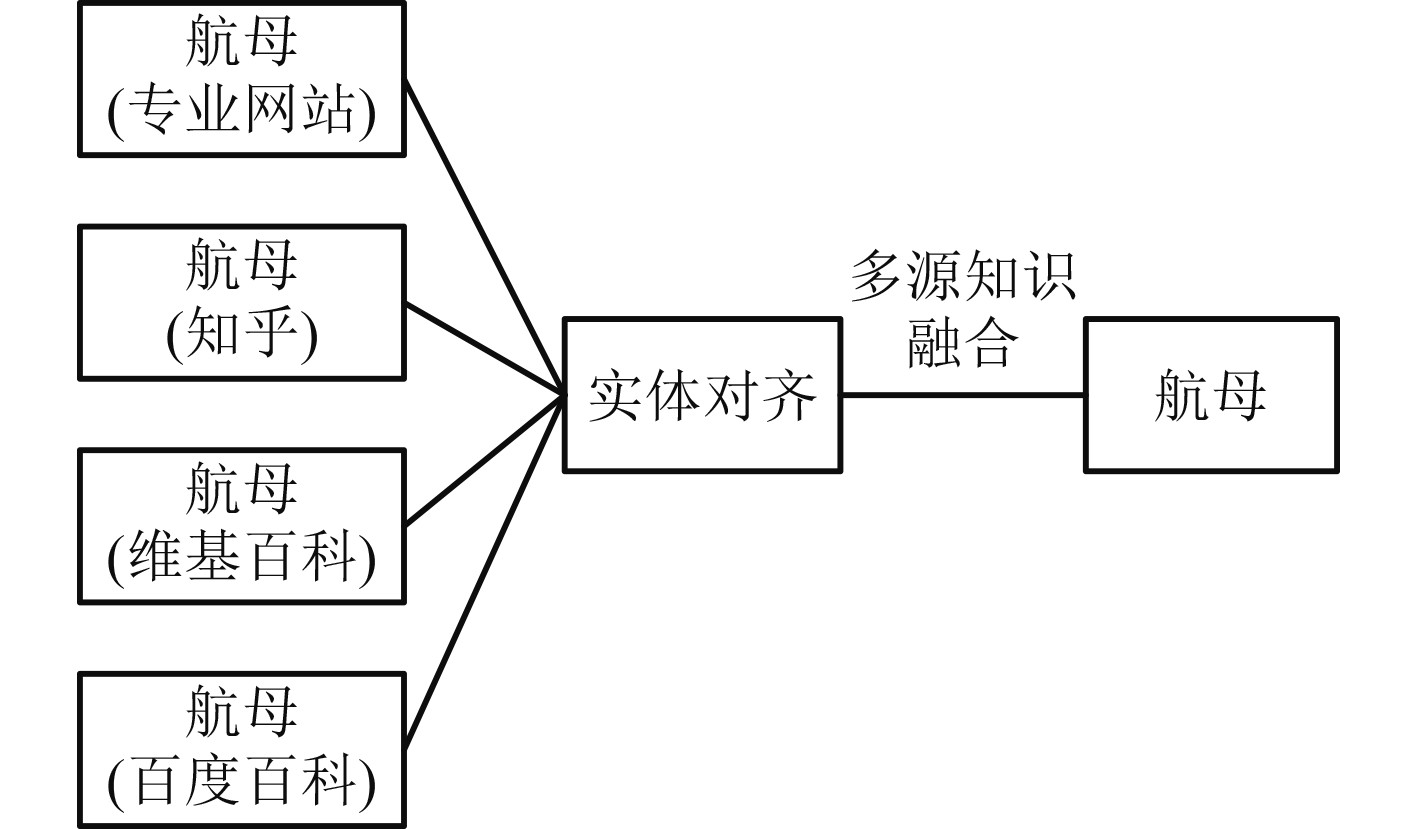
1)实体对齐
实体对齐是判断2个或多个实体是否为同一实体,将具有相同指称的命名实体聚集到一起[6],通过相似度计算等算法把聚集的实体融合的过程。在各类舰船文本数据源中,国家、舰船名称、舰船种类、制造厂、母港和区域等各类实体的表述是多样化的,舰船实体中英文混合、简写、缩写以及国际标准量等不规范表述以及实体的上下文指代不明给实体链接带来了极大困难。如图4中的“航母”融合了多个网站来源的实体信息,实体对齐要尽量聚集实体信息,包括实体的指称、属性、关系以及所属类别等,使实体代表的信息更准确,通过相似度算法在指向相同的实体之间构建对齐关系。实体对齐要解决的问题是尽量避免实例以及关系的冲突问题。
|
图 4 实体对齐示意图 Fig. 4 Schematic diagram of entity alignment |
2)实体消歧
实体消歧是根据上下文信息实现并消除一词多义的歧义现象。实体消歧用于解决同名舰船实体产生歧义问题,通过实体消歧,可以根据语境准确建立实体链接,把具有歧义的命名性指称项映射到其实际所指的实体概念上去。本文主要采用聚类算法实现实体消歧。例如,实体名“航母”可能指的是“福特”号类别中的“航母”,也可能指的是“企业”号类别中的“航母”。实体消歧就是要根据上下文相关信息进行歧义消解。例如通过上下文包含的“核动力”信息确认它是“福特”号航母,其结果为“福特”号航母。
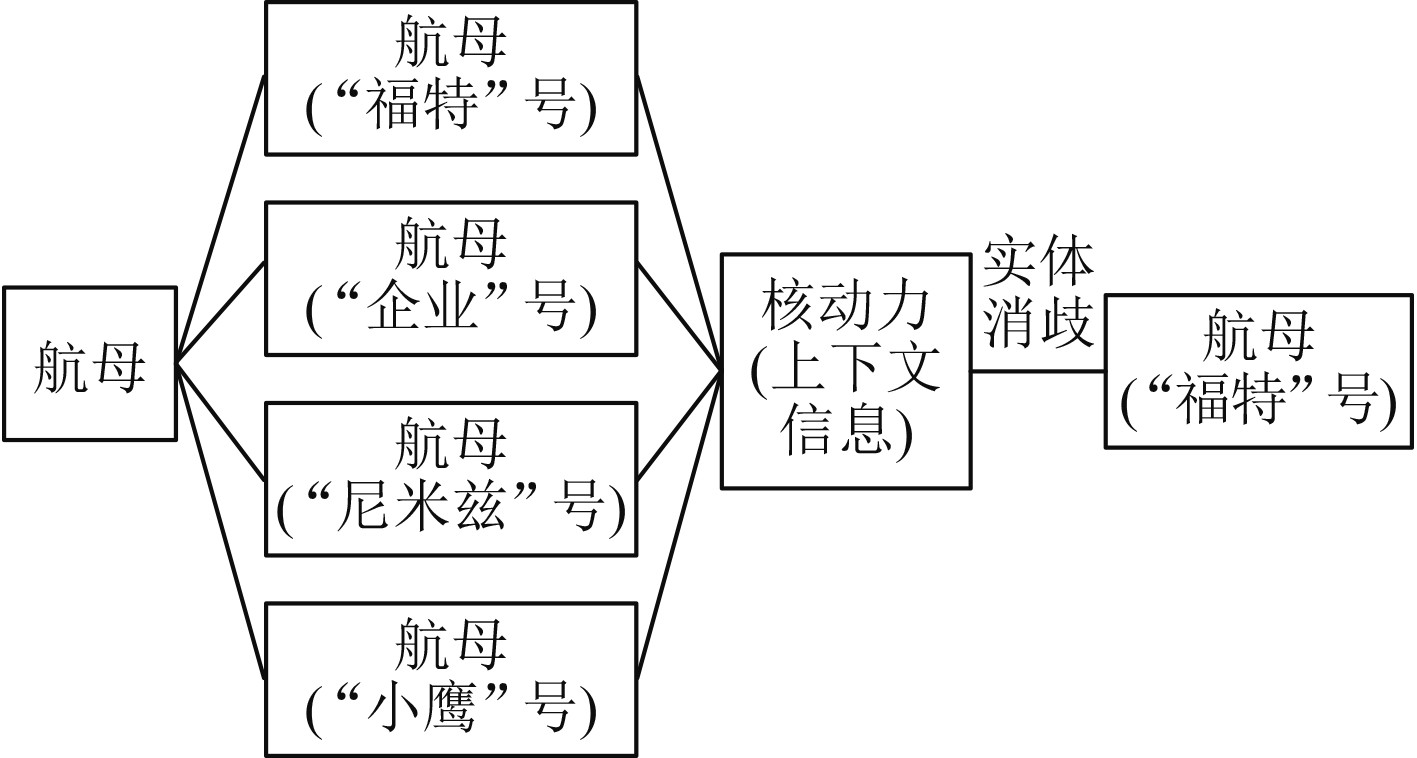
|
图 5 实体消歧示意图 Fig. 5 Schematic diagram of entity disambiguation |
知识图谱通常采用图数据库的方式存储知识。以“图”这种数据结构存储和查询数据非常适合知识图谱。图数据库的数据模型主要是以节点和关系(边)来体现,也可以处理键值对,优点是快速解决复杂的关系问题[7]。
研究中使用了Neo4j进行数据存储。Neo4j[8]是一个高性能的图形数据库。通过Neo4j可以直观呈现实体间的各种关系(见图6),可为舰船活动规律挖掘,信息服务提供更易于理解和交互的知识呈现方式。
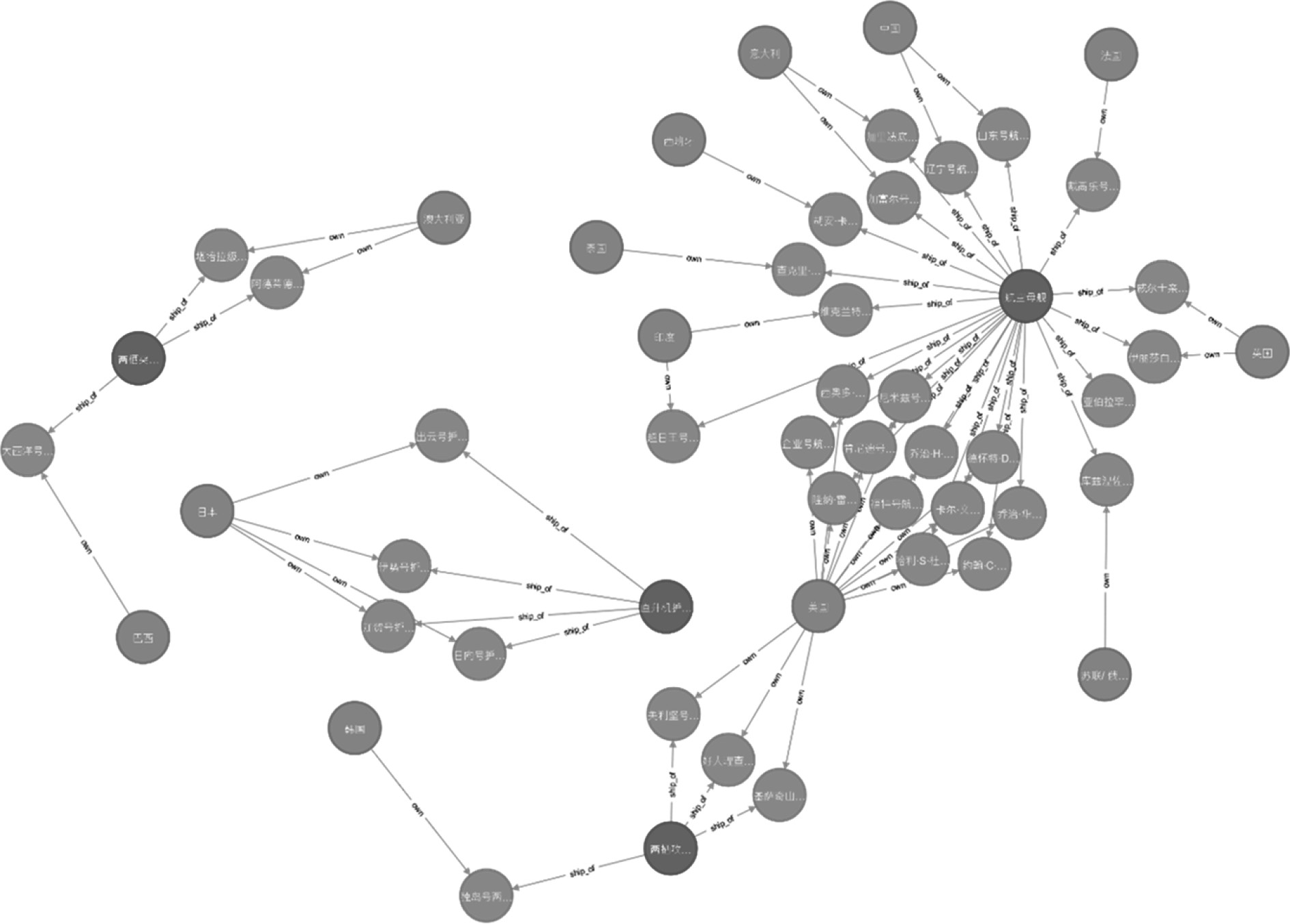
|
图 6 Neo4j数据库存储的部分舰船信息 Fig. 6 Part of ship information stored in Neo4j database |
知识应用主要包括:语义搜索、查询搜索、智能问答、数据分析、图谱可视化和模型解释,根据具体的需求调用相应模块。
4 舰船活动规律挖掘算法设计舰船活动知识图谱存储了大量的舰船事件信息,包括发生时间、地点、事件的结果等,利用数据挖掘技术可以进一步发现蕴含其中的更深层次信息。
模糊C均值聚类(FCM)是一种被证明非常适合处理数据挖掘问题的聚类。根据模糊聚类框架,每个聚类都是一个模糊集,模糊集中的每个数据都有一个与每个聚类相关联的隶属度值,范围在0~1之间,衡量数据属于该特定聚类的程度。FCM提供了一种方法,给出了如何将填充在某些多维空间的数据点分组为特定数量的不同集群[9]。该方法通过迭代产生最佳c分区并计算聚类中心,生成类成员矩阵。假设一个数据集包含紧凑的、分离良好的集群,模糊C均值聚类算法的目标有2个:1)找出这些簇的中心;2)确定数据集中每个点的聚类(即标签)。基于集群紧凑且分离良好的假设,一旦完成了第一个目标,就可以轻松实现第二个目标。给定聚类中心,数据集中的一个点属于中心最近的聚类,即
| $ {x_i} \in {c_j},\quad {\rm{if}}\,\left\| {{x_i} - {v_j}} \right\| < \,\left\| {{x_i} - {v_k}} \right\|,\quad k = 1,2,c,k \ne j,$ |
其中
通常模糊C均值从对聚类中心的初始猜测开始,旨在标记每个聚类的平均位置。这些聚类中心的初始猜测很可能是不正确的。此外,模糊C均值为每个数据点分配每个集群的成员等级。通过迭代更新每个数据点的聚类中心和成员等级,模糊C均值迭代地将聚类中心移动到数据集中的正确位置。此迭代基于最小化目标函数,该目标函数表示从任何给定数据点到由该数据点的成员等级加权的聚类中心的距离[10]。模糊C均值聚类的输出是一个聚类中心列表和每个数据点的几个成员等级。可以使用模糊C均值聚类返回的信息通过创建隶属函数来表示每个聚类的模糊质量帮助构建模糊推理系统。
舰船活动规律挖掘采用最小化广义最小二乘误差函数算法:
| $ {J_{FCM}} = \sum\limits_{i\,j} {} {\sum\limits_{k = 1}^c {{u_k}(i,j)} ^q}{\left\| {F(i,j) - {v_k}} \right\|^2} 。$ | (1) |
其中:F(i,j)={f11, f12, f13···,fnn}
模糊分割通过如下所示目标函数的迭代优化来执行,更新成员函数Uk(i,j) 和聚类中心Vk为:
| $ {U_k}(i,j) = {\left[ {\sum\limits_{n = 1}^c {{{\left( {\frac{{\left\| {F(i,j) - {V_k}} \right\|}}{{\left\| {F(i,j) - {V_n}} \right\|}}} \right)}^{2/(q - 1)}}} } \right]^{ - 1}},\; 1 \leqslant k \leqslant c,$ | (2) |
| $ {V_k} = \frac{{\displaystyle\sum\limits_{i,j} {{U_k}{{(i,j)}^q} \times F(i,j)} }}{{\displaystyle\sum\limits_{i,j} {{U_k}{{(i,j)}^q}} }},\; 1 \leqslant k \leqslant c。$ | (3) |
以上迭代将在||Uk+1−Uk||<ε时停止,其中ε是终止标准,在0~1之间,k是迭代次数。该过程收敛到FCM的局部最小值或鞍点。该算法由以下步骤组成:
1)初始化Uk(i,j)=[u(i,j)]矩阵
2)在k步用 Uk计算中心向量v(k)=[vk]
| $ {V_k} = \frac{{\displaystyle\sum\limits_{i,j} {{U_k}{{(i,j)}^q} \times F(i,j)} }}{{\displaystyle\sum\limits_{i,j} {{U_k}{{(i,j)}^q}} }},\;\; 1 \leqslant {\rm{k}} \leqslant c。$ |
3)更新Uk , Uk+1
| $ {U_k}(i,j) = {\left[ {\sum\limits_{n = 1}^c {{{\left( {\frac{{\left\| {F(i,j) - {V_k}} \right\|}}{{\left\| {F(i,j) - {V_n}} \right\|}}} \right)}^{2/(q - 1)}}} } \right]^{ - 1}},\; 1 \leqslant k \leqslant c。$ |
如果||Uk+1−Uk||<ε ,那么停止,否则回到步骤2。
假设有一个包含6个点的数据集,每个点都有2个特征F1和F2。列出表1中的数据集。假设要使用FCM将数据集划分为2个簇(即参数c=2),假设将FCM中的参数q设置为2,初始样本为v1=(5,5)和v2=(10,10)。
数据集在两维空间的分布如图7所示。
|
|
表 1 数据集 Tab.1 Data set |
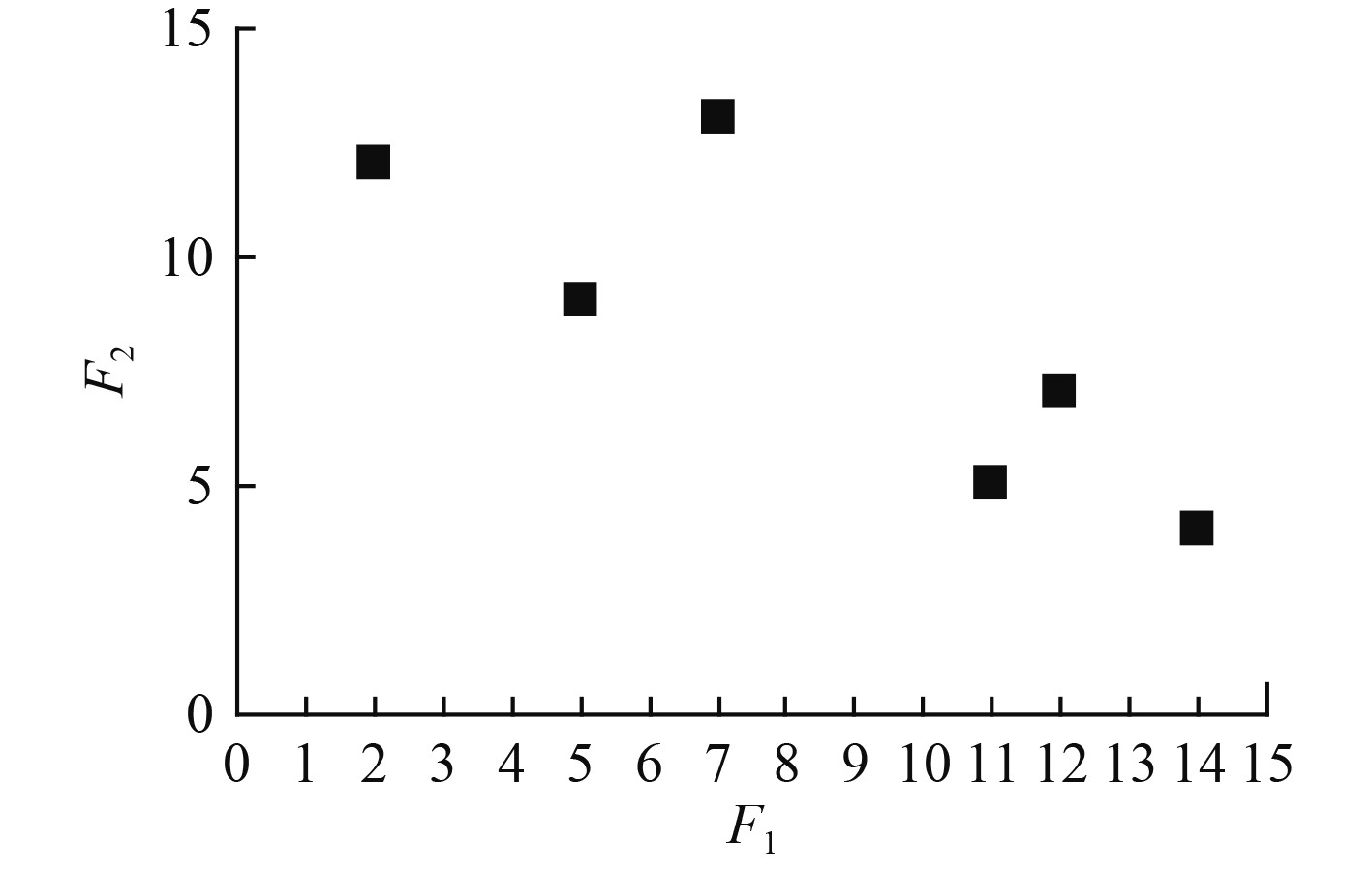
|
图 7 数据集图例 Fig. 7 Data set legend |
2个簇的初始隶属度函数使用等式(2)计算。
| $ {U_k}(i,j) = {\left[ {\sum\limits_{n = 1}^c {{{\left( {\frac{{\left\| {F(i,j) - {V_k}} \right\|}}{{\left\| {F(i,j) - {V_n}} \right\|}}} \right)}^{2/(q - 1)}}} } \right]^{ - 1}},\; 1 \leqslant k \leqslant c,$ |
| $ {\left\| {F\left( {1,1} \right) - {v_1}} \right\|^2} = {3^2} + {7^2} =58,$ |
| $ {\left\| {F\left( {1,1} \right) - {v_2}} \right\|^2} = {8^2} + {2^2}=68 ,$ |
| $ {\mu _1}\left( {{x_1}} \right) = \dfrac{1}{{\dfrac{{58}}{{58}} + \dfrac{{58}}{{68}}}} = 0.539\;7 。$ |
同样地,可以得到如下结果:
| $ {\mu _2}\left( {{x_1}} \right) = \frac{1}{{\dfrac{{68}}{{58}} + \dfrac{{68}}{{68}}}} = 0.460\;3,{\mu _1}\left( {{x_2}} \right) = \dfrac{1}{{\dfrac{{16}}{{16}} + \dfrac{{16}}{{26}}}} = 0.619\;0, $ |
| $ {\mu _2}\left( {{x_2}} \right) = \dfrac{1}{{\dfrac{{26}}{{15}} + \dfrac{{26}}{{26}}}} = 0.381\;0 , {\mu _1}\left( {{x_3}} \right) = \dfrac{1}{{\dfrac{{68}}{{18}} + \dfrac{{68}}{{68}}}} = 0.209\;3 ,$ |
| $ {\mu _2}\left( {{x_3}} \right) = \dfrac{1}{{\dfrac{{18}}{{68}} + \dfrac{{18}}{{18}}}} = 0.790\;7 , {\mu _1}\left( {{x_4}} \right) = \dfrac{1}{{\dfrac{{36}}{{36}} + \dfrac{{36}}{{26}}}} = 0.419\;4, $ |
| $ {\mu _2}\left( {{x_4}} \right) = \dfrac{1}{{\dfrac{{26}}{{36}} + \dfrac{{26}}{{26}}}} = 0.580\;6 ,{\mu _1}\left( {{x_5}} \right) = \dfrac{1}{{\dfrac{{53}}{{53}} + \dfrac{{53}}{{13}}}} = 0.197, $ |
| $ {\mu _2}\left( {{x_5}} \right) = \dfrac{1}{{\dfrac{{13}}{{53}} + \dfrac{{13}}{{13}}}} = 0.803,{\mu _1}\left( {{x_6}} \right) = \dfrac{1}{{\frac{{82}}{{82}} + \dfrac{{82}}{{52}}}} = 0.388\;1, $ |
| $ {\mu _2}\left( {{x_6}} \right) = \dfrac{1}{{\dfrac{{52}}{{82}} + \dfrac{{52}}{{52}}}} = 0.611\;9。$ |
因此,使用这2个簇的初始样本x1和x2隶属于在第1个簇中的属性更多,而数据集中的其余点隶属于第2个簇中的属性更多。
然后,FCM算法根据式(3)更新样本。
| $\begin{split} {v_1} =& {\dfrac{{\displaystyle\sum\limits_{i,j} {{u_1}{{(i,j)}^q} \times F(i,j)} }}{{\displaystyle\sum\limits_{i,j} {{u_1}{{(i,j)}^q}} }}=}\\ &{\dfrac{{0.539\;7}^{2}\left(2,12\right)+{0.619\;0}^{2}\left(5,9\right)+{0.209\;3}^{2}\left(7,13\right)}{{0.539\;7}^{2}+{0.619\;0}^{2}+{0.209\;3}^{2}+{0.419\;4}^{2}+{0.197}^{2}+{0.388\;1}^{2}} +}\\ &{\dfrac{{0.419\;4}^{2}\left(11,5\right)+{0.197}^{2}\left(12,7\right)+{0.388\;1}^{2}\left(14,4\right)}{{0.539\;7}^{2}+{0.619\;0}^{2}+{0.209\;3}^{2}+{0.419\;4}^{2}+{0.197}^{2}+{0.388\;1}^{2}} =}\\ &{\left(4.388\;8,5.560\;3\right),}\end{split} $ |
| $ \begin{split}{v_2} =& {\dfrac{{\displaystyle\sum\limits_{i,j} {{u_2}{{(i,j)}^q} \times F(i,j)} }}{{\displaystyle\sum\limits_{i,j} {{u_2}{{(i,j)}^q}} }}=}\\ &{\dfrac{{0.460\;3}^{2}\left(2,12\right)+{0.381\;0}^{2}\left(5,9\right)+{0.790\;7}^{2}\left(7,13\right)}{{0.460\;3}^{2}+{0.381\;0}^{2}+{0.790\;7}^{2}+{0.580\;6}^{2}+{0.803}^{2}+{0.611\;9}^{2}}+}\\ &{\dfrac{{0.580\;6}^{2}\left(11,5\right)+{0.803}^{2}\left(12,7\right)+{0.611\;9}^{2}\left(14,4\right)}{{0.460\;3}^{2}+{0.381\;0}^{2}+{0.790\;7}^{2}+{0.580\;6}^{2}+{0.803}^{2}+{0.611\;9}^{2}} =}\\ &{\left(\dfrac{22.213\;5}{2.338\;6},\frac{19.673\;9}{2.338\;6}\right) =\left(9.498\;6,8.412\;7\right) 。}\end{split}$ |
如图8所示,更新后的样本v1移动到更靠近由x1,x2,和x3形成的集群中心,而更新后的样本v2则移动到更靠近由x4,x5 和 x6形成的集群中。
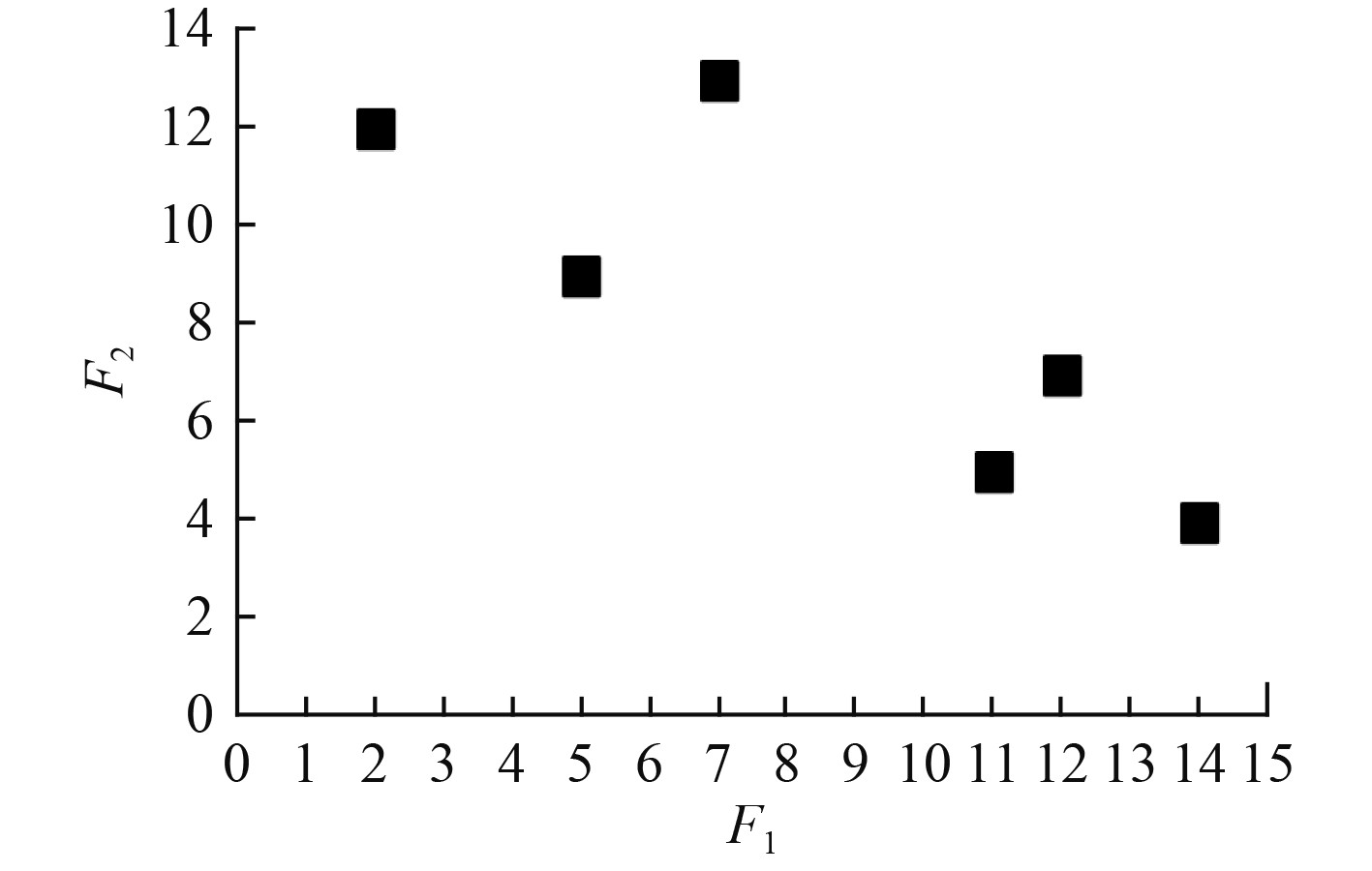
|
图 8 样本更新示意图 Fig. 8 Schematic diagram of sample update |
根据上面的实例可以得出关于FCM算法挖掘舰船规律知识的一些要点:
1)FCM可以找到目标函数Jm的局部极小值(或鞍点),这是因为FCM理论是从一个FCM解的目标函数Jm的梯度应该为0的条件推导出来的;
2)FCM保证在q>1时收敛。可用于数据挖掘[11];
3)FCM应用于给定数据集的挖掘结果不仅取决于参数q和c的选择,还取决于初始样本的选择。
5 系统实现系统开发采用Django框架,该框架用Python语言编写,是遵循MVC模式的开源开发框架,能够开发出功能复杂的带有数据库驱动的网站。
舰船活动规律知识图谱分析系统的主页,展示的是舰船基础信息和统计信息。基础信息给出的是系统收集到的“舰船”节点相关的“服役时间”、“航速”、“下碇时间”、“满载排水量”、“名称”、“级别”、“编制”、“母港”、“舷号”、“满排吨位”、“舰名出处”、“续航距离”、“型宽”、“下水时间”、“动工时间”、“建造厂”、“舰长”等反映舰船基本属性的信息。统计信息给出的是反映舰船分布规律、统计数量、活动次数等反应统计数据的信息。
舰船动态页面,给出的是舰船动态信息,包括某艘舰船当前的活动及与之相关的事件。
关系可视化界面给出某个舰船相关的信息,这部分信息通过查询数据库中的“舰船”节点,输出相关联的“国家”、“舰船种类”、“建造厂”、“乘员与载员”、“母港”、“区域”等。
6 结 语通过研究初步建立了海军垂直领域舰船活动知识图谱,搭建了舰船活动规律知识图谱分析系统。试验表明,系统能够建立概念之间的联系,建立舰船活动及时空事件的关联关系,挖掘一定的舰船活动规律,并能够对舰船活动信息进行多维度画像,具备初步的知识图谱分析能力。下一步将增加信息源网站和航天影像信息,优化图谱计算规则,完善挖掘算法,形成更具实用价值的知识图谱分析系统。
| [1] |
陈成, 陈跃国, 等. 意图知识图谱的构建与应用[J]. 大数据, 2020(6): 57-68. |
| [2] |
PAN JZ, HORROCKS I. RDFS(FA): Connecting RDF(S) and OWL DL[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(2): 192–206.
|
| [3] |
杨秀璋. 实体和属性对齐方法的研究与实现[D]. 北京: 北京理工大学, 2016.
|
| [4] |
刘峤, 李杨, 段宏, 等. 知识图谱构建技术综述[J]. 计算机研究与发展, 2016, 53(3): 582-600. DOI:10.7544/issn1000-1239.2016.20148228 |
| [5] |
SOHN JS, CHUNG IJ. Dynamic FOAF management method for social networks in the social web environment[J]. The Journal of Supercomputing, 2013, 66(2): 633–648.
|
| [6] |
https://blog.csdn.net/panghaomingme/article/details/120271840
|
| [7] |
BOLLACKER K, EVANS C, PARITOSH P, et al. Freebase: a collaboratively created graph database for structuring human knowledge[C]//Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. AcM, 2008: 1247−1250.
|
| [8] |
张佳宇. 基于本体的煤矿安全领域知识图谱研究[D]. 太原: 太原科技大学, 2019.
|
| [9] |
Neo4j[EB/OL].https://neo4j.com/ [2018-03-06].
|
| [10] |
AllegroGraph.https://allegrograph.com/, [2018-02-08].
|
| [11] |
LENT B., SWAMI A., WIDOM J.. Clustering association rules[C]//Proceedings of the 13th International Conference on Data Engine, 1997: 220−231.
|
 2022, Vol. 44
2022, Vol. 44
