近距配置声呐纯方位探测可应用在单平台隐蔽探测目标,也可应用于狭水道下的水雷阵等,具有重要的应用。在多传感器纯方位目标数据关联中,由于信息量少,空间分辨率低,可用的方法不多,较为著名的有多维分配法[1-2],但该方法只能用于3个以上传感器组成的纯方位测量系统中,并且实现较为复杂,计算量大。对于两站纯方位定位,修建娟等[3]利用方位关联假设得到初始的目标位置假设,再在后续的滤波中计算这些假设的概率,并进行概率加权融合,本质上是利用了目标的运动假设信息,当目标机动时,该方法的有效性需要进一步讨论。其他的方法主要是利用信号的某些特征进行关联,如信号能量[4]、特征门限[5]、D-S证据理论组合[6],为了获取这些特征,需要更多的硬件和信号处理的投入。另外可以使用或利用概率数据互联的方法[7],在多假设下跟踪,并计算互联概率,确定关联事件。而对于近距离配置的两声呐,可以根据实时的海上水文条件,估计出传感器的探测范围,根据这一重要的先验信息和两声呐近距离配置的特点,本文提出方位门关联方法。该方法可与其他方法结合,减小关联概率计算量。
1 方位门关联方法方位门关联方法是当声呐探测到目标时,利用单平台2部声呐间距近、观测同一目标的方位接近、方位变化规律一致的特点规律,以其中1部声呐发现的目标方位为基准,设置一个方位门,与另1部声呐发现的目标进行关联的方法。方位门关联方法原理简单、便于实现、关联计算快,更好地实现目标预警的快速目标关联,缩短系统反应时间。
1.1 方位门门限的确定方位门首先需要确定方位门的门限,即方位门的上下限。
下面推导方位门门限的计算方法,这里所有的角度都以顺时针为正,逆时针为负。
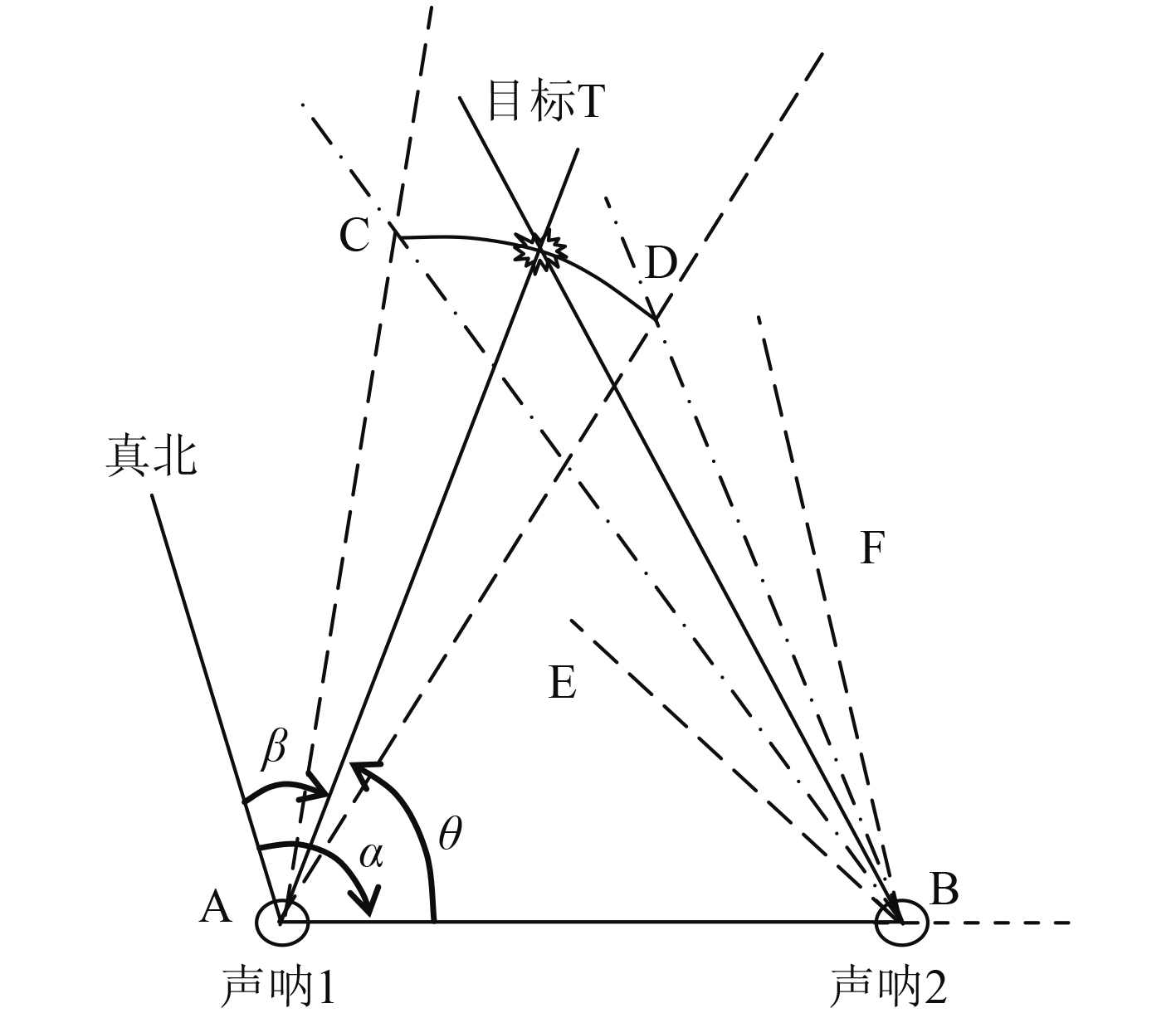
以声呐1作为声呐数据关联中的主传感器,对于选定的高威目标,首先假设目标的距离大于声呐1的作用距离。在该假设下,确定另1部声呐的方位门限,如图1所示,假设目标T刚好在传感器1的作用距离上,即
|
图 1 方位关联门图解 Fig. 1 Bearing door for bearing association |
| $ BC = \sqrt {{L_a}^2 + {L_s}^2 - 2{L_a}{L_s}\cos ( - \theta + {\sigma _{s1}})} \text{,} $ | (1) |
可以使用余弦来计算
| $ \cos \angle ABC = \frac{{B{C^2} + {L_s}^2 - {L_a}^2}}{{2{L_s}*BC}},$ | (2) |
当目标距离更远(目标距离大于
| $ \left( {\angle ABC - {\text{π}} - {\sigma _{s2}},\theta + {\sigma _{s1}} + {\sigma _{s2}}} \right) $ | (3) |
之内。目标在声呐2中的真北方位应当在
| $ \left( {\alpha + \angle ABC - {\text{π}} - {\sigma _{s2}},\beta + {\sigma _{s1}} + {\sigma _{s2}}} \right) $ | (4) |
之内。
当目标在第1部声呐基线方位角
| $ BC = \sqrt {{L_a}^2 + {L_s}^2 - 2{L_a}{L_s}\cos (\theta + {\sigma _{s1}})} \text{,} $ | (5) |
可根据
| $ \cos \angle ABC = \frac{{B{C^2} + {L_s}^2 - {L_a}^2}}{{2{L_s}*BC}} $ | (6) |
计算
| $ \left( {\theta - {\sigma _{s1}} - {\sigma _{s2}},\pi - \angle ABC + {\sigma _{s2}}} \right) 。$ | (7) |
以
式(3)和式(7)形成方位门的上下限,上下限之差称为方位门大小,方位门大小是影响方位门关联主要因素,方位门越小,门内目标就越少,关联精度就越高,错关联的概率就越低,但漏关联概率也随之增大。在2部声呐对目标的测量在其测量误差内,则式(3)和式(7)确定的方位门基本确保没有漏关联。方位门大小与2个传感器的方位测量误差、基线长度、目标的舷角

|
图 2
方位门与
|
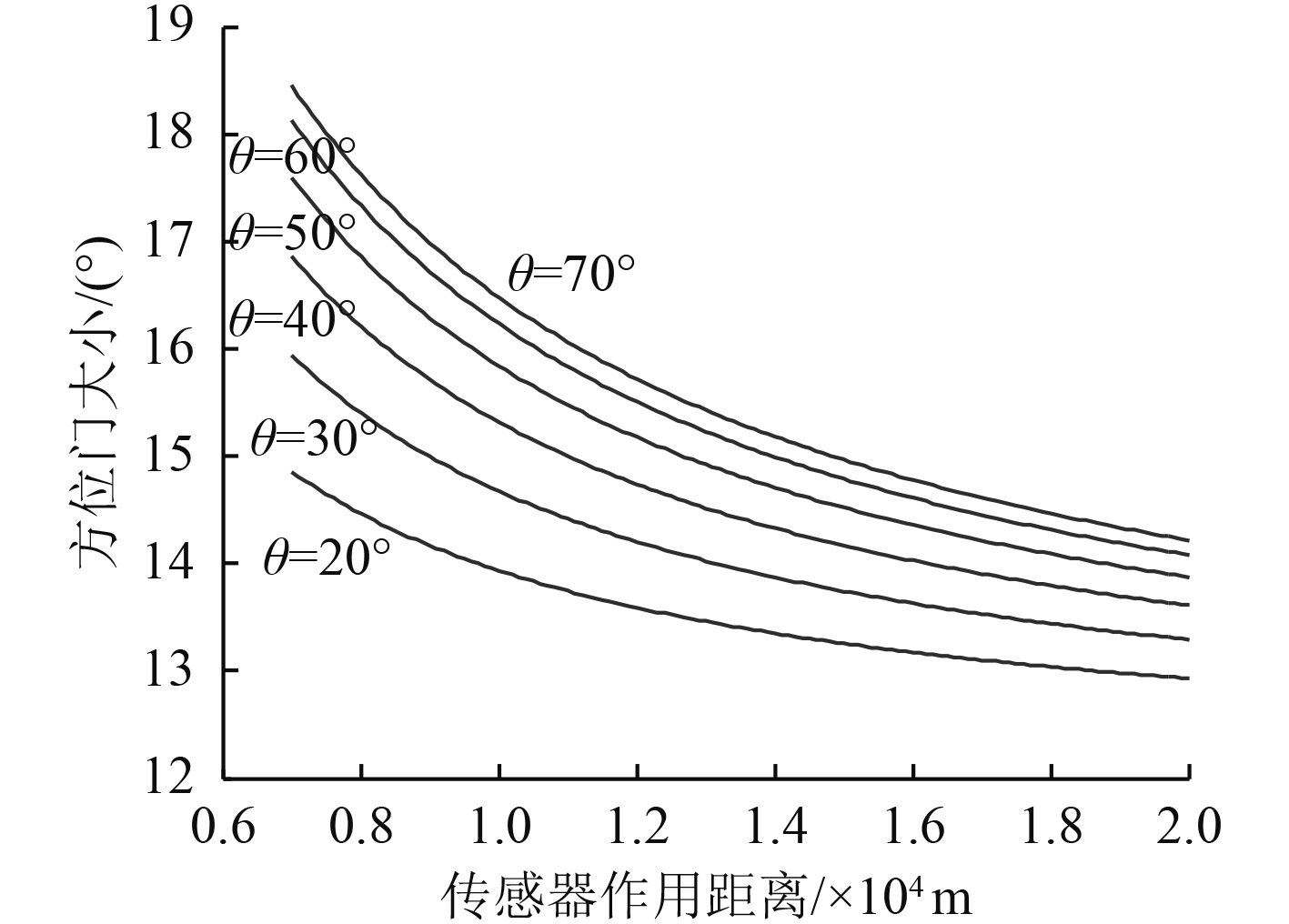
方位门也与传感器的作用距离
|
图 3
传感器作用距离
|
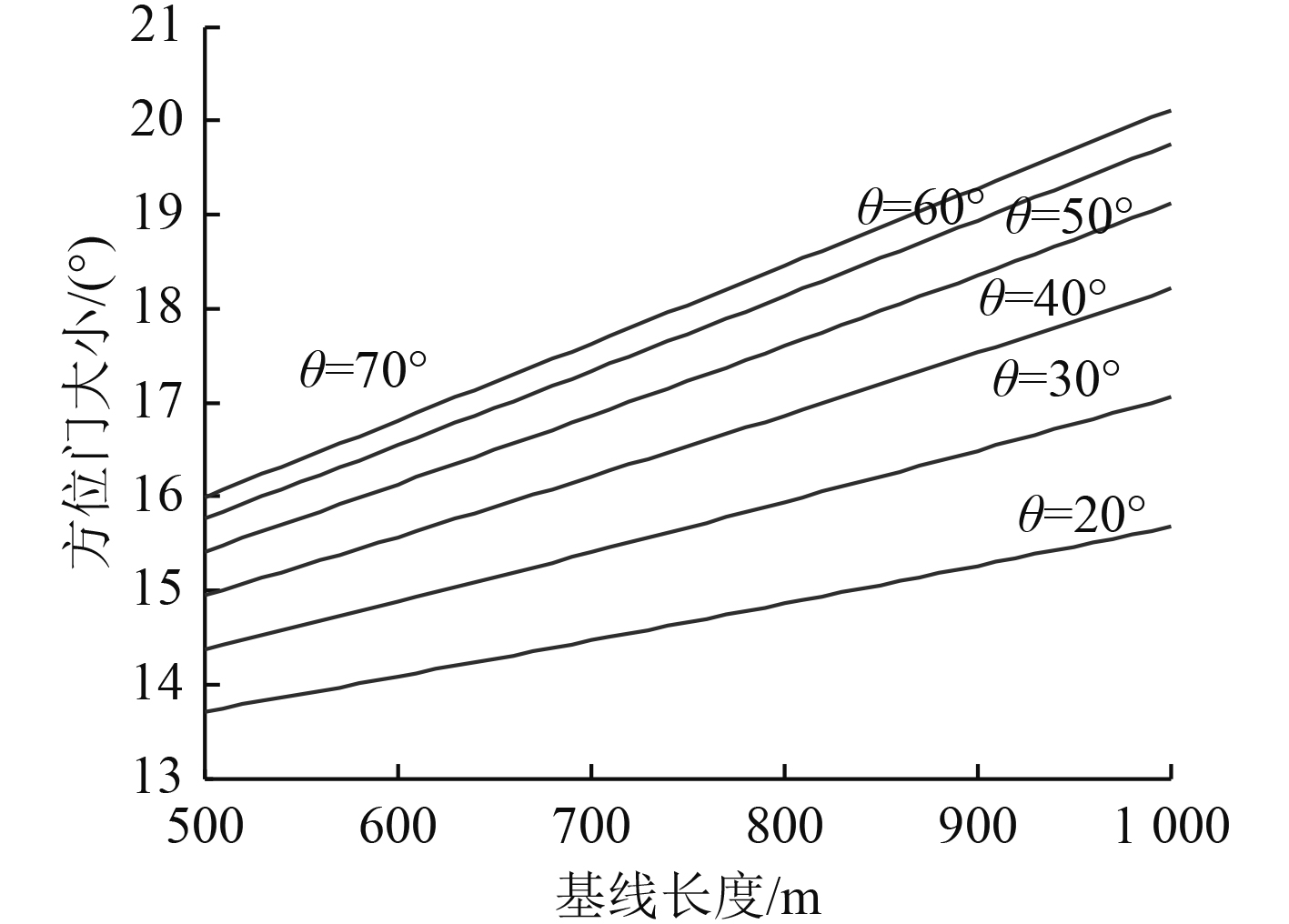
方位门与传感器之间的基线长度
|
图 4
基线长度
|
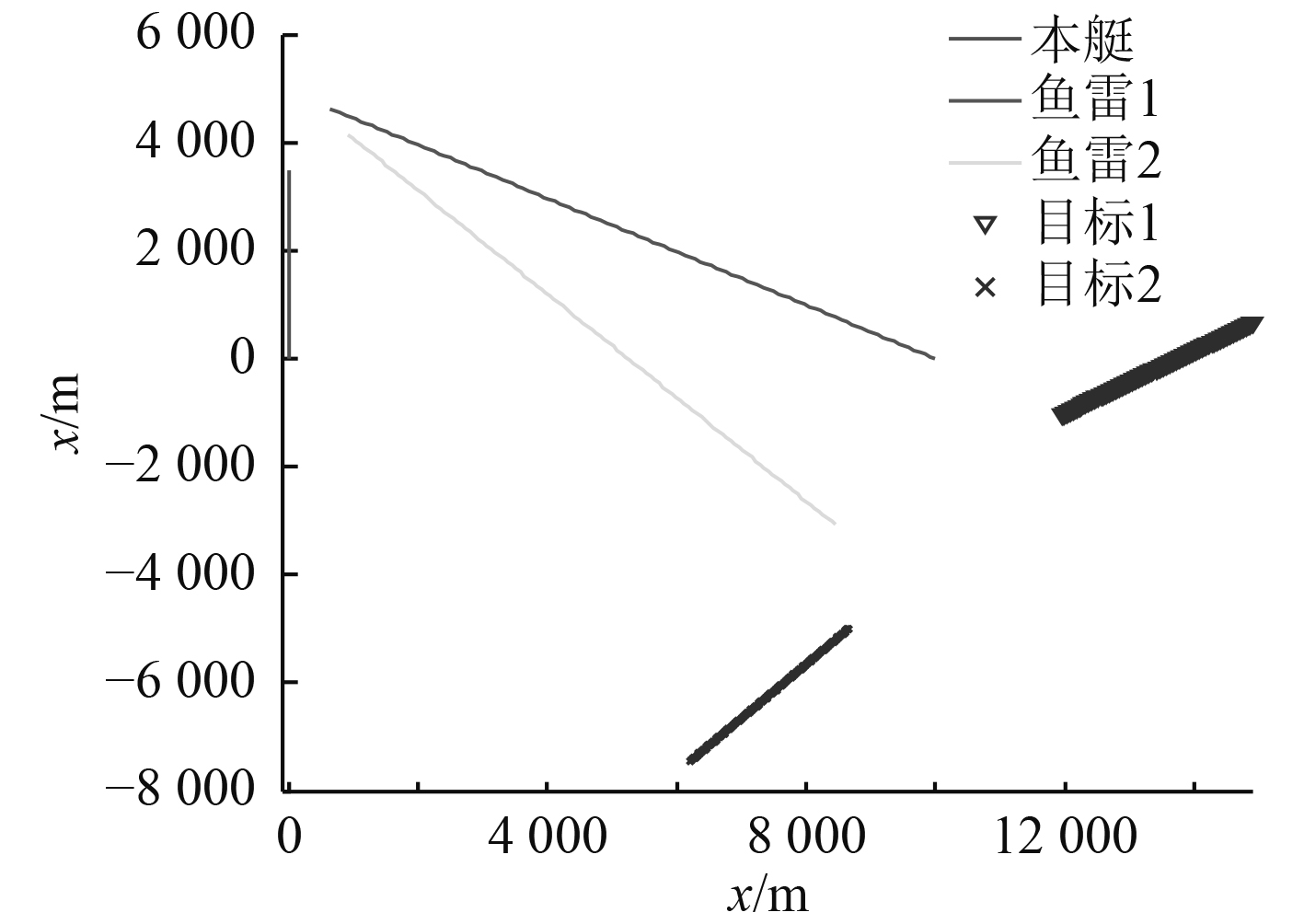
为了验证这种方位门关联的基本性能,进行计算机典型态势下的方位门关联仿真,态势如图5所示。目标1和目标2分别在一定距离上对本艇实施鱼雷攻击,攻击后分别从不同方向撤离。本艇发现鱼雷时,2个鱼雷距离分别为10 km和9 km,方位分别为90º和110º,航向分别为−63.7º和−46.2º,航速都是30 m/s。2个撤离的目标距离分别为12 km和10 km,方位分别为95º和120º,航向分别为60º和−135º,航速都是10 m/s。假设鱼雷目标和撤离目标都作匀速直线运动。本艇沿着正北方向以10 m/s的速度前进,其中一个传感器初始位置在原点,其对目标的方位测量误差3º;另一个传感器在(0,−800) m,即传感器基线
|
图 5 鱼雷攻击态势仿真 Fig. 5 Situation of torpedo attack in sim |
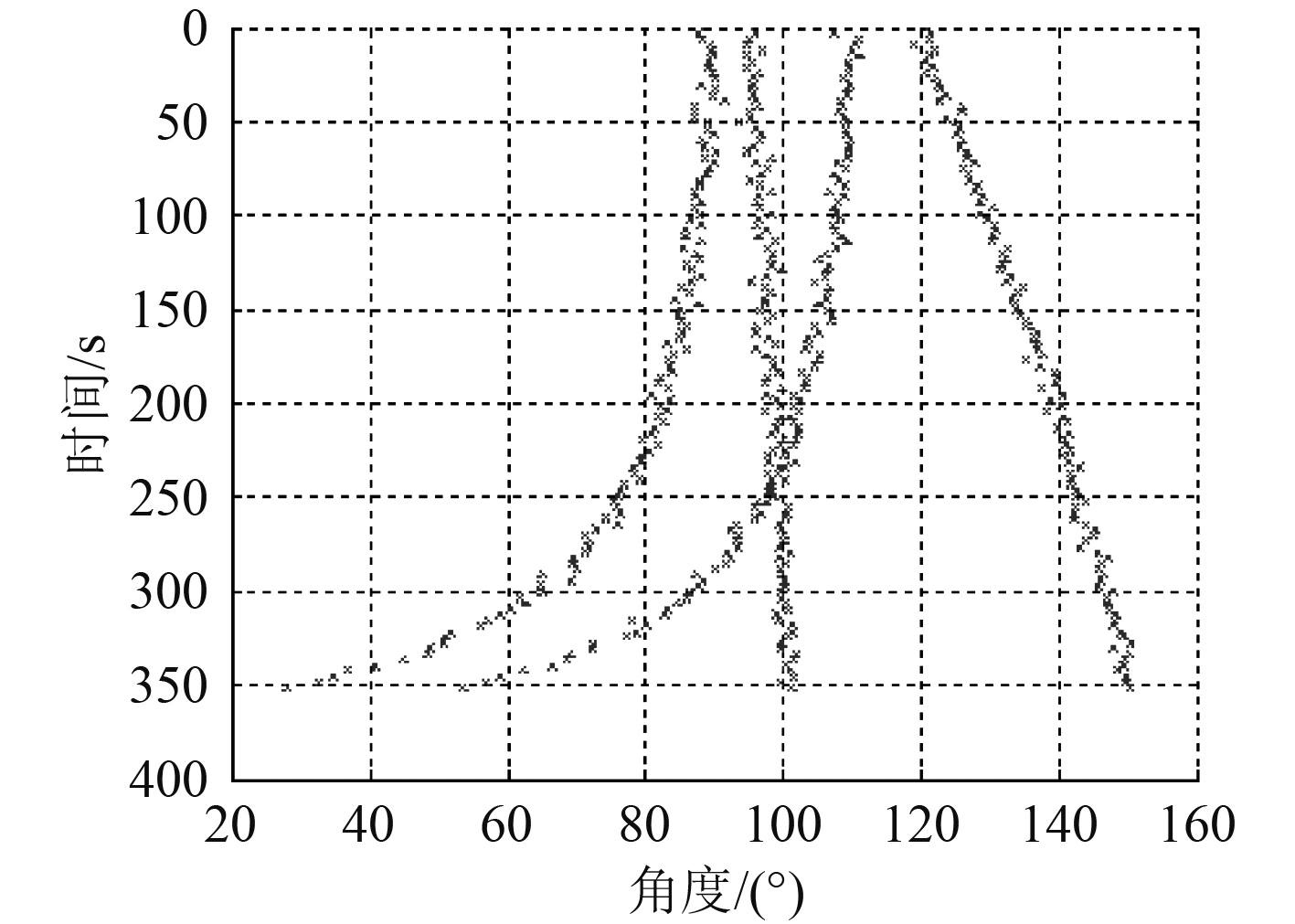
|
图 6 传感器1的方位时间序列仿真 Fig. 6 Bearing-time record in sensor 1 in sim |
仿真结果显示在图7(a)中,关联的前100 s放大显示在图7(b)中。从图中可以看到,在关联的前100 s中,两声呐的关联非常好,100 s的时间足够系统建立航迹,因此方位门关联方法能够为建航提供早期的关联信息。
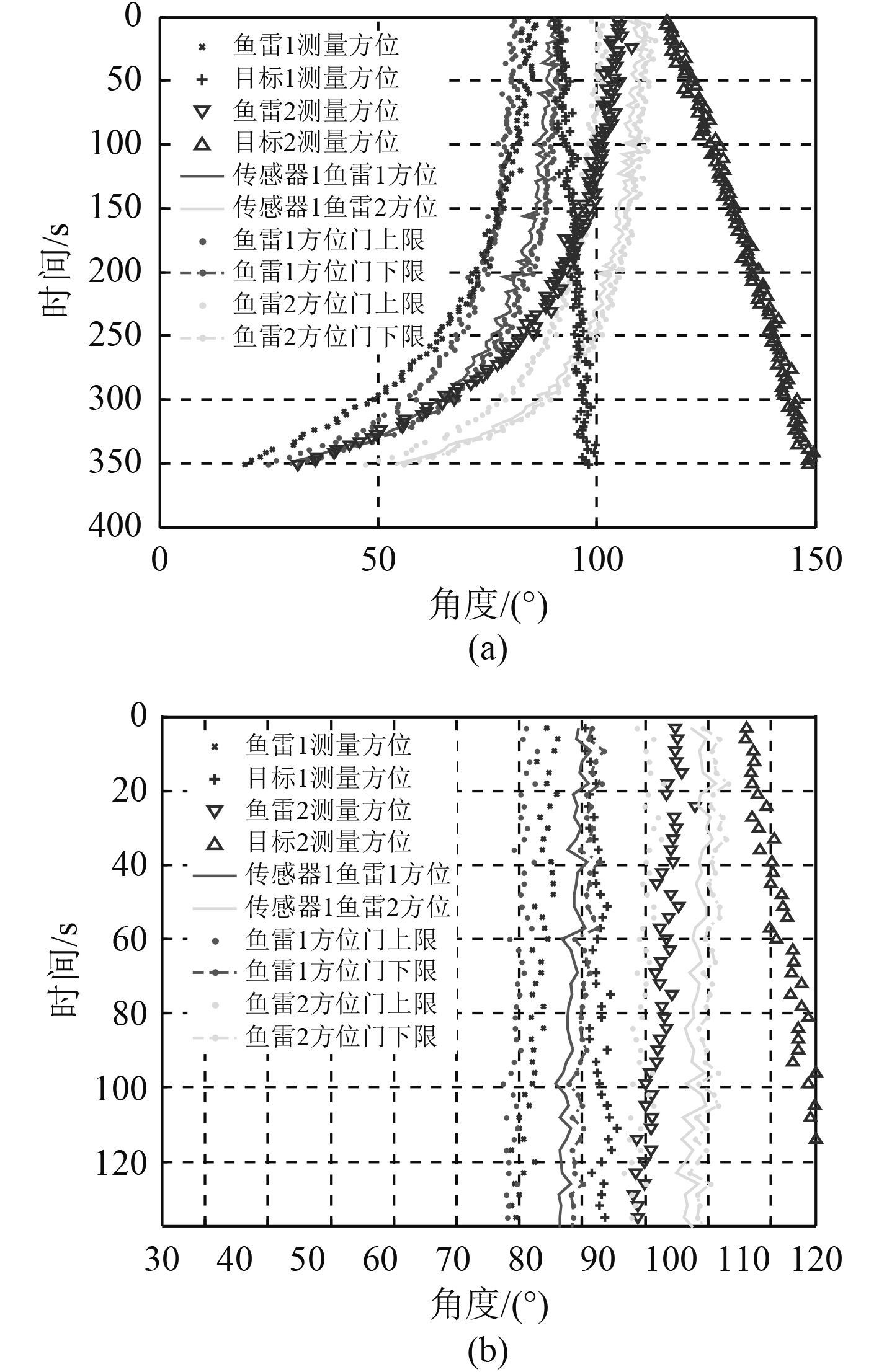
|
图 7 传感器2方位时间序列仿真及鱼雷目标方位门局部放大 Fig. 7 Bearing-time record and bearing door in sensor 1 and their larger image |
虽然在目标发现时利用目标发现最小距离进行关联是可行的,但是随着目标的接近,最小发现距离有可能远远大于目标的真实距离,这样计算出来的关联门就不正确了,这一点从图7中可以看到。但是随着滤波的进行,距离的估计会越来越正确,因此,可以假设目标在一定的距离范围内,也即目标在该距离范围内的概率很高,此时,可以利用目标距离方位建立正确的方位门。
具有距离范围的目标关联门的上下限可以使用距离的上下限来计算,设距离的目标上下限为
首先讨论目标在右舷的情况,即
| $ BC = \sqrt {{L_{low}}^2 + {L_s}^2 - 2{L_{low}}{L_s}\cos ( - \theta + {\sigma _{s1}})} ,$ | (8) |
| $ \cos \angle ABC = \frac{{B{C^2} + {L_s}^2 - {L_{low}}^2}}{{2{L_s}*BC}} 。$ | (9) |
因此,以基线AB的延伸方向为起始边,该目标在传感器2中的方位下限为:
| $ \angle ABC - {\text{π}} - {\sigma _{s2}} ,$ | (10) |
同样,传感器2目标方位线的上限可以用目标距离的上限来计算,只需要将式(1)和式(2)中的
| $ BD = \sqrt {{L_{up}}^2 + {L_s}^2 - 2{L_{up}}{L_s}\cos ( - \theta - {\sigma _{s1}})} \text{,} $ | (11) |
| $ \cos \angle ABD = \frac{{B{D^2} + {L_s}^2 - {L_{up}}^2}}{{2{L_s}*BD}} ,$ | (12) |
因此,以基线AB的延伸方向为起始边,该目标在传感器2中的方位的下限为:
| $ \angle ABD - {\text{π}} + {\sigma _{s2}} 。$ | (13) |
利用与上文仿真条件相同的态势进行仿真,目标距离范围假设在真实距离上下浮动50%,其他仿真条件与上文相同。由于本艇是向正北运动,传感器基线与正北的交角为180°,则传感器2的方位门为:
| $ (\angle ABC - {\sigma _{s2}},\angle ABD + {\sigma _{s2}}) 。$ | (14) |
仿真的结果如图8所示。与图7比较可以看出,在200 s以后,方位门覆盖了传感器2对鱼雷目标的测量方位,说明随着目标距离范围的给出,尽管给出的距离范围较大,达到目标距离本身,但是由于传感器基线较短,使得方位门关联方法仍具有很好的关联性能,特别是在目标数量不是非常密集的水下环境中。
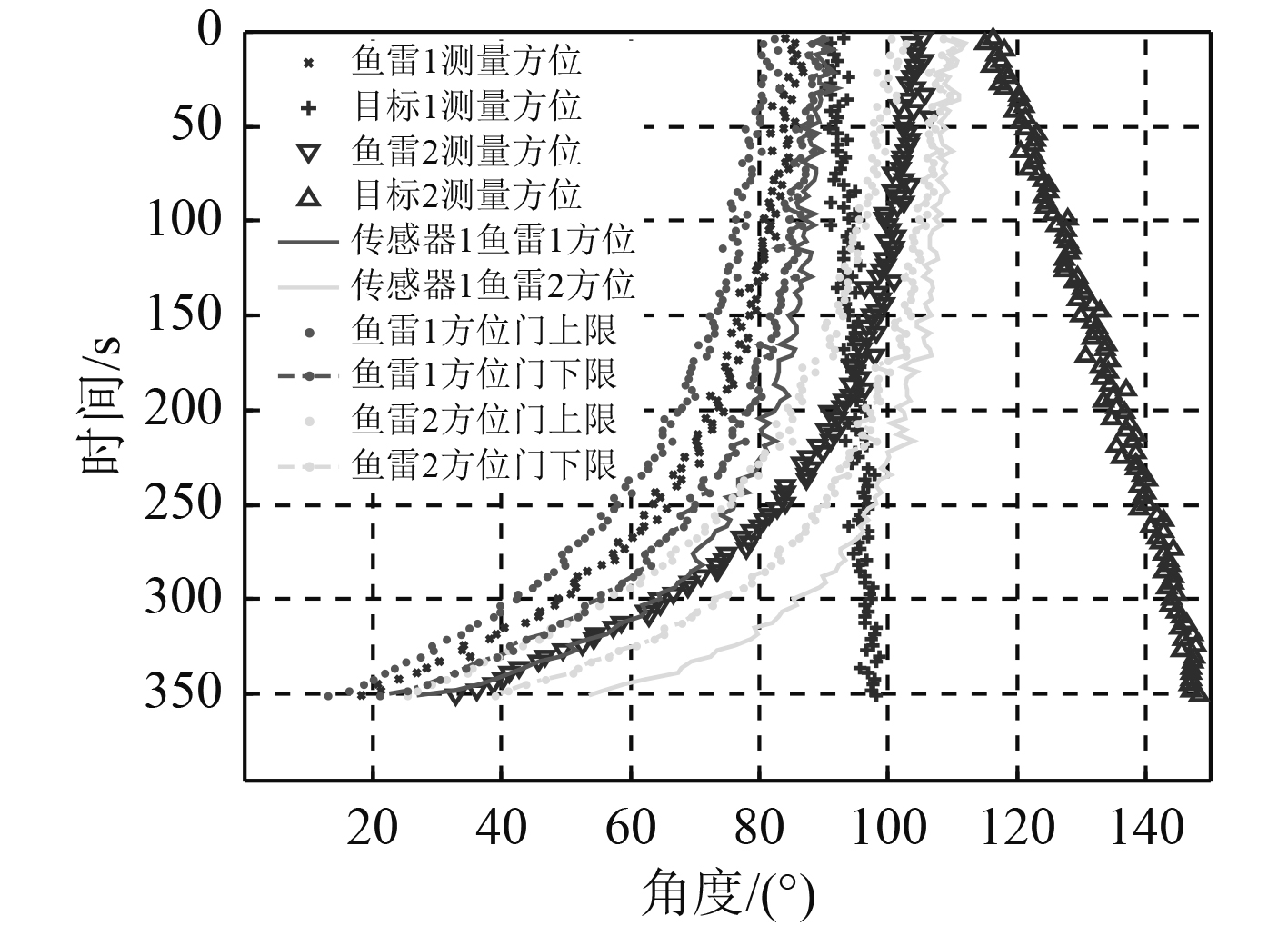
|
图 8 具有距离范围的鱼雷目标方位门关联 Fig. 8 Bearing door of torpedo target with distance scope |
随着目标的关联的进行,目标会进一步确定其目标范围,并且可以进一步地计算传感器2的方位测量与传感器1目标的关联概率,从而可以利用概率数据互联等软判决的方法进行目标跟踪的滤波。
3 结 语2部近距离配置的声呐,可以利用配置的特点,采用方位门关联方法,解决目标接触初期的目标定位问题,而不需要进行机动,对于平台来说,有利于其隐蔽,对于网络雷阵来说,有利于目标初步定位。在接触初期,通过方位门关联,可以进行快速的目标定位,提供早期提供信息;随着跟踪的进行,在较大定位误差的情况下,仍然可以通过具有距离范围的方位门关联,继续定位关联,解决目标接近状态下的目标跟踪问题。
| [1] |
DEB S, PATTIPATI K R, BAR-SHALOM Y. PASSDAT: passive sensor data association for tracking-A PC software[C]//SPIE: Signal and Data Processing of Small Targets. 1990: 274-186.
|
| [2] |
PATTIPATI K R, DEB S, BAR-SHALOM Y, et al. A new relaxation algorithm and passive sensor data association[J]. IEEE Transactions on AC, 1992, 37(2): 198-213. DOI:10.1109/9.121621 |
| [3] |
修建娟, 何友, 王国宏, 等. 两站无源定位系统中的多目标跟踪算法研究[J]. 电子学报, 2002, 30(12): 1763-1767. DOI:10.3321/j.issn:0372-2112.2002.12.008 |
| [4] |
MA N, CHIA C W. Target localization by two fixed non-coherent passive linear arrays[J]. IEEE, 2008.
|
| [5] |
KADAR I. Passive multisensor multitarget feature-aided unconstrained tracking: a geometric perspective[C]//FUSION 2000: 17-24.
|
| [6] |
韩崇昭, 李晨, 朱洪艳. 红外搜索跟踪系统的数据关联算法研究[J]. 控制与决策, 2008, 23(2): 171-176. DOI:10.3321/j.issn:1001-0920.2008.02.010 |
| [7] |
苏骏, 李亚安, 陈晓, 等. 双观测站水下纯方位多目标跟踪的数据关联算法[J]. 水下无人系统学报, 2018, 26(2): 115-121. |
 2022, Vol. 44
2022, Vol. 44
