0 引　言

工程实测中，由于反射声的存在导致近场声全息技术（NAH）^[1]无法重建目标声源单独产生的声场。为解决这一问题，研究人员提出了多种针对反射声的声场分离方法^[2-3]。为便于分析，现有大多数方法对边界反射面各个位置处的声压反射系数进行了简化，即根据边界声阻抗相对于流体介质阻抗的大小，将反射面近似为绝对硬边界^[4](反射系数取为1)或绝对软边界^[5-6](反射系数为−1)。工程实际中反射面的声阻抗特性并不一定满足理想化条件。不考虑边界声阻抗，分离算法的分离精度会降低，甚至可能失效，限制了算法的适用范围。文献[7]提出声场分离时需考虑边界声阻抗，但并未进行专门的研究。2019 年，Elias Zea^[8] 提出一种基于傅里叶变换的方法，完成了平行反射面平面声源的声场分离，分析了反射面阻抗对声场分离和重建的性能影响，表明在声场分离中考虑边界声阻抗确实具有重要意义。

本文结合边界声阻抗的特点，针对存在边界反射的环境，提出结合球面谐波叠加原理和镜像法实现声场分离的算法，将反射面对声场的作用量化，可提高声场分离的精度。仿真实验表明，与硬边界方法和软边界方法的分离效果相比，新算法具有更好的分离精度和实用性。

1 理论模型及其算法实现

声波在理想流体中的传播规律可用波动方程描述，波动方程经傅里叶变换后可得到Helmholtz方程。在球坐标系下，用分离变量法求解Helmholtz方程可得到空间声场中任意一点的声压^[9]如下式：

$ \begin{split}p(r, \phi, \theta, \omega)=&\sum_{n=0}^{\infty} \sum_{m-n}^{n}\left[c_{m n} h_{n}^{(1)}(k r) Y_{n}^{m}(\theta, \phi)+\right.\\ &\left.d_{m n} h_{n}^{(2)}(k r) Y_{m}^{i m}(\theta ; \phi)\right]。\end{split}$

(1)

其中： $ h_n^{(1)}(kr)Y_n^m(\theta ,\phi ) $ 代表声场中的去波分量； $ h_n^{(2)}(kr)Y_n^m(\theta ,\phi ) $ 代表声场中的来波分量； $ h_n^{(1)}(kr) $ 是第一类n阶hankel函数； $ h_n^{(2)}(kr) $ 是第二类n阶hankel函数； $ Y_n^m(\theta ,\phi ) $ 是n阶m次的球面谐波函数；k为波数； $ {c_{mn}} $ 和 $ {d_{mn}} $ 代表权重系数。当目标声源处在自由声场中，声场中仅有远离声源的去波，故式(1)可写为：

$ p(r, \phi, \theta, \omega)=\sum_{n=0}^{\infty} \sum_{m=n}^{n}\left[c_{m n} h_{n}^{(1)}(k r) Y_{n}^{m}(\theta, \phi)\right]，$

(2)

其中， $ Y_n^m(\theta ,\phi ) $ 是n阶m次的球面谐波函数，其表达式为：

$ Y_{n}^{m}(\theta, \phi)=\sqrt{\frac{(2 n+1)}{4 \pi} \frac{(n-m) !}{(n+m) !}} P_{n}^{m}(\cos \theta) \mathrm{e}^{\mathrm{im} \phi}，$

(3)

式中， $ P_n^m(\cos \theta ) $ 为缔合勒让德函数。声场中全息测量面上放置N个测点，则声场测点处声压可根据式(2)写成矩阵的表达形式，如下式：

$ \left[ {\begin{array}{*{20}{c}} {{p_{meas,1}}} \\ {\begin{array}{*{20}{c}} {{p_{meas,2}}} \\ \vdots \\ \vdots \end{array}} \\ {{p_{meas,N}}} \end{array}} \right] \cong \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\psi _{11}^{(1)}}& \cdots &{\psi _{1j}^{(1)}}&{\begin{array}{*{20}{c}} \cdots &{\psi _{1M}^{(1)}} \end{array}} \end{array}} \\ {\begin{array}{*{20}{c}} {\psi _{21}^{(1)}}&{\begin{array}{*{20}{c}} \cdots &{\psi _{2j}^{(1)}} \end{array}}& \cdots &{\psi _{2M}^{(1)}} \end{array}} \\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \vdots &{\begin{array}{*{20}{c}} {}&{} \end{array}}&{\begin{array}{*{20}{c}} \vdots &{\begin{array}{*{20}{c}} {}&{} \end{array}} \end{array}}& \vdots \end{array}} \\ {\begin{array}{*{20}{c}} {\psi _{i1}^{(1)}}&{\begin{array}{*{20}{c}} \cdots &{\psi _{ij}^{(1)}} \end{array}}& \cdots &{\psi _{iM}^{(1)}} \end{array}} \\ {\begin{array}{*{20}{c}} \vdots &{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}& \vdots \end{array}}&{\begin{array}{*{20}{c}} {}&{} \end{array}}& \vdots \end{array}} \end{array}} \\ {\begin{array}{*{20}{c}} {\psi _{N1}^{(1)}}& \cdots &{\begin{array}{*{20}{c}} {\psi _{Nj}^{(1)}}& \cdots \end{array}}&{\psi _{NM}^{(1)}} \end{array}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{c_1}} \\ {{c_2}} \\ {\begin{array}{*{20}{c}} \vdots \\ \vdots \end{array}} \\ {{c_M}} \end{array}} \right]，$

(4)

其中， $ \psi _{ij}^{(1)}\left( {r,\phi ,\theta } \right) = h_n^1(kr)Y_n^m(\phi ,\theta ) $ ;M为扩展项数。 $\left[ {{c_1}}\quad {{c_2}}\quad \cdots \quad \cdots \quad {{c_M}} \right]^{\rm{T}}$ 为球谐波基函数的权重系数向量。为运算方便，将式(4)简记为：

$ {\boldsymbol{P = \psi C}}。$

(5)

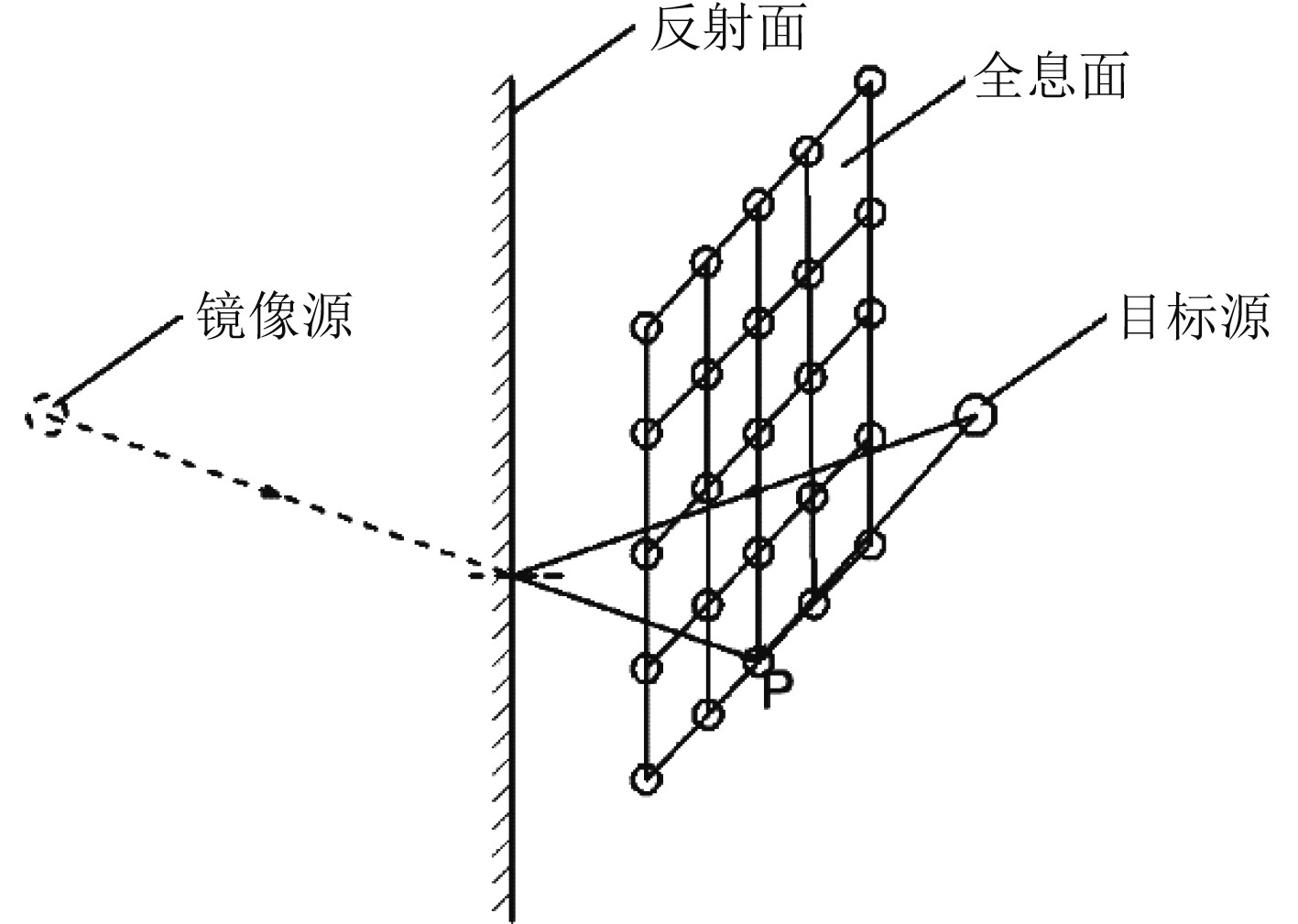
根据图1所示镜像法的原理，假设界面另一侧存在一个与实际声源关于界面对称的虚拟声源，P点是全息面上的一个测点，其测得的声压值一部分是目标源发出的直达声压，另一部分是目标声源经反射面反射后到达该测点的反射声压，可以将反射声压看作是镜像源经过反射面处理后到达测点的“直达声”，处理过程考虑到反射边界声阻抗的影响。那么由式(5)可得目标源在全息面测点上声压 $ {P_1} $ 为：

$ {P_1} = {{\boldsymbol{\psi }}_1}{\boldsymbol{C}}。$

(6)

其中： ${{\boldsymbol{\psi}} _1}$ 为目标源位置到全息面测点位置的传递矩阵； ${\boldsymbol C}$ 为表示目标源的球谐波基函数的权重系数。

同理，考虑反射边界的声阻抗的影响，可以得到镜像源在全息面测点上的声压 $ {P_2} $ 为：

$ {P_2} = {{\boldsymbol{R}}_p}{{\boldsymbol{\psi }}_2}{\boldsymbol C}，$

(7)

其中： ${{\boldsymbol{\psi}} _2}$ 是镜像源位置到全息面测点位置的传递矩阵； ${{\boldsymbol{R}}_p}$ 为经过每个测点位置的声波在反射面上的反射系数 $ {r_p} $ 组成的矩阵，其表达式为：

$ {{\boldsymbol{R}}_p} = {\rm{diag}}({r_{p1}} \cdots {r_{pm}} \cdots {r_{pN}})。$

(8)

式中：N为测点数； $ {r_p} $ 利用反射边界声阻抗得到^[10]，其表达式为：

$ {r_p} = \frac{{Z\cos {\theta _i} - \rho c}}{{Z\cos {\theta _i} + \rho c}}{\text{ = }}\frac{{\cos {\theta _i} - \dfrac{{\rho c}}{Z}}}{{\cos {\theta _i} + \dfrac{{\rho c}}{Z}}}。$

(9)

式中：Z是反射边界声阻抗值； ${\theta _i}$ 是声波的入射角； $\rho $ 为流体介质的密度； $c$ 为声波在流体介质中的声速。由于声压是标量，具有线性可加性，所以全息面测点上的总声压即传声器阵列测得的声压 $ {P_{ce}} $ 为：

$ {P_{ce}} = {P_1} + {P_2}。$

(10)

联立式(6)、式(7)和式(10)，解得目标源在全息面测点上的直达声压为

$ {P_1} = {\psi _1}{({\psi _1} + {R_p}{\psi _2})^\dagger }{P_{ce}} ，$

(11)

式中 $ {({\psi _1} + {R_p}{\psi _2})^\dagger } $ 是 $ {\psi _1} + {R_p}{\psi _2} $ 的广义逆，其表达式为

$ {({\psi _1} + {R_p}{\psi _2})^\dagger }{\text{ = [(}}{\psi _1} + {R_p}{\psi _2}{)^{\rm{H}}}({\psi _1} + {R_p}{\psi _2}){]^{ - 1}}{({\psi _1} + {R_p}{\psi _2})^{\rm{H}}}，$

(12)

式中，上标H表示矩阵的共轭转置。

为了能够定量描述分离算法的精度，定义分离误差为：

$ \varepsilon = \frac{{{{\left\| {{{\boldsymbol P'}_1} - {{\boldsymbol P}_{theo}}} \right\|}_2}}}{{{{\left\| {{{\boldsymbol P}_{theo}}} \right\|}_2}}} \times 100\text{%} 。$

(13)

式中： $ {P_{theo}} $ 表示各测点的直达声压理论值组成的列向量； $ {P'_1} $ 代表各测点分离得到的值组成的列向量； $ {\left\| \cdot \right\|_2} $ 表示2-范数。

2 仿真验证与参数分析

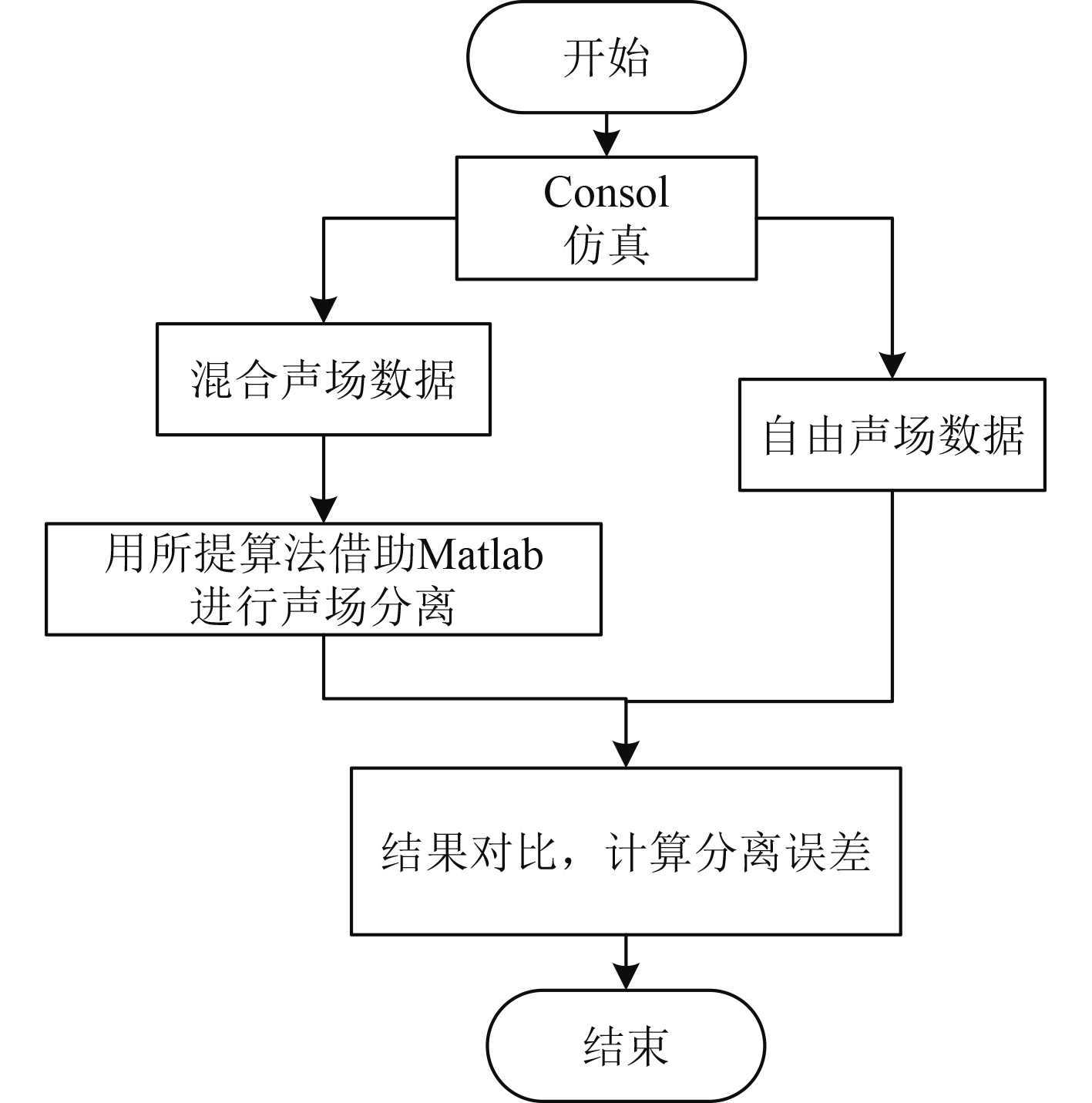
为检验该算法的可行性，用Comsol和Matlab相结合来进行仿真实验，具体的仿真分析流程如图2所示。先用Comsol模拟出没有反射声的自由声场和有反射声的混合声场，再将全息测量面上得到的数据导入Matlab中，用所提的算法对混合声场数据进行分离得到直达声，将结果与自由声场数据进行对比，计算出分离误差，验证算法的可行性。

2.1 模型介绍

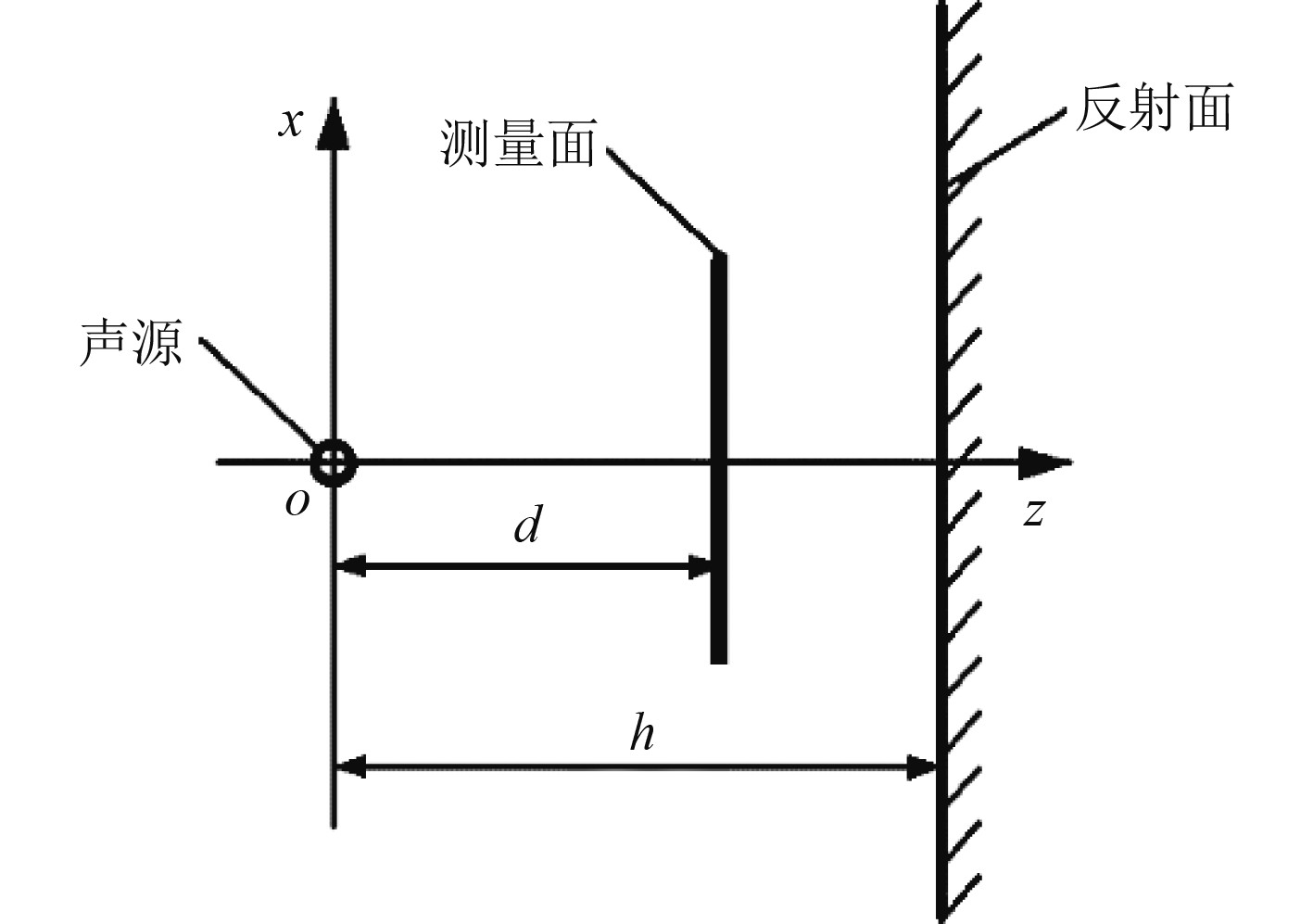
声场模型如图3所示，流体介质为水，其密度 $ {\ \rho _0} $ =1000 kg/m³，声速c = 1500 m/s；以单极点源作为目标声源，幅值取1，其中心O位于坐标(0,0,0)处，与反射面之间的距离为h；反射边界为平面阻抗反射面，边界的表面阻抗值为Z。为检验该算法的有效性，选取不同材质的反射面是空气、硅橡胶和混凝土，分别进行仿真分析，其表面声阻抗值如表1所示。单层方形水听器阵列置于声源与反射面之间，并与反射面平行。依据空间采样定理，当最高分析频率为1000 Hz时，测量距离应≤1.5 m，阵元间距应≤0.75 m，故测量阵列和声源之间距离取为d=1 m，测量阵列为3 m×3 m的规则平面，其上均布7×7个声压测点，选取相邻声压测点的间距为0.5 m。

2.2 结果与讨论

该仿真分析中用单极点源作为目标声源进行3组实验，将每组所得的混合声场数据分别用考虑声阻抗的算法、硬边界方法和软边界方法进行分离，将分离的结果与理论值进行对比，并由式(13)计算各组实验的分离误差，声源中心O与反射面距离h=3m时的结果如图4所示。

图4(a)中，空气反射面的表面声阻抗确实很小，满足绝对软边界的要求，考虑边界声阻抗的分离效果与软边界方法相同；图4(b)中，硅橡胶的表面声阻抗与水相近，既不满足绝对软边界要求，也不满足绝对硬边界要求，所以软边界方法和硬边界方法均失效，只有考虑边界声阻抗的方法能起到分离作用。图4(c)中，混凝土的表面声阻抗比水大，但并没有达到绝对硬边界的要求，所以硬边界方法有一定的分离效果，但其误差高于考虑边界声阻抗的算法，软边界方法则是完全失效。可以看出，考虑边界声阻抗的声场分离方法将各种反射面的性质都考虑在内，定量处理反射面的影响，更具有普适性，因而对于各种反射面都可以得到更好的分离效果。

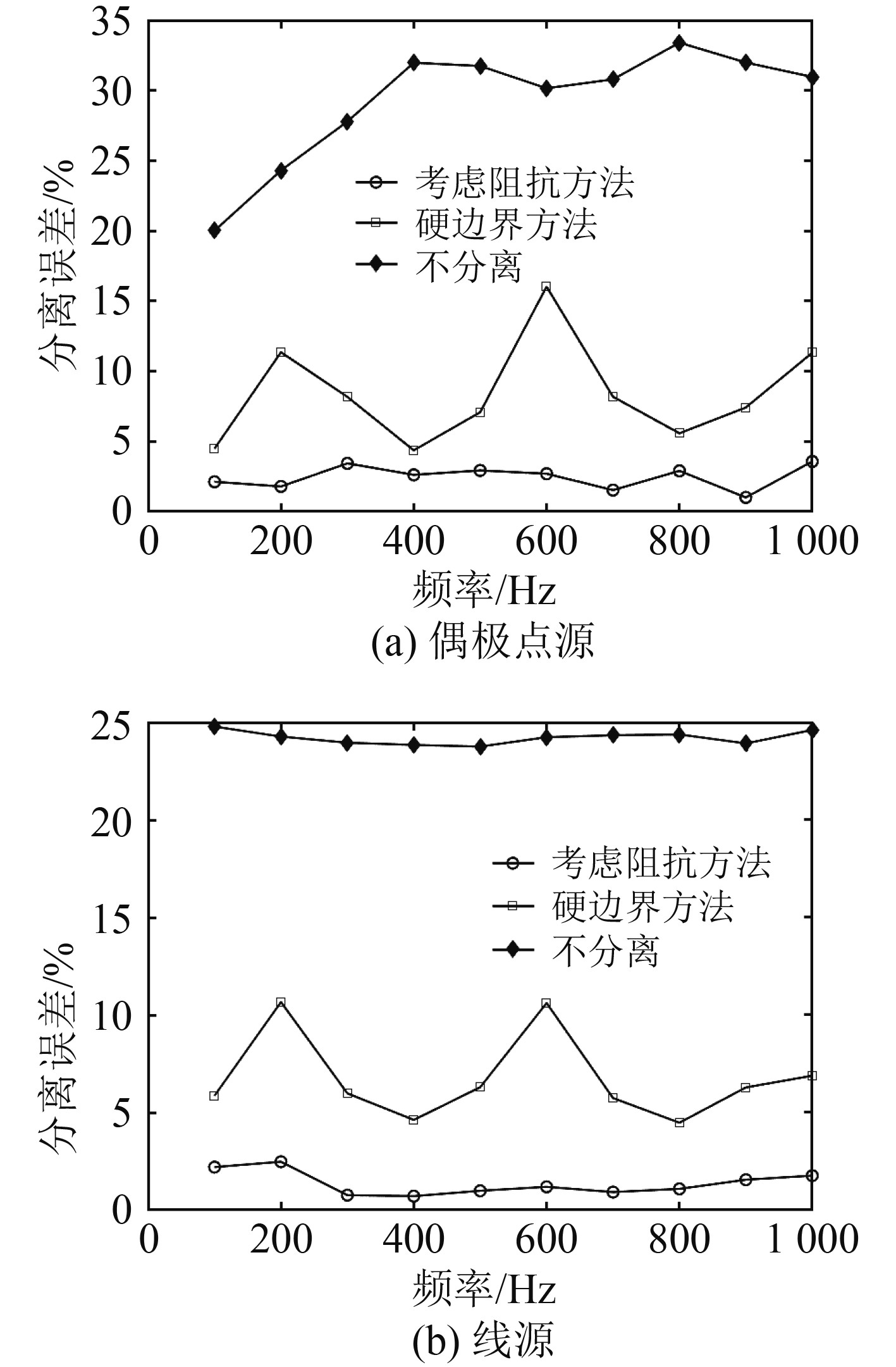
以上仿真中目标声源都是最简单的单极点源，为了检验该算法的适用范围，分别选取偶极点源和线源作为目标声源。偶极点源的偶极矩矢量为(0,0,1)，位置位于坐标原点；线源长度为0.5 m，幅值为1，线源中心位于坐标原点处。选取反射面材质为混凝土，使用图3所示的仿真模型进行仿真实验，不同声源情况下，分离效果如图5所示。从图5可知，在混凝土这种阻抗边界条件下，偶极点源和线源作为目标声源时，考虑边界声阻抗的声场分离算法的分离误差均在5%以下，可见对于不同类型的声源，所提算法都能起到很好的分离效果，且分离精度都比传统的硬边界方法要高，稳定性也比传统硬边界方法要好。

对于不同的声源类型，式（4）中球谐函数的扩展项数M的取值是不同的。对于单极点源，扩展项数M取为1即可达到很好的分离效果；对于偶极点源，扩展项数M需要取到2才能达到较好的分离效果；而线源需要把扩展项数M取到4才能得到很好的分离效果。这是因为球面谐波基函数是一组完备的正交基，声源的辐射声场都可以用球面谐波基函数的叠加来描述，不同类型的声源包含的球谐基函数成分是不同的，单极点源是最简单的声源，对应球谐基函数的 $Y_0^0$ 阶成分，偶极点源也是简单声源，对应球谐基函数的 $Y_1^0$ 阶成分，而线源是一种复杂的声源，并不对应某阶球谐基函数，故需要较多阶球谐基函数叠加逼近才能较好的描述其产生的声场。因此，通过球谐基函数的叠加，可以实现对不同类型声源的辐射声场的描述，证明了所提算法可以较好完成不同声源反射声场的分离。

3 结　语

为分离出各种反射边界情况下的直达声场，方便近场声全息技术的使用，借助反射边界声阻抗，提出一种对存在反射的声场进行声场分离的算法。利用Comsol和Matlab进行仿真实验，并对仿真结果进行对比分析，得到相关结论如下：

1）对于不同类型的反射界面，利用考虑边界声阻抗的声场分离算法均能较好地实现声场分离，相较于不考虑边界声阻抗的方法更具有实用性，也更符合实际。

2）在不同声源情况下，再次检验了本文所提算法的分离效果。结果显示，对于不同声源，考虑边界声阻抗的声场分离算法的分离误差均在5%以下，分离效果精度高稳定性好，进一步证明所提算法的普适性。