相比于电励磁电机,永磁电机高效、节能、轻便等特点使其得到了广泛应用[1-2]。国内外诸多学者对不同结构电机理论、设计进行了深入研究,但是都聚焦于电机内部磁场分析及其结构设计,主要目的是更高功率密度、最优经济性能、更小噪声振动等[3-5]。随着永磁电机的广泛使用,在诸如地磁环境测量、水下航行器等特殊应用领域,电机的外围环境磁场可能会造成地磁测量误差、影响航行器安全隐蔽性。
永磁电机环境磁场仅有少量学者进行研究,文献[6]针对空气中测磁的不同情况仿真,定性得出了磁场泄漏的规律,对实际工程具有一定的参考价值,但缺乏数学模型;文献[7-8]同样也有相应仿真工作,在理论方面,只是罗列了几个电磁场公式,在电机漏磁的数学模型上并无太大实际价值。
文献[9-10]对永磁直流电机分别进行了二维径向漏磁与二维轴向漏磁仿真分析,定性得到了电机环境漏磁场的分布规律,但该文献对电机本体参数描述几乎为零。
文献[11-13]对两极平行充磁电机进行了磁场建模分析,忽略了定子铁芯影响,得到了电机气隙、永磁体的解析模型。
对电机内部磁场建模已有很多文献,但是鲜有学者对电机外部环境磁场进行理论研究。
本文借鉴文献[13]的思路,建立了两极式的表贴式永磁电机环境磁场模型,分析磁场分布规律,利用Comsol软件分别进行静态和空载仿真分析,并在此基础上,分析了电机永磁体充磁方式、极对数、定子铁芯厚度、不导磁粗细、定子铁芯相对磁导率、极弧系数、气隙长度对环境磁场的影响。
1 磁场模型 1.1 模型建立电机模型简化等效为6个区域:不导磁转轴(shaft)、转子铁芯(rotor iron)、永磁体(PM)、气隙(air gap)、定子铁芯(stator iron)、环境(circumstance),并忽略电机定子齿、极弧系数,认为定子、永磁体是规则圆环,不考虑铁芯的饱和,等效模型如图1所示。
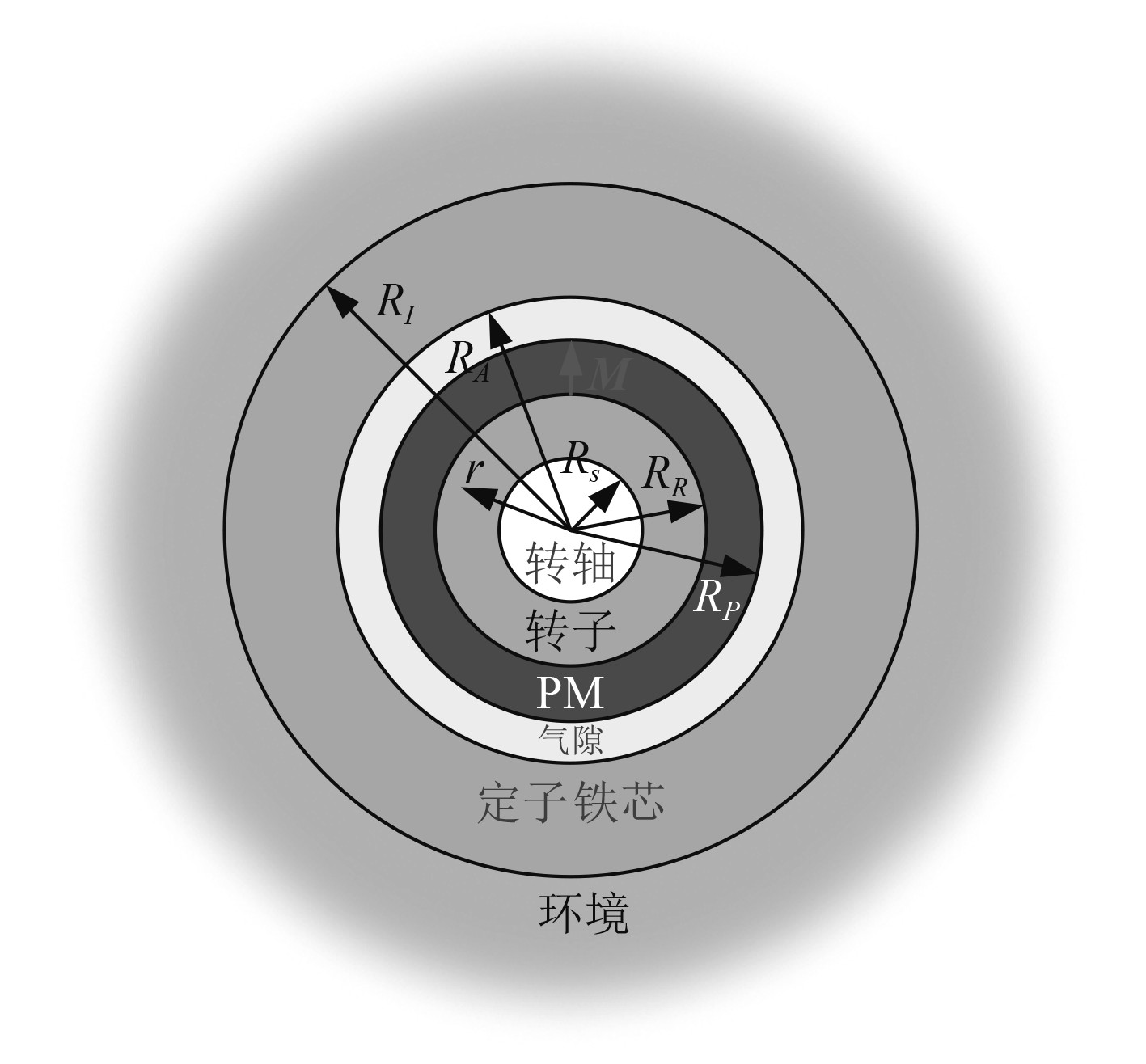
|
图 1 电机等效模型 Fig. 1 Motor′s equivalent model |
为分析其规律,将永磁体认为是两极,对于平行充磁的永磁体,其磁化强度可以写为:
| $ {{{M}}} = {M_r}{{r}} + {M_\theta }{\mathbf{\theta }} ,$ | (1) |
| $ \left\{ \begin{gathered} {M_r} = \left| {{{ M}}} \right|\cos \theta ,\hfill \\ {M_\theta } = - \left| {{{ M}}} \right|\sin \theta 。\hfill \\ \end{gathered} \right. $ | (2) |
式中:
由其分量可知,
| $ \left\{ \begin{gathered} {\nabla ^2}{A_{Sz}} = 0 ,\hfill \\ {\nabla ^2}{A_{Rz}} = 0 ,\hfill \\ {\nabla ^2}{A_{Pz}} = - \nabla \times ({\mu _0}{{M}}) = 0,\hfill \\ {\nabla ^2}{A_{Az}} = 0,\hfill \\ {\nabla ^2}{A_{Iz}} = 0 ,\hfill \\ {\nabla ^2}{A_{Cz}} = 0 。\hfill \\ \end{gathered} \right. $ | (3) |
矢量磁位Az呈现周期性,即
| $ \left\{ \begin{gathered} {B_r}(r,\theta ) = {B_r}(r,-\theta )\qquad (a),\hfill \\ {B_r}(r,\theta ) = -{B_r}(r,\pi -\theta )\quad (b),\hfill \\ \end{gathered} \right. $ | (4) |
| $ \left\{ \begin{gathered} {B_\theta }(r,\theta ) = -{B_\theta }(r,-\theta )\quad(a) ,\hfill \\ {B_\theta }(r,\theta ) = {B_\theta }(r,\pi -\theta )\quad(b) 。\hfill \\ \end{gathered} \right. $ | (5) |
根据图1的电机等效模型,可以知道电机分6个域,5个边界(转子与转子铁芯SR、转子铁芯与永磁体边界RP、永磁体与气隙边界PA、气隙与定子铁芯AI、定子铁芯与环境IC),由边界的磁场强度H的周向连续,磁感应强度B的径向连续[14]和铁芯磁导率远远大于气隙磁导率,且气隙很小,可以得到5组边界条件:
| $ \begin{gathered} SR:\left\{ \begin{gathered} {B_{rS}}(r,\theta ) = {B_{rP}}(r,\theta ){|_{r = {R_S}}},\hfill \\ {H_{\theta S}}(r,\theta ) = {H_{\theta R}}(r,\theta ){|_{r = {R_S}}},\hfill \\ \end{gathered} \right.{\text{ }} \hfill \\ RP:\left\{ \begin{gathered} {B_{rR}}(r,\theta ) = {B_{rP}}(r,\theta ){|_{r = {R_R}}} ,\hfill \\ {H_{\theta R}}(r,\theta ) = {H_{\theta P}}(r,\theta ){|_{r = {R_R}}},\hfill \\ \end{gathered} \right.{\text{ }} \hfill \\ PA:\left\{ \begin{gathered} {B_{rP}}(r,\theta ) = {B_{rA}}(r,\theta ){|_{r = {R_P}}} ,\hfill \\ {H_{\theta P}}(r,\theta ) = {H_{\theta A}}(r,\theta ){|_{r = {R_P}}},\hfill \\ \end{gathered} \right.{\text{ }} \hfill \\ AI:\left\{ \begin{gathered} {B_{rA}}(r,\theta ) = {B_{rI}}(r,\theta ){|_{r = {R_A}}},\hfill \\ {H_{\theta A}}(r,\theta ) = 0{|_{r = {R_A}}} ,\hfill \\ \end{gathered} \right.{\text{ }} \hfill \\ IC:\left\{ \begin{gathered} {B_{rI}}(r,\theta ) = {B_{rC}}(r,\theta ){|_{r = {R_I}}},\hfill \\ {H_{\theta I}}(r,\theta ) = {H_{\theta C}}(r,\theta ){|_{r = {R_I}}}。\hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ | (6) |
当
| $ \left\{ \begin{gathered} {B_{rC}}(r,\theta ) = 0{|_{r \to \infty }},\hfill \\ {H_{\theta C}}(r,\theta ) = 0{|_{r \to \infty }}。\hfill \\ \end{gathered} \right. $ | (7) |
利用分离变量法[15]可以解出各个域的矢量磁位为:
| $ \begin{split} {A_z} =& R(r)\varPhi (\theta ) =\sum\limits_{m = 1}^n ({C_{1m}}{r^m} +\\ & {C_{2m}}{r^{ - m}})({B_{1m}}\cos (m\theta ) + {B_{2m}}\sin (m\theta )) ,\end{split} $ | (8) |
所以环境磁场的解析式为:
| $ \left\{ \begin{gathered} {B_r}(r,\theta ) = \frac{1}{r}\frac{{\partial {A_z}}}{{\partial \theta }}{\text{ = }}\sum\limits_{m = 1}^{2n{\text{ - }}1} {{D_{2m}}{r^{ - m - 1}}\cos (m\theta )},\hfill \\ {B_\theta }(r,\theta ) = - \frac{{\partial {A_z}}}{{\partial r}} = \sum\limits_{m = 1}^{2n{\text{ - }}1} {{D_{2m}}{r^{ - m - 1}}\sin (m\theta )} 。\hfill \\ \end{gathered} \right. $ | (9) |
将式(9)的系数
如果只是关心磁场大小,用磁通密度模可以很好衡量,对于圆柱坐标来说,其表示为:
| $ |B| = \sqrt {|{B_r}{|^2} + |{B_\theta }{|^2}} {\text{ = }}{D_{C2}}{r^{ - 2}}{\text{ = }}{D_{C2}}{(d{\text{ + }}{R_I})^{ - 2}}。$ | (10) |
式(10)表明磁通密度模只与距电机表面距离
利用Comsol软件分别进行电机环境磁场静态和空载仿真分析,并在此基础上,分析电机参数对环境磁场的影响,电机的本体参数如表1所示。
|
|
表 1 电机参数 Tab.1 The parameters of motor |
利用Comsol软件中的无限元域模拟电机外围的无限大空气域,建立电机仿真模型和静态仿真结果如图2所示(无限元域是示意图,实际仿真远大于电机)。
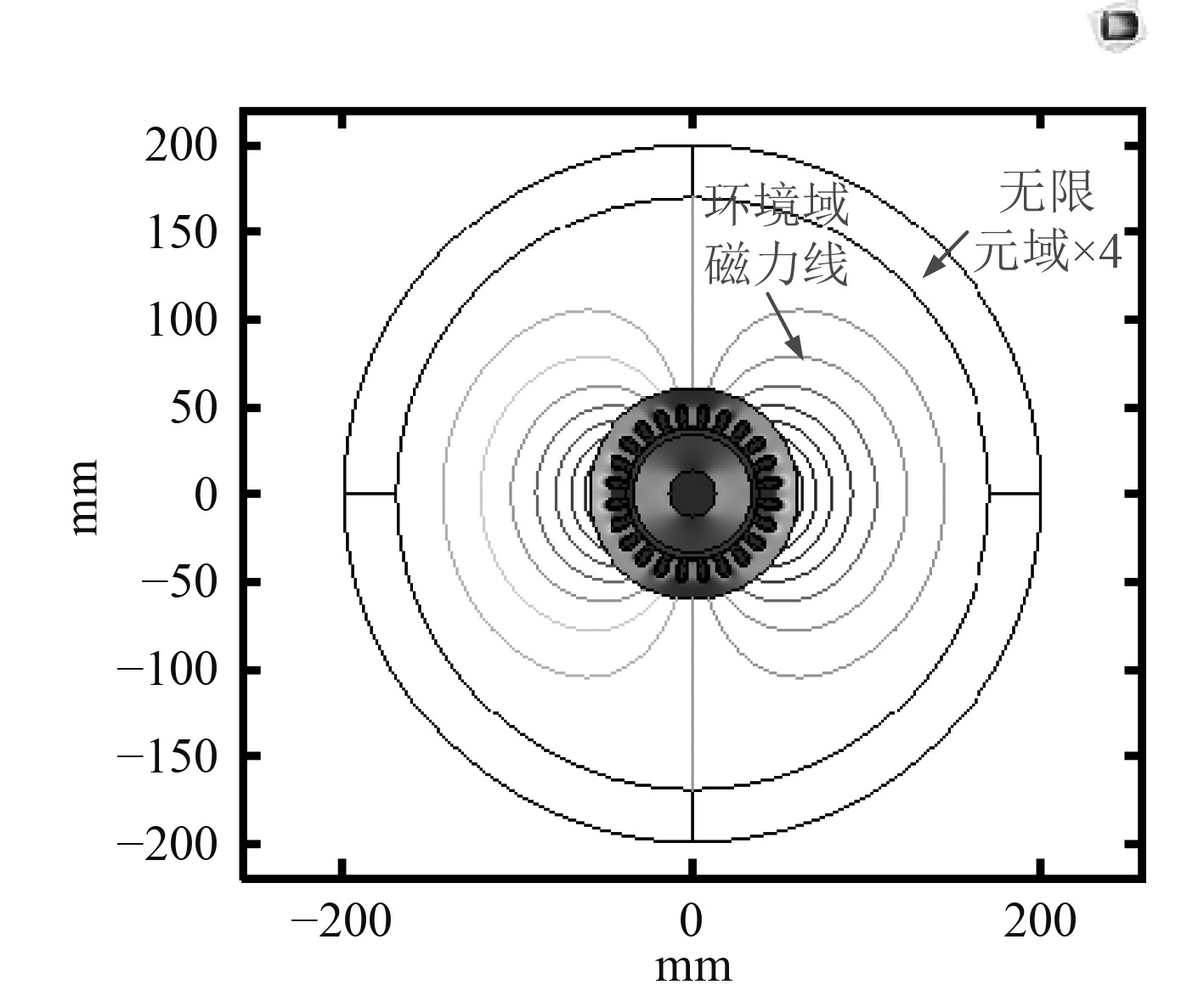
|
图 2 静态仿真磁力线分布 Fig. 2 Distribution of magnetic field lines under static state |
可以看出,电机环境磁场有部分“泄漏”(图2中环境域磁力线是放大效果),永磁体产生的磁通绝大部分经定子铁芯回到永磁体,少量穿出铁芯,进入外部环境。
在距离电机1 mm(r=61 mm)和40 mm(r=100 mm)外表面设置一系列的测量点(测量圆),其磁感应强度周向分量和径向分量如图3所示。
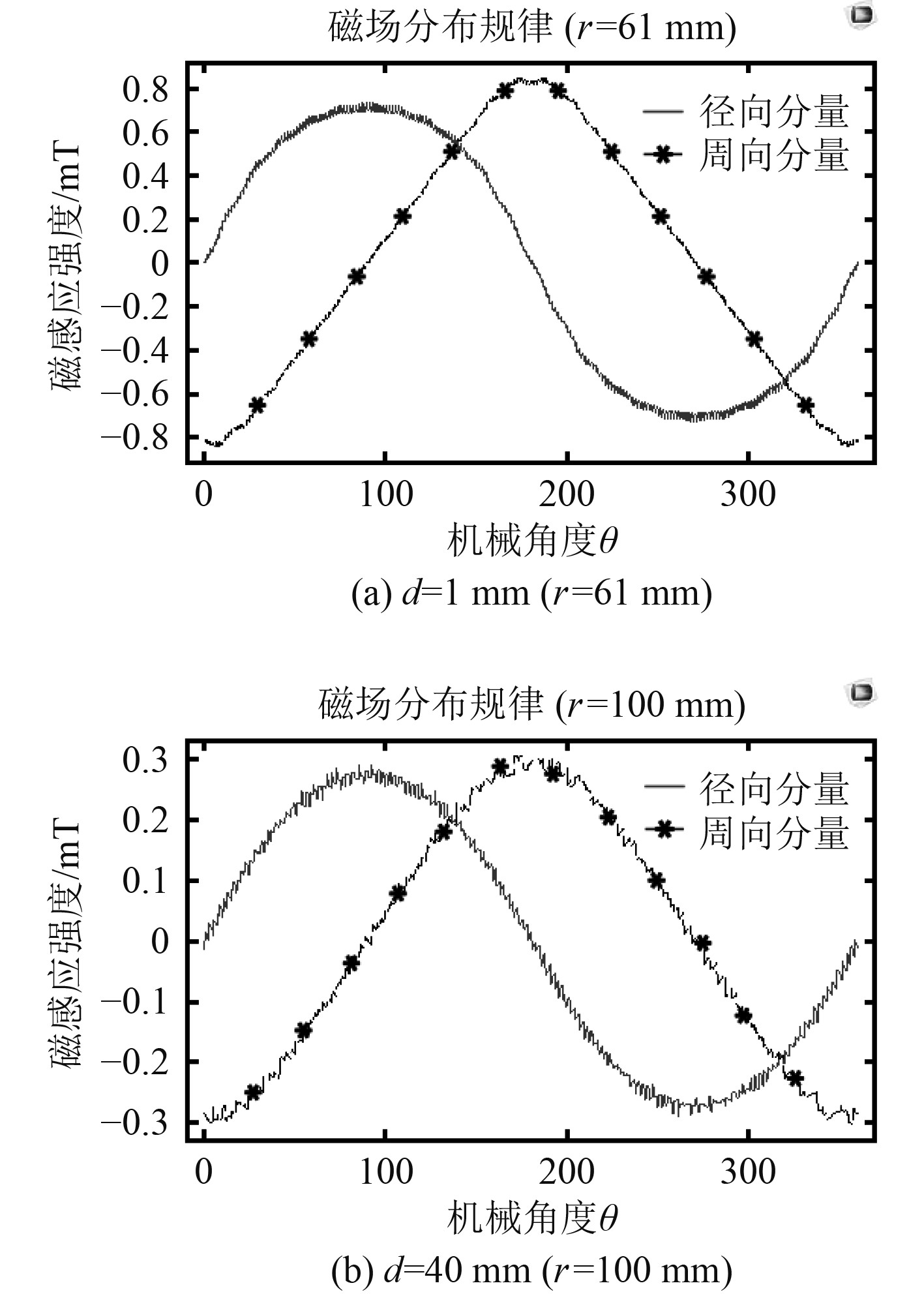
|
图 3 环境中周向与径向磁场分布 Fig. 3 Circumferential and radial flux density distribution in the environment |
径向分量和周向分量均呈现正弦分布规律,周期与极对数一致,在相位上两者相差1/4周期,这符合式(9)所得到的结论。图3(a)显示了在近电机面(d≤约半个电机半径,即d≤30 mm)径向分量类似于平顶波,周向分量类似于尖顶波,这是由于永磁体的极弧系数<1所导致的;在远电机面(d>半个电机半径),两者更接近于正弦波形,在越远的地方越接近。
根据式(10)的分析,磁通密度模在电机等圆周线上不变,即不随机械角度变化,但随距电机表面距离呈平方衰减。利用仿真软件在永磁电机的dq轴方向的环境域中设置一系列测量点(测量线),其结果如图4所示。
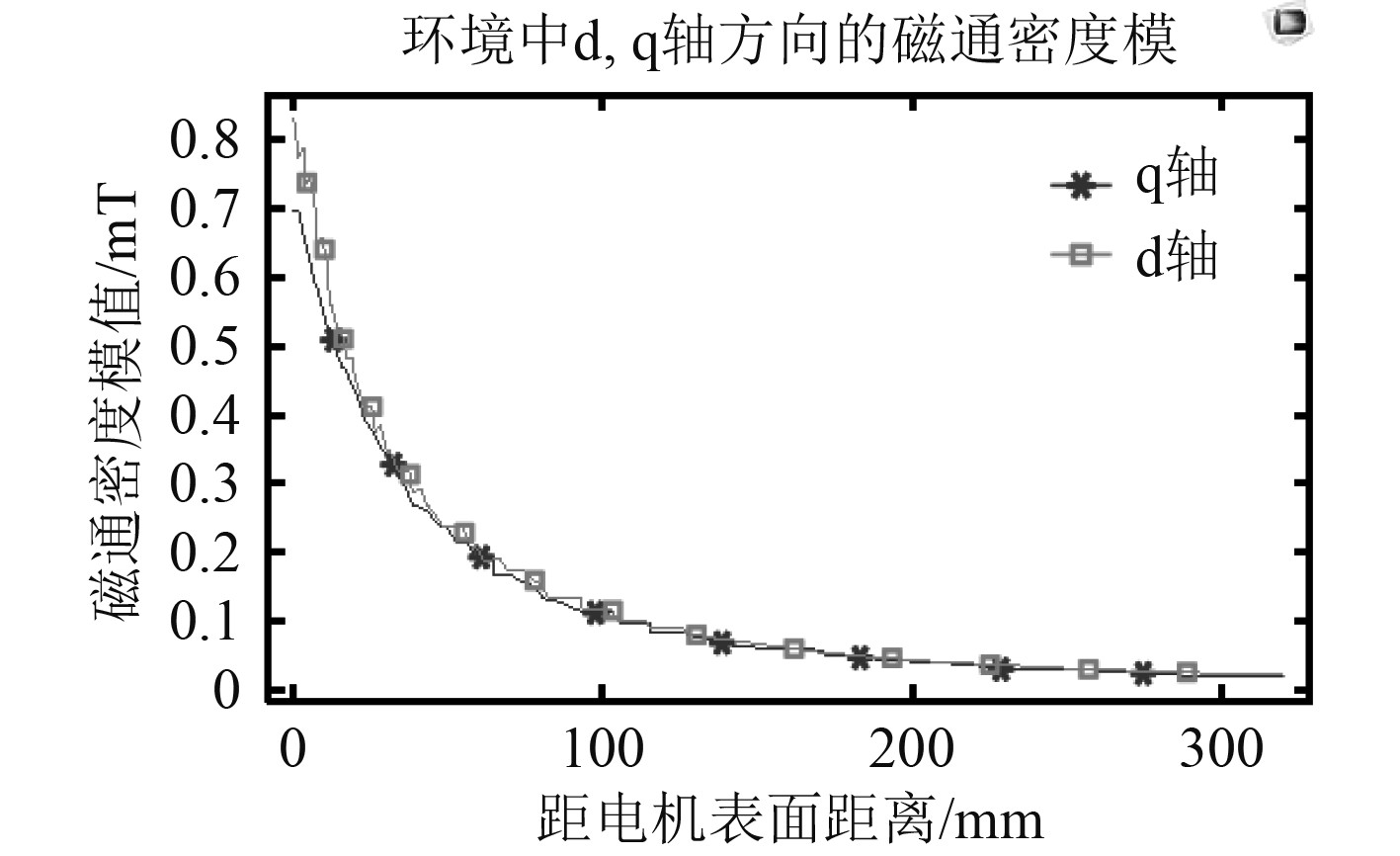
|
图 4 环境中距电机表面不同距离dq轴磁通密度模值 Fig. 4 The modulus of d & q axis flux density at different distances from the motor surface in the environment |
由图4可知,除了在近电机面d轴与q轴的磁通密度模有较小差别,在远电机面几乎无差别。也就可以近似认为电机在等圆周线上磁通密度模是不变的。其环境中的磁通密度模等值线如图5所示。
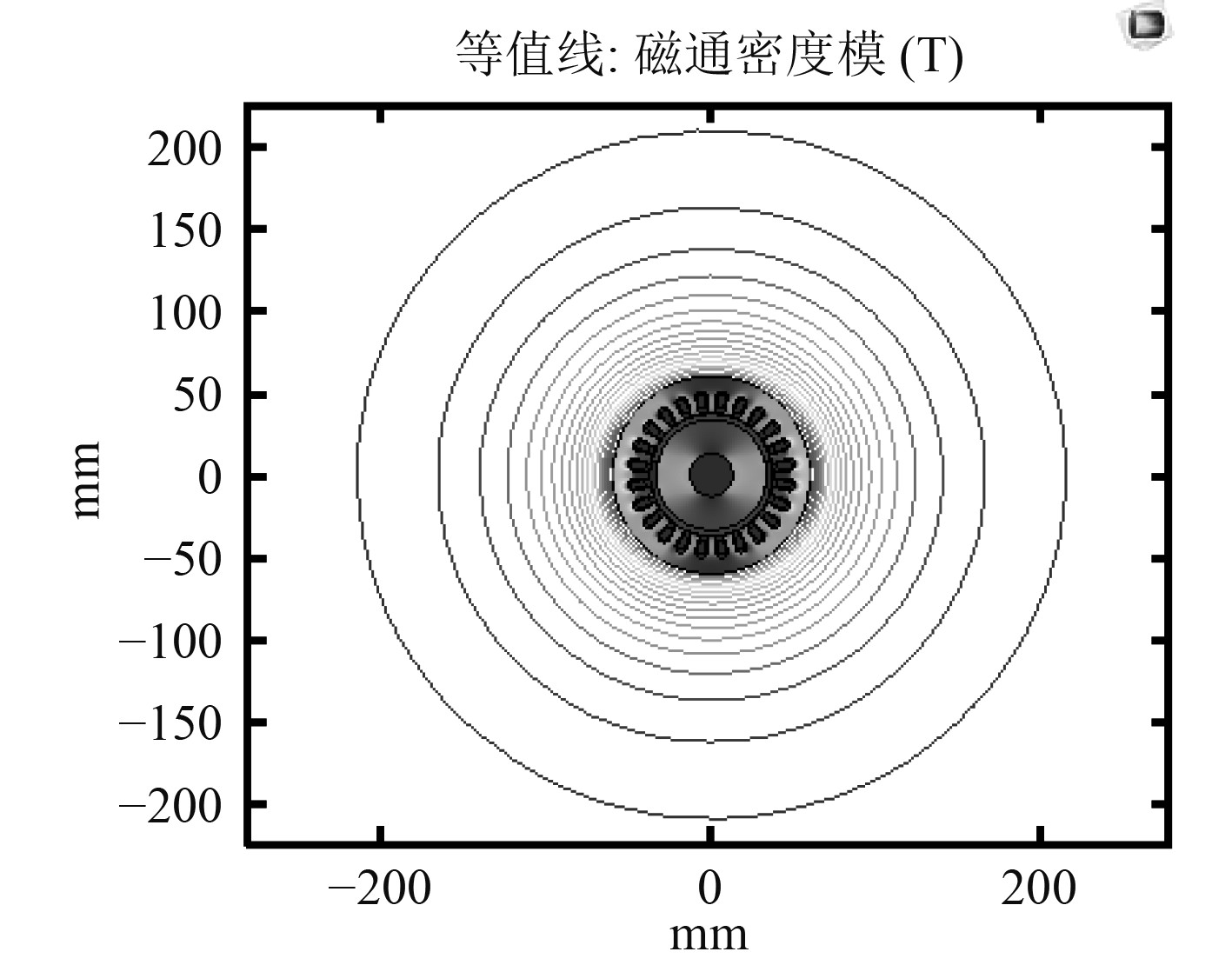
|
图 5 环境磁通密度模等值线 Fig. 5 Contours of ambient magnetic flux density modulus |
需要指出的是,仿真时外部环境区域的大小影响着仿真的结果,主要体现在径向与周向幅值的差别,环境区域越小,电机极数越少,影响越大。
2.2 空载仿真电机空载状态电机转子处于旋转中,所以周向与径向磁感应强度也会随着转子而旋转,周期与转速相同,但磁通密度模在等距圆周上仍然是定值。采用三相60°相带,绕组整距绕法,转速10 r/s,以距电机表面距离40 mm(r=100 mm)为例,不同时间各分量仿真结果如图6所示。
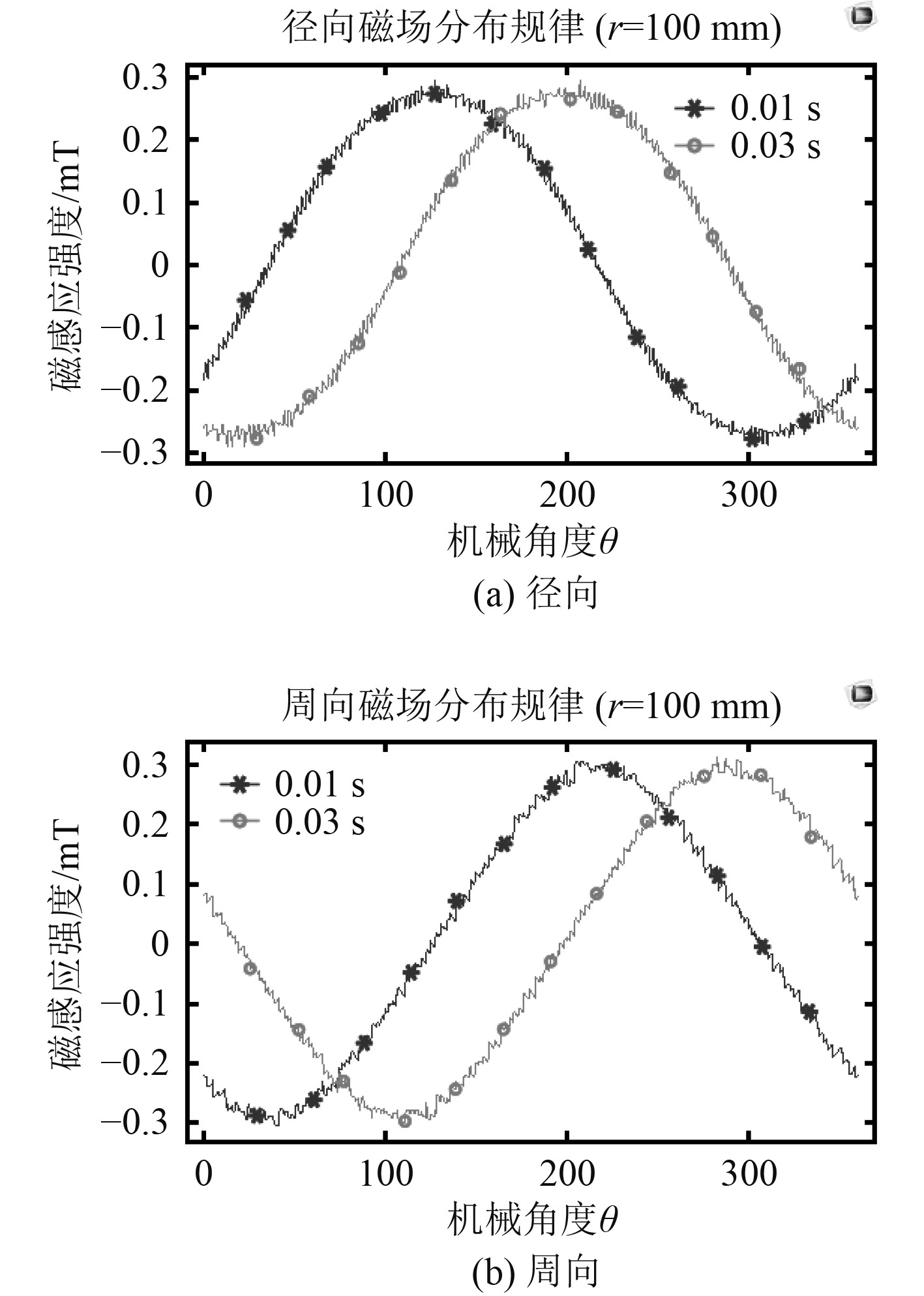
|
图 6 不同时间周向与径向磁场分布 Fig. 6 Distributions of the circumferential and radial flux density at different times |
电机外部环境的某一圆周线上的磁场径向分量和周向分量仍然符合正弦分布,与静态情况不同的是,由于转子的旋转,径向和周向分量也“跟着”旋转,即可以引入时间变量来衡量,空载时两极永磁电机环境域中各分量如下式:
| $ \left\{ \begin{gathered} {B_r}(r,\theta ) = \frac{1}{r}\frac{{\partial {A_z}}}{{\partial \theta }}{\text{ = }}{D_2}{r^{ - 2}}\cos (\omega t{\text{ + }}\theta ) ,\hfill \\ {B_\theta }(r,\theta ) = - \frac{{\partial {A_z}}}{{\partial r}} = {D_2}{r^{ - 2}}\sin (\omega t{\text{ + }}\theta )。\hfill \\ \end{gathered} \right. $ | (11) |
式中ω为转子旋转角频率。
设置空间上固定不动测量线,可以得到不同时间的磁通密度模如图7所示。
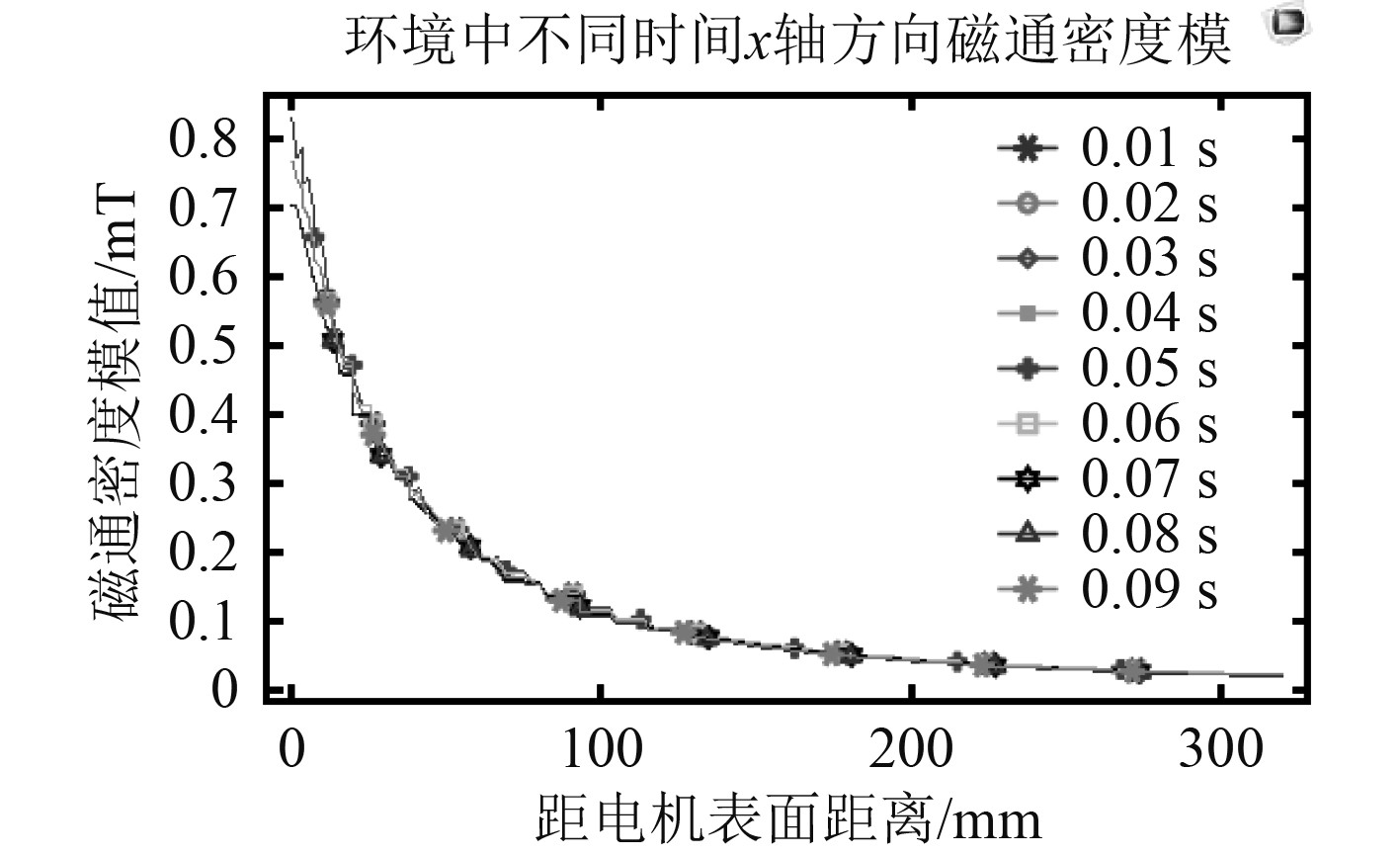
|
图 7 空载不同时间固定方向(x轴)磁通密度模 Fig. 7 Flux density mode of the no-load motor at different times (x axis) |
虽然电机在旋转,但是磁通密度模始终在等圆周线上几乎是不变的(近电机表面有较小影响),与距离电机距离成平方反比关系。
2.3 电机参数影响电机内部的结构不同可能会对环境磁场分布造成影响,下面从永磁体充磁方式、极对数、定子铁芯厚度、不导磁粗细、定子铁芯相对磁导率、极弧系数、气隙长度分别进行讨论。本小节中所有的磁场分布均是距离电机表面40 mm即r=100 mm的等圆周线上测量的。
2.3.1 充磁方式分别设置永磁体充磁方式为经向充磁和平行充磁,其他参数同表1,磁场分布和环境磁通密度模分布如图8所示。
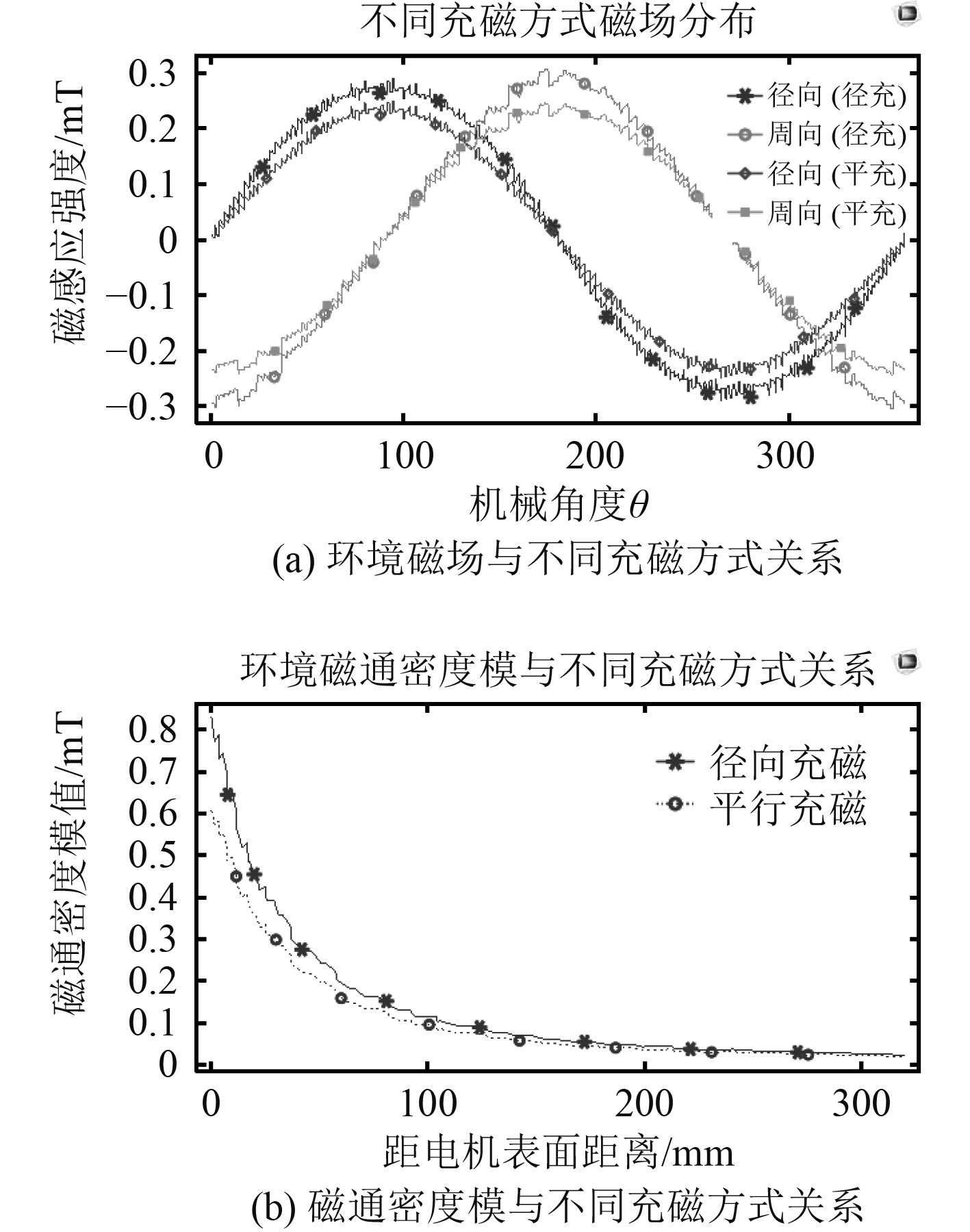
|
图 8 不同充磁方式仿真图 Fig. 8 Different magnetizing methods |
充磁方式的不同对磁场大小有一定影响,但是不影响分布规律,即环境中磁场各分量近似为正弦变化,磁通密度模与距离呈平方反比关系。
2.3.2 极数将电机由2极变为4极,仿真结果如图9所示。
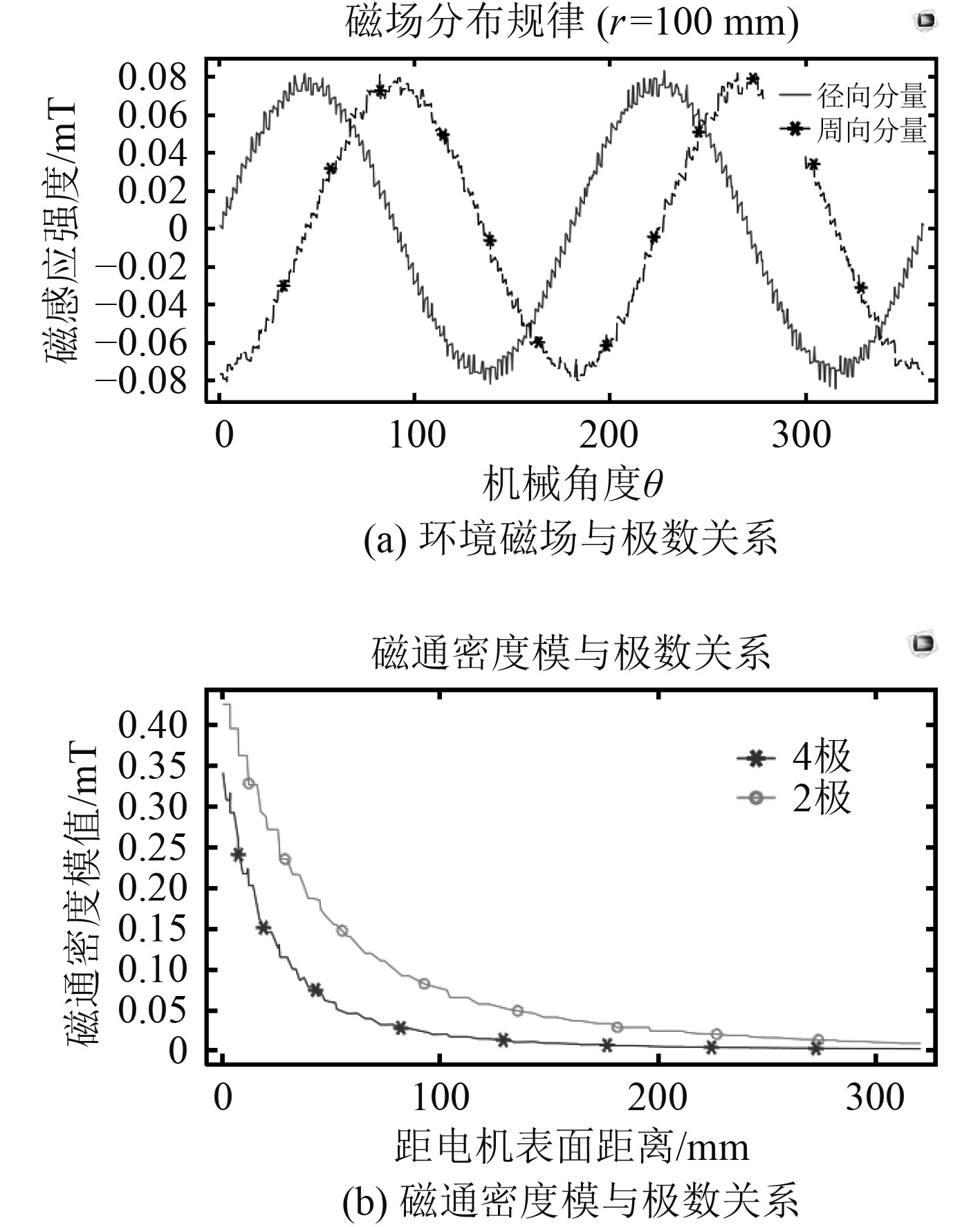
|
图 9 不同极数仿真图 Fig. 9 Different number of poles |
电机极数对环境磁场影响较大,主要体现在周向与径向分量的周期性与极对数一致(2极对应1个周期,4极对应2个周期),环境磁通密度模近似呈现3次方(极对数+1)反比衰减规律,即4极的衰减速度明显大于2极,6极8极电机同样满足此规律。所以极数越多,环境磁场衰减越快,这是由于极数多的电机相对于极数少的电机,环境磁场路径更短,更“容易”回到铁芯。
2.3.3 定子铁芯厚度利用参数化扫描,只变化定子铁芯的厚度,即铁芯的外半径,其他参数同表1,磁场变化情况如图10所示。
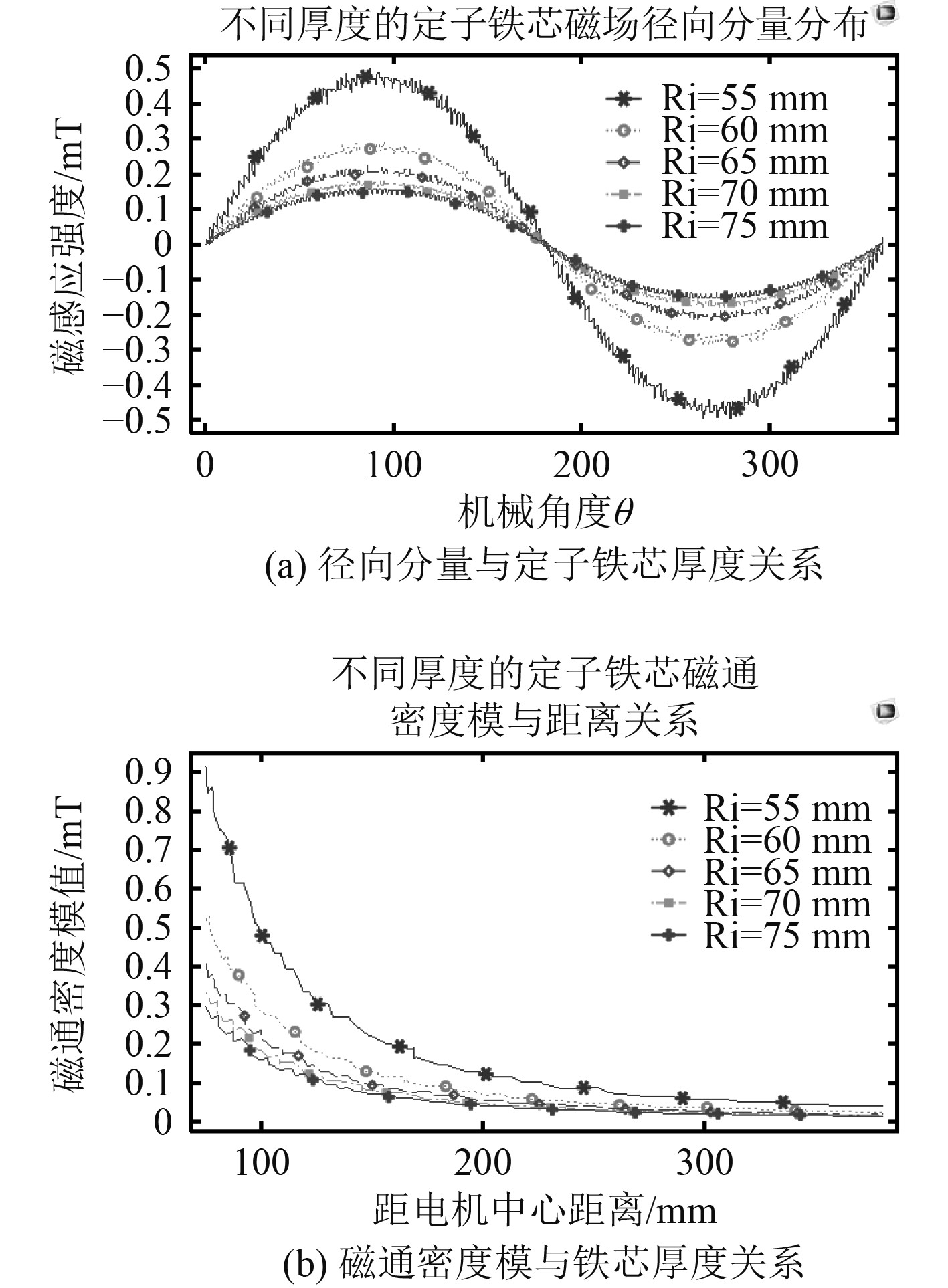
|
图 10 不同定子铁芯厚度仿真图 Fig. 10 Different stator core thickness |
定子铁芯越厚,磁通更容易“束缚”在铁芯中,所以环境中“泄漏”更少,衰减速度更快。需要指出的是,由于定子铁芯半径发生变化,所以图10(b)中x轴坐标更改为距电机中心距离r。
2.3.4 不导磁轴半径利用参数化扫描,只改变不导磁轴半径,磁场变化情况如图11所示。
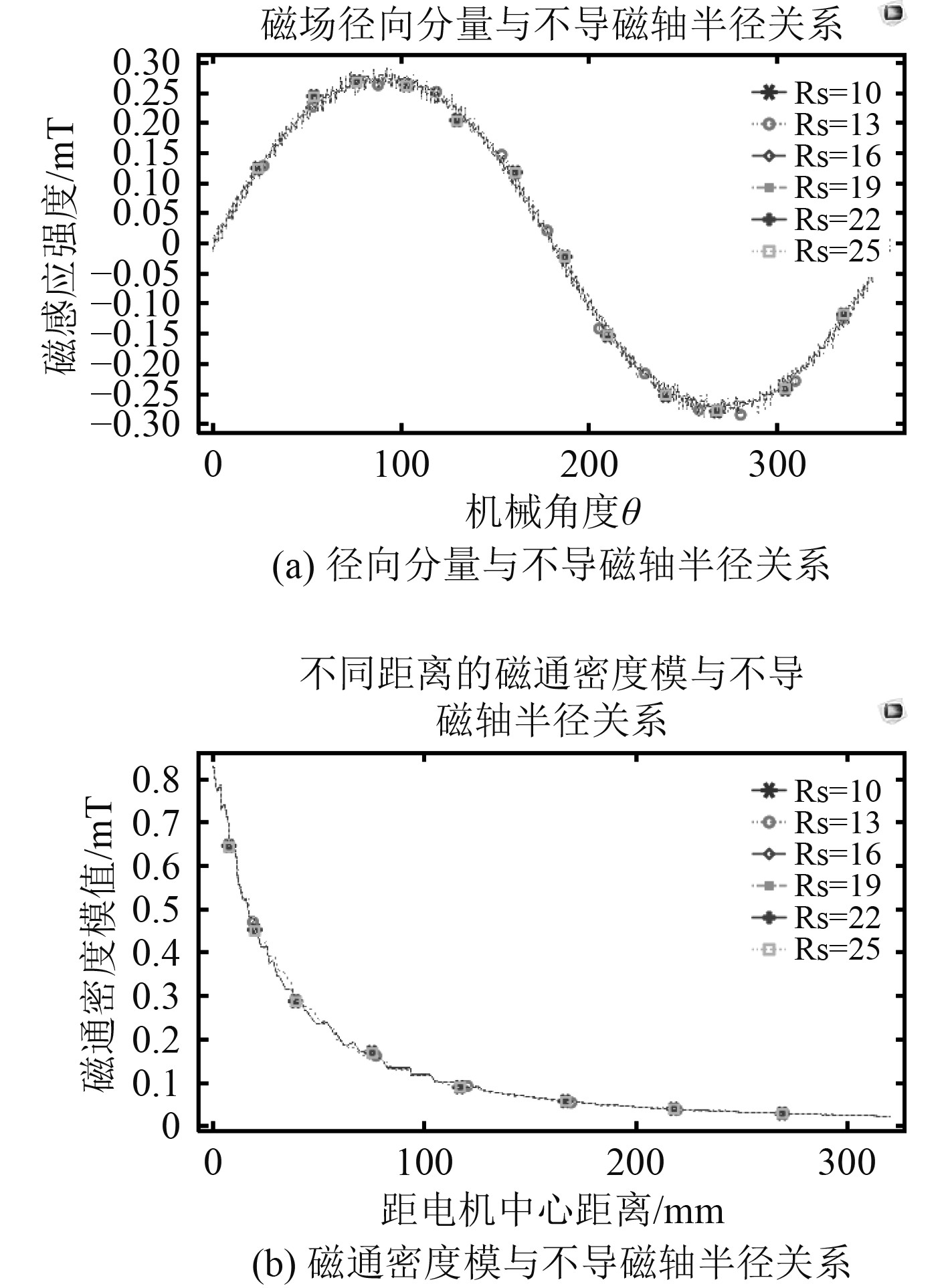
|
图 11 不同不导磁轴半径仿真图 Fig. 11 Different non-magnetic shaft radius |
可知,不导磁轴变化几乎对环境磁场分布没有影响。
2.3.5 不同铁芯磁导率利用参数化扫描只变化定子铁芯的磁导率,其他参数同表1,仿真结果如图12所示。
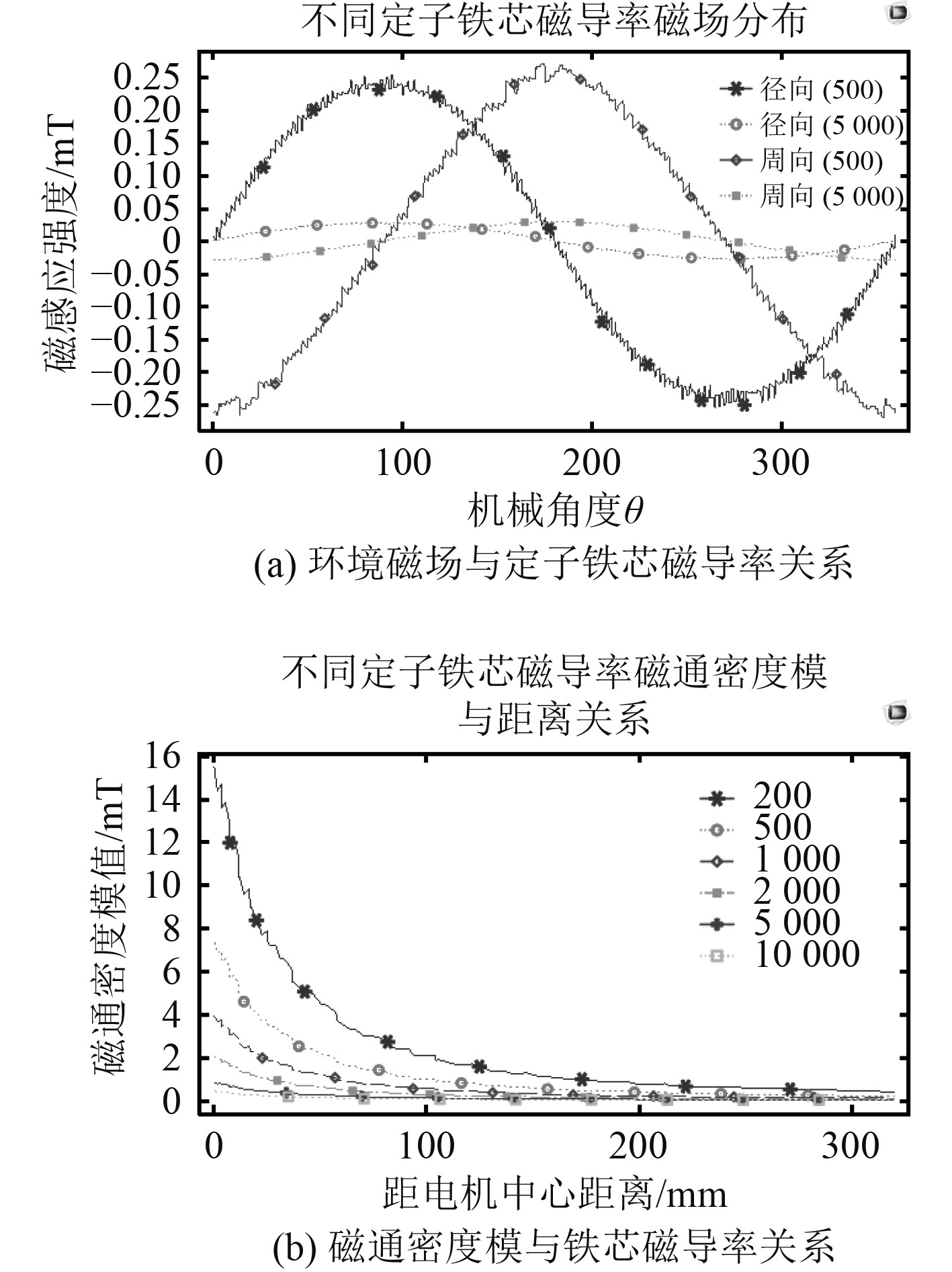
|
图 12 不同定子铁芯磁导率仿真图 Fig. 12 Magnetic permeability of different stator cores |
定子铁芯磁导率虽然不改变磁场分量的正弦分布、磁通密度模的平方衰减规律,但是对环境磁场的大小影响很大;铁芯越饱和,“泄漏”环境中会更多,反之则少。
2.3.6 气隙长度改变电机的气隙长度,可以得到其对环境磁场的影响规律如图13所示。
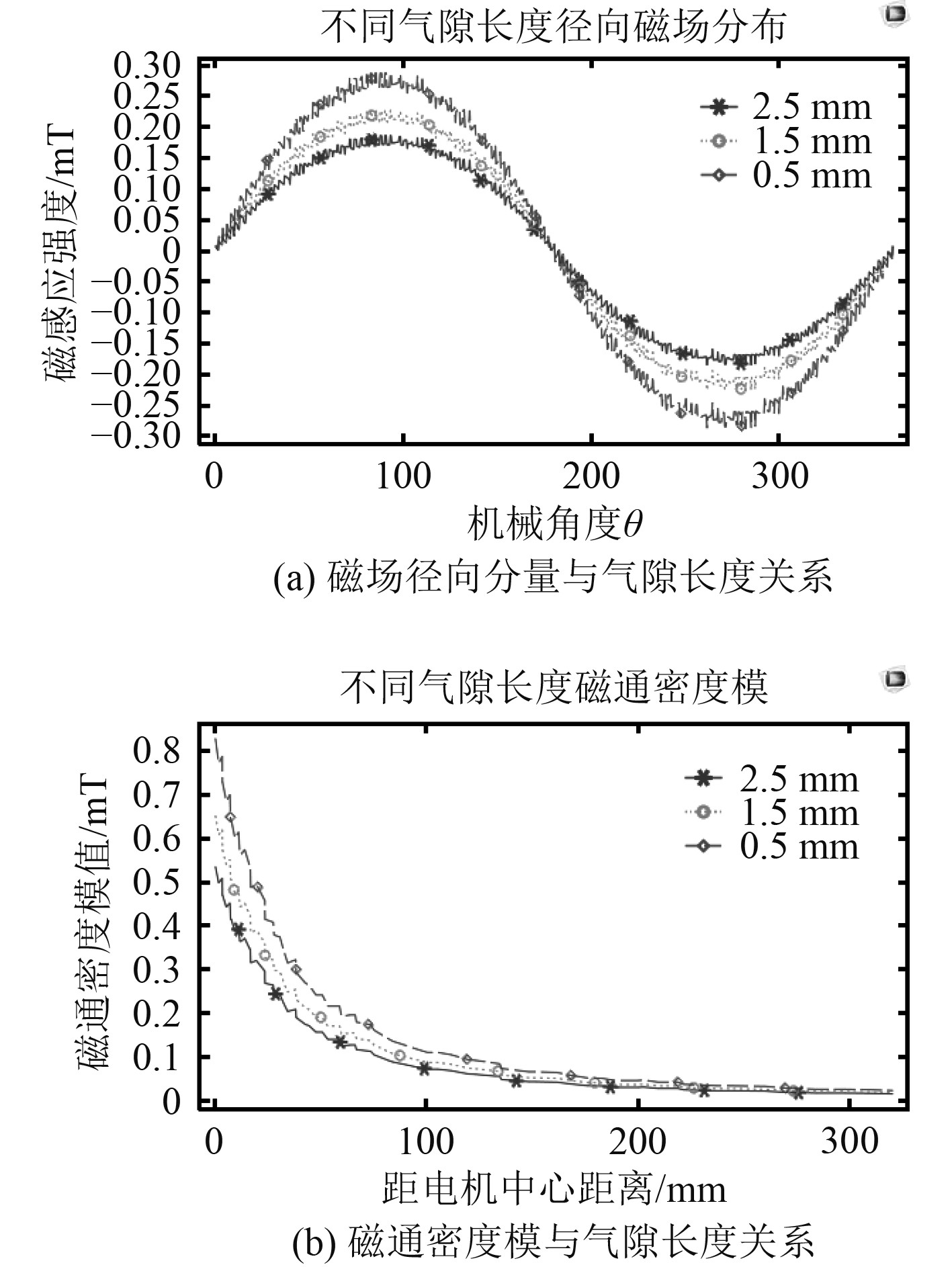
|
图 13 不同气隙长度仿真图 Fig. 13 Different air gap lengths |
气隙长度不仅影响电机的电气性能,同样影响电机的环境磁场大小,气隙越大,环境磁场越小,但不影响波形和衰减规律。
2.3.7 极弧系数改变电机的极弧系数,可以得到其对环境磁场的影响规律如图14所示。
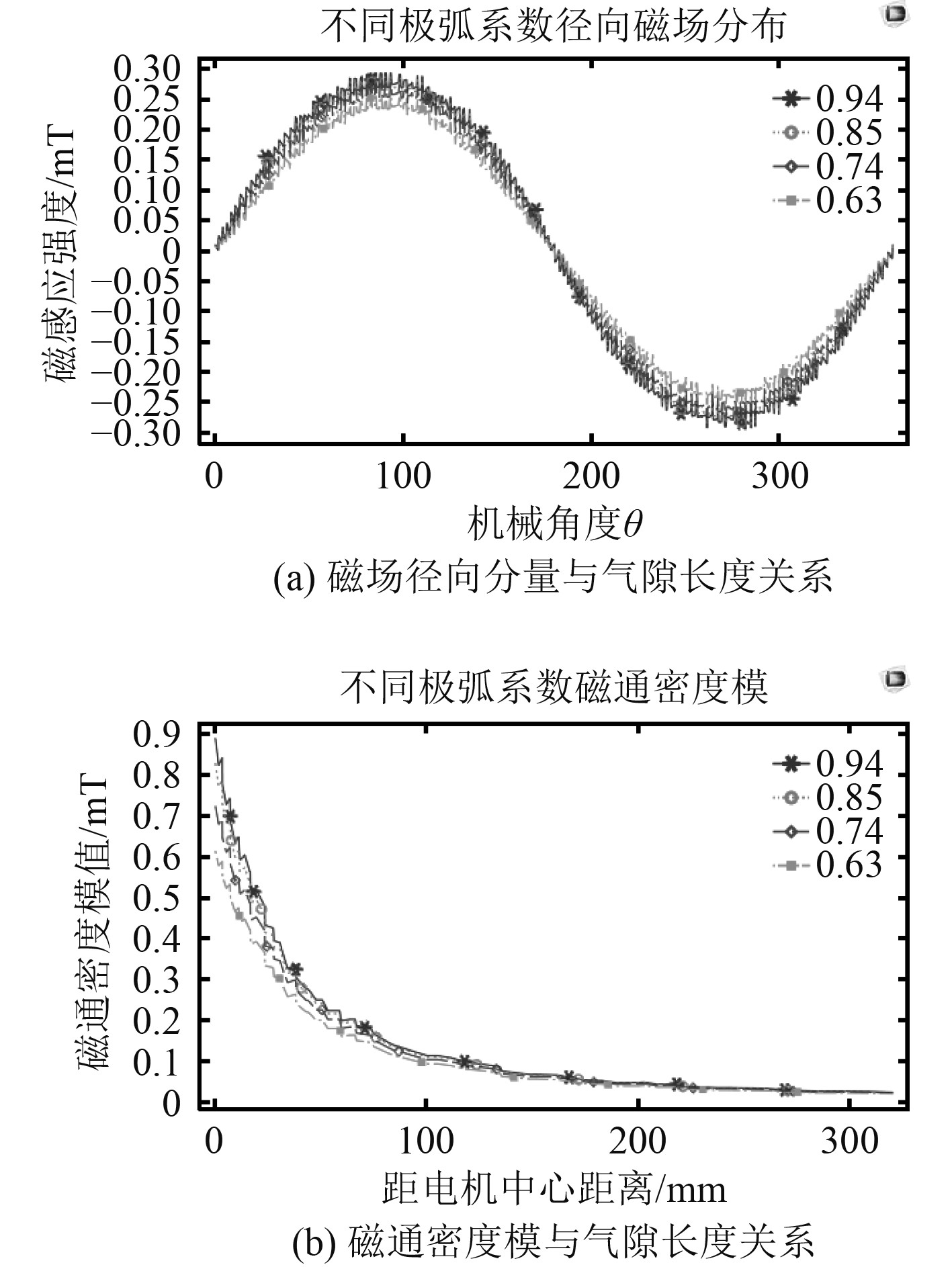
|
图 14 不同极弧系数仿真图 Fig. 14 Different pole arc coefficients |
极弧系数的变化对电机环境磁场影响并是不很大,也不影响其波形和衰减规律。
3 结 语本文建立了两极式的表贴式永磁电机环境磁场模型,利用有限元软件分别进行了静态和空载仿真分析,并在此基础上,分析了电机永磁体充磁方式、极对数、定子铁芯厚度、不导磁粗细、定子铁芯相对磁导率、极弧系数、气隙长度对环境磁场的影响,得出以下结论:
1)电机环境磁场周向分量与径向分量均近似呈现正弦分布,相位上两者相差1/4周期。
2)在近电机面(d≤约半个电机半径)径向分量类似于平顶波,周向分量类似于尖顶波,在远电机面(d>半个电机半径),两者更接近于正弦波形,在越远的地方越接近。
3)电机旋转时,环境磁场各分量也随着旋转,转速和转向与电机同步速一致,但等圆周线上磁通密度模不会发生变化(无论静态与旋转),与距离呈平方反比衰减。
4)定子铁芯厚度、铁芯磁导率对环境磁场大小有很大影响;永磁体的充磁方式、气隙长度、极弧系数对环境磁场大小有一定影响;不导磁轴半径对环境磁场无影响;但这些均不影响磁场的正弦规律和平方衰减规律。
5)电机极对数影响环境磁场的周期性、衰减性,极数越多,环境磁场周期各分量周期数越多,衰减越快,衰减次数等于电机极对数加1。
| [1] |
唐任远. 现代永磁电机理论与设计[M]. 北京: 机械工业出版社, 2016.
|
| [2] |
王秀和. 永磁电机[M]. 北京: 中国电力出版社, 2007.
|
| [3] |
耿连发, 吴延忠. 现代永磁电机发展趋势[J]. 沈阳工业大学学报, 1995(1).
|
| [4] |
我国永磁电机行业运行现状分析[J]. 电器工业, 2020(Z1): 38−44.
|
| [5] |
2018年永磁电机概况及趋势分析[J]. 电器工业, 2019(6): 40−43.
|
| [6] |
王一凡. 面向机载地磁测量的磁干扰补偿技术研究[D]. 武汉: 华中科技大学, 2012.
|
| [7] |
刘哲. 无刷直流电机对地磁测量的干扰分析及补偿研究[D]. 武汉: 华中科技大学, 2012.
|
| [8] |
温家保. 水下机器人对光泵磁力仪的干扰及消除算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [9] |
李尉, 宋保维, 胡欲立. 水下航行器用永磁直流电机漏磁场数值分析[J]. 机械与电子, 2011(3).
|
| [10] |
李富平, 胡欲立, 董金宝. 基于Magnet的永磁直流电动机漏磁仿真分析[J]. 微特电机, 2010, 38(4): 27-29. DOI:10.3969/j.issn.1004-7018.2010.04.009 |
| [11] |
沈建新, 陈利根. 永磁无刷电机中平行充磁2极气隙磁场的解析计算[J]. 电机与控制应用, 2006, 33(1): 7-10. DOI:10.3969/j.issn.1673-6540.2006.01.002 |
| [12] |
张岩岩, 周健, 耿海鹏, 等. 两极平行充磁环形永磁体磁场解析计算[J]. 微特电机, 2019, 47(1): 7-11+16. DOI:10.3969/j.issn.1004-7018.2019.01.002 |
| [13] |
CHENG W J, SUN Y H, YU L, et al. Analytical solution to magnetic field distribution of a parallel magnetised rotor with cylindrical or ring-type permanent magnet[J]. IET Electric Power Applications, 2015, 9(6): 429-437. DOI:10.1049/iet-epa.2014.0162 |
| [14] |
汤蕴璆, 梁艳萍. 电机电磁场的分析与计算[M]. 北京: 机械工业出版社, 2010.
|
| [15] |
姚端正, 梁家宝. 数学物理方法[M]. 北京: 科学出版社, 2010.
|
 2022, Vol. 44
2022, Vol. 44

