2. 中国船舶科学研究中心船舶振动噪声重点实验室,江苏 无锡 214082
2. National Key Laboratory on Ship Vibration and Noise, China Ship Scientific Research Center, Wuxi 214082, China
内孤立波是分层海洋中一种振幅大、传播距离远的海水内部波动,海上实测的最大波幅甚至达到了170 m,诱导的最大流速可达2 m/s[1-2]。内孤立波波面上方和下方存在密度跃变,水下航行器穿越内孤立波时,浮力不均衡,就会产生所谓的“断崖”掉深运动,内孤立波诱发的剪切流动还可导致水下航行器运动姿态发生突变甚至失控。内孤立波作用下水下航行器的运动响应特性有其力学载荷动因,探究载荷形成机理是内孤立波对航行性能影响和控制研究的基础和前提。
内孤立波载荷早期的研究,主要以海洋工程结构物为研究背景,内孤立波诱导的流场采用KDV理论给出,运用Morison公式计算内波流场在结构物上产生的水动力,可分析圆柱等简单构件的内波作用力[3-4]。
近年来,CFD方法也被用于内孤立波的研究,付东明等[5]采用分层流CFD模拟方法,开发了双推板式内孤立波的数值模拟方法,对实尺度海洋分层环境下细长回转体内孤立波载荷特性进行了分析。在此基础上,陈杰[6]采用指定速度入口边界条件实现了内波造波,避免了采用双推板方法必需使用动网格的局限,使得数值造波更稳定可靠,并对Suboff潜艇模型不同潜深工况下的内孤立波载荷特性进行了分析。王旭[7]对内孤立波数值造波方法进行了深入的研究,比较了造波源生成方法的优劣和内孤立波理论表达式的适用范围,并与试验结果进行了比较验证。魏岗与杜辉等[8-9]在分层流内波试验水池中开展细长体模型的内波载荷测量试验,并与数值模拟结果进行了比较,验证了内孤立波载荷数值模拟方法。关晖等[10]数值模拟了Suboff潜艇模型受上凸型和下凹型内孤立波2种情形下,内孤立波与潜艇相互作用的流场演化过程,给出了潜艇在穿越内孤立波时所受水平力、垂向力及力矩特性,并与不分层均匀流体中的结果进行了对比,结果表明潜艇在穿越内孤立波时所受力会在短时间内发生巨变,对潜艇的水动力性能有明显影响。
内孤立波是分层环境下产生的水体内部波动,置于其中的水下航行器所受的载荷除了受内波诱导流场的水动力作用外,还受分层密度差静力的作用。本文在前述研究建立了内孤立波载荷数值模拟方法并分析内孤立波载荷特性基础上,以Suboff潜艇模型为研究对象,深入分析潜体位于内孤立波波面上方、穿越波面、位于波面下方3种情形下,模型受内孤立波流场水动力和分层密度差静力作用过程,对比纵向力、垂向力和俯仰力矩特性差异,以期阐明水下航行器内孤立波载荷形成机理,为内孤立波作用下水下航行器运动响应研究和控制研究打下基础。
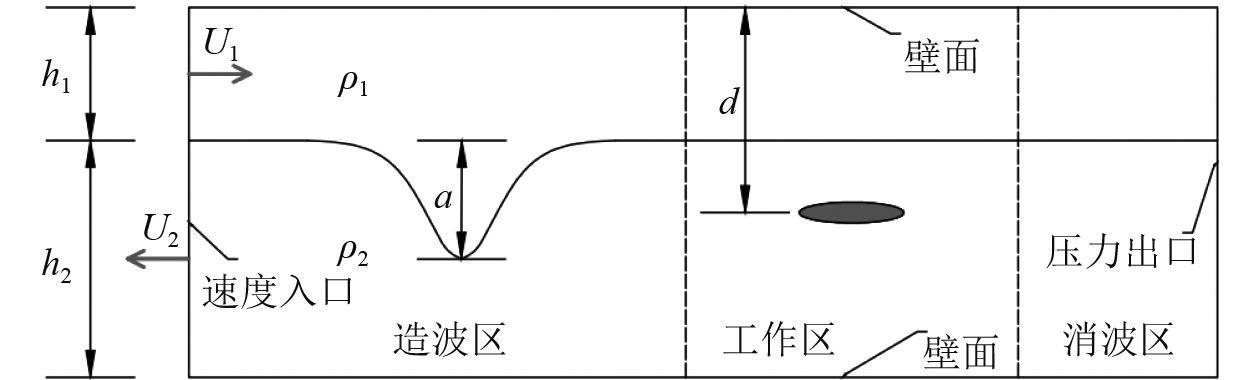
1 数值模拟方法 1.1 内孤立波理论将实际海洋密度层化结构简化为2层流体,如图1所示。上层为密度较轻的流体,厚度为
|
图 1 两层流体中内孤立波作用示意图 Fig. 1 Diagram of the action of internal solitary wave in two layer fluids |
有限深水中内孤立波通常采用KdV方程来表达,为了研究大振幅内孤立波的作用,本研究采用eKdV理论来表达内孤立波,eKdV相比KdV增加了2阶非线性项,eKdV方程如下[11]:
| $ {\mathrm{\eta }}_{{t}}+\left({{c}}_{0}+{{c}}_{1}\mathrm{\eta }+{{c}}_{3}{\mathrm{\eta }}^{2}\right){\mathrm{\eta }}_{\mathrm{x}}+{{c}}_{2}{\mathrm{\eta }}_{\mathrm{x}\mathrm{x}\mathrm{x}}=0 。$ | (1) |
式中:
eKdV方程有如下内孤立波解:
| $ {\eta }\left({x},{t}\right)=\frac{{a}}{{B}+\left(1-{B}\right){{\rm{c}}}{{\rm{o}}}{{\rm{s}}}{{{\rm{h}}}}^{2}\left[{\lambda }\left({x}-{c}{t}\right)\right]}。$ | (2) |
式中:
采用指定速度入口边界的方法实现造波,如图1所示。上层密度较轻的流体入口速度设为U1,下层密度较重的流体入口速度设为U2。由内孤立波的eKdV解,可知在波面上方和下方的水质点的平均水平速度为:
| $ {{U}}_{1}=-{c}\frac{{\eta }}{{{h}}_{1}-{\eta }};$ | (3) |
| $ {{U}}_{2}={c}\frac{{\eta }}{{{h}}_{2}-{\eta }} 。$ | (4) |
由式(3)和式(4)即可确定上层和下层的入口速度表达式,它是时间t的函数。编写场函数控制速度入口动态变化,即可实现内波孤立波的造波。
采用求解RANS方程进行流场的模拟,分层界面的模拟采用类似自由面模拟的VOF多相流模型,将上层和下层2种密度不同的流体看作2种流体相。出口采用压力出口,计算域顶部和底部采用壁面边界条件,前部和后部采用对称边界条件。
1.3 研究对象研究对象采用国际通用的Suboff潜艇模型,包含1个主体、1个指挥台和4个对称的尾翼,如图2所示。将该模型进缩比,缩小后的模型长1 m,直径约11.7 cm。

|
图 2 Suboff模型 Fig. 2 Model of Suboff |
分层流试验水池长25 m,宽3 m,深1.5 m,用盐度分层方法模拟海洋分层,上层冲淡水,下层冲盐水,采用溃坝方法造内孤立波。试验水深80 cm,上层为50 cm深淡水,下层30 cm深盐水,密度为1020 kg/m3。按照试验工况采用数值模拟方法对模型位于分层界面处内孤立波作用下所受的力进行了数值模拟。
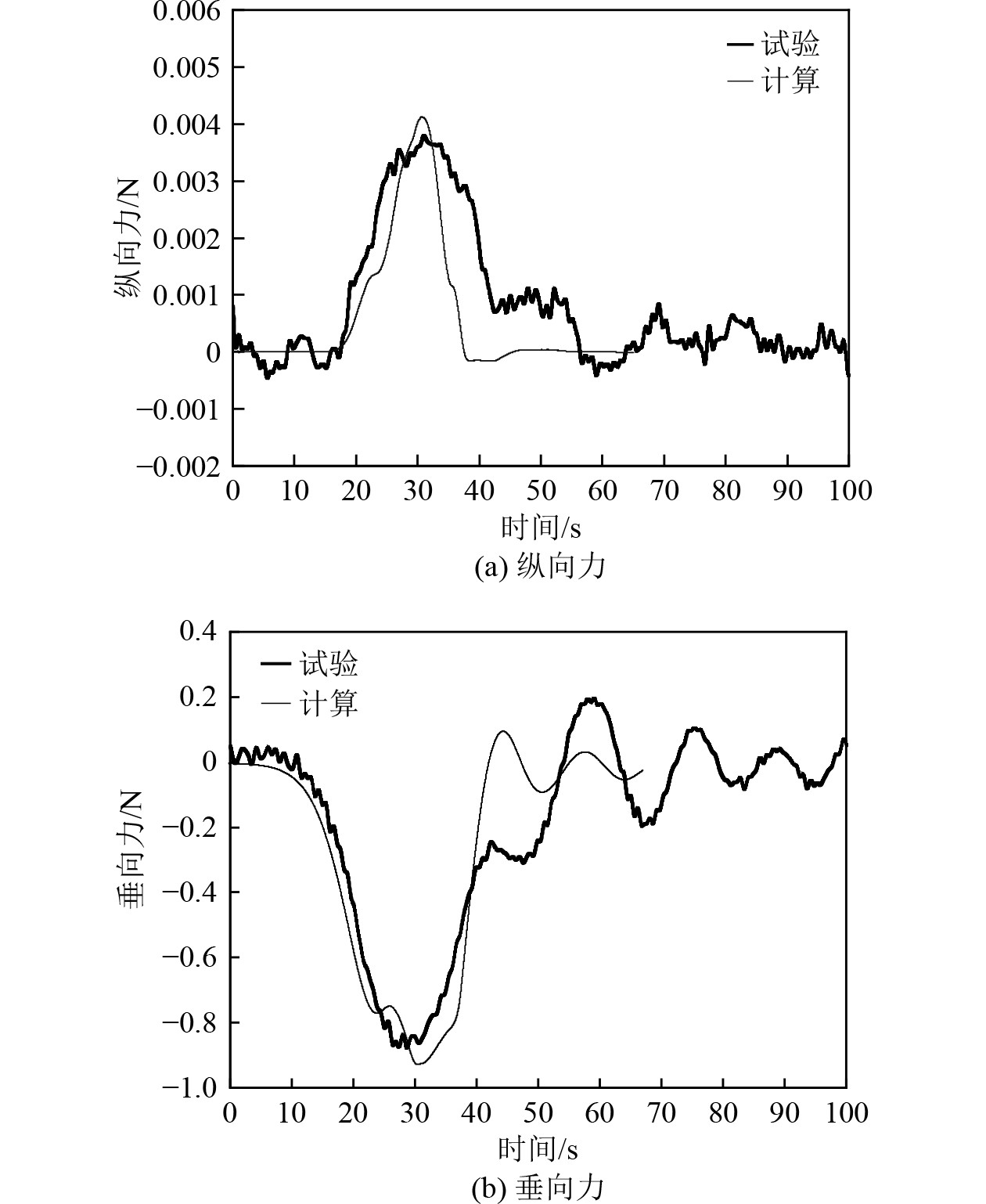
图3给出了模型纵向力和垂向力随时间变化关系曲线,并与试验结果进行了对比。可以看出内孤立波作用过程中模型所受的垂向力和纵向力随时间变化曲线变化规律与试验测试结果基本一致,计算模拟的纵向力幅值比试验结果大9.4%,垂向力的幅值比试验结果大7.5%。
|
图 3 模型受力随时间变化关系曲线 Fig. 3 Time-dependent curves of the forces on model |
从少量工况对比来看,内孤立波载荷数值模拟结果与试验结果有较好的吻合,数值模拟方法得到初步验证。
2 数值模拟结果及分析 2.1 数值模拟工况分层流体上层深度30 cm、密度998 kg/m3,下层流体深度70 cm、密度1025 kg/m3。为了研究不同波幅内孤立波作用下模型的受力特性,取波幅为10 cm,16 cm,20 cm的内孤立波进行数值模拟。为了分析模型相对于内孤立波位置不同时的受力情况,取潜深为20 cm,30 cm,40 cm,50 cm,60 cm,潜深20 cm时模型中心位于界面上方10 cm处,潜深30 cm时模型中心正好处于界面位置,潜深40 cm,50 cm,60 cm时模型中心分别位于界面下方10 cm,20 cm,30 cm处,用以模拟模型在内孤立波上方、穿越内孤立波波面、在内孤立波下方等典型情形。
内孤立波近似二维波,因此模型的受力主要是纵向力(阻力)、垂向力(升力)和俯仰力矩。阻力系数、升力系数和力矩系数的表达式分别为:
| $ {{C}}_{{D}}=\frac{{{F}}_{{x}}}{{{\rho }}_{0}{{g}}^{{、}}{A}{D}} \text{,} {{C}}_{{L}}=\frac{{{F}}_{{z}}}{{{\rho }}_{0}{{g}}^{{、}}{A}{D}} \text{,} {{C}}_{{M}}=\frac{{M}}{{{\rho }}_{0}{{g}}^{{、}}{A}{D}{L}} 。$ | (5) |
式中:
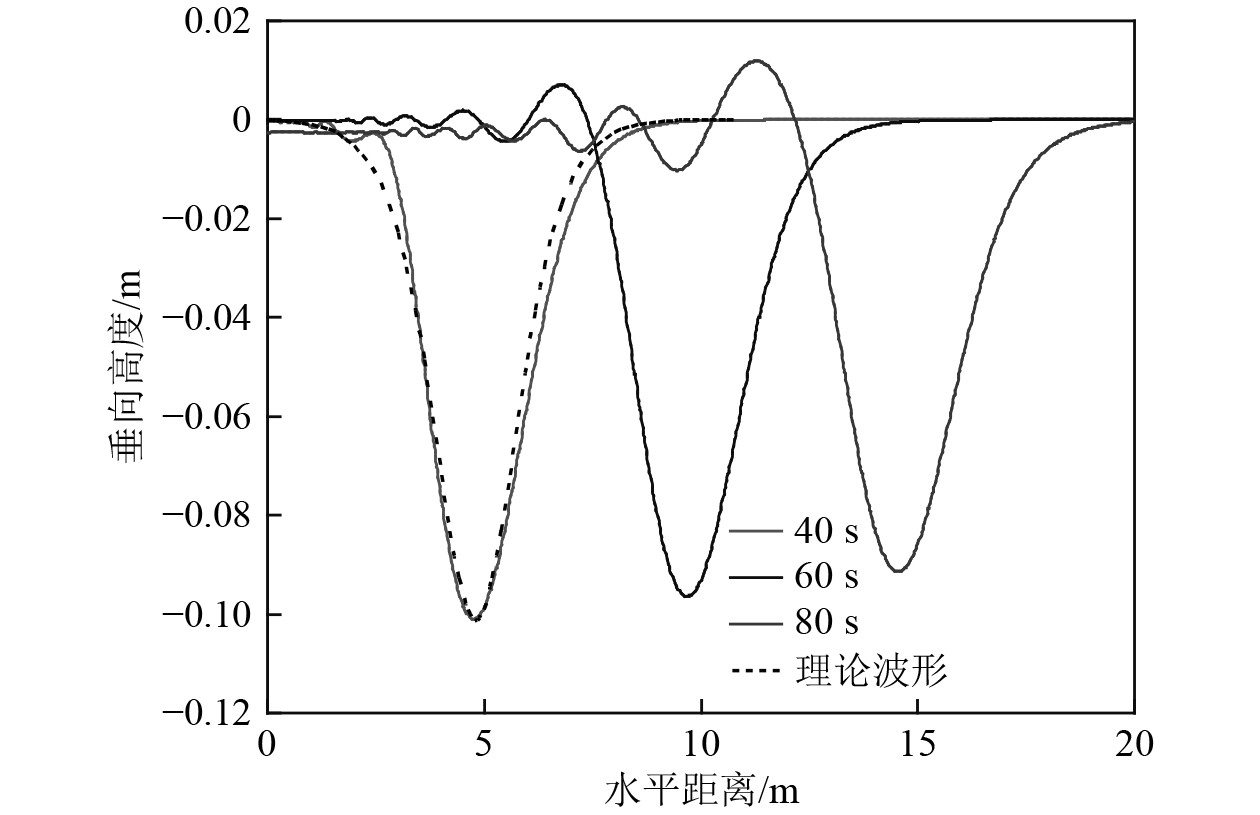
图4给出了数值模拟的内孤立波波形及传播演化情况。从图中可以看出采用速度入口造波方法,计算40 s后生成了完整的内孤立波,与式(2)表达的理论波形吻合良好。内孤立波生成后,以一定的速度向前传播,内孤立波形保持较好,60 s和80 s的波幅有所衰减,同时有内孤立波的尾波列出现,但其波幅远小于内孤立波主波。数值模拟的内孤立波的传播速度约为2.5 m/s,与理论值2.55 m/s吻合较好。
|
图 4 内孤立波波形及传播演化情况 Fig. 4 Waveform of internal solitary wave and propagation evolution |
图5为数值模拟的内孤立波波面处密度分布和流场矢量分布情况。内孤立波波面上方是密度较轻的上层流体,下方密度较重的下层流体,模型在穿越波面时,将产生浮力变化,引起失重或超重。内孤立波波面上方诱导的流场沿内孤立波传播方向,波面下方流场方向与上方相反,这就是所谓的内孤立波剪切流动。内孤立波左侧是上升流,右侧是下降流。整体来看,内孤立波诱导的流场是扁圆形顺时针旋转的回旋流场。

|
图 5 内孤立波诱导的流场特征 Fig. 5 The characteristic of flow filed induced by internal solitary wave |
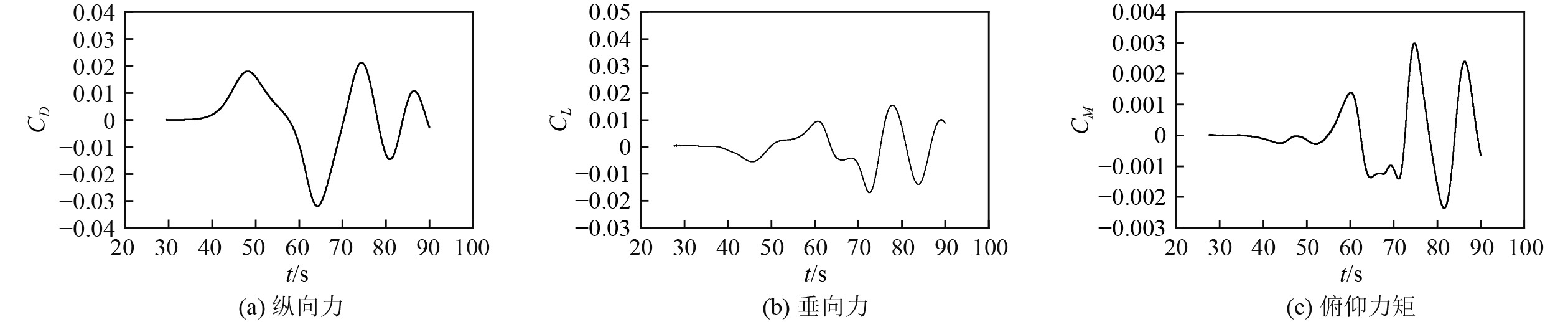
图6给出了模型位于分层界面上方10 cm波幅为20 cm工况时遭遇内孤立波过程中的受力曲线。该工况下,模型位于分层界面上方,下凹型内孤立波经过时,当然也位于波面上方,这意味着,模型没有流体密度差的静力作用,只受内孤立波诱导流场产生的水动力作用。从图6可以看出,受内孤立波作用过程中,纵向力、垂向力和俯仰力矩产生了一定的变化。纵向力变化曲线波动范围比垂向力大一些,量级一致。内孤立波经过后,受尾波列影响,纵向力、垂向力仍维持一定波动变化,由于尾波列波长变短,甚至于俯仰力矩变化曲线的波动幅度比内孤立波主波影响时还要大。可见,即使模型位于分层界面上方,受内孤立波诱导的流场影响,其水动力性能也产生了明显的变化。
|
图 6 模型位于分层界面上方10 cm工况的受力曲线 Fig. 6 Forces curve of the model located 10 cm above the interface |
图7给出了模型位于分层界面下方10 cm处波幅为20 cm工况时不同时刻模型与内孤立波相对位置图,图8给出了遭遇内孤立波过程中的受力曲线。从图中可以看出,该工况下初始时模型处于分层界面下方,内孤立波迎面传过来时,有模型穿入、穿出内孤立波面的过程,内孤立波作用过程中纵向力、垂向力和俯仰力矩产生了较大的变化。大约40 s(见图7(a))时模型开始受内孤立波作用,模型受到向左下方的流场作用,阻力开始增加,升力也开始增加,但幅度不大,模型头部遭受的流场比尾部强,所以在向左下的流场作用下,有埋首力矩产生。从45 s起(见图7(b)),模型抵近波面,即将进入波面上方低密度流体区域,由于浮力的改变,迅速产生向下的垂向力。至56 s(见图7(d))时,模型位于内孤立波正中间位置,完全处于波面上方低密度流体中,垂向力达到极值,此时流场呈水平向右,阻力达到正极大值,俯仰力矩很小,处于平衡状态。从60 s起((见图7(e)),模型开始穿出波面,由于浮力的增加,垂向力迅速减少,模型遭受的流场逐渐变为右向上的方向,产生了仰首力矩。至65 s(见图7(f))时,模型完全穿出波面,位于高密度流体中,此时,垂向力已很小,俯仰力矩也较小。

|
图 7 模型位于界面下方10 cm遭遇内孤立波过程图 Fig. 7 Diagram of the process of the model located 10 cm below the interface encountering internal solitary wave |
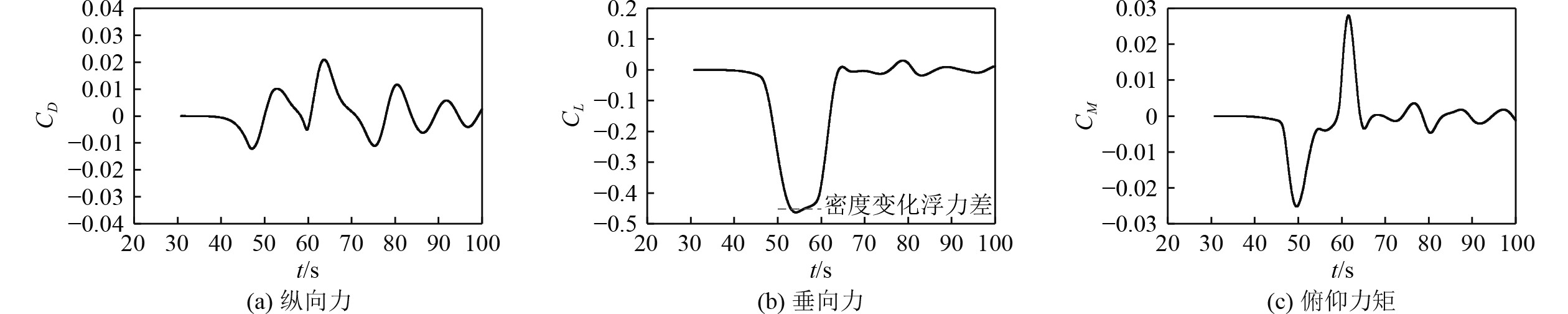
|
图 8 模型位于界面下方10 cm工况的受力曲线 Fig. 8 Forces curve of the model located 10 cm below the interface |
总的来看,有模型穿进穿出波面的情况下,模型所处的流体密度变化起了决定性作用,垂向力比纵向力大一个量级。对于垂向力,根据密度差计算了浮力差,约为2.22 N,换算成升力系数约为0.45。对于俯仰力矩,在模型穿进、穿出波面时,首尾浮力不平衡,俯仰力矩有极大值和极小值产生。
图9给出了模型位于分层界面下方30 cm波幅为20 cm工况时遭遇内孤立波过程中的受力曲线。该工况下模型潜深较深,始终处于波面下方,这意味着,模型没有密度差产生的静力作用,只有内孤立波流场产生的水动力作用。从图9可以看出,受内孤立波作用过程中,纵向力、垂向力和俯仰力矩也产生了一定的变化。从40 s至50 s,模型靠近内孤立波过程,受左向下方向的流场作用,产生了负的纵向力和垂向力。70 s后受内孤立波尾波列产生流场作用,由于尾波列波幅小,对模型的作用力明显减小,受力曲线呈小幅波动。

|
图 9 模型位于界面下方30 cm工况的受力曲线 Fig. 9 Forces curve of the model located 30 cm below the interface |
为了分析潜深对内孤立波载荷的影响,对波幅为20 cm时模型位于分层界面上方10 cm(d20)、界面处(d30),界面下10 cm(d40),20 cm(d50),30 cm(d60)等5种工况进行了模拟,内孤立波作用过程中的受力曲线如图10所示。
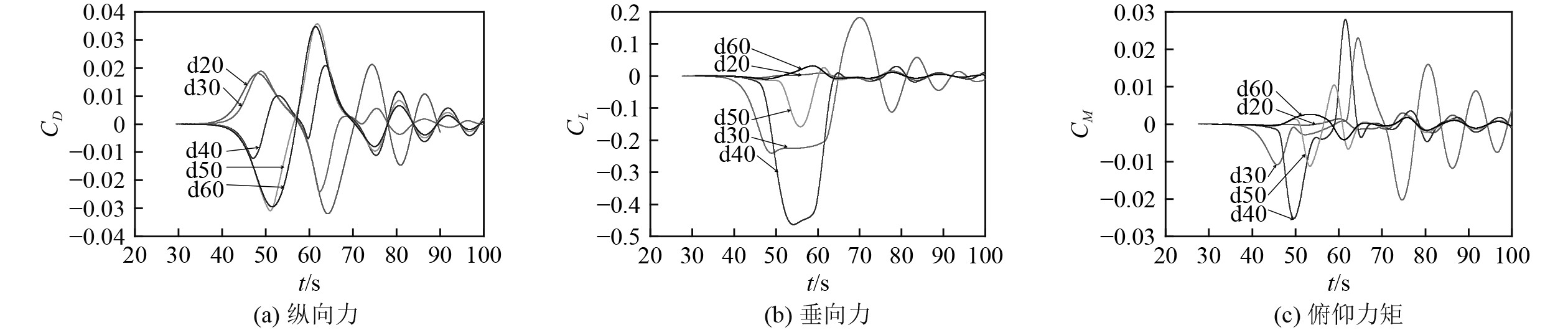
|
图 10 潜深不同时模型受力曲线 Fig. 10 Forces curve of the model for different depths |
对于纵向力,分层界面上方10 cm、界面处2个工况的变化规律与另外3个工况的变化规律相反,这是因为分层界面上方10 cm、界面处2个工况主要受内孤立波诱导的上层流场作用,界面下10 cm,20 cm,30 cm主要受内孤立波诱导的下层流场作用,而波面上方和下方的流场方向相反。
对于垂向力,分层界面上方10 cm和界面下30 cm等2个工况的变化规律与另外3个工况的变化规律不同,这是因为分层界面上方10 cm工况模型始终位于上层轻流体中,界面下30 cm工况模型始终位于下层重流体中,这2个工况都不受密度差静力作用,仅受内孤立波流场的水动力作用,垂向力幅值较小,与另外3个工况的变化规律也相反。
对于俯仰力矩,由于密度差形成的垂向力较大,在形成俯仰力矩过程中起主要作用,与垂向力受潜深影响规律相同,分层界面上方10 cm和界面下30 cm等2个工况的变化规律与另外3个工况的变化规律相反。
2.5 不同波幅时作用力特性分析为了分析内孤立波波幅对内孤立波载荷的影响,对模型位于界面下方10 cm时,波幅为10 cm,16 cm,20 cm 3个工况进行了模拟,内孤立波作用过程中的受力曲线如图11所示。
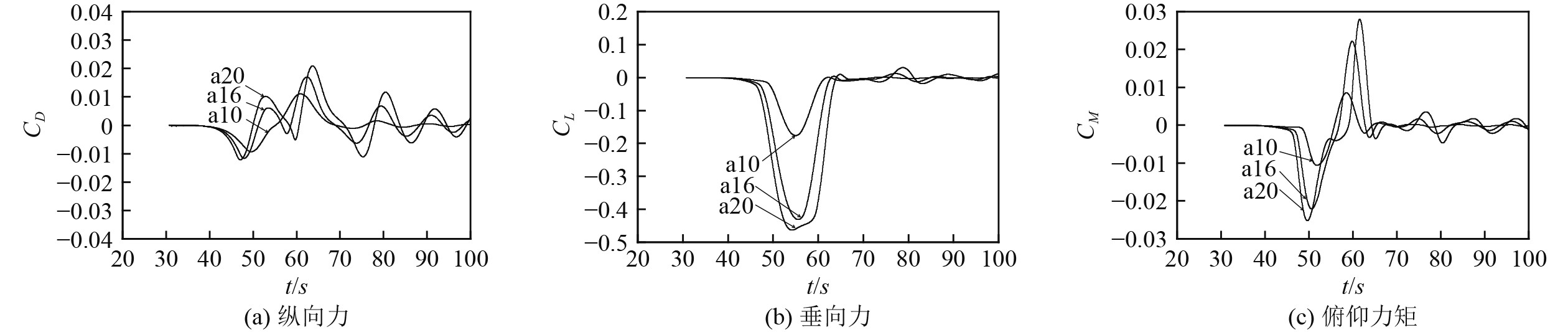
|
图 11 波幅不同时模型受力曲线 Fig. 11 Forces curve of the model for different wave amplitudes |
波幅为10 cm的工况,内孤立波波谷经过模型时,模型基本上刚好一半在波面上方低密度流体中,一半在波面下方高密度流体;波幅为16 cm工况,模型恰好处于波面上方;波幅为20 cm工况,模型完全处于波面上方。从图11可以看出,纵向力、垂向力和俯仰力矩随时间变化过程中极大/小值都随波幅增加大而增大。波幅为10 cm工况的纵向力曲线变化规律与其他2个工况有明显不同,这是因为该工况没有穿越内孤立波波面。对于垂向力曲线,受密度差浮力变化的影响,产生了明显的竖直向下的力,波幅为20 cm的工况,内孤立波波谷经过时,模型完全处于低密度流体中,产生的力最大。3种工况都有密度差的静力作用,垂向力比纵向力大一个量级。对于俯仰力矩,主要是由模型进、出波面时,首尾受垂向力作用不平衡而引起,3种工况的俯仰力矩变化曲线基本一致。
3 结 语经过数值模拟,得出如下结论:
1)有模型穿进、穿出波面的情况下,模型所处的流体密度变化,起了决定性作用,垂向力比纵向力大一个量级;对于俯仰力矩,在穿进、穿出波面的情况时,艏艉浮力不平衡,分别产生了俯仰力矩的极大值和极小值;模型位于分层界面上方或始终位于内孤立波波面下方时,受内孤立波流场的影响,其水动力性能也产生了明显的变化。
2)潜深不同时,受波面上方和下方的流场方向相反影响,模型位于分层界面上方与下方纵向力的变化规律相反;受有无密度差静力作用影响,穿越波面的工况与始终位于分层界面上方或下方的工况垂向力变化规律明显不同。
3)不同波幅时,纵向力、垂向力和俯仰力矩随时间变化规律基本相同,极大/小值都随波幅增加大而增大,波幅大小不影响内孤立波载荷的形成机理;
本文的研究初步阐明了内孤立波作用下潜艇的水动力载荷形成机理,为下一步开展内孤立波作用下潜艇运动响应特性研究和掉深机理分析打下了基础。
| [1] |
BOLE J B, EBBESMEYER C C, ROMEA R D. Soliton curents in the South China Sea : measurements and theoretcal modeling[C]//The 26th Annual OTC in Houston, Texas, U. S. A. , 2-5 May, 1994: 387−396.
|
| [2] |
EBBESMEYER C C, COOMES C A, et al. New observations on internal waves(solitons) in the South China Sea using an acoustic Doopler current proflier[C]//Marine Technology Society 91 Proceedings, New Orleans, 1991: 165−175.
|
| [3] |
沈国光, 叶春生. 内波孤立子的非波导荷载计算[J], 天津大学学报. 2005, 38(12): 1046−1050.
|
| [4] |
CAI S Q, LONG X M, GAN Z J. A method to estimate the forces exerted by internal solitons on cylinder piles[J]. Ocean Engineering, 2003, 30: 673−689.
|
| [5] |
付东明, 尤云祥, 李巍. 两层流体中内孤立波与潜体相互作用的数值模拟[J]. 海洋工程, 2009, 27(3): 38-44. DOI:10.3969/j.issn.1005-9865.2009.03.006 |
| [6] |
陈杰, 尤云祥, 刘晓东, 等. 内孤立波与有航速潜体相互作用数值模拟[J]. 水动力学研究与进展, 2010, 25(3): 343-351. |
| [7] |
王旭. 内孤立波与深海浮式结构物相互作用特性研究[D]. 上海: 上海交通大学, 2015.
|
| [8] |
WEI Gang, DU Hui, XU Xiao-hui, et al. Experimental investigation of the generation of large amplitude internal solitary wave and its interaction with a submerged slender body[J]. Physics, Mechanics & Astronomy, 2014, 57(2): 201-310. |
| [9] |
DU Hui, WEI Gang, GU Meng-meng, et al. Experimental investigation of the load exerted by nonstationary internal solitary waves on a submerged slender body over a slope[J]. Applied Ocean Research, 2016(59): 216-223. |
| [10] |
关晖, 魏岗, 杜辉. 内孤立波与潜艇相互作用的水动力学特性[J]. 解放军理工大学学报, 2012, 13(5): 577-582. |
| [11] |
CHOI W, CAMASSA R. Fully nonlinear internal waves in a two-fluid system[J]. Journal Fluid Mech, 1999, 396: 1−36
|
 2022, Vol. 44
2022, Vol. 44
