2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
滑行艇与普通的排水型船舶在航行时有着明显的区别,根据船速的不同,其航行过程可分为3个阶段:预滑行阶段、半滑行阶段和全滑行阶段。由于滑行艇具有这3个受力完全不同的航行阶段,阻力的预报比排水型船舶困难很多,国际上还尚未实现满足工程要求的滑行艇阻力纯理论预报。长期以来,滑行艇的阻力主要采用模型试验、经验公式或系列图谱进行预报。国内的设计单位也主要依赖于模型试验[1]和利用系列试验资料或图谱来估算滑行艇阻力。
近年来,随着基于RANS方程的粘性流数值计算方法、重叠网格和六自由度运动模型的引入,滑行艇的水动力性能预报取得了快速发展。与基于无粘性甚至是线性假设之上的传统理论对比,CFD方法采用了更接近流体真实流动的数学模型,计算出来的结果更加接近实际情况[2-6]。
本文以某型槽道滑行艇为计算对象,采用结构化动态重叠网格,引入艇体垂向及纵摇方向2个自由度,对滑行艇稳定直航时的受力、姿态、流场进行预报分析。
1 数值计算 1.1 控制方程及湍流模型连续性方程和动量方程如下:
| $ \frac{{\partial ({{\bar u}_i})}}{{\partial {x_i}}} = 0 \text{,}$ | (1) |
| $ \frac{{\partial ({{\bar u}_i})}}{{\partial t}} + {\bar u_j}\frac{{\partial ({{\bar u}_i})}}{{\partial {x_i}}} + \frac{{\partial (\overline {{{u'}_i}{{u'}_j}} )}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial \bar p}}{{\partial {x_j}}} + \frac{{\partial {{\bar \tau }_{ij}}}}{{\partial {x_j}}} \text{。}$ | (2) |
式中:
| $ {\bar \tau _{ij}}{\text{ = }}\nu \left( {\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}}{\text{ + }}\frac{{\partial {{\bar u}_j}}}{{\partial {x_i}}}} \right) \text{。}$ | (3) |
湍流模型采用SST
| $ \begin{split} &\frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}}(\rho k{{\bar u}_i}) = \frac{\partial }{{\partial {x_j}}}\left({\varGamma _k}\frac{{\partial k}}{{\partial {x_j}}}\right) + {G_k} - {Y_k} ,\\ &\frac{\partial }{{\partial t}}(\rho \omega ) + \frac{\partial }{{\partial {x_i}}}(\rho \omega {{\bar u}_i}) = \frac{\partial }{{\partial {x_j}}}\left({\varGamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}\right) + {G_\omega } - {Y_\omega } + {S_\omega }\text{。} \end{split} $ | (4) |
式中:
重叠网格是指划分网格时,对物体的各个部件单独划分网格,然后将各个部件网格嵌入到背景网格中,网格之间存在重叠区域。经过挖洞等预处理将计算域之外的网格(如船体内部的网格)排除在计算之外,然后对剩余重叠区域的网格建立插值关系,以达到对整个计算域的求解。赵发明等[7]在重叠网格方面进行了大量的研究,并指出水平集方法与重叠网格能较好地模拟带自由液面的船舶绕流问题。
1.3 Level-Set水平集方法在计算流体力学领域,Level-Set水平集方法常用于预报流体的自由液面。水平集方法的基本原理是将二维闭合曲线或三维闭合曲面表示为比其高一维的形状的等值线或等值面,等值线或等值面称为水平集,高维形状对应的函数称为水平集函数。水平集方法的优势主要发挥在构造物理模型演变过程中。
1.4 船体姿态变化预报方法滑行艇在不同航速下船体表面压力分布及航行姿态会产生较大的变化。这种姿态变化的预报需要采用URANS方程求解艇体绕流场获取船体表面实时受力,并结合刚体六自由度运动方程计算姿态变化,最终利用结构化动态重叠网格进行网格变形来实现。
2 计算对象采用某水面槽道滑行艇模型进行计算,主尺度如表1所示。
|
|
表 1 槽道滑行艇主尺度 Tab.1 Main dimensions of channel planing craft |
|
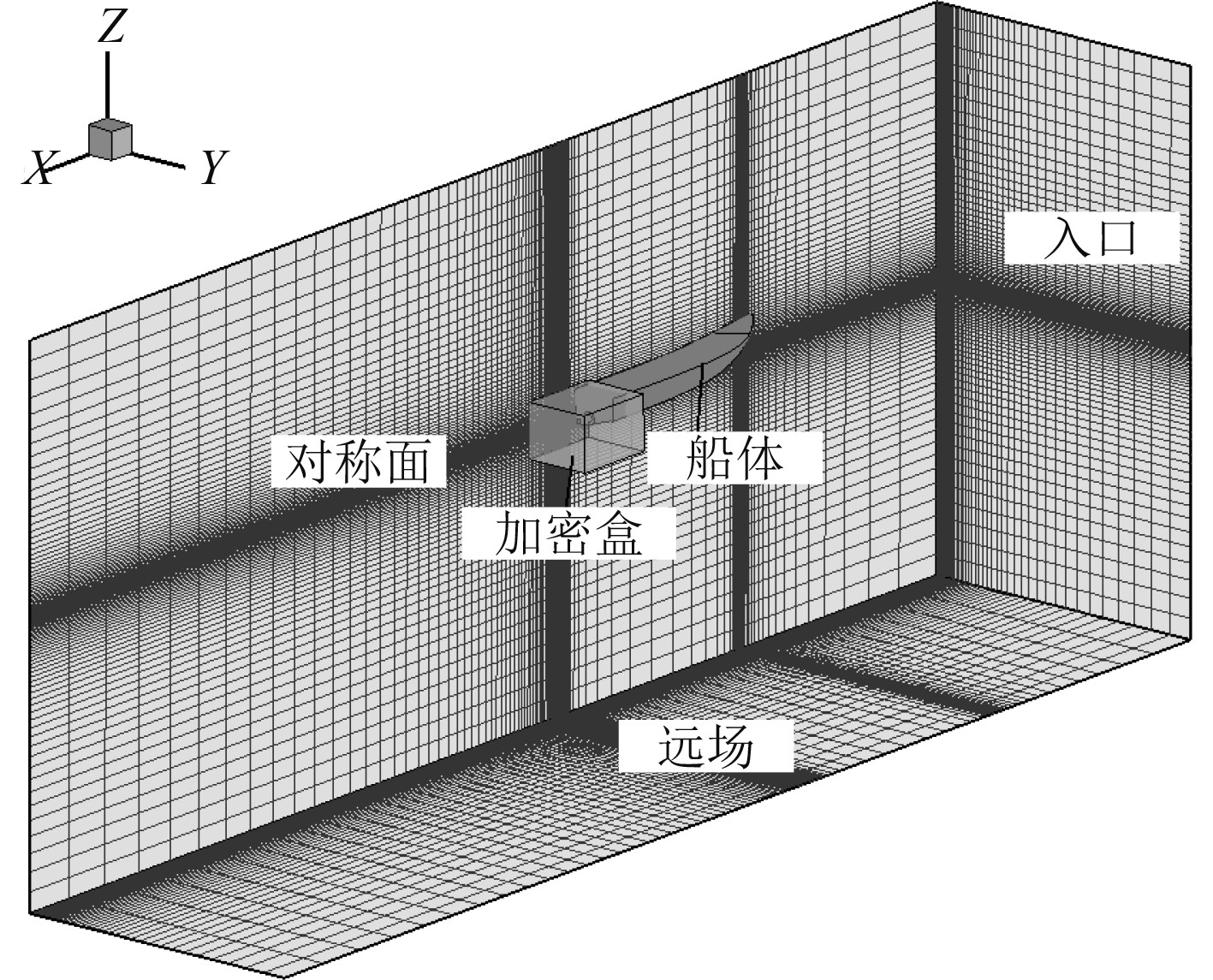
图 1 计算域及边界条件 Fig. 1 Computational region and boundary conditions |
|
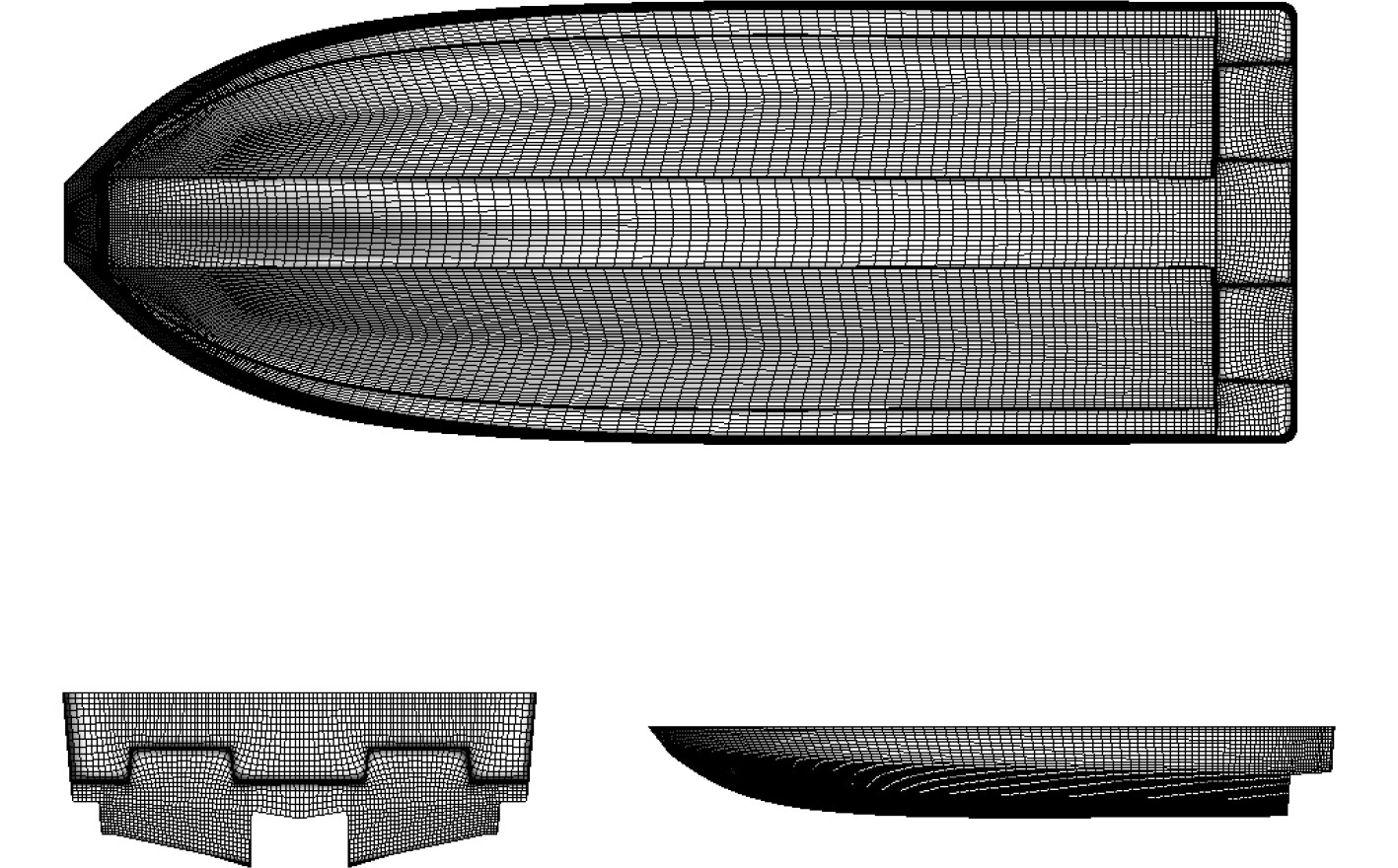
图 2 艇体网格 Fig. 2 Mesh generation |
通过对不同航速下槽道艇的直航计算,最终形成结果如表2所示。其中Fr定义为:
|
|
表 2 快速性计算结果 Tab.2 Calculation results of resistance performance |
| $ Fr = \frac{V}{{\sqrt {{{gL}}} }} \text{。}$ |
式中:V为滑行艇航速;L为滑行艇长度;g为重力加速度。
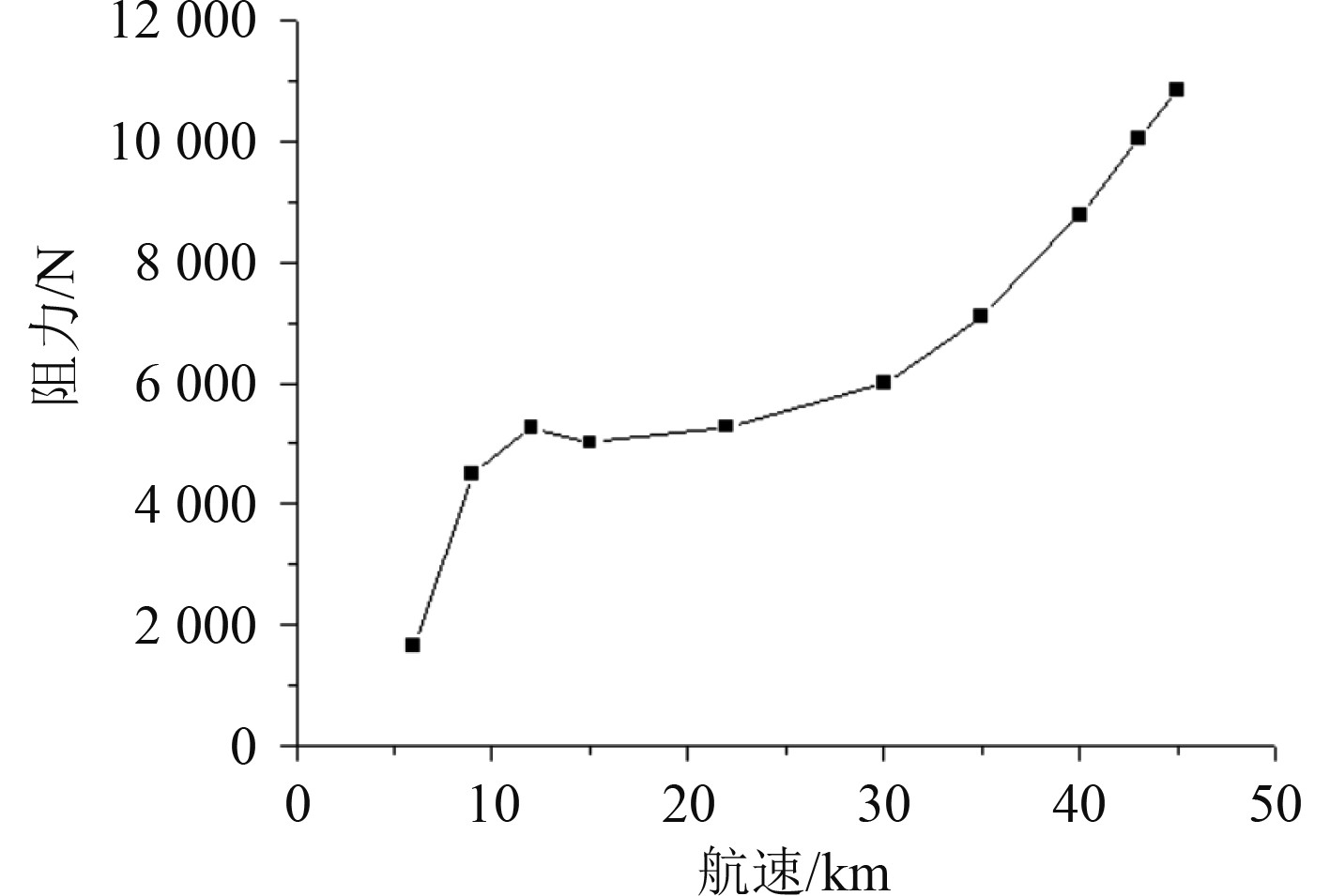
可以看到,槽道艇在12 kn左右会有一次阻力峰的出现,当越过阻力峰后,阻力在一定范围内不升反降,如图3所示。通过阻力对比能发现,槽道艇12 kn的航行阻力与22 kn航行阻力十分接近,据此可知,槽道艇在达到起滑速度12 kn后,艇体航速将迅速上升至22 kn。
|
图 3 阻力-航速曲线 Fig. 3 Resistance curve |
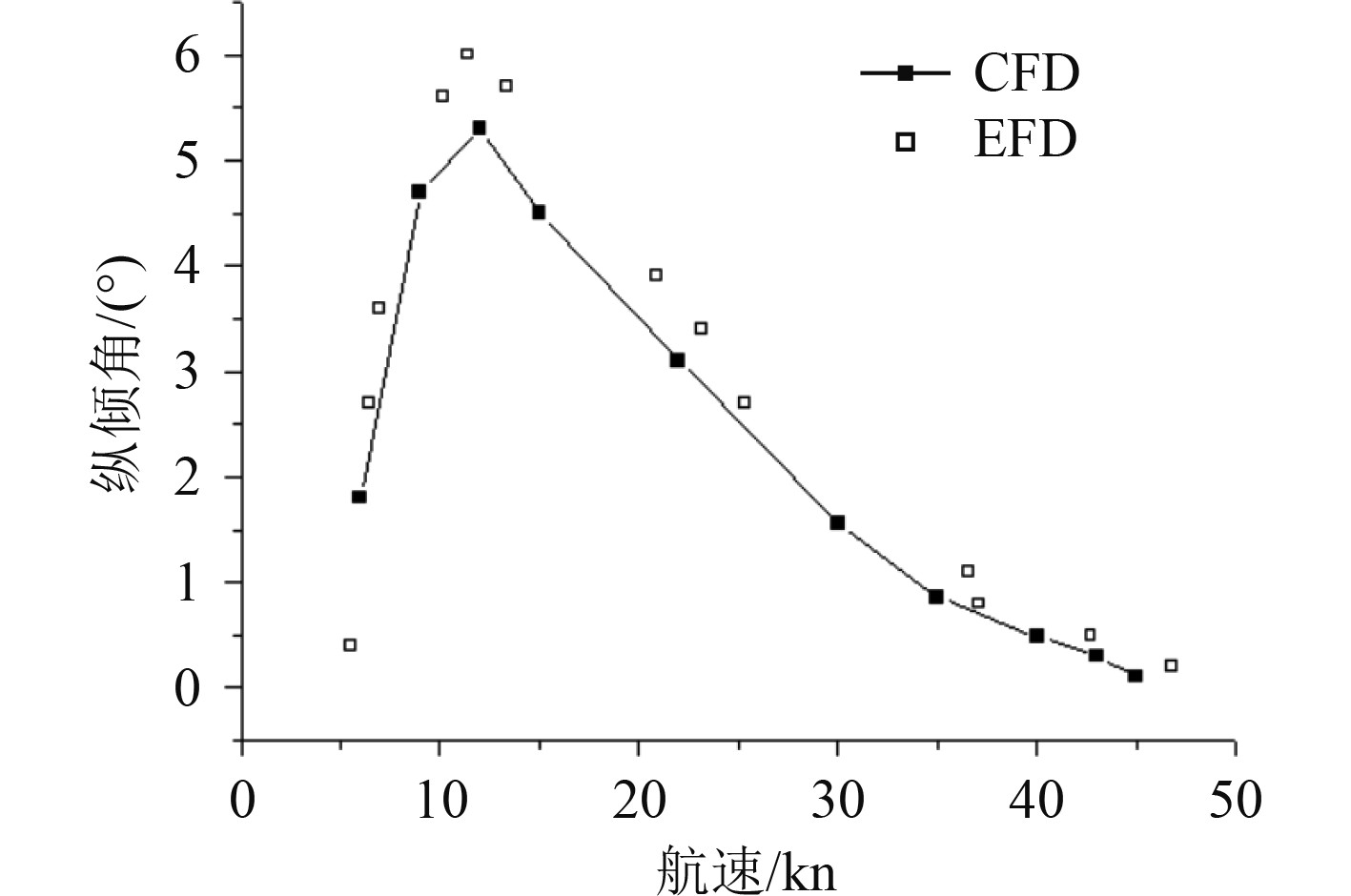
滑行艇的纵倾角则体现出先上升后下降的趋势,该角度的峰值点为5.3°,恰好对应阻力曲线中的阻力峰。而当航速超过起滑速度后,纵倾角逐渐下降,该特征可作为实际航行时起滑的判断依据。图4给出了槽道艇实船试验数据与仿真数据的对比结果,吻合较好。
|
图 4 纵倾角-航速曲线 Fig. 4 Pitch curve |
图5~图8给出了不同航速时的自由液面波形图。通过对不同航速时自由液面波形图的观察可以发现,槽道艇在航速较低时,呈现明显的排水航行特征,首尾波系接近凯尔文波。随着航速增大,船体兴波的变化较为明显,船侧和船底的水流在船尾的某个位置交汇,形成了明显的鸡尾状水丘,散波角度减小。而随着槽道艇航速的进一步增大,兴波逐渐减弱,槽道喷出水柱的距离增长,尾流场向内收缩。该种特征被认为增加了槽道艇的虚长度,有利于减小兴波阻力[8]。
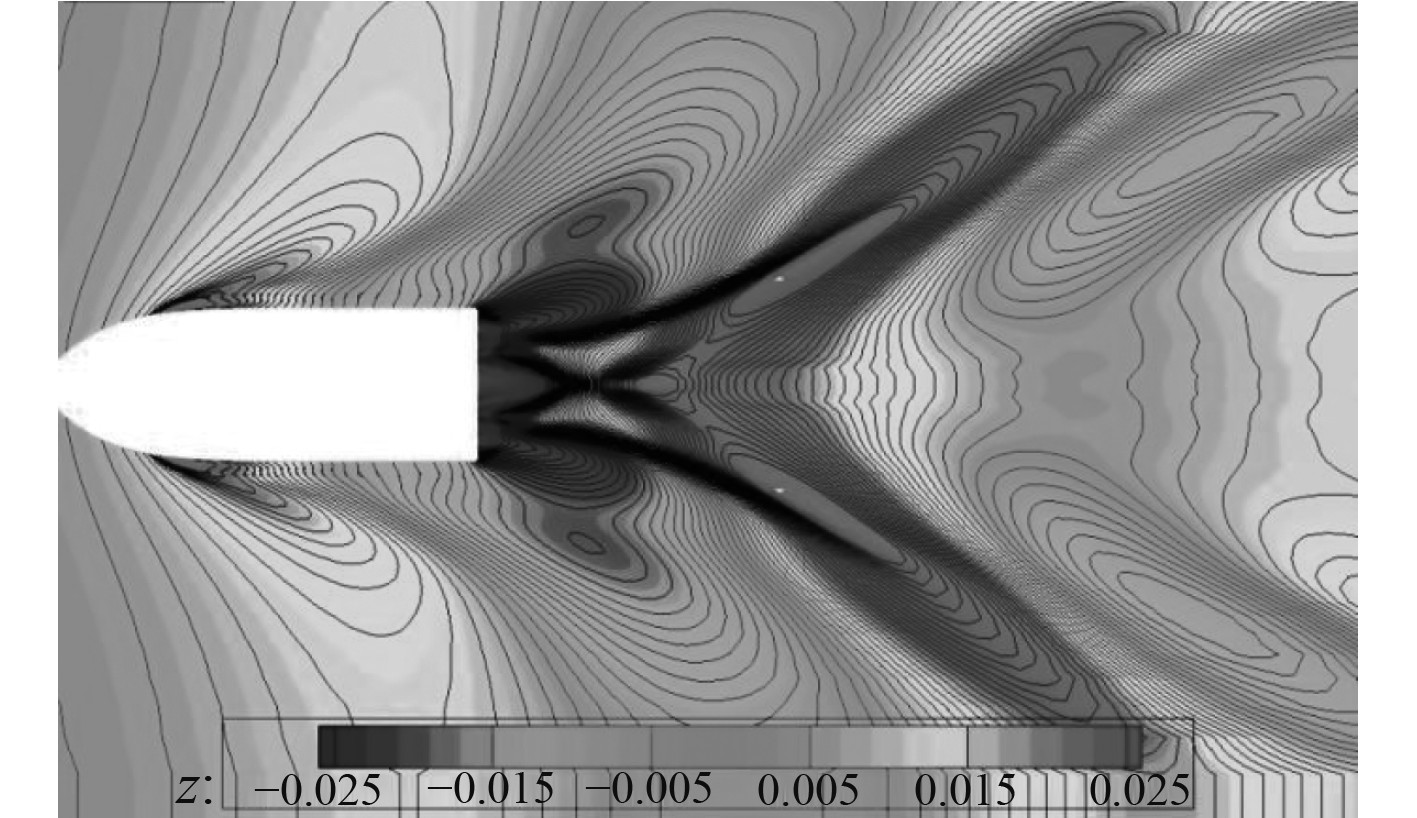
|
图 5 自由液面波形(Fr = 0.54) Fig. 5 Free surface(Fr = 0.54) |
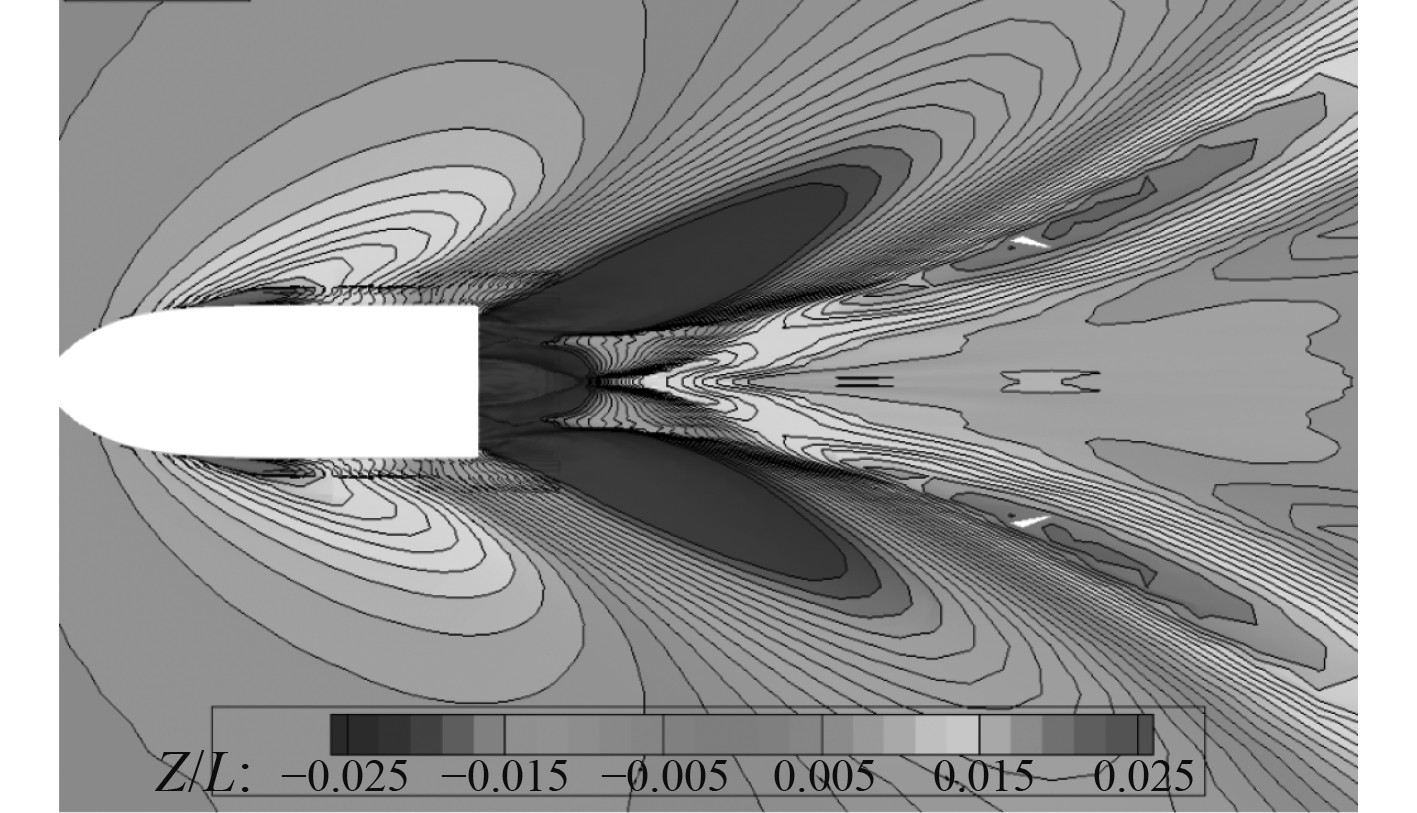
|
图 6 自由液面波形(Fr = 0.73) Fig. 6 Free surface(Fr = 0.73) |
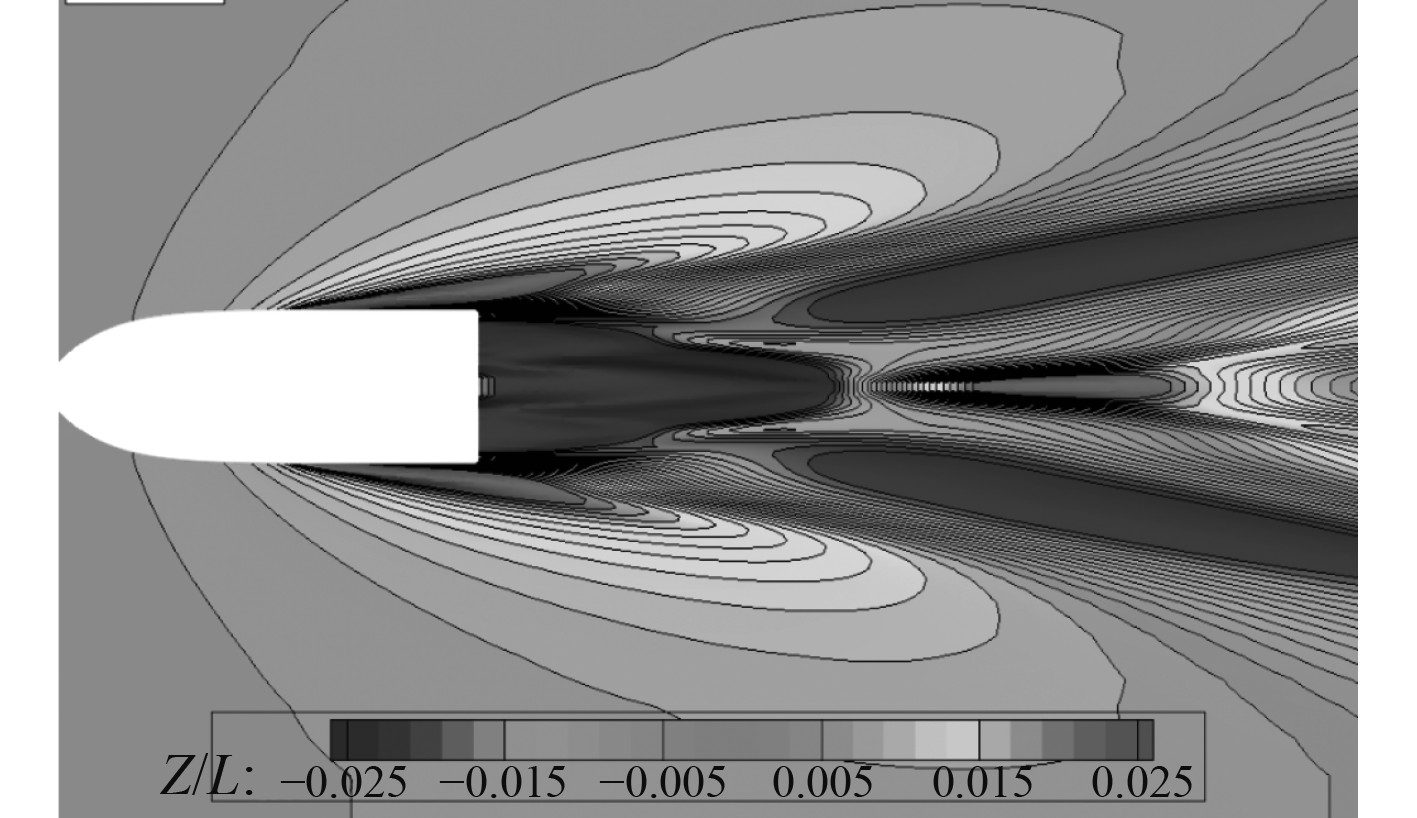
|
图 7 Fr = 1.33自由液面波形(Fr = 1.33) Fig. 7 Free surface(Fr = 1.33) |

|
图 8 自由液面波形(Fr = 2.72) Fig. 8 Free surface(Fr = 2.72) |
图9~图12给出了不同航速时槽道滑行艇内槽道中纵剖面气液两相分布情况。浅色为水,深色为空气。可以看出,当滑行艇的傅汝德数达到Fr = 0.73时,滑行艇的纵倾角度最大,此时滑行艇受到的阻力达到极大值,随着滑行艇航速的变大,滑行艇达到滑行状态,滑行艇浸湿长度逐渐减小,槽道内空气占比不断增加,当滑行艇的Fr = 2.72时,滑行艇槽道仅仅在船尾的一小部分和水面相接。

|
图 9 中纵剖面气液分布(Fr = 0.54) Fig. 9 Gas-liquid distribution in middle longitudinal section(Fr = 0.54) |

|
图 10 中纵剖面气液分布(Fr = 0.73) Fig. 10 Gas-liquid distribution in middle longitudinal section(Fr = 0.73) |

|
图 11 中纵剖面气液分布(Fr = 1.33) Fig. 11 Gas-liquid distribution in middle longitudinal section(Fr = 1.33) |

|
图 12 中纵剖面气液分布(Fr = 2.72) Fig. 12 Gas-liquid distribution in middle longitudinal section(Fr = 2.72) |
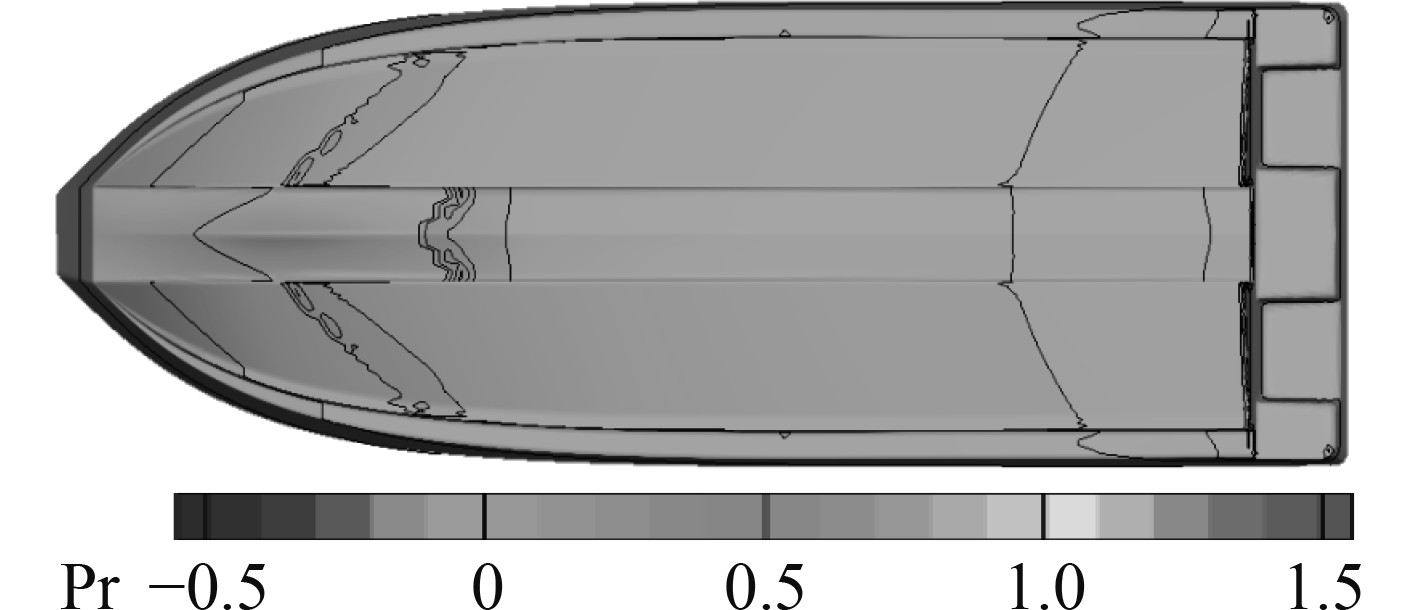
图13~图16给出了滑行艇船体压力分布的无量纲云图。可以看出,滑行艇底部的高压区,即空气和水的交界处随航速的增加,不断后移,使得滑行艇的湿表面积也从初始的排水状态到起滑状态不断减小。
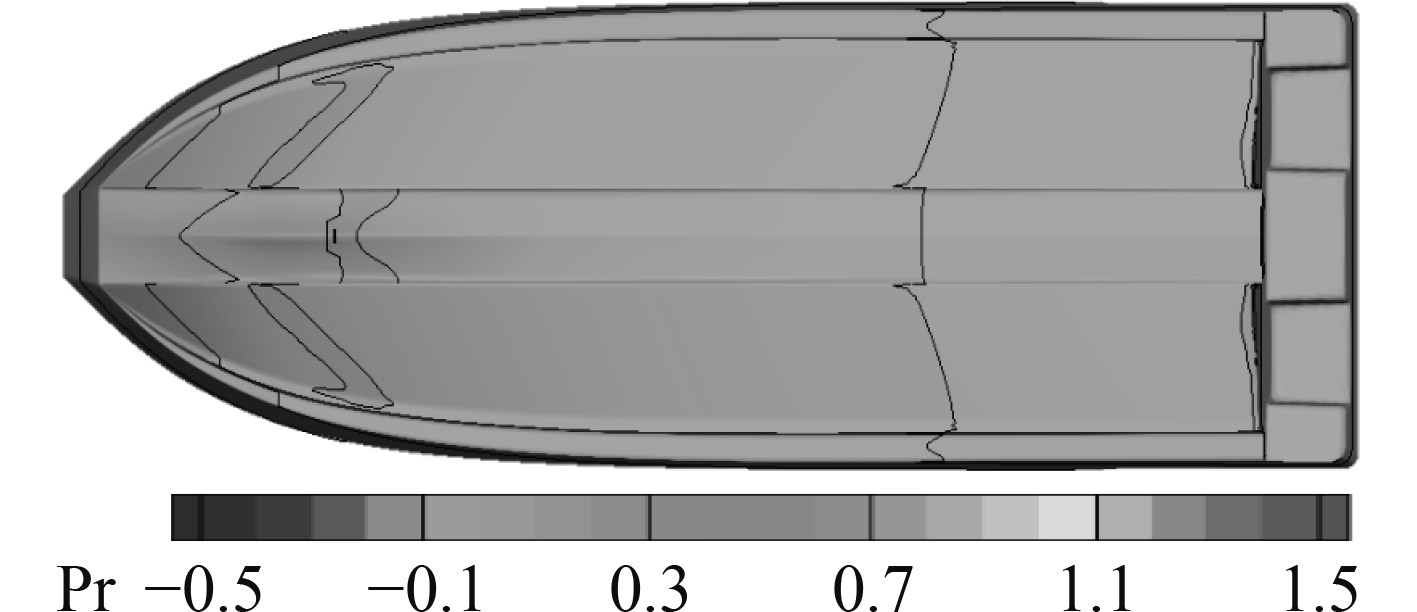
|
图 13 船底压力分布(Fr = 0.54) Fig. 13 Bottom pressure distribution(Fr = 0.54) |
|
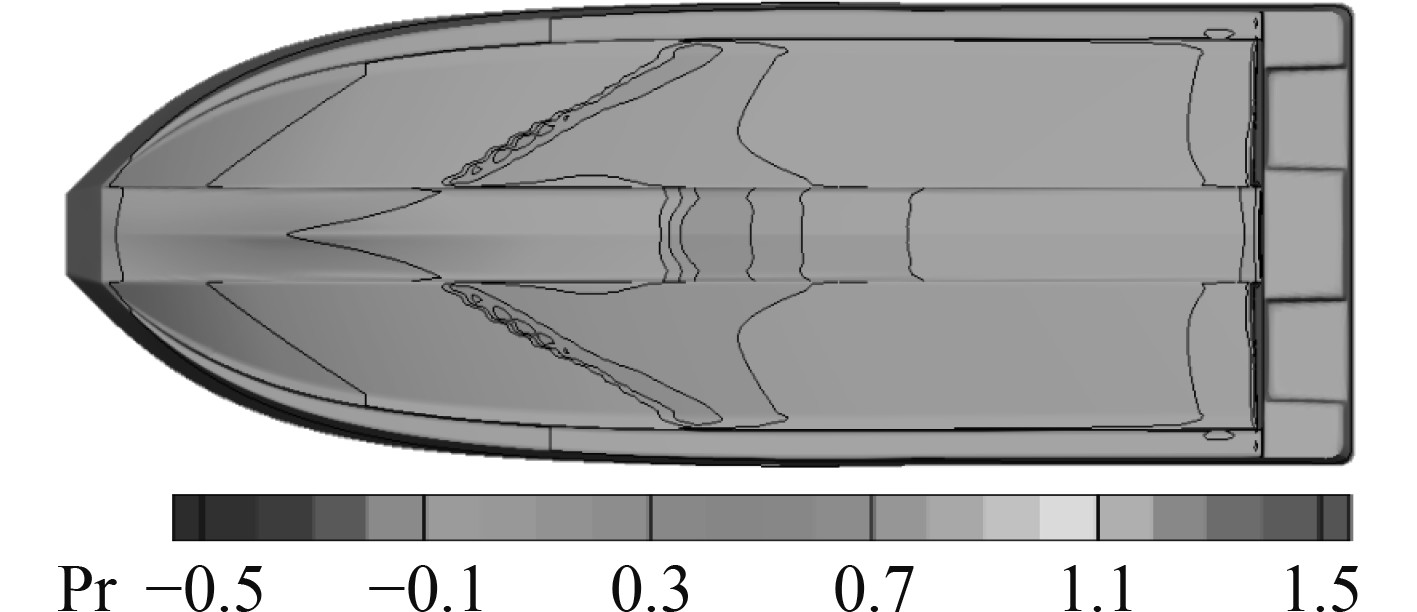
图 14 船底压力分布(Fr = 0.73) Fig. 14 Bottom pressure distribution(Fr = 0.73) |
|
图 15 船底压力分布(Fr = 1.33) Fig. 15 Bottom pressure distribution(Fr = 1.33) |

|
图 16 船底压力分布(Fr = 2.72) Fig. 16 Bottom pressure distribution(Fr = 2.72) |
本文通过全结构网格划分计算域,基于动态重叠网格与Level-Set水平集方法,实现对某型槽道艇进行静水直航仿真,得到以下结论:
1)该槽道艇的阻力曲线在12 kn左右出现阻力峰,越过阻力峰后,阻力先下降后上升。而纵倾角随航速增加呈先上升后下降趋势,最大纵倾角5.3°出现在阻力峰位置,仿真结果与试验吻合较好;
2)槽道艇自由液面波形在低速时呈明显的排水型船特征,随着艇体起滑,槽道喷出较长尾流,兴波收束减少,尾流主要分布在船宽范围内;
3)槽道滑行艇的槽道随着航速增加,逐渐脱离水面,最后只剩下尾部局部面积在水中受力,这种现象使得槽道升力较容易受风浪影响。
| [1] |
罗富强, 霍聪, 高霄鹏, 等. 多航态高速无人艇阻力试验研究[J]. 舰船科学技术, 2019, 41(23): 58-63. |
| [2] |
李昆鹏, 魏成柱, 梁晓锋. 多面体网格在滑行艇数值仿真计算中的应用[J]. 舰船科学技术, 2020, 42(3): 33-37. |
| [3] |
李岩, 柳存根. 基于CFD的新型高速艇艇型静水性能研究[J]. 舰船科学技术, 2020, 42(13): 70-73. |
| [4] |
王志东, 窦朋, 凌宏杰, 等. 高速滑行艇喷溅特性研究方法[J]. 中国造船, 2018, 59(3): 116-125. DOI:10.3969/j.issn.1000-4882.2018.03.012 |
| [5] |
申云磊, 高霄鹏, 霍聪. 阻流板对滑行艇阻力性能的影响[J]. 舰船科学技术, 2020, 42(5): 30-33. |
| [6] |
王慧, 朱仁传, 杨云涛, 黄山. 基于CFD的滑行艇兴波与姿态模拟分析[J]. 中国造船, 2020, 61(3): 1-14. DOI:10.3969/j.issn.1000-4882.2020.03.001 |
| [7] |
赵发明, 高成君, 夏琼. 重叠网格在船舶CFD中的应用研究[J]. 船舶力学, 2011, 15(4): 332-341. DOI:10.3969/j.issn.1007-7294.2011.04.002 |
| [8] |
马继强. 基于STAR CCM+的单槽道滑行艇阻力和兴波性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
 2022, Vol. 44
2022, Vol. 44
