随着人们生活水平的提高以及休闲方式的改变,大型邮轮作为国际高端旅游休闲方式,其建造与运营备受业界关注。大型邮轮具有船体修长、重心位置高、上层建筑层次分明、各种结构设施复杂的特征,其耐波性能有别于普通船舶,需要对其开展有针对性的研究。曹宇等[1]基于三维线性频域势流理论对大型邮轮的耐波性能进行评估,研究了重心高度、惯性半径等参数对邮轮耐波性的影响;李辉等[2]应用三维线性频域水动力软件对豪华邮轮的波浪载荷进行计算,研究了《钢制海船入级规范》对于邮轮波浪载荷计算的适用性。章新智[3]等结合现有船舶规范,对豪华邮轮耐波性衡准要素进行分析研究并提出了邮轮耐波性衡准的优化建议。马网扣等[4]从满足SOLAS 2020的破舱稳性要求方面对大型邮轮的主尺度规划提出了一些建议。Dallinga R P等[5]讨论了大型邮轮组合运动及横摇对晕船率的影响以及波浪砰击造成的不适。Jae-Han Kim等[6]从乘客舒适性角度研究了实际运行状态下邮轮的耐波性,并评估了减摇鳍对提高邮轮耐波性的作用效果。
大型邮轮作为发展中的高性能船舶,特殊的船体构型及使用功能决定了其耐波性衡准要素中的安全性与舒适性标准尤为重要。目前,公认的船舶耐波性衡准是北欧合作研究计划和中国船舶科学研究中心提出的,其他专家学者如毛筱菲、戴仁元等也提出了一些衡准,而各船级社尚未对邮轮的耐波性评估建立单独的标准。国际标准化组织(ISO)卫生与安全委员会(HSC)对于船舶耐波性的评估方法为各船级社制定规范时所认可并引用,本文在对大型邮轮进行耐波性评估时以该标准为依据,如表1所示。
|
|
表 1 国际标准化组织(ISO)卫生与安全委员会(HSC)船舶耐波性执行标准 Tab.1 International Organization for Standardization (ISO) Health and Safety Committee (HSC) marine seakeeping standard |
以1艘大型邮轮为研究对象,采用数值模拟与模型试验相结合的研究方法,对大型邮轮的耐波性能进行研究,重点关注大型邮轮的横摇、纵摇、垂荡三自由度运动以及重心位置处的垂向及横向运动加速度。数值模拟以三维线性时域势流理论为理论依据,所用软件工具为挪威船级社开发的SESAM-Wasim,邮轮模型为以缩尺比1∶55制作的水面自航模型,试验在可模拟各种海况条件的上海交通大学海洋深水试验池中实施。
1 三维线性时域势流理论设船体在水面上做任意形式的摇荡运动,运动可以由入射波及其在船体上的绕射影响所引起。流场中任一空间点
控制方程
| $ {\nabla }^{2}{\varPhi }\left({P},{t}\right)=0 \text{,}$ | (1) |
自由面条件
| $ \frac{{\partial }^{2}{\varPhi }}{\partial {t}^{2}}+\mathrm{g}\frac{\partial {\varPhi }}{\partial z}=0 \text{,}$ | (2) |
物面条件
| $ \frac{\partial {\varPhi }}{\partial n}{|}_{{S}_{0}}={V}_{n}\left(x,y,z,t\right)=\sum _{j=1}^{6}\dot{{x}_{0j}}\left(t\right){n}_{j}\text{,}$ | (3) |
水底条件
| $ \underset{z\to -\mathrm{\infty }}{\mathrm{lim}}\nabla {\varPhi }=0 \text{或} \frac{\partial {\varPhi }}{\partial n}{|}_{z=-H}=0 \text{。}$ | (4) |
式中:
除上述方程和条件外,速度势还应满足辐射条件和初始条件。
流场中速度势可分解为船体振荡的辐射势
| $ {\varPhi }\left({P},{t}\right)={{\varPhi }}_{I}+{{\varPhi }}_{D}+{{\varPhi }}_{R} \text{,}$ | (5) |
通常入射波速度势
辐射条件
| $ \underset{R\to \mathrm{\infty }}{\mathrm{lim}}\nabla {{\varPhi }}_{D\left(R\right)}=0 \text{,} {R}=\sqrt{{x}^{2}+{y}^{2}+{z}^{2}} \text{,}$ | (6) |
物面条件
| $ \frac{\partial {{\varPhi }}_{D}}{\partial n}{|}_{{S}_{0}}=-\frac{\partial {{\varPhi }}_{I}}{\partial n}{|}_{{S}_{0}} \text{,} \frac{\partial {{\varPhi }}_{R}}{\partial n}{|}_{{S}_{0}}=\sum _{j=1}^{6}\dot{{x}_{0j}}{n}_{j} \text{。}$ | (7) |
在物面上,初始条件可令式(3)中
| $ \frac{\partial {\varPhi }}{\partial n}{|}_{{S}_{0}}={V}_{n}\left(x,y,z,0\right)=\sum _{j=1}^{6}\dot{{x}_{0j}}\left(0\right){n}_{j}\text{,} $ | (8) |
在自由面上,初始条件为:
| $ {\varPhi }\left({P},0\right)={f}\left({P}\right) ,\text{且} \frac{\partial {\varPhi }\left({P},0\right)}{\partial \mathrm{t}}={f}{\text{′}}\left(P\right)=-gZ\left(P,0\right) \text{。}$ | (9) |
式中:
流场内速度势的定解问题可用格林函数转化为物面积分方程求解。然后可按照线性伯努利方程求得流场中的动压力和作用于船体的流体动力,并依此建立时域运动方程。
设辐射势
| $ {{\varPhi }}_{R}\left(P,t\right)={{\varPhi }}_{RI}\left({P},{t}\right)+{{\varPhi }}_{RM}({P},{t}) \text{,}$ | (10) |
由辐射势初始条件产生的流体动力为:
| $ {F}_{i}^{RI}\left(t\right)=-\rho {\iint }_{{S}_{0}}^{}\frac{\partial {{\varPhi }}_{RI}\left({P},{t}\right)}{\partial t}{n}_{i}{\rm{d}}S \text{,}$ | (11) |
由物体运动引起的流体动力为:
| $ {F}_{i}^{RM}\left(t\right)=-\rho {\iint }_{{S}_{0}}^{}\frac{\partial {{\varPhi }}_{RM}\left(\mathrm{P},\mathrm{t}\right)}{\partial t}{n}_{i}{\rm{d}}S \text{,}$ | (12) |
入射波及其绕射引起的流体动力为:
| $ {F}_{i}^{W}\left(t\right)=-\rho {\iint }_{{S}_{0}}^{}\frac{\partial }{\partial t}[{{\varPhi }}_{I}\left({P},{t}\right)+{{\varPhi }}_{D}\left({P},{t}\right)]{n}_{i}{\rm{d}}S \text{,}$ | (13) |
船体运动偏离平衡位置的静回复力为:
| $ {F}_{i}^{S}\left(t\right)=-{{\boldsymbol{C}}}_{ij}\cdot {x}_{0j}\left(t\right) \text{,}$ | (14) |
式中
于是,时域中船体线性运动方程可写为:
| $ {\sum }_{j=1}^{6}{{\boldsymbol{m}}}_{ij}\ddot{{x}_{ij}}\left(t\right)={F}_{i}^{RI}+{F}_{i}^{RM}+{F}_{i}^{W}+{F}_{i}^{S},(i=\mathrm{1,2},\cdots ,6) \text{。}$ | (15) |
式中
大型邮轮数值计算输入参数为邮轮实际尺度,模型试验所制作的模型缩尺比为1∶55,大型邮轮主要参数如表2所示。
|
|
表 2 大型邮轮主要参数 Tab.2 Main parameters of large cruise |
邮轮数值计算与模型试验采用规则波与不规则波2种环境波浪参数。规则波有10个,波长/船长比(λ/L)分别为0.2,0.4,0.6,0.8,1.0,1.2,1.4,1.6,1.8,2.0,波高均为2m;不规则波浪有5个,采用JONSWAP波浪谱,其参数如表3所示。
|
|
表 3 不规则波参数 Tab.3 Irregular wave parameters |
大型邮轮数值模拟应用的计算工具是基于三维时域势流理论以及Rankine面元法的水动力分析软件SESAM-Wasim。Rankine面元法即应用简单格林函数法求解速度势微分方程的方法,该方法的优点是形式简单易于实现,可避免计算复杂自由面格林函数,自由面和船体的非线性效应也便于计入。因为Rankine源格林函数不满足任何边界条件,所以必须在边界上划分网格,布置源汇来保证满足边界条件。Wasim程序生成的船体表面网格与自由液面网格如图1所示。

|
图 1 大型邮轮船体及自由面网格 Fig. 1 Large cruise ship hull and free surface mesh |
邮轮模型设有动力推进装置,可以通过遥控装置使其以设定的速度及方向在试验水池中航行。模型试验分为2个模块:规则波试验和不规则波试验。
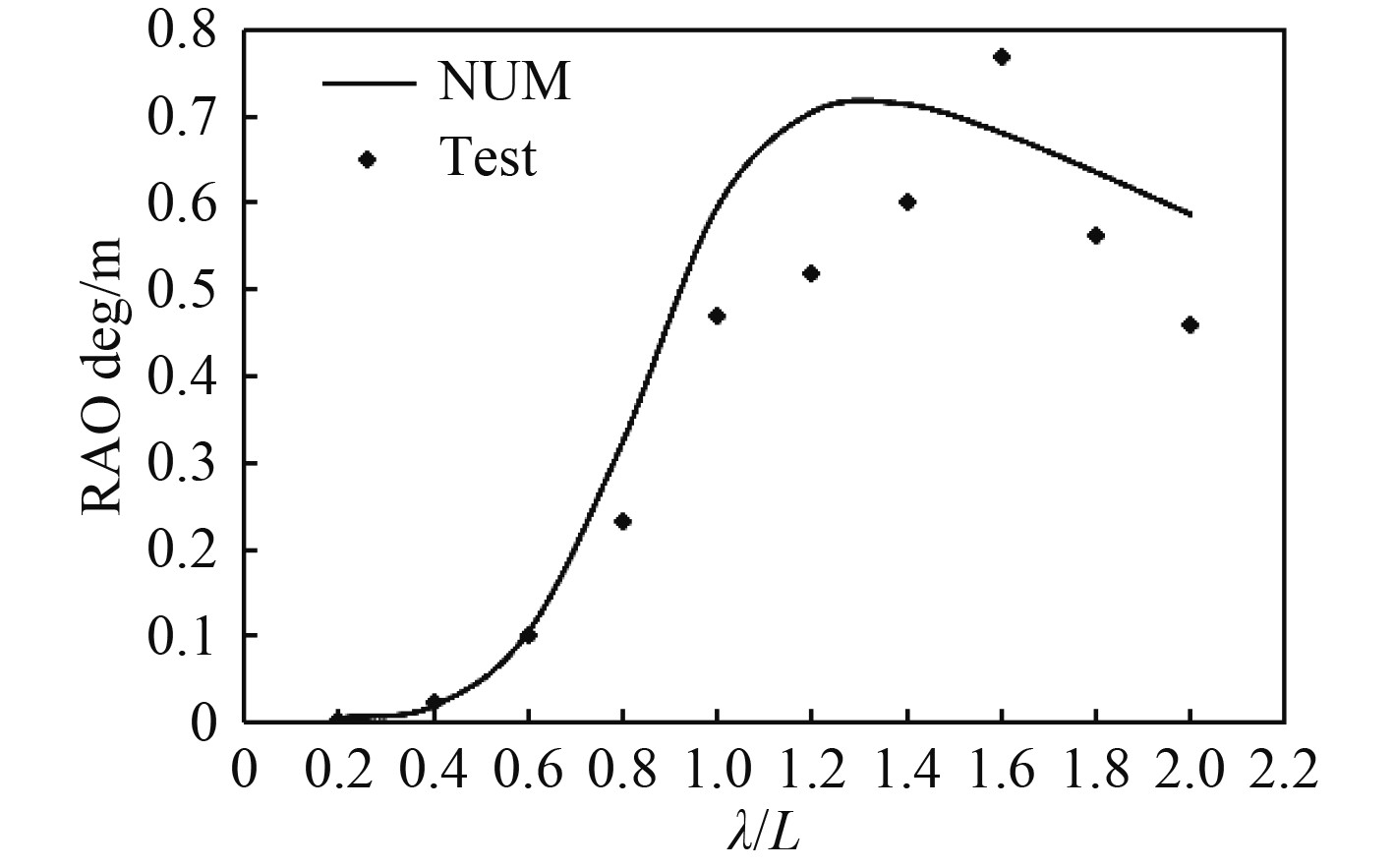
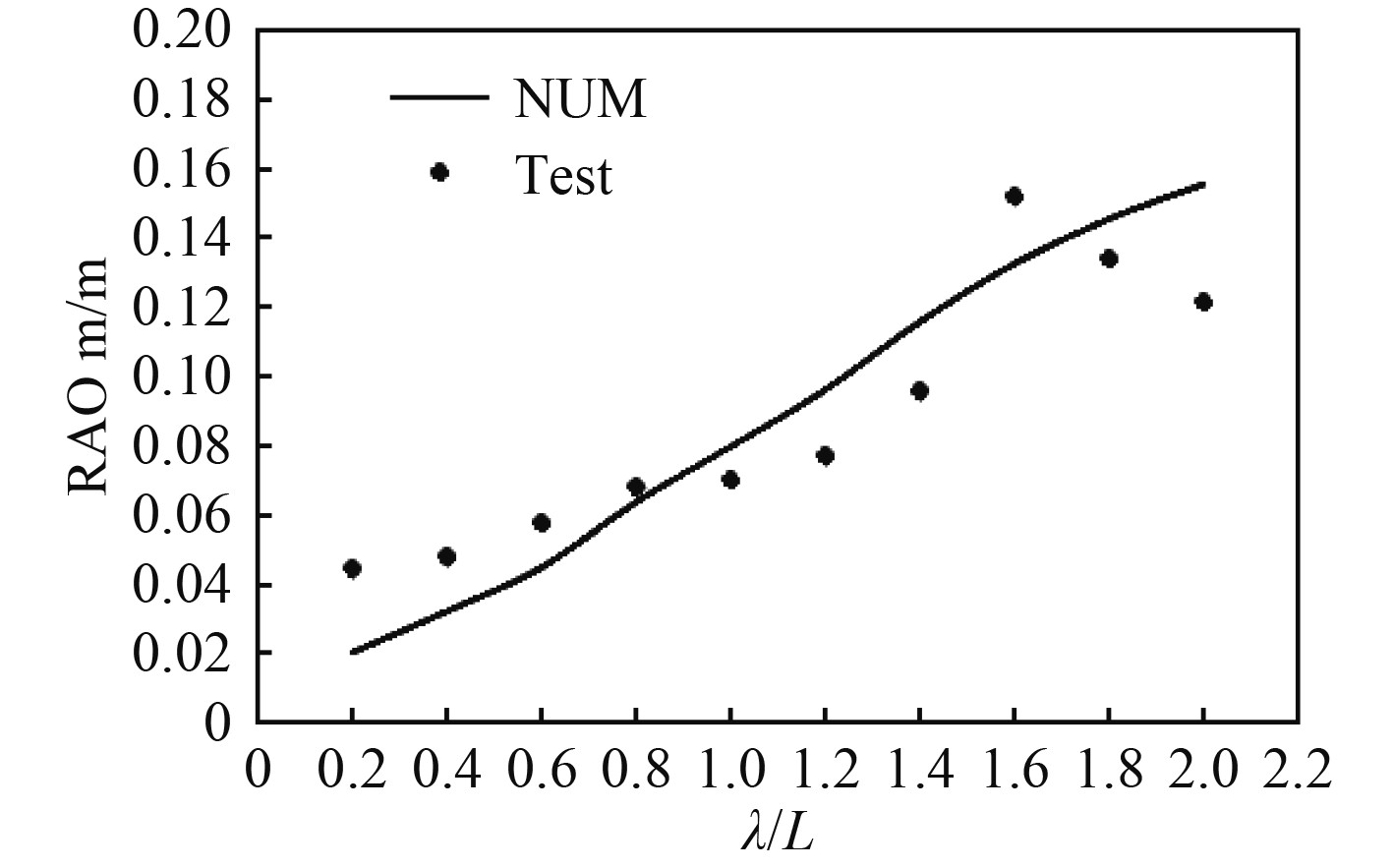
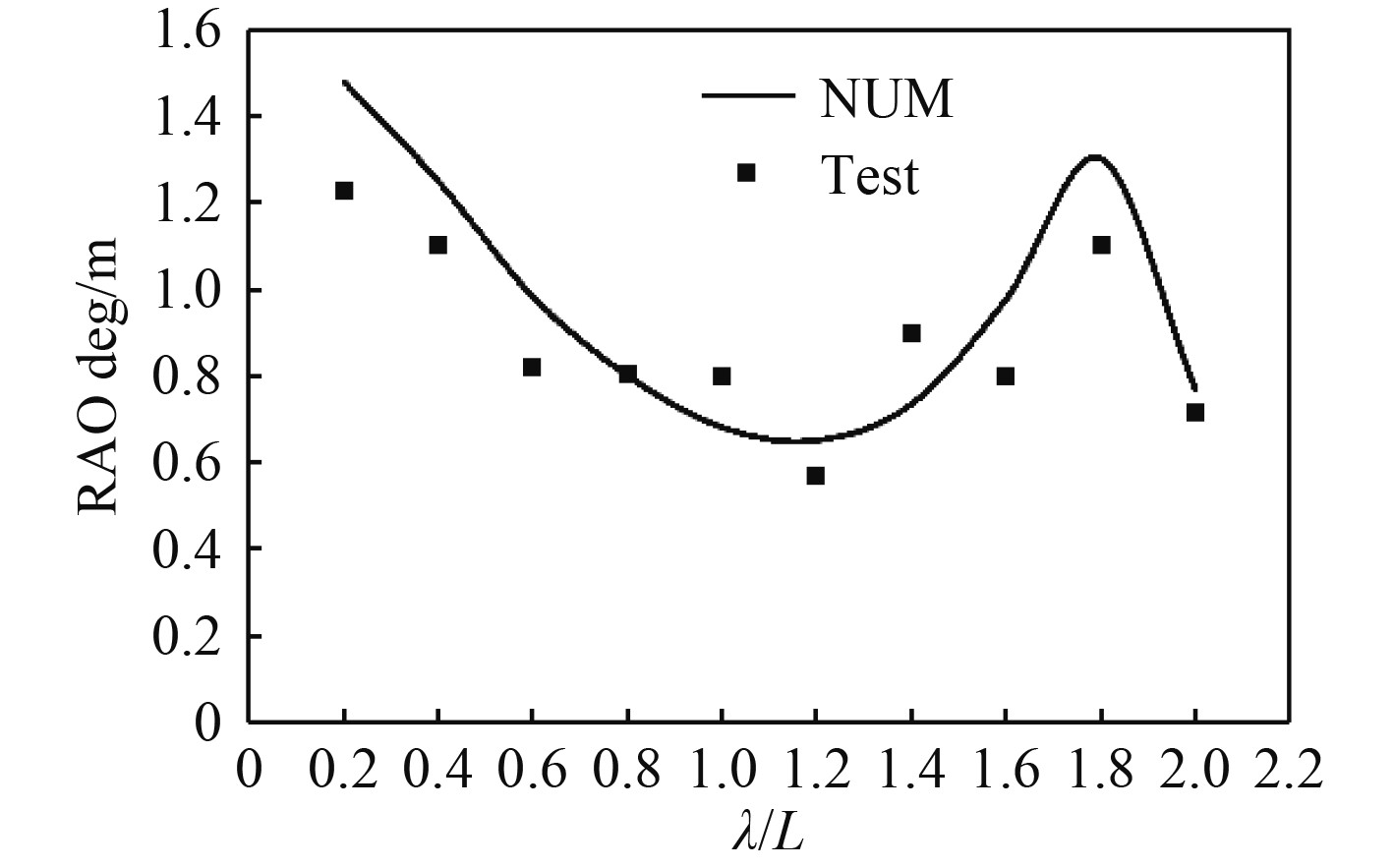
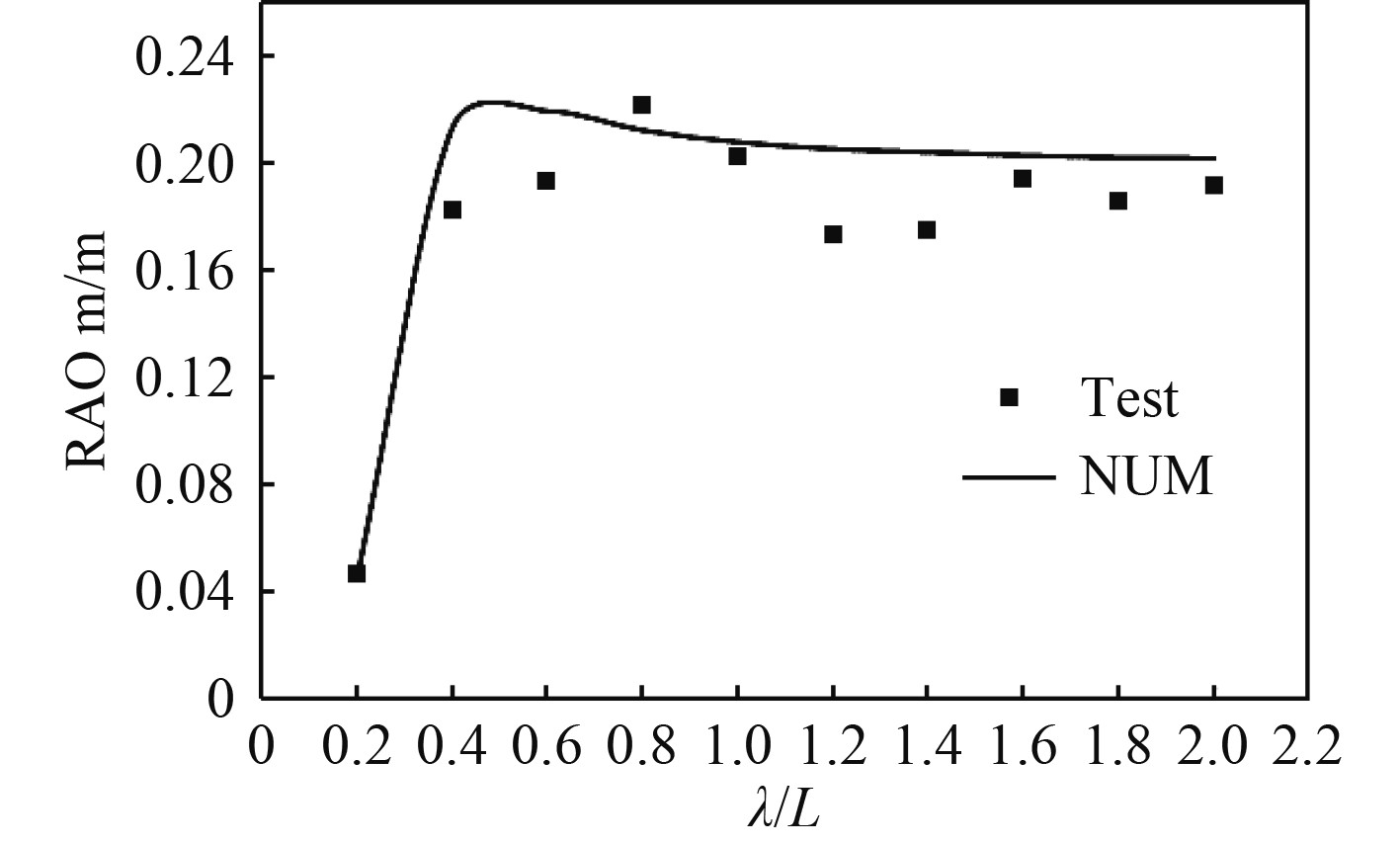
3 邮轮计算与试验结果对比 3.1 规则波中邮轮运动响应在规则波中,大型邮轮计算与试验的对比数据为设计航速18 kn下重心位置处的横摇、纵摇、垂荡运动RAO,如图2~图5所示。图中曲线代表计算结果,散点代表试验结果。
|
图 2 迎浪纵摇运动RAO Fig. 2 Pitch RAO in head wave |
|
图 3 迎浪垂荡运动RAO Fig. 3 Heave RAO in head wave |
|
图 4 横浪横摇运动RAO Fig. 4 Roll RAO in beam wave |
|
图 5 横浪垂荡运动RAO Fig. 5 Heave RAO in beam wave |
由图2~图5可知,在规则波作用下,邮轮运动响应幅值随波长与船长比的变化趋势计算结果与试验数据比较吻合。迎浪条件下,邮轮纵摇运动响应在波长与船长比为1.4时趋于最大值,邮轮垂荡运动响应随波长增大而持续增大;横浪条件下,邮轮横摇运动响应与波长与船长比的变化关系较为复杂,在波长与船长比为1.2时趋于最小值,邮轮垂荡运动在波长较短时迅速增加,当波长与船长比大于0.4时,运动幅值受波浪波长的影响相对较小。
3.2 不规则波中邮轮运动响应在不规则波中,邮轮计算与试验结果的对比分析包括4级海况与6级海况下迎浪作用下纵摇、垂荡运动的有义双幅值,以及横浪作用下横摇、垂荡运动的有义双幅值,如图6~图9所示。
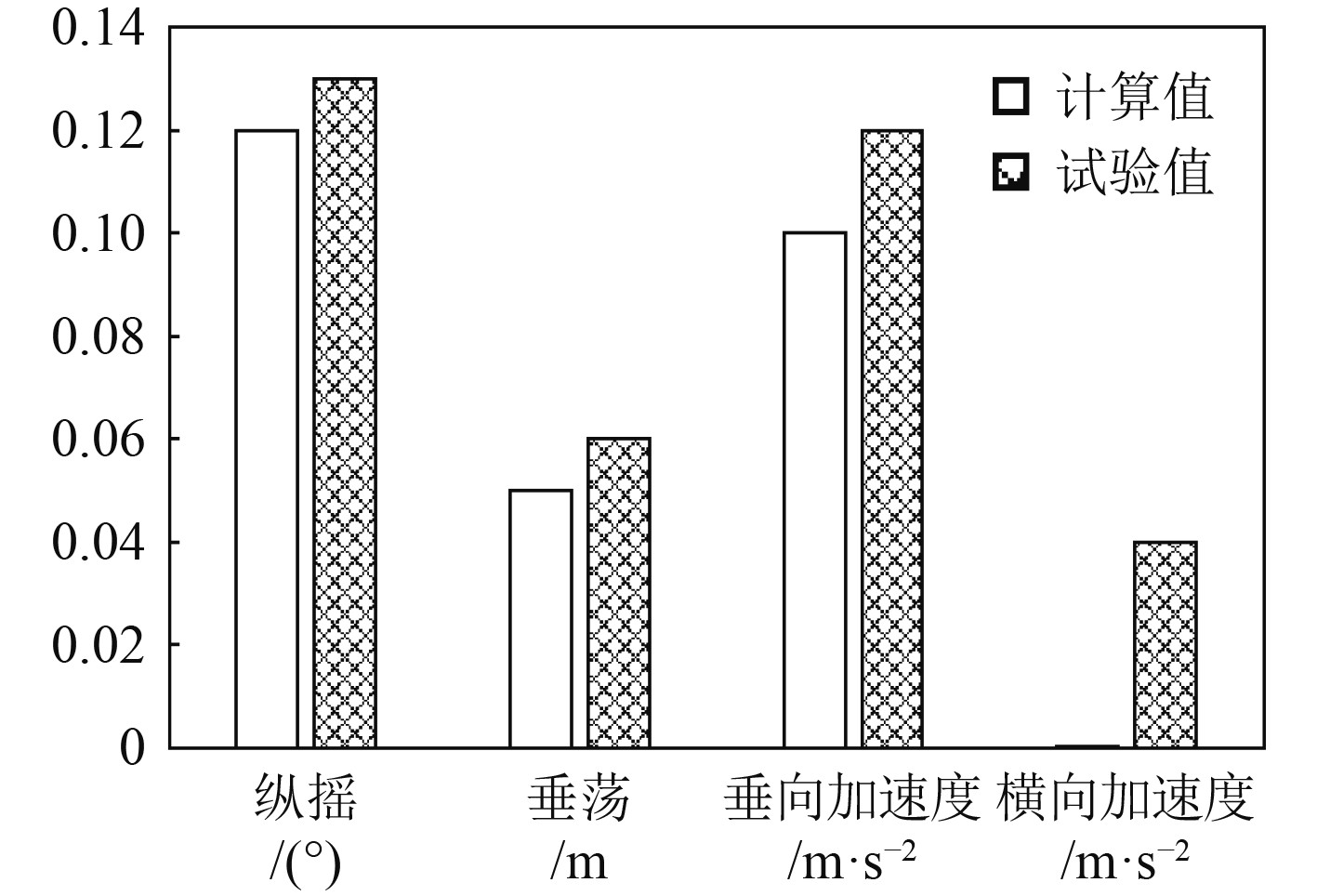
|
图 6 迎浪邮轮运动响应有义双幅值(4级海况) Fig. 6 Double significant amplitude of cruise motion response in head wave (sea state 4) |
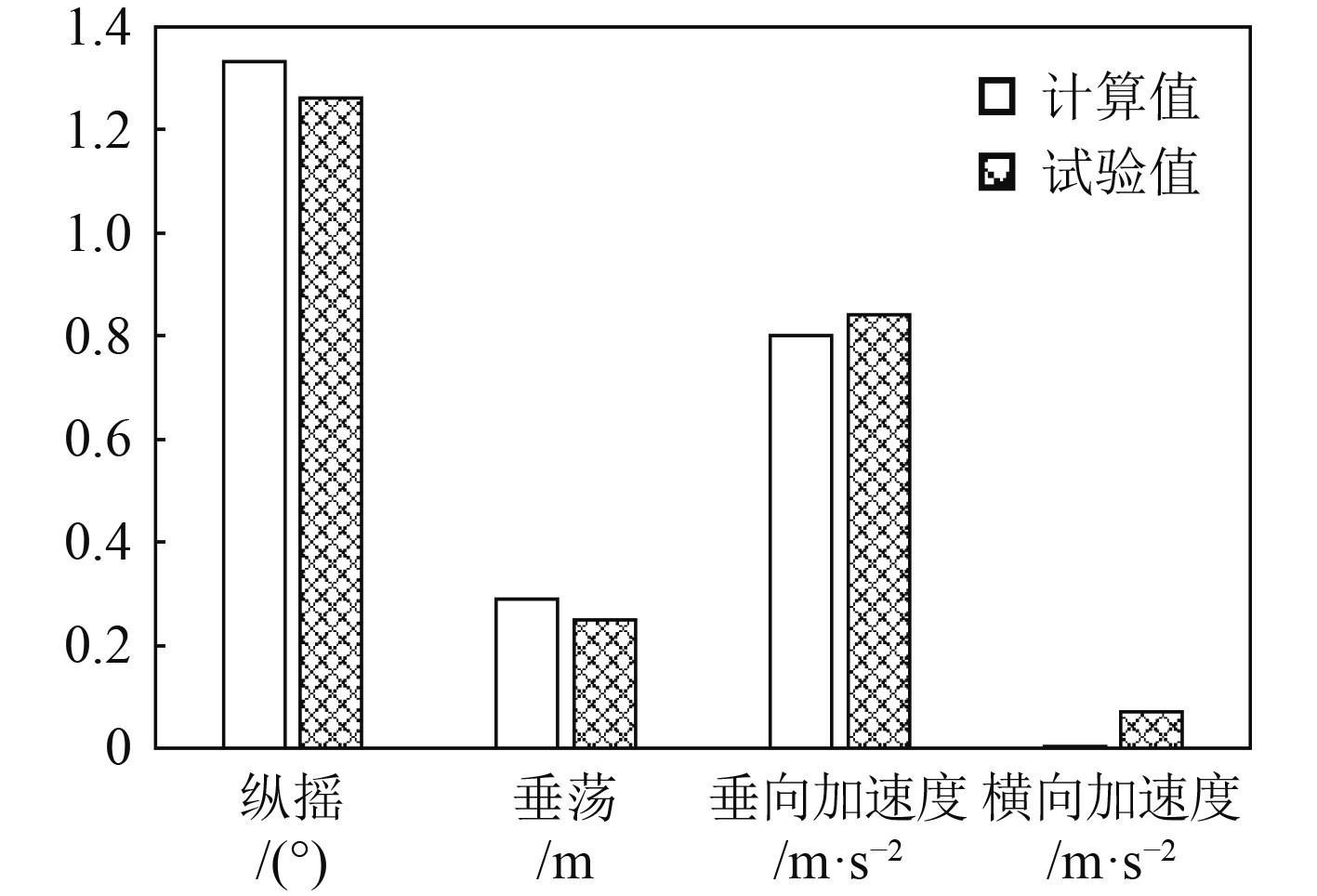
|
图 7 迎浪邮轮运动响应有义双幅值(6级海况) Fig. 7 Double significant amplitude of cruise motion response in head wave (sea state 6) |
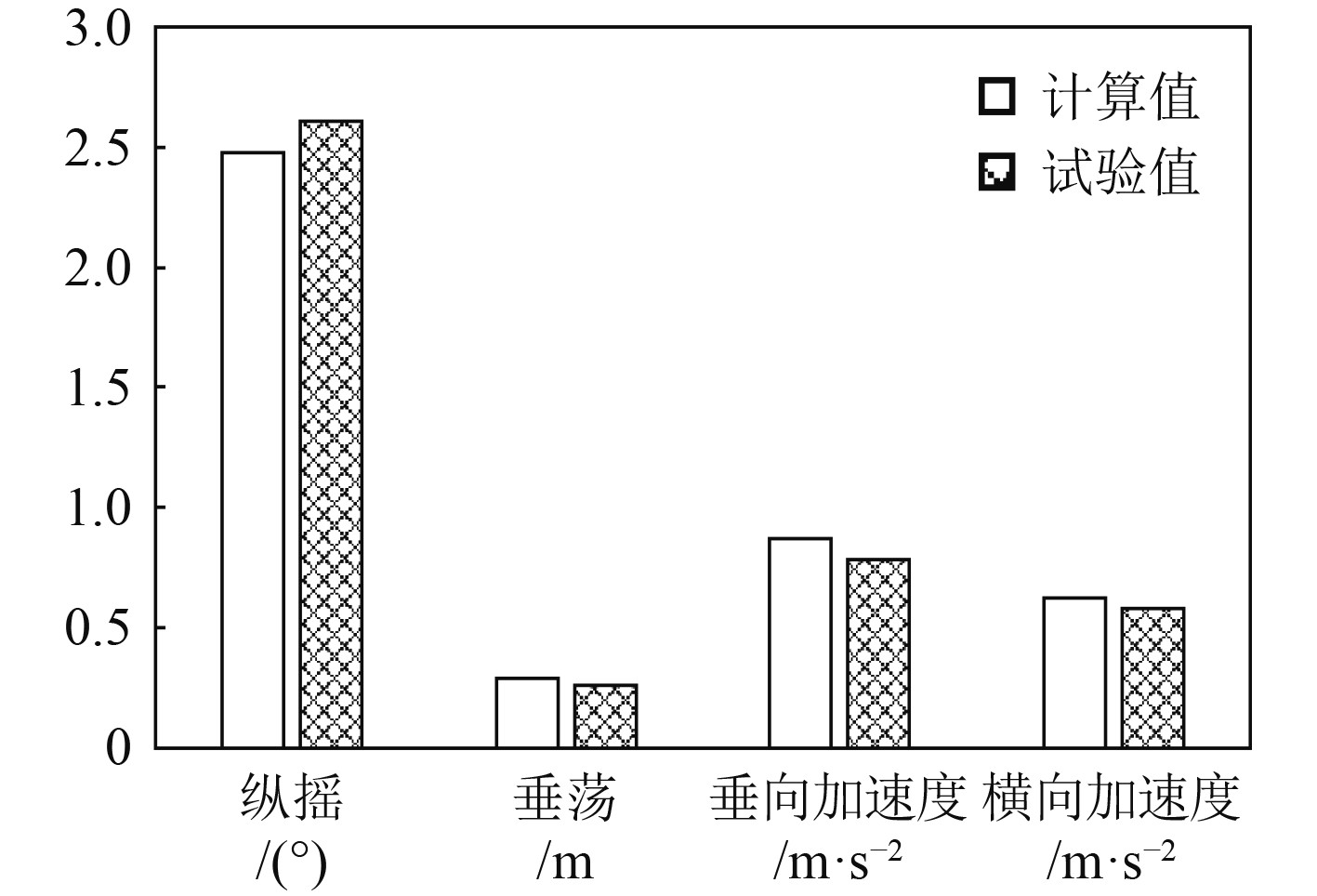
|
图 8 横浪邮轮运动响应有义双幅值(4级海况) Fig. 8 Double significant amplitude of cruise motion response in beam wave (sea state 4) |
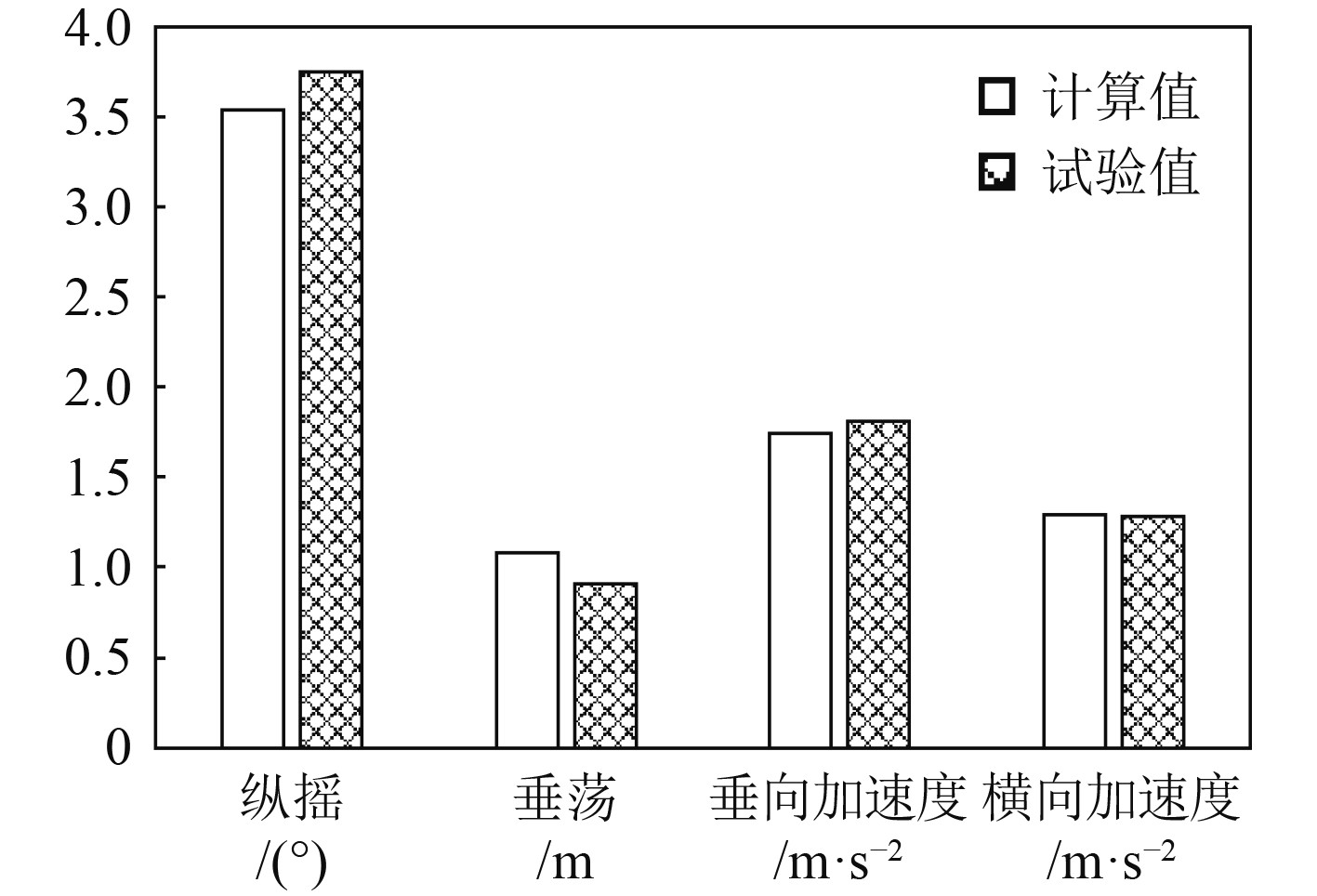
|
图 9 横浪邮轮运动响应有义双幅值(6级海况) Fig. 9 Double significant amplitude of cruise motion response in beam wave (sea state 6) |
由图6~图9可知,迎浪条件4级海况下,邮轮运动响应计算值均小于试验值,最大误差为20%,6级海况下,邮轮运动响应计算值与试验值最大误差为13.7%;横浪条件4级海况下,邮轮运动响应计算值与试验值最大误差为10.3%,6级海况下,邮轮运动响应计算值与试验值最大误差为5.9%。因此,经邮轮模型试验与计算结果对比分析,SESAM-Wasim对邮轮的运动数值模拟精度较高,计算结果具有良好的可靠性。
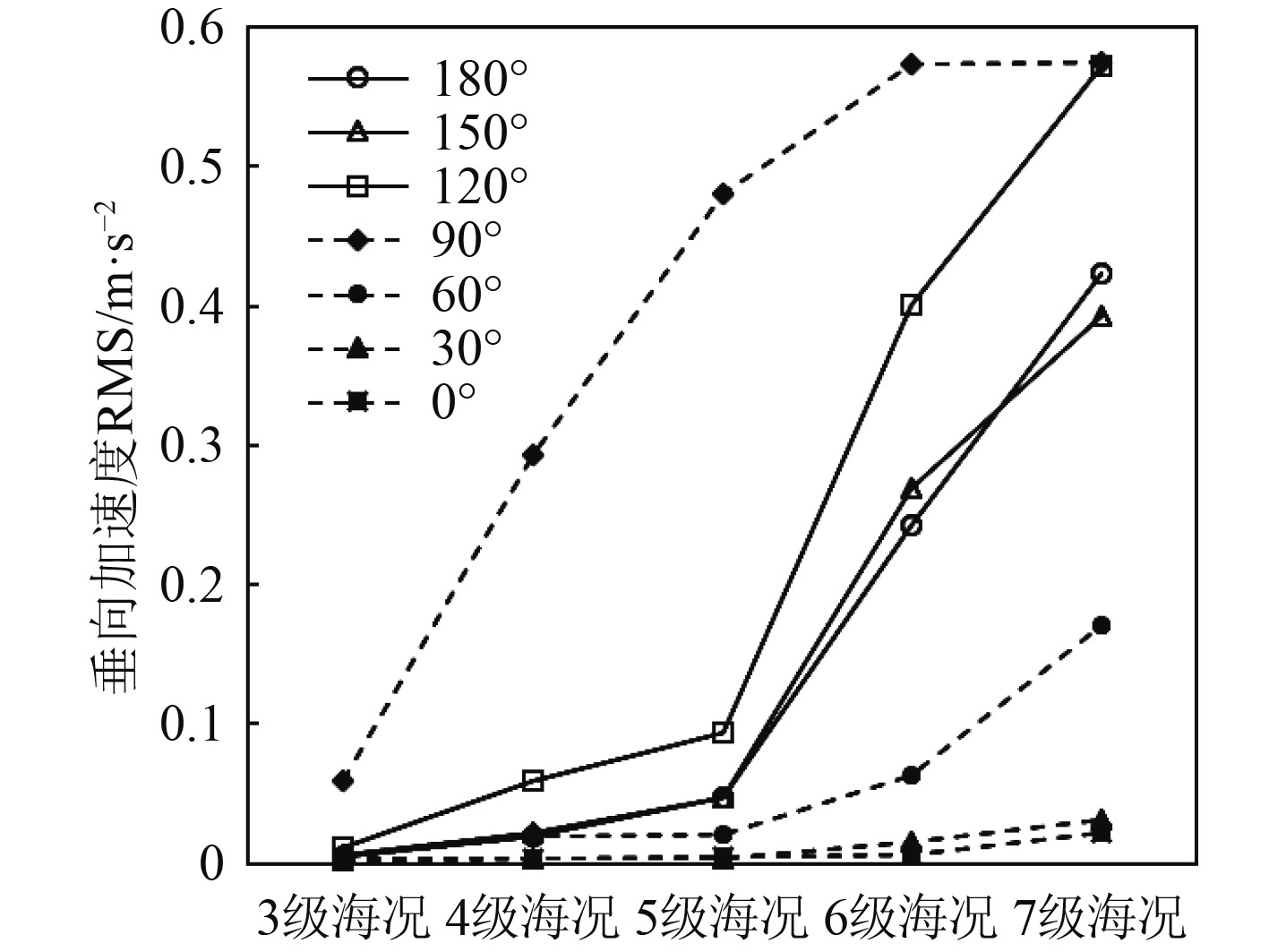
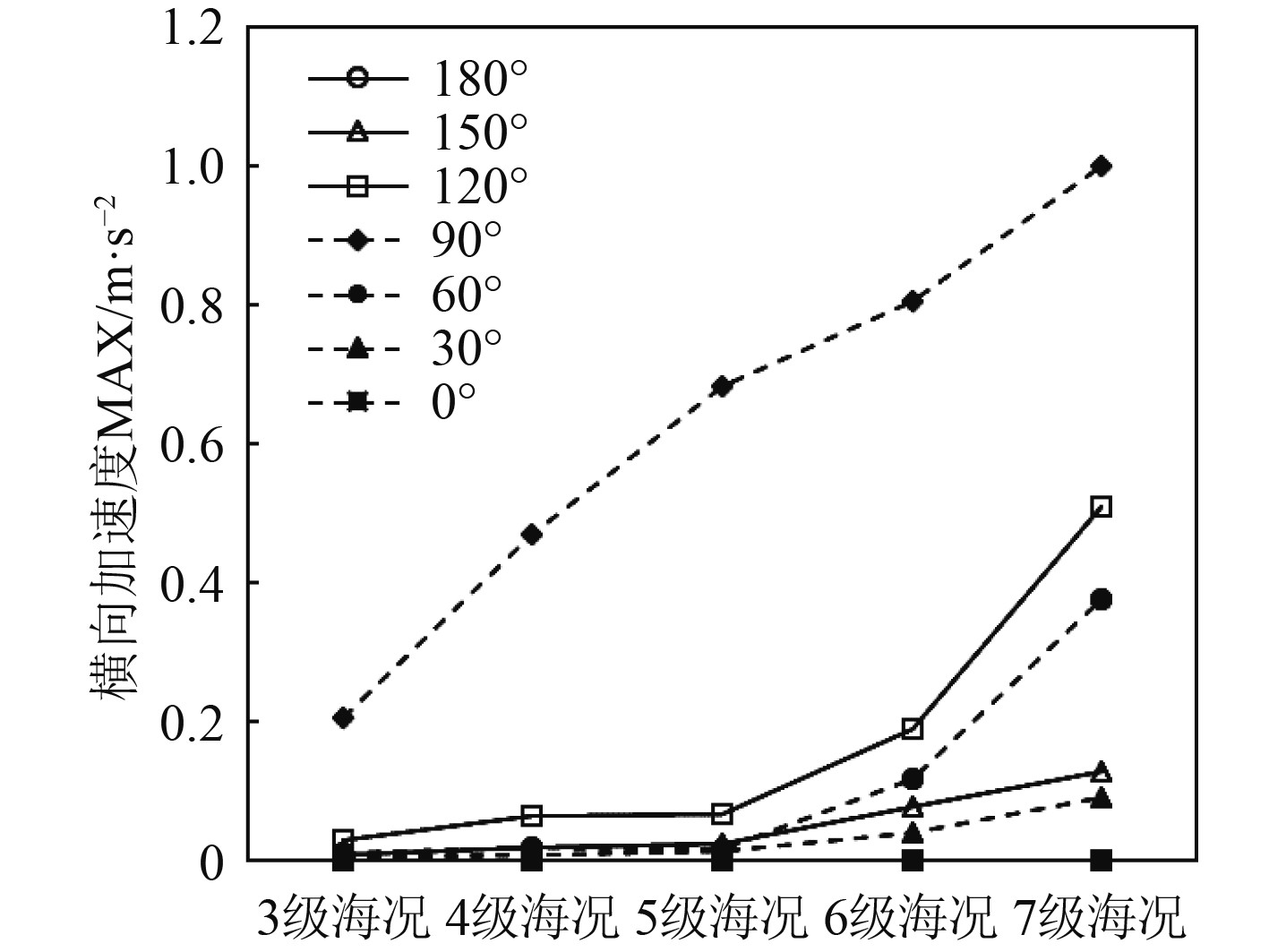
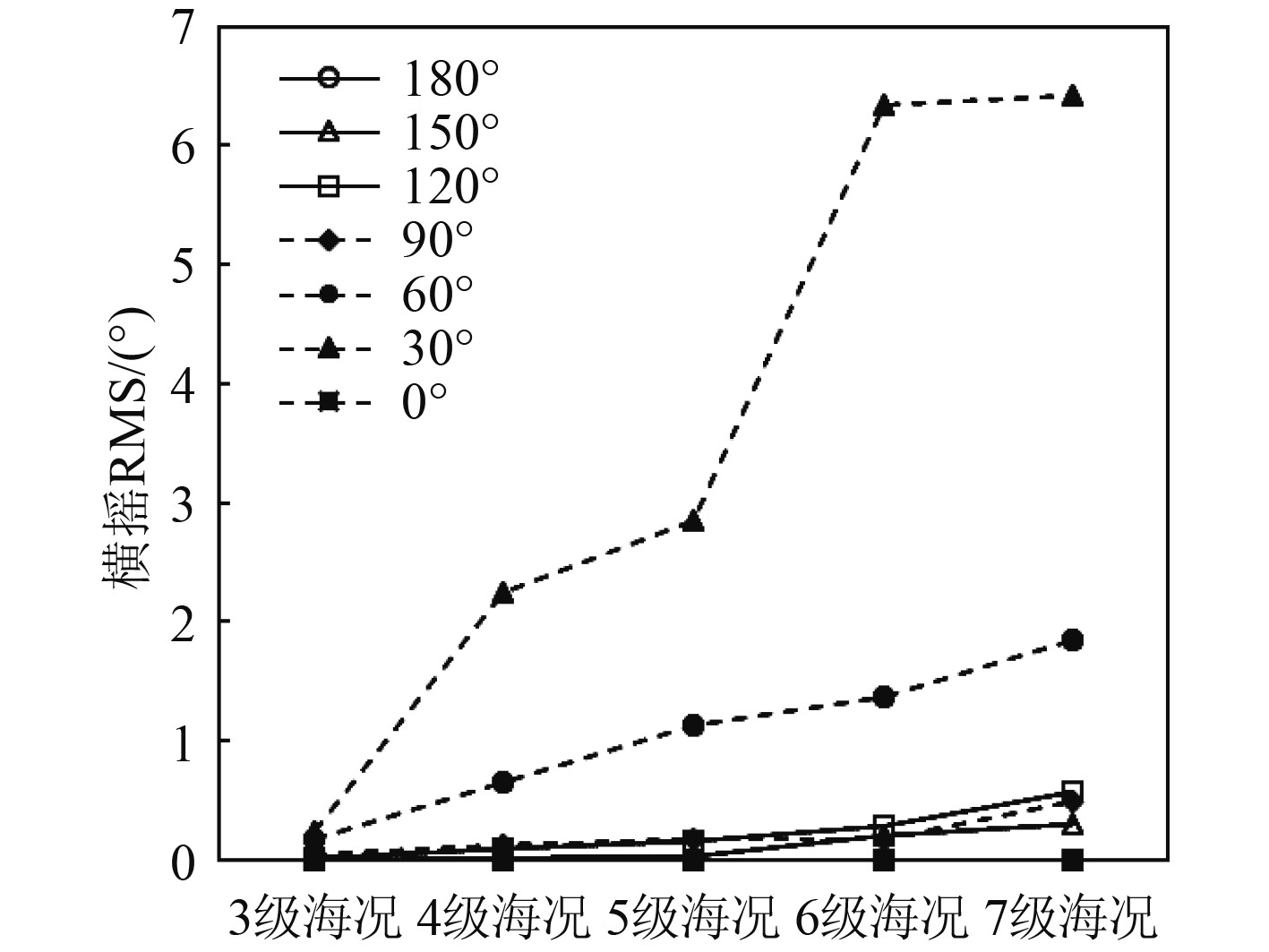
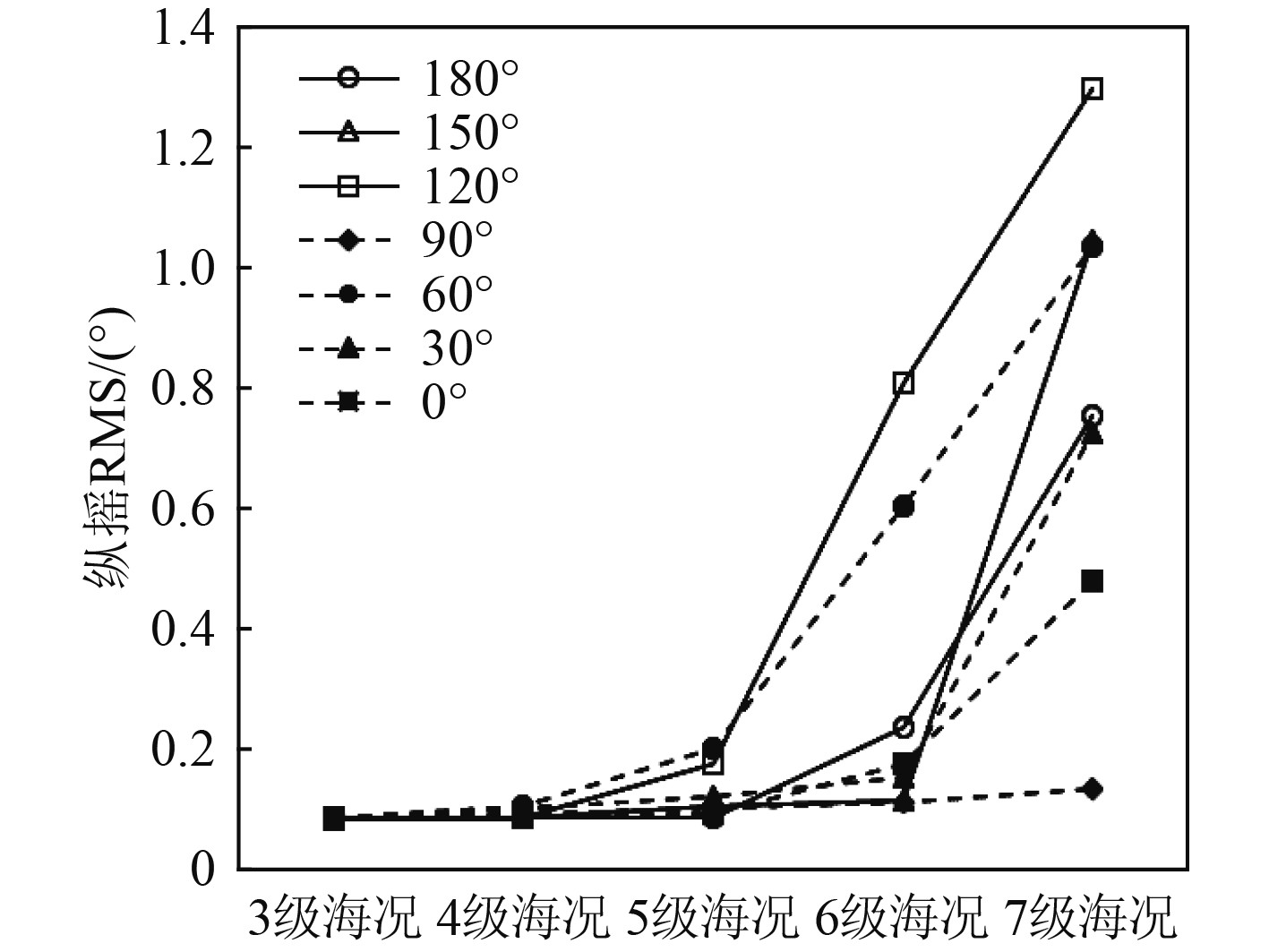
4 邮轮耐波性能评估分析 4.1 不同浪向下邮轮的耐波性能邮轮以设计航速18 kn在海上航行会遭遇不同方向的波浪,图10~图13展示了不同海况等级下,邮轮在不同浪向下的运动响应。
|
图 10 邮轮垂向加速度 Fig. 10 Vertical acceleration of cruise ship |
|
图 11 邮轮横向加速度 Fig. 11 Lateral acceleration of cruise ship |
|
图 12 邮轮横摇运动 Fig. 12 Roll motion of cruise ship |
|
图 13 邮轮纵摇运动 Fig. 13 Pitch motion of cruise ship |
由图10~图13可知,大型邮轮垂向加速度及横向加速度均在浪向为90°时较其他浪向大,说明横浪对大型邮轮的运动加速度影响最大;横摇运动在浪向30°时达到最大,浪向为60°时次之;5级海况以下,纵摇运动在浪向60°时最大,6级海况以上时,纵摇运动在浪向120°时最大。
经评估,5级及以下海况条件下,大型邮轮的垂向加速度、横向加速度、横摇运动和纵摇运动在任意浪向下均符合舒适性标准;6级海况下,大型邮轮的垂向加速度、横向加速度和纵摇运动在任意浪向下满足舒适性标准,但横摇运动在浪向30°时超过了正常营运安全标准;7级海况下,大型邮轮的垂向加速度、纵摇运动在任意浪向下均符合舒适性标准,横向加速度在浪向90°时超过了舒适性标准,但满足正常营运安全标准,横摇运动在浪向30°时超过了安全性标准。
因此,当大型邮轮以设计航速18 kn航行时,在5级及以下海况,可忽略浪向的影响,在6级海况应避免在浪向30°下航行,在7级海况应避免在浪向30°及90°下航行。
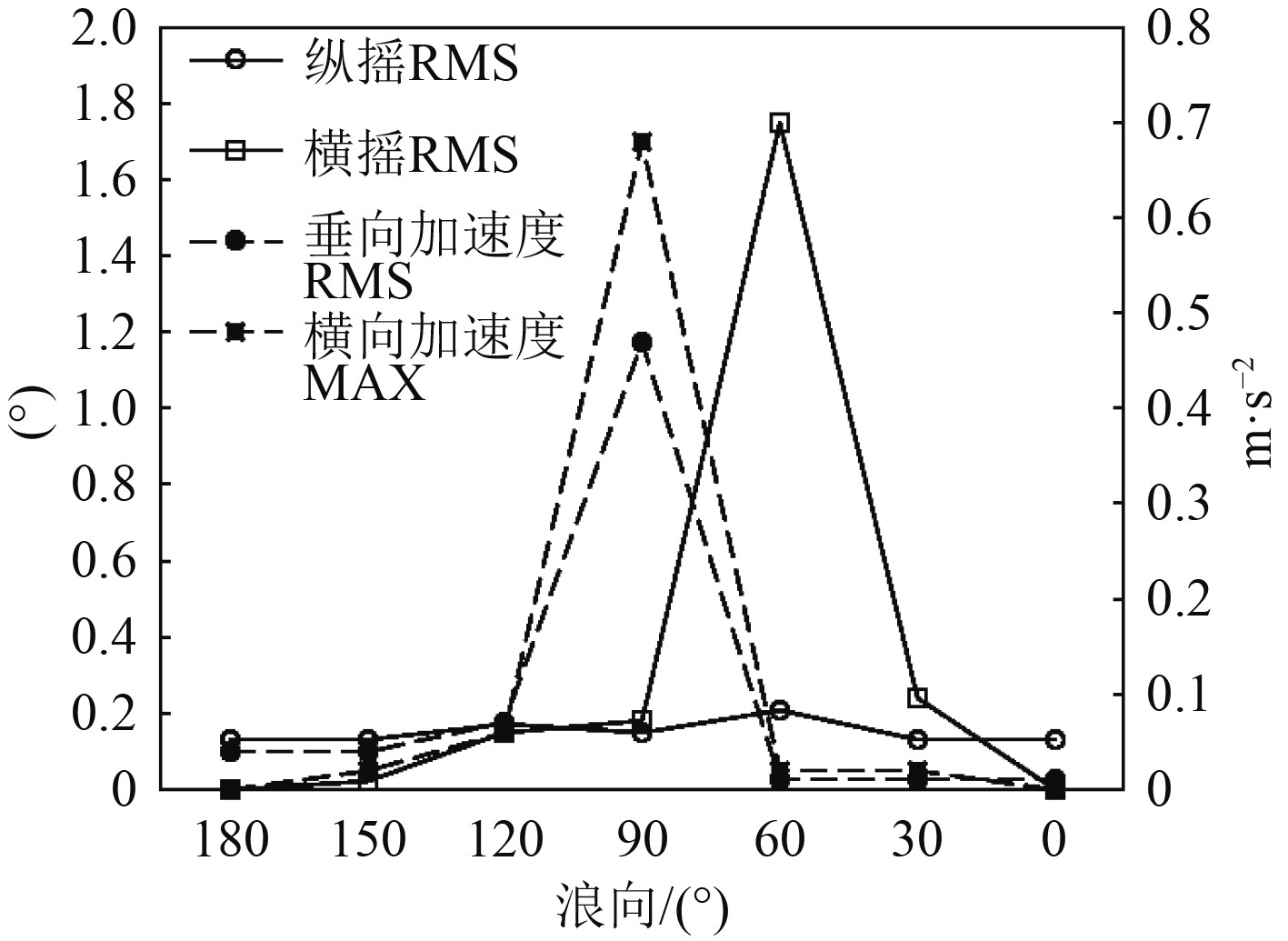
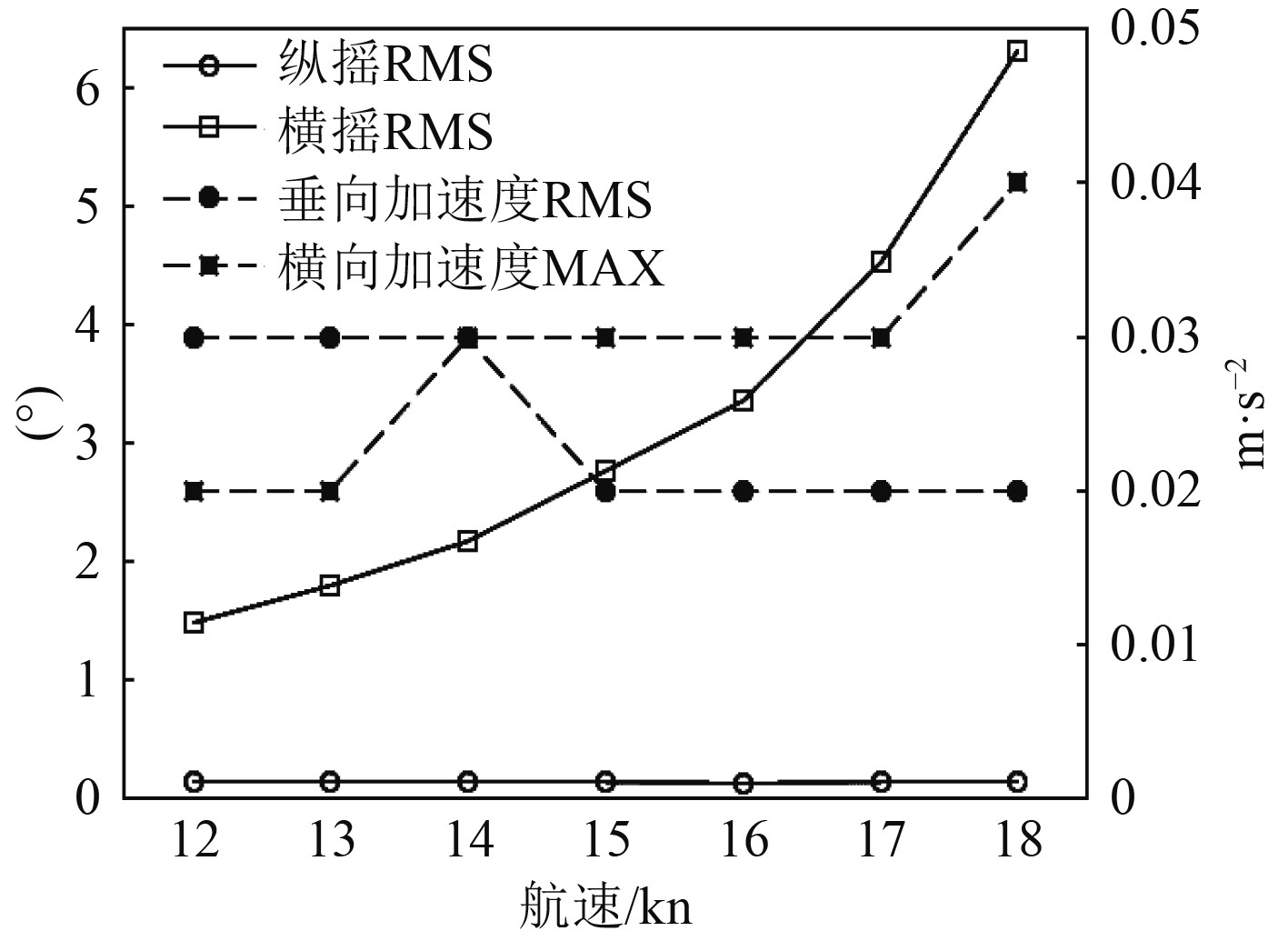
4.2 不同航速下邮轮的耐波性能5级海况下,大型邮轮在最大航速22 kn时的运动响应如图14所示。6级海况下,浪向30°时,大型邮轮在不同航速的运动响应如图15所示。
|
图 14 邮轮运动响应(5级海况,航速22 kn) Fig. 14 Motion response of cruise ship (sea state 5, 22 kn ) |
|
图 15 邮轮运动响应(6级海况,浪向30°) Fig. 15 Motion response of cruise ship (sea state 6, wave direction 30°) |
由图14可知,在5级海况下,大型邮轮以最大航速22 kn航行时,其垂向加速度最大均方根值、横向加速度最大值均小于0.98 m/s2,横摇最大均方根值小于3.0°,纵摇最大均方根值小于1.5°,符合舒适性标准。由图15可知,在6级海况、浪向30°条件下,大型邮轮航速不超过18kn时,其垂向加速度、横向加速度和纵摇运动均满足舒适性标准,但其横摇均方根值在航速为16 kn时即超过了3.0°,不满足舒适性标准,在航速为17 kn时即超过了4.0°,不符合正常营运安全标准。
因此,在5级及以下海况,大型邮轮可以以最大航速22 kn航行,不必考虑波浪的影响;在6级海况下,大型邮轮在航行时应控制航速不超过15 kn。
5 结 语本文通过数值模拟与模型试验相结合的方法,针对大型邮轮对安全性与舒适性的特别需求,研究大型邮轮的耐波性能,重点关注邮轮横摇、纵摇、垂荡运动以及重心位置处的横向及垂向运动加速度,并选取相关耐波性衡准对其进行了安全性与舒适性评估。结论如下:
1) 由邮轮模型试验与数值计算结果对比分析可知,应用基于三维时域势流理论以及Rankine面元法开发的水动力软件SESAM-Wasim对邮轮进行数值模拟可得到比较准确可靠的结果。
2) 邮轮以设计航速18 kn运行时,在5级及以下海况,其耐波性能完全满足安全营运与舒适性标准,可在任意浪向下航行;当海况条件达到6级时,邮轮应避免在浪向30°航行;当海况条件达到7级时,邮轮应避免在浪向30°及90°航行。
3) 当海况条件未超过5级时,大型邮轮在最大航速22 kn以内航行,可忽略海浪影响,耐波性满足安全营运与舒适性标准。当邮轮在更高海况下航行时,可通过降低航速的方法使其耐波性符合标准。在6级海况下,大型邮轮航速降至15 kn即可。
| [1] |
CAO Yu, YU Bao Jun, WANG Jian Fang. Modeling the seakeeping performance of luxury cruise ships[J]. Journal of Marine Science & Application, 2010, 9(3): 292-300. |
| [2] |
李辉, 王宇博, 许会芬, 等. 豪华邮轮波浪载荷预报方法[J]. 船舶工程, 2018, 40(S1): 71-74+145. |
| [3] |
章新智, 王驰明, 郭昂. 豪华邮轮耐波性衡准分析[J]. 船舶标准化工程师, 2014, 47(4): 13-17. DOI:10.3969/j.issn.1005-7560.2014.04.004 |
| [4] |
马网扣, 王露, 董良志, 等. SOLAS 2020破舱稳性对大型邮轮主尺度规划的影响[J]. 中国造船, 2019, 60(3): 46-54. |
| [5] |
DALLINGA R P, BOS J E. Cruise ship seakeeping and passenger comfort[J]. Cruise Ship Seakeeping & Passenger Comfort Tno Repository, 2010.
|
| [6] |
JAE-H K, YONGHWAN K. Study on assessment of passenger comfort and its improvement by using motion stabilization for a cruise ship[C]//International Conference on Maritime Technology. 2012
|
| [7] |
赵连恩, 谢永和. 高性能船舶原理与设计[M]. 北京: 国防工业出版社, 2009.
|
| [8] |
朱仁传, 缪国平. 船舶在波浪上的运动理论[M]. 上海: 上海交通大学出版社, 2019.
|
 2022, Vol. 44
2022, Vol. 44
