0 引　言

船舶在真实航行条件下，航向稳定性，转首性和回转性的优劣将直接影响到船舶的航行安全性和经济性。对于全附体船舶的操纵运动，其周围的流场非常复杂，这使得预测船舶的运动存在很大的困难。传统的船舶操纵性能预报方法是缩比模型试验，试验能够直接获取部分船舶操纵性能指标，但也有其局限性。相比于实际海况，试验通常会简化试验条件，并且很难获取流场信息特别是船桨舵干扰引起的剧烈流场变化。同时，试验周期较长，成本较高，并且很难对已建造好的船模进行调整^[1].

基于系统的操纵模拟方法也被广泛地用来研究船舶操纵性能。袁桂蓉^[2]建立了吊舱推进器船舶的操纵运动模型和海上干扰作用力模型，对吊舱推进器船舶的运动进行了仿真试验。陈纪军等^[3]研究了十字形和X 形尾舵布局对航行体的操纵性水动力特性的影响。而近年来，随着计算机技术的发展，CFD (计算流体动力学)已被越来越广泛地使用。由于 CFD是基于物理原理的高保真度方法，并且能在没有经验输入的情况下得出较为可靠的结果，它也越来越多地被用于预测船舶操纵性^[4]。Carrica等^[5]使用CFD Ship-Iowa对KCS模型在浅水中的Z形机动进行了数值模拟，并将仿真结果与试验数据进行了比较。Martin等^[6]使用了离散桨和体积力2种方法对ONRB1潜艇模型进行了2个航速下的水平/垂直面Z型以及回转的操纵仿真模拟。仿真结果与试验对比发现，2种方法都能很好地复现试验的时历结果，仿真误差均小于10%。邱云明等^[7]使用RANS方法研究了船舶危险对遇时的水动力相互作用，计算结果与试验的对比验证了方法的可靠性，分析了船舶受力和运动特征，该结果为危险对遇时两船操纵研究提供了参考依据。随着技术的发展和进步，以及对船舶操纵性的越来越高的要求，2017年于中国无锡召开的第28届拖曳水池会议正式成立了专注于波浪中操纵性问题研究的专门委员会，为船舶操纵性的研究提出了新的指导方向。王建华等^[8-9]使用CFD求解器naoe-FOAM-SJTU进行了ONRT波浪中的回转、Z型和航向保持的操纵性数值仿真，将船舶波浪操纵仿真的六自由度运动、螺旋桨的推力和扭矩、舵角的历时曲线，以及船舶运动轨迹的时历结果同Tokyo 2015 CFD 研讨会上的模型试验数据进行了对比，发现波浪中回转试验模拟关键参数误差均小于10%，波浪中Z型试验模拟关键参数误差小于15%，结果吻合良好，验证了直接数值求解波浪中船舶操纵问题的可靠性。

目前，已有的许多研究结果已经验证了使用CFD方法预报船舶操纵性与耐波性的可行性，但仍然很少有研究直接评估船舶在波浪中的操纵性能。在实际的海上航行时，船舶经常处于波浪环境中，因此，对船舶在波浪中的回转特性进行研究，具有重要意义。本方案用非稳态RANS方法预测ONRT在规则波中迎浪航行时的回转特性．研究使用了自主研发的粘性流CFD代码HUST-Ship求解RANS方程，并结合六自由度刚体运动方程预测船体运动，自研结构化动态重叠网格代码HUST-Overset用于处理大幅的船舶运动。螺旋桨推进模型使用了迭代型体积力模型OUM（大阪大学方法）^[10]。研究过程中，采用了移动域方法^[11]进行造波。首先使用PI速度控制器^[12]进行静水自航的转速匹配，然后定转速在波浪中自航至稳定状态，当波峰到达船中是开始转舵，进行波浪回转的仿真模拟。仿真得到的静水自航，波浪自航以及波浪回转结果均与Tokyo2015^[13]以及Simman2020^[14]提供的试验结果进行比较，并进一步分析了ONRT波浪自航过程中的六自由度运动和舵力变化。

1 数值方法和数学模型

本文所有的计算包括敞水，波浪和静水中的拖航和自航仿真都是使用URANS求解器HUST-Ship进行的。HUST-Ship已经通过大量不同的螺旋桨，潜艇以及水面船的仿真验证了其可靠性^[15~17]。

1.1 改进体积力模型

RANS方程是通过对连续性方程和动量方程时均化得到：

$ \frac{{\partial {U_i}}}{{\partial {x_i}}} = 0 ，$

$ \frac{{\partial {U_i}}}{{\partial t}} + {U_j}\frac{{\partial {U_i}}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial P}}{{\partial {x_i}}} + \frac{1}{\rho }\frac{\partial }{{\partial {x_j}}}(\mu \frac{{\partial {U_i}}}{{\partial {x_j}}} - \rho \overline {u_i'u_j'} ) + {f_{bi}}。$

其中： $ {U_i} $ 为雷诺平均速度成分； $ {x_i}{\text{ = (}}x,y,z{\text{)}} $ 为独立坐标方向； $ P $ 为流体动压； $ \overline {u_i'u_j'} $ 为雷诺应力； $ {f_{bi}} $ 为螺旋桨每单元体积的力； $ {F_r} = {U_0}/\sqrt {gL} $ 为傅汝德数， $ {R_e} = {U_0}L/\nu $ 为雷诺数。 $ {U_0} $ 和 $ L $ 分别为船舶设计速度，船舶垂线间长。另外，选择了双方程涡粘性 $ k - \omega $ 模型作为湍流模型^[18]。

体积力方法，即在船后添加一个简化的圆柱区域代替螺旋桨，同时在动量方程右端添加一体积力项 $ {f_{bi}} $ 产生螺旋桨相应的力和力矩。体积力求解流场信息是用螺旋桨的性能参数和RANS方程求解来得到螺旋桨-船的相互作用形式，根据实际的叶片载荷得到 $ {f_{bi}} $ 的分布。计算时将计算出的 $ {f_{bi}} $ 代入动量守恒公式中，求得舰船在自航时的有效伴流及其他流场信息。迭代型体积力模型OUM^[10]是一种基于考虑三维螺旋桨粘性效应的BEMT（叶元-动量方法）的方法，在迭代计算中采用该时刻桨盘面处的瞬时速度作为螺旋桨进速进行计算。

1.2 自由液面模拟方法

仿真中，使用了单相level-set方法捕捉自由液面的变化，忽略空气的密度和黏性影响。这种方法中定义流场中任意一点距自由液面的距离为 $ \varphi $ ，自由液面即可表示为 $ \varphi {\text{ = }}0 $ ，level-set方程可写为^[19]：

$ \frac{{\partial \varphi }}{{\partial t}} + v\nabla \varphi = 0 {。}$

其中： $v$ 为速度矢量； $ \varphi {\text{ = }}0 $ 表示自由液面， $ \varphi > 0 $ 表示在空气中， $ \varphi < 0 $ 表示在水中。

1.3 坐标系与六自由度运动

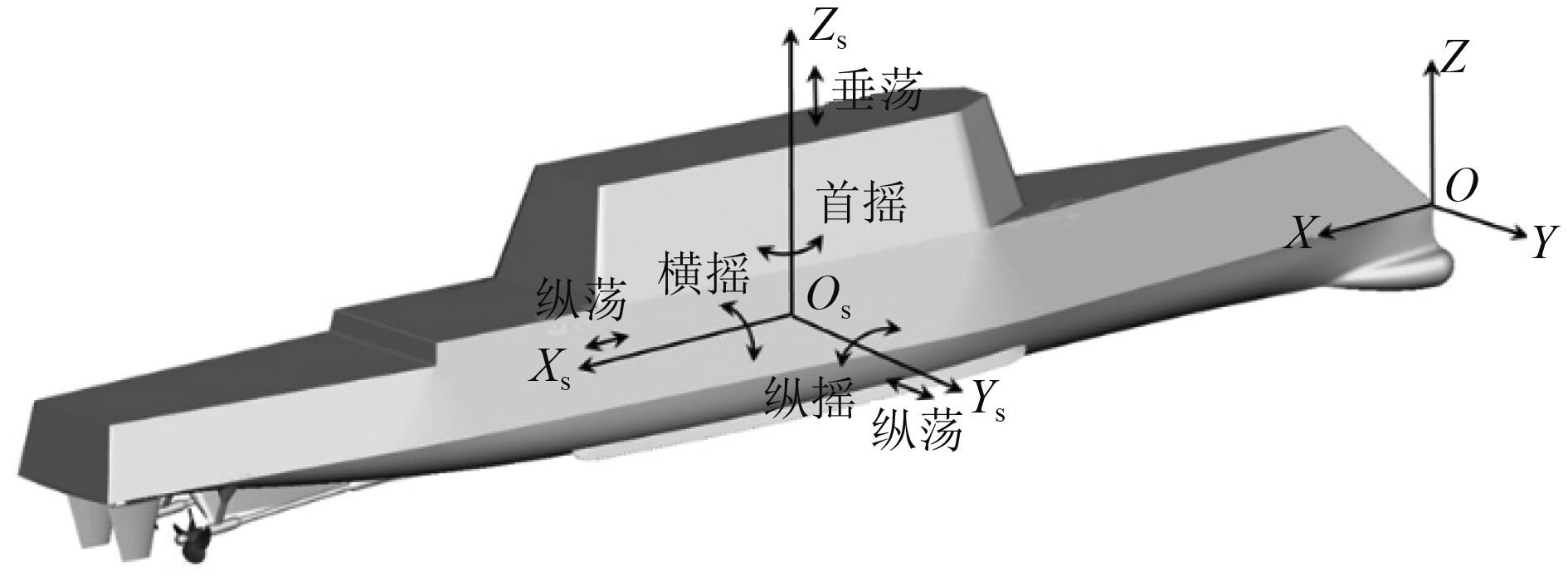
HUST-Ship中船舶运动的求解涉及2个右手的笛卡尔坐标系分别为大地坐标系O-XYZ与船体坐标系O_S-X_SY_SZ_S，如图1所示。为预报船舶运动姿态的变化，HUST-Ship中集成了六自由度运动模块，六自由度运动方程在船体坐标系下求解，船体的平动和转动在大地坐标系下表示，船体的速度、加速度以及所受力和力矩在船体坐标系中表达。根据刚体动力学与动量矩定理，船舶六自由度运动方程^[10]可表示为：

$ {m[\dot u - vr + wq] = X}，$

$ {{m[\dot v - wp + ur] = Y}}，$

$ {{m[\dot w - uq + vp] = Z}}，$

$ {{{I}}_x}{{\dot p + [}}{{{I}}_z}- {{{I}}_y}{{]qr = K}}，$

$ {{{I}}_{{y}}}{{\dot q + [}}{{{I}}_x} - {{{I}}_z}{{]rp = M}}，$

$ {{{I}}_{{z}}}{{\dot r + [}}{{{I}}_y} - {{{I}}_x}{{]pq = N}} 。$

式中：u，v，w，p，q，r分别为纵荡，横荡，垂荡，横摇，纵摇，首摇速度；x正方向指向船尾，y左舷指向右舷为正，z方向向上为正；I_x，I_y，I_z分别为船体坐标系下X_S，Y_S，Z_S轴的无量纲惯性矩；X，Y，Z，K，M，N分别为作用于船体的外力和外力矩在船体坐标系下X_S，Y_S，Z_S轴的分量。

1.4 数值造波^[20]

HUST-Ship中使用速度边界造波方法产生目标波浪。当仿真的目标波浪波长为 $ \lambda $ ，波高为 $ A $ 时，其入口处的自由液面变化为：

$ {{\eta (t) = A{\rm{cos}}(kx - \omega t + \varphi )}}，$

对应边界上的速度为：

$ {{u = A\omega }}\frac{{{{{\rm{cos}}hk(z + d)}}}}{{{{{\rm{sin}}hkd}}}}{{{\rm{cos}}(kx - \omega t + \varphi )}} ，$

$ {{w = A\omega }}\frac{{{{{\rm{sin}}hk(z + d)}}}}{{{{{\rm{sin}}hkd}}}}{{{\rm{sin}}(kx - \omega t + \varphi )}} 。$

其中： $ {{A}} $ ， $ {{k}} $ ， $ {{\omega }} $ ， $ {{\varphi }} $ 为分别为子成分规则波的波幅，波数，圆频率，初始相位。

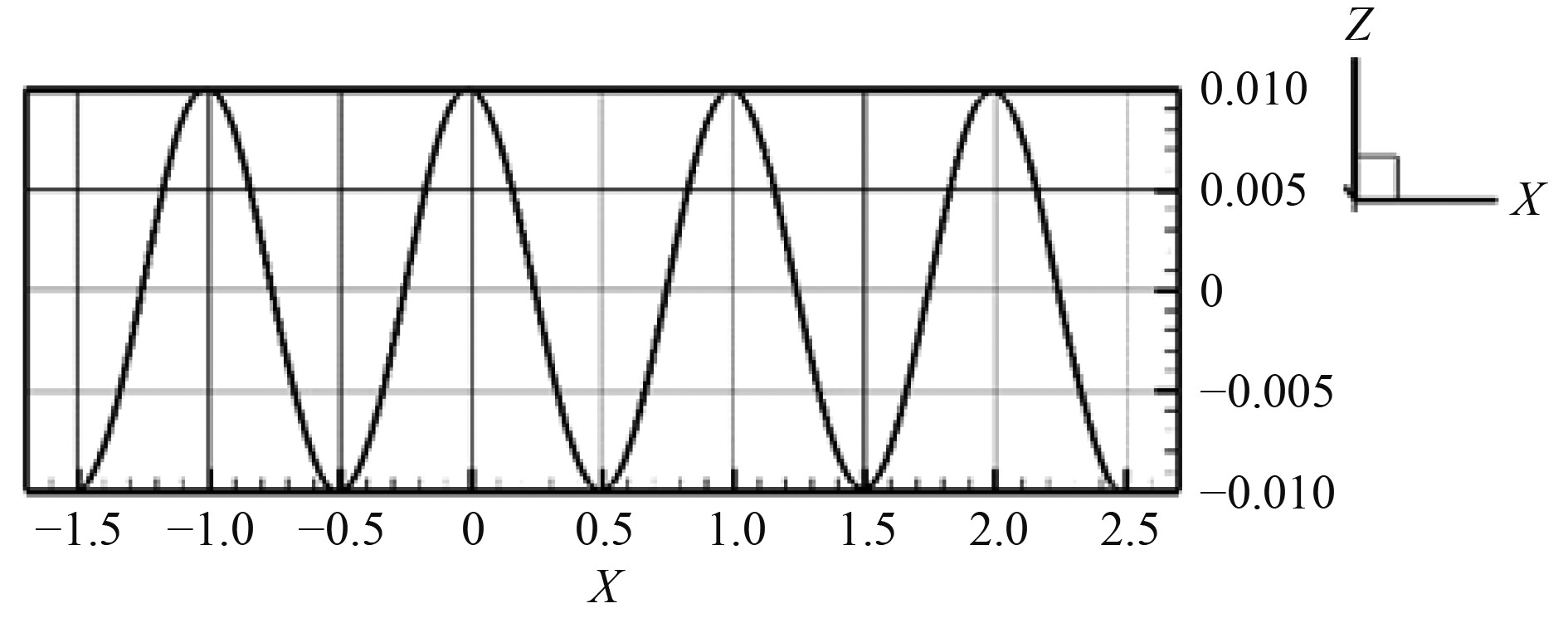
基于以上边界造波方法，对所需λ/L_wl = 1和H/L_wl = 0.02的规则波网格分布进行讨论。由于迎浪是波浪沿着X方向，经测验Y方向的网格节点数对最后的造波结果几乎没有影响，可与静水中网格节点相同(Y方向)，通过多次测量验证，确定其网格分布为：单位波长范围60个网格节点(X方向)，波高1.5倍的高度范围内加密且单位波高20个网格节点(即−0.03<Z<0.03节点数为30)，造波效果如图2所示。

2 研究对象与计算域 2.1 研究对象

本文选用的研究对象为ONRT(ONR Tumblehome)模型，该模型是现代水面作战舰艇的初步设计，是国际上公布用于基础研究的模型之一，模型参数来自SIMMAN 2020^[14] 研讨会，波浪回转工况按照SIMMAN 2020工况case5.3设置。

该船的主尺度参数由表1给出。

2.2 网格划分

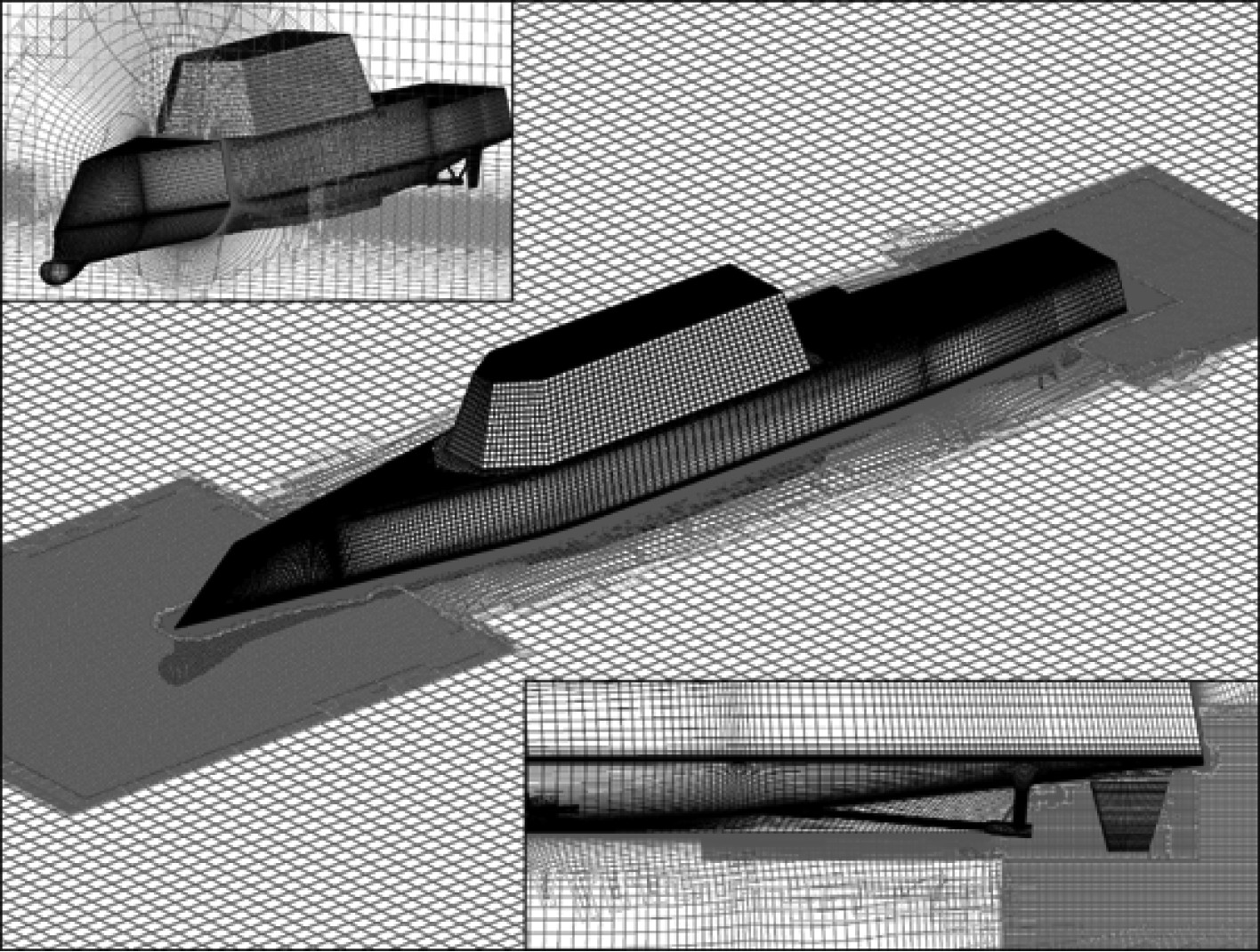
对于全附体船模，要考虑不同附体周围流场与船体的相互干扰，导致对问题的求解变得复杂。为了解此，基于自研重叠程序HUST-Overset使用了动态重叠网格方法。如图3所示，由于船舶首尾流场变化较为剧烈，所以需要单独进行加密。设置加密区不仅可以使船体和各个附体之间重叠插值时孤点减少，更有助于船体周围流场的捕捉。本HUST-Overset基于结构网格的格点式重叠方法，具体可分为3步^[1]：挖洞，识别插值点以及寻找插值点的贡献单元。其中，洞映射方法用于进行挖洞，ADT方法用于寻找插值点的贡献单元，并采用三线性插值获得来贡献单元与插值点关系。

2.3 计算域与边界条件

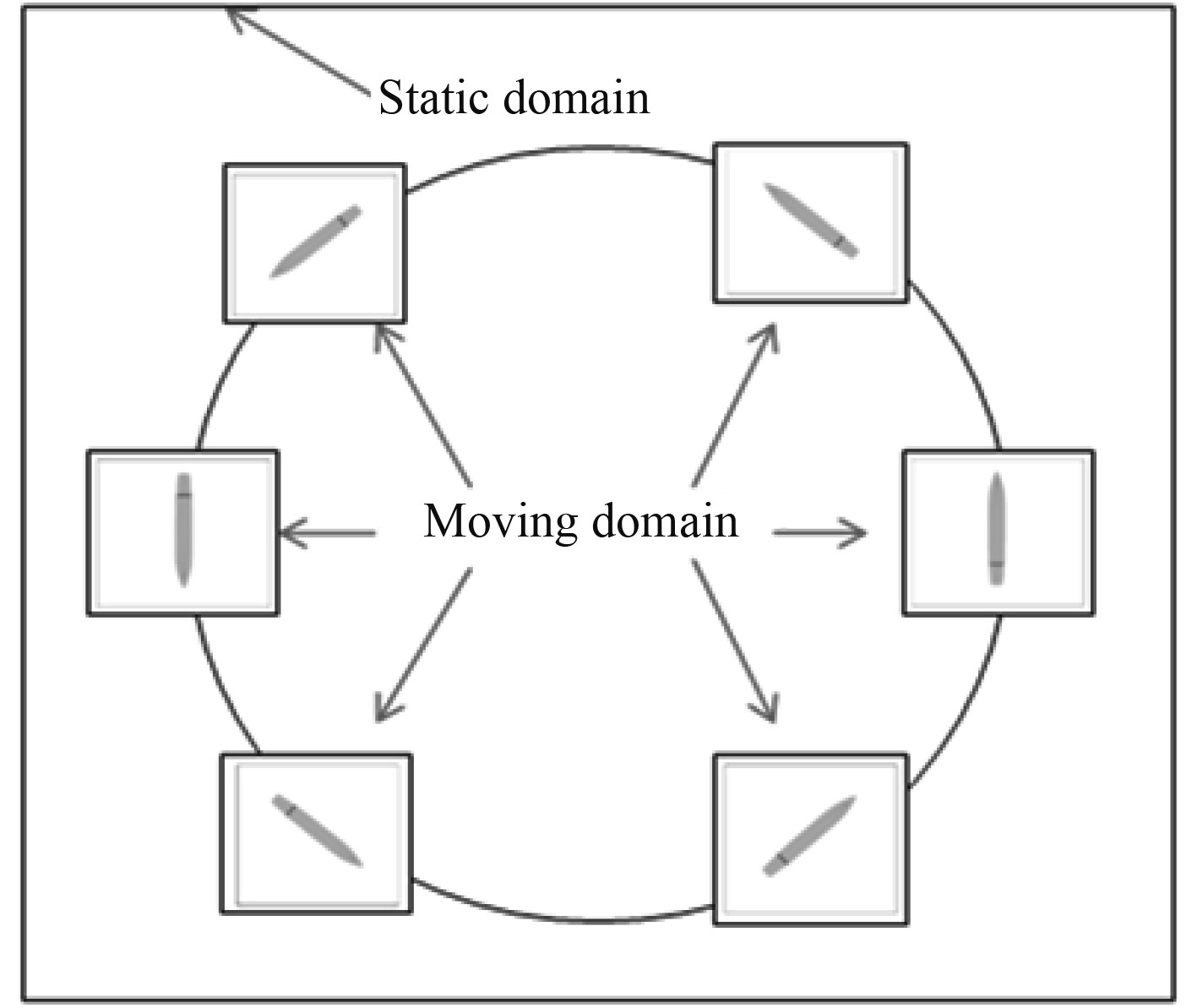
如图4所示，针对船舶在波浪中的大幅度操纵运动的问题，将数值造波技术与移动域模型^[8]相结合，以保证移动域中浪向、浪高等波浪参数不受背景网格相对位置改变带来的影响，可以最大程度减小动态计算对超大背景网格的需求，减小背景网格域移动对波浪参数改变的影响。

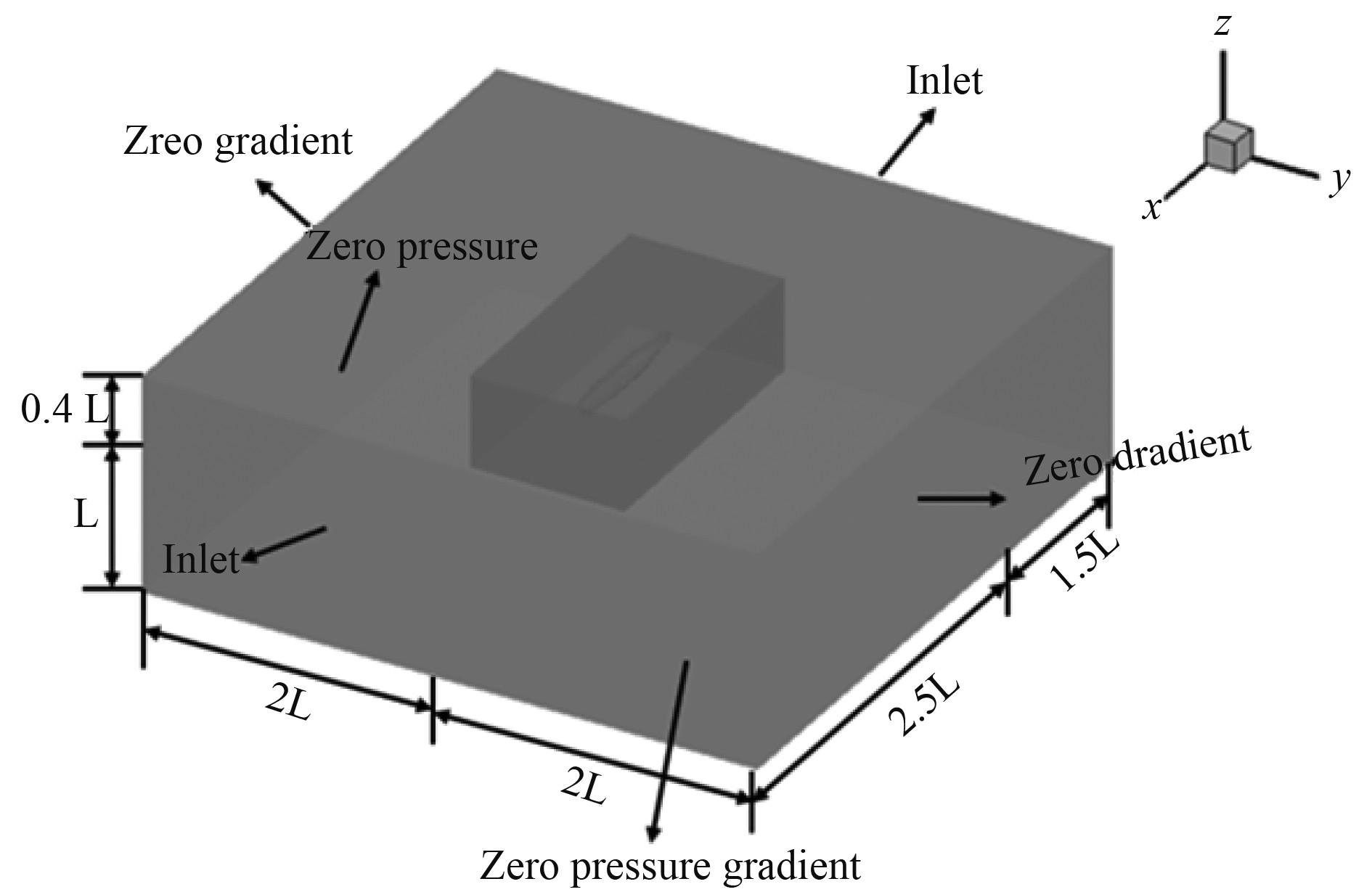
为了进行船舶波浪回转的数值仿真，如图5所示，建立一个长宽均为4L的方形计算域，以便能模拟出精确的波浪条件。经过一系列数值造波试验后，确定了该方形计算域的节点分布。初始船宽方向的2个边界均设置为零速度梯度边界条件“Zero gradient”，底部和顶部分别设置为远场边界条件“Zero pressure gradient”（压力梯度为0）与“Zero pressure”（压力为0），使用的移动域造波方法中，船长方向的双边界均设置为速度入口边界条件“Inlet”。

3 结果与分析

为进行试验工况为Fr=0.2时，35°舵角波浪回转仿真模拟，首先需进行Fr=0.2时，静水自航的转速匹配，然后定转速在波浪中自航至稳定状态，当波峰到达船中是开始转舵，进行波浪回转的仿真模拟。

3.1 静水自航转速匹配

HUST-Ship中，比例积分速度控制器(PI speed controller)^[12]用于在静水自航仿真时匹配对应目标航速的螺旋桨转速：

$ {{n = p(}}{{{U}}_{t{\rm{arg}} et}} - {{{U}}_{{\rm{ship}}}}{{) + I}}\int {{{(}}{{{U}}_{t{\rm{arg}} et}}-{{{U}}_{{\rm{ship}}}}{\text{)}}{\rm{dt}}}。$

式中：P和I分别为比例与积分常数。

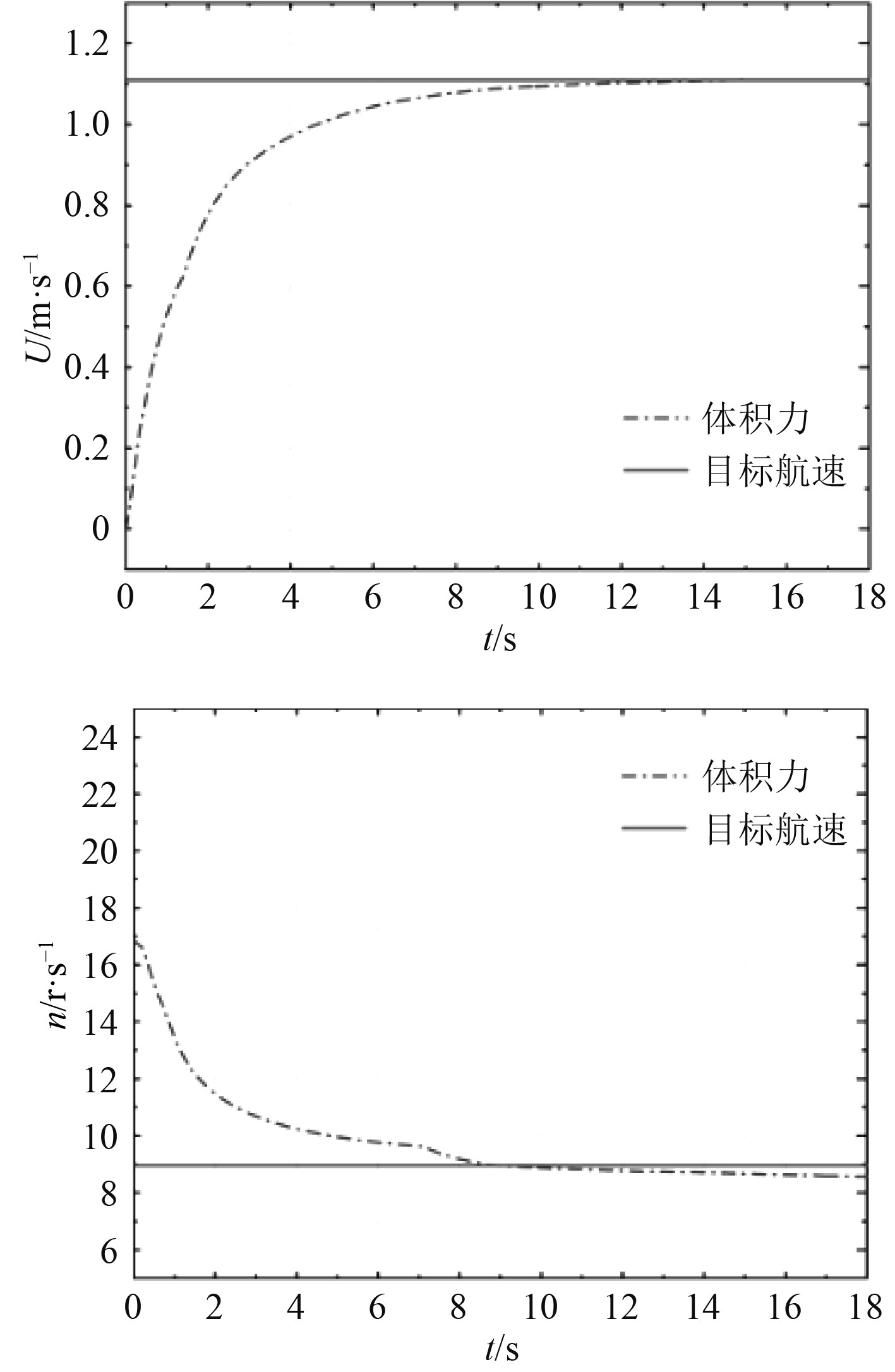
静水自航航速-转速匹配的整个过程如图6所示。使船舶达到目标航速所匹配的螺旋桨转速8.57 r/s与Tokyo 2015^[13]提供的试验结果8.97 r/s相近，相差4.46%，由此可知迭代型体积力OUM可较为精确地预报船舶自航转速。

3.2 定转速波浪自航仿真

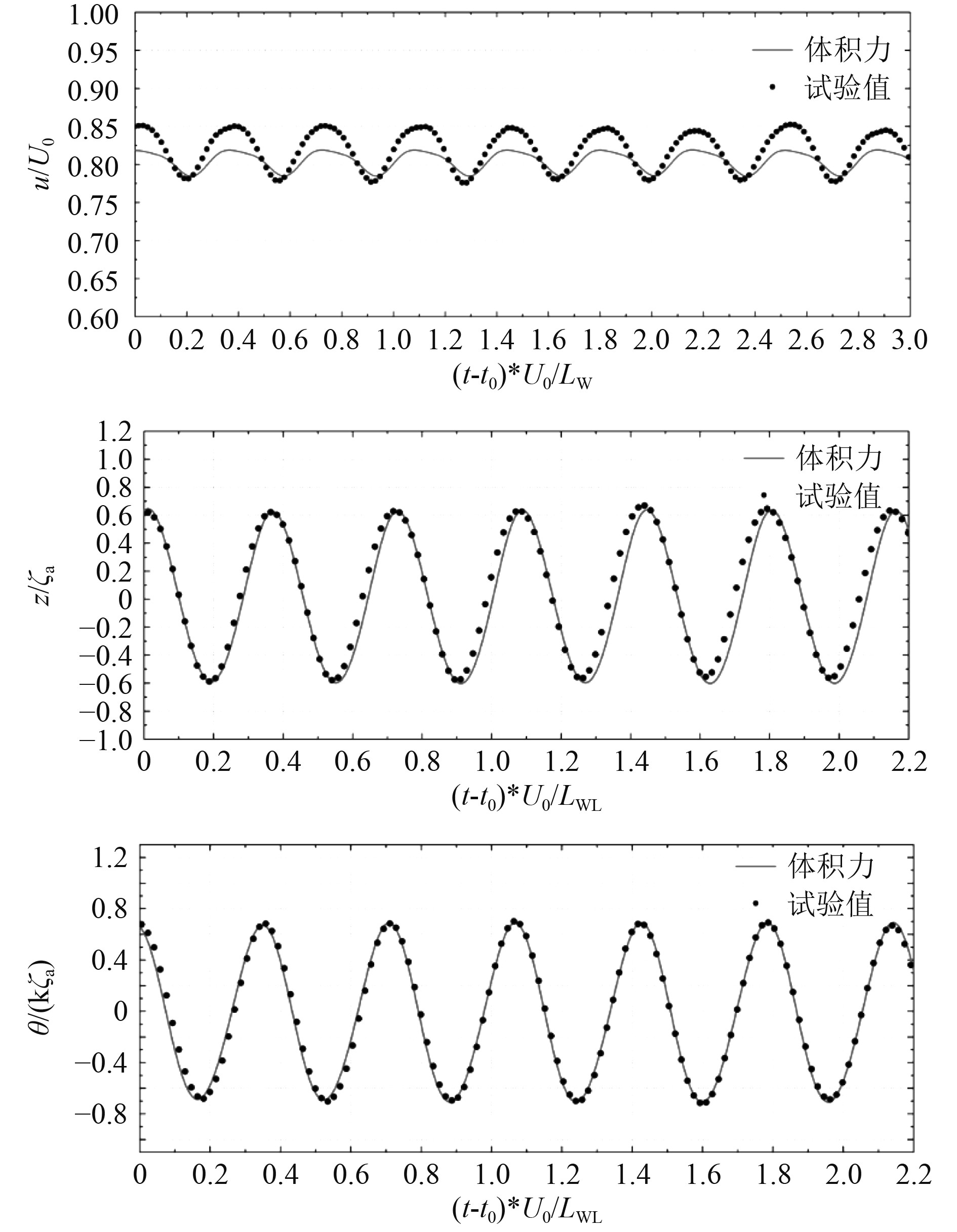
根据静水自航转速匹配结果，OUM体积力迎浪自航设定螺旋桨转速分别为8.57 r/s，取ONRT船模波浪自航的航速，垂荡，纵摇稳定状态时历结果与试验时历曲线对比如图7所示。可以发现，体积力仿真结果与试验吻合良好。为进一步分析，得到其量化结果如表2所示。可以发现，仿真结果与试验差别不大于3%。

3.3 波浪回转仿真结果

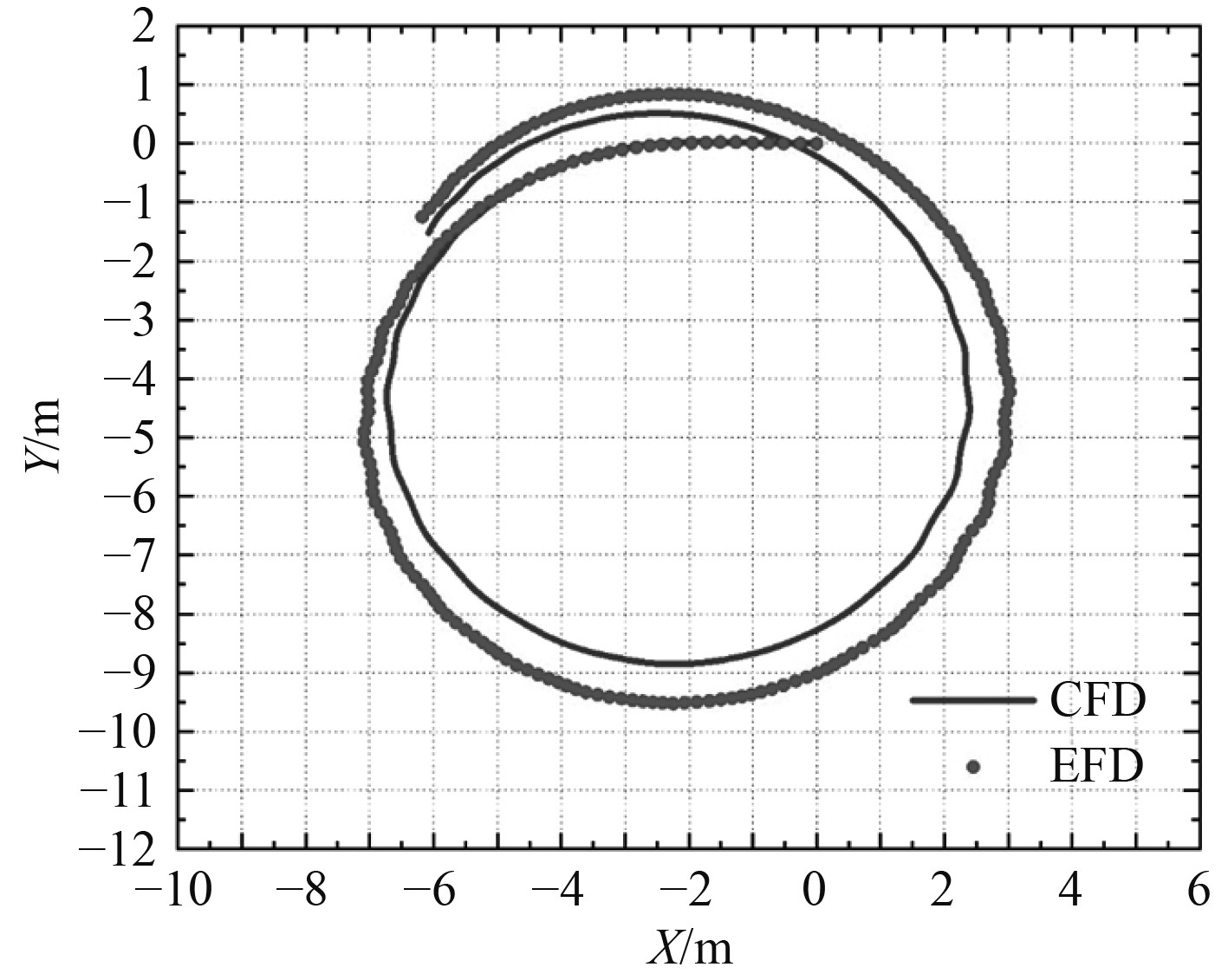
为了验证HUST-Ship具有波浪条件下船舶操纵性数值仿真的能力，基于边界造波法的数值波浪操纵水池的构建已经被详细地分析和研究^[11]。基于体积力法仿真ONRT船模35°波浪回转轨迹与试验对比如图8所示，对比两者轨迹可知数值预报结果与试验结果匹配度较高，仿真所得到的回转圈偏小，在首向角为90°与270°时ONRT运动轨迹有明显的波动现象。

以纵距、正横距和战术直径等特征参数量化，CFD结果与EFD结果之间的差别如表3所示，数值预报的误差均在10%以内，表明迭代型体积力方法预报波浪回转是可信的。

ONRT波浪回转过程中的六自由度运动如图9所示。可以发现，首向角为300°时横摇角幅值最大，达到9.5°，而纵摇运动幅值最小时船模处于横浪状态，当垂荡运动幅值小幅波动时ONRT遭遇随浪。另外，由于规则波具有周期性，导致垂荡、横摇、纵摇运动的时历曲线有显著波频振荡特性，但在XY面的平动如纵荡、横荡、首摇没有展现大的波频特性，该特征与前人研究一致^[9]，进一步证明了计算结果的可靠性。如图10所示，ONRT波浪回转过程中航速和首摇角速度变化与试验结果的整体趋势一致，波动频率与试验吻合，波动幅值会稍有不同。

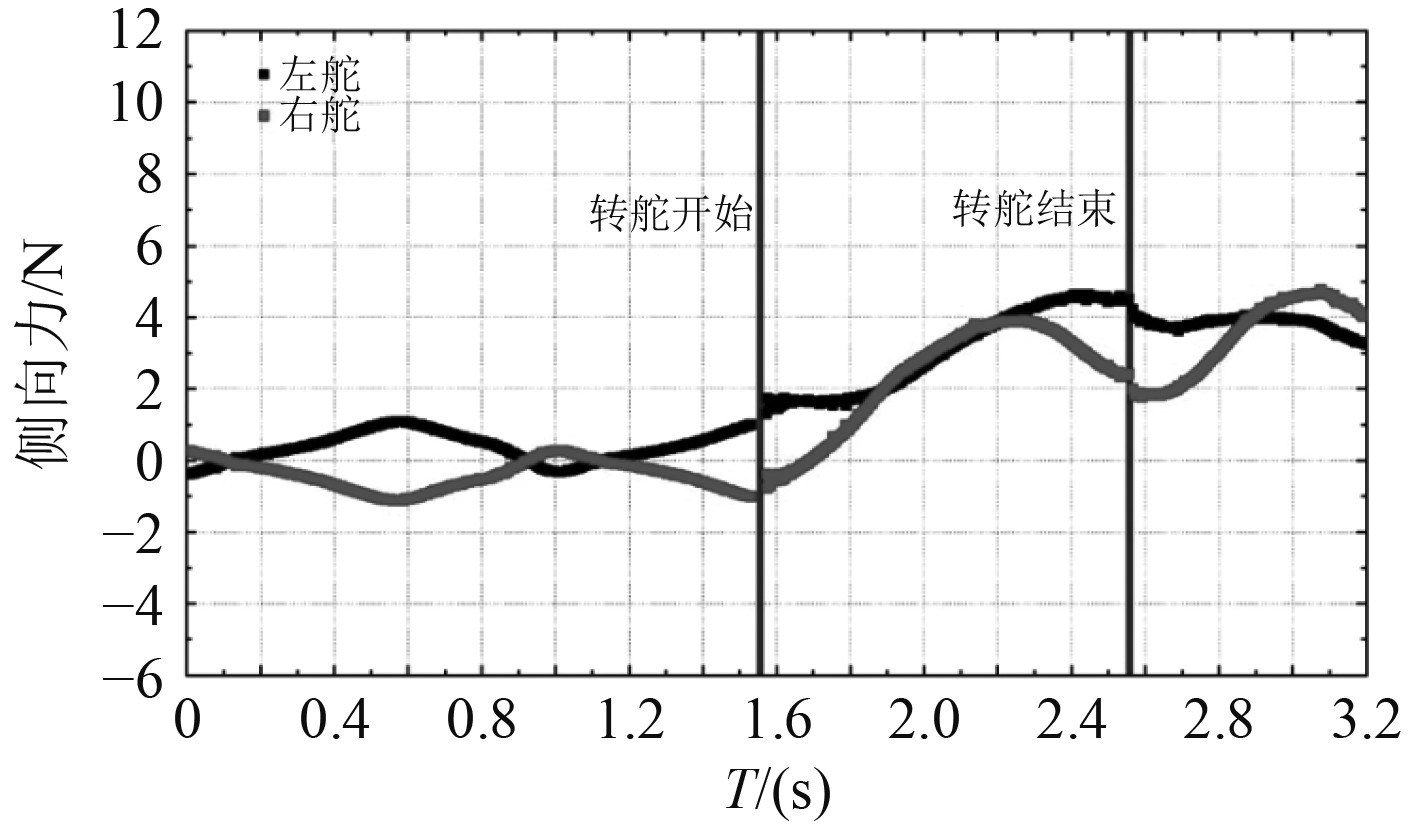
图11为ONRT波浪回转过程中在操舵前后左舵和右舵所受侧向力的变化。转舵开始之前，由于波浪的作用左、右舵所受侧向力不断变化，但合力始终为零，船舶保持直线航行，执行转舵操作后左、右舵所受侧向力同时增加，且侧向力方向相同合力不为0，提供船舶转向所需要的力与力矩。

4 结　语

本文基于自研URANS求解器HUST-Ship和自研重叠程序HUST-Overset对船模ONRT在波浪中的回转操纵运动进行直接CFD仿真，对静水自航，波浪自航以及波浪回转仿真结果均与Tokyo2015以及Simman2020提供的试验结果进行了比较。结果显示，静水自航转速误差在5%以内，波浪自航运动速降误差均小于3%，波浪回转轨迹的特征参数误差在8.5%以内，验证了HUST-Ship对静水以及波浪中船舶自由自航运动预报的适用性和可靠性，证明了迭代型体积力可以较为可靠且快速地预报船-桨-舵-波浪相互耦合作用，并且进一步分析了ONRT在波浪自航过程中的六自由度运动和舵力变化规律。由于体积力方法是一种平均的概念，无法捕捉桨周围更加真实的流动，会导致目前的数值预报存在一定的误差，后期将采用离散桨模型进一步对该问题进行研究，以获取更高的求解精度和更加详细的流场信息。