0 引　言

不沉性是舰船在舱室破损浸水后，具有足够稳性和浮性而能漂浮于水面不沉的固有能力^[1]。潜艇不沉性包含水上不沉性和水下自浮能力2个方面，其中水上不沉性是根本，它决定潜艇水上浸水或在水下破损浸水后，依靠抗沉措施浮至水面，能否保有足够的浮性和稳性，不至于沉没或倾覆。各国潜艇设计规范对与水上不沉性相关的破舱制、破损浮性和破损稳性均有明确的指标要求，我国潜艇设计中也需要对其各分项指标进行校核。鉴于潜艇水上不沉性既涉及破舱制、破损浮性和破损稳性，又受艇体姿态角、稳性高、抗海面风浪等级等多因素影响，评估难度大，目前国内外相关量化评估方法少见报道。为此，本文综合运用AHP^[2]和S型函数，建立一套潜艇水上不沉性评估方法，并结合案例进行了分析。

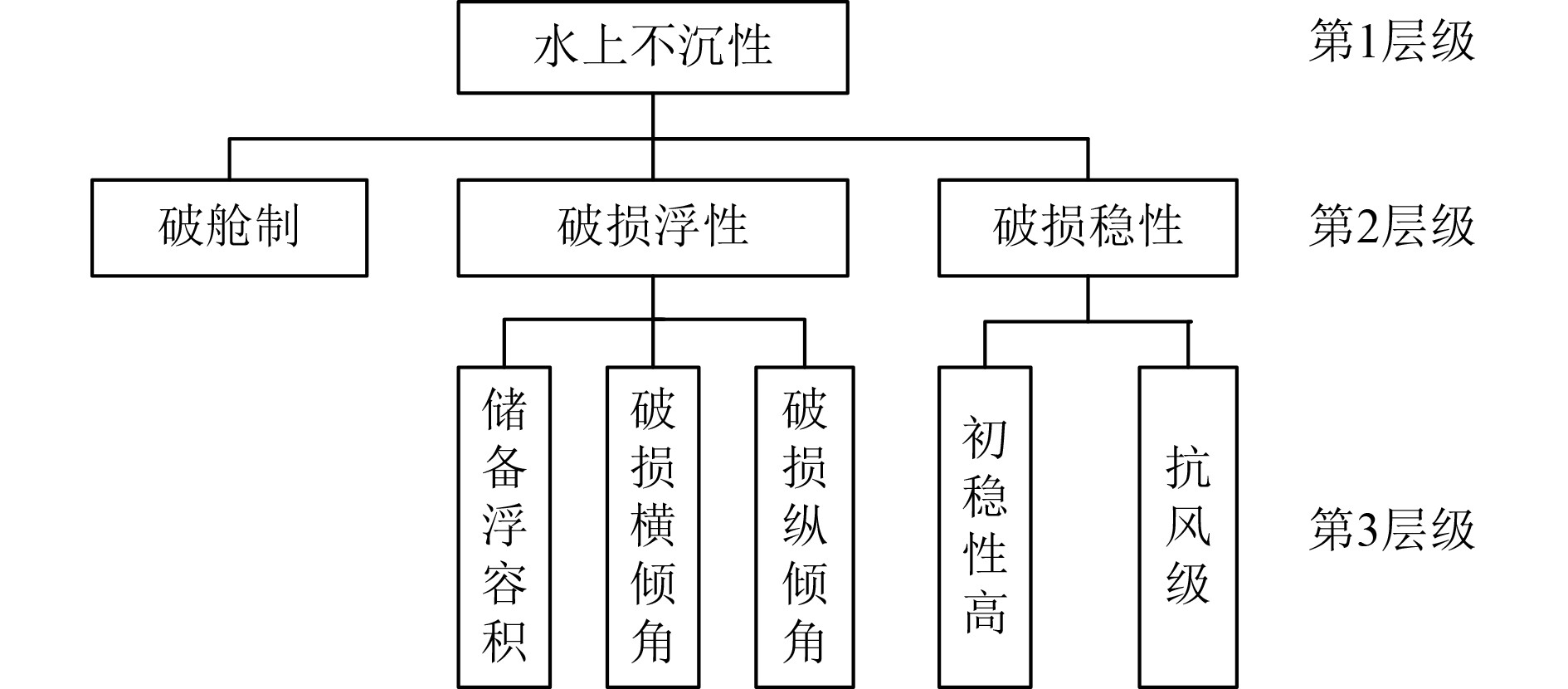
1 评估体系构建

构建潜艇水上不沉性的评估体系，主要基于其各分项考核指标进行。通常，潜艇水上不沉性主要通过对主压载水舱实施注水的静力方式，使破损潜艇在水上状态获得符合规范要求的浮性和稳性，具备稳定漂浮于水面的能力^[3]。我国规范明确潜艇水上不沉性包含满足水上不沉性的破舱制、破损浮性和破损稳性的具体要求。其中，破舱制是潜艇不沉性设计和校核计算中，对破损浸水的隔舱及与其相邻的主压载水舱数量和组合的选择原则，既是对潜艇总体设计的硬性要求，也是指导潜艇破损浸水后正确保持水上不沉的操作原则，目前各国规范对潜艇不沉性破舱制均有明确规定。潜艇破损后能否维持水上状态漂浮，主要取决于储备浮容积的大小，同时潜艇浮至水面后，正确控制艇体姿态非常关键，应确保其姿态角不超出规范值，其破损浮性还与潜艇的破损横倾角和纵倾角有关。水上破损浸水的潜艇，因自由液面的存在和风浪的影响，稳性保持难度大，潜艇稳性由破损后初稳性高和抗风级共同决定。由此，确定潜艇水上不沉性评估指标体系如图1所示。

2 评估衡准建立

潜艇水上不沉性评估的目的，在于指导不沉性的优化设计，提高潜艇生命力和安全性，以潜艇水上不沉性评估衡准值P作为不沉性评估的目标函数。鉴于潜艇设计规范对水上不沉性相关的各分项有明确的指标要求，任意分项未达到考核指标要求，潜艇不沉性校核将不予通过。显然，具备开展水上不沉性评估的潜艇，首先必须通过不沉性校核，各分项指标达标。如果以[0,1]表示潜艇水上不沉性评估衡准值的大小范围，对未通过校核的潜艇，其水上不沉性评估衡准值设置为0；对各分项均达到指标要求的潜艇，其水上不沉性评估衡准值应在[0.6,1]之间，可根据评估衡准的大小，评估潜艇的水上不沉性能为优良、中等或一般，并给出改进设计建议，具体如表1所示。

3 评估方法研究 3.1 评估流程

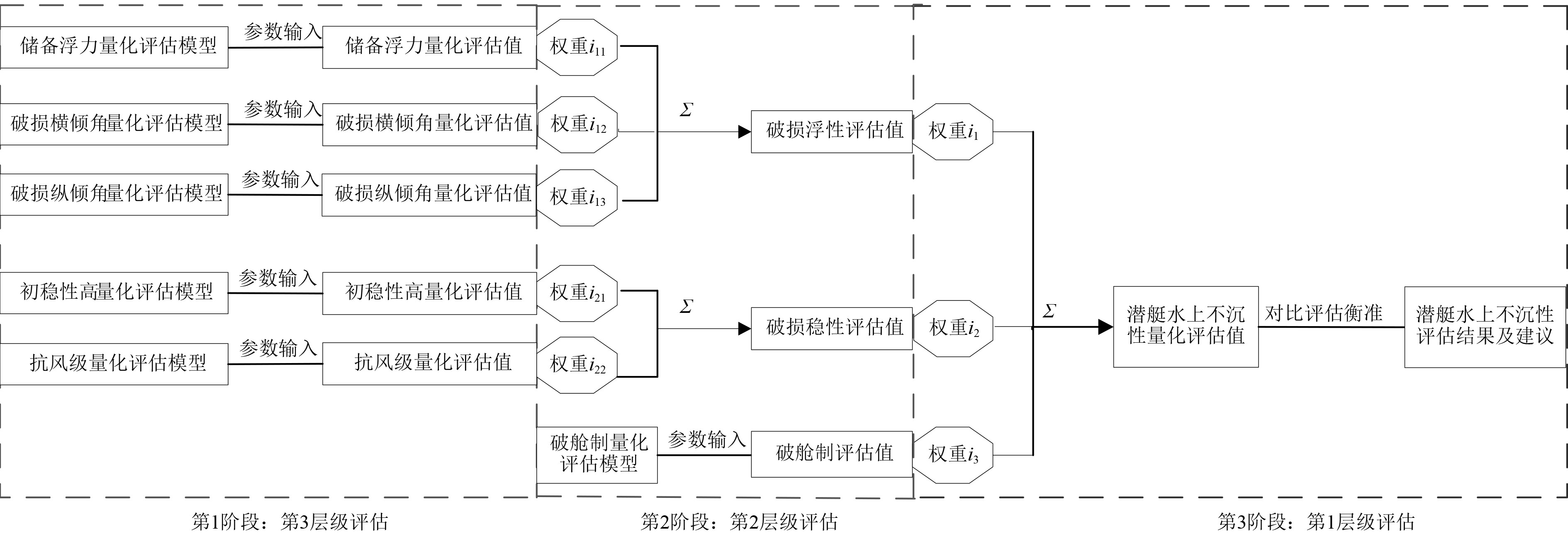
潜艇水上不沉性评估共分3个阶段，第1阶段主要通过S型函数方法，构建第3层级中储备浮容积、破损横倾角、破损纵倾角、初稳性高、抗风级等分项指标量化评估模型，并根据设计参数，计算各分项指标量化评估值；第2阶段通过专家评比，以AHP确立储备浮容积、破损横倾角、破损纵倾角在破损浮性中的权重，以及初稳性高、抗风级在破损稳性中的权重，通过加权计算破损浮性和破损稳性评估值，同时构建潜艇破舱制量化评估模型，计算破舱制评估值；第3阶段通过专家评比，以AHP确立破舱制、破损浮性、破损稳性在潜艇水上不沉性评估中的权重，通过加权求和，计算潜艇水上不沉性量化评估值，对比表1中的评估衡准，确定潜艇水上不沉性评估结果，并出具评估报告。潜艇水上不沉性评估流程如图2所示。

3.2 评估模型

设潜艇水上不沉性量化评估值为P，破损浮性、破损稳性和破舱制的评估值分别为P₁,P₂,P₃，权重分别为i₁,i₂,i₃，则

$ P = \sum\limits_{x = 1}^3 {{p_x} \cdot {{\text{i}}_x}}，$

(1)

设储备浮容积、破损横倾角、破损纵倾角的评估值分别为P₁₁,P₁₂,P₁₃，权重分别为i₁₁,i₁₂,i₁₃，则

$ {P_1} = \sum\limits_{y = 1}^3 {{P_{1y}}} \cdot {{\text{i}}_{1y}} 。$

(2)

设初稳性高、抗风级的评估值分别为P₂₁,P₂₂，权重分别为i₂₁,i₂₂，则

$ {P_2} = \sum\limits_{{\text{z}} = 1}^2 {{P_2}_z} \cdot {{\text{i}}_{2z}}，$

(3)

综合式（1）~式（3），潜艇水上不沉性量化评估值为：

$ P = \left( {\sum\limits_{y = 1}^3 {{P_{1y}}} \cdot {{\text{i}}_{1y}}} \right) \cdot {i_{\text{1}}} + \left( {\sum\limits_{z = 1}^2 {{P_2}_z} \cdot {{\text{i}}_{2z}}} \right) \cdot {i_{\text{2}}} + {P_{\text{3}}} \cdot {i_{\text{3}}}。$

(4)

3.3 评估方法

根据评估流程及评估模型可知，潜艇水上不沉性量化评估的关键在于构建储备浮容积、破损横倾角、破损纵倾角、设初稳性高、抗风级和破舱制的量化评估模型，进而求解相应分量的量化评估值，以及确定各层级中不同分量的权重。

3.3.1 破损浮性量化评估方法

1）储备浮容积量化评估模型

潜艇储备浮容积的大小应满足水上不沉性的基本要求，同时总体还需综合其他性能的要求进行选取。目前，除俄罗斯“台风”级核潜艇采用3个耐压壳体，其储备浮容积高达35%外，目前世界在役常规艇型的潜艇储备浮容积一般设置在30%内，单壳体潜艇一般在10%～15%，双壳体潜艇、核潜艇一般在15%～30%^[3]。以 $ \overline \Delta $ 表示潜艇储备浮容积，令 $ \overline \Delta {\text{ = }}30{\text{% }} $ ，P₁₁=1； $ \overline \Delta {\text{ = }}10{\text{% }} $ ，P₁₁=0.6。根据S型函数，建立评估模型为：

$ {P_{11}} = \left\{ \begin{array}{*{20}{c}} \dfrac{1}{{1 + {e^{11 \times (0.3 - \overline \Delta )}}}} + 0.5，&{{\text{1}}0\% \leqslant \overline \Delta \leqslant {\text{3}}0\% } ，\\ 0 ，&\overline \Delta < 10{\text{% }} 。\end{array} \right. $

(5)

2）破损横倾角量化评估模型

为保证水上状态的破损潜艇不倾覆，潜艇的静横倾角不允许过大，通常要求控制在±15°内。以 $ \varphi $ 表示破损横倾角，令 $ \varphi {\text{ = }}0^\circ $ ，P₁₂=1； $ \left| \varphi \right|{\text{ = }}15^\circ $ ，P₁₂=0.6。根据S型函数，建立评估模型为：

$ {P_{12}} = \left\{ {\begin{array}{*{20}{c}} \dfrac{1}{{1 + {e^{8.4\left| \varphi \right|}}}} + 0.5，&{0 \leqslant \left| \varphi \right| \leqslant 15^\circ } ，\\ 0，&{\left| \varphi \right| > 15^\circ } 。\end{array}} \right. $

(6)

3）破损纵倾角量化评估模型

为保证水上状态的破损潜艇不倾覆，潜艇的静纵倾角不允许过大，通常要求控制在±9°内。以 $ \theta $ 表示破损横倾角，令 $ \theta {\text{ = }}0^\circ $ ，P₁₃=1； $ \left| \theta \right|{\text{ = }}9^\circ $ ，P₁₂=0.6。根据S型函数，建立评估模型为：

$ {P_{13}} = \left\{ {\begin{array}{*{20}{c}} \dfrac{1}{{1 + {e^{14\left| \theta \right|}}}} + 0.5，&{0 \leqslant \left| \theta \right| \leqslant 9^\circ } ，\\ 0，&{\left| \varphi \right| > 9^\circ } 。\end{array}} \right. $

(7)

4）破损浮性量化评估权重模型

考虑到潜艇储备浮容积在潜艇设计之初即确定，事关潜艇水上不沉的重要方面为潜艇姿态角的控制与扶正。为此，经专家综合评估，在破损浮性中的重要性排序为静纵倾角、静横倾角和储备浮容积，并基于AHP，建立破损浮性量化评估矩阵，如表2所示。

由此，计算确定i₁₁=0.136，i₁₂=0.238，i₁₃=0.625。

3.3.2 破损稳性量化评估方法

1）初稳性高量化评估模型

潜艇水上状态破损后，稳性高随之下降，即低于潜艇完整稳性时的初稳性高（通常不超出0.4m^[4]），但通常要求不小于0.15m。以 $ \overline {GM} $ 表示潜艇初稳性高，令 $ \overline {GM} $ =0.15 m， $ {P_{21}} $ =0.6； $ \overline {GM} $ =0.4 m， $ {P_{21}} $ =1。根据S型函数，建立评估模型为：

$ {P_{21}} = \left\{ {\begin{array}{*{20}{c}} \dfrac{1}{{1 + {e^{8.8 \times }}^{(0.4 - \overline {GM} )}}} + 0.5，&0.15 \leqslant \overline {GM} \leqslant 0.4，\\ 0，&{\overline {GM} < 0.15} 。\end{array}} \right. $

(8)

2）抗风级量化评估模型

潜艇水上状态破损后，需保有一定的抗风能力，通常要求破损后在4级海况下潜艇稳性衡准数不小于1.0。4级海况对应的风级为5～7级，以 $ {W_K} $ 表示抗风级，令 $ {W_K}{\text{ = }}5 $ ， $ {P_{22}}{\text{ = }}0.6 $ ； $ {W_K}{\text{ = }}6 $ ， $ {P_{22}}{\text{ = }}0.8 $ ； $ {W_K}{\text{ = }}7 $ ， $ {P_{22}}{\text{ = }}1 $ 。

3）破损稳性量化评估权重模型

潜艇水上破损后，采取措施防止初稳性高大幅降低非常必要，对于保证潜艇的抗风浪能力同样重要。为此，经专家综合评估，在破损稳性中的重要性排序为初稳性高、抗风级，同样基于AHP，建立破损浮性量化评估矩阵，如表3所示。

由此，计算确定i₂₁=0.75，i₂₂=0.25。

3.3.3 破舱制量化评估方法

一般双壳体潜艇需满足 $ {I_2} $ 破舱制要求，但单壳体潜艇要完全满足 $ {I_2} $ 破舱制要求很难，但达到 $ {I_1} $ 破舱制的要求则必须保证。以 $ {\rm I} $ 表示潜艇破舱制，令 $ {I} = {{I}_1} $ ， $ {P_3} = 0.6 $ ； $I = {I_2}$ ， $ {P_3} = 1 $ ； $I = {{\rm I}_0}$ ， $ {P_3} = 0 $ 。

3.3.4 水上不沉性量化评估方法

对潜艇水上不沉性的量化评估，需要确定破舱制、破损浮性和破损稳性的权重，经专家综合评估，并基于AHP，建立潜艇水上不沉性量化评估矩阵，如表4所示。

由此，计算确定i₁=0.342，i₂=0.0.577，i₃=0.081。

4 案例分析

假设某单壳体潜艇设计储备浮容积13%，满足I₁破舱制要求，完整初稳性高0.3 m，假设在水下航行发生碰撞，I舱破损进水，破口面积0.1 m²，以高压气吹除浮至海面，受海面6级风力和自由液面影响，潜艇破损初稳性高将降至0.18 m或以下，静横倾角将达到或超过11º、静纵倾角将达到或超过−7°。根据式（1）～式（8），潜艇水上不沉性评估衡准值计算结果如表5所示。

根据计算结果，该潜艇的水上不沉性评估衡准值为0.659，综合评定为“一般”，建议进一步优化设计方案。通过增加潜艇破损下的初稳性高，提升潜艇水上不沉能力，或者采取向尾压载水舱注水等方式，扶正艇体姿态，增加潜艇初稳性高，提高潜艇在风浪条件下的稳性衡准数，以及现行设计方案下的水面抗沉能力。

5 结　语

潜艇水上不沉性量化评估，对优化潜艇设计，辅助潜艇水上抗沉均有现实意义。过去由于潜艇不沉性不方便试验考核，多以单项指标校核和总体定性分析为主，潜艇不沉性设计水平不高，潜艇实际水面不沉性能难有效保证。本文以提升潜艇生命力和安全性的需求为牵引，基于AHP和S型函数，建立一种可量化评估的潜艇水上不沉性评估方法及评估衡准，并结合实例进行了分析。