2. 广州市顺海造船有限公司,广东 广州 511440
2. Guangzhou Shunhai Shipyards Ltd., Guangzhou 511440, China
自20世纪以来,潜艇作为一种具有良好隐蔽性和战略作用的水下装备,在各国军事国防领域扮演着越来越重要的角色。随着计算机技术的快速发展,对潜艇的操纵性研究方法也逐渐成熟,对艇体型线及操纵面形式的研究也逐渐成为一大热点。操纵面的类型通常由首围壳舵和尾舵两部分组成,常见的尾操纵面形式包括十字型、X型、H型、木字型等[1]。目前大多数潜艇均采用十字型尾舵,而H型尾舵作为一种新型尾舵具有结构简单和控制方便等优点,有较大的开发空间。
目前对潜艇操纵性的研究主要有模型试验方法、基于势流的面源法、基于CFD的间接预报和直接预报方法[2]。针对传统的十字型尾操纵面,国内学者对其开展了大量的研究。张峰丽[3]通过CFD方法对十字型尾操纵面潜艇模型进行了斜托试验和PMM实验,验证了CFD方法在求解水动力系数时的准确性。黄晨冉[4]通过重叠网格方法对十字型尾操纵面潜艇进行操纵运动模拟并与实验结果进行了对比验证。针对其他操纵面形式及几何参数影响,国内学者也做了大量研究。陈纪军等[5]通过CFD方法对十字型和X型尾操纵面航行体的水动力特性进行了对比分析,得到不同尾操纵面布局下平面静不稳定系数及舵力特性的大小关系。林俊兴等[6]在ITTC坐标系中比较十字型舵和X型舵的水动力特性,并建立了相同舵面积下不同尾操纵面的操纵力等效关系。曾广会等[7]以潜艇垂直面操纵运动线性方程为基础,提出了潜艇操纵面几何参数敏感性的概念,并开展了大量的敏感性计算。
H型尾操纵面和十字型尾操纵面结构相似,较X型尾操纵面控制简单,而针对H型尾操纵面这一尾舵形式的研究却很少。本文通过有限体积方法对十字型尾操纵面模型和H型尾操纵面模型的超越运动进行数值模拟,对比2种不同尾操纵面形式模型在超越运动过程中的运动特性,并通过对比分析不同翼板宽度的H型尾操纵面模型在超越运动中的运动情况,获得H型尾操纵面模型矩形翼板宽度的最优解。
1 数学模型 1.1 控制方程本文计算模型为不可压单相流,对不可压流体进行数值求解的主要基本方程为连续性方程和N-S方程,本文采用雷诺时均方法对N-S方程进行离散,控制方程如下:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $ \begin{split} \frac{\partial }{{\partial t}}(\rho {u_i}) +& \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\Biggr({\mu _0}\Biggr(\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}\Biggr) - \\ & \frac{2}{3}{\mu _0} \cdot \frac{{\partial {u_l}}}{{\partial {x_l}}}{\delta _{ij}}\Biggr) + \frac{\partial }{{\partial {x_j}}}( - \rho \overline {u_i^,u_j^,} ) + \rho {f_i} 。\end{split} $ | (2) |
式中:
通过补充湍流方程方法对控制方程进行封闭,本文重点分析潜艇在大尺度空间内的操纵性问题,同时关注黏性阻力和形状阻力对艇体的影响。分析得到边界层首层落在粘性底层且选取Y+≤5。选取标准
| $ \frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}}(\rho k{u_i}) = \frac{\partial }{{\partial {x_j}}}\left(\left(\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}\right)\frac{{\partial k}}{{\partial {x_j}}}\right) + {G_k} - {Y_k} + {S_k},$ | (3) |
| $ \frac{\partial }{{\partial t}}(\rho \omega ) + \frac{\partial }{{\partial {x_i}}}(\rho \omega {u_i}) = \frac{\partial }{{\partial {x_j}}}\left(\left(\mu + \frac{{{\mu _t}}}{{{\sigma _\omega }}}\right)\frac{{\partial \omega }}{{\partial {x_j}}}\right) + {G_\omega } - {Y_\omega } + {S_\omega }。$ | (4) |
在直接数值模拟时,对于船舵桨耦合计算通常用2种方法对螺旋桨问题进行处理,第1种是通过采用均布模型、
| $ {f_{bx}} = {A_x}{r^*}\sqrt {1 - {r^*}} {f_{b\theta }} = {A_\theta } \cdot \frac{{{r^*}\sqrt {1 - {r^*}} }}{{{r^*}(1 - r_h^,) + r_h^,}} ,$ | (5) |
| $ {r^*} = \frac{{{r^,} - r_h^,}}{{1 - r_h^,}} r_h^, = \frac{{{R_H}}}{{{R_P}}} {r^,} = \frac{r}{{{R_P}}} ,$ | (6) |
| $ \begin{split}&{A_x} = \frac{{105}}{8} \cdot \frac{T}{{{\text{π}} \Delta (3{R_H} + 4{R_p})({R_p} - {R_H})}},\\ &{A_\theta } = \frac{{105}}{8} \cdot \frac{Q}{{{\text{π}} \Delta {R_P}(3{R_H} + 4{R_P})({R_P} - {R_H})}}\end{split}。$ | (7) |
其中:
针对美国国防研究计划署提出的Suboff项目中的Suboff-1模型进行数值模拟分析,该模型已在泰勒水池进行了水动力实验并形成详细的实验报告[8],对于验证本文数值方法的准确性有参考作用。通过采用体积力模型模拟螺旋桨旋转产生推力的方法,对不同形式尾操纵面的Suboff-1模型进行水平超越运动模拟,表1为选取的全附体Suboff-1计算模型的主要尺度要素。
|
|
表 1 计算模型主尺度要素 Tab.1 Main scale elements of calculation model |
针对H型尾操纵面模型进行超越运动计算,为与不同操纵面运动过程中的优劣进行直观对比,选取结构形式简单的平面矩形板作为H型尾操纵面的翼板结构。将延舵面来流方向定义为翼板长边方向,其垂直方向定义为翼板宽边方向。
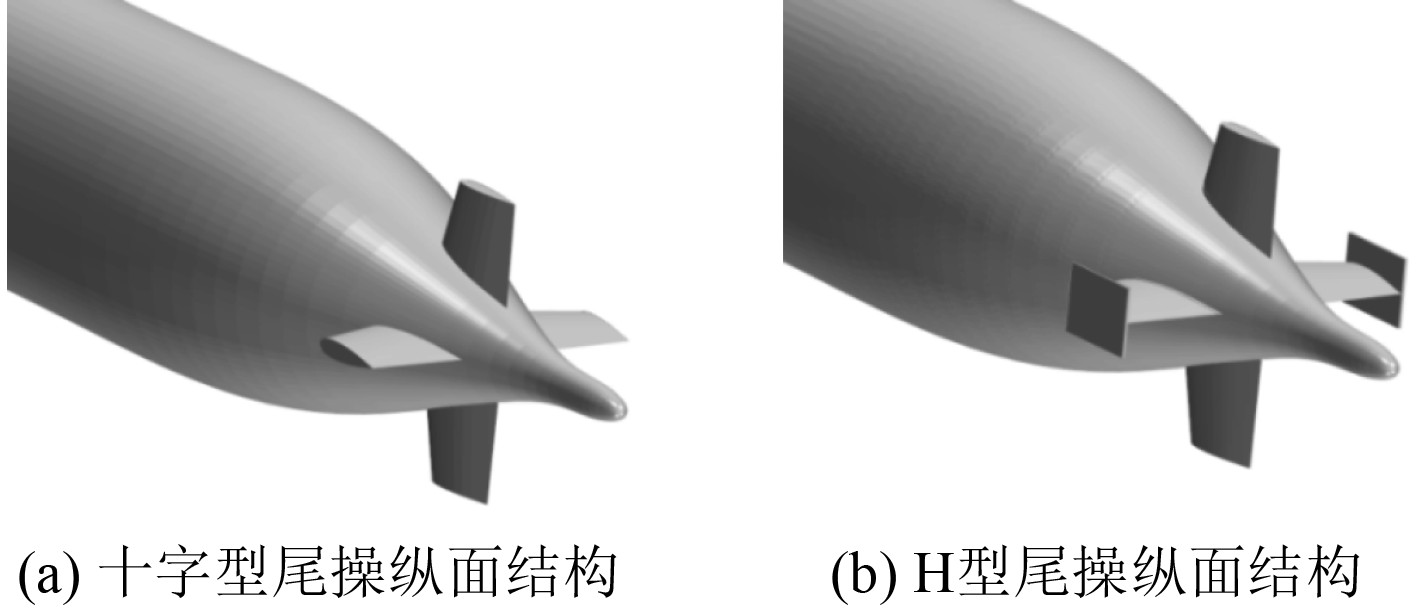
选取H型尾操纵面翼板长度与舵长相等,由于翼板厚度将对艇体阻力产生较大影响,选取翼板厚度选取为0.01 m。研究不同矩形翼板宽度对H型尾操纵面的潜艇模型在超越运动中的影响,选取5组不同宽度的H型尾操纵面模型进行计算。为消除其他几何因素影响,5组不同翼板宽度的H型尾操纵面模型的翼板长度与厚度均相等。不同尾操纵面尾部结构和H型尾操纵面的翼板结构如图1和图2所示。
|
图 1 不同尾操纵面结构形式 Fig. 1 Different tail control surface structures |

|
图 2 不同尾操纵面形式的水平舵结构 Fig. 2 Horizontal rudder structures with different stern control plane |
以H型操纵面的翼板宽度为参数,对5组不同翼板宽度的H型尾舵模型分别进行超越运动模拟计算。其中5组翼板宽度分别取为艇体平行中体直径的20%,30%,40%,50%,60%,并编以A,B,C,D,E等5组。翼板的具体宽度见表2。
|
|
表 2 5组不同翼板宽度编号 Tab.2 Five groups of different flange width numbers |
通过采用嵌套重叠网格方法和刚体运动模型对方向舵进行控制,在艇体自由运动的前提下使方向舵相对艇体运动。以自航点位置为操舵的开始时刻,转舵速度设置为60°/s、预定舵角为20°、预定首向角设置为10°。当艇首到达预定首向角位置时,方向舵立刻反向操舵,当艇首方向第二次达到预定首向角位置时超越运动完成。为对不同尾操纵面形式数值结果进行直观对比,本文计算模型均采取相同的操舵控制。
| $ \theta_{\delta}= \left\{\begin{array}{c} -60^{\circ} / {\rm{s}},\varphi \leqslant 10^{\circ} \cup \delta \geqslant-20^{\circ} ,\\ 0^{\circ} / {\rm{s}},|\delta| \geqslant 20^{\circ} ,\\ 60^{\circ} / {\rm{s}},\text { others }。\end{array}\right. $ |
其中:
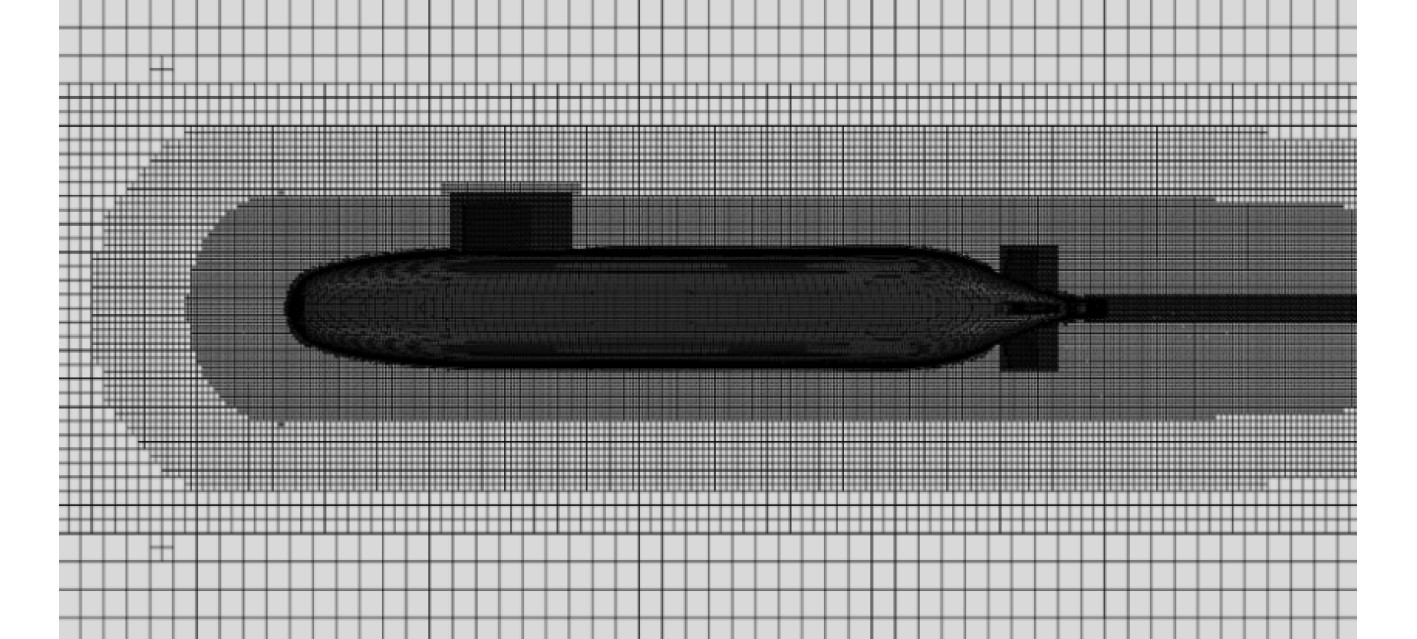
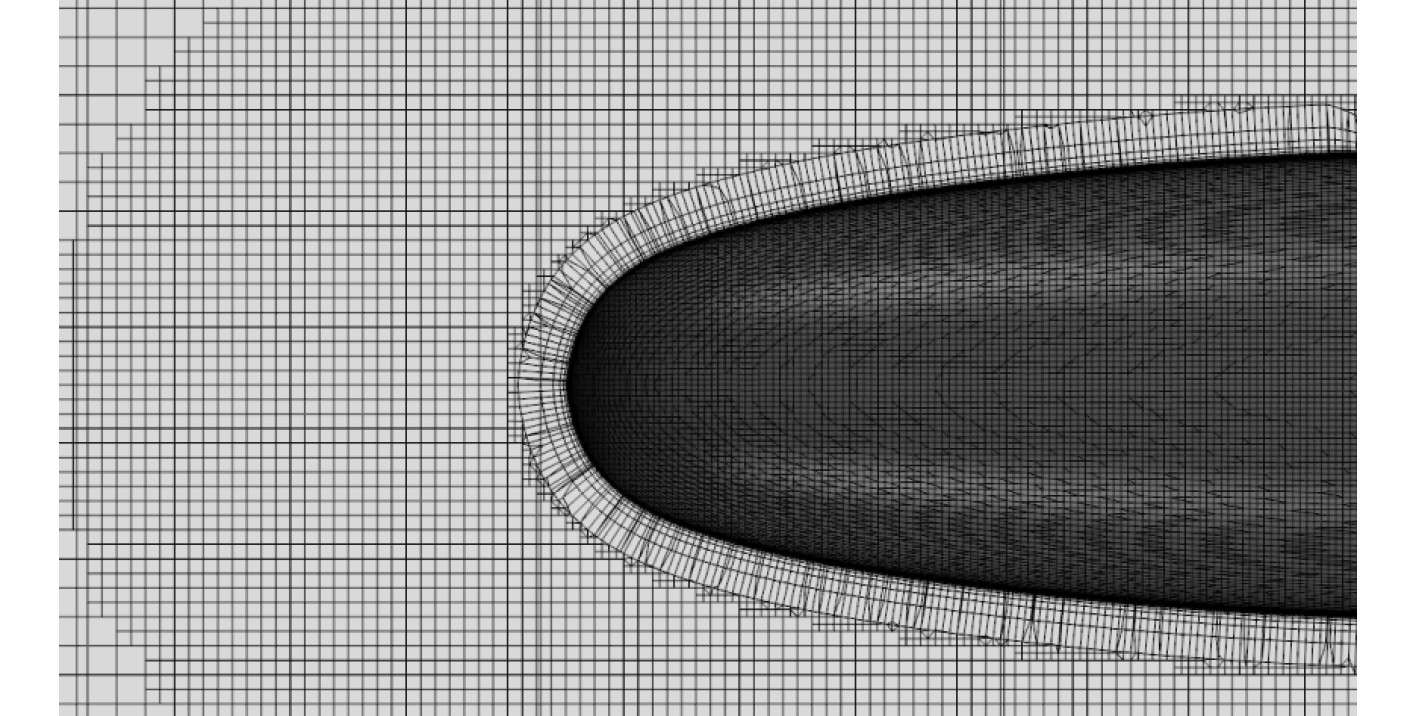
使用嵌套重叠网格方法对艇身和尾舵区域进行网格划分,在保证艇身网格达到计算精度的前提下采用多层网格加密技术,最终使艇身计算域外部网格与计算流场网格达到插值精度要求。通过重叠网格方法和刚体运动设置对方向舵的运动进行处理。选取标准k-ω模型作为湍流补充方程,为满足湍流模型要求选取Y+≤5,此时计算边界层总厚度为0.055 m。艇身多层网格加密技术划分情况和首部边界层分布如图3和图4所示。
|
图 3 模型整体网格划分 Fig. 3 Global mesh generation of the model |
|
图 4 首部边界层网格划分 Fig. 4 Meshing of head boundary layer |
由图3和图4可见,通过多层网格加密技术,内层潜艇模型表面已比较光滑且外层可以达到重叠网格的差值条件。潜艇边界层为0.055 m的前提下边界层设置为13层,确保边界层首层落至粘性子层满足标准k-ω湍流模型的要求。
3.1 网格收敛性分析在保证计算精度的前提下使网格数量较小,选取由Clake[9]提出的切割体网格作为主要划分网格,对不同计算域进行网格划分。在边界层网格保持一致的前提下,通过更改基础网格的大小得到4套不同网格方案,对不同网格方案的计算模型进行直航阻力计算。网格收敛性验证结果见表3。
|
|
表 3 网格收敛性验证结果 Tab.3 Grid convergence verification results |
分析可得,当取方案2中网格总量为398万时,模型直航总阻力已逐渐收敛。此时随着网格数量的增加计算阻力最大相对误差仅为0.9%。在保证计算精度和计算速率的前提下,本文选取方案2的网格作为后续计算网格。
3.2 艇体阻力预报以方案2为计算网格计算不同航速下模型的艇体阻力,通过将数值模拟结果与实验结果[10]进行对比分析,验证计算模型的准确性。不同进速下的模型阻力测算与实验值对比见表4。结果显示计算模型阻力数值计算结果与实验结果的误差均能控制在5%以内。虽然随模型的进速增大误差略增大,但均在合理的误差内。
|
|
表 4 艇体阻力预报 Tab.4 Hull resistance prediction |
以潜艇常用的DTMB 4679螺旋桨作为模型桨,计算出该桨的敞水曲线后,采用体积力方法代替实际桨叶模型实现运动控制。对艇体和推力盘产生的推力及阻力进行监测,通过曲线拟合方法获得Suboff-1模型与DTMB 4679螺旋桨模型配合时的自航点位置。如图5所示,当螺旋桨转速取值780 r/min时螺旋桨推力与艇体阻力相等,此时自航点航速为2.34 m/s。

|
图 5 自航点推阻力预报 Fig. 5 Prediction of self propelled point thrust resistance |
首先针对不同的尾操纵面形式在超越运动中的运动情况进行对比,分析获得相较十字型尾操纵面形式,H型尾操纵面形式对潜艇在超越运动过程中的应舵性能、跟从性能、减摇作用上的影响。再针对翼板宽度不同的5组模型进行超越运动模拟,获取在本文选取的矩形翼板情况下,H型尾操纵面翼板宽度最优解。
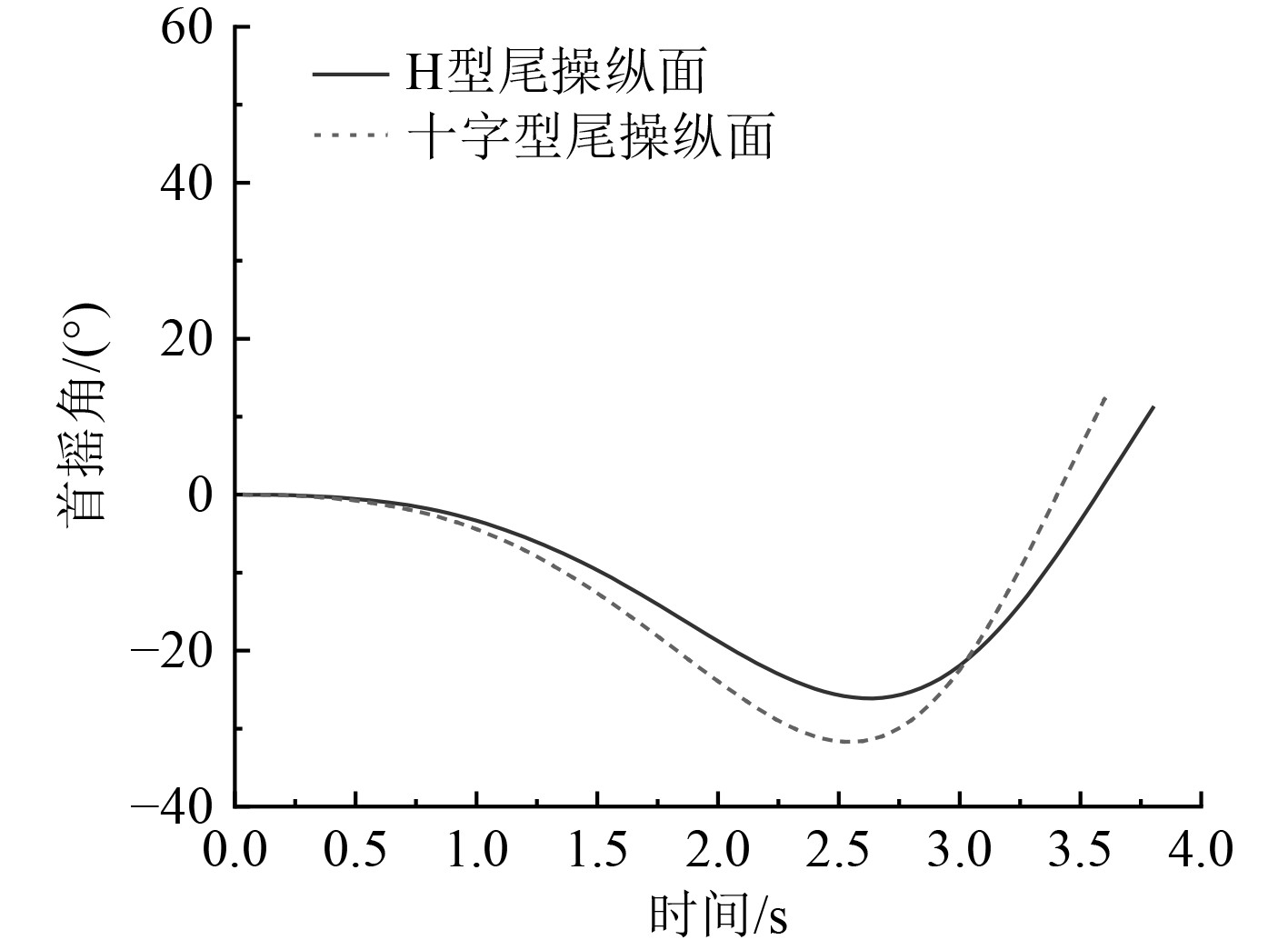
4.1 十字型操纵面与H型操纵面操纵效果对比选取H型操纵面模型与十字型操纵面模型进行水平超越运动模拟计算,并进行数值计算结果对比分析。在潜艇模型超越运动模拟中,选取自航点位置转舵节点为开始时刻,模型经过2次转舵后再次达到预定首向角时为结束时刻。针对超越运动过程中不同尾操纵面模型的首次达到预定首向角时间、超越运动完成时间和运动过程中的最大横摇进行数值模拟结果分析。超越运动过程中的艇首摇角时历曲线如图6所示。
|
图 6 水平超越运动首摇角时历曲线 Fig. 6 Time history curve of yaw angle of horizontal overrunning motion |
由图6结果对比分析可得,2种不同尾操纵面模型在相同操舵控制下,达到预定首向角的时间略有不同,其中H型尾操纵面模型较十字型尾操纵面模型首次达到预定首向角时间慢0.22 s。
对于2种不同的尾操纵面模型的超越运动总完成时间,H型尾操纵面模型较十字型尾操纵面模型慢0.24 s。由前文所述,可得在两模型首次达到预定首向角完成第2次操舵后两模型再次回转到预定首向角所需时间几乎相同。结果对比表明,H型尾操纵面模型的应舵性能较十字型尾操纵面模型略差。当方向舵固定时,跟从性能较十字型尾操纵面大致相同。
在潜艇超越运动过程中,潜艇方向舵偏转将引起其两侧压力的差异,同时方向舵两侧大小不同的水动压力将产生绕潜艇纵轴线的横倾力矩,从而引起潜艇发生横摇。图7为2种不同尾操纵面潜艇模型在运动过程中的横摇时历曲线。

|
图 7 水平超越运动横摇角时历曲线 Fig. 7 Time history curve of roll angle in horizontal transcendental motion |
由图7的计算结果可以看到,两不同模型在超越运动的过程中,随着潜艇达到预定首向角后的第2次转舵,首摇加速度减小的同时两模型开始出现反向剧烈横摇。最大横摇出现时刻均为潜艇第2次操舵后的首向角回复的过程中,且十字型尾操纵面模型较H型尾操纵面模型的最大横摇角度更大。对比最大横摇角度可知,H型尾操纵面模型有较好的减摇作用,较十字型尾操纵面模型最大横摇角可减少32.7%。
综合分析可得,H型尾操纵面较十字型尾操纵面模型的应舵性能略差但对于潜艇的跟从性能影响较小,通过添加翼板这一结构形式将产生良好的减摇作用。
4.2 翼板宽度差异对H舵响应的影响在设计H型尾操纵面这一结构形式时需要考虑翼板的宽度大小,通过对表2所列的5组不同翼板宽度的H型尾操纵面模型进行超越运动数值模拟,对运动过程中这5组具有不同翼板宽度的模型首次达到预定首向角时间、超越运动完成时间和运动过程中的最大横摇角进行对比分析,进而优选出矩形翼板形式的最佳翼板宽度。表5给出了数值模拟后的5组H型尾操纵面模型在超越运动中首次达到预定首向角时间和超越运动完成时间的结果。
|
|
表 5 5组H型尾操纵面模型超越运动的响应时间 Tab.5 Response time of overtaking motion of five H-shaped stern control plane models |
对表5的计算结果分析有以下结论:5组模型首次达到预定首向角的时间随翼板宽度的增加而增加,5组模型随翼板宽度增加,首次达到预定首向角时间最大增幅为4.11%;通过增加翼板宽度将使潜艇的应舵性能造成损失,当翼板宽度由艇体直径的20%增至60%时,时间增幅为12.67%;分析超越运动完成时间与潜艇达到预定首向角时间差值,在第2次转舵后5组模型转首至完成超越运动所需时间变化幅度微小,最大幅度仅为1.71%。可得随翼板宽度的增加,对潜艇的跟从性能改变很小。
H型尾操纵面较十字型尾操纵面在潜艇超越运动中有明显减摇效果的前提下,对5组H型尾操纵面模型在超越运动中的最大横摇角进行计算。通过曲线拟合,得到5组H型尾操纵面模型在超越运动过程中的最大横摇角,如表6所示。
|
|
表 6 不同翼宽模型在超越运动中的最大横摇角度 Tab.6 Maximum roll angle of different wing width models in overtaking motion |
从表6结果可以看出,随着翼板宽度的增加,最大横摇角逐渐减小。翼板宽度相对艇体直径为20%~50%时,减摇幅度保持在22.18%~45.10%之间。当翼板宽度增加至0.25m时,随翼板宽度的增加,模型的横摇减小幅度仅为1.78%。综合H型尾操纵面对于潜艇在应舵性能和跟从性能的影响,当翼板宽度取值为艇体直径的50%时,应舵时间较十字舵增加16.2%,艇体最大横摇减小43.32%。随翼板宽度增加,横摇较小幅度减小,此时翼板宽度为最佳翼板宽度。
4.3 涡场分析通过改变尾操纵面形式,对潜艇在运动中的减摇性能进行改善,伴随尾部结构形式的改变潜艇周围的涡场也会发生变化。
选取的2组计算模型为十字型尾操纵面模型和前文中翼宽为0.254 m的H型尾操纵面模型。对雷诺数为Re=1.2×107时的潜艇直航涡场进行数值模拟,从数值模拟结果来分析2种不同尾操纵面形式对尾部涡场造成影响。图8给出了在这一雷诺数下数值模拟所得到模型艇首及控制台周边区域中围壳涡场内的马蹄涡系、项链涡对、围壳尾涡等的涡量场分布,图9则给出了十字型和H型尾操纵面的涡量场分布,其中涡强由图形左侧标尺给出。

|
图 8 艇首及控制台的涡场分布 Fig. 8 Vortex field distribution of bow and console |

|
图 9 尾操纵面涡量场 Fig. 9 Vortex field of tail control surface |
计算结果表明,不管是十字型或H型尾操纵面,艇首及控制台周边区域的涡量场分布没有差别。而由图9可以看出,不同尾操纵面的尾涡场大致相同,H型操纵面添加的翼板结构产生的尾涡系由螺旋桨的远前方向螺旋桨盘面处延伸。
在螺旋桨前部的潜艇尾部收缩结构前,两模型的涡强有较大不同,其中十字型尾舵模型在此处的平均涡强为51 s−1而H型尾操纵面模型的涡强为12 s−1,且聚集更多的尾舵马蹄涡系尾涡。在方向舵的涡场范围,2种模型不同的尾结构形式并没有造成方向舵后的尾涡结构变化。由于潜艇的流噪声主要产生于艇首围壳舵后部的湍流转捩区,在图8和图9给出的涡场细节可以看出,更改尾操纵面结构形式仅引起艇体尾部的涡场变化,而对艇首涡场的影响几乎可以忽略。
对于尾部总体涡场,H型尾操纵面结构降低了十字型操纵面在艇尾收缩处的总体涡强,同时由于翼板的增加,引起了较多的尾涡流向后方。
5 结 语本文通过重叠网格方法和体积力方法,针对不同尾操纵面形式的Suboff-1模型进行超越运动数值模拟。通过结果分析,获得H型尾操纵面这一控制简单的结构形式在超越运动中较十字型尾操纵面在应舵性能、转首性能、减摇作用上的影响,并通过分析5组不同翼面宽度的H型尾操纵面模型在超越运动中的数值结果,获得矩形翼板形式翼宽的最优解。得到结论如下:
1)H型尾操纵面作为一种控制简单的舵面形式,在超越运动过程中较十字型尾操纵面有良好的减摇性能,当设计翼宽为潜艇平行中体直径的20%时,最大横摇角度减少32.7%;
2)由十字型尾操纵面改进为H型尾操纵面形式时将造成潜艇应舵性能的损失,达到预定首摇角时间将增大,但对潜艇的跟从性能影响较小;
3)对于本文设计的矩形面板型H型操纵面翼板形式,通过对5组不同翼宽的减摇性能、应舵性能和跟从性能综合分析,翼板宽度的最优解为潜艇平行中体直径的50%;
4)2种尾操纵面形式的改变对艇身流噪声产生的重要部位影响较小,而H型尾操纵面较十字型尾操纵面在螺旋桨盘面前产生大量尾涡。
| [1] |
王京齐, 施生达. 现代潜艇尾操纵面的发展状况[J]. 舰船科学技术, 2007, 29(1): 33-40. |
| [2] |
柏铁朝, 许建, 陈炫树, 等. 基于CFD的潜艇操纵性数值仿真发展综述[J]. 舰船科学技术, 2020, 42(5): 1-7. DOI:10.3404/j.issn.1672-7649.2020.05.001 |
| [3] |
张风丽. 潜艇操纵性水动力系数预报方法研究[J]. 中国水运, 2018, 18(1): 13-15. |
| [4] |
黄晨冉. 基于重叠网格的水下潜器操纵运动直接模拟[D]. 武汉: 武汉理工大学, 2018.
|
| [5] |
陈纪军, 潘子英, 彭超, 等. 十字形和X形艉舵航行体的水动力特性对比[J]. 中国舰船研究, 2020, 15(2): 8-16. |
| [6] |
林俊兴, 戴余良, 张涛. X形舵和十字形舵操纵力等效关系的研究[J]. 舰船科学技术, 2004, 26(5): 5-13. |
| [7] |
曾广会, 朱军, 黄昆仑. 潜艇操纵面几何参数敏感性计算研究[J]. 舰船科学技术, 2009, 30(2): 44-48. DOI:10.3404/j.issn.1672-7649.2009.02.006 |
| [8] |
王庆云, 庞永杰, 李伟坡, 等. 系列舵翼潜艇水动力系数数值计算及试验研究[J]. 舰船科学技术, 2015, 37(11): 21-26. DOI:10.3404/j.issn.1672-7649.2015.11.004 |
| [9] |
CLAKE D K, HASSAN H A, SALAS M D. Euler calculations for multielement airfoils using cartesian grids[J]. Aiaa Journal, 2012, 24(3): 353-358. |
| [10] |
汪小翔, 廉滋鼎, 许靖峰, 等. SUBOFF标模水下阻力试验方法[C]//第十四届全国水动力学学术会议暨第二十八届全国水动力学研讨会文集. 上海: 《水动力学研究与进展》出版社, 2017.
|
 2022, Vol. 44
2022, Vol. 44
