当外部激励作用于储液容器时造成容器内部流体运动的现象称为晃荡,该现象具有很强的非线性和随机性,其产生的冲击力是液舱结构破坏和船舶失稳的主要原因之一。随着各种液化船的广泛使用,液舱晃荡现象越发成为人们关注的焦点。目前,对于晃荡的研究主要有理论分析方法、数值方法和实验方法3种方法。其中数值方法由于其适应性强、成本低、效率高的特点受到广泛欢迎。因此本文采用基于OpenFOAM的CFD技术进行数值模拟。
晃荡问题最早出现在航天航空领域,1966年Abramson[1]对球型和矩形容器内的液体晃荡问题开展了相关研究,揭示了晃荡对于燃料箱稳性的影响。Abramosn是研究液舱晃荡问题的先驱,但由于当时条件的制约,该研究无论是结果精度还是条件考虑都有所欠缺。随着计算机和计算流体力学(CFD)的发展,晃荡研究的缺陷逐步完善。Faltinsen等[2]对于二维情况下不同形状液舱的晃荡进行了分析,揭示了二维情况下方形液舱晃荡载荷特性。黄硕等[3]对于二维液舱在非线性水动力影响下的运动特性进行了研究,得到了能量耗散系数的选取规律。孙士艳等[4]对二维楔形储罐内液体进入平静水面的水动力问题进行了研究,揭示了二维楔形槽内液体进入平静水面的运动特性。张书谊等[5]基于CFD软件Fluent探索了二维情况下矩形液舱内液体水动力特性,但是没有考虑液舱长度的影响。Kim[6]和朱仁庆等[7]对船舱内液体的三维晃荡特性进行了分析,揭示了三维情况下液舱晃荡特性。王庆丰等[8]使用HydroSTAR对带液舱的FSRU船舶进行运动响应分析,揭示了液舱载液率和液舱布置对FSRU运动的影响。甄长文等[9]对于三维共振频率下油船液舱舱内液体晃荡情况进行了模拟研究,发现当晃荡稳定后舱内液体以驻波与行波组合的方式运动。李裕龙等[10]基于OpenFOAM对船舶与晃荡在波浪中的时域耦合运动进行研究,揭示了船舶在液舱晃荡时的横摇特性。Clearly[11]和Bass等[12]综合使用Matlab与CFD软件针对不同形式液舱液体晃荡进行了数值计算比较,并针对矩形舱室提出了抑制晃荡的方法。但上述研究皆默认水作为介质的情况,SoutoIglesias[13]首先对不同宽度液舱在不同介质中的晃荡载荷进行研究,分析了液舱宽度以及介质变化引起的三维效应对冲击载荷的影响。在此之后,Zou[14]系统地研究了介质粘性变化对于冲击载荷的影响,发现高粘度液体的冲击压力在黏性阻尼的作用下需要更长的时间才能达到稳定状态。Lee等[15]模拟了流体粘度、密度比以及可压缩性对晃动载荷的影响等。
国内外已经取得了关于液舱晃荡的大量研究成果,但是很少有学者开展当液舱内流体状态发生变化时船舶的运动特性研究。本文将研究液舱内水冻成冰时,船舱的运动特性,基于对结构体的固有频率和共振特性分析,深入研究流体状态的发生改变时内部水或冰、船舱和外部波浪之间的耦合作用机理。
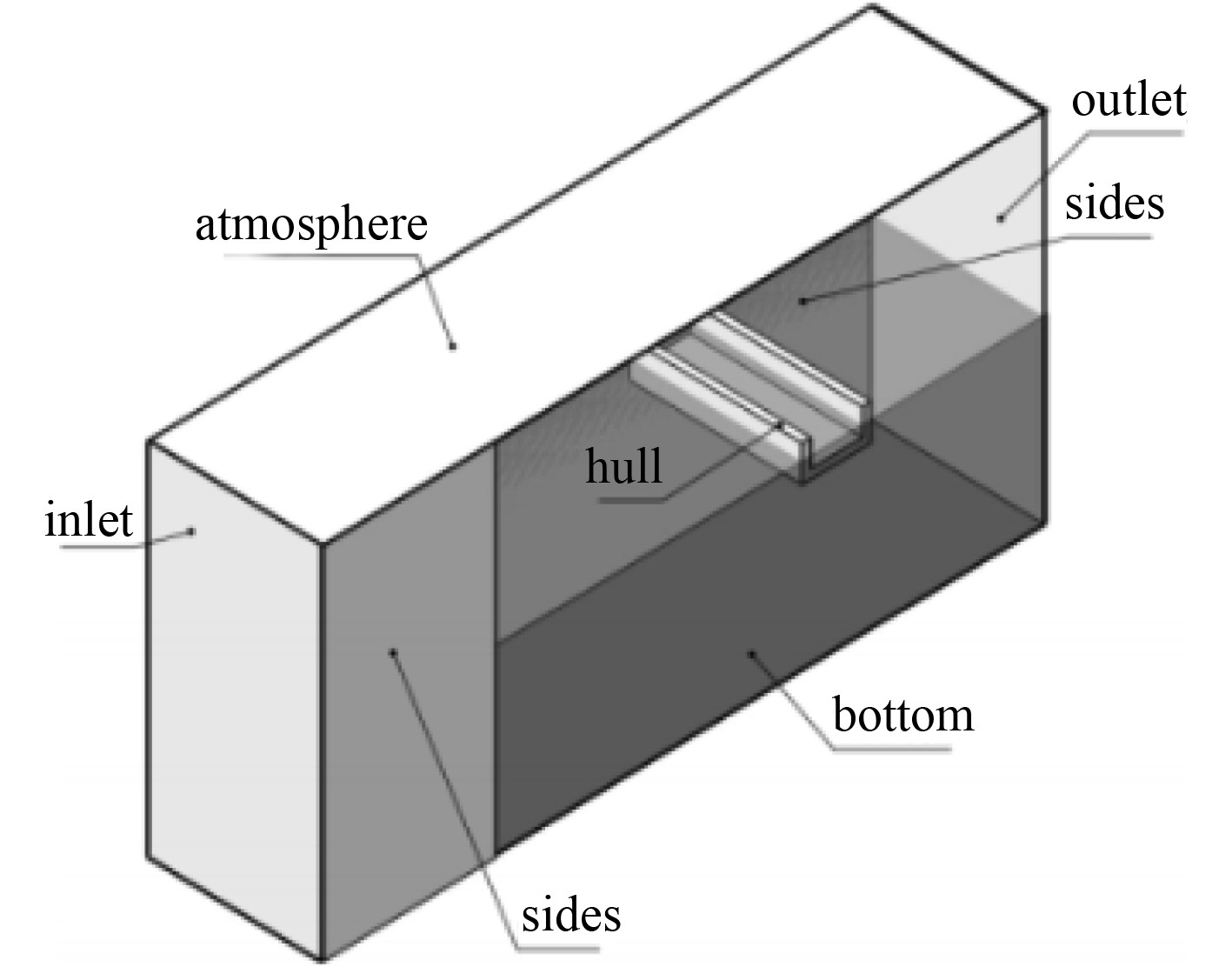
1 数学模型本文采用OpenFOAM开源软件,建立液舱在波浪中运动的CFD数值计算模型,研究舱内流体力学特性对液舱运动和受力的影响。为进行对比分析,假设液舱内水被冻成冰块,忽略热力学热胀冷缩规律,在建模时让水体与冰块密度相同,质量相同,并且让冰块形状与液舱未发生运动时水体的初始形状相同。建立一个内部结构为矩形的二维液舱计算域示意图,如图1所示。在此基础上,定义一个笛卡尔空间固定坐标系
|
图 1 液舱计算域 Fig. 1 Computational domain of tank |
|
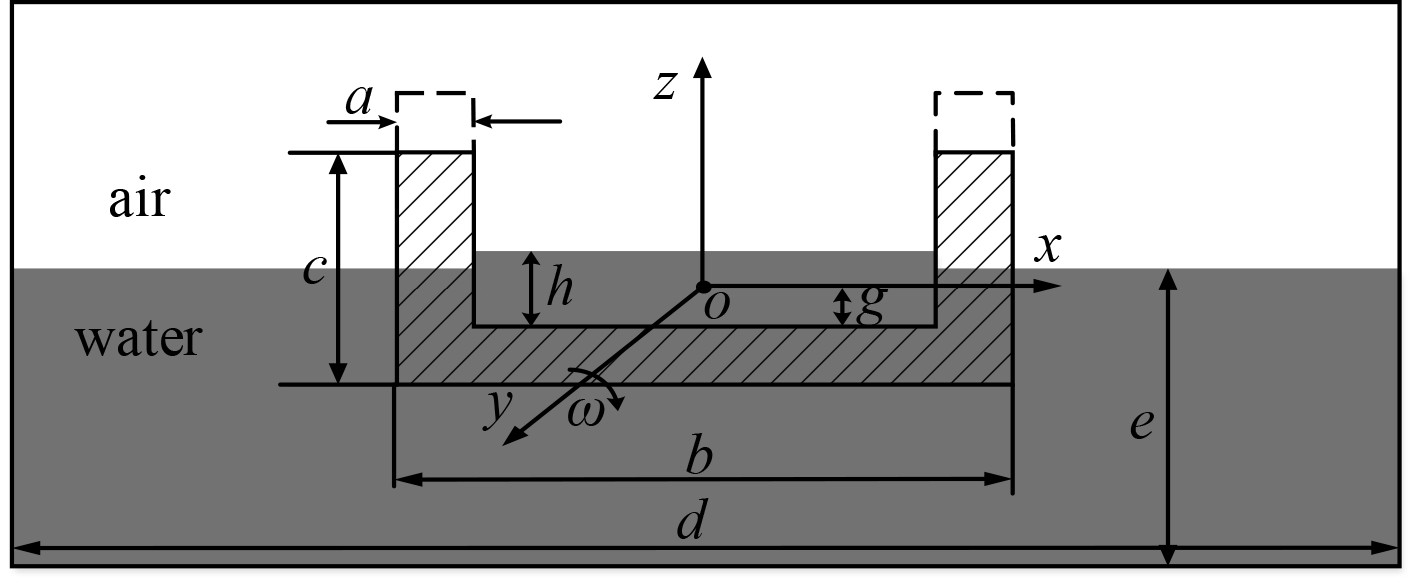
图 2 数学模型及坐标定义 Fig. 2 Mathematical model and coordinate system |
忽略流场可压缩性,采用适用于不可压缩流的连续性方程和N-S方程来建立流场的基本控制方程。
| $ \nabla \cdot {{\boldsymbol{U}}} = 0 ,$ | (1) |
| $ \frac{{{\rm{D}}{\boldsymbol{U}}}}{{{\rm{D}}t}} = {{{F}}_b} - \frac{1}{\rho }\nabla p + \nu {\nabla ^2}{U}。$ | (2) |
式中:
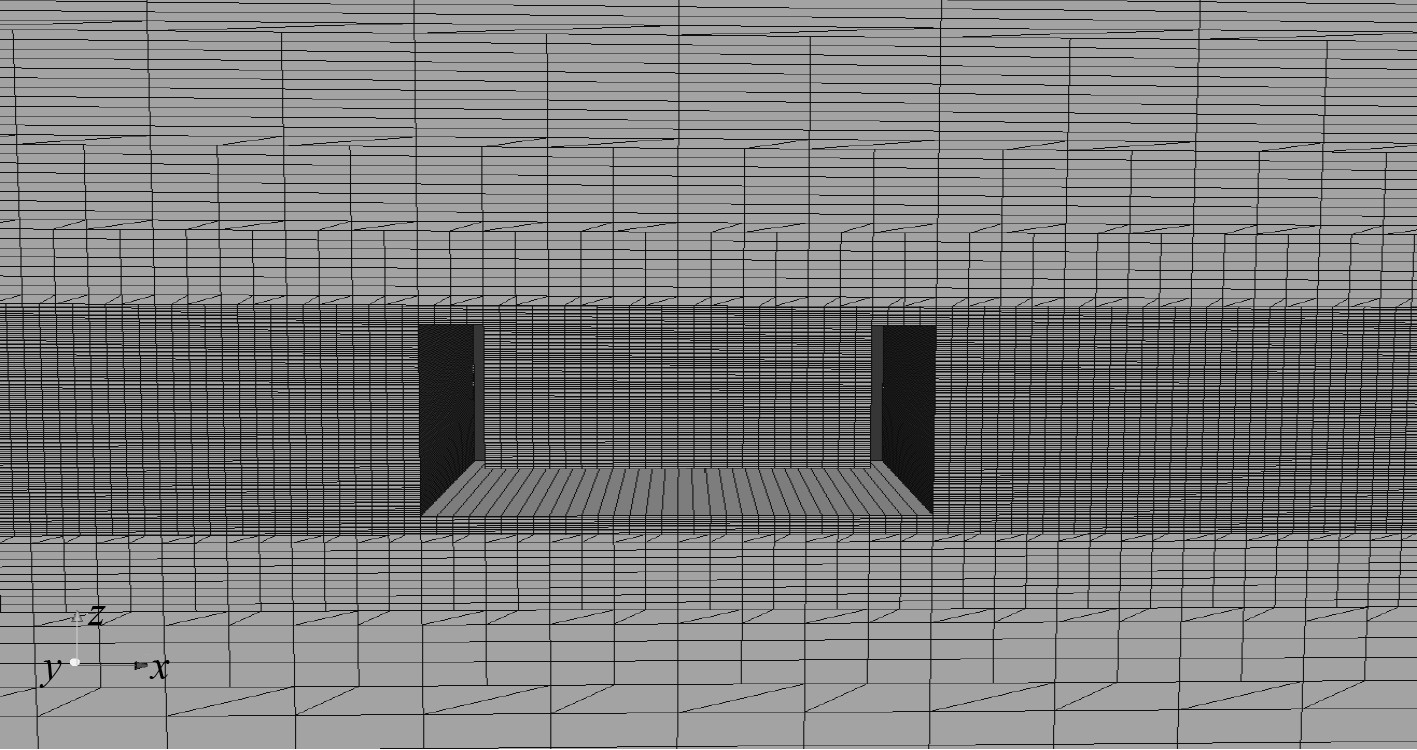
当物体运动时,液固交界面必然发生改变,如何处理物面附近网格则是一个难题。为此,本文在物体外部选定一个区域作为动网格区域,动网格求解器设置为dynamicMotionSolverFvMesh,该求解器是根据边界条件与扩散方程计算动网格区域网格的运动,不改变拓扑结构,较其他方法该方法适用于任何类型的小幅运动,并且能够保证较高的网格质量。动网格区域的内部边界设置为0.3,外部边界设置为1。图3为网格示意图,在布置网格时需要注意,在物体和自由面附近,采用精细网格,远离物体和自由面,网格逐步过渡到粗网格。
|
图 3 网格示意图 Fig. 3 Grid diagram |
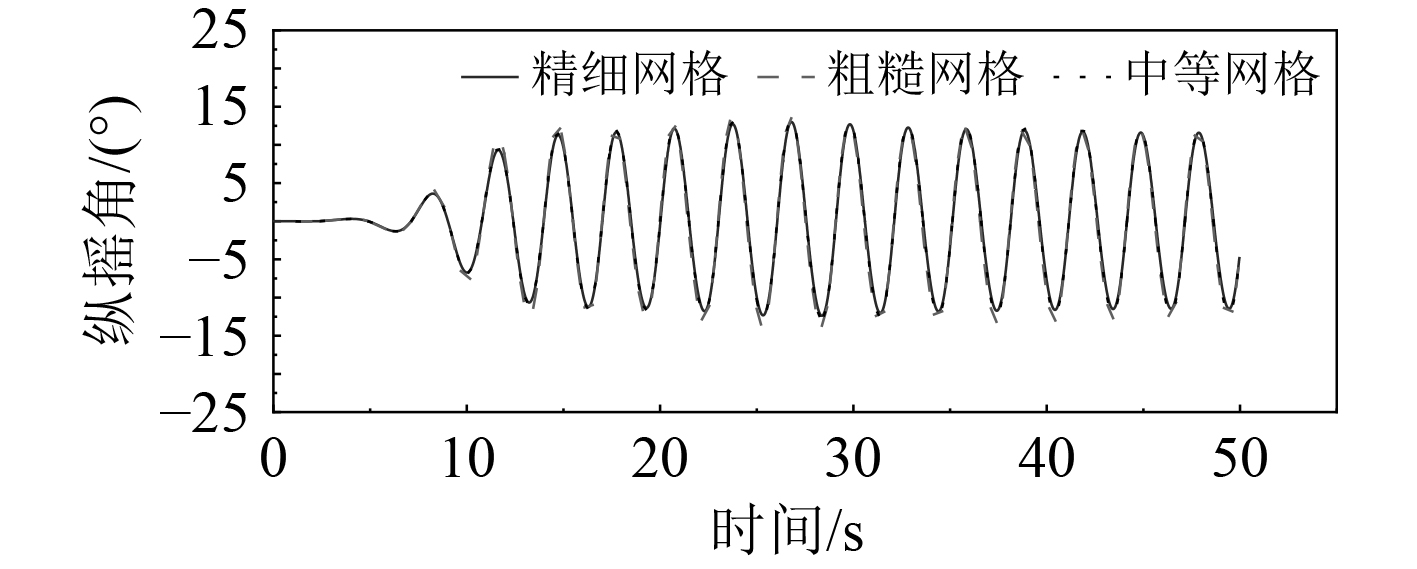
选择一个载水液舱对网格收敛性进行验证。液舱壁质量
|
图 4 网格收敛性分析 Fig. 4 Grid convergence analysi |

|
图 5 液舱自由晃荡纵摇角随时间变化曲线 Fig. 5 Pitch angle of the tank varying with time at free sloshing |
在进行数值结果分析时,仍沿用收敛性分析中使用的船舱参数,即舱壁质量
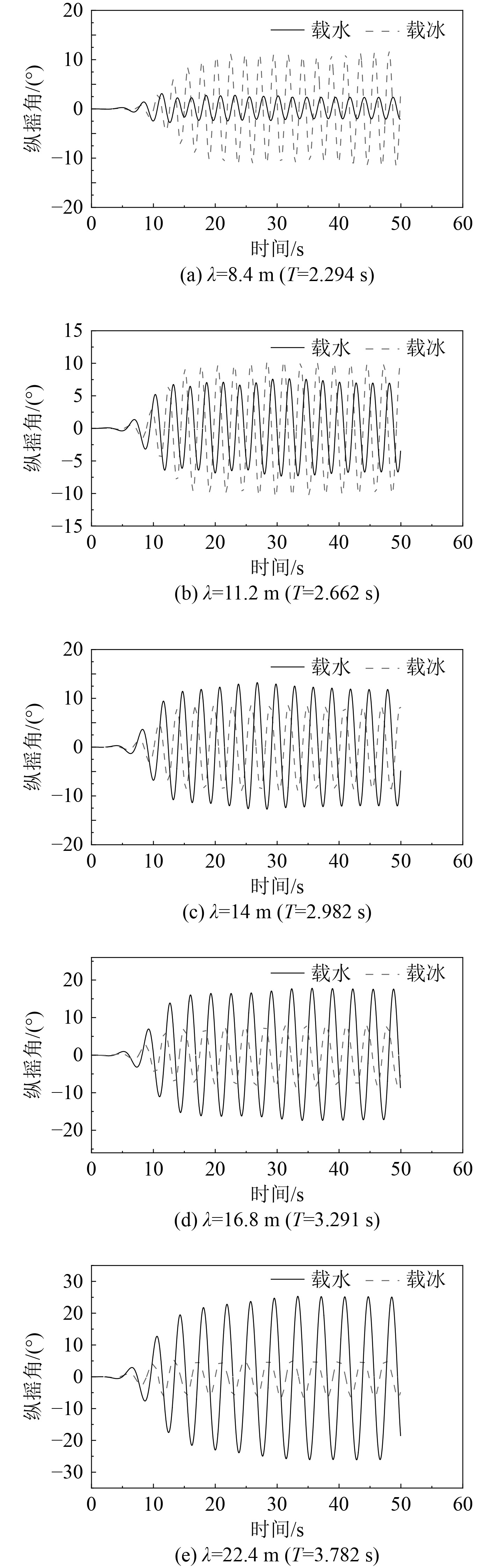
图6给出了波高为0.2 m时不同波长条件下水舱和冰舱的运动时历曲线。波长分别取为8.4 m,11.2 m,14 m,16.8 m和22.4 m,基于5阶无限水深斯托克斯波波长与周期的色散关系,可以得到周期分别为2.294,2.662,2.982,3.291和3.782 s。在初始时刻,水舱和冰舱均处于静止状态,在波浪激励下开始运动,然后逐渐达到稳定。观察图6,可以发现一个规律,随着波长的增加,载冰舱运动幅值逐渐减小,而载水舱幅值逐渐增大。与波长相比,0.2 m波高对应的最大波陡只有0.024。因此,可以基于线性共振理论对问题进行分析。由图5可知,载水舱固有频率为3.7 s,在图6所计算的所有波长中,最大波长所对应的波浪周期最接近于载水舱固有周期,从共振角度出发,载水舱运动幅值将越来越大,图6的计算结果完全符合关于水舱的分析。而对于冰,结果则恰恰相反,即波长越大,幅值越低,这是由于冰的固有周期是2.17 s,与最小波长所对应的固有周期最接近。
|
图 6 当波高为0.2 m时不同波长下船舱纵摇角度随时间变化曲线 Fig. 6 The time history of pitch angle with different wavelengths at wave height is 0.2 m |
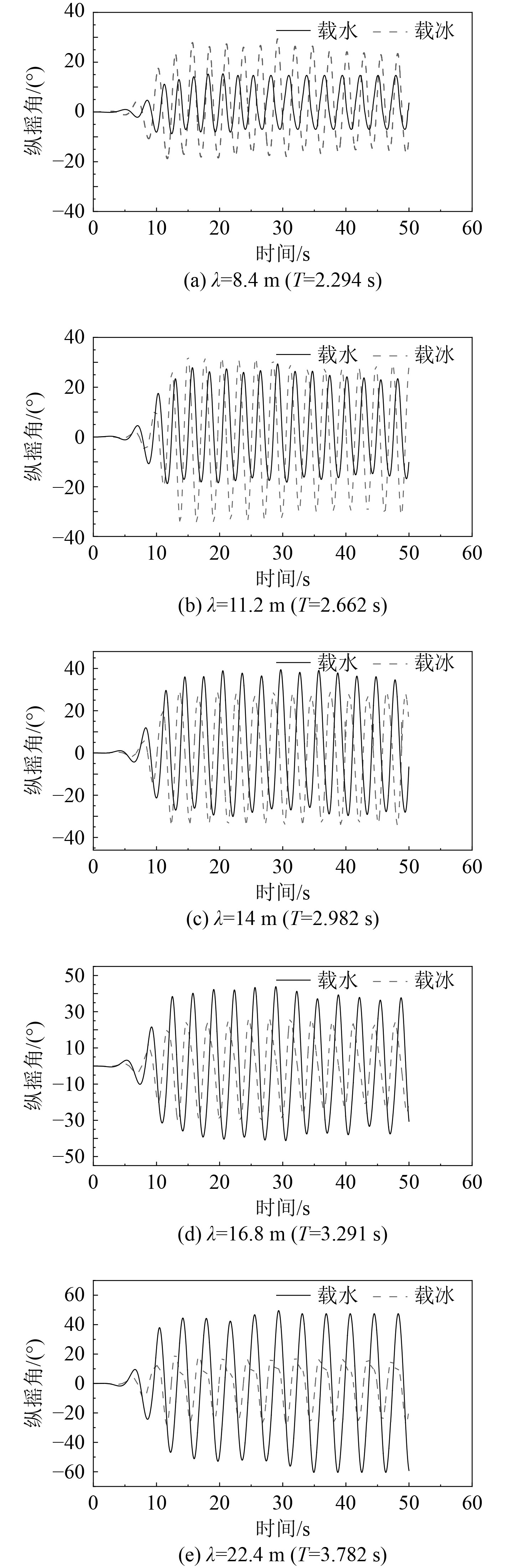
图7给出了波高为0.6 m时不同波长条件下水舱和冰舱的运动时历曲线。波长分别取为8.4 m,11.2 m,14 m,16.8 m和22.4 m。随着波陡的增加,此时非线性波的周期分别为2.098,2.483,2.888,3.199和3.734 s。与图6类似,由于冰舱固有周期接近于小波长固有周期,液舱固有周期接近于大波长固有周期。因此对于小波长情况冰舱运动幅值大,对于大波长情况液舱运动幅值大。此外,计算结果也表现出一些非线性特性,与图6相比,图7的波高是图6的3倍,但在相同工况下,图7的运动幅值并未达到图6的3倍,约为2倍左右。其次由于水舱的固有周期较大,图中没有表现出明显的高频共振特征。但对比冰舱,由于其固有频率较高,周期较短,运动时历结果表现出高频运动特征,尤其是图7(e),由于此时波浪周期约为固有周期的1.7倍,因此运动时历结果的波峰处出现双峰特征。由图6和图7可知,相同质量的水和冰,运动特性差异极大,水舱和冰舱最主要的变化特征是固有频率的变化,因此在实际工程计算中,应尽量避免液舱固有频率接近波浪频率,可极大降低船舶航行风险。
|
图 7 当波高为0.6 m时不同波长下船舱纵摇角度随时间变化曲线 Fig. 7 The time history of pitch angle with different wavelengths at wave height is 0.6 m |
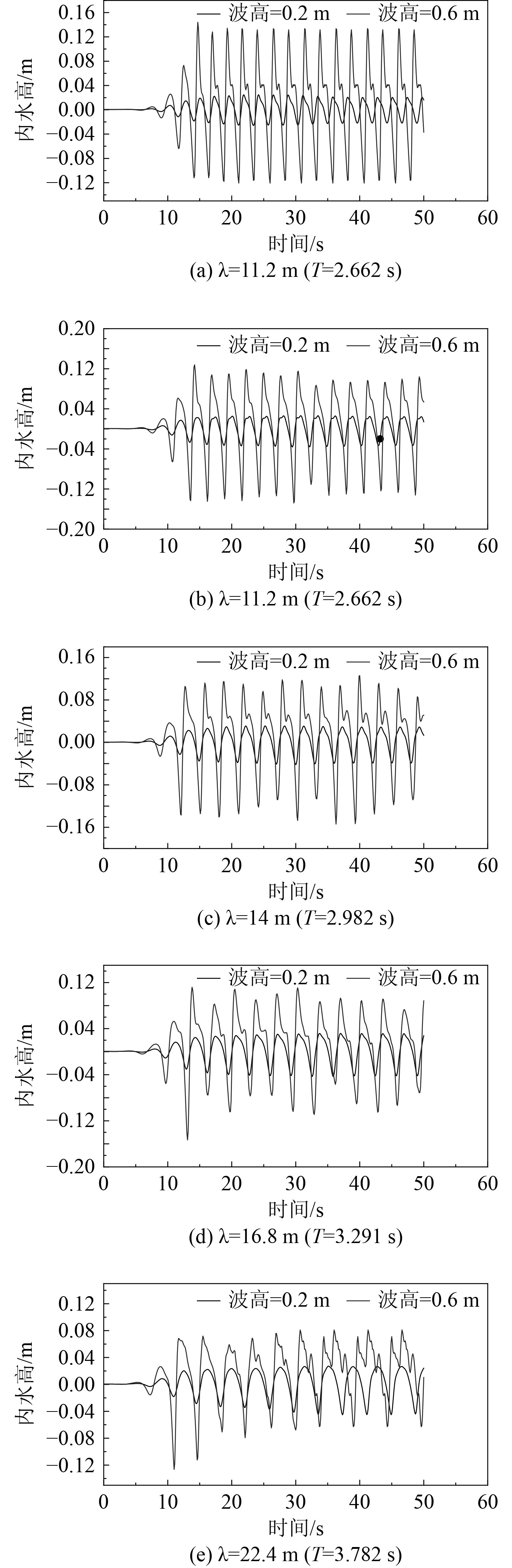
图8给出以上2个算例的液舱内部自由面高度变化情况,取液舱内部监测点
|
图 8 液舱内水晃荡随时间变化曲线 Fig. 8 The times history of inner liquid sloshing |
本文基于OpenFOAM开源软件,从连续性方程和N-S方程出发,采用动网格技术,将载冰舱与载水液舱运动特性进行对比,研究液舱内水运动对于液舱运动特性的影响。
1)相同形状和相同密度水舱固有周期大于冰舱固有周期,这是由于冰块相当于是刚体,每个质点的加速度都是相同的,而对于水,每个质点的加速度都不相同,这使得水舱即难加速度也难减速,最终导致水舱的固有周期大于冰舱。
2)受船舱固有周期与波浪周期相对关系的影响,在本文算例中,当波长逐步增加时,载冰舱运动幅值逐渐减小,而载水舱幅值逐渐增大,其深层次的原因是,船舱固有频率和波浪频率接近时,船舱将发生共振,此时运动幅值最大。
3)当波高不大时,液舱内流体随波浪柔和振荡,随着波高的增加,非线性效应逐渐显现,液舱内流体的高频振动特征也随之出现,在一个波浪周期内,流体质点可能出现双峰或三峰振动特征。
| [1] |
ABRAMSON H. The dynamic behavior of liquids in moving containers. NASA SP-106[J]. NASA Special Publication, 1966, 106. |
| [2] |
O. M. Faltinsen. Sloshing[J]. 力学进展, 2017: 1−24.
|
| [3] |
黄硕, 段文洋. 液舱晃荡与船体非线性时域耦合运动计算[J]. 哈尔滨工程大学学报, 2014(9): 1045-1052. HUANG S, DUAN W Y. Nonlinear time domain simulation of sloshing and coupled ship motion[J]. Journal of Harbin Engineering University, 2014(9): 1045-1052. |
| [4] |
SUN. S. Y, WU. G. X, XU.G.. Free fall water entry of a wedge tank into calm water in three degrees of freedom[J]. Applied Ocean Research, 2019, 92: 101920. DOI:10.1016/j.apor.2019.101920 |
| [5] |
张书谊, 段文洋. 矩形液舱横荡流体载荷的Fluent数值模拟[J]. 中国舰船研究, 2011, 6(5): 73-77. ZHANG S. Y, DUAN W. Y. Numerical Simulation of Sloshing Loads on Rectangular Tank Based on Fluent. [J]. Chinese Journal of Ship Research, 2011, 6(5): 73-77. |
| [6] |
KIM Y. Numerical simulation of sloshing flows with impact load[J]. Applied Ocean Research, 2001, 23(1): 53-62. DOI:10.1016/S0141-1187(00)00021-3 |
| [7] |
朱仁庆, 侯玲. LNG船液舱晃荡数值模拟[J]. 江苏科技大学学报(自然科学版), 2010, 24(1): 1-6. |
| [8] |
王庆丰, 焦经纬, 徐刚, 等. FSRU晃荡的耦合分析[J]. 江苏科技大学学报(自然科学版), 2017, 31(5): 684-688. WANG Q F, JIAO J W, XU G, et al. Analysis of coupling effects of sloshing and ship motion for FSRU[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2017, 31(5): 684-688. |
| [9] |
甄长文, 吴文锋, 朱柯壁, 等. 共振频率下油船液舱晃荡数值模拟研究[J]. 中国修船, 2019, 32(1): 40-43. |
| [10] |
李裕龙, 朱仁传, 缪国平, 等. 基于OpenFOAM的船舶与液舱流体晃荡在波浪中时域耦合运动的数值模拟[J]. 船舶力学, 2012, 16(7): 750-758. LI Y L, ZHU R C, MIAO G P, et al.. Simulation of ship motion coupled with tank sloshing in time domain based on OpenFOAM[J]. Journal of Mechanics, 2012, 16(7): 750-758. DOI:10.3969/j.issn.1007-7294.2012.07.004 |
| [11] |
CLEARY J,WILLIAM A. Subdivision, stability, liability[J]. Safety, 1981, 19(3): 228-244. |
| [12] |
BASS R L, E BOWLES B, COX P A. Liquid dynamic loads in LNG cargo tanks[J]. Sname Transactions, 1980, 88: 103-126. |
| [13] |
IGLESIAS. A. S, BULIAN. G,VERA. E. B.. A set of canonical problems in sloshing. Part 2: Influence of tank width on impact pressure statistics in regular forced angular motion[J]. Ocean Engineering, 2015, 105(SEP.1): 136-159. |
| [14] |
ZOU C F, WANG D Y, et al. The effect of liquid viscosity on sloshing characteristics[J]. Journal of Marine Science and Technology, 2015, 20(4): 765-775. DOI:10.1007/s00773-015-0329-y |
| [15] |
LEE. D. H, KIM. M. H,KWON. S. H, et al.. A parametric sensitivity study on LNG tank sloshing loads by numerical simulations[J]. Ocean Engineering, 2007, 34(1): 3-9. DOI:10.1016/j.oceaneng.2006.03.014 |
 2022, Vol. 44
2022, Vol. 44

